Quantum transport observed in films of magnetic topological semimetal EuSb2
Abstract
We report fabrication of EuSb2 single-crystalline films and investigation of their quantum transport. First-principles calculations demonstrate that EuSb2 is a magnetic topological nodal-line semimetal protected by nonsymmorphic symmetry. Observed Shubnikov-de Haas oscillations with multiple frequency components exhibit small effective masses and two-dimensional field-angle dependence even in a 250 nm thick film, further suggesting possible contributions of surface states. This finding of the high-mobility magnetic topological semimetal will trigger further investigation of exotic quantum transport phenomena by controlling magnetic order in topological semimetal films.
I INTRODUCTION
Topological semimetals are characterized by nontrivial band crossings at nodal points or nodal lines in the momentum space Fang et al. (2016); Burkov et al. (2011); Lu and Shen (2017); Wang et al. (2017a); Armitage et al. (2018). In topological nodal-point semimetals, Dirac or Weyl semimetals, these gapless points give rise to exotic quantum transport phenomena Lu and Shen (2017); Wang et al. (2017a). Under magnetic fields, for example, Fermi-arcs of the surface state merge with the bulk state and form so-called Weyl orbits Potter et al. (2014); Wang et al. (2017b), as recently observed in its quantum Hall state Zhang et al. (2017); Lin et al. (2019); Zhang et al. (2019); Nishihaya et al. (2019).
Topological nodal line semi-metals (TNLSMs) are characterized by the Zak phase Zak (1989) in loops encircling the nodal lines. It has been theoretically suggested that this topological feature appears in bulk Oroszlány et al. (2018); Yang et al. (2018) and surface Chan et al. (2016); Bian et al. (2016); Yamakage et al. (2016); Hirayama et al. (2017, 2018) quantum oscillations. In this context, it is important to prepare high-mobility films of TNLSMs. On the other hand, many compounds which possess nodal lines without spin-orbit coupling (SOC) turn into topological insulators or nodal point semimetals when considering SOC Fang et al. (2015); Kobayashi et al. (2017). In order to protect these nodal lines from gapping by strong SOC, nonsymmorphic symmetry is required Fang et al. (2015); Kobayashi et al. (2017); Zhao and Schnyder (2016).
In general, time-reversal symmetry breaking destroys the robustness of nodal lines Okugawa and Murakami (2017), while they remain stable only when the magnetic ordering still respects space group symmetries Bzdušek et al. (2016); Wang (2017). Therefore, there are very few reports about intrinsic magnetic TNLSMs under SOC (single-layer GdAg2 Ormaza et al. (2016); Feng et al. (2019) and GdSbTe Hosen et al. (2018); Sankar et al. (2019)). Many of the nodes are slightly gapped on the entire lines (Fe3GeTe2 Chen et al. (2013); Kim et al. (2018) and Fe (Ga, Al) Sakai et al. (2020)) or except the Weyl points (Co3Sn2S2 Liu et al. (2018) and Co2MnGa Chang et al. (2017); Sakai et al. (2018); Belopolski et al. (2019)) under SOC. Moreover, quantum oscillations have not been observed in all of these compounds. Hence, to identify new magnetic TNLSMs is strongly called for exploring unique quantum transport phenomena.
CaSb2 is a novel TNLSM where nodal lines are protected by two-fold screw symmetry along axis even in the presence of SOC Funada et al. (2019a). Recently, superconductivity has been also observed in polycrystalline samples Ikeda et al. (2020). In EuSb2, on the other hand, large magnetic moments are expected to be introduced while keeping the unique crystal structure. Although antiferromagnetic (AFM) ordering of nearly Eu2+ spins has been investigated in the 1980s Hulliger and Schmelczer (1978); Niggli and Hulliger (1984), electronic structures and transport properties have long been unknown for EuSb2. Here we demonstrate that EuSb2 is a new magnetic TNLSM protected by nonsymmorphic symmetry of the space group /. We fabricate single-crystalline EuSb2 films by molecular beam epitaxy and investigate their magnetotransport. Observed Shubnikov-de Haas (SdH) oscillations with multiple frequency components indicate small effective masses and two-dimensional (2D) field-angle dependence characteristics in topological semimetals.
II EXPERIMENTAL METHODS
EuSb2 epitaxial films were grown on single-crystalline (110) Al2O3 substrates in an Epiquest RC1100 chamber. The molecular beams were simultaneously provided from conventional Knudsen cells containing 3N Eu and 6N Sb. The growth temperature was set at 850 ∘C, and the beam equivalent pressures, measured by an ionization gauge, were set to 110-5 Pa for Eu and 4.010-4 Pa for Sb, considering the Eu-Sb binary phase diagram Abdusalyamova and Vasilyeva (2011). The film thicknesses were typically set at 250 nm for structural characterization and magnetotransport measurements, and 750 nm for magnetization measurements. The growth rate was about 0.3 Å/s. High-field resistivity and magnetization measurements were performed at the International MegaGauss Science Laboratory in the Institute for Solid State Physics at the University of Tokyo. Resistivity up to 58 T was measured by a standard four-probe method for 200 m-width multi-terminal Hall bars, using a non-destructive pulsed magnet Uchida et al. (2017). Temperature dependence was also measured using a Quantum Design Physical Properties Measurement System. Magnetization up to 27 T was measured by a conventional induction method with coaxial pickup coil Yoshida et al. (2009). Temperature dependence was also measured using a superconducting quantum interference device magnetometer in a Quantum Design Magnetic Property Measurement System. First-principles calculations of the band structure with SOC were performed by using the VASP package Kresse and Furthmüller (1996a, b); Kresse and Joubert (1999), with the experimentally determined lattice constants Hulliger and Schmelczer (1978). The generalized gradient approximation of Perdew-Burke-Ernzerhof was adopted for the exchange-correlation functional Perdew et al. (1996). -point mesh with Monkhorst-Pack scheme Monkhorst and Pack (1976) was used for the Brillouin zone sampling of the primitive cell and Gaussian smearing with a width of eV was applied.
III RESULTS AND DISCUSSION
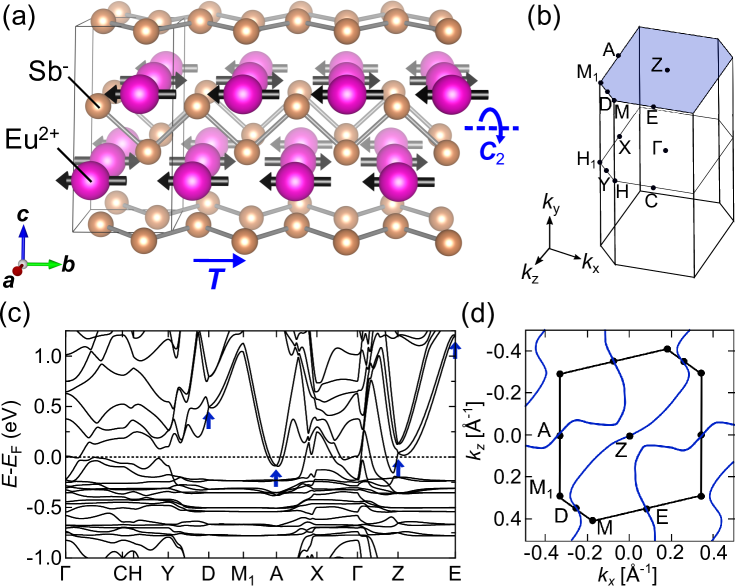
Figure 1(a) shows the crystal structure of EuSb2. This structure is characterized by Sb zigzag chains running parallel to the axis and mirror planes in the plane. This Sb chain forms Sbnn- and the valence of Eu becomes divalent (Eu2+). These Eu spin moments are oriented along the [010] direction and antiferromagnetically ordered with a propagation vector of , corresponding to the magnetic space group Niggli and Hulliger (1984). Therefore, this AFM ordering does not break the two-fold screw symmetry () which protects the nodal lines on the plane. It is thus expected that the nodal lines stably exist in the AFM phase.
The Brillouin zone and band structure calculated for the AFM phase are presented in Figs. 1(b) and 1(c). While flat bands located between -0.3 and -0.7 eV are attributed to the Eu 4 orbitals, dispersive bands crossing originate from the Sb 5 ones, resembling TNLSM CaSb2. There are band crossing points at the high-symmetry points Z, A, E, and D as in CaSb2 Funada et al. (2019a), and which are connected by nodal lines on the plane, as shown in Fig. 1(d). This indicates that EuSb2 is a magnetic TNLSM even in the presence of SOC.
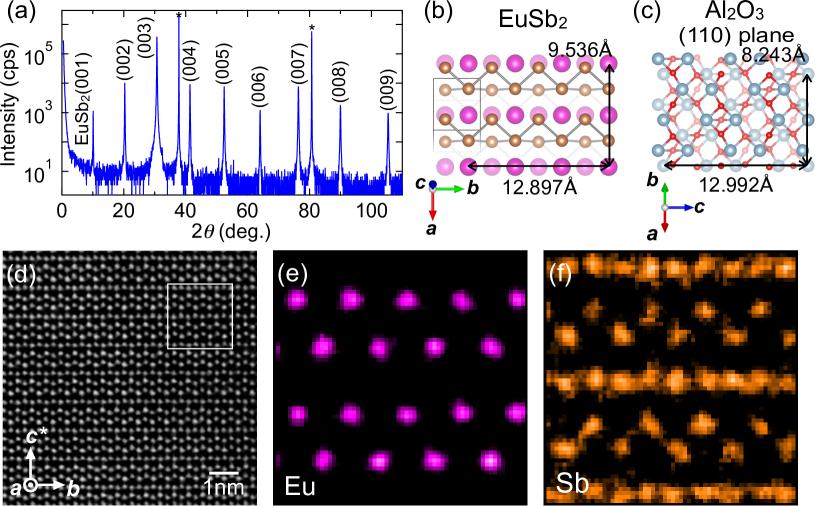
X-ray diffraction (XRD) - scan in Fig. 2(a) reveals sharp reflections from the (001) EuSb2 lattice plane without any impurity phases. Figures. 2(b) and 2(c) show the epitaxial relation viewed along the out-of-plane axis, with a mismatch of 0.7 % between the axis of the (110) Al2O3 plane and the axis of the (001) EuSb2 plane. The axis of EuSb2 is tilted by approximately deg. from the axis perpendicular to the - plane. Figure 2(d) shows a cross-section image of the EuSb2 film, taken by high-angle annular dark-field scanning transmission electron microscopy. The periodic arrangement of EuSb2 is clearly confirmed which corresponds to the EuSb2 crystal structure determined by single-crystal XRD Hulliger and Schmelczer (1978). Elemental maps are taken by energy dispersive X-ray spectrometry as shown in Figs. 2(e) and 2(f). The Sb zigzag chains along the axis are atomically resolved. Further XRD characterization was also performed to confirm high crystallinity and in-plane orientation (see Supplementary Materials Supplement ).
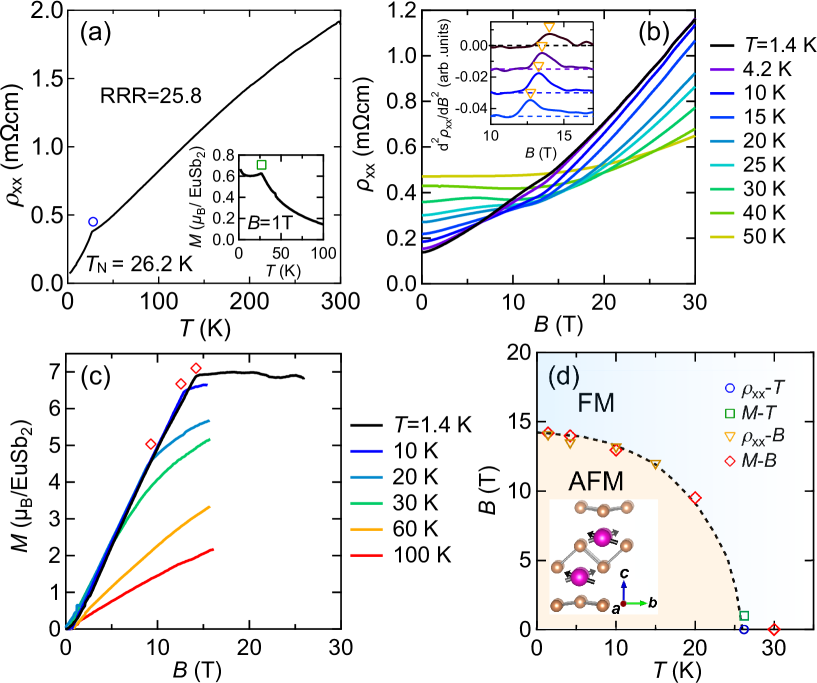
Figure 3(a) summarizes temperature dependence of the resistivity. The resistivity exhibits metallic behavior down to K with a residual resistivity ratio (RRR) of , reflecting high quality of the film. A clear kink observed at 26.2 K corresponds to the Néel temperature () Hulliger and Schmelczer (1978), which is also seen in temperature dependence of the magnetization (inset). The resistivity decreases rapidly with decreasing temperature below probably due to suppression of the magnetic fluctuations. Figure 3(b) presents out-of-plane magnetic field sweeps of the resistivity up to 58 T at various temperatures. The resistivity at the base temperature of 1.4 K exhibits a cusp-like behavior at 14.1 T, which is more clearly seen in its second derivative (inset). This saturation field shifts to the lower values with increasing temperature and then disappears above . Figure 3(c) shows magnetization curves measured at various temperatures. The magnetization taken at K increases approximately linearly with field and then saturates at about 7, indicating transition from the AFM phase at low fields to the forced ferromagnetic (FM) one. This behavior is consistent with previous magnetization measurements Hulliger and Schmelczer (1978). Below , the saturation field shifts to lower values with increasing temperature, as confirmed in the resistivity change. Above , the kink indicating saturation disappears and the magnetization curve follows the Brillouin function. Therefore, the kink indicates the phase transition from AFM to FM phase, where Eu2+ spins are polarized along the direction by the magnetic field.
Figure 3(d) summarizes a - phase diagram as determined by the above transport and magnetization measurements. Upon increasing the out-of-plane magnetic field, the Eu2+ spin moments, which are initially oriented along the axis at zero field, are gradually canted toward the axis without spin-flop transition. For the in-plane field, on the other band, the magnetization below exhibits a spin-flop transition at T, corresponding to reorientation of the spin moments perpendicular to the applied field (see Supplementary Materials Supplement ). EuSb2 exhibits large positive magnetoresistance both in the AFM and FM phases, similar to nonmagnetic TNLSMs (such as ZiSiS Sankar et al. (2017) and CaSb2 Funada et al. (2019a)). In the FM phase, the Eu2+ localized spins are polarized along the magnetic-field direction and electron scattering by the localized spins is expected to be further suppressed.
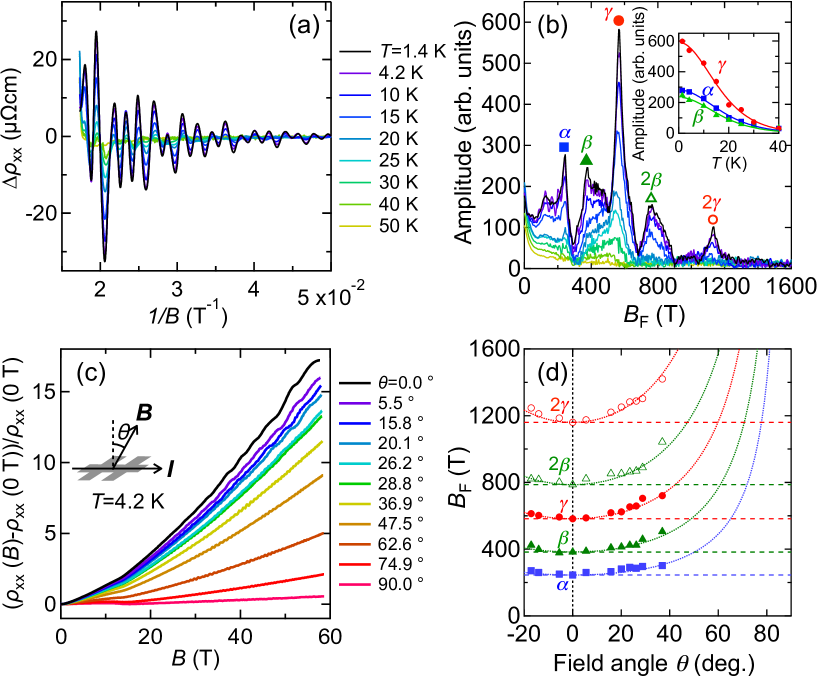
The SdH oscillations appear at high fields below 40 K, where the Eu2+ spin moments are oriented along the out-of-plane direction and band structures for the FM phase are expected to be realized (see Supplementary Materials Supplement ). Figure 4(a) plots the oscillatory component of the resistivity as a function of involved at various temperatures. Apparently, there is more than one type of frequency. As shown in Fig. 4(b), the fast Fourier transform (FFT) of yields three major frequencies at T, T, and T and their harmonics. The obtained frequencies suggest the presence of three Fermi pockets (, , ) perpendicular to the axis. As summarized in Table 1, the Fermi surface cross-section areas perpendicular to the applied magnetic field are calculated to be , , and Å-2, using the Lifshitz-Onsager relation, with the electron charge and the reduced Planck constant . These cross-sectional areas are typically small, taking only % of the entire BZ on the - plane. The FFT amplitudes of these three peaks gradually decrease with elevating temperature. As confirmed in the inset, their temperature dependence can be suitably fitted using the standard Lifshitz-Kosevich formula with thermal damping factors
| (1) |
where is Boltzman constant and the cyclotron frequency. The effective masses are estimated as small as about 0.11 for all three peaks with the free electron mass , as listed in Table 1. Importantly, this value is comparable to or even smaller than one reported in many other topological semimetals, e.g., 0.049 (bulk) Uchida et al. (2017) and 0.27 (surface) Nishihaya et al. (2019) in Cd3As2, 0.07 (bulk) Zhang et al. (2017b) and 0.50 (surface) Nair et al. (2020) in TaAs, and 0.04-0.18 (bulk) Matusiak et al. (2017) in ZrSiS. The Fermi velocity is also estimated as large as ms-1, similar to other topological semimetals Uchida et al. (2017); Nishihaya et al. (2019); Zhang et al. (2017b); Nair et al. (2020); Matusiak et al. (2017). More detailed analysis of the SdH oscillations indicates that the mobility is estimated as high as about cm2V-1s-1 (for details see Supplementary Materials Supplement ).
| carrier | (T) | (Å-2) | () | ( ms-1) |
|---|---|---|---|---|
| 247 | 0.023 | 0.109 | 3.66 | |
| 372 | 0.036 | 0.113 | 4.39 | |
| 566 | 0.056 | 0.117 | 5.24 |
Figure 4(c) shows field-angle dependence of the SdH oscillations taken at K. The magnetoresistance is significantly suppressed with rotation of the field direction from the out-of-plane (, ) to the in-plane (, -) direction. In addition, peaks and valleys of the oscillations shift to higher fields upon increasing . As confirmed in Fig. 4(d), although the oscillation amplitude becomes small and it is difficult to follow the frequency at higher angles (), all frequencies extracted from the FFT spectra can be fitted to , indicating that the quantum transport observed in these EuSb2 films originates from the 2D electronic structure.
One possible origin of the 2D field-angle dependence is that EuSb2 hosts a 2D bulk Fermi surface structure. However, most of the calculated Fermi surfaces are three-dimensional (3D), except only one 2D-like Fermi surface with low Fermi velocity (for details see Supplementary Materials Supplement ). Another possible origin is the quantum confinement effect. When the film thickness is comparable to the de Broglie wavelength of the carriers, the 3D bulk state is confined to form a 2D quantum-well state. However, the film thickness of 250 nm is considered large enough to maintain the 3D state, because even in Dirac semimetal Cd3As2 with extremely low carrier density and large Fermi velocity exhibits a 3D state above 100 nm film thickness Uchida et al. (2017). A third possibility is surface states of EuSb2. By fitting using the LK formula, we obtain nontrivial Berry Phases for the and pockets (for details see Supplementary Materials Supplement ). These bands may be non-trivial surface states, which are likely to be protected by the combination of two-fold screw and time reversal symmetry. Another possibility is that they are trivial surface states formed on the polar surface, which can also obtain non-trivial phases with the Rashba splitting. In any case, it is unobvious why the 2D conduction state is much more dominant than the 3D state and further studies are needed to determine its origin.
IV CONCLUSION
In summary, we have fabricated single-crystalline EuSb2 films by molecular beam epitaxy and have studied quantum transport at high fields. First-principles calculations have demonstrated that EuSb2 hosts topological nodal lines protected by nonsymmorphic symmetry, which remains preserved even under AFM ordering. Effective masses extracted from multiple SdH oscillations are fairly small, which is characteristic of topological semimetals. The 2D field-angle dependence of the SdH oscillations suggests the possibility of surface quantum transport in EuSb2. Our finding of the new magnetic TNLSM and observation of quantum transport will stimulate further investigations of exotic quantum transport as represented by Weyl orbit and topological phase transitions in magnetic topological semimetals.
V ACKNOWLEDGMENTS
We thank M.-T. Huebsch and T. Yu for fruitful discussions. This work was supported by JST PRESTO No. JPMJPR18L2 and CREST Grant No. JPMJCR16F1, Japan and by Grant-in-Aids for Scientific Research on Innovative Areas No. 19H05825, Scientific Research (S) No. 16H06345, and Scientific Research (B) No. JP18H01866 from MEXT, Japan.
References
- Fang et al. (2016) C. Fang, H. Weng, X. Dai, and Z. Fang, Chin. Phys. B 25, 117106 (2016).
- Burkov et al. (2011) A. A. Burkov, M. D. Hook, and L. Balents, Phys. Rev. B 84, 235126 (2011).
- Lu and Shen (2017) H.-Z. Lu and S.-Q. Shen, Front. Phys. 12, 127201 (2017).
- Wang et al. (2017a) S. Wang, B. C. Lin, A. Q. Wang, D. P. Yu, and Z. M. Liao, Adv. Phys.-X 2, 518 (2017).
- Armitage et al. (2018) N. P. Armitage, E. J. Mele, and A. Vishwanath, Rev. Mod. Phys. 90, 15001 (2018).
- Potter et al. (2014) A. C. Potter, I. Kimchi, and A. Vishwanath, Nat. Commun. 5, 5161 (2014).
- Wang et al. (2017b) C. M. Wang, H. P. Sun, H. Z. Lu, and X. C. Xie, Phys. Rev. Lett. 119, 136806 (2017).
- Zhang et al. (2017) C. Zhang, A. Narayan, S. Lu, J. Zhang, H. Zhang, Z. Ni, X. Yuan, Y. Liu, J. H. Park, E. Zhang, W. Wang, S. Liu, L. Cheng, L. Pi, Z. Sheng, S. Sanvito, F. Xiu, Nat. Commun. 8, 1272 (2017).
- Lin et al. (2019) B. C. Lin, S. Wang, S. Wiedmann, J. M. Lu, W. Z. Zheng, D. Yu, and Z. M. Liao, Phys. Rev. Lett. 122, 36602 (2019).
- Zhang et al. (2019) C. Zhang, Y. Zhang, X. Yuan, S. Lu, J. Zhang, A. Narayan, Y. Liu, H. Zhang, Z. Ni, R. Liu, E. S. Choi, A. Suslov, S. Sanvito, L. Pi, H.-Z. Lu, A. C. Potter, F. Xiu, Nature 565, 331 (2019).
- Nishihaya et al. (2019) S. Nishihaya, M. Uchida, Y. Nakazawa, R. Kurihara, K. Akiba, M. Kriener, A. Miyake, Y. Taguchi, M. Tokunaga, and M. Kawasaki, Nat. Commun. 10, 2564 (2019).
- Zak (1989) J. Zak, Phys. Rev. Lett. 62, 2747 (1989).
- Oroszlány et al. (2018) L. Oroszlány, B. Dóra, J. Cserti, and A. Cortijo, Phys. Rev. B 97, 205107 (2018).
- Yang et al. (2018) H. Yang, R. Moessner, and L. K. Lim, Phys. Rev. B 97, 165118 (2018).
- Chan et al. (2016) Y. H. Chan, C. K. Chiu, M. Y. Chou, and A. P. Schnyder, Phys. Rev. B 93, 205132 (2016).
- Bian et al. (2016) G. Bian, T. R. Chang, H. Zheng, S. Velury, S. Y. Xu, T. Neupert, C. K. Chiu, S. M. Huang, D. S. Sanchez, I. Belopolski, N. Alidoust, P.-J. Chen, G. Chang, A. Bansil, H. T. Jeng, H. Lin, M. Z. Hasan, Phys. Rev. B 93, 121113 (2016).
- Yamakage et al. (2016) A. Yamakage, Y. Yamakawa, Y. Tanaka, and Y. Okamoto, J. Phys. Soc. Jpn. 85, 013708 (2016).
- Hirayama et al. (2017) M. Hirayama, R. Okugawa, T. Miyake, and S. Murakami, Nat. Commun. 8 (2017).
- Hirayama et al. (2018) M. Hirayama, R. Okugawa, and S. Murakami, J. Phys. Soc. Jpn. 87, 041002 (2018).
- Fang et al. (2015) C. Fang, Y. Chen, H. Y. Kee, and L. Fu, Phys. Rev. B 92, 081201(R) (2015).
- Kobayashi et al. (2017) S. Kobayashi, Y. Yamakawa, A. Yamakage, T. Inohara, Y. Okamoto, and Y. Tanaka, Phys. Rev. B 95, 245208 (2017).
- Zhao and Schnyder (2016) Y. X. Zhao and A. P. Schnyder, Phys. Rev. B 94, 195109 (2016).
- Okugawa and Murakami (2017) R. Okugawa and S. Murakami, Phys. Rev. B 96, 115201 (2017).
- Bzdušek et al. (2016) T. Bzdušek, Q. S. Wu, A. Rüegg, M. Sigrist, and A. A. Soluyanov, Nature 538, 75 (2016).
- Wang (2017) J. Wang, Phys. Rev. B 96, 081107(R) (2017).
- Ormaza et al. (2016) M. Ormaza, L. Fernández, M. Ilyn, A. Magana, B. Xu, M. J. Verstraete, M. Gastaldo, M. A. Valbuena, P. Gargiani, A. Mugarza, A. Ayuela, L. Vitali, M. Blanco-Rey, F. Schiller, J. E. Ortega, Nano Lett. 16, 4230 (2016).
- Feng et al. (2019) B. Feng, R. W. Zhang, Y. Feng, B. Fu, S. Wu, K. Miyamoto, S. He, L. Chen, K. Wu, K. Shimada, T. Okuda, Y. Yao, Phys. Rev. Lett. 123, 116401 (2019).
- Hosen et al. (2018) M. M. Hosen, G. Dhakal, K. Dimitri, P. Maldonado, A. Aperis, F. Kabir, C. Sims, P. Riseborough, P. M. Oppeneer, D. Kaczorowski, T. Durakiewicz, M. Neupane, Sci. Rep. 8, 13283 (2018).
- Sankar et al. (2019) R. Sankar, I. P. Muthuselvam, K. R. Babu, G. S. Murugan, K. Rajagopal, R. Kumar, T. C. Wu, C. Y. Wen, W. L. Lee, G. Y. Guo, F. C. Chou, Inorg. Chem. 58, 11730 (2019).
- Chen et al. (2013) B. Chen, J. H. Yang, H. D. Wang, M. Imai, H. Ohta, C. Michioka, K. Yoshimura, and M. H. Fang, J. Phys. Soc. Jpn. 82, 124711 (2013).
- Kim et al. (2018) K. Kim, J. Seo, E. Lee, K. T. Ko, B. S. Kim, B. G. Jang, J. M. Ok, J. Lee, Y. J. Jo, W. Kang, J. S. Shim, C. Kim, H. W. Yeom, B. I. Min, B. J. Yang, J. S. Kim, Nat. Mat. 17, 794 (2018).
- Sakai et al. (2020) A. Sakai, S. Minami, T. Koretsune, T. Chen, T. Higo, Y. Wang, T. Nomoto, M. Hirayama, S. Miwa, D. Nishio-Hamane, F. Ishii, R. Arita, S. Nakatsuji, Nature 581, 53 (2020).
- Liu et al. (2018) E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S. Y. Yang, D. Liu, A. Liang, Q. Xu, Q. Kroder, V. Süß, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Writh, Y. Chen, S. T. B. Goennenwein, C. Felser, Nat. Phys. 14, 1125 (2018).
- Chang et al. (2017) G. Chang, S. Y. Xu, X. Zhou, S. M. Huang, B. Singh, B. Wang, I. Belopolski, J. Yin, S. Zhang, A. Bansil, Phys. Rev. Lett. 119, 156401 (2017).
- Sakai et al. (2018) A. Sakai, Y. P. Mizuta, A. A. Nugroho, R. Sihombing, T. Koretsune, M. T. Suzuki, N. Takemori, R. Ishii, D. Nishio-Hamane, R. Arita, P. Goswami, S. Nakatsuji, Nat. Phys. 14, 1119 (2018).
- Belopolski et al. (2019) I. Belopolski, K. Manna, D. S. Sanchez, G. Chang, B. Ernst, J. Yin, S. S. Zhang, T. Cochran, N. Shumiya, H. Zheng, B. Singh, G. Bian, D. Multer, M. Litskevich, X. Zhou, S.-M. Huang, B. Wang, T.-R. Chang, S.-Y. Xu, A. Bansil, C. Felser, H. Lin, M. Z. Hasan, Science 365, 1278 (2019).
- Funada et al. (2019a) K. Funada, A. Yamakage, N. Yamashina, and H. Kageyama, J. Phys. Soc. Jpn. 88, 044711 (2019).
- Ikeda et al. (2020) A. Ikeda, M. Kawaguchi, S. Koibuchi, T. Hashimoto, T. Kawakami, S. Yonezawa, M. Sato, and Y. Maeno, Phys. Rev. Mater. 4, 041801(R) (2020).
- Hulliger and Schmelczer (1978) F. Hulliger and R. Schmelczer, J. Solid State Chem. 26, 389 (1978).
- Niggli and Hulliger (1984) A. Niggli and F. Hulliger, Z. Kristallogr. 167, 125 (1984).
- Abdusalyamova and Vasilyeva (2011) M. N. Abdusalyamova and I. G. Vasilyeva, J. Solid State Chem. 184, 2751 (2011).
- Uchida et al. (2017) M. Uchida, Y. Nakazawa, S. Nishihaya, K. Akiba, M. Kriener, Y. Kozuka, A. Miyake, Y. Taguchi, M. Tokunaga, N. Nagaosa, Y. Tokura, M. Kawasaki, Nat. Commun. 8, 2274 (2017).
- Yoshida et al. (2009) H. Yoshida, Y. Okamoto, T. Tayama, T. Sakaktbara, M. Tokunaga, A. Matsuo, Y. Narumi, K. Kindo, M. Yoshida, M. Takigawa, Z. Hiroi, J. Phys. Soc. Jpn. 78, 043704 (2009).
- Kresse and Furthmüller (1996a) G. Kresse and J. Furthmüller, Comput. Mater. Sci. 6, 15 (1996).
- Kresse and Furthmüller (1996b) G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
- Kresse and Joubert (1999) G. Kresse and D. Joubert, Phys. Rev. B 59, 1758 (1999).
- Perdew et al. (1996) J. P. Perdew, M. Ernzerhof, and K. Burke, J. Chem. Phys. 105, 9982 (1996).
- Monkhorst and Pack (1976) H. J. Monkhorst and J. D. Pack, Phys. Rev. B 13, 5188 (1976).
- Sankar et al. (2017) R. Sankar, G. Peramaiyan, I. P. Muthuselvam, C. J. Butler, K. Dimitri, M. Neupane, G. N. Rao, M. T. Lin, and F. C. Chou, Sci. Rep. 7, 40603 (2017).
- (50) See Supplementary Material [URL] for detailed characterization, which includes Refs. [51-53].
- (51) K. S. Takahashi, H. Ishizuka, T.i Murata, Q. Y. Wang, Y. Tokura, N. Nagaosa, M. Kawasaki, Sci. Adv. 4, eaar7880 (2018).
- (52) G. P. Mikitik and Y. V. Sharlai, Phys. Rev. Lett. 82, 2147 (1999).
- (53) Z. Wang, Y. Zheng, Z. Shen, Y. Lu, H. Fang, F. Sheng, Y. Zhou, X. Yang, Y. Li, C. Feng, and Z.-A. Xu, Phys. Rev. B 93, 121112(R) (2016).
- Zhang et al. (2017b) C. L. Zhang, Z. Yuan, Q. D. Jiang, B. Tong, C. Zhang, X. C. Xie, and S. Jia, Phys. Rev. B 95, 085202 (2017).
- Nair et al. (2020) N. L. Nair, M.-E. Boulanger, F. Laliberté, S. Griffin, S. Channa, A. Legros, W. Tabis, C. Proust, J. Neaton, L. Taillefer, J. G. Analytis, Phys. Rev. B 102, 075402 (2020).
- Matusiak et al. (2017) M. Matusiak, J. R. Cooper, and D. Kaczorowski, Nat. Commun. 8, 15219 (2017).