Quantum state transfer of superposed multi-photon states via phonon-induced dynamic resonance in an optomechanical system
Abstract
We propose a method to transfer macroscopically superposed states between two optical cavities mediated by a mechanical oscillator, which works in a nonlinear regime of optomechanical interaction. Our approach relies on the phonon-induced dynamic resonance, where the motion of mechanical oscillator dynamically sets on/off the resonance between two cavities. Our method assumes high amplitude limit of oscillator, weak coupling between optical cavities, and adiabatic approximation. We show that, under these conditions, various multi-photon quantum states, especially, Schrödinger cat states, can be transferred with nearly perfect fidelity in a deterministic process. We show that transfer fidelity of 0.99 can be achieved using the experimental parameters in currently available technology.
I Introduction
Quantum state transfer (QST), the faithful transmission of quantum states from one place to another, plays a pivotal role in quantum information processing and communication [1, 2, 3, 4, 5]. Such a process has been pursued through different methods. Quantum teleportation [6, 7, 8, 9, 10] exploits entanglement between distant subsystems and classical communication of measurement outcomes. Alternatively, double-swap protocol [11] facilitates state transfer through the exchange of flying qubits. Another notable approach involves adiabatic passage via photonic dark states [12], akin to stimulated Raman adiabatic passage [13, 14, 15], providing yet another avenue for efficient quantum state transfer. Inspired by these proposals, a variety of theoretical studies and practical realizations have been explored, spanning diverse quantum systems, such as atoms [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32], spins [33, 34, 35, 36, 37, 38, 39], ions [40, 41, 42, 43, 44, 45], superconducting circuits [46, 47, 48, 49, 50, 51, 52, 53, 54, 55], solid qubits [56, 57, 58, 59], and optics [60, 61, 62].
Optomechanical system (OMS), a composite system of light and mechanical modes interacting by radiation pressure force [63], has emerged as a potential platform for quantum information tasks. Near-ground state cooling for mechanical resonators and strong optomechanical coupling were investigated [64, 65, 66, 67, 68, 69]. These facilitated the successful realization [70, 71, 72] of an optical-to-mechanical QST [73, 74, 75, 76, 77, 78, 79, 80]. A notable feature of OMS is that the coupling is independent of the resonant properties of the intra-cavity component, enabling it to function as a quantum interface for QST across systems with significant energy gaps. Both approaches of double-swap and adiabatic passage were employed to transfer a quantum state between optical modes of different frequencies in a three-mode OMS [81, 82, 83, 84, 85], with experimental demonstrations validating their efficacy [86, 87, 88, 89]. Efforts to improve these schemes were also explored, including the utilization of hybrid solutions [90, 91, 92] and shortcut-to-adiabaticity techniques [93, 94, 95]. Additionally, QST between two mechanical resonators coupled to a common cavity mode [96, 97, 98, 99], across distant optomechanical sites [100, 101], and in hybrid atom-optomechanical systems [103, 104, 105, 106, 107] were investigated. Moreover, progress of controlling entanglement in OMS [108] opens a promising route towards realizing quantum teleportation in OMS [109, 110, 111, 112, 113, 114]. However, these works on QST in OMS rely on the linearized cavity-mechanical interaction [63], limiting the amplitude of quantum states to transfer [77, 78].
In this work, we propose a model to transfer quantum states between two coupled optical cavities via a mechanical oscillator, operating in a nonlinear regime. In particular, we focus on a three-mode OMS consisting of two cavities coupled to a movable in-between mirror via optomechanical interactions [115], while also interacting each other. Unlike prior approaches reliant on beam-splitter interactions for the transfer mechanism, we exploit the dynamic resonance transfer [116]. Here, the motion of the mechanical oscillator induces dynamic resonance between two cavities, by which a quantum state is transferred between the cavity modes of (initially) different wavelengths without necessitating linearization. To the end we require high amplitude limit of oscillator, weak coupling between optical cavities, and adiabatic approximation. The high amplitude limit, achievable by preparing an initial state in a large number of photons, allows to approximately neglect quantum fluctuations and thermal noise inherent in the mechanical oscillator. As a result, there is an advantage experimental that it does not need to initialize the mechanical mode in its ground state nor to maintain extremely low bath temperatures, as typically required in a double-swap approach [81]. The conditions of weak optical coupling and adiabaticity, readily attained through appropriate parameterization of the system, enable the passive transfer assisted by the dynamic resonance, in other words, no external control fields are demanded except the preparation of initial state. Our approach is expected to be practical compared to the adiabatic passage method, as in Refs. [83, 84]. Under the conditions, we demonstrate the near-perfect transfer of high-amplitude quantum states between the cavities. We employ Fock states, displaced squeezed states, and Schrödinger cat states, which are at the heart of quantum optics and applications for quantum information processing [117, 118, 119, 120, 121].
The paper is organized as follows. In Section II, we introduce our system and derive its dynamics. Section III discusses the conditions requisite for achieving phonon-induced dynamic resonance. Subsequently, in Section IV, we assess the efficiency of our model by analyzing the transfer fidelity of quantum states. Summaries of our results are represented in Section V. In addition, Appendix A offers a detailed exposition of adiabatic approximation and Appendix B provides explicit expressions for the transfer fidelity of displaced squeezed states.
II System and its dynamics
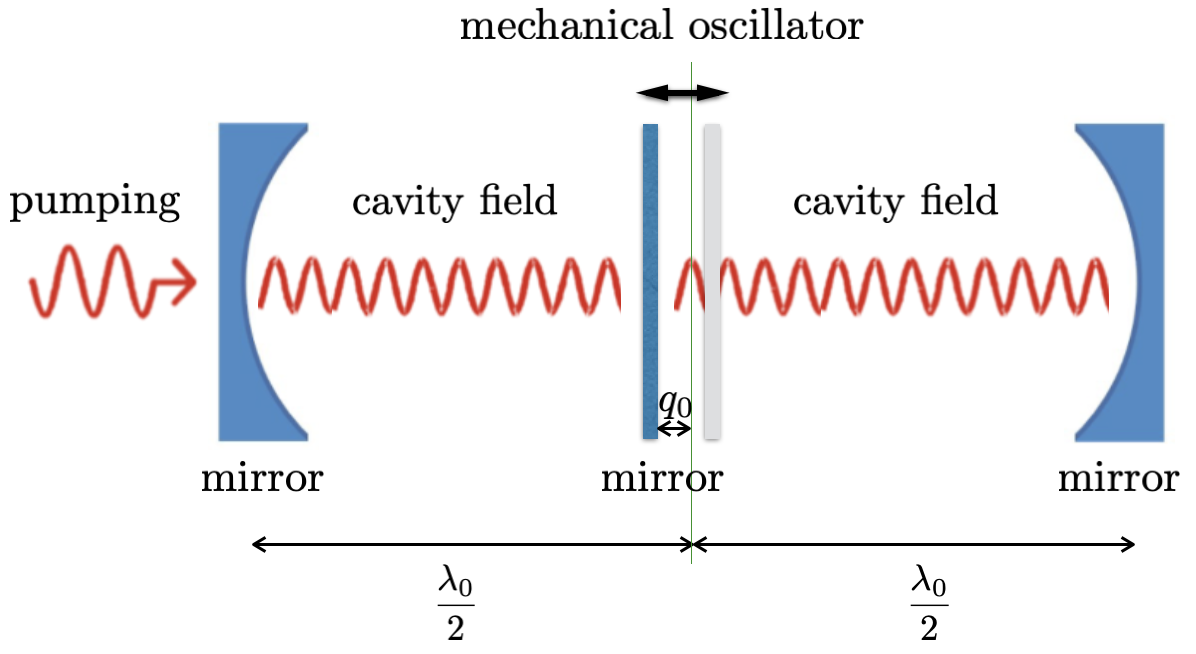
We present an optomechanical model tailored for QST between two optical cavities. This model consists of two optical Fabry-Perot cavities that share a two-sided mirror, as depicted in Fig. 1. The in-between mirror of mass is allowed to vibrate with frequency around its equilibrium position, located by from the middle of the end mirrors. If the equilibrium position were located exactly at the middle, the two cavities would have the same fundamental frequency with wavelength . Here, the position is located by to the left with . The fundamental frequencies in the left and right cavities are therefore different by , where with and . The vibrating mirror, called a mechanical oscillator (or simply an oscillator), is assumed to be slightly transparent so as to couple the two cavities with a coupling constant . The effective Hamiltonian in the rotating frame at the frequency is given by (in the unit of ) [115]
| (1) |
Here, and are the annihilation operators of the left (right) cavity and the oscillator, respectively, and with the number operators for . The optomechanical coupling constant and the dimensionless shift with being the mechanical zero-point fluctuation amplitude [63]. The first term in Eq. (1) describes the optical coupling between cavities, the second term is the optomechanical coupling between the oscillator and the cavities, and the third is the free energy of the oscillator. We note that does not explicitly depend on time .
In addition, we consider the coherent control of the cavity amplitudes by external fields with the interaction Hamiltonian . The cavities and oscillator are also affected by damping and noise processes due to their coupling with the environment. Taking into account control and dissipation terms, the Langevin equations for the system operators are then written by [122]
| (2) |
Here, is the annihilation operator vector and . Vectors and are coherent controlling and noise fields, respectively. are the decay rates of cavities 1, 2, and oscillator . We assume the reservoirs are independent of one another with their correlations , where (for ) are the thermal average numbers. The dynamic matrix is given by
| (3) |
where the frequency operator is a function of the oscillator’s operators and .
It is worth noting that the dynamic equation in Eq. (2) is nonlinear. Nevertheless, if the oscillator is treated classically and oscillates slowly enough (), the dynamics simplify to a beam-splitter-type interaction between two cavities with time-dependent frequencies. This interaction becomes resonant when the frequencies of the two become mutually equal depending on the oscillator’s amplitude. This phenomenon, known as phonon-induced dynamic resonance [116], is discussed in more detail in the next section.
III Phonon-induced dynamic resonance in adiabatic process
In this section, we show how our model enables the manifestation of phonon-induced dynamic resonance between two cavities. We begin by providing an intuitive description from a classical perspective, followed by the comprehensive solution of quantum dynamics. Meanwhile, we also explore the specific conditions necessary to establish phonon-induced dynamic resonance, providing a detailed discussion of their significance.
We assume a weak coupling between optical cavities, characterized by , ensuring that the two cavities are initially in far-off resonance. In contrast, under strong optical coupling, direct hopping between the cavities dominates, leading to a conventional quantum state exchange [123]. We also assume the oscillator frequency . Let us suppose that the left cavity is coherently excited by turning on and off the external driving fields in a short time . The driving fields are switched off at onward. In this way, we prepare the initial quantum state of the optomechanical system, while leaving the the oscillator’s state unchanged, . In other words, during the preparation, the oscillator is nearly immobilized at its initial equilibrium position. Consequently, the two cavities remain far from resonance and do not exchange energy (photons). Starting from , as the oscillator is allowed to vibrate, the radiation pressure by the left cavity pushes the oscillator toward a new equilibrium position at the right. The oscillator then approaches the middle of the two cavities, depending on the excited energy in the left cavity, so that the cavities become resonant and exchange photons. The resonance condition is temporally satisfied with the oscillator’s position, so-called a phonon-induced dynamic resonance [116].
The oscillator’s equilibrium position of average is determined by the radiation pressures or the photon numbers of the cavity fields. The initial photon-number average in the left cavity, denoted as , needs to be so large that the dynamic resonance condition can be fulfilled with , or equivalently, , where the threshold number of photons . In this regime of dynamic resonance and the time duration much shorter than (i.e., ), one may neglect the quantum fluctuation of the oscillator if the following condition is satisfied [124]
| (4) |
Here we expand , where the average amplitude is the solution to . The high amplitude limit in Eq. (4), as assumed throughout this paper, is that the average amplitude from the equilibrium, , is much larger than the quantum fluctuation [124]. In terms of the number fluctuation of cavities, the condition in Eq. (4) is reformulated as
| (5) |
In this limit, the frequency operator in Eq. (3), a function of , is reduced to the scalar function of the average , i.e., is replaced by , where is the real part of . In the oscillator’s equation, we replace the operators by their averages, i.e., by and by . We also remove the noise operator by assuming the thermal phonon number . The dynamic equation (2) becomes, divided into two types,
| (6) | |||||
| (7) |
where and are vectors for the cavities, and
| (8) |
The absence of the coherent terms for the cavities in Eq. (6) is due to the assumption that the diabatic processes of initializing the cavities are performed in a very short time .
To apply adiabatic approximation to the cavity dynamics with the phonon-induced dynamic resonance, we assume (see Appendix A). This adiabatic condition, when combined with the weak optical coupling, results in
| (9) |
Accordingly, Eq. (6) is transformed, as in Appendix A, to the dynamic equation for eigen modes of annihilation operators ,
| (10) |
where , , and is a diagonal matrix with diagonal elements . For , the eigenvalues are given by , where . The transformation is expressed as
| (11) |
with and . The solution to Eq. (10) is given by
| (12) |
where . It is remarkable that the two coupled cavities are described by two independent eigen modes. On the other hand, each eigen mode remains coupled with the oscillator in a way that its frequency depends temporally on the amplitude of oscillator, which is the solution to Eq. (7),
| (13) | |||||
where , with . Here we neglected the terms including , by the rotating wave approximation, as they are fast rotating with .
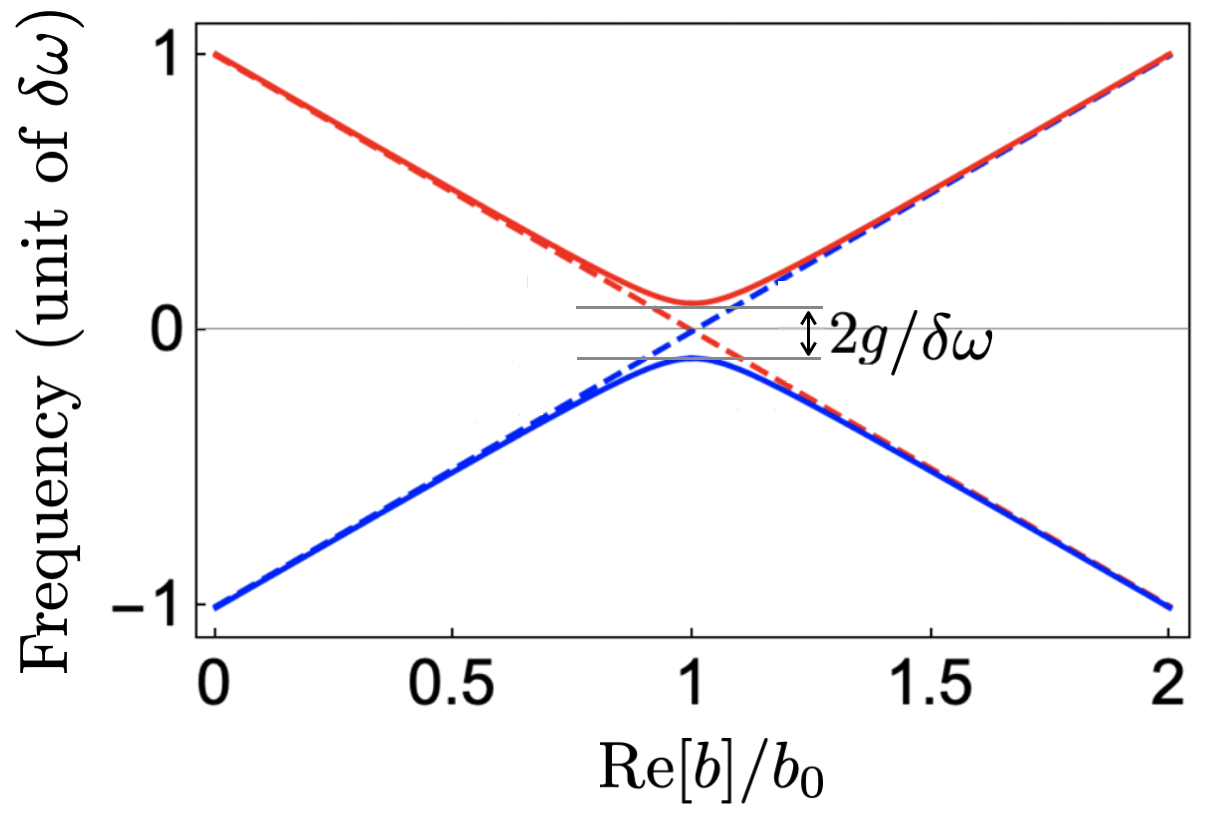
Figure 2 presents optical frequencies in terms of , with real amplitude , which shows a typical feature of the adiabatic process. For zero optical coupling of , the width of the left (right) cavity is linearly increased (decreased) when the oscillator moves to the right. As a result, the frequency of cavity mode () is linearly decreased (increased), leading to a frequency crossing at . When , a gap emerges between the two eigen-mode frequencies, characterized by the order of . It’s essential for this order to be small enough, say , that the two frequencies nearly touch each other.

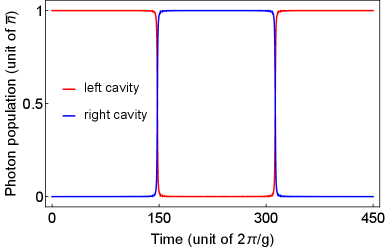
Given and , we illustrate the phonon-induced dynamic resonant transfer by presenting the semiclassical solution of on phase space of in Fig. 3 and photon populations of cavities in Fig. 4. The phase-space trajectory of the oscillator (in Fig. 3) starts at the origin and moves clock-wise to the resonant position of if . Around here, all the photons are transferred to the right cavity mode (as seen in Fig. 4) and the oscillator moves along the other larger circle. Turning back to the resonant position of , all the photons are transferred back to the left mode (as seen in Fig. 4) and the oscillator moves along the original circle.
The phonon-induced dynamic resonance in a three-mode optomechanical system is at the heart of our approach to QST. The nearly perfect population transfer between two cavities is achievable when the key assumptions are satisfied. Specifically, the high amplitude limit is feasible with the large number of photons (as indicated in the subsequent section). The conditions of adiabaticity and weak optical coupling are met by appropriately configuring the system’s parameters, for instance, setting , , and , which are experimentally available [125, 126].
IV Transfer quantum states with the large number of photons
In this section, we propose two schemes to transfer quantum states between two cavities. Initially, the cavities are prepared in a composite state , where the left cavity is in the state and the right cavity is in the vacuum (ground) state . The local state is to be transferred from the left cavity to the right through the phonon-induced dynamic resonance. In the first scheme, we aim that the cavities are in a fixed target state , similar to the conventional state-swapping. In the second scheme, we introduce a moving target state , where the transferred state depend on time in terms of the phase. Under the assumptions required to establish phonon-induced dynamic resonance, we derive expressions for the transfer fidelity (section IV.1) and evaluate the efficiency of our schemes by employing Fock states, displaced squeezed states, and Schrödinger cat states (section IV.2). These states, fundamental to quantum optics, are pivotal for applications in quantum information processing.
IV.1 Transfer fidelity
The state transfer is evaluated in terms of fidelity , which is defined by the probability that the cavities initially in are found in a target state at time ,
| (14) |
where and the time evolution operator with being the time-ordering operator. Here is for the fixed target state or for the moving target state. To distinguish the fidelity between the two schemes, we will also use the subscripts “fix” and “mov” for , corresponding to the fixed and moving target states, respectively.
With the fixed target state , by expanding the local state as , where is a complete set of number states, we get
| (15) |
Here . The fidelity in Eq. (14) is then obtained by applying the solutions in Eq. (12) to the operator in Eq. (15).
To analytically examine the state-transfer process, we assume in this work that . The effects of damping and noise, as well as the effects neglected in the adiabatic approximation and high-amplitude limit (introduced in the previous section), will be presented in future work.
By assuming no noise in Eq. (12), we derive
| (16) |
where . The transmittance matrix is composed of elements
| (17) | ||||
| (18) |
where and are defined by Eq. (11), and . Thus, and the fidelity
| (19) |
Noting that is a complex function of , expressed as . It is necessary for some that to achieve nearly perfect fidelity. From Eq. (18), we have
| (20) |
For , this can be approximated as
| (21) |
Given that and , holds if
| (22) |
which requires and . Since , the condition is trivial under the assumption , provided . Meanwhile the requirement is equivalent to , consistent with the scenario where population transfer is complete, as illustrated in Figs. 3 and 4. In other words, the unit fidelity in QST can be achieved on the condition that the population transfer is perfect. On the other hand, the fidelity can oscillate rapidly at a frequency of the order of , as does the phase term of , .
To account the oscillations in the phase and the fidelity, we introduce an alternative scheme that the target state is let depend on time in terms of the phase, called a moving target state, . The phase , derived from Eq. (18) as
| (23) |
can be implemented using a linear phase shifter [127, 128]. With this approach, the fidelity depends solely on the magnitude of , given by
| (24) |
This formulation simplifies the time dependency of the fidelity and effectively addresses the oscillatory behavior.
IV.2 Examples
As examples, we first consider the transfer of the Fock state . The state must have a large photon number to satisfy the high amplitude limit in Eq. (5). The fidelity is given by
| (25) |
Here the fidelities with the moving target state and the fixed target state are equal to each other. This is because differs from by a global phase. When and , the magnitude of in Eq. (21) can be approximated as
| (26) |
Then, the fidelity in Eq. (25) becomes
| (27) |
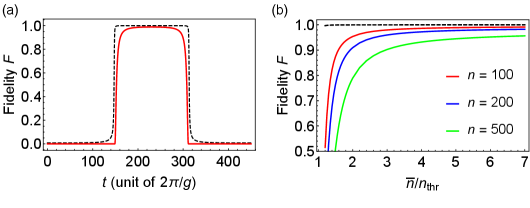
which approaches unity if . This establishes an upper bound on the initial photon number of the local state to attain high fidelity. To illustrate the possibility of achieving faithful state transfer when population transfer is successful, we plot the fidelity in Eq. (25) as a function of time, compared with the transmittivity , in Fig. 5(a). Fidelities of transferring Fock states with different photon numbers are presented in Fig. 5(b). As predicted by Eq. (27), the fidelity decreases as increasing the initial number of photons . Additionally, Fig. 5(b) shows that the fidelity depends on the ratio , however, it rapidly increases to the unity with the ratio. Therefore, this ratio does not need to be very large, noting that an excessively high initial photon number in the left cavity, far exceeding the threshold , would violate the adiabatic assumption and destabilizes the mechanical oscillator’s motion.
Schrödinger cat states, as iconic examples of quantum superposition, are crucial for exploring the boundaries of quantum mechanics and advancing quantum information processing. We consider Schrödinger cat states to transfer [118, 119, 120, 121]
| (28) |
where are coherent states with amplitude and . The high amplitude limit in Eq. (5) satisfies
| (29) |
for the large amplitude . The fidelities with the fixed target state and the moving target state are given, respectively, by
| (30) |
and
| (31) |
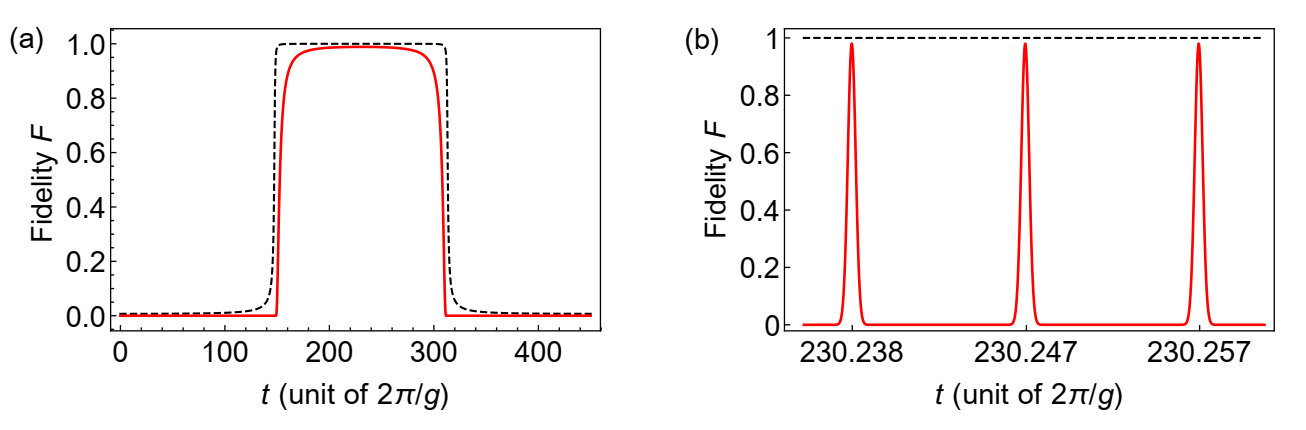
Using Eq. (26), both and approach unity if . Noting that for large , this condition can be expressed as , which is the same as that for Fock states. Fig. 6 displays the fidelities of transferring a Schrödinger cat state with the initial number of photons . In Fig. 6(a), the fidelity with the moving target state, , consistently approaches unity over a prolonged period (red curve), closely matching the interval when the transmittivity reaches unity (dashed black curve). On the other hand, in Fig. 6(b), the fidelity with the fixed target state, , reaches unity at specific times but then decays to zero, even when the population transfer is perfect (indicated by the unity of the dashed black line). The interval between adjacent peaks is approximately , suggesting the rapid oscillation of .
Displaced squeezed states are a class of Gaussian states that play a vital role in quantum optics. They provide enhanced control over quantum uncertainties, making them essential for improving precision in measurements and advancing quantum communication. To evaluate the performance of our model on Gaussian states, we consider the displaced squeezed states [117]
| (32) |
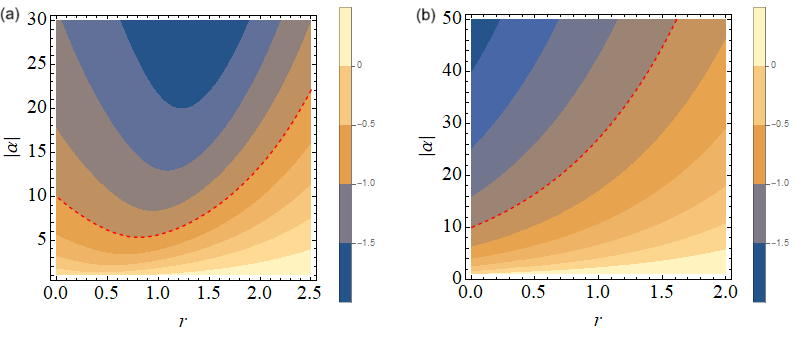
where is the displacement operator and the squeezing operator with complex amplitudes and , respectively. Applying the high amplitude limit Eq. (5) to results in
| (33) |
where . The condition (33) is satisfied by high-amplitude states with large , along with an appropriate chosen value of , as illustrated in Fig. 7. The explicit expressions for fidelities of transferring the displaced squeezed states are provided in Appendix B. The numerical results, in Eq. (39) and in Eq. (38), for states to transfer and are plotted in Fig. 8. Figure 8(a) illustrates the achievement of nearly perfect fidelity with the moving target state, while Fig. 8(b) demonstrates the oscillation of fidelity with the fixed target state.
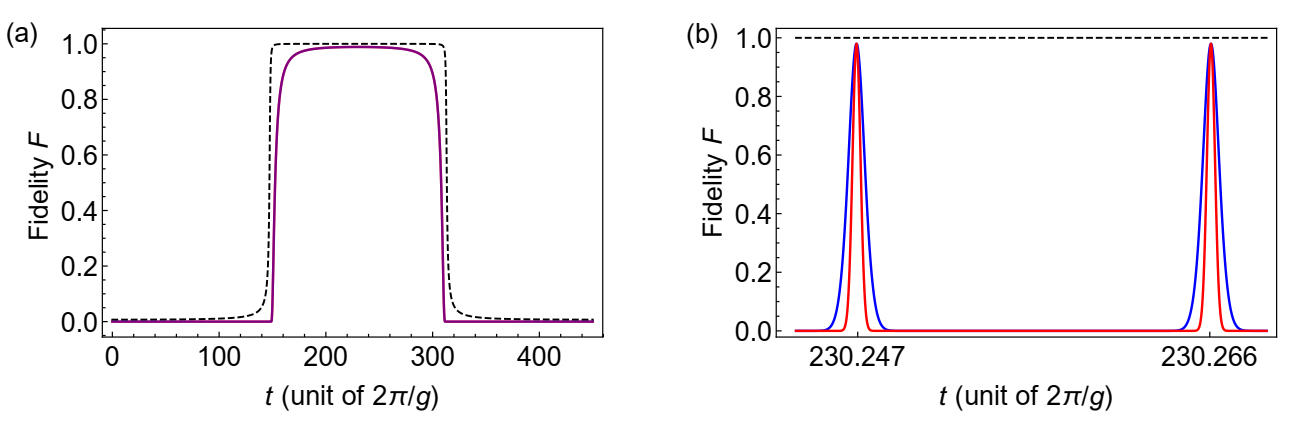
We explore the transfer of quantum states, including both Gaussian and non-Gaussian types, between two cavities in a three-mode optomechanical system. The results suggest that our model is particularly effective for states with large photon numbers (). In the scheme with the fixed target state, the fidelity rapidly oscillates with time, reaching unity only at specific instances (except the Fock state). However, the oscillation of fidelity can be addressed using a phase shifter [127, 128], as demonstrated in the scheme with the moving target state. In this case, nearly perfect fidelity is maintained over extended periods, comparable to the timescale of the mechanical oscillator.
This section demonstrates how phonon-induced dynamic resonance contributes to efficient quantum state transfer. Once population transfer via phonon-induced dynamic resonance is achieved, the fidelity of the quantum state transfer approaches unity. With currently available technology [125, 126], the transfer fidelity as high as 0.99 is attainable. Recent prospects in the ultrastrong regime of nonlinear optomechanical coupling [131, 132] are expected to improve fidelity further, bringing it closer to perfection.
V Conclusion
We propose a novel model to transfer quantum states between two optical cavities mediated by a mechanical oscillator in a three-mode optomechanical system. The system operates in the nonlinear regime of optomechanical interaction and with parameters set to satisfy three key assumptions: high amplitude limit of mechanical oscillator, weak coupling between optical cavities, and adiabatic approximation. These assumptions are essential to establish phonon-induced dynamic resonance, the heart of our approach to quantum state transfer.
We examine two schemes: the first involves the fixed target state, akin to conventional state-swapping, while the second assumes the moving target state whose phase evolves over time. Our results demonstrate that both schemes can achieve nearly perfect fidelity once population transfer via phonon-induced dynamic resonance is reliable. In the first scheme, the transfer fidelity rapidly oscillates with time. However, by introducing a phase shifter in the second scheme, the oscillation is mitigated, enabling nearly perfect fidelity to be maintained over extended periods, comparable to the timescale of the mechanical oscillator.
A defining strength of our scheme is its capacity to transfer high-amplitude quantum states, a capability unattainable in approaches relying on linearized optomechanical interactions. Quantum states with large numbers of photons tend to be resilient to specific types of noise and errors including thermal noise, shot noise and photon losses, enhancing the overall fidelity of quantum state transfer [133]. Efficiently transferring such high-amplitude quantum states is essential for large-scale quantum computing based on continuous-variable systems [134, 135].
In this work, the efficiency of quantum state transfer is analyzed under the assumption that quantum fluctuations and thermal noises of the mechanical oscillator are negligible. Furthermore, damping and noise effects are excluded to enable the derivation of analytical expressions for fidelity. An investigation that includes all of these effects will be addressed in future studies.
Acknowledgment
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2023M3K5A1094813).
Appendix
Appendix A ADIABATIC APPROXIMATION
We derive the adiabatic approximation to the cavity dynamics. We perform an eigendecomposition for the cavity modes to obtain for some invertible matrix so that is a diagonal matrix at every instance time ; the column vectors of are instantaneous eigenvectors of the dynamic matrix in Eq. (8),
| (34) |
where is the -th column vector of and is the -th diagonal element of .
Applying from the left, Eq. (6) is transformed to the dynamic equation for the eigenmode vector ,
| (35) |
where , . Here, we use for all . We neglect by the adiabatic approximation [129]
| (36) |
for . Using the expressions for quantities associated with , given in sections II and III, the adiabatic is rephrased to be
| (37) |
Appendix B Fidelity of transferring the displaced squeezed state
References
- [1] D. P. DiVincenzo, ”The physical implementation of quantum computation,” Fortschr. Phys. 48, 771-783 (2000).
- [2] N. Gisin and R. Thew, ”Quantum communication,” Nat. Photonics 1, 165-171 (2007).
- [3] H. J. Kimble, ”The quantum internet,” Nature (London) 453, 1023-1030 (2008).
- [4] D. Awschalom, K. K. Berggren, H. Bernien, et al., ”Development of quantum interconnects (QuICs) for next-generation information technologies,” PRX Quantum, 2, 017002 (2021).
- [5] G. Moody, V. J. Sorger, D. J. Blumenthal, et al., ”2022 Roadmap on integrated quantum photonics,” J. Phys. Photonics 4, 012501 (2022).
- [6] C. H. Bennett, G. Brassard, C. Crépeau, et al., ”Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Phys. Rev. Lett. 70, 1895 (1993).
- [7] S. L. Braunstein and H. J. Kimble, ”Teleportation of continuous quantum variables,” Phys. Rev. Lett. 80, 869 (1998).
- [8] J. Lee, M. S. Kim, Y. J. Park, et al., ”Partial teleportation of entanglement in a noisy environment,” J. Mod. Opt. 47, 2151-2164 (2000).
- [9] J. Lee, M. S. Kim, ”Entanglement teleportation via Werner states,” Phys. Rev. Lett. 84, 4236 (2000).
- [10] J. Lee, H. Min, and S. D. Oh, ”Multipartite entanglement for entanglement teleportation,” Phys. Rev. A 66, 052318 (2002).
- [11] J. I. Cirac, P. Zoller, H. J. Kimble, et al., ”Quantum state transfer and entanglement distribution among distant nodes in a quantum network,” Phys. Rev. Lett. 78, 3221 (1997).
- [12] T. Pellizzari, ”Quantum networking with optical fibres,” Phys. Rev. Lett. 79, 5242 (1997).
- [13] U. Gaubatz, P. Rudecki, S. Schiemann, et al., ”Population transfer between molecular vibrational levels by stimulated Raman scattering with partially overlapping laser fields. A new concept and experimental results,” J. Chem. Phys. 92, 5363-5376 (1990).
- [14] K. Bergmann, H. Theuer, and B. W. Shore, ”Coherent population transfer among quantum states of atoms and molecules,” Rev. Mod. Phys. 70, 1003 (1998).
- [15] N. V. Vitanov, A. A. Rangelov, B. W. Shore, et al., ”Stimulated Raman adiabatic passage in physics, chemistry, and beyond,” Rev. Mod. Phys. 89, 015006 (2017).
- [16] M.D. Lukin, S. F. Yelin, and M. Fleischhauer, ”Entanglement of atomic ensembles by trapping correlated photon states,” Phys. Rev. Lett. 84, 4232 (2000).
- [17] M. Fleischhauer and M. D. Lukin, ”Dark-state polaritons in electromagnetically induced transparency,” Phys. Rev. Lett. 84, 5094 (2000).
- [18] D. F. Phillips, A. Fleischhauer, A. Mair, et al., ”Free to read storage of light in atomic vapor,” Phys. Rev. Lett. 86, 783 (2001).
- [19] A. Mair, J. Hager, D. F. Phillips, et al., ”Phase coherence and control of stored photonic information,” Phys. Rev. A 65, 031802(R) (2002).
- [20] S. Lloyd, M. S. Shahriar, J. H. Shapiro, et al., ”Long Distance, Unconditional Teleportation of Atomic States via Complete Bell State Measurements,” Phys. Rev. Lett. 87, 167903 (2001).
- [21] T. V. Leent, M. Bock, F. Fertig, et al., ”Entangling single atoms over 33 km telecom fibre,” Nature 607, 69-73 (2022).
- [22] B. Julsgaard, A. Kozhekin, and E. S. Polzik, ”Experimental long-lived entanglement of two macroscopic objects,” Nature 413, 400-403 (2001).
- [23] L. M. Duan, M. D. Lukin, J. I. Cirac, et al., ”Long-distance quantum communication with atomic ensembles and linear optics,” Nature 414, 413-418 (2001).
- [24] M. Razavi and J. H. Shapiro, ”Long-distance quantum communication with neutral atoms,” Phys. Rev. A 73, 042303 (2006).
- [25] J. F. Sherson, H. Krauter, R. K. Olsson, et al., ”Quantum teleportation between light and matter,” Nature 443, 557-560 (2006).
- [26] W. Yao, R. B. Liu, and L. J. Sham, ”Theory of control of the spin-photon interface for quantum networks,” Phys. Rev. Lett. 95, 030504 (2005).
- [27] S. Ritter, C. Nölleke, C. Hahn, et al., ”An elementary quantum network of single atoms in optical cavities,” Nature 484, 195-200 (2012).
- [28] G. F. Peñas, R. Puebla, and J. J. García-Ripoll, ”Improving quantum state transfer: correcting non-Markovian and distortion effects,” Quantum Sci. Technol. 8, 045026 (2023).
- [29] A. Serafini, St. Mancini, and S. Bose, ”Distributed Quantum Computation via Optical Fibers,” Phys. Rev. Lett. 96, 010503 (2006).
- [30] S. Kato, N. Nemet, K. Senga, et al., ”Observation of dressed states of distant atoms with delocalized photons in coupled-cavities quantum electrodynamics,” Nat. Commum. 10, 1160 (2019).
- [31] B. Vogell, B. Vermersch, T. E. Northup, et al., ”Deterministic quantum state transfer between remote qubits in cavities,” Quantum Sci. Technol. 2, 045003 (2017).
- [32] A. Gogyan and Yu. Malakyan, ”Deterministic quantum state transfer between remote atoms with photon-number superposition states,” Phys. Rev. A 98, 052304 (2018).
- [33] S. Bose, ”Quantum communication through an unmodulated spin chain,” Phys. Rev. Lett. 91, 207901 (2003).
- [34] A. Lyakhov and C. Bruder, ”Quantum state transfer in arrays of flux qubits,” New J. Phys. 7, 181 (2005).
- [35] M. Christandl, N. Datta, A. Ekert, et al., ”Perfect state transfer in quantum spin networks,” Phys. Rev. Lett. 92, 187902 (2004).
- [36] V. Giovannetti and D. Burgarth, ”Improved transfer of quantum information using a local memory,” Phys. Rev. Lett. 96, 030501 (2006).
- [37] J. Fitzsimons and J. Twanley, ”Globally controlled quantum wires for perfect qubit transport, mirroring, and computing,” Phys. Rev. Lett. 97, 090502 (2006).
- [38] D. Burgarth and S. Bose, ”Conclusive and arbitrarily perfect quantum-state transfer using parallel spin-chain channels,” Phys. Rev. A 71, 052315 (2005).
- [39] M. S. Wei, M. J. Liao, Y. Q. Wang, et al., ”Quantum state transfer on square lattices with topology,” Phys. Rev. A 108, 062401 (2023).
- [40] A. S. Parkins and H. J. Kimble, ”Quantum state transfer between motion and light,” J. Opt. B: Quantum Semiclass. Opt. 1, 496 (1999).
- [41] F. K. Nohama and J. A. Roversi, ”Two-qubit state transfer between trapped ions using electromagnetic cavities coupled by an optical fibre,” J. Phys. B: At. Mol. Opt. Phys. 41, 045503 (2008).
- [42] M. Riebe, H. Häffner, C. F. Roos, et al., ”Deterministic quantum teleportation with atoms,” Nature 429, 734-737 (2004).
- [43] M. D. Barrett, J. Chiaverini, T. Schaetz, et al., ”Deterministic quantum teleportation of atomic qubits,” Nature 429, 737-739 (2004).
- [44] M. Riebe, M. Chwalla, J. Benhelm, et al., ”Quantum teleportation with atoms: quantum process tomography,” New J. Phys. 9, 211 (2007).
- [45] S. Olmschenk, D. N. Matsukevich, P. Maunz, et al., ”Quantum teleportation between distant matter qubits,” Science 323, 486-489 (2009).
- [46] K. Jahne, B. Yurke, and U. Gavish, Phys. Rev. A 75, 010301 (2007).
- [47] S. J. Srinivasan, N. M. Sundaresan, D. Sadri, Y. Liu, J. M. Gambetta, T. Yu, S. M. Girvin, and A. A. Houck, ibid 89, 033857 (2014).
- [48] A. N. Korotkov, ”Flying microwave qubits with nearly perfect transfer efficiency,” Phys. Rev. B 84 , 014510 (2011).
- [49] E. A. Sete, E. Mlinar, and A. N. Korotkov, ”Robust quantum state transfer using tunable couplers” Phys. Rev. B 91, 144509 (2015).
- [50] J. Wenner, Yi Yin, Yu Chen, et al., ”Catching time-reversed microwave coherent state photons with 99.4% absorption efficiency,” Phys. Rev. Lett. 112, 210501 (2014).
- [51] C. J. Axline, L. D. Burkhart, W. Pfaff, et al., ”On-demand quantum state transfer and entanglement between remote microwave cavity memories,” Nature 14, 705-710 (2018).
- [52] P. Kurpiers, P. Magnard, T. Walter, et al., ”Deterministic quantum state transfer and remote entanglement using microwave photons,” Nature 558, 264-267 (2018).
- [53] A. Bienfait, K. J. Satzinger, Y. P. Zhong, et al., ”Phonon-mediated quantum state transfer and remote qubit entanglement,” Science 364, 368-371 (2019).
- [54] N. Leung, Y. Lu, S. Chakram,et al., ”Deterministic bidirectional communication and remote entanglement generation between superconducting qubits,” npj Quantum Inf. 5, 18 (2019).
- [55] K. G. Fedorov, M. Renger, S. Pogorzalek, et al., ”Experimental quantum teleportation of propagating microwaves,” Sci. Adv. 7, eabk0891 (2021).
- [56] M. A. Lemonde, S. Meesala, A. Sipahigil, et al., ”Phonon Networks with Silicon-Vacancy Centers in Diamond Waveguides,” Phys. Rev. Lett. 120, 213603 (2018).
- [57] F. Rozpedek, R. Yehia, K. Goodenough, et al., ”Near-term quantum-repeater experiments with nitrogen-vacancy centers: Overcoming the limitations of direct transmission,” Phys. Rev. A 99, 052330 (2019).
- [58] W. Pfaff, B. J. Hensen, H. Bernien, et al., ”Unconditional quantum teleportation between distant solid-state quantum bits,” Science 345, 532-535 (2014).
- [59] M. Pompili, S. L. N. Hermans, S. Baier, et al., ”Realization of a multinode quantum network of remote solid-state qubits,” Science 372, 259-264 (2021).
- [60] Q. Lin and B. He, ”Bi-directional mapping between polarization and spatially encoded photonic qutrits,” Phys. Rev. A 80, 062312 (2009).
- [61] B. He, Y. Ren, and A. Bergou, ”Creation of high-quality long-distance entanglement with flexible resources,” Phys. Rev. A 79, 052323 (2009).
- [62] X. M. Jin, J. G. Ren, B. Yang, et al., ”Experimental free-space quantum teleportation,” Nat. Photon. 4, 376-381 (2010).
- [63] M. Aspelmeyer, T. J. Kippenberg, K. Marquardt, ”Cavity optomechanics,” Rev. Mod. Phys. 86, 1391 (2014).
- [64] D. Kleckner and D. Bouwmeester, ”Sub-kelvin optical cooling of a micromechanical resonator,” Nature 444, 75-78 (2006).
- [65] S. Gröblacher, K. Hammerer, M. R. Vanner, et al., ”Observation of strong coupling between a micromechanical resonator and an optical cavity field,” Nature 460, 724-727 (2009).
- [66] A. O’Connell, M. Hofheinz, M. Ansmann, et al., ”Quantum ground state and single-phonon control of a mechanical resonator,” Nature 464, 697-703 (2010).
- [67] J. D. Teufel, T. Donner, Dale Li, et al., ”Sideband cooling of micromechanical motion to the quantum ground state,” Nature 475, 359-363 (2011).
- [68] J. Chan, T. P. Mayer Alegre, A. H. Safavi-Naeini, et al., ”Laser cooling of a nanomechanical oscillator into its quantum ground state,” Nature 478, 89-92 (2011).
- [69] E. Verhagen, S. Deléglise, S. Weis, et al., ”Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode,” Nature 482, 63-67 (2012).
- [70] T. A. Palomaki, J. W. Harlow, J. D. Teufel, et al., ”Coherent state transfer between itinerant microwave fields and a mechanical oscillator,” Nature 495, 210-214 (2013).
- [71] V. Fiore, Y. Yang, M. C. Kuzyk, et al., ”Storing optical information as a mechanical excitation in a silica optomechanical resonator,” Phys. Rev. Lett. 107, 133601 (2017).
- [72] A. P. Reed, K. H. Mayer, J. D. Teufel, et al., ”Faithful conversion of propagating quantum information to mechanical motion,” Nat. Phys. 13, 1163-1167 (2017).
- [73] J. Zhang, K. Peng, and S. L. Braunstein, ”Quantum-state transfer from light to macroscopic oscillators,” Phys. Rev. A 68, 013808 (2003).
- [74] K. Jähne, C. Genes, K. Hammerer, et al., ”Cavity-assisted squeezing of a mechanical oscillator,” Phys. Rev. A 79, 063819 (2009).
- [75] U. Akram, N. Kiesel, M. Aspelmeyer, et al., ”Single-photon opto-mechanics in the strong coupling regime,” New J. Phys. 12, 083030 (2010).
- [76] F. Khalili, S. Danilishin, H. Miao, et al., ”Preparing a mechanical oscillator in non-Gaussian quantum states,” Phys. Rev. Lett. 105, 070403 (2010).
- [77] R. Y. Teh, S. Kiesewetter, M. D. Reid, et al., ”Simulation of an optomechanical quantum memory in the nonlinear regime,” Phys. Rev. A 96, 013854 (2017).
- [78] R. Y. Teh, S. Kiesewetter, P. D. Drummond, et al., ”Creation, storage, and retrieval of an optomechanical cat state,” Phys. Rev. A 98, 063814 (2018).
- [79] J. Cheng, X. T. Liang, W. Z. Zhang, et al., ”Optomechanical state transfer in the presence of non-Markovian environments,” Opt. Commun. 430, 385-390 (2019).
- [80] S. Lei, X. Wang, H. Li, et al., ”High-fidelity and robust optomechanical state transfer based on pulse control,” Appl. Phys. B 129, 193 (2023).
- [81] L. Tian and H. Wang, ”Optical wavelength conversion of quantum states with optomechanics,” Phys. Rev. A 82, 053806 (2010).
- [82] C. A. Regal and K. W. Lehnert, ”From cavity electromechanics to cavity optomechanics,” J. Phys.: Conf. Ser. 264, 012025 (2011).
- [83] L. Tian, ”Adiabatic state conversion and pulse transmission in optomechanical systems,” Phys. Rev. Lett. 108, 153604 (2012).
- [84] Y. D. Wang and A. A. Clerk, ”Using interference for high fidelity quantum state transfer in optomechanics,” Phys. Rev. Lett. 108, 153603 (2012).
- [85] L. Tian, ”Optoelectromechanical transducer: Reversible conversion between microwave and optical photons,” Ann. Phys. (Berlin) 527, 1-14 (2015)
- [86] J. Hill, A. Safavi-Naeini, J. Chan, et al., ”Coherent optical wavelength conversion via cavity optomechanics,” Nat. Commun. 3, 1196 (2012).
- [87] J. Bochmann, A. Vainsencher, D. D. Awschalom, et al., ”Nanomechanical coupling between microwave and optical photons,” Nat. Phys. 9, 712-716 (2013).
- [88] R. W. Andrews, R. W. Peterson, T. P. Purdy, et al., ”Bidirectional and efficient conversion between microwave and optical light,” Nat. Phys. 10, 321-326 (2014).
- [89] M. Forsch, R. Stockill, A. Wallucks, et al., ”Microwave-to-optics conversion using a mechanical oscillator in its quantum ground state,” Nat. Phys. 16, 69-74 (2020).
- [90] Y. D. Wang and A. A. Clerk, ”Using dark modes for high-fidelity optomechanical quantum state transfer,” New J. Phys. 14, 105010 (2012).
- [91] S. Sainadh U and A. Narayanan, ”Mechanical switch for state transfer in dual-cavity optomechanical systems,” Phys. Rev. A 88, 033802 (2013).
- [92] S. A. McGee, D. Meiser, C. A. Regal, et al., ”Mechanical resonators for storage and transfer of electrical and optical quantum states,” Phys. Rev. A 87, 053818 (2013).
- [93] D. G. Odelin, A. Ruschhaupt, A. Kiely, et al., ”Shortcuts to adiabaticity: Concepts, methods, and applications,” Rev. Mod. Phys. 91, 045001 (2019).
- [94] F. Y. Zhang, W. L. Li, W. B. Yan, et al., ”High-performance supercapacitor carbon electrode fabricated by large-scale roll-to-roll micro-gravure printing,” J. Phys. B: At. Mol. Opt. Phys. 52, 115501 (2019).
- [95] C. L. Zhang, X. Chen, C. G. Liao, et al., ”Reversible quantum state transfer in a three-mode optomechanical system,” Laser Phys. Lett. 18, 065206 (2021).
- [96] M. Schmidt, M. Ludwig, and F. Marquardt, ”Optomechanical circuits for nanomechanical continuous variable quantum state processing,” New J. Phys. 14, 125005 (2012).
- [97] M. J. Weaver, F. Buters, F. Luna, et al., ”Coherent optomechanical state transfer between disparate mechanical resonators,” Nat. Commun. 8, 824 (2017).
- [98] Y. X. Zeng, J. Shen, M. S. Ding, et al., ”Macroscopic Schrödinger cat state swapping in optomechanical system,” Opt. Express 28, 9587-9602 (2020).
- [99] V. Fedoseev, F. Luna, I. Hedgepeth, et al., ”Stimulated Raman adiabatic passage in optomechanics,” Phys. Rev. Lett. 126, 113601 (2021).
- [100] A. H. Safavi-Naeini and O. Painter, ”Proposal for an optomechanical traveling wave phonon–photon translator,” New J. Phys. 13, 013017 (2011).
- [101] K. Fang, M. H. Matheny, X. Luan, et al., ”Optical transduction and routing of microwave phonons in cavity-optomechanical circuits,” Nat. Photonics 10, 489-496 (2016).
- [102] G. D. de Moraes Neto, F. M. Andrade, V. Montenegro, et al., ”Quantum state transfer in optomechanical arrays,” Phys. Rev. A 93, 062339 (2016).
- [103] K. Hammerer, M. Wallquist, C. Genes, et al., ”Strong coupling of a mechanical oscillator and a single atom,” Phys. Rev. Lett. 103, 063005 (2009).
- [104] M. Wallquist, K. Hammerer, P. Zoller, et al., ”Single-atom cavity QED and optomicromechanics,” Phys. Rev. A 81, 023816 (2010).
- [105] S. Singh, H. Jing, E. M. Wright, et al., ”Quantum-state transfer between a Bose-Einstein condensate and an optomechanical mirror,” Phys. Rev. A 86, 021801(R) (2012).
- [106] F. Momeni and M. H. Naderi, ”Atomic quadrature squeezing and quantum state transfer in a hybrid atom–optomechanical cavity with two Duffing mechanical oscillators,” J. Opt. Soc. Am. B 36, 775-785 (2019).
- [107] H. Molinares, V. Eremeev, and M. Orszag, ”High-fidelity synchronization and transfer of quantum states in optomechanical hybrid systems,” Phys. Rev. A 105, 033708 (2022).
- [108] A. K. Sarma, S. Chakraborty, and S. Kalita, ”Continuous variable quantum entanglement in optomechanical systems: A short review,” AVS Quantum Sci. 3, 015901 (2021).
- [109] S. Pirandola, S. Mancini, D. Vitali, et al., ”Continuous-variable entanglement and quantum-state teleportation between optical and macroscopic vibrational modes through radiation pressure,” Phys. Rev. A 68, 062317 (2003).
- [110] S. G. Hofer, W. Wieczorek, M. Aspelmeyer, et al., ”Quantum entanglement and teleportation in pulsed cavity optomechanics,” Phys. Rev. A 84, 052327 (2011).
- [111] S. Barzanjeh, M. Abdi, G. J. Milburn, et al., ”Reversible optical-to-microwave quantum interface,” Phys. Rev. Lett. 109, 130503 (2012).
- [112] S. Pautrel, Z. Denis, J. Bon, et al., ”Optomechanical discrete-variable quantum teleportation scheme,” Phys. Rev. A 101, 063820 (2020).
- [113] J. Li, A. Wallucks, R. Benevides, et al., ”Proposal for optomechanical quantum teleportation,” Phys. Rev. A 102, 032402 (2020).
- [114] N. Fiaschi, B. Hensen, A. Wallucks, et al., ”Optomechanical quantum teleportation,” Nat. Photonics 15, 817-821 (2021).
- [115] C. K. Law, ”Interaction between a moving mirror and radiation pressure: A Hamiltonian formulation,” Phys. Rev. A 51, 2537 (1995).
- [116] J. Lim, M. Tame, K. H. Yee, et al., ”Phonon-induced dynamic resonance energy transfer,” New J. Phys. 16, 053018 (2014).
- [117] C. C. Gerry and P. L. Knight, Introductory quantum optics (Cambridge University Press, 2005).
- [118] C. W. Lee, J. Lee, H. Nha, et al., ”Generating a Schrödinger-cat-like state via a coherent superposition of photonic operations,” Phys. Rev. A 85, 063815 (2012).
- [119] B. Vlastakis, G. Kirchmair, Z. Leghtas, et al., ”Deterministically encoding quantum information using 100-photon Schrödinger cat states,” Science 342, 607-610 (2013).
- [120] J. Q. Liao and L. Tian, ”Macroscopic quantum superposition in cavity optomechanics,” Phys. Rev. Lett. 116, 163602 (2016).
- [121] U. B. Hoff, J. Kollath-Bönig, J. S. Neergaard-Nielsen, et al., ”Measurement-Induced Macroscopic Superposition States in Cavity Optomechanics,” Phys. Rev. Lett. 117, 143601 (2016).
- [122] C. Gardiner and P. Zoller, Quantum Noise (Springer Berlin, Heidelberg, 2004).
- [123] A. Yariv, Y. Xu, R. K. Lee, et al., ”Coupled-resonator optical waveguide: A proposal and analysis,” Opt. Lett. 24, 711-713 (1999).
- [124] M. Ludwig, B. Kubala, and F. Marquardt, ”The optomechanical instability in the quantum regime,” New J. Phys. 10, 095013 (2008).
- [125] K. W. Murch, K. L. Moore, S. Gupta, et al., ”Observation of quantum-measurement backaction with an ultracold atomic gas,” Nat. Phys. 4, 561-564 (2008).
- [126] R. Burgwal and E. Verhagen, ”Enhanced nonlinear optomechanics in a coupled-mode photonic crystal device,” Nat. Commun. 14, 1526 (2023).
- [127] B. J. Smith, D. Kundys, N. Thomas-Peter, et al., ”Phase-controlled integrated photonic quantum circuits,” Opt. Express 17, 13516-13525 (2009).
- [128] R. Kokkoniemi, T. Ollikainen, R. E. Lake, et al., ”Flux-tunable phase shifter for microwaves,” Sci. Rep. 7, 14713 (2017).
- [129] M. S. Sarandy and D. A. Lidar, ”Adiabatic approximation in open quantum systems,” Phys. Rev. A 71, 012331 (2005).
- [130] K. B. Møller, T. G. Jørgensen, and J. P. Dahl, ”Displaced squeezed number states: Position space representation, inner product, and some applications,” Phys. Rev. A 54, 5378 (1996).
- [131] M. A. Lemonde, N. Didier, and A. Clerk, ”Enhanced nonlinear interactions in quantum optomechanics via mechanical amplification,” Nat. Commun. 7, 11338 (2016).
- [132] J. Manninen, M. T. Haque, D. Vitali, et al., ”Enhancement of the optomechanical coupling and Kerr nonlinearity using the Josephson capacitance of a Cooper-pair box,” Phys. Rev. B 105, 144508 (2022).
- [133] F. Fröwis, P. Sekatski, W. Dür, et al., ”Macroscopic quantum states: Measures, fragility, and implementations,” Rev. Mod. Phys. 90, 025004 (2018).
- [134] S. L. Braunstein and P. van Loock, ”Quantum information with continuous variables,” Rev. Mod. Phys. 77, 513 (2005).
- [135] K. Fukui and S. Takeda, ”Building a large-scale quantum computer with continuous-variable optical technologies,” J. Phys. B: At. Mol. Opt. Phys. 55, 012001 (2022).