Quantum spherical codes
Abstract
We introduce a framework for constructing quantum codes defined on spheres by recasting such codes as quantum analogues of the classical spherical codes. We apply this framework to bosonic coding, obtaining multimode extensions of the cat codes that can outperform previous constructions while requiring a similar type of overhead. Our polytope-based cat codes consist of sets of points with large separation that at the same time form averaging sets known as spherical designs. We also recast concatenations of CSS codes with cat codes as quantum spherical codes, revealing a new way to autonomously protect against dephasing noise.
Bosonic (a.k.a. oscillator) codes offer alternative qubit blueprints that are compatible with continuous-variable (CV) quantum platforms [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
and that can reduce overhead by offering an extra layer of protection
[11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25].
Qubits defined on a few bosonic modes or more exotic spaces [26] are likely to prove useful as control of quantum systems improves, but the field remains relatively unexplored [27, 28]
in part because structures and intuition from qubit-based coding theory need not apply.
We develop a framework that yields generalizations of a class of bosonic codes called the cat codes
[29, 30] and unifies such codes with several others.
Our key observation is that all such codes are particular instances of quantum versions of spherical codes
[31, 32], a family well known in classical coding theory.
We overview the framework and demonstrate its utility with several new multimode cat codes.
A rigorous study of general features
is left to a companion follow-up work.
General codes on the sphere
Codewords of qubit codes are quantum superpositions of bit-strings.
By analogy, we start with a spherical code, which is a set, or constellation, of points on the unit sphere.
To construct a quantum spherical code, or QSC, we take a collection of logical constellations, each of which gives rise to a codeword of the QSC obtained by taking a quantum superposition of all points .
We consider uniform superpositions here, leaving more general codes to future work.
Taken together, the logical constellations yield the code constellation, .
In the electromagnetic setting, spherical codes protect classical information against signal fluctuations during transmission, which correspond to small shifts acting on points in the constellation. A code’s ability to protect against such errors can be quantified by the minimum (squared) Euclidean distance between any pair of distinct points. QSCs naturally inherit as a figure of merit for protecting against such “bit-flip” noise.
Since QSCs store quantum information, they also suffer from “phase” noise, which comes from, e.g., fiber attenuation. Such noise can be expressed in terms of “potential-energy” functions on the sphere whose evaluation can be used to distinguish logical constellations (cf. [26, Sec. VI.B; 33]). If the average of a function over points in a constellation depends on , then the function’s underlying physical process causes an undetectable “phase” error.
An spherical code contains points on the -dimensional unit sphere such that the squared Euclidean distance between any two points is at least . An QSC is a -dimensional subspace of a quantum system’s vector space whose states are labeled by points on an -dimensional (real or complex) unit sphere, and whose protection against rotations is quantified by . Protection against “phase” noise is designated by the proxy “” because the notion of a “phase-flip” distance depends on the physical system embedding the QSC.
In principle, the above framework applies to any quantum state space parameterized by points on a sphere.
CV systems [34, 35] admit several such spaces, and there exist examples of QSCs expressed using ordinary [29, 30, 36], squeezed [37, 38, 39], and pair-coherent states [40].
Collective atomic systems described by spin-coherent states as well as rotational state spaces of diatomic molecules also admit QSCs, namely, various large-spin codes [41] and diatomic molecular codes
[26, Sec. VI], respectively.
We focus on coherent-state QSCs because
such codes naturally generalize the cat codes, and error-correction procedures for these new multimode cat codes require a similar type of overhead as what has already been realized [1, 2, 3, 4, 5].
We note that the discussion below can be modified to apply to other manifestations of QSCs.
Coherent-state formalism
A single-mode coherent state is a quantum representation of a standing wave of a fixed-frequency signal. An -mode coherent state is parameterized by a complex -dimensional point . The point’s norm corresponds to the state’s energy, and points of all states with a fixed energy form a complex -sphere, .
Coherent-state QSCs consist of disjoint logical constellations of points picked from the -sphere and superimposed to form logical codewords,
| (1) |
where we restrict logical constellations to lie on the unit -sphere and delegate the overall scaling of the sphere’s radius to . An example to keep in mind is the four-component cat code defined by and .
The normalization in Eq. (1) is only valid asymptotically as because coherent states are not quite orthogonal due to the uncertainty principle,
| (2) |
The above “quantum corrections” for two coherent states of a code are suppressed exponentially with the energy and the minimum distance between two points in the code’s constellation ,
| (3) |
Since sets the scale of resolution of the constellation points, we refer to it as the resolution from now on.
Coherent states are subjected to two essentially different types of distortion — angular dephasing due to fluctuations in a mode’s frequency and changes in the mode’s excitations [42, Sec. II.A]. These induce “bit” and “phase” noise on QSCs, respectively. The corresponding relevant noise operators are passive linear-optical transformations and products of modal ladder operators , whose commutator is . Products of transformations and ladder operators can be used to express any physical noise channel [43, Eq. (39)].
Transformations on modes are parameterized by the unitary group [35, Sec. 5.1.2]. A transformation corresponding to the -dimensional unitary matrix rotates a coherent state into . If the rotation satisfies , the transformation is detectable in the limit. Codes with larger resolution protect against larger sets of transformations.
A general ladder error,
| (4) |
is a monomial in the operators and their adjoints. It is parameterized by non-negative integer vectors and quantifying how many energy carriers (e.g., photons or phonons) are gained and lost in each mode, respectively.
Lowering operators are “diagonal” in the coherent-state basis, satisfying , where is the th component of . This “diagonality” relation and its adjoint imply that the expectation value of a ladder error over the th codeword (1) reduces to the average of the operator’s corresponding monomial over ,
| (5) |
where the one-norm is the degree of . A ladder error can be detected whenever the above average is independent of [44].
Polytope QSCs
We have found numerous QSCs whose constellations form vertices of real [45] or complex [46, 47] polytopes .
Polytope vertices are both sufficiently well-separated and uniform, providing protection against both types of noise.
Code and polytope tables for the two cases are in Appxs. A and B, respectively.
We characterize ladder-error protection of polytope QSCs with three “distances”: , , and . The first is the number of detectable losses (plus one), signifying that any pure-loss ladder error with is detectable. Similarly, is the number of correctable losses (plus one), signifying that any ladder error with is detectable. The degree distance signifies that the code detects ladder errors with degree . These three parameters satisfy
| (6) |
and can vary quite significantly.
Our notation for an -mode polytope QSC with logical codewords is or, more generally, . The four-component cat code is a QSC, detecting loss error while sporting the relatively high resolution of . Since it can detect one gain simultaneously with one loss, this code also corrects loss error.
Each logical constellation of the four-component cat code is a line segment, and the code constellation forms the vertices of a square. More generally, logical constellations of the -component cat code are two -gons whose vertices interleave for maximal resolution. There is a tradeoff between loss protection and resolution, with the latter of order for a large number of correctable losses. Utilizing higher dimensions, we pick other complex polytopes that maintain the same resolution while offering increased loss protection over the cat codes.
A simple code straddling the cat codes in terms of performance is the simplex code,
| (7) |
where . This code admits a lower resolution than the cat code, but detects one more loss in any of the two modes. Equivalently, it admits a higher resolution than the cat code’s resolution of unity, but corrects one fewer loss. Simplices exist in any dimension, yielding the infinite QSC family that approaches the resolution of the cat code with increasing while detecting one more loss in any mode.
The Möbius-Kantor code maintains the resolution of the cat code while adding one more logical state and detecting one more loss.
Each of its three logical constellations form the 8 vertices of a Möbius-Kantor polygon ( in Coxeter notation; see Appx. B), and such polygons combine to form the 24 vertices of a polygon.
This code corrects one more loss than the -qutrit [36], a QSC whose logical constellations each make up the 8 vertices of a complex octagon .
These two codes differ despite the fact that both code constellations map to the vertices of the same real 4D polytope via the mapping , demonstrating subtleties in using real polytopes to define complex QSCs.
Logical constellations of the powerful Hessian code consist of the 27 vertices of a Hessian polytope,
| (8) |
where , and “perms.” is shorthand for the two cyclic permutations of the vector to the left for each . This code corrects as many losses as the cat code, but has the resolution of the cat code. Moreover, it can detect up to 8 losses, a feature available only to the cat codes.
There is a code that maintains the same resolution as the cat code, but corrects one more and detects 8 more losses. Its logical constellations each form the 24 vertices of a polygon, combining into a 48-vertex polygon.
An overachieving cousin of the above code is the Witting code, consisting of two Witting polytopes with 240 vertices each.
This code corrects as many losses as a cat code, has the resolution of a cat code, and detects up to 11 losses.
It is the first member of the infinite family of codes that are based on orbits of the real Clifford group [48, 49, 50, 51].
A lower bound on for Clifford, simplex, or other QSCs can be obtained whenever their logical constellations form designs [52]. A constellation is a complex spherical design [53, 54] of strength if averages of monomials of total degree over (1) are equal to those over the entire unit -sphere,
| (9) |
Design strength is preserved under unitary rotations , so logical constellations consisting of rotated versions of a complex spherical -design yield a QSC whose degree distance is at least . In this way, construction of good QSCs can be accomplished by finding well-separated spherical designs of high strength coupled with a choice of rotations (with the identity) that permits to control the resolution of the code constellation while achieving high logical dimension .
Corroborating our parameter-based analysis, we numerically compare the performance of multi- and single-mode codes using the channel fidelity [55, 56, 57, 58, 59]. We observe that, for quKit encodings (for ), even simple multi-mode constellations, such as the simplex (7), are able to utilize the extra dimensions efficiently and outperform single-mode constellations over a range of loss rates (see Appx. D). The more non-trivial Möbius-Kantor encoding (see Table B.1) consistently outperforms various combinations of cat codes for a wide range of energies and noise parameters.
CSS-based QSCs
Concatenations of CSS codes [60, 61, 62] with the two-component cat code
[29], , can also be interpreted as QSCs, albeit with a weight-based notion of ladder-error protection. Such codes are actively studied [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25], but have so far been interpreted in the framework of the outer qubit code and not in terms of underlying modal degrees of freedom.
Our interpretation parallels a standard way to construct (classical) spherical codes
by mapping binary codes to the (real) sphere
[31, Sec. 2.5; 32, Sec. 1.2].
A qubit CSS code is constructed from two binary linear codes with distances and , guaranteeing detection of Pauli -type and -type errors with weights less than the distances, respectively. Its codewords are equal superpositions of multi-qubit states labeled by binary strings. Concatenation is equivalent to mapping each binary string into a point on the -sphere via the coordinate-wise antipodal mapping and . This yields an QSC that detects all errors with Hamming weight (see Appx. C). Asymptotically good qubit CSS codes thus yield QSCs whose distances are both separated from 0 as .
X-type gates & stabilizers
Rotations on the -sphere provide groups of -type logical gates and stabilizers for QSCs. Elements of a logical group permute logical constellations. Elements of a stabilizer subgroup permute points within each constellation, thereby leaving codewords invariant. Rotations are realized by passive linear-optical transformations using [35, Eq. (3.24)]. Rotation-based gates are noise-bias preserving [63] in that they do not convert rotations into losses.
For cat codes with components, with , the 1D rotation permutes the two constellations, while powers of leave each constellation invariant. These rotations generate and are realized by transformations and .
Simplex constellations (7) can be permuted with the rotation and are invariant under powers of , corresponding to the groups , respectively. The latter group is generated by the two-mode transformations and .
A stabilizer group for the Hessian code (8) is , the 27-element qutrit Pauli/isenberg group consisting of powers of and the qutrit Pauli matrices. Appending by the logical- rotation , where is the 3-by-3 identity, yields the logical group . These groups are realized by phase-shifters and SWAP gates. Larger can be picked using the fact that all constellations form polytopes. The largest such groups are the 648-element and 1296-element symmetry groups of the corresponding Hessian and double-Hessian polytopes, respectively. These offer other ways to implement the logical- Pauli gate, but do not yield other gates.
Qudit QSCs offer larger logical-gate groups. The two groups are for the 24-cell real polytope code, with the former generated by the 5-by-5 matrix , and the latter the binary icosahedral group . Since the stabilizer group acts trivially, the logical group acts on the 5 codewords as a 5D permutation representation of the icosahedral group .
CSS-based QSCs inherit logical- stabilizers (gates) by mapping each -type stabilizer (logical Pauli) to a transversal linear-optical transformation via the component-wise mapping . For example, the stabilizer of the code is mapped to the joint parity .
Z-type gates & stabilizers
The -type “stabilizer” for -component cat codes is , which annihilates each point in the dilated code constellation . The corresponding polynomial can be thought of as a potential on the sphere that is minimized only at the code-constellation points [64].
Polytope QSCs can require multiple polynomials to be stabilized.
Simplex codes (7) are stabilized by and .
Hessian codewords (8) are stabilized by the , , and .
The degree of is lower than the code’s degree distance () and detectable-loss distance (), unlike for the cat codes.
This property makes this code similar to degenerate stabilizer codes , i.e., codes whose check-operator weight is smaller than their distance.
Stabilizer polynomials commute with logical transformations for any in the logical group and can be obtained by averaging ladder operators (4) over the symmetry group of the code constellation’s polytope.
Other polynomials act as logical gates on QSCs, evaluating to the same value for all points in in a way that depends on . For the cat codes, evaluates to on the two codewords, respectively, yielding a logical- gate. The monomial projects to a logical- gate within the simplex codespace. The smallest loss-only -gate of the Hessian code is or its two cyclic permutations, and only a permutation-symmetric combination of all three operators commutes with the stabilizer group. A lower-degree monomial realizes another -gate with the help of gain operators. Combinations generate logical -rotations within the -annihilated subspace [64], and have been realized for cat codes [4].
CSS-based QSCs inherit gates/stabilizers by mapping each -type gate/stabilizer to a monomial via the component-wise mapping . For example, the code’s gate is mapped to . These codes also require stabilizers on each mode in order to stabilize the inner cat-code constellation.
Correcting errors
Protection against rotation-based noise for -component cat codes is done passively using a Lindbladian whose jump operator is the -type stabilizer [64] and/or a Hamiltonian [65, 66]. Both techniques have been realized for [3, 5]. General QSCs admit the same type of passive protection but require several ’s.
Microwave cavities coupled to superconducting circuits [67] provide a fertile ground for realizing such passive protection, and we outline how an existing superconducting circuit element called an “ATS” [68] can be tuned to realize the more complicated jump operators of several QSCs (see Appx. E). In particular, we show that a recent surface-cat concatenated-code proposal [17] can be readily modified with a -type surface-code stabilization scheme, thereby utilizing the full power of the code against -type noise in exclusively passive fashion.
Ladder errors (4) map the th codeword (1) into error states in . The stabilizer group splits up into several irreducible representations (irreps) acting on this span. Ladder-error protection is done by measuring syndromes associated with irreps and mapping back into the codespace. In order for correction to be possible, the stabilizer group has to be able to resolve all error spaces associated with a given error set.
The -component cat-code stabilizer is the parity . Its eigenvalues correspond to the two irreps of , distinguishing between no error and a single loss . This technique [1] led to the first demonstration of break-even QEC using cat codes [2]. Similar multimode parities detect -errors for CSS-based QSCs.
For the simplex code (7), eigenvalues of the two-mode stabilizer label the five irreps of . They allow for correction of , falling short of correcting all two-mode losses due to not being simultaneously correctable with .
Conclusion
We introduce a framework for constructing quantum analogs of the classical spherical codes, encapsulating several physically relevant quantum coding schemes for bosonic, spin, and molecular systems. We apply our framework to obtain multi-mode coherent-state codes based on polytopes, CSS codes, and classical codes. These QSCs outperform previous cat-code constructions [29, 30, 36] both in terms of code parameters and a numerical performance comparison. We show how passive protection of several instances of these QSCs can be realized in microwave cavities.
There are many other ways of constructing spherical codes, e.g.,
as group-orbit codes
[69, 70, 71], as spherical embeddings of association schemes [32],
through computer searches [72, 73], and many others [74, 31, 32, 75], as well as ways of constructing spherical designs
[76, 77, 78].
As such, we anticipate that this work will pave the way for many novel, well-protected, and experimentally feasible logical qubits.
Data availability statement
Mathematica notebooks generated during the current study are available from the corresponding author on reasonable request. Further details and references about spherical codes described in this manuscript are available at the Error-correction Zoo website at http://errorcorrectionzoo.org and the corresponding repositories at http://github.com/errorcorrectionzoo.
Acknowledgements.
We thank Francesco Arzani, Ansgar Burchards, Jonathan Conrad, Aurélie Denys, Philippe Faist, Michael Gullans, Wenhao He, Liang Jiang, Greg Kuperberg, Gideon Lee, Anthony Leverrier, Pavel Panteleev, Shraddha Singh, and Guo (Jerry) Zheng for helpful discussions. VVA is especially grateful to Kyungjoo Noh for discussion about realizations of these codes. This work is supported in part by NSF QLCI grant OMA-2120757 and NSF grants CCF-2110113 (NSF-BSF) and CCF-2104489. JTI thanks the Joint Quantum Institute at the University of Maryland for support through a JQI fellowship. Our figures were drawn using Mathematica 13 following the prescription of Ref. [79]. Contributions to this work by NIST, an agency of the US government, are not subject to US copyright. Any mention of commercial products does not indicate endorsement by NIST. VVA thanks Ryhor Kandratsenia and Olga Albert for providing daycare support throughout this work.Appendix A Real-polytope QSCs
| logical constellation | code constellation | related code | ||||
| line segment | -gon | two-component cat quit | ||||
| icosahedron | ||||||
| dodecahedron | ||||||
| 24-cell | group-GKP | |||||
| 288-cell | group-GKP | |||||
| hyper-icosahedron | group-GKP | |||||
| hyper-dodecahedron | ||||||
| -orthoplex | : group-GKP | |||||
| -cube | ||||||
| -gon | -gon | -component cat quit | ||||
| tetrahedron | dodecahedron | |||||
| octahedron | 5-octahedron | |||||
| icosahedron | 2-icosahedron | |||||
| hyper-tetrahedron | hyper-dodecahedron | |||||
| hyper-octahedron | 24-cell | group-GKP, -qutrit | ||||
| 288-cell | group-GKP | |||||
| hyper-icosahedron | group-GKP | |||||
| hyper-dodecahedron | ||||||
| hyper-cube, -octahedron | 24-cell | |||||
| 24-cell | 288-cell | group-GKP | ||||
| hyper-icosahedron | group-GKP | |||||
| hyper-dodecahedron | ||||||
| hyper-icosahedron | hyper-dodecahedron | |||||
| -simplex | -bisimplex | |||||
| -simplex | -cube | shortened Hadamard | ||||
| -demicube | -cube | single parity-check | ||||
| -orthoplex | -cube | augmented Hadamard |
Logical constellations of a real polytope QSC form the vertices of a real polytope. The figure that results from the union of all logical polytopes is called a polytope compound, and its vertices form the code constellation . Polytope QSCs can thus be constructed from established polytope compounds.
Regular real polytope compounds have been classified in three [80] and four [45, 81] dimensions. We collect all QSCs whose logical and code constellations each form a single regular real polytope in Table A.1. We leave to future work QSCs made up of polytope compounds whose code constellation forms vertices of multiple regular polytopes [80][45, Table VII][81, Sec. 10] as well as recently discovered variations of compounds with the same parameters [81, Sec. 10]. We include a few QSCs constructed from notable non-regular polytopes. All polytopes used in our constructions are listed in Table A.2.
The first column of the table lists the polytope whose vertices make up the logical constellations . All make up the same polytope for every code, with the exception being the “hyper-cube, -octahedron” code, in which () makes up the vertices of a hyper-cube (hyper-octahedron).
Since the -sphere is complex while the polytopes are real, we have to embed the polytopes into the sphere. For even dimension , the standard method of doing this is via the mapping
| (A1) |
Other mappings can be obtained by permuting the real coordinates. For odd , one has to embed the polytope into dimensions and then apply a mapping like the one above. Convenient coordinates exist for polytopes embedded in higher dimensions, e.g., vertices of a -simplex have coordinates and permutations thereof [32, Sec. 1.5]. Mappings into higher-dimensional spaces can also be used, e.g., the -component cat-code constellation can be mapped into for any -dimensional unit vector . If one prefers to use real-valued vertices, then can be directly embedded into .
The parameters can depend on which of the above mappings one uses; we calculate them numerically by evaluating Eq. (5) for a given . A mapping-independent lower bound on the degree distance can be obtained from the strength of the design formed by the logical polytopes. Real polytope vertices can form (real) spherical designs [52], which are convertible into complex spherical designs via [53, Lemma 3.3]. The design strengths of -dimensional polytope vertices are listed in Table A.2, column 5, yielding for a code consisting of such polytopes. This bound appears to be tight for real polytopes and holds as long as the polytope formed by is the same dimension as those formed by each . Otherwise, the logical polytopes will not share a common sphere on which their vertices form designs. An exception to this restriction is for that are 1D line segments and is due to the fact that any pair of segments shares a common circle. The degree distance of a QSC consisting of segments is thus at least two.
| polytope | dim | Schlafli/Coxeter | vertices | design | (numerical) | reference | |
| line segment | |||||||
| triangle | |||||||
| square | |||||||
| pentagon | |||||||
| -gon | |||||||
| tetrahedron | |||||||
| octahedron | |||||||
| cube | |||||||
| icosahedron | |||||||
| dodecahedron | |||||||
| 2-icosahedron | [80] | ||||||
| 5-octahedron | [80] | ||||||
| hyper-tetrahedron | [82] | ||||||
| hyper-octahedron | [82] | ||||||
| hyper-cube | [82] | ||||||
| 24-cell |
|
||||||
| 288-cell | o3m4m3o |
|
|||||
| hyper-icosahedron |
|
||||||
| hyper-dodecahedron |
|
||||||
| -simplex | |||||||
| -bisimplex | [83] | ||||||
| -orthoplex | |||||||
| -demicube | [83] | ||||||
| -cube |
Points on the real 4D sphere are in one-to-one correspondence with quaternions, which in turn parameterize the group [84].
Vertices of the hyper-octahedron, 24-cell, (disphenoidal) 288-cell, and hyper-icosahedron correspond to quaternions forming the quaternion , binary tetrahedral , binary octahedral , and binary icosahedral subgroups, respectively.
Polytope QSCs consisting of such polytopes thus are related to group-GKP codes [26].
The -qutrit code [36] is similarly related to the group-GKP code, but the idea of using groups this way is limited to two modes because spheres in higher dimensions no longer correspond to groups.
An binary linear code can be converted into a QSC by taking logical constellations to be cosets of in under the antipodal mapping.
The table lists QSCs arising this way from the Hadamard
and single parity-check
codes.
These codes all have non-trivial because the cosets correspond to known polytope compounds when embedded into the sphere [47, pg. 287].
Appendix B Complex-polytope QSCs
| logical const-n | code const-n | related code | ||||
| Möbius-Kantor | ||||||
| group-GKP | ||||||
| -orthoplex | group-GKP, -qutrit | |||||
| group-GKP | ||||||
| -orthoplex | rectified Hessian | |||||
| -orthoplex | rectified Hessian | |||||
| Hessian | double Hessian | |||||
| Witting | double Witting | Clifford group-orbit | ||||
| -cube | -cube | |||||
| -orthoplex | -orthoplex |
Complex polytopes are polytopes whose vertices are complex. As with real polytopes, there are a myriad polygons in the two complex dimensions, a handful of special polytopes in a few of the higher dimensions, and only two infinite families of non-real complex polytopes present in any dimension.
The two families are straightforward complex generalizations of the cube and orthoplex, respectively. A simple set of vertices of a real -dimensional cube consists of vectors with coordinates . The vertices of the complex -cube (a.k.a. ) consist of complex vectors of dimension with th roots of unity at each coordinate. A similar generalization holds for the -orthoplex (a.k.a. ), whose coordinates are -dimensional vectors whose single nonzero entry is an th root of unity.
A union of complex polytopes sharing a common center forms a complex polytope compound. Complex compounds yield complex QSCs whose code constellations are formed by the vertices of the compound and whose logical constellations are formed by the vertices of the participating polytopes. Complex compounds have not been as thoroughly studied as their real counterparts, and most of our codes come from the handful of constructions from Refs. [85, 86, 47]. In Table B.1, we collect the complex polytope QSCs that are the most interesting for a comparative study with the real polytope codes. All the polytopes used in our constructions are listed in Table B.2.
Complex polygons yield several interesting QSCs not available in the real case. We mentioned already in the main text that multiple complex polytopes can reduce to the same real polytope when mapped into the reals. As another example, compounds consisting of polygonal code constellations have exceptional loss detection capabilities, with as high as 30, but suffer from low resolution. There are many more polygons, and we leave a more extensive list of complex polytope QSCs to a follow-up work.
Complex polytopes also offer interesting many-mode alternatives to cat codes. The tensor product of single-mode -component cat codes is an QSC whose code constellation can be thought of as an -cube, constructed as a Kronecker product of -cubes. The resolution of this code decreases as order , meaning that a constant energy per mode (usually picked to be [17, 2]) is required in order to be able to resolve codewords without substantial intrinsic memory error. On the other hand, the -orthoplex QSC, whose logical constellations are -orthoplexes, maintains constant resolution and has extra loss detection at the expense of a linear increase in the codespace dimension and no loss correction. It is an interesting open problem to find a QSC with that can correct one or more losses.
| polytope | dim | Schlafli/Coxeter | vertices | design | (numerical) | reference | |
| Möbius-Kantor | [46, 85] | ||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| [46, 85] | |||||||
| Hessian |
|
||||||
| double Hessian | [86] | ||||||
| rectified Hessian |
|
||||||
| Witting |
|
||||||
| double Witting | [2 3{3}3{3}3{3}3] | ||||||
| -cube | [46] | ||||||
| -orthoplex | [46] |
Appendix C CSS-based QSCs
The antipodal mapping converts binary strings labeling -qubit states into -mode coherent states normalized to an energy of unity,
| (C1) |
Using [87, Thm. 7.3], there exists a basis of codewords for an CSS code that is labeled by length- binary strings and that is expressed in terms of , the dual of one of the underlying binary linear codes. Applying the antipodal mapping to the th element of such a basis yields a codeword for the corresponding QSC,
| (C2) |
Phase-flip errors
Using Eq. (5), the projection of a general ladder error acting a subset of modes into the QSC codespace is equivalent to a -type error,
| (C3) |
where we define . As long as the support size of the region is less than , the distance of , the properties of CSS codes can be used to show that the above error is detectable. This means that any ladder error with Hamming weight is detectable.
Bit-flip errors
The squared Euclidean distance between two code constellation elements and can be expressed in terms of the Hamming distance between their corresponding binary strings,
| (C4a) | ||||
| (C4b) | ||||
| (C4c) | ||||
| (C4d) | ||||
This quantity is bounded by , where is the distance of the other underlying binary linear code .
Appendix D Performance of quKit QSCs
| cat | simplex | ||||||
|---|---|---|---|---|---|---|---|
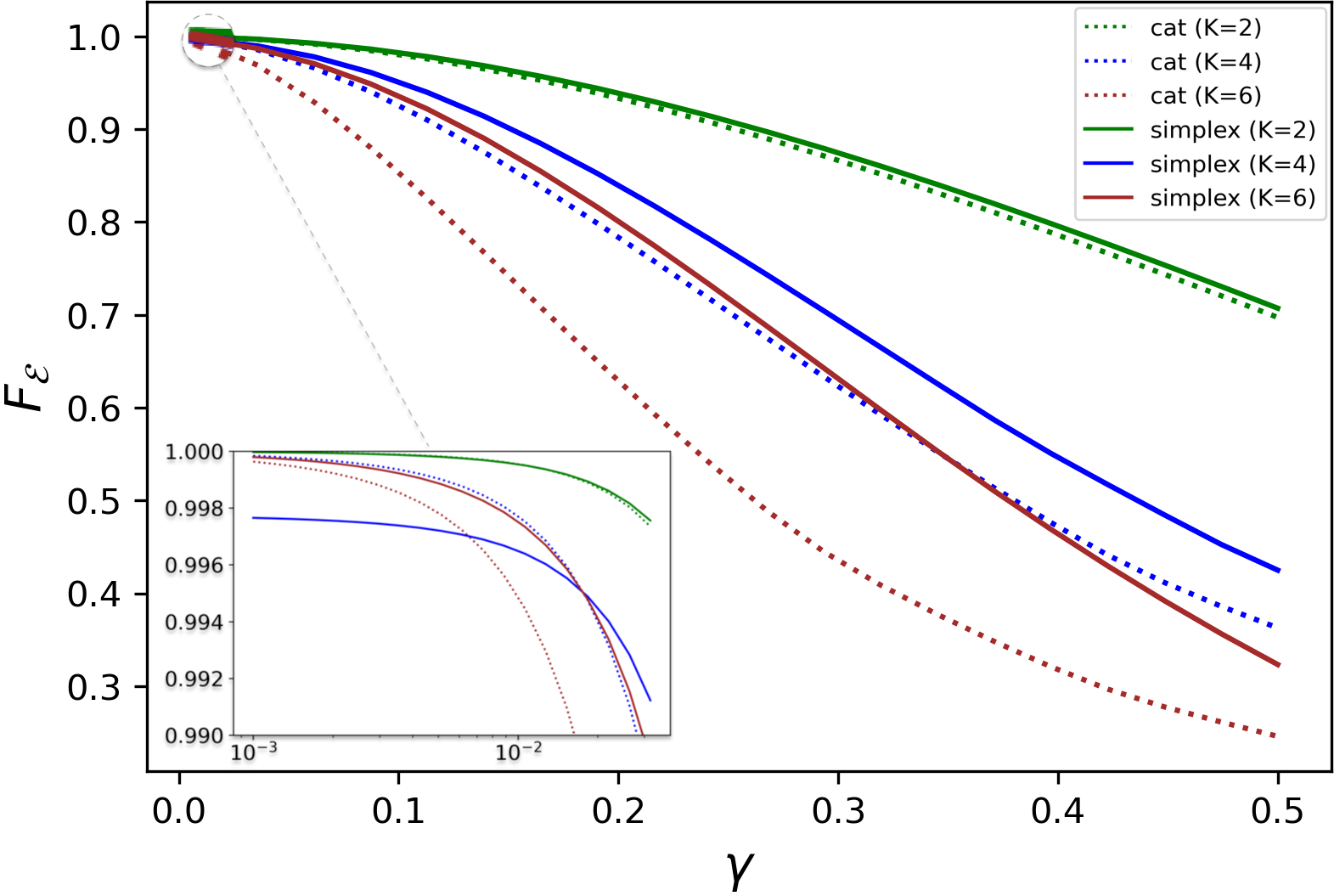
Here, we present results of a numerical comparison of several new intrinsically multi-mode polytope constellations to single-mode and multi-mode instantiations of cat-code (i.e., polygon-based) constellations. We observe that multi-mode QSCs efficiently utilize the extra dimensions to store more logical information, all while consuming a comparable (in most cases, lower) energy per mode.
Our performance metric, as guided by [55, 56, 57, 58], is the channel fidelity
| (D1) |
where, for a qubit state, is the maximally entangled state between the source qubit and the ancilla qubit . The outgoing density matrix, , is obtained by the action of the combined encoding-noise-recovery channel on the source qubit and identity on the ancilla. The channel fidelity is an intrinsic property of the channel which measures how well the entanglement between the information qubit and an ancillary system in preserved upon application of the channel . For more motivation behind our choice of metric, we refer the interested reader to [59, Appx. A].
The channel is considered to be the composition of the encoding, noise and recovery channels. We assume that noise occurs only via the pure-loss channel, described by Kraus operators [88]
| (D2) |
where quantifies the amount of photons lost, and where is the loss rate. For a selected encoding and this error channel, we optimize the recovery to obtain the maximum . This optimization problem can be formulated as a semidefinite program [57], which we solve using the Python library CVXPY [89, 90].
The above technique can be adapted to bosonic codes by setting a maximum Fock-space cutoff (in order to make the underlying space finite-dimensional) [59]. We avoid such truncation by working in the coherent-state basis. In such a basis, the action of the pure loss channel can be expressed using a different set of Kraus operators whose cardinality and matrix dimension are equal to the size of the code constellation [36, Appx. A]. That way, we are constrained more by the size of the code constellation than the number of modes.
A -dimensional code is constructed by replicating a “base” logical constellation times while maintaining good resolution . Cat codes use -gons as the base constellations, while simplex codes employ from Eq. (7).
The th logical constellation of a -gon quit code with is generated by multiplying the base line segment with . The th logical constellation for the quit simplex codes with is obtained by letting , where is the two-dimensional identity and is the Pauli- matrix. The () simplex constellations are generated using the unitary rotations ().
Sweet-spot comparison
Given a loss rate , one can tune the energy of a given code to obtain the sweet spot energy value — the that gives the highest fidelity . For cat codes, it has been observed [91, 92, 59] that this sweet spot value is finite, and that it does not drastically change with small changes in the loss rate . We observe similar behavior in all the QSCs we examine.
We evaluate the performance of each code at its respective sweet spot in order to compare the highest possible performance of each code under a given loss rate. Figure 1(a) lists the code parameters of the simplex and -gon based cat quKit codes. The advantage of using simplex codes over the cat becomes pronounced for larger memories. As we scan the table in the figure, we see that the fidelity of simplex codes decreases slower with growing dimension compared to that of cat codes, meaning that simplex codes utilize the available phase space more effectively when packing more quantum information. This is corroborated by the simplex quits maintaining higher resolution for large .
The energy required per mode () for optimal simplex performance also increases at a slower rate than that of cat codes. Notably, for , even the total energy () needed by simplex codes is lower than that of the corresponding cat code. This trend is consistent in code performance, quantified by the channel fidelity, as shown in Fig. 1(b).
| logical const-n | code const-n | |||||
|---|---|---|---|---|---|---|
| -gon | -gon | |||||
| -gon | -gon | |||||
| Möbius-Kantor |
Overall advantage of a qudit encoding
We also compare overall performance of a multi-mode QSC to various cat-like codes by sweeping both energy and loss rate. We fix and construct codes out of various logical constellations: the -gon, -gon (), () and the Möbius-Kantor polygon. The first two are single-mode cat codes, the third distributes logical information over two modes using tensor products of single-mode cat codes, while the last is an intrinsically two-mode code.
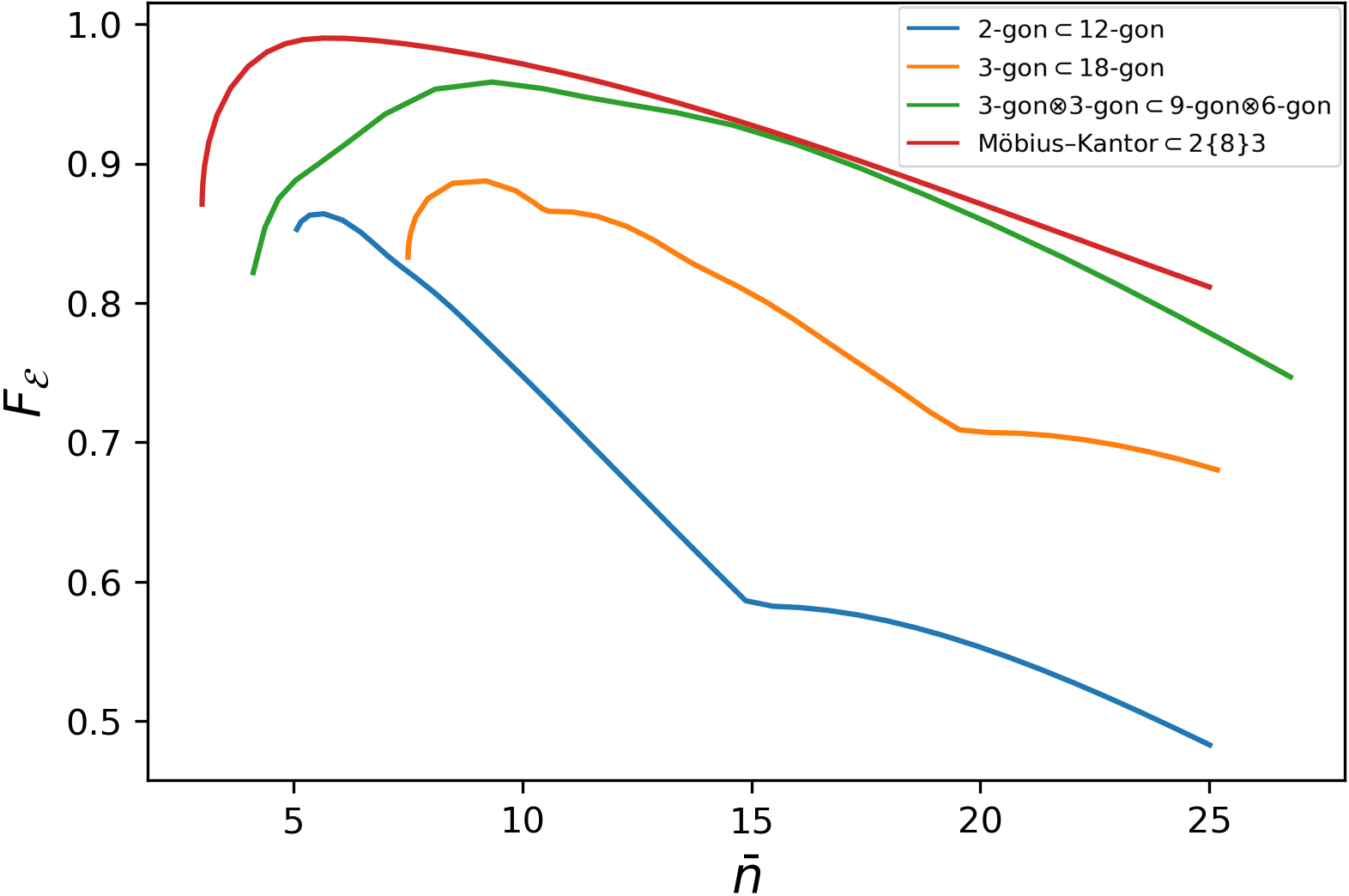
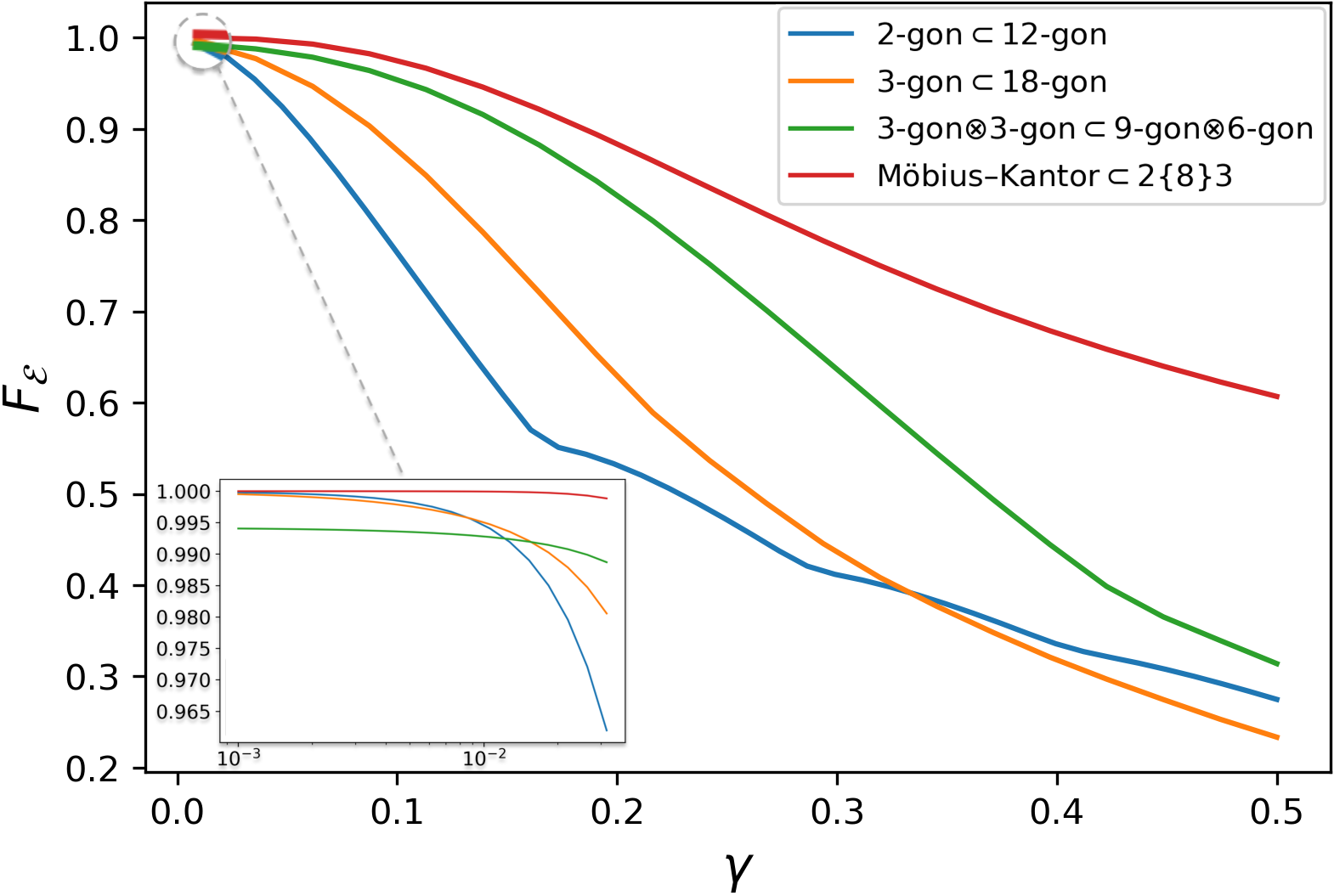
Results from a numerical comparison in Fig. 2(a) show a universal advantage across the swept energy-and-loss-rate parameter space. Similar trends are observed for various other values (not shown here). Notably, the Möbius-Kantor surpasses other codes even at their optimal values, as exemplified in Fig. 2(b), where we choose the corresponding to the -gon -gon code’s sweet spot.
We append sweet-spot data for this set of codes in Tab. D.1, which corroborates the simplex-cat-code data in Fig. 1(a). We observe that the Möbius-Kantor code provides robust protection against up to 2 losses, boasts higher resolution (), requires lower energy per mode, and consistently outperforms all the mentioned polygon based codes in the sweet-spot comparison.
When encoding a greater number of logical dimensions, multimodal QSCs prove significantly more resource efficient and clearly outperform cat codes.
Appendix E Lindbladian stabilization
The -type (i.e., dephasing or rotation error) correction for cat codes is done autonomously by engineering Lindbladians with a desired “correcting” jump operator and correction rate . Engineering such terms is possible in microwave cavities coupled to superconducting circuits [67]. The typical scheme proceeds by coupling the physical system to an ancillary or buffer mode via the Hamiltonian coupling , setting the ancillary mode to have a high loss rate, and then showing that the effective Lindbladian acting on the physical -mode system has jump operator (see, e.g., Ref. [64]).
Multi-mode coherent-state QSCs require more jump operators, and each jump operator can now consist of multiple monomials in the lowering operators . However, due to the flexibility provided by a recently developed circuit element called an asymmetrically threaded SQUID, or ATS [68], the above scheme can be extended to realize the more complex jumps required for QSCs. We sketch out a general scheme below and apply it to a CSS and a polytope QSC.
The cost of our basic scheme — one ancillary mode per jump — is only an upper bound. While more advanced schemes are outside the scope of this work, we note that a single ATS can be used to simulataneously realize multiple jumps using as little as one ancillary mode [17, Appx. B.2].
E.0.1 General scheme
A desired jump operator is a sum of monomials of some maximum degree and a potential constant term that is the th power of ,
| (E1) |
Leveraging previous schemes [68, supplement][17, Appx. B.2], we describe a slightly more general scheme to implement a dissipator with this jump operator, which generates time evolution according to the equation of motion (E4).
Let the harmonic component of the th physical mode have frequency , while the ancilla -mode evolves at . In the rotating frame w.r.t. these components, the multi-mode density matrix describing a set of modes coupled via an ATS evolves according to
| (E2) |
We describe each term and its purpose:
-
1.
The drive term, , will yield the constant part of the jump operator (E1) once the effective equation of motion on the physical modes is derived. This term can be set to zero if no constant term is necessary.
-
2.
All of the magic comes from the ATS term [17, Eq. (B11)]111Up to constant prefactors, this term is also obtained from the last two terms in [68, Eq. (S2)] by setting , , and , and expanding to first order in . The quadratic term in that equation can absorbed into the bare oscillator Hamiltonian prior going into the rotating frame by expanding in a set of normal modes.,
(E3) which depends on static real parameters and tunable real parameters . The static flux [68, Eq. (S3)] allows us to interpolate between a sine and cosine ATS term. One pump tone, with amplitude and frequency , is necessary for each monomial in the jump operator (E1). Tuning the frequency allows us to select the specific desired monomial, while tuning the drive allows us to tune the monomial’s coefficient.
-
3.
The dissipative part, for sufficiently large , ensures that the ancilla is sufficiently lossy. The steady-state space of this evolution is spanned by any state of the modes, tensored with the vacuum Fock state on the mode. Assuming the Hamiltonian terms to be perturbations to this strong Lindbladian evolution, one can then derive an effective equation of motion within this steady-state space using either second-order perturbation theory or what is colloquially known as “adiabatic elimination” [94, 95, 96].
Expanding the ATS term yields an infinite series, with combinatorially many monomials consisting of products of drive-tone terms , physical mode operators , the ancillary mode term , and the flux bias . The expansion is approximated by truncating to an order such that the highest-degree term is one higher than the degree of the highest-order monomial in the desired jump operator (E1). The phase term ensures that the expansion contains the monomial of correct (even or odd) degree.
The pump-tone frequencies are then tuned to particular linear combinations of so that any of the monomials that are also present in the desired jump operator become time-independent. That way, all other terms can be treated as higher-order “fast-rotating” corrections in what is known as the “rotating-wave approximation”. Combining with the drive term, the Hamiltonian terms in Eq. (E3) are then approximated by . Verifying that the many remaining terms in the expansion are all time-dependent can be done using the algebraic manipulation plugin sneg [97, 98] in Mathematica.
The desired equation of the density matrix on the physical modes upon adiabatically eliminating the ancilla is then
| (E4) |
for a to-be-determined correction rate , and up to higher-order corrections “” stemming from corrections to the approximations.
E.0.2 CSS QSCs
Our -type stabilization for CSS-type concatenated encodings provides an autonomous alternative to the discrete measurement of -type error syndromes. Such jump operators can be readily “plugged in” to any concatenated cat-CSS code, including a recent concatenated surface-cat code proposal [17].
Our jump operator for the surface-cat code example consists of a product of lowering operators acting on sides one through four of each plaquette, , of a square lattice. This is a special case of the general form (E1) with one degree-four monomial and constant term with . The sole monomial requires only one pump tone, with amplitude and frequency , and zero flux bias, . The ATS sine term is expanded to fifth order. The condition selecting the desired monomial is
| (E5) |
This monomial is multiplied by a product of accompanying constants, , to yield an effective correction rate , after adiabatic elimination.
The above scheme is done for each plaquette of the surface-code architecture. The additional dissipators — required for restricting each mode to antipodal coherent states — are realized in said architecture using a single ATS [17, Appx. B.2]. Together, these provide autonomous protection against all -type errors, utilizing the full error-correcting power of the (outer) surface code for such noise. Extension to other QLDPC codes is straightforward, barring any issues with long-range physical connectivity.
E.0.3 Hessian QSC
The Hessian code requires three jump operators, two of which consist of three monomials. Each jump operator can be realized using the general scheme above, providing a non-trivial QSC example that should be realizable with state-of-the-art ATS technology.
-
1.
The jump has no constant term, so no drive term is necessary. Only one pump tone, with amplitude and frequency , is required, and to obtain a cosine ATS. The ATS term is expanded to second order. The conditions selecting the desired monomial are
(E6) This monomial corresponds to an effective correction rate after adiabatic elimination.
-
2.
The jump also has no constant term. The three terms require three drive tones, with parameters for . The phase so that the ATS term becomes a cosine. The ATS cosine term is expanded to second order. The conditions selecting the desired monomials are
(E7) Each of these monomials is multiplied by a product of respective accompanying constants, , where we have used the drive-tone amplitudes to cancel the non-tunable coupling strengths . This yields an effective correction rate , after adiabatic elimination.
-
3.
The jump has three monomials and a constant term with power and coefficient . The three monomials require three drive tones, with parameters for . The phase so that the ATS term remains a sine. This term is then expanded to fourth order. The conditions selecting the desired monomials are
(E8) Each of these monomials is multiplied by . The fluxes are required to be equal for all three in order to realize the jump. This yields an effective correction rate , after adiabatic elimination.
References
- Sun et al. [2014] L. Sun, A. Petrenko, Z. Leghtas, B. Vlastakis, G. Kirchmair, K. M. Sliwa, A. Narla, M. Hatridge, S. Shankar, J. Blumoff, L. Frunzio, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, Tracking photon jumps with repeated quantum non-demolition parity measurements., Nature 511, 444 (2014).
- Ofek et al. [2016] N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, Extending the lifetime of a quantum bit with error correction in superconducting circuits, Nature 536, 441 (2016).
- Leghtas et al. [2015] Z. Leghtas, S. Touzard, I. M. Pop, A. Kou, B. Vlastakis, A. Petrenko, K. M. Sliwa, A. Narla, S. Shankar, M. J. Hatridge, M. Reagor, L. Frunzio, R. J. Schoelkopf, M. Mirrahimi, and M. H. Devoret, Confining the state of light to a quantum manifold by engineered two-photon loss, Science 347 (2015).
- Touzard et al. [2018] S. Touzard, A. Grimm, Z. Leghtas, S. Mundhada, P. Reinhold, C. Axline, M. Reagor, K. Chou, J. Blumoff, K. Sliwa, S. Shankar, L. Frunzio, R. J. Schoelkopf, M. Mirrahimi, and M. Devoret, Coherent Oscillations inside a Quantum Manifold Stabilized by Dissipation, Phys. Rev. X 8, 021005 (2018).
- Grimm et al. [2020] A. Grimm, N. E. Frattini, S. Puri, S. O. Mundhada, S. Touzard, M. Mirrahimi, S. M. Girvin, S. Shankar, and M. H. Devoret, Stabilization and operation of a Kerr-cat qubit, Nature 584, 205 (2020).
- Campagne-Ibarcq et al. [2020] P. Campagne-Ibarcq, A. Eickbusch, S. Touzard, E. Zalys-Geller, N. E. Frattini, V. V. Sivak, P. Reinhold, S. Puri, S. Shankar, R. J. Schoelkopf, L. Frunzio, M. Mirrahimi, and M. H. Devoret, Quantum error correction of a qubit encoded in grid states of an oscillator, Nature 584, 368 (2020).
- Flühmann et al. [2019] C. Flühmann, T. L. Nguyen, M. Marinelli, V. Negnevitsky, K. Mehta, and J. Home, Encoding a qubit in a trapped-ion mechanical oscillator, Nature 566, 513 (2019).
- de Neeve et al. [2022] B. de Neeve, T.-L. Nguyen, T. Behrle, and J. P. Home, Error correction of a logical grid state qubit by dissipative pumping, Nat. Phys. 18, 296 (2022).
- Sivak et al. [2022] V. V. Sivak, A. Eickbusch, B. Royer, S. Singh, I. Tsioutsios, S. Ganjam, A. Miano, B. L. Brock, A. Z. Ding, L. Frunzio, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, Real-time quantum error correction beyond break-even (2022).
- Dahan et al. [2022] R. Dahan, G. Baranes, A. Gorlach, R. Ruimy, N. Rivera, and I. Kaminer, Creation of Optical Cat and GKP States Using Shaped Free Electrons (2022).
- Cohen and Mirrahimi [2014] J. Cohen and M. Mirrahimi, Dissipation-induced continuous quantum error correction for superconducting circuits, Phys. Rev. A 90, 062344 (2014).
- Fukui et al. [2017] K. Fukui, A. Tomita, and A. Okamoto, Analog Quantum Error Correction with Encoding a Qubit into an Oscillator, Phys. Rev. Lett. 119, 180507 (2017).
- Fukui et al. [2018] K. Fukui, A. Tomita, A. Okamoto, and K. Fujii, High-Threshold Fault-Tolerant Quantum Computation with Analog Quantum Error Correction, Phys. Rev. X 8, 021054 (2018).
- Guillaud and Mirrahimi [2019] J. Guillaud and M. Mirrahimi, Repetition Cat Qubits for Fault-Tolerant Quantum Computation, Phys. Rev. X 9, 041053 (2019).
- Vuillot et al. [2019] C. Vuillot, H. Asasi, Y. Wang, L. P. Pryadko, and B. M. Terhal, Quantum error correction with the toric Gottesman-Kitaev-Preskill code, Phys. Rev. A 99, 032344 (2019).
- Noh and Chamberland [2020] K. Noh and C. Chamberland, Fault-tolerant bosonic quantum error correction with the surface–Gottesman-Kitaev-Preskill code, Phys. Rev. A 101, 012316 (2020).
- Chamberland et al. [2022] C. Chamberland, K. Noh, P. Arrangoiz-Arriola, E. T. Campbell, C. T. Hann, J. Iverson, H. Putterman, T. C. Bohdanowicz, S. T. Flammia, A. Keller, G. Refael, J. Preskill, L. Jiang, A. H. Safavi-Naeini, O. Painter, and F. G. Brandão, Building a Fault-Tolerant Quantum Computer Using Concatenated Cat Codes, PRX Quantum 3, 010329 (2022).
- Larsen et al. [2021] M. V. Larsen, C. Chamberland, K. Noh, J. S. Neergaard-Nielsen, and U. L. Andersen, Fault-Tolerant Continuous-Variable Measurement-based Quantum Computation Architecture, PRX Quantum 2, 030325 (2021).
- Guillaud and Mirrahimi [2021] J. Guillaud and M. Mirrahimi, Error Rates and Resource Overheads of Repetition Cat Qubits, Phys. Rev. A 103, 042413 (2021).
- Noh et al. [2022] K. Noh, C. Chamberland, and F. G. Brandão, Low-Overhead Fault-Tolerant Quantum Error Correction with the Surface-GKP Code, PRX Quantum 3, 010315 (2022).
- Zhang et al. [2022] J. Zhang, Y.-C. Wu, and G.-P. Guo, Concatenation of the Gottesman-Kitaev-Preskill code with the XZZX surface code (2022).
- Régent et al. [2022] F.-M. L. Régent, C. Berdou, Z. Leghtas, J. Guillaud, and M. Mirrahimi, High-performance repetition cat code using fast noisy operations (2022).
- Stafford and Menicucci [2022] M. P. Stafford and N. C. Menicucci, Biased Gottesman-Kitaev-Preskill repetition code (2022).
- Lieu et al. [2022] S. Lieu, Y.-J. Liu, and A. V. Gorshkov, Candidate for a passively-protected quantum memory in two dimensions (2022).
- Gouzien et al. [2023] E. Gouzien, D. Ruiz, F.-M. L. Regent, J. Guilland, and N. Sangouard, Computing 256-bit Elliptic Curve Logarithm in 9 Hours with 126133 Cat Qubits (2023).
- Albert et al. [2020] V. V. Albert, J. P. Covey, and J. Preskill, Robust Encoding of a Qubit in a Molecule, Physical Review X 10, 031050 (2020).
- Byron Bay Quantum Computing Workshop [2021] Byron Bay Quantum Computing Workshop, GKP retrospective & bosonic codes panel discussion with Gottesman, Devoret, Divincenzo, & Girvin (2021).
- Gottesman [2022] D. Gottesman, Opportunities and Challenges in Fault-Tolerant Quantum Computation (2022).
- Cochrane et al. [1999] P. T. Cochrane, G. J. Milburn, and W. J. Munro, Macroscopically distinct quantum-superposition states as a bosonic code for amplitude damping, Phys. Rev. A 59, 2631 (1999).
- Leghtas et al. [2013] Z. Leghtas, G. Kirchmair, B. Vlastakis, R. J. Schoelkopf, M. H. Devoret, and M. Mirrahimi, Hardware-Efficient Autonomous Quantum Memory Protection, Phys. Rev. Lett. 111, 120501 (2013).
- Conway and Sloane [1999] J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices and Groups, Grundlehren der mathematischen Wissenschaften, Vol. 290 (Springer New York, New York, NY, 1999).
- Ericson and Zinoviev [2001] T. Ericson and V. Zinoviev, Codes on Euclidean Spheres (North Holland, 2001).
- Pedernales et al. [2020] J. S. Pedernales, F. Cosco, and M. B. Plenio, Decoherence-Free Rotational Degrees of Freedom for Quantum Applications, Phys. Rev. Lett. 125, 090501 (2020).
- Cerf et al. [2007] N. J. Cerf, G. Leuchs, and E. S. Polzik, Quantum Information with Continuous Variables of Atoms and Light (Imperial College Press, 2007).
- Serafini [2017] A. Serafini, Quantum Continuous Variables: A Primer of Theoretical Methods (CRC Press, Boca Raton FL, 2017).
- Denys and Leverrier [2022] A. Denys and A. Leverrier, The 2T-qutrit, a two-mode bosonic qutrit (2022).
- Schlegel et al. [2022] D. S. Schlegel, F. Minganti, and V. Savona, Quantum error correction using squeezed Schrodinger cat states, Physical Review A 106, 022431 (2022).
- Xu et al. [2022] Q. Xu, G. Zheng, Y.-X. Wang, P. Zoller, A. A. Clerk, and L. Jiang, Autonomous quantum error correction and fault-tolerant quantum computation with squeezed cat qubits (2022).
- Hillmann and Quijandr\́mathrm{missing}ia [2022] T. Hillmann and F. Quijandr\́mathrm{i}a, Quantum error correction with dissipatively stabilized squeezed cat qubits (2022).
- Albert et al. [2019] V. V. Albert, S. O. Mundhada, A. Grimm, S. Touzard, M. H. Devoret, and L. Jiang, Pair-cat codes: autonomous error-correction with low-order nonlinearity, Quantum Sci. Technol. 4, 035007 (2019).
- Gross [2021] J. A. Gross, Encoding a qubit in a spin, Phys. Rev. Lett. 127, 010504 (2021).
- Turchette et al. [2000] Q. A. Turchette, C. J. Myatt, B. E. King, C. A. Sackett, D. Kielpinski, W. M. Itano, C. Monroe, and D. J. Wineland, Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs, Phys. Rev. A 62, 053807 (2000).
- Grimsmo et al. [2020] A. L. Grimsmo, J. Combes, and B. Q. Baragiola, Quantum Computing with Rotation-Symmetric Bosonic Codes, Phys. Rev. X 10, 011058 (2020).
- Knill and Laflamme [1997] E. Knill and R. Laflamme, Theory of quantum error-correcting codes, Phys. Rev. A 55, 900 (1997).
- Coxeter [1973] H. S. M. Coxeter, Regular polytopes, 3rd ed. (Dover Publications, New York, 1973).
- Shephard [1952] G. C. Shephard, Regular Complex Polytopes, P. Lond. Math. Soc. s3-2, 82 (1952).
- Coxeter [1991] H. S. M. Coxeter, Regular complex polytopes, 2nd ed. (Cambridge University Press, Cambridge [England]; New York, 1991).
- Sidelnikov [1997a] V. Sidelnikov, On a finite group of matrices and codes on the Euclidean sphere, Problems Inform. Transmission 33, 29 (1997a).
- Sidelnikov [1997b] V. Sidelnikov, On a finite group of matrices generating orbit codes on Euclidean sphere, in IEEE Int. Symp. Inf. Theory - Proc. (IEEE, Ulm, Germany, 1997) p. 436.
- Sidelnikov [1999] V. Sidelnikov, Spherical 7-Designs in 2n-Dimensional Euclidean Space, J. Algebraic Comb. 10, 279 (1999).
- Nebe et al. [2001] G. Nebe, E. M. Rains, and N. J. A. Sloane, The Invariants of the Clifford Groups, Designs, Codes and Cryptography 24, 99 (2001).
- Delsarte et al. [1977] P. Delsarte, J. M. Goethals, and J. J. Seidel, Spherical codes and designs, Geom. Dedicata 6, 363 (1977).
- Roy and Suda [2014] A. Roy and S. Suda, Complex Spherical Designs and Codes, J. Combin. Designs 22, 105 (2014).
- Mohammadpour and Waldron [2023] M. Mohammadpour and S. Waldron, Complex spherical designs from group orbits (2023).
- Schumacher [1996] B. Schumacher, Sending entanglement through noisy quantum channels, Phys. Rev. A 54, 2614 (1996).
- Reimpell and Werner [2005] M. Reimpell and R. F. Werner, Iterative Optimization of Quantum Error Correcting Codes, Phys. Rev. Lett. 94, 080501 (2005).
- Fletcher et al. [2007] A. S. Fletcher, P. W. Shor, and M. Z. Win, Optimum quantum error recovery using semidefinite programming, Phys. Rev. A 75, 012338 (2007).
- Fletcher et al. [2008] A. S. Fletcher, P. W. Shor, and M. Z. Win, Channel-Adapted Quantum Error Correction for the Amplitude Damping Channel, IEEE Trans. Inf. Theory 54, 5705 (2008).
- Albert et al. [2018] V. V. Albert, K. Noh, K. Duivenvoorden, D. J. Young, R. T. Brierley, P. Reinhold, C. Vuillot, L. Li, C. Shen, S. M. Girvin, B. M. Terhal, and L. Jiang, Performance and structure of single-mode bosonic codes, Phys. Rev. A 97, 032346 (2018).
- Calderbank and Shor [1995] A. R. Calderbank and P. W. Shor, Good Quantum Error-Correcting Codes Exist, Phys. Rev. A 54, 1098 (1995).
- Steane [1996a] A. M. Steane, Error Correcting Codes in Quantum Theory, Phys. Rev. Lett. 77, 793 (1996a).
- Steane [1996b] A. Steane, Multiple-particle interference and quantum error correction, Proc. R. Soc. A 452, 2551 (1996b).
- Puri et al. [2020] S. Puri, L. St-Jean, J. A. Gross, A. Grimm, N. E. Frattini, P. S. Iyer, A. Krishna, S. Touzard, L. Jiang, A. Blais, S. T. Flammia, and S. M. Girvin, Bias-preserving gates with stabilized cat qubits, Sci. Adv. 6, 10.1126/sciadv.aay5901 (2020).
- Mirrahimi et al. [2014] M. Mirrahimi, Z. Leghtas, V. V. Albert, S. Touzard, R. J. Schoelkopf, L. Jiang, and M. H. Devoret, Dynamically protected cat-qubits: a new paradigm for universal quantum computation, New J. Phys. 16, 045014 (2014).
- Goto [2016] H. Goto, Bifurcation-based adiabatic quantum computation with a nonlinear oscillator network: Toward quantum soft computing, Sci. Rep. 6, 21686 (2016).
- Puri et al. [2017] S. Puri, S. Boutin, and A. Blais, Engineering the quantum states of light in a Kerr-nonlinear resonator by two-photon driving, npj Quantum Inf. 3, 18 (2017).
- Girvin [2023] S. M. Girvin, Introduction to Quantum Error Correction and Fault Tolerance (2023).
- Lescanne et al. [2020] R. Lescanne, M. Villiers, T. Peronnin, A. Sarlette, M. Delbecq, B. Huard, T. Kontos, M. Mirrahimi, and Z. Leghtas, Exponential suppression of bit-flips in a qubit encoded in an oscillator, Nat. Phys. 16, 509 (2020).
- Slepian [1968] D. Slepian, Group Codes for the Gaussian Channel, Bell Syst. Tech. J. 47, 575 (1968).
- Loeliger [1991] H.-A. Loeliger, Signal sets matched to groups, IEEE Trans. Inform. Theory 37, 1675 (1991).
- Mittelholzer and Lahtonen [1996] T. Mittelholzer and J. Lahtonen, Group codes generated by finite reflection groups, IEEE Trans. Inform. Theory 42, 519 (1996).
- Sloane et al. [2000] N. Sloane, R. Hardin, W. Smith, and others, Spherical codes (2000).
- Ballinger et al. [2009] B. Ballinger, G. Blekherman, H. Cohn, N. Giansiracusa, E. Kelly, and A. Schürmann, Experimental Study of Energy-Minimizing Point Configurations on Spheres, Exp. Math. 18, 257 (2009).
- Cameron et al. [1978] P. Cameron, J. Goethals, and J. Seidel, Strongly regular graphs having strongly regular subconstituents, Journal of Algebra 55, 257 (1978).
- Waldron [2018] S. F. D. Waldron, An Introduction to Finite Tight Frames, Appl. Harm. Numer. Anal. (Springer New York, New York, NY, 2018).
- Bajnok [1991] B. Bajnok, Construction of Designs on the 2-Sphere, Eur. J. Combin. 12, 377 (1991).
- Reznick [1995] B. Reznick, Some constructions of spherical 5-designs, Linear Algebra Appl. 226-228, 163 (1995).
- Xiang [2022] Z. Xiang, Explicit spherical designs, J. Algebraic Comb. 5, 347 (2022).
- Coxeter and Shephard [1992] H. S. M. Coxeter and G. C. Shephard, Portraits of a Family of Complex Polytopes, Leonardo 25, 239 (1992).
- Skilling [1976] J. Skilling, Uniform compounds of uniform polyhedra, Math. Proc. Camb. Phil. Soc. 79, 447 (1976).
- McMullen [2018] P. McMullen, New Regular Compounds of 4-Polytopes, in New Trends in Intuitive Geometry, Vol. 27 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2018) pp. 307–320.
- Mamone et al. [2010] S. Mamone, G. Pileio, and M. H. Levitt, Orientational Sampling Schemes Based on Four Dimensional Polytopes, Symmetry 2, 1423 (2010).
- Klitzing [2023] R. Klitzing, Polytopes & their Incidence Matrices (2023).
- Hanson [2005] A. J. Hanson, Visualizing quaternions, in ACM SIGGRAPH 2005 Courses on - SIGGRAPH ’05 (ACM Press, Los Angeles, California, 2005) p. 1.
- Coxeter et al. [1997] H. S. M. Coxeter, J. C. Fisher, and J. B. Wilker, Coordinates for the Regular Complex Polygons, J. London Math. Soc. 55, 527 (1997).
- Coxeter [1997] H. S. M. Coxeter, Reciprocating the Regular Polytopes, J. London Math. Soc. 55, 549 (1997).
- Bruss and Leuchs [2007] D. Bruss and G. Leuchs, eds., Lectures on quantum information (Wiley-VCH, Weinheim, 2007).
- Nielsen and Chuang [2011] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed. (Cambridge University Press, New York, NY, USA, 2011).
- Agrawal et al. [2018] A. Agrawal, R. Verschueren, S. Diamond, and S. Boyd, A rewriting system for convex optimization problems, Journal of Control and Decision 5, 42 (2018).
- Diamond and Boyd [2016] S. Diamond and S. Boyd, CVXPY: A Python-Embedded Modeling Language for Convex Optimization, Journal of Machine Learning Research 17, 1 (2016).
- Michael et al. [2016] M. H. Michael, M. Silveri, R. T. Brierley, V. V. Albert, J. Salmilehto, L. Jiang, and S. M. Girvin, New Class of Quantum Error-Correcting Codes for a Bosonic Mode, Phys. Rev. X 6, 031006 (2016).
- Li et al. [2017] L. Li, C.-l. Zou, V. V. Albert, S. Muralidharan, S. M. Girvin, and L. Jiang, Cat Codes with Optimal Decoherence Suppression for a Lossy Bosonic Channel, Phys. Rev. Lett. 119, 030502 (2017).
- Note [1] Up to constant prefactors, this term is also obtained from the last two terms in [68, Eq. (S2)] by setting , , and , and expanding to first order in . The quadratic term in that equation can absorbed into the bare oscillator Hamiltonian prior going into the rotating frame by expanding in a set of normal modes.
- Reiter and Srensen [2012] F. Reiter and A. S. Srensen, Effective operator formalism for open quantum systems, Phys. Rev. A 85, 032111 (2012).
- Azouit et al. [2016] R. Azouit, A. Sarlette, and P. Rouchon, Adiabatic elimination for open quantum systems with effective Lindblad master equations, in 2016 IEEE 55th Conf. Decis. Control (IEEE, 2016) pp. 4559–4565.
- Azouit et al. [2017] R. Azouit, F. Chittaro, A. Sarlette, and P. Rouchon, Towards generic adiabatic elimination for bipartite open quantum systems, Quantum Sci. Technol. 2, 044011 (2017).
- Zitko [2011] R. Zitko, SNEG – Mathematica package for symbolic calculations with second-quantization-operator expressions, Computer Physics Communications 182, 2259 (2011).
- Zitko [2022] R. Zitko, rokzitko/sneg: April 2022 release (2022).