Quantum simulation of topological zero modes on a 41-qubit superconducting processor

The Aubry-Andr$\acute{\mathrm{e}}$-Harper (AAH) model [1, 2] has been attracting considerable attention in various topics of condensed matter physics, including Hofstadter butterfly [3, 4], Anderson localization [5], quasicrystals [6], and topological phases of matter [7, 8]. The incommensurate diagonal AAH model describes a one-dimensional (1D) tight bonding lattice with quasi-periodic potential. In this model a localization transition is predicted [2], which has been observed experimentally [9, 10]. Moreover, the diagonal AAH model can be exactly mapped to the two-dimensional (2D) Hofstadter model [3], showing a 2D quantum Hall effect (QHE) with topologically protected edge states, which have been observed in experiments [6, 11]. The energy spectra of Bloch electrons in perpendicular magnetic fields versus the dimensional perpendicular magnetic field $b$ form the Hofstadter butterfly [3, 4], showing the splitting of energy bands for a specific value of $b$. The Hofstadter butterfly energy spectrum has been measured in quasi-periodic lattices [12, 13, 14], superlattices [15, 16, 17], and Floquet dissipative quasicrystal [18]. A further generalization to commensurate off-diagonal AAH models, with the hopping amplitude being cosine-modulated commensurate with the lattice, indicates the existence of topological zero-energy edge states in the gapless regime [19]. The topological zero modes differ from the edge states in the 1D diagonal AAH models (similar to the quantum Hall edge) and have never been observed in experiments before.

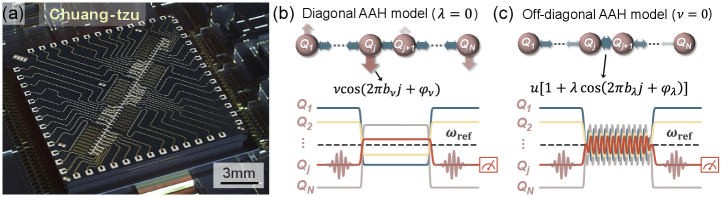
Rapid developments in quantum techniques allow for programming non-trivial topological models and observing their topological states on quantum simulating platforms with a fast-growing number of qubits [20, 21, 11, 22]. Even without fault tolerance, the programmability of a noisy intermediate-scale quantum (NISQ) processor helps to explore various topological phases that are still challenging in real materials [23, 24, 25, 26, 27]. Here, we develop a 43-qubit superconducting quantum processor arranged in a 1D array, named as Chuang-tzu [Fig. 1(a)], to simulate the generalized 1D AAH model. The mean energy relaxation time and pure dephasing time of 41 qubits in our experiments are 21.0 and 1.2$\mu$s, respectively. Since our processor is designed to fulfill the hard-core limit [28, 11], the effective Hamiltonian reads

where $\hat{a}^{{\dagger}}$ ($\hat{a}$) denotes the hard-core bosonic creation (annihilation) operator. In our sample, the frequency $\omega_{j}$ of each qubit $Q_{j}$ is tunable, but the hopping strength $g_{j,j+1}$ between nearest-neighbor (NN) $Q_{j}$ and $Q_{j+1}$ cannot be tuned directly. Here we use the Floquet engineering technique as demonstrated in [29, 30, 31, 32, 33, 34, 35] to simulate the generalized 1D AAH model with a form

with $\lambda\!=\!0$ and $v\!=\!0$ corresponding to the diagonal and off-diagonal AAH models, respectively. In our system, we can independently vary the effective on-site potential $\omega^{\textrm{eff}}_{j}$ and the effective hopping strength $g^{\textrm{eff}}_{j,j+1}$ by the rectangle flux bias and time-periodic driving on the Z control lines of qubits, respectively. The effective $g^{\textrm{eff}}_{j,j+1}$ can be adjusted from about $-3.0$ to $7.6$MHz. Thus, the dynamics of the generalized AAH models are simulated with an approximately effective Hamiltonian using Floquet engineering, and our simulator behaves as a programmable hybrid analogue-digital quantum simulator from the viewpoint in [25]. Details of tuning hopping strength via Floquet engineering are discussed in [36].

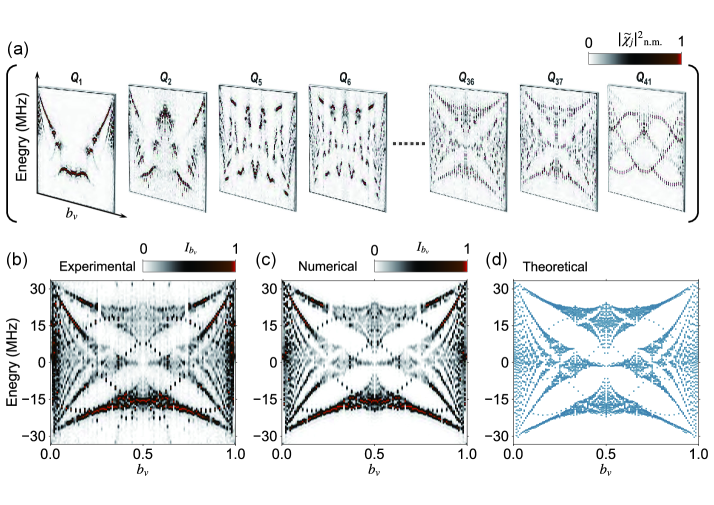
First, we engineer the diagonal AAH model [37, 38] with $N=41$ qubits and measure the Hofstadter butterfly spectrum in the quasi-periodic lattices by setting $\lambda=0$ and tuning the on-site potential as $v\cos(2\pi b_{v}j)$ with $v/(2\pi)\simeq 15.2$MHz and $\varphi_{v}=0$ [Fig. 1(b)]. We simulate 121 instances of diagonal AAH chains when varying $b_{v}$ from 0 to 1. Using the band structure spectroscopic technique [12, 11], we obtain the squared Fourier transformation (FT) magnitude $|\widetilde{\chi}_{j}|^{2}$ of the response function $\chi_{j}(t)\equiv\langle\hat{\sigma}_{j}^{x}(t)\rangle+i\langle\hat{\sigma}_{j}^{y}(t)\rangle$, after preparing a selected qubit $Q_{j}$ at $|+_{j}\rangle=(|0_{j}\rangle+|1_{j}\rangle)/\sqrt{2}$. Figure 2(a) plots $|\widetilde{\chi}_{j}|^{2}$ for several selected qubits $Q_{j}$, and each of them only contains partial information about the energy spectrum. The summation of the squared FT magnitudes [Fig. 2(b)] of all chosen qubits $I_{b_{v}}\equiv\sum_{j}|\widetilde{\chi}_{j}|^{2}$ clearly shows the Hofstadter butterfly energy spectrum, which agrees well with the numerical calculation by simulating the system’s dynamics [Fig. 2(c)] and the theoretical prediction [Fig. 2(d)]. Note that the fractal structure of “Hofstadter’s butterfly”, splitting of energy bands for several $b_{v}$, are clearly shown, which is attributed to the sufficiently large qubit number of our quantum processor [13]. In addition, the wing-like gaps emerge because of the topological feature of the diagonal AAH models, and the 2D integer QHE is characterized by the Chern number [39], which has been experimentally investigated in [11] for $b_{v}={1}/{3}$.

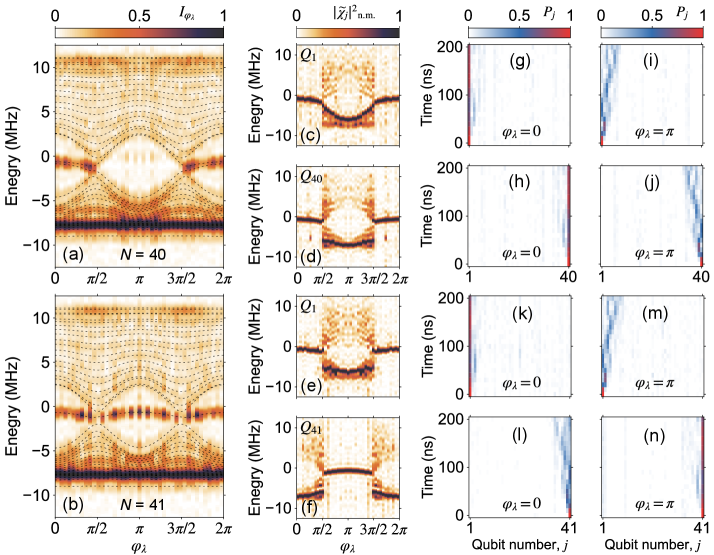
Next, we perform a hybrid analogue-digital quantum simulation of the off-diagonal AAH models with $v=0$ and $\lambda\neq 0$ using Floquet engineering [30] [Fig. 1(c)], which show no QHE [19]. With the bulk-edge correspondence [40, 11], we characterize their topological zero-energy modes, of which the experimental observation is still absent. We first engineer the commensurate off-diagonal AAHs for $b_{\lambda}={1}/{2}$ that can be mapped to a 2D Hofstadter model with $\pi$-flux per plaquette. We experimentally extract the band structures of the lattices with $N=40$ (even) and $41$ (odd) sites by measuring $I_{\varphi_{\lambda}}$ for $\varphi_{\lambda}\in[0,2\pi]$ as shown in Fig. 3(a) and 3(b), respectively, which agrees well with the theoretical prediction (dashed curves). The measured gapless band structure clearly shows two Dirac points with a linear dispersion, which is similar to those observed in graphene [19]. On the lattice with $N=40$ (even) sites, two topological zero modes appear for $\varphi_{\lambda}\in(-{\pi}/{2},{\pi}/{2})$ [Fig. 3(a)], while the topological zero edge mode exists for the whole parameter regime [Fig. 3(b)] with $N=41$ (odd) sites. These exotic topological edge states are also verified from the experimentally measured squared FT magnitudes $|\widetilde{\chi}_{j}|^{2}$ for boundary qubits, as shown in Fig. 3(c–f). For even sites, the $|\widetilde{\chi}_{1}|^{2}$ [Fig. 3(c)] and $|\widetilde{\chi}_{40}|^{2}$ [Fig. 3(d)] for $Q_{1}$ and $Q_{40}$, respectively, both contain information of topological zero edge states in the regime $(-{\pi}/{2},{\pi}/{2})$. However, for odd sites, the $|\widetilde{\chi}_{1}|^{2}$ [Fig. 3(e)] for $Q_{1}$ shows left edge state for $(-{\pi}/{2},{\pi}/{2})$ and the $Q_{41}$’s $|\widetilde{\chi}_{41}|^{2}$ [Fig. 3(f)] implies the existence of the right edge mode for $({\pi}/{2},{3\pi}/{2})$. The small shift of the zero energy of the edge state is attributed to the existence of weak next-nearest-neighboring (NNN) hopping (with an average of about $0.7$MHz) of our sample that slightly breaks the particle-hole symmetry, see details in [36]. Our experiments therefore verify the robustness of the topological zero-energy edge states in the commensurate off-diagonal AAH models.

Furthermore, the topological edge state can also be identified in real space by witnessing the localization of an edge excitation during its quantum walks (QWs) on the 1D qubit chain [29, 11], due to its main overlap with the edge state. We monitor the time evolution of the excitation probabilities $P_{j}$ for all qubits during the QWs. For even sites, QWs of an excitation at either boundary qubit present localization for $\varphi_{\lambda}\!\!=\!\!0$ [Fig. 3(g,h)] in the topological regime and dispersion for $\varphi_{\lambda}\!\!=\!\!\pi$ [Fig. 3(i,j)] in the trivial regime, respectively. In comparison, as shown in Fig. 3(k–n), the QWs of an excitation at $Q_{1}$ ($Q_{41}$) shows localization (diffusion) for $\varphi_{\lambda}\!\!=\!\!0$ and diffusion (localization) for $\varphi_{\lambda}\!=\!\pi$. Thus, our experimental results assert that there always exists only one zero-energy mode localized at either edge in the commensurate off-diagonal AAH models for $\pi$-flux with odd sites. Note that it is still challenging to observe these different behaviors of topological edge modes between even and odd sites in real materials or some other quantum simulating platforms without a fixed number of lattice sites. In our NISQ device, the individually addressable superconducting qubits assisted by Floquet engineering help to overcome these difficulties and show its potential for investigating various exotic topological phenomena.

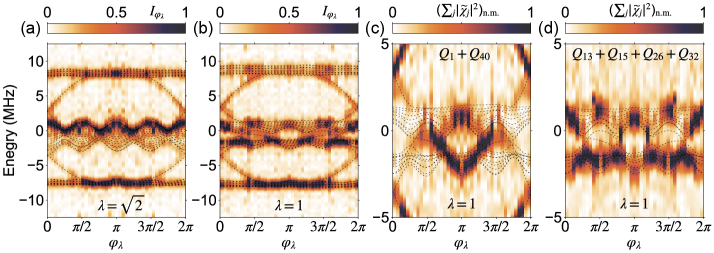
As the $\pi$-flux off-diagonal AAH model can be mapped to the Su-Schrieffer-Heeger (SSH) model [41], the off-diagonal AAH models as a new class of topological models are given by $b_{\lambda}=1/(2q)$ with an integer $q>1$ [19]. Here, we apply 40 qubits to experimentally investigate the generic off-diagonal AAH model for $b_{\lambda}={1}/{4}$ by tuning $g_{j,j+1}^{\textrm{eff}}\!=\!u[1\!+\!\lambda\cos(2\pi b_{\lambda}j+\varphi_{\lambda})]$, with $\varphi_{\lambda}$ varying from 0 to $2\pi$. This model has four energy bands, and the top and bottom bands are fully gapped, where the quantum Hall edge states are clearly exhibited from the measured band structure, see Fig. 4. By tuning $\lambda\!=\!\sqrt{2}$, we see that the central gap closes as theoretically predicted in [19], see Fig. 4(a), which is difficult to be realized with a small-scale quantum simulator. Then, we tune $\lambda\!=\!1$ and measure the band structure as shown in Fig. 4(b), where the central two bands are shown to have four band crossing points near $\varphi_{\lambda}\!=\!{\pi}/{4}$, ${3\pi}/{4}$, ${5\pi}/{4}$, and ${7\pi}/{4}$. Although the mid-gap is very small to observe, we can imply from the measured energy spectrum [Fig. 4(b)] that the central two bands are gapped in the regime $(-{\pi}/{4},{\pi}/{4})$ and $({3\pi}/{4},{5\pi}/{4})$; the topological edge states appear in the regime $({\pi}/{4},{3\pi}/{4})$ and $({5\pi}/{4},{7\pi}/{4})$. To further analyze these two central bands, we separately study the edge and bulk states from the FT signals by only considering the boundary and bulk qubits, respectively. In Fig. 4(c), we plot the summation of the squared FT magnitudes of two boundary qubits $Q_{1}$ and $Q_{40}$ versus $\varphi_{\lambda}$, which mainly shows the information for both the quantum Hall edges in the top and bottom gaps and the zero-energy edges between two central bands. We also illustrate in Fig. 4(d) the summed FT signals for selected bulk qubits $Q_{13}$, $Q_{15}$, $Q_{26}$, and $Q_{32}$, indicating the existence of four band crossing points. Note that the NNN hopping merely causes the shift of zero-energy edge states to mid-gap edges, which verifies the robustness of the topological properties of the commensurate off-diagonal AAH model.

In summary, we experimentally measure the celebrated Hofstadter butterfly energy spectra of up to 41 superconducting qubits and verify the existence of topological zero-energy edge modes in the gapless commensurate AAH models. We introduce multi-qubit Floquet engineering in superconducting circuits, which can be used to realize a wider range of models in condensed matter physics than AAH models, e.g., lattice gauge theories [42] and non-Hermitian systems [43]. In addition, we provide a general automatic calibration scheme for the devices with Floquet engineering (see details in [36]), which is also adaptable to other quantum simulating platforms. Our universal 1D hybrid analogue-digital quantum simulator shows the potential to use programmable NISQ device to investigate exotic topological phases of quantum matter that is still arduous to do in real materials.