Quantum reservoir probing of quantum phase transitions

Quantum phase transitions emerge as quintessential manifestations of the interplay among quantum many-body phenomena [1, 2]. They are characterized by the universal description across microscopically different systems, which has been central to our understanding of quantum matters. Nevertheless, precisely detecting these transitions in equilibrium systems poses significant challenges both theoretically and experimentally. This has led recent investigations to focus on nonequilibrium dynamics, which is inherently related to quantum phase transitions through dynamical quantum critical phenomena. Indeed, nonequilibrium signatures of quantum phase transitions have been identified in a diverse range of systems, spanning integrable, nonintegrable, and topological systems [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. A prevalent strategy in these explorations involves a global quantum quench, wherein the entire system is initially configured in a specific state and subsequently undergoes time evolution under a Hamiltonian with suddenly changed parameters. Recent experimental advancements in isolating and manipulating quantum systems have facilitated such sophisticated control in various platforms, including trapped ions [18, 19, 20, 21], ultracold atoms [22, 23, 24, 25], Rydberg atoms [26, 27, 28, 29], and nitrogen-vacancy centers [30].

A pertinent question then emerges regarding the feasibility of dynamically detecting equilibrium quantum phase transitions through local quantum quenches. Given that the local quench operation, in contrast to its global counterpart, selectively influences nontrivial excitations or quasiparticles in specific regions characteristic of the system [31, 32, 33, 34], the resulting dynamics may potentially unveil signatures of quantum phase transitions. However, the complexity lies in isolating and analyzing the response dynamics directly ascribed to the local quench operation. Since the dynamics is influenced by both the local quantum quench and the intrinsic dynamics of the quantum system itself, the latter obscures the former, thereby diminishing the potential benefit of local quenches in facilitating access to localized physics.

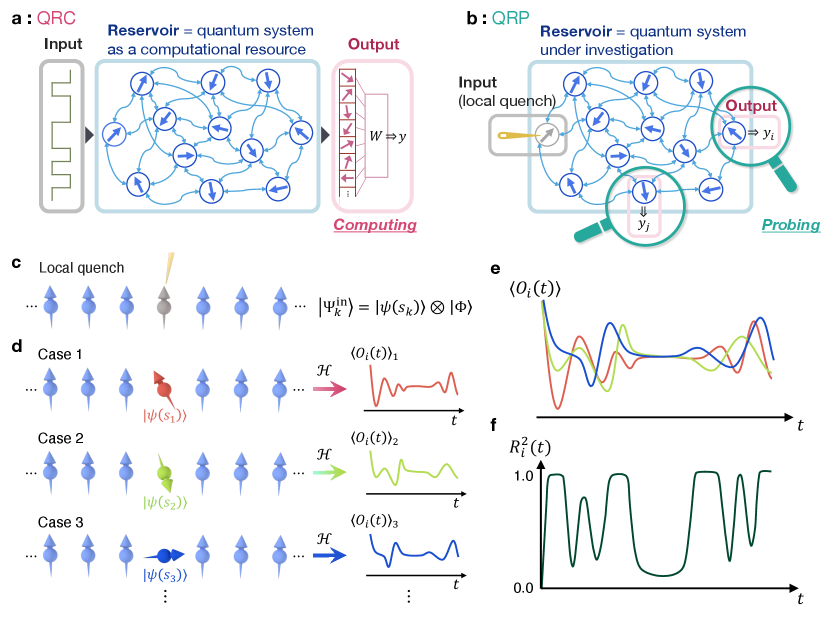
In this paper, we reveal that signatures of quantum phase transitions manifest themselves in out-of-equilibrium local observables subsequent to local quantum quenches. To this end, we develop the methodology of “quantum reservoir probing” (QRP) [35], which selectively extracts the effects of the local quench from the dynamics influenced by multiple factors. Through the lens of the QRP, we observe that the local quantum quench exerts varied influences on a single-site operator depending on the inherent characteristics of quantum phases. Moreover, at the quantum critical points, these influences are notably suppressed due to the enhanced quantum fluctuations. These observations highlight the capability of our QRP to effectively detect quantum phase transitions, as exemplified in both integrable and nonintegrable models herein. Furthermore, notwithstanding the use of a single-site operator, we demonstrate that the QRP can identify topological quantum phase transitions, which are typically distinguished by the absence of local order parameters beyond the Landau-Gintzburg-Wilson paradigm. The broad applicability and design flexibility of our QRP establish it as a versatile tool for probing quantum phenomena, opening the door to further understanding of quantum many-body physics.

Before going to the QRP,we provide an overview of a brain-inspired machine learning framework called reservoir computing [36, 37, 38]. In this paradigm, information is nonlinearly processed by networks of artificial neurons, termed the “reservoir”. A distinguishing feature is that all weight parameters within the reservoir part remain fixed, while only the output weight, which transforms the reservoir state into the final output, is trained utilizing a simple linear regression scheme. Consequently, optimization costs are markedly reduced compared to alternative schemes where the entire network weights are optimized. Importantly, due to this fixed nature, a physical system can embody the reservoir part; the quantum reservoir computing (QRC) harnesses a quantum system as the reservoir (Fig. 1a) [39]. The quantum reservoir system evolves under the influence of the input data, and a read-out vector, constructed through repeated measurements on various degrees of freedom, undergoes linear transformation to yield the final output.

The QRP is an inverse extension of the QRC, wherein the quantum system employed as the reservoir part is investigated by linking physical phenomena with information processing (Fig. 1b). As introduced below, the input is provided via the local quench, and the output is calculated from a local observable; the calculation objective is to estimate the original input value. Given that information is provided solely through the local quench, the estimation succeeds when the local quench exerts an influence on the observed degree of freedom, whereas it fails when the operator is entirely unaffected by the local quench. By systematically scanning local observation operators, the QRP selectively probes the impacts of the local quench on the quantum system through the input estimation performance.

To elaborate, the central feature underlying the QRP is the manipulation of a local degree of freedom, parametrized by a random input value $s_{k}$. Our focus is on a local operator $O$ defined per site $i$ and time $t$, denoted as $O_{i}(t)$, with particular attention to the variations induced by the input variable $s_{k}$. In the statistical analysis across various instances with different inputs subscripted by $k$, the expectation value $\langle O_{i}(t)\rangle_{k}$ may display diverse characteristics that closely reflect the corresponding input values. In such cases, the value of $s_{k}$ can be precisely deduced from $\langle O_{i}(t)\rangle_{k}$ through straightforward calculations. Hence, the successful estimation of the original input value $s_{k}$ provides evidence that the local manipulation exerts an influence on the operator $O_{i}(t)$ at that particular spatiotemporal coordinate. In contrast, the operator $O_{j}(t^{\prime})$ at a different spatiotemporal point may demonstrate consistent behavior across all instances, not accurately mirroring the local quench operation. In this latter case, the operator is predominantly governed by the inherent characteristics of the quantum system independent of the local quench. Therefore, the dependency of the operator $O_{i}(t)$ on the input value $s_{k}$ explores how the local quantum quench influences the operator, while isolating it from other intrinsic phenomena. Remarkably, this linkage is highly sensitive to the Hamiltonian governing the quantum system. The operator’s dependency on the local quench operation thus serves as a witness to the properties of the quantum system, shedding light on the underlying quantum processes at play.

Here, we explain the specific procedures of the QRP on the one-dimensional (1D) quantum systems. The protocol consists of four steps: (i) the preparation of the initial state (Fig. 1c), (ii) the local quench on the central spin, parameterized by the input value $s_{k}$ (Figs. 1c and 1d), (iii) the observation of the dynamics of a local operator $\langle O_{i}(t)\rangle$ under the Hamiltonian $\mathcal{H}$ (Figs. 1d and 1e), and (iv) the statistical evaluation of the performance in estimating the input value $s_{k}$ from the observed dynamics, quantified via the determination coefficient $R_{i}^{2}(t)$ (Fig. 1f). We provide a comprehensive description of each step in the following.

First, the system is prepared in a specified initial state in step (i); for simplicity, a product state is assumed here (e.g., the all-up state in Fig. 1c). Subsequently, in step (ii), the central spin undergoes local manipulation based on the input value $s_{k}$. The resultant state is expressed as

$$|\Psi_{k}^{\mathrm{in}}\rangle=|\psi(s_{k})\rangle\otimes|\Phi\rangle,$$

(1)

where $|\psi(s_{k})\rangle$ represents the state of the locally manipulated spin, while $|\Phi\rangle$ denotes the prepared initial state for the remaining subsystem (Fig. 1d). The input value $s_{k}$ is randomly sampled from a uniform distribution, specifically $s_{k}\in[0,1]$. For the spin-$1/2$ case, we consider the initial state as

$$|\psi(s_{k})\rangle=\sqrt{1-s_{k}}|+\rangle+\sqrt{s_{k}}|-\rangle,$$

(2)

where $|\pm\rangle=\left(\mid\uparrow\rangle\pm\mid\downarrow\rangle\right)/\sqrt{2}$. This state can be prepared by applying a single-gate pulse or a local magnetic field $\bm{h}\propto(2s_{k}-1,0,-2\sqrt{s_{k}(1-s_{k})})$.

We then let the system to evolve under the Hamiltonian $\mathcal{H}$ in step (iii), resulting in the state $|\Psi_{k}(t)\rangle=e^{-i\mathcal{H}t}|\Psi_{k}^{\mathrm{in}}\rangle$ (see Methods section). The expectation value of a local operator $O_{i}(t)$ is calculated as $\langle O_{i}(t)\rangle_{k}=\langle\Psi_{k}(t)|O_{i}|\Psi_{k}(t)\rangle$; we omit the subscript $k$ unless necessary. By iterating this procedure across various instances with different $s_{k}$, we generate multiple time series of the dynamics, as illustrated in Fig. 1e.

Finally in step (iv), we assess the influence of the local quantum quench on the local operator. As a criterion, we employ the precision in estimating the input value $s_{k}$ through the linear transformation of $\langle O_{i}(t)\rangle_{k}$, following the standard methodology used in reservoir computing paradigm [36, 37, 38, 39, 35]. For a given instance $k$, the output of this linear transformation is derived as

$$y_{i,k}(t)=w_{i,O}(t)\langle O_{i}(t)\rangle_{k}+w_{i,c}(t),$$

(3)

where $w_{i,O}(t)$ and $w_{i,c}(t)$ represent the $k$-independent coefficients. These weights are finely tuned for training instances so that the output $y_{{i,k}}(t)$ approximates the original input value $s_{k}$ as closely as possible over all $k$, based on the least squares method. Subsequently in the testing phase, the estimation performance for unknown instances is quantified by the determination coefficient

$$R_{i}^{2}(t)=\frac{\mathrm{cov}^{2}(\{y_{{i,k}}(t)\},\{s_{k}\})}{\sigma^{2}(\{y_{{i,k}}(t)\})\sigma^{2}(\{s_{k}\})},$$

(4)

where $\mathrm{cov}$ and $\sigma^{2}$ represent covariance and variance, respectively; see Methods section for more details. The value of $R^{2}_{i}(t)$ ranges between $0$ and $1$, with an approach towards $1$ indicating that the outputs $\{y_{{i,k}}(t)\}$ closely reproduce the inputs $\{s_{k}\}$ for all testing cases.

Figures 1e and 1f visually elucidate the relationship between the dynamics of $\langle O_{i}(t)\rangle_{k}$ and the corresponding $R^{2}_{i}(t)$. A high $R^{2}_{i}(t)$ value suggests that $\langle O_{i}(t)\rangle_{k}$ varies systematically in response to the input value $s_{k}$. In contrast, $R^{2}_{i}(t)$ close to $0$ indicates that $\langle O_{i}(t)\rangle_{k}$ is largely independent of $s_{k}$, such as at the crossing points resulting from intrinsic oscillations in the quantum system. Therefore, $R^{2}_{i}(t)$ serves as an indicator of the extent to which $O_{i}(t)$ is influenced by the local quench operation. Under different parameters of the Hamiltonian $\mathcal{H}$, the local quench operation exerts varying influences on the resultant dynamics, hence the behavior of $R^{2}_{i}(t)$ is instrumental in examining the unique properties of each quantum phase. It is worth emphasizing that restricting the transformation generating $y_{{i,k}}(t)$ from $\langle O_{i}(t)\rangle_{k}$ to a linear form is crucial. Any additional nonlinearity could lead to either an overestimation or underestimation of the effects of the local quench, while simultaneously impeding interpretability as the output is influenced by the extraneous characteristics of the transformation itself.

Let us first apply our QRP protocol to the paradigmatic 1D Ising model with a transverse magnetic field under the open boundary condition. The Hamiltonian is given by

$$\mathcal{H}=-J\sum_{i}\sigma^{z}_{i}\sigma^{z}_{i+1}+g\sum_{i}\sigma^{x}_{i},$$

(5)

where ${\sigma}_{i}^{x}$ and ${\sigma}_{i}^{z}$ are the $x$ and $z$ Pauli matrices at site $i$, respectively. $g$ signifies the magnitude of the transverse magnetic field and $J>0$ denotes the strength of the nearest-neighbor ferromagnetic interaction; we set $J=1$ as our energy scale. This model manifests a quantum phase transition at the quantum critical point $g_{c}=1$ in the thermodynamic limit, which separates a ferromagnetically ordered phase for $g<1$ from a quantum disordered phase for $g>1$ [40, 1]. Notably, the model is solvable through the Jordan-Wigner transformation and the subsequent Bogoliubov transformation, where the spin system is mapped to the free quasiparticle picture [1].

The system is initialized in the all-up state. Following the local quantum quench, the resultant state $|\Psi^{\mathrm{in}}_{k}\rangle$ in Eq. (1) is explicitly expressed as:

$$|\Psi^{\mathrm{in}}_{k}\rangle=\mid\uparrow\uparrow\uparrow\dots\rangle\otimes|\psi(s_{k})\rangle\otimes\mid\uparrow\uparrow\uparrow\dots\rangle.$$

(6)

Subsequently, we monitor the dynamics of the local spin $\langle\sigma^{x}_{i}(t)\rangle$ at each site $i$ under the Hamiltonian $\mathcal{H}=\mathcal{H}(g)$. Repeating the procedure for many instances with varying $s_{k}$, the estimation performance $R^{2}_{i}(t)$ in Eq. (4) is methodically evaluated.

Figure 2 encapsulates the results of the QRP under various magnetic fields $g$. In Fig. 2a, we show the spatiotemporal representation of the estimation performance $R^{2}_{i}(t)$, which reveals a discernible light-cone structure emanating from the quenched central site. The broad distribution of nonzero $R^{2}_{i}(t)$ suggests that the local spin operator $\langle\sigma_{i}^{x}(t)\rangle$ across diverse spatial locations and temporal moments adequately reflect the impact of the local quantum quench. In the quantum disordered phase, where the ground state exhibits spins aligned along the $x$ direction, the effects of the local quench along the $x$ axis in spin space propagate akin to a spin wave, characterized by pronounced wavefronts of $R^{2}_{i}(t)$. In contrast, in the ferromagnetically ordered phase, the local quenching effects are preserved predominantly within the quasiparticles, manifesting as alterations in phase and amplitude. This influence is evidenced by the ripple-like patterns of the nonzero $R^{2}_{i}(t)$. An exception occurs near the quantum critical point at $g_{c}=1$, characterized by maximized fluctuations that lead to an effective breakdown of the quasiparticle picture. Here, the effects of the local quench are passed on the intrinsic fluctuations of the system, though such influences rapidly diminish as indicated by the noticeably small $R^{2}_{i}(t)$ after the passage of the wavefront. This observation highlights an anomalous suppression of the propagation of local quenching effects at the quantum critical point, which is distinct from other non-critical phases.

In Fig. 2b, the early-time dynamics of $\langle\sigma^{x}_{i}(t)\rangle$ at the nearest-neighbor spin from the central one is depicted for three distinct input values $s_{k}$ at different magnetic fields $g$. At $g=0.5$ and $1.5$, the quasiparticles induce periodic spin oscillations, the phase and amplitude of which are dependent on the input $s_{k}$. In contrast, at $g=1.0$, the dynamics of $\langle\sigma^{x}_{i}(t)\rangle$ exhibits significant variation when the wavefronts pass at approximately $t\simeq 1$, thereafter stabilizing into a uniform pattern that does not reflect the influence of quench operation. Figure 2c displays the corresponding estimation performance at the same site (a vertical cross-section of the color map in Fig. 2a). Over broad temporal spans at $g=0.5$ and $1.5$, $R^{2}_{i}(t)$ becomes close to $1$, which statistically underscores the input dependency of the phase and amplitude of the spin oscillations. Notably, their frequency is governed not by the local quench on the initial state, but rather by the intrinsic characteristics of the quasiparticles themselves. This is evidenced by $R^{2}_{i}(t)$ periodically approaching $0$ (Fig. 2c) at points where oscillations of $\langle\sigma_{i}^{x}(t)\rangle$ intersect for different inputs (Fig. 2b). In contrast, at $g=1.0$, while $R^{2}_{i}(t)$ nears $1$ around $t\simeq 1$ where the wavefronts induce variations in the spin dynamics, the similarity of $\langle\sigma_{i}^{x}(t)\rangle$ in other temporal regions leads to $R^{2}_{i}(t)\simeq 0$, signifying the reduced influence of the local quench by the intrinsic fluctuations enhanced near the quantum critical point.

As described above, the effects of the local quantum quench on the resultant quantum dynamics of local operators manifest qualitatively different characteristics across various phases (Fig. 2a). The distribution of $R^{2}_{i}(t)$ thus serves as a marker for identifying the quantum phase transition. To enhance the clarity of the results, in Fig. 2d, we display the mean value of $R^{2}_{i}(t)$ over a specific subset of spatiotemporal indices $\{(i,t)\}$, denoted as $\overline{R^{2}}$. This analysis focus on $(i,t)$ within the central eleven sites during the time interval $0<t\leq 10$ to minimize the effects from the edges of the system; selecting different subsets does not qualitatively alter the results (see the Supplemental Information). We note that $\overline{R^{2}}$ represents a simple average of local quantities, and therefore, does not include nonlocal quantum effects. As $g$ approaches $g_{c}=1$ from the ferromagnetically ordered state, the fluctuations progressively intensify and interfere with the estimation of the original input, resulting in a decrease in $\overline{R^{2}}$. At the quantum critical point, $\overline{R^{2}}$ reaches its minimum, which corresponds to the emergence of a dark region between the wavefronts observed in Fig. 2a for $g=1.0$. Upon further augmentation of $g$ into the quantum disordered phase, the fluctuations weaken again and the effects of the quench operation become dominant, leading to an increase in $\overline{R^{2}}$. The pronounced dip in Fig. 2d is therefore a definitive indicator of the quantum phase transition occurring at $g_{c}$. Consequently, by focusing on the effects of the local quench, our QRP successfully detects the quantum phase transition only by measurements of single-site spin dynamics.

To illustrate the applicability of our QRP framework to nonintegrable models, we extend the model to the anisotropic next-nearest-neighbor Ising (ANNNI) chain [41, 42, 43, 44]. The Hamiltonian is given by

$$\mathcal{H}=-J\sum_{i}\sigma^{z}_{i}\sigma^{z}_{i+1}-\kappa\sum_{i}\sigma^{z}_{i}\sigma^{z}_{i+2}+g\sum_{i}\sigma^{x}_{i},$$

(7)

where we take $J=1$ and $\kappa$ represents the strength of the next-nerarest-neighbor interaction. The latter term makes the system nonintegrable by introducing the four-body interactions for the quasiparticles derived by the Jordan-Wigner transformation. This model hosts a rich phase diagram in the $\kappa$-$g$ plane [45]. Our investigation focuses on the case of $\kappa=0.5$, where the quantum phase transition occurs at $g_{c}\simeq 1.6$ with the Ising universality, separating ferromagnetically ordered ($g<g_{c}$) and quantum disordered ($g>g_{c}$) phases. The initial state is prepared in the same manner as Eq. (6).

Figure 3a displays the spatiotemporal representation of $R^{2}_{i}(t)$ obtained from $\langle\sigma^{x}_{i}(t)\rangle$, revealing a scenario similar to the transverse-field Ising model. For the majority of sites and times, the local spin $\langle\sigma_{i}^{x}(t)\rangle$ mirrors the input value $s_{k}$ employed in the local quantum quench, as evidenced by the nonzero values of $R^{2}_{i}(t)$. Above the critical field at $g_{c}\simeq 1.6$, particularly for $g=2.2$ in the right panel, the effects of the local manipulation propagate primarily through the excitation wavefronts, while the local spin oscillations exhibit weaker dependence on the local quench with small $R^{2}_{i}(t)$. Conversely, below the critical point the opposite behavior is noted in the left panel for $g=1.0$. Furthermore, in the vicinity of the quantum critical point, the influence of the local quench manifest itself predominantly along the wavefronts, while in the other regions it is suppressed by the enhanced fluctuations, as demonstrated by the emergence of a discernible dark zone between the wavefronts. These fundamental dependencies of the local spin operators on the local quench retain a similarity to those observed in the integrable model presented in Fig. 2a.

In Fig. 3b, we present the mean value $\overline{R^{2}}$, calculated over the indices $(i,t)$ corresponding to the central eleven sites within the time frame $0<t\leq 15$ (see the Supplemental Information for other subsets). Analogous to the observation in Fig. 2d, $\overline{R^{2}}$ demonstrates a pronounced decrease around the quantum critical point at $g\simeq 1.6$, precisely locating the boundary between the different spatiotemporal distribution patterns of $R^{2}_{i}(t)$ in the ferromagnetically ordered phase and the quantum disordered phase. This observation confirms that, even in nonintegrable systems, $R^{2}_{i}(t)$ is an effective marker for detecting quantum phase transitions.

The preceding sections have demonstrated the effectiveness of our QRP in identifying quantum phase transitions, particularly between conventional phases where the internal physics is well-characterized and understood within the Landau-Ginzburg-Wilson theory. Building on this foundation, we now aim to broaden our exploration to more complex quantum phenomena. In particular, we apply the QRP framework to the detection of topological quantum phase transitions, which lack local order parameters that can distinguish adjacent phases. This raises the question of whether the QRP framework, which solely utilizes a single-site spin operator, can still be effective in identifying these transitions beyond the Landau-Gintzburg-Wilson paradigm.

Here, we study the spin-$1$ XXZ model with open boundaries [46, 47], which is defined by

$$\mathcal{H}=\sum_{i}J(S^{x}_{i}S^{x}_{i+1}+S^{y}_{i}S^{y}_{i+1})+\lambda S^{z}_{i}S^{z}_{i+1},$$

(8)

where $S^{\alpha}_{i}$ denotes the $\alpha$-component of spin-$1$ operator at site $i$ and $\lambda$ represents the Ising anisotropy; we set the interaction strength $J=1$. This model is renowned for hosting a prototypical symmetry-protected topological phase, known as the Haldane phase, observed for the anisotropy within $0<\lambda<\lambda_{c}$ with $\lambda_{c}\simeq 1.18$ [48, 49, 50]. The Haldane phase is distinguished by its protection under a $Z_{2}\times Z_{2}$ symmetry, and is characterized by nonlocal string order parameters [51, 52, 53]. With increasing the anisotropy, the topological quantum phase transition into the topologically trivial spin-$1$ Néel state occurs at the quantum critical point, which belongs to the two-dimensional (2D) Ising universality class [49, 54, 55].

The QRP framework can be naturally extended to the spin-$1$ XXZ model. Here, $|\Phi\rangle$ is initialized as the Néel state, and the input spin state $|\psi^{\prime}(s_{k})\rangle$, the spin-$1$ extension of Eq. (2), is prepared by applying a local magnetic field $\bm{h}^{\prime}\propto(s_{k}-1,0,-\sqrt{s_{k}(2-s_{k})})$. Explicitly, the resultant state $|\Psi^{\mathrm{in}}_{k}\rangle$ is expressed as:

$$|\Psi^{\mathrm{in}}_{k}\rangle=\mid\uparrow\downarrow\uparrow\downarrow\dots\uparrow\downarrow\rangle\otimes|\psi^{\prime}(s_{k})\rangle\otimes\mid\downarrow\uparrow\downarrow\uparrow\dots\downarrow\uparrow\rangle.$$

(9)

Following this setup, the impact of the local quench on $\langle S^{x}_{i}(t)\rangle$ is evaluated through the estimation performance $R^{2}_{i}(t)$, analogous to the previous cases.

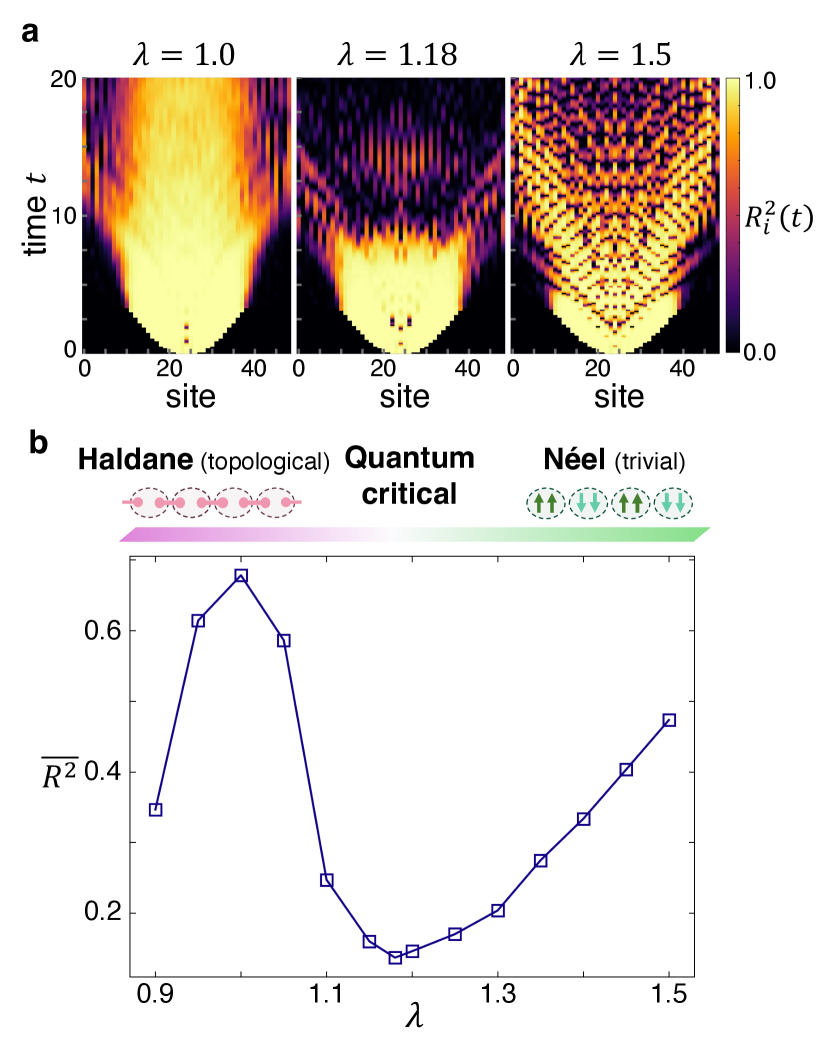
In Fig. 4a, we present the estimation performance $R^{2}_{i}(t)$ under the Hamiltonian $\mathcal{H}$ for three different anisotropies: $\lambda=1.0$ in the Haldane phase, $\lambda=1.3$ in the Néel phase, and $\lambda=1.18$ at the vicinity of the quantum critical point. The spread of nonzero $R^{2}_{i}(t)$ values indicates that the operator $S_{i}^{x}(t)$ is reflective of the local quantum quench at various spatiotemporal points, similar to what is observed in $S=1/2$ spin systems. Following an initial transient period, $R^{2}_{i}(t)$ shows a disturbed ripple-like pattern in the Néel phase, reminiscent of those in the ordered phases in Figs. 2a and 2b. In contrast, in the Haldane phase, $R^{2}_{i}(t)$ becomes more uniform, presumably due to the nonlocal sharing of quenching effects via the underlying singlet pairs. Around the critical point, a notable trend is observed wherein $R^{2}_{i}(t)$ progressively declines over time. This precisely mirrors the trend observed at the quantum critical point in conventional quantum phase transitions (Figs. 2a and 3a).

Figure 4b presents the mean value $\overline{R^{2}}$, which effectively distinguishes these three distinct distributions of $R^{2}_{i}(t)$. $\overline{R^{2}}$ is computed as the average of $R^{2}_{i}(t)$ for the entire system within the time interval $10<t\leq 20$. A key observation in Fig. 4b is the pronounced dip at approximately $\lambda\simeq\lambda_{c}$, signifying the suppression of the impact of local quench. This dip thus marks the quantum critical point characterized by enhanced fluctuations, clearly delineating the boundary between the topological Haldane phase and the trivial Néel phase. Consequently, despite the absence of local order parameters in the Haldane phase, our QRP, based on the local quench and local observables, demonstrates itself as a potent instrument for detecting the topological quantum phase transition.

Finally, we analyze the extended Su-Schrieffer-Heeger (eSSH) model [56, 57, 58, 59, 60, 61]:

	$\displaystyle\mathcal{H}=$	$\displaystyle J\sum_{i=1}^{N/2}(\sigma^{x}_{2i-1}\sigma^{x}_{2i}+\sigma^{y}_{2i-1}\sigma^{y}_{2i}+\delta\sigma^{z}_{2i-1}\sigma^{z}_{2i})$
	$\displaystyle+$	$\displaystyle J^{\prime}\sum_{i=1}^{N/2-1}(\sigma^{x}_{2i}\sigma^{x}_{2i+1}+\sigma^{y}_{2i}\sigma^{y}_{2i+1}+\delta\sigma^{z}_{2i}\sigma^{z}_{2i+1}).$		(10)

Here, $J$ and $J^{\prime}$ represent the strength of alternating nearest-neighbor interactions, and $\delta$ denotes the anisotropy in the $z$ direction; we set $J=1$. Our analysis focuses on the scenario at $\delta=0.5$, where a topological phase transition occurs around $J^{\prime}_{c}\simeq 1$, typically examined through many-body topological invariants [62, 60, 61]. For $J^{\prime}<J^{\prime}_{c}$, the trivial dimer phase manifests, with spins forming singlet pairs with their nearest neighbors, while for $J^{\prime}>J^{\prime}_{c}$, the topological phase emerges, characterized by the emergence of edge states. Importantly, these phases are entirely topological and devoid of local orderings on both sides of the quantum critical point, unlike the spin-1 XXZ model, which exhibits the local Néel order on one side.

The initial state $|\Psi_{k}\rangle$ is prepared as the ground state of $\mathcal{H}$ in the topological phase with $J^{\prime}=6.0$, subject to a weak magnetic field $\bm{h}\propto(2s_{k}-1,0,-2\sqrt{s_{k}(1-s_{k})})$ applied locally to one of the central sites for encoding input information. To ensure that any variations in $|\Psi_{k}\rangle$ across different instances arise solely from differences in $s_{k}$, a magnetic field is applied at both edge spins along the $+z$ direction; this edge field resolves the ground state degeneracy associated with edge degrees of freedom. Both central and edge fields are set to a magnitude of $0.1$ and deactivated following state preparation. Although the prepared state is not a product state and thus not representable in the form of Eq. (1), the effects of the local field are essentially confined to the central region, thereby presenting a virtually identical scenario to the local quench operation. Commencing from this initial state, we monitor the dynamics of the local spin $\langle\sigma_{i}^{x}(t)\rangle$ across multiple cases with different $s_{k}$. The resultant discrepancies in the observed dynamics are attributed to the initial localized manipulation parameterized by $s_{k}$, analogous to prior models.

Figure 5a illustrates the estimation performance $R^{2}_{i}(t)$ under the Hamiltonian $\mathcal{H}$ for three different values of $J^{\prime}$. In all scenarios, $R^{2}_{i}(t=0)$ acquires nonzero values only around the central region, confirming that the information regarding $s_{k}$ is indeed introduced locally through the application of the local magnetic field. During the subsequent time evolution, the effects of the initial localized manipulation begin to propagate throughout the system, where the distinctions between the phases become evident. Notably, in proximity to the quantum critical point at $J^{\prime}=1.0$, $R^{2}_{i}(t)$ is markedly suppressed, displaying a discernibly dark spatiotemporal region in Fig. 5a. This behavior contrasts with the topological phase at $J^{\prime}=1.3$, which exhibits a ripple-like pattern, and the trivial phase at $J^{\prime}=0.7$, characterized by a strip-shaped pattern. In Fig. 5b, we illustrate the $J^{\prime}$ dependence of $\overline{R^{2}}$, defined by averaging $R^{2}_{i}(t)$ over the central $24$ sites within the time frame $8<t\leq 20$. Consistent with previous models, $\overline{R^{2}}$ exhibits a pronounced dip at the quantum critical point, which precisely delineates the boundary between the trivial and topological phases. Indeed, although the transition is entirely topological and the local orderings are absent, the quantum fluctuations are consistently enhanced at the critical point. The QRP locally detect such fluctuations as a witness of the topological quantum phase transition.

To summarize, we have proposed the QRP as an versatile tool for identifying the quantum phase transitions in a variety of quantum systems, including integrable, nonintegrable, and topological systems. The QRP selectively evaluates the effects of the local quench in a manner similar to the pump-probe paradigm. Here, the parametrized local quantum quench, acting as the “pump”, injects random disturbance into the dynamics. The estimation performance of this random input parameter, through the linear transformation of the single-site operator, serves as the “probe”. This pump-probe-like process informationally discerns the underlying relationship between the local quench and the resultant dynamics of operators. Using the QRP, we have observed that the local quench operation exerts varied influence depending on the nature of the quantum phases. At the quantum critical points, the introduced disturbance becomes subordinate to the maximally enhanced quantum fluctuations. A noticeable decline in the estimation performance observed therein serves as a marker for the transition between distinct quantum phases. These findings have established that local, nonequilibrium excitations bear the signatures of quantum phase transitions concerning global, equilibrium many-body ground states. The crux of our methodology lies in the suppression of local quenching effects on local dynamics due to amplified quantum fluctuations, the rigorous justification of which is left for future study.

Our investigations have focused on 1D quantum spin systems; however, the QRP methodology is applicable to a broader range of quantum systems in more than one dimension as well. Indeed, the conformal field theories governing quantum phase transitions in two and higher-dimensional systems exhibit significant differences from their 1D counterparts [63]. These differences manifest themselves as changes in nature of excitations, intrinsic dynamics, and critical behaviors near quantum critical points, all of which would be detectable through the QRP. Moreover, geometric frustrations in high-dimensional quantum spin systems, coupled with the inherent quantum fluctuations, give rise to a plethora of topological quantum phase transitions in a variety of systems. For instance, in certain systems, such transitions are associated with the emergence of anyons, which have promising potential for applications in topological quantum computing [64]. The examination of how anyons respond to local quantum operations through the QRP holds significant importance in light of the aforementioned applications. We leave the high-dimensional applications of the QRP for future investigations.

Finally, let us remark on the design flexibility of the QRP. A fundamental advantage of employing local quantum quenches, in contrast to global ones, lies in their capability to access and elucidate quantum phenomena induced by local operations, such as specific classes of excitations. Indeed, the concept of excitation in quantum systems is intrinsically linked to the relative relationship between local manipulations and initial states; thus, identical local quench operations can lead to varying outcomes based on the differences in the initial states. When one possesses prior knowledge regarding the physics of the targeted system, especially for discerning partially understood phenomena, the optimal selections for the initial state, local quantum quench, and read-out operators in the QRP become intuitively evident. In contrast, the true value of the QRP framework becomes markedly pronounced in the exploration of completely unknown quantum systems. Therein, the underlying physics remains undisclosed, rendering the interpretation of the complex dynamics observed a formidable task. Our QRP introduces a systematic methodology to address this complexity, categorizing operators by meticulously investigating their dependence on various local operations through a scan of the aforementioned conditions of the QRP. Furthermore, the experimental simplicity of the QRP is noteworthy, as it necessitates solely single-site measurements during the initial stages of the dynamics. Consequently, we believe that the QRP presents a promising methodology for eliciting novel insights into a broad spectrum of exotic quantum many-body phenomena, extending beyond quantum phase transitions.

To construct the initial state, we define $\mathcal{H}_{\mathrm{DMRG}}$ that yields $|\Psi_{k}^{\mathrm{in}}\rangle$ as its ground state obtained from the density matrix renormalization group (DMRG) method [65, 66, 67]. For the transverse-field Ising model, the ANNNI model, and the spin-$1$ XXZ model, the initial states are prepared in product states as described in Eqs. (6) and (9). The Hamiltonian $\mathcal{H}_{\mathrm{DMRG}}$ is correspondingly defined, consisting of the local up or down magnetic field along the $z$-axis, which yields the all-up or Néel states as the ground state. A local magnetic field is applied to the central spin to prepare it as $|\psi(s_{k})\rangle$ in the spin-$1/2$ systems and $|\psi^{\prime}(s_{k})\rangle$ in the spin-$1$ system. For the eSSH model, we set $\mathcal{H}_{\mathrm{DMRG}}=\mathcal{H}(J^{\prime}=6.0)$, applying the $s_{k}$-dependent central field and an edge field in $+z$-axis with a strength of $0.1$. The initial state is then obtained as the ground state of $\mathcal{H}_{\mathrm{DMRG}}$ using the DMRG method, expressed as a matrix product state with a bond dimension $\chi$. For the time-evolution $e^{-i\mathcal{H}t}|\Psi_{k}^{\mathrm{in}}\rangle$, we employ the time-dependent variational principle [68, 69, 70] with a bond dimension $\chi$ and a time step $\Delta t=0.005$. The tensor network calculations are implemented using the Julia version of the ITensor library [71, 72].

From a uniform distribution $[0,1]$, a set of $256$ input values $\{s_{k}\}$ is sampled. Each input $s_{k}$ produces a distinct initial state $|\Psi_{k}^{\mathrm{in}}\rangle$, and the dynamics of operator $\langle O_{i}(t)\rangle_{k}$ is subsequently calculated. Among them, $l^{\mathrm{tr}}=128$ instances are designated for training, while the remaining $l^{\mathrm{ts}}=128$ instances are reserved for testing. The linear transformation is represented using a 2D vector $\bm{x}_{i,k}(t)=\left(\langle O_{i}(t)\rangle_{k},1\right)$ and expressed as $y_{i,k}(t)=\bm{x}_{i,k}(t)\bm{w}_{i}(t)$, with the weight vector $\bm{w}_{i}(t)=(w_{i,O}(t),w_{i,c}(t))^{\top}$.

In the training phase, an ($l^{\mathrm{tr}}\times 2$)-dimensional matrix $X_{i}^{\mathrm{tr}}(t)=\{\bm{x}_{i,k}(t)\}_{k=1}^{l^{\mathrm{tr}}}$ is constructed by summing up the observed dynamics. The output, represented as an $l^{\mathrm{tr}}$-dimensional vector $\bm{y}_{i}^{\mathrm{tr}}(t)=\{y_{i,k}\}_{k=1}^{l^{\mathrm{tr}}}$, is calculated as $\bm{y}_{i}^{\mathrm{tr}}(t)=X^{\mathrm{tr}}_{i}(t)\bm{w}_{i}(t)$. The weight vector is trained to closely match the output $\bm{y}_{i}^{\mathrm{tr}}(t)$ with the original input ${\bm{{s}}}^{\mathrm{tr}}=\{s_{k}\}_{k=1}^{l^{\mathrm{tr}}}$. The optimal solution, which minimizes the least squared error between these vectors, is given by

$$\bm{w}_{i}(t)={{X}_{i}^{\mathrm{tr}}}(t)^{+}{\bm{{s}}}^{\mathrm{tr}},$$

(11)

where ${{X}_{i}^{\mathrm{tr}}}(t)^{+}$ denotes the Moore-Penrose pseudoinverse-matrix of ${{X}_{i}^{\mathrm{tr}}}(t)$.

In the testing phase, an ($l^{\mathrm{ts}}\times 2$)-dimensional matrix $X_{i}^{\mathrm{ts}}(t)=\{\bm{x}_{i,k}(t)\}_{k=l^{\mathrm{tr}}+1}^{l^{\mathrm{tr}}+l^{\mathrm{ts}}}$ is similarly composed, yielding the output $\bm{y}_{i}^{\mathrm{ts}}(t)=X_{i}^{\mathrm{ts}}(t)\bm{w}_{i}(t)$ using the trained weights. The estimation performance is assessed by comparing this testing output with the corresponding input ${\bm{{s}}}^{\mathrm{ts}}=\{s_{k}\}_{k=l^{\mathrm{tr}}+1}^{l^{\mathrm{tr}}+l^{\mathrm{ts}}}$ using the determination coefficient

$$R^{2}_{i}(t)=\frac{\mathrm{cov}^{2}(\bm{y}^{\mathrm{ts}}_{i}(t),{\bm{{s}}}^{\mathrm{ts}})}{\sigma^{2}(\bm{y}^{\mathrm{ts}}_{i}(t))\sigma^{2}({\bm{{s}}}^{\mathrm{ts}})}.$$

(12)

Here, $\mathrm{cov}$ and $\sigma^{2}$ denote covariance and variance, respectively. The coefficient $R^{2}_{i}(t)$ statistically assesses the extent to which $O_{i}(t)$ is influenced by the local quantum quench parameterized by $s_{k}$. We have verified that a smaller dataset with $l^{\mathrm{tr}}=100$ and $l^{\mathrm{ts}}=100$ produces quantitatively similar results.

As explained above, the QRP analyzes the variation of dynamics under different $s_{k}$ values. $R^{2}_{i}(t)$ should ideally be zero when no systematic variations dependent on the input $s_{k}$ are observed. However, in numerical simulations, $R^{2}_{i}(t)$ might accidentally exhibit nonzero values, sensitively reflecting the small deviations comparable to numerical errors. To avoid this numerical artifact, we introduce a threshold $\Delta_{\mathrm{th}}$ for the deviation of the operator across different instances. We employ the average absolute deviation $\Delta_{i}(t)$, defined as

$$\Delta_{i}(t)=\frac{1}{l_{\mathrm{tr}}}\sum_{k=1}^{l_{\mathrm{tr}}}\left|\langle O_{i}(t)\rangle_{k}-\frac{1}{l_{\mathrm{tr}}}\sum_{k=1}^{l_{\mathrm{tr}}}\langle O_{i}(t)\rangle_{k}\right|.$$

(13)

When $\Delta_{i}(t)$ is negligibly small, $R^{2}_{i}(t)$ calculated from the above $\langle O_{i}(t)\rangle$ should approach zero. We thus manually set $R^{2}_{i}(t)=0$ when $\Delta_{i}(t)<\Delta_{\mathrm{th}}$; we utilize $\Delta_{\mathrm{th}}=10^{-5}$, and $\Delta_{\mathrm{th}}$ dependency is presented in the Supplemental Information. This procedure does not qualitatively alter our methodology and is experimentally feasible.

The data that support the findings of this study are available from the corresponding author upon reasonable request.

The simulation codes used in this study are available from the corresponding author upon reasonable request.

This research was supported by a Grant-in-Aid for Scientific Research on Innovative Areas “Quantum Liquid Crystals” (KAKENHI Grant No. JP19H05825) from JSPS of Japan and JST CREST (No. JP-MJCR18T2). K.K. was supported by the Program for Leading Graduate Schools (MERIT-WINGS) and JSPS KAKENHI Grant Number JP24KJ0872. The computation in this work has been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo.

K.K. and Y.M. conceived the project. K.K performed the detailed calculations and analyzed the results under the supervision of Y.M. All authors contributed to writing the paper.

The authors have no conflicts of interest directly relevant to the content of this article.

Supplementary Note 1: Average of the estimation performance over various subsets of spatiotemporal indices

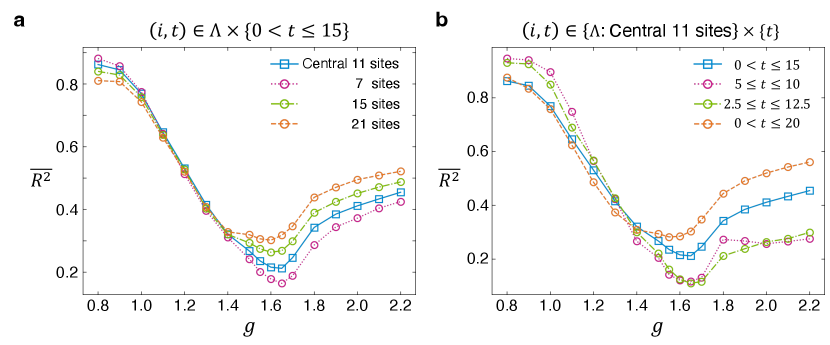
In the main text, we have demonstrated the efficacy of the quantum reservoir probing (QRP) in identifying quantum phase transitions through a statistical analysis of the effects of a local quantum quench, as described by the estimation performance $R^{2}_{i}(t)$ in Eq. (5) in the main text. Figures 2d and 3b in the main text illustrate the signatures of quantum phase transitions and quantum critical points, utilizing the mean value of $R^{2}_{i}(t)$, which is calculated over selected spatiotemporal indices $(i,t)$ to minimize extraneous effects from the edges of the systems. Particularly, in the case of the transverse-field Ising model in Fig. 2d, we have presented the field dependence of the mean estimation performance $\overline{R^{2}}$, which is obtained by averaging $R^{2}_{i}(t)$ for indices $(i,t)\in\Lambda\times\{0<t\leq 10\}$, where $\Lambda$ encompasses the central $11$ sites. Similarly for the ANNNI model in Fig. 3b, we have exhibited $\overline{R^{2}}$ defined over $(i,t)$ drawn from the set $\Lambda\times\{0<t\leq 15\}$, where $\Lambda$ also contains central $11$ sites. It is imperative to note that the quantum phases manifest distinguishable characteristics in $R^{2}_{i}(t)$ (Figs. 2a and 3a in the main text), and $\overline{R^{2}}$ serves as an ancillary tool to further clarify these characteristics. In other words, this averaging operation is implemented only to enhance the clarity of the results, and $\overline{R^{2}}$, defined as the simple average of local quantities, remains inherently local, and does not include nonlocal quantum effects. In this Supplementary Note, we present $\overline{R^{2}}$ defined for various subsets of spatiotemporal indices $(i,t)$, thus demonstrating the robustness of the QRP in detecting quantum phase transitions independent of the employed spatiotemporal subset.

Figure S1 displays the average $\overline{R^{2}}$ in the transverse-field Ising model as a function of the field $g$ in the evolution Hamiltonian $\mathcal{H}(g)$. In Fig. S1a, we show $\overline{R^{2}}$ computed over various spatial index sets $\Lambda$, while the temporal index range is held constant at $\{0<t\leq 10\}$. Conversely, in Fig. S1b, we present $\overline{R^{2}}$ calculated over fixed sets $\Lambda$, which encompass the central eleven sites, while changing the temporal index range. While each curve corresponding to the subset $\{(i,t)\}$ exhibits distinct shapes, the qualitative characteristics are consistent: $\overline{R^{2}}$ decreases as it approaches $g=1.0$, reaches a minimum at $g_{c}$ due to the strong fluctuations, and subsequently rises with further increasing $g$. These patterns robustly indicate the occurrence of a quantum phase transition, with the quantum critical point at $g_{c}$ demarcating the transition between the ferromagnetically ordered phase and the quantum disordered phase.

Figure S2 demonstrates the averaged estimation performance in the ANNNI model as a function of the field strength. Figure S2a illustrates $\overline{R^{2}}$ calculated over various spatial index sets $\Lambda$ with the temporal index range consistently set at $\{0<t\leq 15\}$. In addition, Fig. S2b illustrates $\overline{R^{2}}$ calculated over a fixed spacial indices set $\Lambda$ that includes the central eleven sites, while varying the temporal index range. Similar to the observations in the transverse-field Ising model, the qualitative behaviors of $\overline{R^{2}}$ in the ANNNI model remain consistent across different subsets $\{(i,t)\}$, with all results corroborating the occurrence of a quantum phase transition around $g_{c}\simeq 1.6$. However, a notable feature in the ANNNI model is the broader shape of the dip in $\overline{R^{2}}$ near the quantum critical point, which leads to variations in the identified field strength at which $\overline{R^{2}}$ reaches its minimum depending on the specific subset employed. Nevertheless, it is anticipated that this variance would decrease as the system size increases. A larger system would reduce the influence of edge effects, which are the principal cause of the subset $\{(i,t)\}$ dependency in $\overline{R^{2}}$. Consequently, in a larger system, the quantum critical point is expected to be identified with greater precision and clarity.

Supplementary Note 2: Dependence of the estimation performance on the deviation threshold

As explained in the Methods section in the main text, we introduced the threshold for deviations in the dynamics over multiple cases in the evaluation of the estimation performance. The average absolute deviation $\Delta_{i}(t)$, defined in Eq. (13) in the main text, is employed as a criterion. $R^{2}_{i}(t)$ should be zero when $\Delta_{i}(t)$ is negligible at the level of the numerical error, however, it may accidentally become nonzero sensitively reflecting the small deviations. To circumvent such numerical artifacts, we manually set $R^{2}_{i}(t)=0$ when $\Delta_{i}(t)$ is smaller than the threshold $\Delta_{\mathrm{th}}$. Figures in the main text are obtained under $\Delta_{\mathrm{th}}=10^{-5}$, whereas the qualitative behaviors remain consistent with different $\Delta_{\mathrm{th}}$ as shown in the following.

In Fig. S3, we present $R^{2}_{i}(t)$ in the transverse-field Ising model for three different $\Delta_{\mathrm{th}}$; the results with $\Delta_{\mathrm{th}}=10^{-5}$ are illustrated in Fig. 2a in the main text. In Fig. S3a, $R^{2}_{i}(t)$ without the threshold is presented, where $R^{2}_{i}(t)$ is depicted as obtained. Remarkably, we observe nonzero $R^{2}_{i}(t)$ even outside the light cone, likely due to numerical artifacts. In Figs. S3b and S3c, we introduce the threshold $\Delta_{\mathrm{th}}=10^{-6}$ and $\Delta_{\mathrm{th}}=10^{-4}$, respectively. The unphysical nonzero values of $R^{2}_{i}(t)$ outside the wavefronts are eliminated, mitigating numerical artifacts. Furthermore, the introduction of the threshold narrows the “width” of the wavefront, particularly evident at $g=0.5$. However, once the effects of the local quench have propagated (i.e., inside the wave fronts), the behavior of $R^{2}_{i}(t)$ changes minimally, and the phase-dependent behavior remains consistent. Therefore, the introduction of the threshold to the QRP does not qualitatively alter the outcomes.