Quantum liquid crystals in the finite-field K model for -RuCl3
Abstract
We study the extended Kitaev model called the K model, using a perturbative expansion combined with a well-controlled mean-field approximation and a cutting-edge exact diagonalization. In the phase diagram, we discover a nematic Kitaev spin liquid and a Kekulé Kitaev spin liquid. The former potentially explains the high-field nematic state with zero Chern number experimentally observed in -RuCl3, even for sufficiently small values of . The latter has a Majorana zero mode in its vortex core, which can be potentially controlled by the domain wall motion. This opens a possible application of the quantum liquid crystal phases in the K model to the topological quantum computation.
Introduction. — The Kitaev model Kitaev (2006) is a prominent example of exactly solvable models with a quantum spin liquid (QSL) property, which is characterized by various topological signatures O’Brien et al. (2016); Yamada (2021). However, it is known that real materials cannot fully be described by this fine-tuned model and include additional interactions Wang et al. (2020), which potentially change the topological property of the ground state. Recently the K model Rau et al. (2014); Gohlke et al. (2018); Catuneanu et al. (2018); Liu and Normand (2018); Samarakoon et al. (2018); Gordon et al. (2019); Chern et al. (2020); Lee et al. (2020); Yamada et al. (2020); Gohlke et al. (2020); Buessen and Kim (2021); Luo et al. (2021); Zhang et al. (2021) has been investigated intensively in connection with a Kitaev material -RuCl3, and various kinds of topological transitions were expected theoretically. Whereas various numerical methods have been used, most studies treat itinerant Majorana fermions of the Kitaev model indirectly, and the role of Majorana fermions is unclear.
Among many possible realizations of the proximate Kitaev model Jackeli and Khaliullin (2009); Plumb et al. (2014); Yamada et al. (2017a, b); Liu and Khaliullin (2018); Sano et al. (2018); Jang et al. (2019), -RuCl3 is an outstanding material because a half-integer quantization of the thermal Hall conductivity has been observed Kasahara et al. (2018); Yokoi et al. (2021). At higher field, the breaking of the threefold rotation symmetry has been observed from the field angle dependence of the heat capacity at the same time as the disappearance of the thermal Hall effect Tanaka et al. (2020). The coincidence is attributed to the first-order transition from Kitaev’s phase with a Chern number 1 to Kitaev’s phase with a Chern number 0, which occurs directly maintaining an energy gap Takahashi et al. (2021). A theoretical characterization is necessary for the high-field nematic phase based on a microscopic model like the K model. While some studies Gohlke et al. (2018); Lee et al. (2020) find the nematic phase within the K model, the property of the associated nematic phase transition from the Kitaev spin liquid is not well discussed Gohlke et al. (2020).
Another interesting phase with a broken threefold rotation symmetry is a Kekulé phase. Though both a nematic phase and a Kekulé phase are spin liquids with a toric code topological order, some properties are different. The most significant difference is the presence of a Majorana zero mode (MZM) in the vortex for a Kekulé phase Jackiw and Rossi (1981); Yang et al. (2019). Here a vortex means a crossing point of boundaries of three different domains of the -broken Kekulé phases. MZMs can potentially be braided by the domain wall motion, which leads to a nontrivial phase. Thus, by controlling such topological defects in this liquid crystalline phase, the protected quantum computation in the MZM states is possible.
Both of these phases are relevant to the K model even in the mean-field level, and thus we investigate these phases precisely. From now on we call the nematic phase nematic Kitaev spin liquid (NKSL) and the Kekulé phase Kekulé-Kitaev spin liquid (KKSL).
From the mean-field approximation and the exact diagonalization, we discover a vast region of NKSL and KKSL with a broken threefold rotation symmetry. Both of these phases can be regarded as quantum spin analogues of liquid crystals Kivelson et al. (1998). These phases are enabled to be discovered by the methods which treat itinerant Majorana fermions directly.
In this Letter, we study a phase diagram of the finite-field K model using the third-order perturbation. The effective model is an interacting Majorana model with four-body and six-body interactions Bravyi et al. (2010); Vijay et al. (2015); Affleck et al. (2017); Li and Franz (2018); Kamiya et al. (2018); Wamer and Affleck (2018); Rahmani et al. (2019); Rahmani and Franz (2019); Li et al. (2019); Tummuru et al. (2021). Based on the mean-field solution and the exact diagonalization, we find the phase diagram is rich enough to predict various exotic spin liquids like NKSL and KKSL.
Third-order perturbation. — We begin with the following Kitaev- or K model. These two terms are known to be dominant in -RuCl3.
| (1) |
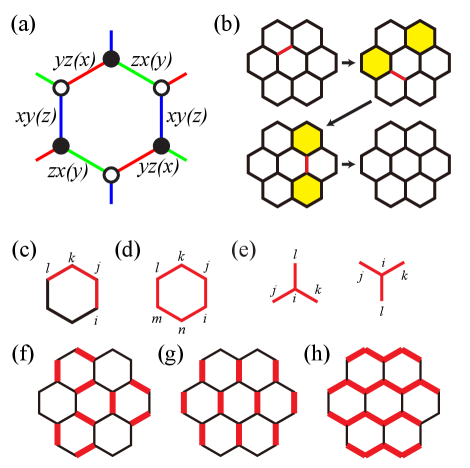
where we assume , and to be a real number, and and are spin-1/2 and Pauli operators defined on the th site, respectively. means that a nearest-neighbor (NN) bond belongs to -bonds as shown in Fig. 1(a), and the -plane is perpendicular to the -direction. We note that our study is based on the original Kitaev model with an additional interaction, not the so-called Kekulé-Kitaev model Kamfor et al. (2010); Quinn et al. (2015); Mirmojarabian et al. (2020). The Kekulé-Kitaev model explicitly breaks the symmetry, while our model spontaneously breaks this symmetry in the Kekulé phase.
As is usually the case, the nontrivial contribution begins from the third order in . The third-order perturbation leads to the following effective Hamiltonian.
| (2) |
where means that , , and are two possible patterns for -, -, and -bonds, respectively, inside each hexagon. The factor comes from the intermediate vortex pattern Yamada (2020); Takahashi et al. (2021), as shown in Fig. 1(b).
We then move on to the effective Majorana interacting model.
| (3) |
where , represents armchair-type interactions shown in Fig. 1(c), and represents six-body interactions shown in Fig. 1(d). The site ordering of and is counterclockwise, as shown in Figs. 1(c)-(d).
The same process applies to the case with a magnetic field. We can consider the Hamiltonian with
| (4) |
where is an applied magnetic field. By tracking intermediate vortex states, we would finally get
| (5) |
where , means that a bond belongs to -bonds with the -plane perpendicular to the -direction, represents a next-nearest-neighbor (NNN) bond, and represents a -shaped, or -shaped interaction for sites , where , , and are connected by -, -, and -bonds, respectively, as shown in Fig 1(e). means the next-next-nearest-neighbor (NNNN) bond which is a diagonal of hexagons in the -direction, where is even and is odd as usual.
From now on, we set for simplicity. The absolute value of is undecidable, so we set as a simple normalization. We note that two-body terms are not antisymmetrized, so the hopping amplitude is in the Hermitian form.
The model. — Let us begin with the zero-field model. First, we extend the model to the following form:
| (6) |
with and being real parameters. When , this model becomes the original (K) model with .
The operator
| (7) |
can be defined for each hexagon plaquette , and plays an important role as they commute with each other. Indeed, the model is integrable in the limit . Eigenstates are constructed by assigning for each plaquette.
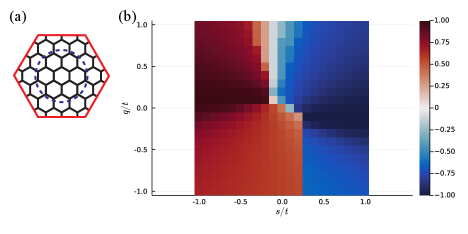
This limit () is also known as the Vijay-Hsieh-Fu (VHF) surface code Vijay et al. (2015) and has a characteristic topological order with an exact anyon symmetry. To check the existence of such a phase we did exact diagonalization of the 54-site cluster, which is shown in Fig. 2(a). This VHF surface code is indeed realized in the model with a large region, as shown in Fig. 2(b). In Fig. 2(b) the right half is mostly blue connected to the limit, and the left half is mostly red connected to the limit. This means that the large phase is rather stable with respect to the perturbation of and .
It seems that even on the line, most of the region is connected to this VHF surface code phase, and from this we conclude that even in the original (K) model Eq. (5) this phase is realized in the large region. Since the resolution of Fig. 2(b) is not good enough, the exact region of where this phase is realized will be discussed later.
K model with a magnetic field. — Then, we go back to the original (K) model Eq. (5). With a magnetic field, it indeed becomes easy to identify the phase because we can use a Chern number to diagnose gapped topological phases. The Chern number is connected to the topological order of the spin model according to Kitaev’s 16-fold way. For example, phases with a Chern number in the Majorana model can be identified with the Ising topological order, which we call a chiral spin liquid (CSL) with a Chern number in the following.
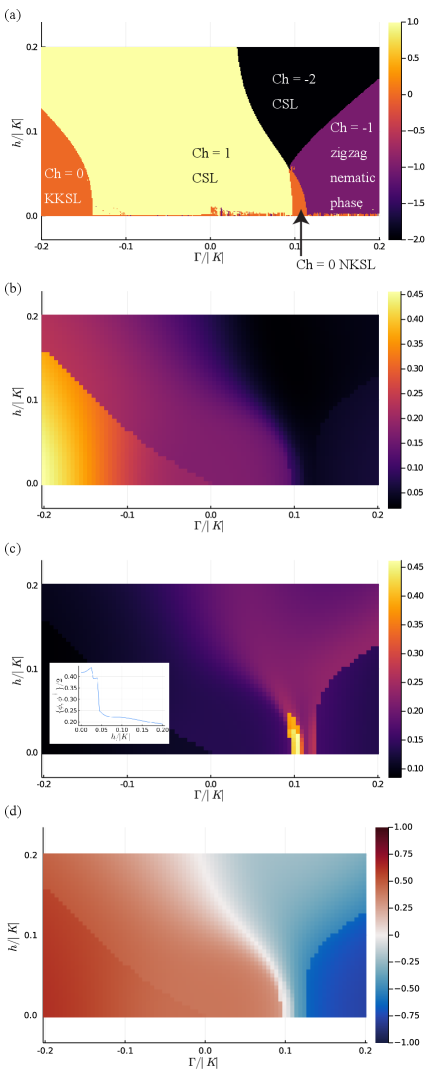
The mean-field phase diagram is shown in Fig. 3(a) Phases are identified from the Chern number and bond order parameters. The Chern number is computed by the Fukui-Hatsugai-Suzuki method Fukui et al. (2005). The details of the calculation is included in Supplemental Material (SM) SM . The method is based on Refs. Li and Franz (2018); Takahashi et al. (2021). From the phase diagram we find the following phases:
-
1.
a KKSL with a Chern number .
-
2.
Kitaev’s non-Abelian CSL with a Chern number .
-
3.
an Abelian CSL with a Chern number .
-
4.
an NKSL with a Chern number .
-
5.
a zigzag nematic phase with a Chern number .
The bond ordering patterns for a KKSL, an NKSL, and a zigzag nematic phase are shown in Figs. 1(f), (g), and (h), respectively.
Exact diagonalization. — From now on we will confirm the results of the mean-field theory by exact diagonalization of Eq. (5). The exact diagonalization is done using the 54-site cluster again. We note that this size is much larger than what has been used for the Kitaev model exact diagonalization. We take an average of expectation values for all the degenerate ground states. First, we check the operator , corresponding to the absolute value of the Kekulé order parameter Pujari et al. (2015) with
| (8) |
where the definition of (–) is included in SM SM . In Fig. 3(b), the orange triangular region with corresponds to the Kekulé-ordered phase. The area of this phase becomes larger than that of the mean-field phase diagram. Surprisingly, it looks like the Kekulé order appears with an infinitesimal in the 54-site calculation. This implies that the Kitaev spin liquid is unstable with respect to a negative perturbatively and it is possible that the Kekulé order opens a gap for Dirac cones (see SM SM for more details).
Next we check the nematic order parameter Pujari et al. (2015) with
| (9) |
where the definition of (–) is included in SM SM . In Fig. 3(c), NKSL is identified with the small orange region around . The area of this phase becomes smaller than that of the mean-field phase diagram. We now confirmed the existence of NKSL even in the exact diagonalization, but the zigzag nematic phase disappears in the same calculations. There remains a violet region which is different from the zigzag nematic phase found in the mean-field approach. We note that the order parameter is nonzero on the whole parameter space in Fig. 3(b) and (c) due to the finite-size effect.
Finally, we check the value of to identify the mysterious area which cannot be identified by the calculation of the nematic order parameter. As shown in Fig. 3(d), the value of reaches around 0.75, which is very close to the highest value . Combined with what is obtained from the model, we believe that this phase is connected to the large phase of the model. Thus, this phase appearing in the large region should be described by the VHF surface code. This region indeed has the largest value of the entanglement entropy (see Fig. 4), which reconfirms that it is a highly entangled phase which cannot be described by the mean-field picture.
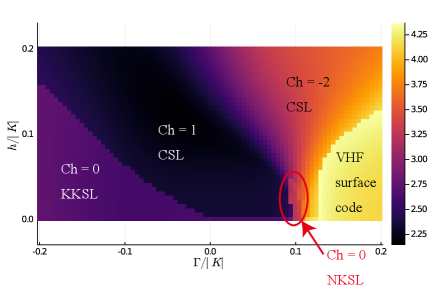
Phase diagram of the model. — As shown in Fig. 4, we find the following phases.
-
1.
a KKSL with a Chern number .
-
2.
Kitaev’s non-Abelian CSL with a Chern number .
-
3.
an Abelian CSL with a Chern number .
-
4.
an NKSL with a Chern number .
-
5.
a VHF surface code.
Except for the fact that the zigzag nematic phase is replaced by the VHF surface code, the phases obtained are the same as those found in the mean-field theory. We note that Kitaev’s non-Abelian CSL with a Chern number is identified because this phase is stable on the line Takahashi et al. (2021), while an Abelian CSL with a Chern number is just a speculation.
Especially in the experimentally relevant region, , we find an NKSL phase with a Chern number 0, which potentially explains the observed topological nematic transition from Kitaev’s non-Abelian CSL to the toric code phase.
Overall, we have obtained a very rich phase diagram within the flux-free assumption, and disclosed the existence and properties of NKSL expected from experiments. Though our calculation is somewhat idealized, a more realistic phase diagram should be obtained by dealing with a term, for example, additionally Takikawa and Fujimoto (2019, 2020). In addition, in the future it is important to check whether an Abelian CSL with a Chern number is connected to the one discovered previously in the K model Takikawa and Fujimoto (2020).
Effect of the Heisenberg term. — Here we will discuss the effect of the Heisenberg term. With this term the third-order perturbation leads to the following additional interaction.
| (10) |
where represents an zigzag-type interaction for sites , and represents an NNNN hopping which is not a diagonal of hexagons. This term promotes nematic order, and potentially enhances NKSL. Thus, the additional small Heisenberg term should be relevant to the field-induced nematic transition, and will be investigated in the future.
Discussion. — We invent a systematic approach to treat non-Kitaev interactions in a perturbative manner by fully incorporating many-body effects of Majorana interactions. We discover the emergence of a Kekulé order in the K model for , and a nematic order for , as well as a more exotic VHF surface code phase. We also discover an Abelian CSL with a Chern number -2, which can be detected by the sign change of the thermal Hall effect or spin Seebeck effect Takikawa et al. (2021).
In the experimentally relevant region for -RuCl3, the discovered nematic phase potentially explains the nematic transition observed in the high-field phase. While the position of the NKSL phase is consistent the density matrix renormalization group Gohlke et al. (2018, 2020), its nature is totally different from nematic phases discovered previously Lee et al. (2020). NKSL is not a simple nematic phase but a spin liquid phase with a partial symmetry breaking. We believe that NKSL discovered in our study is not the same phase as the ones in the previous studies, and that the approximate coincidence of the nematic region is only accidental. Our study endorses the topological nematic transition scenario proposed in Ref. Takahashi et al. (2021) with a more realistic model and interactions. This state is potentially detectable by nuclear magnetic resonance (NMR) or Mössbauer spectroscopy Yamada and Fujimoto (2021).
Another direction to explore is to engineer the Kekulé order in artificial systems. The sign and magnitude of the term is known to be strongly dependent on the spin-orbit coupling (SOC), so it can potentially be controlled by the proximity effect with a substrate. The substrate with heavy elements may strengthen the SOC of -RuCl3, and allow the fine tuning of . The signature of the Kekulé phase is the existence of an MZM at the vortex core, which would potentially be discovered by scanning tunneling microscope (STM), leading to a possible topological quantum computation.
Acknowledgements.
We thank M. Gohlke, I. Kimchi, Y. Tada, M. O. Takahashi, D. Takikawa for fruitful discussions. This work was supported by JSPS KAKENHI Grant No. JP21H01039, and by JST CREST Grant Number JPMJCR19T5, Japan. M.G.Y. is supported by Multidisciplinary Research Laboratory System for Future Developments, Osaka University. This research was supported in part by the National Science Foundation under Grant No. NSF PHY-1748958. The computation in this work has been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo.References
- Kitaev (2006) A. Kitaev, Ann. Phys. 321, 2 (2006), january Special Issue.
- O’Brien et al. (2016) K. O’Brien, M. Hermanns, and S. Trebst, Phys. Rev. B 93, 085101 (2016).
- Yamada (2021) M. G. Yamada, Phys. Rev. Research 3, L012001 (2021).
- Wang et al. (2020) Y. Wang, G. B. Osterhoudt, Y. Tian, P. Lampen-Kelley, A. Banerjee, T. Goldstein, J. Yan, J. Knolle, H. Ji, R. J. Cava, J. Nasu, Y. Motome, S. E. Nagler, D. Mandrus, and K. S. Burch, npj Quantum Mater. 5, 14 (2020).
- Rau et al. (2014) J. G. Rau, E. K.-H. Lee, and H.-Y. Kee, Phys. Rev. Lett. 112, 077204 (2014).
- Gohlke et al. (2018) M. Gohlke, G. Wachtel, Y. Yamaji, F. Pollmann, and Y. B. Kim, Phys. Rev. B 97, 075126 (2018).
- Catuneanu et al. (2018) A. Catuneanu, Y. Yamaji, G. Wachtel, Y. B. Kim, and H.-Y. Kee, npj Quantum Mater. 3, 23 (2018).
- Liu and Normand (2018) Z.-X. Liu and B. Normand, Phys. Rev. Lett. 120, 187201 (2018).
- Samarakoon et al. (2018) A. M. Samarakoon, G. Wachtel, Y. Yamaji, D. A. Tennant, C. D. Batista, and Y. B. Kim, Phys. Rev. B 98, 045121 (2018).
- Gordon et al. (2019) J. S. Gordon, A. Catuneanu, E. S. Sørensen, and H.-Y. Kee, Nat. Commun. 10, 2470 (2019).
- Chern et al. (2020) L. E. Chern, R. Kaneko, H.-Y. Lee, and Y. B. Kim, Phys. Rev. Research 2, 013014 (2020).
- Lee et al. (2020) H.-Y. Lee, R. Kaneko, L. E. Chern, T. Okubo, Y. Yamaji, N. Kawashima, and Y. B. Kim, Nat. Commun. 11, 1639 (2020).
- Yamada et al. (2020) T. Yamada, T. Suzuki, and S.-i. Suga, Phys. Rev. B 102, 024415 (2020).
- Gohlke et al. (2020) M. Gohlke, L. E. Chern, H.-Y. Kee, and Y. B. Kim, Phys. Rev. Research 2, 043023 (2020).
- Buessen and Kim (2021) F. L. Buessen and Y. B. Kim, Phys. Rev. B 103, 184407 (2021).
- Luo et al. (2021) Q. Luo, J. Zhao, H.-Y. Kee, and X. Wang, npj Quantum Mater. 6, 57 (2021).
- Zhang et al. (2021) S.-S. Zhang, G. B. Halász, W. Zhu, and C. D. Batista, Phys. Rev. B 104, 014411 (2021).
- Jackeli and Khaliullin (2009) G. Jackeli and G. Khaliullin, Phys. Rev. Lett. 102, 017205 (2009).
- Plumb et al. (2014) K. W. Plumb, J. P. Clancy, L. J. Sandilands, V. V. Shankar, Y. F. Hu, K. S. Burch, H.-Y. Kee, and Y.-J. Kim, Phys. Rev. B 90, 041112 (2014).
- Yamada et al. (2017a) M. G. Yamada, H. Fujita, and M. Oshikawa, Phys. Rev. Lett. 119, 057202 (2017a).
- Yamada et al. (2017b) M. G. Yamada, V. Dwivedi, and M. Hermanns, Phys. Rev. B 96, 155107 (2017b).
- Liu and Khaliullin (2018) H. Liu and G. Khaliullin, Phys. Rev. B 97, 014407 (2018).
- Sano et al. (2018) R. Sano, Y. Kato, and Y. Motome, Phys. Rev. B 97, 014408 (2018).
- Jang et al. (2019) S.-H. Jang, R. Sano, Y. Kato, and Y. Motome, Phys. Rev. B 99, 241106 (2019).
- Kasahara et al. (2018) Y. Kasahara, T. Ohnishi, Y. Mizukami, O. Tanaka, S. Ma, K. Sugii, N. Kurita, H. Tanaka, J. Nasu, Y. Motome, T. Shibauchi, and Y. Matsuda, Nature 559, 227 (2018).
- Yokoi et al. (2021) T. Yokoi, S. Ma, Y. Kasahara, S. Kasahara, T. Shibauchi, N. Kurita, H. Tanaka, J. Nasu, Y. Motome, C. Hickey, S. Trebst, and Y. Matsuda, Science 373, 568 (2021).
- Tanaka et al. (2020) O. Tanaka, Y. Mizukami, R. Harasawa, K. Hashimoto, N. Kurita, H. Tanaka, S. Fujimoto, Y. Matsuda, E.-G. Moon, and T. Shibauchi, (2020), arXiv:2007.06757 [cond-mat.str-el] .
- Takahashi et al. (2021) M. O. Takahashi, M. G. Yamada, D. Takikawa, T. Mizushima, and S. Fujimoto, Phys. Rev. Research 3, 023189 (2021).
- Jackiw and Rossi (1981) R. Jackiw and P. Rossi, Nucl. Phys. B 190, 681 (1981).
- Yang et al. (2019) Z.-C. Yang, T. Iadecola, C. Chamon, and C. Mudry, Phys. Rev. B 99, 155138 (2019).
- Kivelson et al. (1998) S. A. Kivelson, E. Fradkin, and V. J. Emery, Nature 393, 550 (1998).
- Bravyi et al. (2010) S. Bravyi, B. M. Terhal, and B. Leemhuis, New J. Phys. 12, 083039 (2010).
- Vijay et al. (2015) S. Vijay, T. H. Hsieh, and L. Fu, Phys. Rev. X 5, 041038 (2015).
- Affleck et al. (2017) I. Affleck, A. Rahmani, and D. Pikulin, Phys. Rev. B 96, 125121 (2017).
- Li and Franz (2018) C. Li and M. Franz, Phys. Rev. B 98, 115123 (2018).
- Kamiya et al. (2018) Y. Kamiya, A. Furusaki, J. C. Y. Teo, and G.-W. Chern, Phys. Rev. B 98, 161409 (2018).
- Wamer and Affleck (2018) K. Wamer and I. Affleck, Phys. Rev. B 98, 245120 (2018).
- Rahmani et al. (2019) A. Rahmani, D. Pikulin, and I. Affleck, Phys. Rev. B 99, 085110 (2019).
- Rahmani and Franz (2019) A. Rahmani and M. Franz, Rep. Prog. Phys. 82, 084501 (2019).
- Li et al. (2019) C. Li, E. Lantagne-Hurtubise, and M. Franz, Phys. Rev. B 100, 195146 (2019).
- Tummuru et al. (2021) T. Tummuru, A. Nocera, and I. Affleck, Phys. Rev. B 103, 115128 (2021).
- Kamfor et al. (2010) M. Kamfor, S. Dusuel, J. Vidal, and K. P. Schmidt, J. Stat. Mech.: Theory Exp. 2010, P08010 (2010).
- Quinn et al. (2015) E. Quinn, S. Bhattacharjee, and R. Moessner, Phys. Rev. B 91, 134419 (2015).
- Mirmojarabian et al. (2020) F. Mirmojarabian, M. Kargarian, and A. Langari, Phys. Rev. B 101, 115116 (2020).
- Yamada (2020) M. G. Yamada, npj Quantum Mater. 5, 82 (2020).
- Fukui et al. (2005) T. Fukui, Y. Hatsugai, and H. Suzuki, J. Phys. Soc. Jpn. 74, 1674 (2005).
- (47) See Supplemental Material at [URL will be inserted by publisher] for more details.
- Pujari et al. (2015) S. Pujari, F. Alet, and K. Damle, Phys. Rev. B 91, 104411 (2015).
- Takikawa and Fujimoto (2019) D. Takikawa and S. Fujimoto, Phys. Rev. B 99, 224409 (2019).
- Takikawa and Fujimoto (2020) D. Takikawa and S. Fujimoto, Phys. Rev. B 102, 174414 (2020).
- Takikawa et al. (2021) D. Takikawa, M. G. Yamada, and S. Fujimoto, (2021), arXiv:2104.11115 [cond-mat.str-el] .
- Yamada and Fujimoto (2021) M. G. Yamada and S. Fujimoto, Phys. Rev. Lett. 127, 047201 (2021).