Quantum gates with weak van der Waals interactions of neutral Rydberg atoms
Abstract
Neutral atoms are promising for large-scale quantum computing, but accurate neutral-atom entanglement depends on large Rydberg interactions which strongly limit the interatomic distances. Via a phase accumulation in detuned Rabi cycles enabled by a Rydberg interaction of similar magnitude to the Rydberg Rabi frequency, we study a controlled-phase gate with an arbitrary phase and extend it to the controlled-NOT gate. The gates need only three steps for coupling one Rydberg state, depend on easily accessible van der Waals interaction that naturally arises between distant atoms, and have no rotation error in the weak interaction regime. Importantly, they can work with very weak interactions so that well-separated qubits can be entangled. The gates are sensitive to the irremovable fluctuation of Rydberg interactions, but can still have a fidelity over 98% with realistic position fluctuation of qubits separated over 20 m.
I introduction
Neutral atoms can be rapidly entangled when they are excited to high-lying Rydberg states, which renders the possibility to use neutral atoms for large-scale quantum computing Saffman et al. (2010); Saffman (2016); Weiss and Saffman (2017); Adams et al. (2020); Wu et al. (2021); Morgado and Whitlock (2021). There have been several experiments demonstrating entanglement between individual neutral atoms by Rydberg interactions Wilk et al. (2010); Isenhower et al. (2010); Zhang et al. (2010); Maller et al. (2015); Jau et al. (2016); Zeng et al. (2017); Levine et al. (2018); Picken et al. (2019); Levine et al. (2019); Graham et al. (2019); Jo et al. (2020); Madjarov et al. (2020) primarily via the blockade mechanism Jaksch et al. (2000) where two nearby Rydberg atoms should possess a strong interaction . The value of drops quickly when the qubit spacing increases, so it is necessary to place the qubits close enough for the blockade condition to hold. For example, the interatomic distance was in the range m in recent experiments of high-fidelity neutral-atom entanglement Levine et al. (2018, 2019); Graham et al. (2019); Madjarov et al. (2020). On the other hand, the yet to be large-scale quantum processor is supposed to host a large number of qubits in which entanglement operations between distant qubits are required in a general computational task. To tackle this issue, Ref. Weimer et al. (2012) suggested a method to entangle two qubits separated by a chain of ancillary qubits by adiabatically following the many-body ground state of the qubit chain coupled via the Rydberg blockade mechanism, and Ref. Cesa and Martin (2017) proposed to entangle distant qubits by coupling two targeted qubits with a group of ancillary atoms via Rydberg interactions. These methods depend on strong interactions of nearby Rydberg atoms. For example, Ref. Weimer et al. (2012) analyzed a model by assuming a large enough enabled by a small average interatomic spacing m, so that the entanglement of two logic qubits separated by m would require a coherent control over around 19 ancillary qubits.
In this work, we analyze an entangling gate between two well-separated neutral atoms by partially exciting them to Rydberg states. In contrast to the gate protocols dependent on the blockade mechanism, we find that a tiny can rapidly generate entanglement between ground hyperfine levels via detuned ground-Rydberg Rabi oscillations, and a controlled phase gate with an arbitrary phase can be created accurately. The intrinsic fidelity of the gate is perfect when is frozen and when the Rydberg-state decay is ignored, but for realistic setups where there will be fluctuations of qubit positions Graham et al. (2019) and Rydberg-state decay, the gate can still have a fidelity with qubit spacing over m. Compared to the Rydberg gate by a dynamical phase shift from the Rydberg interactions Jaksch et al. (2000), our gate does not require the Rydberg Rabi frequency to be much larger than and, thus, a high-fidelity implementation is less technically demanding, where is the (reduced) Planck constant. Compared to the Rydberg gates in Shi (2017) that work with similar condition but need five pulses to couple multiple Rydberg states, the gate in this work needs fewer pulses to couple only one Rydberg state. In contrast to previous Rydberg gates based on Förster resonances Shi (2017); Beterov et al. (2016); Petrosyan et al. (2017); Beterov et al. (2018a, b); Khazali and Molmer (2020); Beterov et al. (2020); Stojanovic (2021), our gate depends on van der Waals interactions that naturally appear in well separated atoms without resorting to external fields for tuning a Förster resonance. Since entangling operations between well-separated qubits are necessary for large-scale quantum computing, our method can simplify the quantum circuit in quantum computing because otherwise many standard Rydberg gates are needed to entangle two distant qubits.
The remainder of this article is organized as follows. In Sec. II, we study the controlled-phase gate with an arbitrary phase, and then extend it to a CNOT gate. In Sec. III, we study the achievable gate fidelity with realistic parameters and fluctuation of qubit positions. Section IV gives a comparison between the gate protocols here and previous Rydberg gates with distant qubits. A brief summary is given in Sec. V.
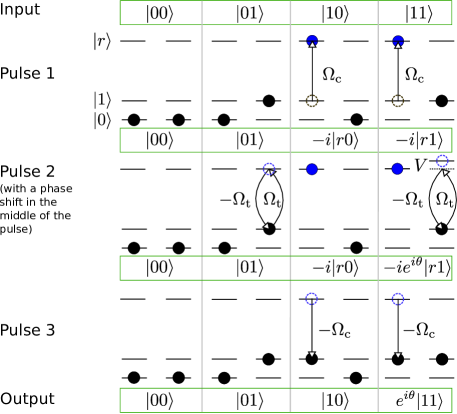
II Two-qubit controlled gates with weak van der Waals interactions
II.1 A controlled-phase gate with an arbitrary phase
We first present the protocol for a controlled-phase gate and then extend it to a CNOT gate in Sec. II.2. In particular, we consider a quantum entanglement operation
| (1) |
by exciting two qubits to Rydberg states via external laser fields, where is tunable via adjustment of the frequency and magnitude of the laser field, and and are the two states of a qubit defined by the two hyperfine-Zeeman ground substates of a heavy alkali-metal atom such as 87Rb and 133Cs. External laser fields are sent to the qubits for exciting to a Rydberg state . Equation (1) is realized effectively by three pulses, where “effectively” means that the total number of pulses is four, but since the middle two pulses only differ by a phase which can be rapidly inserted in the laser fields, the total number of pulses is effectively three as shown in Fig. 1. Pulses 1 and 3 are for exciting and deexciting the control qubits with Rabi frequencies of magnitude , and pulse 2 is for exciting the target qubit with Rabi frequencies of magnitude . Upon the application of pulse 1 with a rotation for the control qubit enabled by the Hamiltonian H.c. in a rotating frame, the input eigenstates evolve as
where the other input state does not evolve since it is not excited because the energy separation between and is GHz for 87Rb which is orders of magnitude larger than ( times) the Rydberg Rabi frequency MHz that we will consider. Then, the probability Saffman and Walker (2005) of Rydberg excitation of is on the order of , which can be ignored.
The Hamiltonian for pulse 2 sent upon the target qubit is H.c., where the sign applies for the first (second) half of pulse 2. During the first half of pulse 2, laser fields are sent to the target qubit for the transition with a Rabi frequency for a pulse duration , where is the Rydberg interaction of the state . As previous studied in Refs. Shi (2017, 2019, 2018); Levine et al. (2019), the interaction will detune the transition between and so that the state rotation has a generalized Rabi frequency . In contrast to the resonant Rabi rotation between two states where one full Rabi cycle results in a phase change to the state, the detuned Rabi cycle will lead to a phase change Shi (2017), so that the state evolution in the first half of pulse 2 is
where
The second half of pulse 2 is similar to its first half, but with a Rabi frequency . With a radiation duration , the input state returns to itself since its total time-evolution operator in the second pulse reduces to an identity because . On the other hand, remarkably, the change of the sign of the Rydberg Rabi frequency does not change the picture of the detuned Rabi oscillation, so that another phase change appears for the input state . As a consequence, the state evolution is
| (2) |
in the second half of pulse 2.
Pulse 3 is similar to pulse 1 but with a phase change to the Rabi frequency which becomes . The rotation restores the state of the control qubit back to the ground state, leading to
With the understanding that the input state does not evolve in the rotating frame, the state transform in Eq. (1) is realized as shown in Fig. 1.

II.2 A CNOT gate
The controlled phase gate studied in Sec. II.1 becomes a CZ gate when , which has the same entangling power Williams (2011) as a CNOT gate. On the other hand, the pulse sequence in Sec. II.1 can be slightly modified so as to directly create a CNOT gate,
| (3) |
The CNOT gate sequence shown in Fig. 2 is similar to that described in Fig. 1 with two modifications. First, pulse 1 and pulse 3 use the same set of laser fields, i.e., no need to have a relative sign difference in the Rabi frequencies as in Fig. 1. Second, in pulse 2, we replace the Rydberg-excitation Hamiltonian H.c. in Fig. 1 by
| (4) |
i.e., (i) the first half of pulse 2 requires two sets of laser fields, one for the Rydberg excitation , and the other for the Rydberg excitation , and (ii) the second half of pulse 2 requires two sets of laser fields, one for the Rydberg excitation , and the other for the Rydberg excitation . This requires simultaneous excitation of both qubit states to a Rydberg state. For two-photon Rydberg excitations, different intermediate states should be used with an example shown in Figs. 2(a) and 2(b). To understand the time evolution of the wavefunctions for different input states in pulse 2, we follow Ref. Shi (2020a) and consider , where as shown in Fig. 2(c). In this basis, Eq. (4) becomes
With the condition (corresponding to in the picture of Sec. II), the first half and the second half of pulse 2, each with duration , lead to
for which a detailed proof is given above Eq. (2). Figure 2(c) shows that the Rydberg deexcitation via pulse 3 leads to a CNOT gate of Eq. (3) with the fact that
III Gate fidelity
The gates can be fast. The total gate duration is according to the pulse sequence in Fig. 1 or Fig. 2. For a CZ or CNOT gate where , we should have the condition
| (5) |
so that the total gate duration is . Rydberg Rabi frequencies around MHz were used for entanglement of individual neutral atoms in Ref. Graham et al. (2019), so the CZ or CNOT gates can have a short duration s if similar Rabi frequencies are employed.
A high fidelity (about ) can be realized with our gates. Because the gate sequences for the CZ and the CNOT gates are similar, we consider the CZ gate as an example. In order to avoid slow gate speed, a Rydberg interaction around or over MHz is desirable. Then, higher Rydberg states are preferred so that the Rydberg interaction can still be around MHz even if the qubits are separated by tens of m. Among the previous demonstrations of neutral atom quantum gates, the highest -orbital Rydberg state of 87Rb atoms ever used had a principal quantum number Isenhower et al. (2010); Zhang et al. (2010). The excitation of -orbital Rydberg states with was demonstrated in an ensemble of 87Rb atoms where coherent many-body phenomena were observed Dudin and Kuzmich (2012). To avoid the anisotropic interaction of -orbital Rydberg states, we consider -orbital Rydberg states whose interaction is highly isotropic in real space Walker and Saffman (2008). For these reasons, we analyze the gate performance with and Rydberg Rabi frequencies
| (6) |
so that the duration will be s for a CZ gate. We note that a similar Rydberg Rabi frequency MHz was used in Zhang et al. (2010) for entanglement of individual 87Rb atoms via the excitation of the states. The Rydberg interaction of for well separated qubits is characterized by Walker and Saffman (2008); Saffman et al. (2010), where THzm6 Shi et al. (2014) is the van der Waals coefficient and is the qubit spacing. To analyze the performance of a CZ gate where in Eq. (1), the condition in Eq. (5) requires that the distance between the centers of the traps for the two qubits should be m with Eq. (6) [which leads to MHz according to Eq. (5)].
There are intrinsic errors from the Rydberg-state decay and the position fluctuations of the atomic qubits when the traps are turned off during the gate sequence (there is also an error due to Doppler dephasing but it is not an intrinsic issue since it is removable by the methods in, e.g., Refs Ryabtsev et al. (2011); Shi (2020b)). The former can be estimated as , where is the lifetime of the Rydberg state and is the total duration for the input state to stay in the Rydberg state averaged over the four input eigenstates,
where is the wavefunction calculated by unitary time evolution from the initial state . Numerical simulation shows in general and s with Eq. (6), and is ms (or 1.10 ms) at room temperature (or at K) Beterov et al. (2009), leading to (or .

The fluctuation of the qubit positions contributes the major error because our gate works perfectly only when the interaction is equal to the desired value. There will be random position fluctuation of the qubits before the traps are switched off, and the atoms fly freely during the gate sequence. This leads to fluctuation of the qubit spacing which results in fluctuation of . A numerical investigation of this matter requires information for realistic r.m.s. qubit-position fluctuations in reference to the trap center. Though most publications on entanglement experiments did not show such details, Ref. Graham et al. (2019) showed that the longitudinal and transverse r.m.s. position fluctuations of the atoms in their traps were m and m, respectively. In order to incorporate the effect of the free flight of the atoms during the gate sequence, we would like to modify the values of r.m.s. fluctuations. The change of the atomic locations during the gate sequence will change the interatomic distance. For an atomic temperature around K (e.g., qubits with K were studied in the entanglement experiments of Refs. Picken et al. (2019), Levine et al. (2018), and Graham et al. (2019), respectively), the r.m.s. distance for a qubit to fly during the gate sequence is about , where is the r.m.s. speed of the atom along one of the three directions in the 3D space, is the effective temperature of the atom, and and are the Boltzmann constant and the atomic mass, respectively. For a free flight of qubits, the average change of distance will be for a duration . So, we analyze the fluctuation of the qubit positions by increasing the r.m.s. fluctuations to
which leads to m in the condition of Eq. (6).
The schematic of position fluctuation is shown in Fig. 3(a). We suppose that the quantization axis is along , and polarized Rydberg laser lights travel along . The Rydberg excitation scheme is shown in Fig. 3(b). The centers of the traps for the control and target qubits are and , respectively. Because of the finiteness of the trap depths, the positions of the control and target qubits are and , respectively, where the distribution function
characterizes , and
is the distribution function for or . In the numerical simulation, the value of is calculated by using the actual distance of the qubits . The average fidelity is sampled with
where the fidelity is defined by Pedersen et al. (2007)
Here, is the actual gate matrix evaluated by using the unitary dynamics with the Rydberg-state decay ignored, and =diag is the ideal gate matrix in the basis . The integral for each is approximated by taking discrete values; for example, for , the sampling is approximated by with , and the total gate fidelity is sampled by similar approximations for . The numerical simulation is resource-demanding, but we can obtain an estimate about the convergence of the integration via slowly varying the steps. For equal to , and , the sampled average fidelities are , and respectively, from which we estimate . With Rydberg-state decay included, the intrinsic fidelity would be (or ) at K (or 4.2 K).
IV Comparison with other methods
The gates in this work have several advantages compared to other gates Jaksch et al. (2000); Shi (2017, 2019); Beterov et al. (2016) that can also work with weak interactions in distant Rydberg atoms.
The first advantage is that our gate does not have rotation errors in the weak interaction regime. It was proposed in Ref. Jaksch et al. (2000) that phase gates can be created via the dynamical phase shift of the van der Waals interaction between two weakly interacting Rydberg atoms as experimentally demonstrated in Ref. Jo et al. (2020). The method of Jaksch et al. (2000) involves the excitation which has an intrinsic error due to the failure for exciting the state from as analyzed in Ref. Saffman and Walker (2005). In contrast, the intrinsic accuracy of the gate here is limited only by the Rydberg-state decay in the weak interaction regime.
The second advantage is that our gate depends on van der Waals interaction that naturally appears between two distant Rydberg atoms. As has been experimentally tested Jo et al. (2020), such a strategy allows an easy access to an experimental demonstration. In comparison, by using Förster resonance one can also design entangling gates between well-separated qubits Beterov et al. (2016, 2020, 2018a, 2018b) but fine tuning via external fields is required Safinya et al. (1981); Anderson et al. (1998); Mourachko et al. (1998); Westermann S. et al. (2006); Nipper et al. (2012); Richards and Jones (2016); Kondo et al. (2016); Ryabtsev et al. (2010); Tretyakov et al. (2014); Faoro et al. (2015); Tretyakov et al. (2017); Cheinet et al. (2020). However, it will be useful to investigate, if possible, an extension of our method to the regime of Förster resonance. If it is indeed possible, high-fidelity entanglement should be reachable with qubits separated even longer than the estimate in this work. This is because the Förster resonant interaction falls off as , while the van der Waals interaction falls off as when increases.
The third advantage is that our method can more easily realize a CZ gate compared to previous high-fidelity gates based on weak van der Waals interactions Shi (2017, 2019). Compared to Ref. Shi (2017) which uses five pulses for coupling two different Rydberg states, the gate here needs only three steps to couple one Rydberg state. Compared to Shi (2019) which proposes a quantum entangling gate that should be repeated several times to form a CZ gate when assisted by single-qubit gates, our method can realize a controlled-phase gate (such as CZ) with any desired phase by only three laser pulses as shown in Fig. 1.
V conclusions
We study a controlled-phase gate based on weak van der Waals interactions between neutral Rydberg atoms. The gate is realized via phase accumulations in detuned Rabi oscillations enabled by weak Rydberg interactions. The gate is easily realizable and can have a high fidelity because it only needs three steps to couple one type of Rydberg state, has no intrinsic rotation errors in the weak interaction regime, and does not depend on fine tuning of Förster resonant processes. We use practical parameters to show that it is possible to create a CZ gate in two qubits separated by m with a fidelity about or at 4.2 K (or at room temperature). We also show that a similar pulse sequence can lead to a CNOT gate which is realizable with similarly small van der Waals interactions. The theory brings hope to simplify the quantum circuit for large-scale quantum computing in which entanglement between distant qubits is required.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China under Grants No. 12074300 and No. 11805146, the Natural Science Basic Research plan in Shaanxi Province of China under Grant No. 2020JM-189, and the Fundamental Research Funds for the Central Universities.
References
- Saffman et al. (2010) M. Saffman, T. G. Walker, and K. Mølmer, Quantum information with Rydberg atoms, Rev. Mod. Phys. 82, 2313 (2010).
- Saffman (2016) M. Saffman, Quantum computing with atomic qubits and Rydberg interactions: Progress and challenges, J. Phys. B 49, 202001 (2016).
- Weiss and Saffman (2017) D. S. Weiss and M. Saffman, Quantum computing with neutral atoms, Phys. Today 70, 44 (2017).
- Adams et al. (2020) C. S. Adams, J. D. Pritchard, and J. P. Shaffer, Rydberg atom quantum technologies, J. Phys. B: At. Mol. Opt. Phys. 53, 012002 (2020).
- Wu et al. (2021) X. Wu, X. Liang, Y. Tian, F. Yang, C. Chen, Y. C. Liu, M. K. Tey, and L. You, A concise review of Rydberg atom based quantum computation and quantum simulation, Chin. Phys. B 30, 020305 (2021).
- Morgado and Whitlock (2021) M. Morgado and S. Whitlock, Quantum simulation and computing with Rydberg-interacting qubits, AVS Quantum Sci. 3, 023501 (2021).
- Wilk et al. (2010) T. Wilk, A. Gaëtan, C. Evellin, J. Wolters, Y. Miroshnychenko, P. Grangier, and A. Browaeys, Entanglement of Two Individual Neutral Atoms Using Rydberg Blockade, Phys. Rev. Lett. 104, 010502 (2010).
- Isenhower et al. (2010) L. Isenhower, E. Urban, X. L. Zhang, A. T. Gill, T. Henage, T. A. Johnson, T. G. Walker, and M. Saffman, Demonstration of a Neutral Atom Controlled-NOT Quantum Gate, Phys. Rev. Lett. 104, 010503 (2010).
- Zhang et al. (2010) X. L. Zhang, L. Isenhower, A. T. Gill, T. G. Walker, and M. Saffman, Deterministic entanglement of two neutral atoms via Rydberg blockade, Phys. Rev. A 82, 030306(R) (2010).
- Maller et al. (2015) K. M. Maller, M. T. Lichtman, T. Xia, Y. Sun, M. J. Piotrowicz, A. W. Carr, L. Isenhower, and M. Saffman, Rydberg-blockade controlled-not gate and entanglement in a two-dimensional array of neutral-atom qubits, Phys. Rev. A 92, 022336 (2015).
- Jau et al. (2016) Y.-Y. Jau, A. M. Hankin, T. Keating, I. H. Deutsch, and G. W. Biedermann, Entangling atomic spins with a Rydberg-dressed spin-flip blockade, Nat. Phys. 12, 71 (2016).
- Zeng et al. (2017) Y. Zeng, P. Xu, X. He, Y. Liu, M. Liu, J. Wang, D. J. Papoular, G. V. Shlyapnikov, and M. Zhan, Entangling Two Individual Atoms of Different Isotopes via Rydberg Blockade, Phys. Rev. Lett. 119, 160502 (2017).
- Levine et al. (2018) H. Levine, A. Keesling, A. Omran, H. Bernien, S. Schwartz, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić, and M. D. Lukin, High-fidelity control and entanglement of Rydberg atom qubits, Phys. Rev. Lett. 121, 123603 (2018).
- Picken et al. (2019) C. J. Picken, R. Legaie, K. McDonnell, and J. D. Pritchard, Entanglement of neutral-atom qubits with long ground-Rydberg coherence times, Quantum Sci. Technol. 4, 015011 (2019).
- Levine et al. (2019) H. Levine, A. Keesling, G. Semeghini, A. Omran, T. T. Wang, S. Ebadi, H. Bernien, M. Greiner, V. Vuletić, H. Pichler, and M. D. Lukin, Parallel implementation of high-fidelity multi-qubit gates with neutral atoms, Phys. Rev. Lett. 123, 170503 (2019).
- Graham et al. (2019) T. M. Graham, M. Kwon, B. Grinkemeyer, Z. Marra, X. Jiang, M. T. Lichtman, Y. Sun, M. Ebert, and M. Saffman, Rydberg mediated entanglement in a two-dimensional neutral atom qubit array, Phys. Rev. Lett. 123, 230501 (2019).
- Jo et al. (2020) H. Jo, Y. Song, M. Kim, and J. Ahn, Rydberg atom entanglements in the weak coupling regime, Phys. Rev. Lett. 124, 033603 (2020).
- Madjarov et al. (2020) I. S. Madjarov, J. P. Covey, A. L. Shaw, J. Choi, A. Kale, A. Cooper, H. Pichler, V. Schkolnik, J. R. Williams, and M. Endres, High-fidelity entanglement and detection of alkaline-earth Rydberg atoms, Nat. Phys. 16, 857 (2020).
- Jaksch et al. (2000) D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté, and M. D. Lukin, Fast Quantum Gates for Neutral Atoms, Phys. Rev. Lett. 85, 2208 (2000).
- Weimer et al. (2012) H. Weimer, N. Y. Yao, C. R. Laumann, and M. D. Lukin, Long-Range Quantum Gates using Dipolar Crystals, Phys. Rev. Lett. 108, 100501 (2012).
- Cesa and Martin (2017) A. Cesa and J. Martin, Two-qubit entangling gates between distant atomic qubits in a lattice, Phys. Rev. A 95, 052330 (2017).
- Shi (2017) X.-F. Shi, Rydberg Quantum Gates Free from Blockade Error, Phys. Rev. Appl. 7, 064017 (2017).
- Beterov et al. (2016) I. I. Beterov, M. Saffman, E. A. Yakshina, D. B. Tretyakov, V. M. Entin, S. Bergamini, E. A. Kuznetsova, and I. I. Ryabtsev, Two-qubit gates using adiabatic passage of the Stark-tuned Forster resonances in Rydberg atoms, Phys. Rev. A 94, 062307 (2016).
- Petrosyan et al. (2017) D. Petrosyan, F. Motzoi, M. Saffman, and K. Mølmer, High-fidelity Rydberg quantum gate via a two-atom dark state, Phys. Rev. A 96, 042306 (2017).
- Beterov et al. (2018a) I. I. Beterov, G. N. Hamzina, E. A. Yakshina, D. B. Tretyakov, V. M. Entin, and I. I. Ryabtsev, Adiabatic passage of radiofrequency-assisted Forster resonances in Rydberg atoms for two-qubit gates and generation of Bell states, Phys. Rev. A 97, 032701 (2018a).
- Beterov et al. (2018b) I. I. Beterov, I. N. Ashkarin, E. A. Yakshina, D. B. Tretyakov, V. M. Entin, I. I. Ryabtsev, P. Cheinet, P. Pillet, and M. Saffman, Fast three-qubit Toffoli quantum gate based on the three-body Forster resonances in Rydberg atoms, Phys. Rev. A 98, 042704 (2018b).
- Khazali and Molmer (2020) M. Khazali and K. Molmer, Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits, Phys. Rev. X 10, 021054 (2020).
- Beterov et al. (2020) I. I. Beterov, D. B. Tretyakov, V. M. Entin, E. A. Yakshina, I. I. Ryabtsev, M. Saffman, and S. Bergamini, Application of adiabatic passage in Rydberg atomic ensembles for quantum information processing, J. Phys. B 53, 182001 (2020).
- Stojanovic (2021) V. M. Stojanovic, Scalable W -type entanglement resource in neutral-atom arrays with Rydberg-dressed resonant dipole-dipole interaction, Phys. Rev. A 103, 022410 (2021).
- Saffman and Walker (2005) M. Saffman and T. G. Walker, Analysis of a quantum logic device based on dipole-dipole interactions of optically trapped Rydberg atoms, Phys. Rev. A 72, 022347 (2005).
- Shi (2019) X.-F. Shi, Fast, Accurate, and Realizable Two-Qubit Entangling Gates by Quantum Interference in Detuned Rabi Cycles of Rydberg Atoms, Phys. Rev. Appl. 11, 044035 (2019).
- Shi (2018) X.-F. Shi, Accurate Quantum Logic Gates by Spin Echo in Rydberg Atoms, Phys. Rev. Appl. 10, 034006 (2018).
- Williams (2011) C. P. Williams, Explorations in Quantum Computing, 2nd ed., edited by D. Gries and F. B. Schneider, Texts in Computer Science (Springer-Verlag, London, 2011).
- Shi (2020a) X.-F. Shi, Transition Slow-Down by Rydberg Interaction of Neutral Atoms and a Fast Controlled- NOT Quantum Gate, Phys. Rev. Appl. 14, 054058 (2020a).
- Dudin and Kuzmich (2012) Y. O. Dudin and A. Kuzmich, Strongly interacting Rydberg excitations of a cold atomic gas. Science 336, 887 (2012).
- Walker and Saffman (2008) T. G. Walker and M. Saffman, Consequences of Zeeman degeneracy for the van der Waals blockade between Rydberg atoms, Phys. Rev. A 77, 032723 (2008).
- Shi et al. (2014) X.-F. Shi, F. Bariani, and T. A. B. Kennedy, Entanglement of neutral-atom chains by spin-exchange Rydberg interaction, Phys. Rev. A 90, 062327 (2014).
- Ryabtsev et al. (2011) I. I. Ryabtsev, I. I. Beterov, D. B. Tretyakov, V. M. Entin, and E. A. Yakshina, Doppler- and recoil-free laser excitation of Rydberg states via three-photon transitions, Phys. Rev. A 84, 053409 (2011).
- Shi (2020b) X.-F. Shi, Suppressing Motional Dephasing of Ground-Rydberg Transition for High-Fidelity Quantum Control with Neutral Atoms, Physical Review Applied 13, 024008 (2020b).
- Beterov et al. (2009) I. I. Beterov, I. I. Ryabtsev, D. B. Tretyakov, and V. M. Entin, Quasiclassical calculations of blackbody-radiation-induced depopulation rates and effective lifetimes of Rydberg nS, nP, and nD alkali-metal atoms with n80, Phys. Rev. A 79, 052504 (2009).
- Pedersen et al. (2007) L. H. Pedersen, N. M. Møller, and K. Mølmer, Fidelity of quantum operations, Phys. Lett. A 367, 47 (2007).
- Safinya et al. (1981) K. A. Safinya, J. F. Delpech, F. Gounand, W. Sandner, and T. F. Gallagher, Resonant Rydberg-Atom-Rydberg-Atom Collisions, Phys. Rev. Lett. 47, 405 (1981).
- Anderson et al. (1998) W. R. Anderson, J. R. Veale, and T. F. Gallagher, Resonant Dipole-Dipole Energy Transfer in a Nearly Frozen Rydberg Gas, Phys. Rev. Lett. 80, 249 (1998).
- Mourachko et al. (1998) I. Mourachko, D. Comparat, F. de Tomasi, A. Fioretti, P. Nosbaum, V. M. Akulin, and P. Pillet, Many-Body Effects in a Frozen Rydberg Gas, Phys. Rev. Lett. 80, 253 (1998).
- Westermann S. et al. (2006) Westermann S., Amthor T., d. O. A. L., Deiglmayr J., Reetz-Lamour M., and Weidemüller M., Dynamics of resonant energy transfer in a cold Rydberg gas, Eur. Phys. J. D 40, 37 (2006).
- Nipper et al. (2012) J. Nipper, J. B. Balewski, A. T. Krupp, B. Butscher, R. Löw, and T. Pfau, Highly Resolved Measurements of Stark-Tuned Förster Resonances between Rydberg Atoms, Phys. Rev. Lett. 108, 113001 (2012).
- Richards and Jones (2016) B. G. Richards and R. R. Jones, Dipole-dipole resonance line shapes in a cold Rydberg gas, Phys. Rev. A 93, 042505 (2016).
- Kondo et al. (2016) J. M. Kondo, D. Booth, L. F. Goncalves, J. P. Shaffer, and L. G. Marcassa, Role of multilevel Rydberg interactions in electric-field-tuned Förster resonances, Phys. Rev. A 93, 012703 (2016).
- Ryabtsev et al. (2010) I. I. Ryabtsev, D. B. Tretyakov, I. I. Beterov, and V. M. Entin, Observation of the stark-tuned Forster resonance between two rydberg atoms, Phys. Rev. Lett. 104, 073003 (2010).
- Tretyakov et al. (2014) D. B. Tretyakov, V. M. Entin, E. a. Yakshina, I. I. Beterov, C. Andreeva, and I. I. Ryabtsev, Controlling the interactions of a few cold Rb Rydberg atoms by radio-frequency-assisted Forster resonances, Phys. Rev. A 90, 041403(R) (2014).
- Faoro et al. (2015) R. Faoro, B. Pelle, A. Zuliani, P. Cheinet, E. Arimondo, and P. Pillet, Borromean three-body FRET in frozen Rydberg gases, Nat. Comm. 6, 8173 (2015).
- Tretyakov et al. (2017) D. B. Tretyakov, I. I. Beterov, E. A. Yakshina, V. M. Entin, I. I. Ryabtsev, P. Cheinet, and P. Pillet, Observation of the Borromean three-body Förster resonances for three interacting Rb Rydberg atoms, Phys. Rev. Lett. 119, 173402 (2017).
- Cheinet et al. (2020) P. Cheinet, K. L. Pham, P. Pillet, I. I. Beterov, I. N. Ashkarin, D. B. Tretyakov, E. A. Yakshina, V. M. Entin, and I. I. Ryabtsev, Three-body Förster resonance of a new type in Rydberg atoms, Quantum Electronics 50, 213 (2020).