Quantum entanglement estimation via symmetric measurement based positive maps

Quantum entanglement is the key resource in quantum information processing and plays an important role in quantum communication, quantum computing and other modern quantum technologies Hor2009 . Therefore, it is of significance to distinguish the entangled states from the separable ones and estimate degree of entanglement for the entangled states. However, generally the separability problem and the estimation of entanglement are very difficult and even NP-hard 2 . For low dimensional systems like $\mathbb{C}^{2}\otimes\mathbb{C}^{2}$ (qubit-qubit) and $\mathbb{C}^{2}\otimes\mathbb{C}^{3}$ (qubit-qutrit), the celebrated positive partial transposition (PPT) criterion is both necessary and sufficient for separability 3 ; 4 . For higher dimensional systems, more sophisticated methods are needed to detect the entanglement.

One separability criterion to detect entanglement is given by positive maps. A bipartite state $\rho$ is separable if and only if $(\mathbb{I}\otimes\Phi)(\rho)\geq 0$ for any positive map $\Phi$ 5 , where $\mathbb{I}$ is the identity operator. Namely, $\rho$ is entangled if $(\mathbb{I}\otimes\Phi)(\rho)$ has negative eigenvalues for some positive map $\Phi$.

Entanglement can be also detected by entanglement witnesses. A Hermitian operator $W$ is called an entanglement witness if $\text{Tr}(W\rho_{sep})\geq 0$ for all separable states $\rho_{sep}$, and $\text{Tr}(W\rho)<0$ for some entangled sates $\rho$ 6 ; 7 . By Choi-Jamiołkowski isomorphism an entanglement witness is related to a positive but not completely positive map $\Phi$. One kind of entanglement witnesses is the decomposable one, for which an entanglement witness can be written as $W=A+B^{\Gamma}$, where $A,B\geq 0$ and $B^{\Gamma}=(\mathbb{I}\otimes T)B$ with $T$ denoting the transpose. However, the decomposable witness cannot detect the positive partial transpose (PPT) entangled states that are positive under partial transpose. The indecomposable witnesses can detect the PPT states 5 ; 9 ; 10 ; 11 ; 12 , which can be constructed by using realignment separability criterion 13 ; 14 ; 15 and covariance matrix criterion 16 ; 17 ; 18 . In 19 , the authors constructed a class of indecomposable witnesses by using MUBs (mutually unbiased bases). This method was extended to the one by using MUMs (mutually unbiased measurements) and SIC-POVMs (symmetric informationally complete measurements). New entanglement witnesses have been also obtained 20 ; 21 ; 22 . Recently, a new kind of measurements, called symmetric measurements, has been proposed in 23 . Based on the symmetric measurements a class of positive maps and entanglement witnesses are constructed in 24 .

To quantify the entanglement, many measures have been presented such as the entanglement of formation (EOF) 25 ; 26 and concurrence 27 ; 28 ; 29 . However, it is a challenge to evaluate the entanglement measures for general quantum states. Instead of analytic formulas, progress has been made toward the lower bounds of EOF and concurrence. Based on a positive map, a new lower bound of concurrence for arbitrary dimensional bipartite systems has been derived in 30 , which detects the entanglement that is not detected by the previous lower bounds 31 ; 32 .

In this paper, we first present a family of positive and trace-preserving maps based on symmetric measurements. Then we present new separability criteria and show that these separability criteria detect better entanglement of quantum states by a exact example. We then construct a series of entanglement witnesses which include some existing ones as special cases. These entanglement witnesses are shown to detect better entanglement including bound entanglements. At last we give a family of lower bounds of concurrence and demonstrate that the bounds estimate better the quantum entanglement than the existing ones.

A positive operator-valued measure (POVM) is given by a set of positive operators $\{E_{\alpha}\mid E_{\alpha}\geq 0,~{}\sum_{\alpha}E_{\alpha}=\mathbb{I}\}$. For a given state $\rho$, the probability of the measurement outcome with respect to $E_{\alpha}$ is $p_{\alpha}=\text{Tr}(E_{\alpha}\rho)$. Recently, a new POVM called symmetric measurement has been provided in 23 . A set of $N$ $d$-dimensional POVMs $\{E_{\alpha,k}|\,E_{\alpha,k}\geq 0,\,\sum\limits_{k=1}^{M}E_{\alpha,k}=\mathbb{I}_{d}\}$, $\alpha=1,\ldots,N$ is called $(N,M)$-POVM, which satisfies the following symmetry properties,

$\displaystyle\begin{split}\text{Tr}(E_{\alpha,k})&=\frac{d}{M},\\ \text{Tr}(E_{\alpha,k}^{2})&=x,\\ \text{Tr}(E_{\alpha,k}E_{\alpha,\ell})&=\frac{d-Mx}{M(M-1)},\quad\ell\neq k,\\ \text{Tr}(E_{\alpha,k}E_{\beta,\ell})&=\frac{d}{M^{2}},\quad\beta\neq\alpha,\end{split}$

(1)

where

$\displaystyle\frac{d}{M^{2}}<x\leq\min\left\{\frac{d^{2}}{M^{2}},\frac{d}{M}\right\}.$

(2)

For any fixed dimension $d<\infty$, there are at least four different types of information complete $(N,M)$-POVMs: i) $M=d^{2}$ and $N=1$ (general SIC POVM) 34 ; ii) $M=d$ and $N=d+1$ (MUMs) 35 ; iii) $M=2$ and $N=d^{2}-1$; iv) $M=d+2$ and $N=d-1$. A general construction of informationally complete $(N,M)$-POVMs has been presented by using orthonormal Hermitian operator bases $\{G_{0}=\mathbb{I}_{d}/\sqrt{d},\,G_{\alpha,k};\,\alpha=1,\ldots,N,\,k=1,\ldots,M-1\}$ with $\text{Tr}(G_{\alpha,k})=0$,

$\displaystyle E_{\alpha,k}=\frac{1}{M}\mathbb{I}_{d}+tH_{\alpha,k},$

(3)

where

$$H_{\alpha,k}=\left\{\begin{aligned} &G_{\alpha}-\sqrt{M}(\sqrt{M}+1)G_{\alpha,k},\,k=1,\ldots,M-1,\\ &(\sqrt{M}+1)G_{\alpha},\,k=M,\end{aligned}\right.$$

(4)

and $G_{\alpha}=\sum\limits_{k=1}^{M-1}G_{\alpha,k}$. The parameters $t$ and $x$ satisfy the following relation,

$\displaystyle x=\frac{d}{M^{2}}+t^{2}(M-1)(\sqrt{M}+1)^{2}.$

(5)

The optimal value $x_{\rm opt}$, which is the greatest $x$ such that $E_{\alpha,k}\geq 0$, depends on the operator bases. There always exist informationally complete $(N,M)$-POVMs for any integer $d$.

In 24 the following class of positive maps have been presented,

$$\Phi(X)=\frac{1}{b}\Big{[}a\Phi_{0}(X)+\sum_{\alpha=L+1}^{N}\Phi_{\alpha}(X)-\sum_{\alpha=1}^{L}\Phi_{\alpha}(X)\Big{]},$$

(6)

where $a=b-N+2L$, $b=\frac{(d-1)M(x-y)}{d}$, $\Phi_{0}(X)=\frac{\text{Tr}(X)}{d}\mathbb{I}_{d}$ and

$$\Phi_{\alpha}(X)=\frac{M}{d}\sum_{k,l=1}^{M}\mathcal{O}^{(\alpha)}_{k\ell}E_{\alpha,k}\text{Tr}(XE_{\alpha,l})$$

(7)

are $N$ trace-preserving maps given by $(N,M)$-POVMs $\{E_{\alpha,k}\}$ with $\{\mathcal{O}^{(\alpha)}|\mathcal{O}^{(\alpha)}=(\mathcal{O}^{(\alpha)}_{k\ell}),\,\alpha=1,\cdots,N\}$ being a set of $M\times M$ orthogonal rotation operators that preserve the vector $\mathbf{n}_{\ast}=(1,\ldots,1)/\sqrt{d}$.

Using the maps (6), we have the following theorem.

Theorem 1. A bipartite state $\rho$ is entangled if $(\mathbb{I}\otimes\Phi_{z})(\rho)\ngeq 0$, where

$$\Phi_{z}(X)=(1-z)\Phi_{0}(X)+z\Phi(X),~{}\forall X\in\mathbb{M}_{d}$$

(8)

are positive and trace preserving linear maps with $z\in[-1,1]$.

By entanglement witnesses one can detect the entanglement of unknown quantum states experimentally. An entanglement witness $W$ can be obtained based on positive but not completely positive map $\Phi$ through Choi-Jamiołkowski isomorphism J ,

$\displaystyle W=\sum_{k,\ell=1}^{d}|k\rangle\langle\ell|\otimes\Phi[|k\rangle\langle\ell|],$

(12)

where $\{|k\rangle\}^{d}_{k=1}$ is an orthonormal basis in $\mathbb{C}^{d}$. Therefore, by using the positive maps in Theorem 1, we get the following entanglement witnesses,

$\displaystyle W=\frac{1}{b}\left(\frac{aw}{d}\mathbb{I}_{d^{2}}+\sum_{\alpha=L+1}^{N}K_{\alpha}-\sum_{\alpha=1}^{L}K_{\alpha}\right),$

(13)

where

$\displaystyle K_{\alpha}=\frac{Mz}{d}\sum_{k,\ell=1}^{M}\mathcal{O}_{k\ell}^{(\alpha)}\overline{E}_{\alpha,\ell}\otimes E_{\alpha,k}$

(14)

with $\overline{E}_{\alpha,\ell}$ the conjugation of $E_{\alpha,l}$. In particular, when $z=1$ our witnesses includes the one given in 24 as a special case.

As the informationally complete $(N,M)$-POVMs can be constructed by using an orthogonal basis $\{\mathbb{I}_{d}/\sqrt{d},G_{\alpha,k}\}$ of traceless Hermitian operators $G_{\alpha,k}$ for any dimension $d$, we have the following entanglement witnesses,

$$\mathaccent 869{W}=\frac{b}{t^{2}}W=\frac{d-1}{d^{2}}M^{2}(\sqrt{M}+1)^{2}\mathbb{I}_{d^{2}}+\sum_{\alpha=L+1}^{N}J_{\alpha}-\sum_{\alpha=1}^{L}J_{\alpha},$$

(15)

where

$\displaystyle J_{\alpha}=\frac{Mz}{d}\sum_{k,\ell=1}^{M}\mathcal{O}_{kl}^{(\alpha)}\overline{H}_{\alpha,\ell}\otimes H_{\alpha,k}$

(16)

with $\overline{H}_{\alpha,\ell}$ the conjugation of $H_{\alpha,l}$. Note that these witnesses don’t depend on the parameter $x$ that characterizes the symmetric measurements. But $\mathaccent 869{W}$ are relate to the number $M$ of operators in a single POVM. The larger the value of $M$ is, the larger the $L$ can be.

Notice that $J_{\alpha}$ in (16) can be directly represented by the operator basis $\{G_{0}=\mathbb{I}_{d}/\sqrt{d},G_{\alpha,k};\,\alpha=1,\ldots,N,\,k=1,\ldots,M-1\}$, since $H_{\alpha,k}$ are directly given by $G_{\alpha,k}$. By using (4), we further obtain

$\displaystyle J_{\alpha}=\frac{Mz}{d}\sum_{k,\ell=1}^{M-1}\mathcal{Q}_{kl}^{(\alpha)}\overline{G}_{\alpha,\ell}\otimes G_{\alpha,k},$

where

	$\displaystyle\mathcal{Q}_{k\ell}^{(\alpha)}=$		$\displaystyle M(\mathcal{O}_{MM}^{(\alpha)}-1)+M(\sqrt{M}+1)^{2}\mathcal{O}_{k\ell}^{(\alpha)}$		(17)
			$\displaystyle-M(\sqrt{M}+1)(\mathcal{O}_{M\ell}^{(\alpha)}+\mathcal{O}_{kM}^{(\alpha)}).$

Since

$\displaystyle\mathcal{Q}^{(\alpha)T}\mathcal{Q}^{(\alpha)}=\mathcal{Q}^{(\alpha)}\mathcal{Q}^{(\alpha)T}=M^{2}(\sqrt{M}+1)^{4}\mathbb{I}_{M-1},$

$\mathcal{Q}^{(\alpha)}=(\mathcal{Q}_{k\ell}^{(\alpha)})$ $(\alpha=1,\cdots,N)$ are $M\times M$ rescaled orthogonal matrices. When $\mathcal{O}^{(\alpha)}=\mathbb{I}_{M}$, (17) can be rewritten as

$\displaystyle\mathcal{Q}_{k\ell}^{(\alpha)}=M(\sqrt{M}+1)^{2}\delta_{k\ell}.$

(18)

Next, we illustrate that $\mathaccent 869{W}$ (15) are related to a well-known class of entanglement witnesses. Suppose the $(N,M)$-POVM is informationally complete and $L=N$. The corresponding witnesses is

$\displaystyle\mathaccent 869{W}=\frac{M^{2}}{d}(\sqrt{M}+1)^{2}\Bigg{[}\mathbb{I}_{d^{2}}-G_{0}\otimes G_{0}-\frac{d}{M^{2}(\sqrt{M}+1)^{2}}\sum_{\alpha=1}^{N}J_{\alpha}\Bigg{]},$

(19)

where $G_{0}=\mathbb{I}_{d}/\sqrt{d}$. By a simple relabelling of the indices $(\alpha,k)\longmapsto\mu$, we have

$\displaystyle\mathaccent 869{W}^{\prime}=\frac{d\mathaccent 869{W}}{M^{2}(\sqrt{M}+1)^{2}}=\mathbb{I}_{d^{2}}-\sum_{\mu,\nu=0}^{d^{2}-1}Q_{\mu\nu}G_{\mu}^{T}\otimes G_{\nu},$

(20)

where $Q_{\mu\nu}$ are the entries of the following block-diagonal orthogonal matrix,

$\displaystyle Q=\frac{1}{M(\sqrt{M}+1)^{2}}\left[\begin{array}[]{c c c c c}M(\sqrt{M}+1)^{2}&&&&\\ &z\mathcal{Q}^{(1)T}&&&\\ &&z\mathcal{Q}^{(2)T}&&\\ &&&\ddots&\\ &&&&z\mathcal{Q}^{(N)T}\end{array}\right].$

(26)

Therefore, the entanglement witnesses $\mathaccent 869{W}$ constructed from symmetric measurements belong to a larger category of witnesses

$\displaystyle W^{\prime}=\mathbb{I}_{d^{2}}-\sum_{\mu,\nu=0}^{d^{2}-1}Q_{\mu\nu}G_{\mu}^{T}\otimes G_{\nu},$

(27)

which are related to the CCNR criterion Y . The $G_{\mu}$ (27) are the elements of an arbitrary orthonormal Hermitian basis, and $Q=(Q_{\mu\nu})$ is an arbitrary $d^{2}\times d^{2}$ orthogonal matrix with $Q^{T}Q=\mathbb{I}_{d^{2}}$ (in fact, $Q^{T}Q\leq\mathbb{I}_{d^{2}}$ is sufficient).

For any informationally complete $(N,M)$-POVM, assume that $\mathcal{O}^{(\alpha)}=\mathbb{I}_{M}$ and $L=N$. According to $(\ref{Id})$ we have $Q=\text{diag}(1,z,z,\cdots,z)$. The associated entanglement witnesses write

$\displaystyle\mathaccent 869{W}^{\prime}=\mathbb{I}_{d^{2}}-G_{0}\otimes G_{0}-z\sum_{\mu=1}^{d^{2}-1}G_{\mu}^{T}\otimes G_{\mu}.$

(28)

Therefore, it is possible to use different $(N,M)$-POVMs to generate the same witnesses $\mathaccent 869{W}^{\prime}$, provided that the same Hermitian orthonormal basis is used.

Let $M=2$. Then the rotation matrices can only be $\mathcal{O}^{(\alpha)}=\mathbb{I}_{2}$ or $\mathcal{O}^{(\alpha)}=\sigma_{1}=\left[\begin{array}[]{c c}0&1\\ 1&0\end{array}\right]$. In this case, all witnesses constructed from $(N,2)$-POVMs have the following form,

	$\displaystyle\mathaccent 869{W}^{\prime}=$		$\displaystyle\mathbb{I}_{d^{2}}-G_{0}\otimes G_{0}+z(\sum_{\alpha=L+1}^{N}G_{\alpha}^{T}\otimes G_{\alpha}$		(29)
			$\displaystyle-\sum_{\alpha=1}^{L}G_{\alpha}^{T}\otimes G_{\alpha}),$

where $N\leq d^{2}-1$.

To show the advantages of our entanglement witnesses in detecting quantum entanglement, we compare our entanglement witnesses with the ones presented in 24 by three examples, which show that our entanglement witnesses can detect more entangled quantum states, see Appendix D.

Let $H_{1}$ and $H_{2}$ be $d$-dimensional vector spaces. A bipartite quantum pure state $|\psi\rangle$ in $H_{1}\otimes H_{2}$ has a Schmidt form

$\displaystyle|\psi\rangle=\sum_{i}\alpha_{i}|e_{i}^{1}\rangle\otimes|e_{i}^{2}\rangle,$

(30)

where $|e_{i}^{1}\rangle$ and $|e_{i}^{2}\rangle$ are the orthonormal bases in $H_{1}$ and $H_{2}$, respectively, and $\alpha_{i}$ are the Schmidt coefficients satisfying $\sum_{i}\alpha_{i}^{2}=1$. The concurrence $C(|\psi\rangle)$ of the state $|\psi\rangle$ is given by

$\displaystyle C(|\psi\rangle)=\sqrt{2(1-\text{Tr}\rho_{1}^{2})}=2\sqrt{\sum_{i<j}\alpha_{i}^{2}\alpha_{j}^{2}},$

(31)

where $\rho_{1}=\text{Tr}_{2}(|\psi\rangle\langle\psi|)$ is the reduced state obtained by tracing over the second space C .

The concurrence is extended to mixed states $\rho$ by the convex roof,

$\displaystyle C(\rho)=\text{min}\sum_{i}p_{i}C(|\psi_{i}\rangle),$

(32)

where the minimum is taken over all possible pure state decompositions of $\rho=\sum_{i}p_{i}|\psi_{i}\rangle\langle\psi_{i}|$, where $p_{i}\geq 0$ and $\sum_{i}p_{i}=1$. Generally it is formidably difficult to calculate $C(\rho)$. Instead, one considers the lower bound of $C(\rho)$.

In 32 the authors presented a lower bound of $C(\rho)$,

$\displaystyle C(\rho)\geq\sqrt{\frac{2}{d(d-1)}}f(\rho),$

(33)

where $f(\rho)$ is a real-valued and convex function satisfying

$\displaystyle f(|\psi\rangle\langle\psi|)\leq 2\sum_{i<j}\alpha_{i}\alpha_{j}$

(34)

for all pure states $|\psi\rangle$ given by (30).

A lower bound (33) of concurrence can be obtained from a function $f$ satisfying (34) for arbitrary pure states. Nevertheless, it is still a problem to find such function $f$. In fact, there are positive maps which can be used as separability criteria, but one has difficulties to use them to obtain lower bounds of concurrence by finding such functions $f$. Based on the positive map defined in (8), we construct below new functions $f$ to obtain new lower bounds of concurrence $C(\rho)$. Setting $M=d$, $L=N=d+1$ and using the $(N,M)$-POVM constructed from the Gell-Mann matrices 35 in $\Phi$, we have the following theorem, see the proof given in Appendix E.

Theorem 2. For any bipartite quantum state $\rho\in H_{1}\otimes H_{2}$, the concurrence $C(\rho)$ satisfies

$\displaystyle C(\rho)\geq\sqrt{\frac{2}{d(d-1)}}(\|(\mathbb{I}_{d}\otimes\Phi_{z})\rho\|-1),$

(35)

where $\mathbb{I}_{d}$ is identity operator, $\Phi_{z}$ is given in (8), $\|\cdot\|$ stands for the trace norm.

It has been always a challenging problem to find new separability criteria which detect better entanglement, and new lower bounds of entanglement which are larger than the existing ones, at least for some quantum states. We have presented such separability criterion and lower bounds. We illustrate our results below by a detailed example.

Example 1. Let us consider the state (11). From (35) we have

$\displaystyle C(\rho)\geq\sqrt{\frac{1}{6}}(\|(\mathbb{I}_{4}\otimes\Phi_{z})(\rho)\|-1)=\frac{1}{2\sqrt{6}}(\frac{2}{3}q_{1}z-\frac{1}{24}z-\frac{1}{8}+|\frac{2}{3}q_{1}z-\frac{1}{24}z-\frac{1}{8}|).$

(36)

In 30 , a lower bound of the concurrence is given by

$\displaystyle C(\rho)\geq\sqrt{\frac{1}{6}}(\|(\mathbb{I}_{4}\otimes\Phi^{{}^{\prime}})(\rho)\|-3)=\frac{1}{4\sqrt{6}}(q_{1}-q_{4}+|q_{1}-q_{4}|).$

(37)

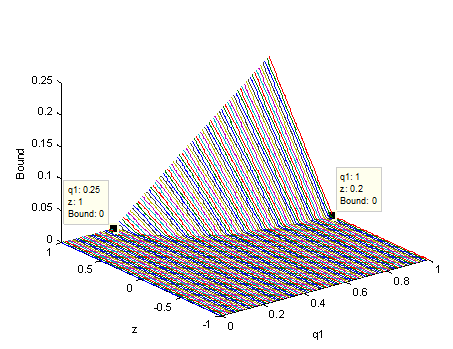
Fig. 1 shows the lower bounds of concurrence given in (36) for the state (11) versus parameters $z$ and $q_{1}$. We see that the lower bounds of concurrence are greater than 0 when $0.2<z\leq 1$, namely, the entanglement of states (11) are detected in this case. When $z=1$ and $0.25<q_{1}<1$, the lower bound of concurrence is greater than 0. When $z<1$, from Fig. 1 one sees the detected entanglement range of $\rho$ and the lower bound of concurrence decreases with $z$. When $z\leq 0.2$, it can be seen from Fig. 1 that the lower bounds of concurrence becomes 0. The lower bound of (36) reaches the maximum at $z=1$.

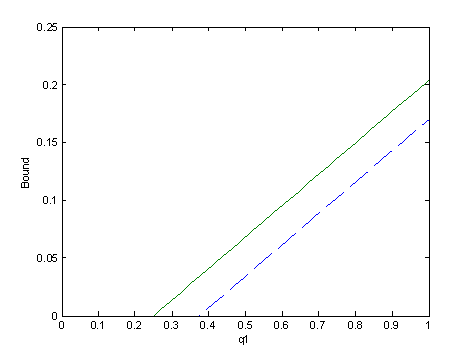
Our lower bounds of concurrence in (36) are better than the lower bounds of concurrence in (37) given in 30 at least for some states. Let us take $z=1$ and $q_{4}=-\frac{1}{3}q_{1}+\frac{1}{2}$. Then (36) can be written as $C(\rho)\geq\frac{1}{2\sqrt{6}}(\frac{2}{3}q_{1}-\frac{1}{6}+|\frac{2}{3}q_{1}-\frac{1}{6}|)$, while (37) can be written as $C(\rho)\geq\frac{1}{4\sqrt{6}}(\frac{4}{3}q_{1}-\frac{1}{2}+|\frac{4}{3}q_{1}-\frac{1}{2}|)$. From Fig. 2 it is seen that our bound of concurrence (36) detects the entanglement for $q_{1}>0.25$, while the bound of concurrence in (37) detects entanglement for $q_{1}>0.375$.

Based on symmetric measurements we have presented a family of positive and trace-preserving maps. From these maps we have obtained separability criteria which detect better the entanglement of quantum states. We have also constructed a series of entanglement witnesses which include some existing ones as special cases and detect even the entanglement of bound entangled states. We have derived a family of lower bounds of concurrence which are tighter than the related existing ones. Since our approach is based on the symmetric measurements, the entanglement of any known quantum states can be experimentally estimated. Moreover, our results may be also applied to the investigation on multipartite entanglement, and highlight on the detection of entanglement in optimal entanglement manipulations jpa .

We thank referees for their valuable suggestions to improve the manuscript.This work is supported by JCKYS2021604SSJS002, JCKYS2023604SSJS017, G2022180019L, the National Natural Science Foundation of China (NSFC) under Grants 12075159 and 12171044, and the specific research fund of the Innovation Platform for Academicians of Hainan Province under Grant No. YSPTZX202215.