Quantum-Enhanced Metrology for Molecular Symmetry Violation
using Decoherence-Free Subspaces

Precision measurements of time-reversal (T) symmetry violation in molecular systems provide stringent tests of new physics beyond the Standard Model [1]. For example, searches for the electron’s electric dipole moment (eEDM) have excluded a broad parameter space of T violating leptonic physics at energy scales up to $\sim 50~{}\mathrm{TeV}$ [2, 3, 4, 5]. Experiments aiming to laser cool and trap eEDM-sensitive neutral molecules [6, 7, 8, 9, 10, 11] are currently under construction and promise significantly improved measurement precision. The immediate impact of cooling and trapping is the substantially longer coherence time compared to beam experiments, a result of both long trapping time and easier field control for quasi-stationary molecules confined in a small volume. Furthermore, quantum metrology techniques [12, 13], such as entanglement and squeezing, promise routes to additional enhancement of eEDM sensitivity. However, a specific scheme providing metrological gain without added susceptibility to classical noise from electromagnetic fields has, to our knowledge, not yet been conceived.

Additionally, contemporary eEDM searches with molecular ions are conducted in non-stationary rotating traps [14, 2], since an external electric field is used to polarize the molecules. Although various improvements will be implemented for near-future experiments [15, 16], molecule motion in the rotating trap during spin precession remains a challenge for implementing entanglement-enhanced metrology.

In this manuscript, we show that the eEDM can be observed as a coupling between two entangled molecules within a decoherence-free subspace. The eEDM sensitivity scales linearly with the entangled molecule number, thereby offering Heisenberg-limited sensitivity beyond the standard quantum limit, while the susceptibility to electromagnetic fields remains mitigated. In addition, the two molecules do not have to be aligned in the lab frame by an external electric field; instead, they are prepared in orthogonal superpositions of opposite parity states. As a result, the scheme is applicable to neutral molecules in optical lattices or tweezer arrays [17, 18] as well as molecular ions in quasi-stationary traps [19, 20], which enable entanglement generation and are a well-established platform for precision measurement [21, 22]. Importantly, the entangled molecular states involved are experimentally achievable using existing entanglement protocols [23, 24, 25, 26, 27, 28, 29], some of which have been demonstrated recently [17, 18, 19], together with single molecule operations [30, 31]. Our discussion here focuses on the eEDM as an example, but the method can be straightforwardly extended to measure other T violating moments, including the nuclear Schiff moment [32] and nuclear magnetic quadrupole moment [33].

The energy shift of the eEDM ($d_{e}$) in an effective internal molecular electric field ($\mathcal{E}_{\mathrm{eff}}$) is $d_{e}\cdot\mathcal{E}_{\mathrm{eff}}$. The internal field points along the molecule axis ($\hat{n}$) and its amplitude is determined by the electronic structure of the molecule, while the eEDM is collinear with the total electron spin ($S$). Conventional eEDM experiments [1, 34, 35, 2, 3] orient the molecule axis in the lab frame by mixing opposite parity states with an external electric field, and subsequently polarize the electron spin in the lab frame as well. The eEDM interaction then manifests as a small spin-dependent energy shift, measured by performing spin precession in the polarized molecules. However, the polarized molecular dipoles and electron spins also make these experiments sensitive to uncontrolled external fields. As a consequence, the most common quantum metrology methods, such as spin squeezing [36, 37, 38], increase sensitivity to external electromagnetic fields by the same amount as the gain in eEDM sensitivity. The resulting increased susceptibility to decoherence and systematic errors from these fields, which are a main concern for eEDM experiments, can counteract the eEDM sensitivity boost.

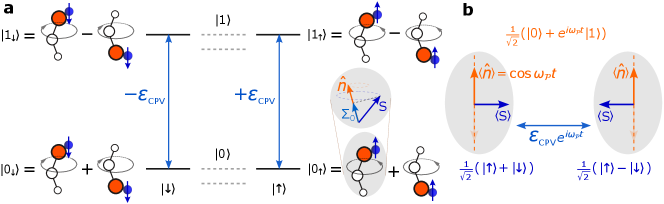
Here we instead probe the eEDM as a coupling between two opposite-parity states in a molecule. We first consider the effects of this coupling in a single molecule to build understanding of the system, and then discuss how we can engineer entangled states in a two (or more) molecule system which have Heisenberg-limited sensitivity $(\propto N)$ to the eEDM but without concurrent increases in collective electric or magnetic field sensitivity. Again, we consider the eEDM as it provides the simplest possible system, but the methods are applicable to symmetry violating nuclear moments as well.

In Fig. 1, we provide an example of a single molecule in the parity-doubled bending mode of a ${}^{2}\Sigma$ triatomic molecule [9], though the method should be generalizable to other types of parity-doubled states. The opposite-parity states are labeled as $\ket{0}$ and $\ket{1}$, and the spin states in the lab basis are labeled by $\ket{\uparrow}$ and $\ket{\downarrow}$. The eEDM causes a spin-dependent coupling between $\ket{0}\leftrightarrow\ket{1}$ with a coupling strength $\varepsilon_{\mathrm{CPV}}=\bra{0_{\uparrow}}\mathcal{E}_{\mathrm{eff}}d_{e}\Sigma\ket{1_{\uparrow}}=2\mathcal{E}_{\mathrm{eff}}d_{e}\Sigma_{0}$, where $\Sigma=S\cdot\hat{n}$ is the projection of spin on the molecule axis and $\Sigma_{0}$ is the expectation value of $\Sigma$ when averaged over other angular momentum quantum numbers of the molecule wavefunction [39]. The coupling changes sign to $-\varepsilon_{\mathrm{CPV}}$ for the time-reversed state $\ket{\downarrow}$.

In a superposition state such as $\frac{1}{2}(\ket{0}+\ket{1})(\ket{\uparrow}+e^{i\theta}\ket{\downarrow})$, which corresponds to an orientation of $\mathcal{E}_{\mathrm{eff}}$ perpendicular to the electron spin, the eEDM interaction causes spin precession that changes the phase $\theta$ of the spin superposition. Note that this is conceptually similar to the usual idea of creating a superposition of $\ket{0},\ket{1}$ by polarizing the molecule with a static external electric field. However, here we consider creating a superposition of these states without static applied fields, meaning that the orientation of the molecular dipole, and therefore $\mathcal{E}_{\mathrm{eff}}$, will be oscillating in the lab frame at a frequency given by the parity splitting $\omega_{\mathcal{P}}$ (typically $\sim 2\pi\times 100~{}\mathrm{kHz}$ to $\sim 2\pi\times 100~{}\mathrm{MHz}$) between $\ket{0}$ and $\ket{1}$ [9]. Thus, the eEDM spin precession ($\lesssim 100~{}\mathrm{\mu Hz}$) can only accumulate phase in the frame rotating at $\omega_{\mathcal{P}}$; in the lab frame, the direction of spin precession oscillates rapidly and averages to zero, so there is no eEDM-induced energy shift or spin precession.

However, with two (or more) molecules, we can engineer states where eEDM precession does not average to zero, yet the oscillation in the lab frame makes the molecules highly insensitive to external fields. Furthermore, we shall see that these states have a metrological gain in sensitivity due to entanglement. We denote the superpositions $\frac{1}{\sqrt{2}}(\ket{0}+e^{i\omega_{\mathcal{P}}t}\ket{1})=\widetilde{\ket{\Uparrow}}$ and $\frac{1}{\sqrt{2}}(\ket{0}-e^{i\omega_{\mathcal{P}}t}\ket{1})=\widetilde{\ket{\Downarrow}}$, suggestive of the fact that these states have opposite orientation of the (rotating) molecular dipole. Consider two molecules in the state $\widetilde{\ket{\Uparrow\Downarrow}}$, as shown in Fig. 2, where we label rotating frame spin states using $\widetilde{\ket{\uparrow}}$ and $\widetilde{\ket{\downarrow}}$. The rotation of the frame is described as $H_{\mathrm{rot}}=\hbar\omega_{\mathcal{P}}\widetilde{\sigma}_{x}$ in the rotating frame basis [40] (also see Supplemental Material). An eEDM shifts $\widetilde{\ket{\uparrow\downarrow}}$ and $\widetilde{\ket{\downarrow\uparrow}}$ oppositely, as they have opposite relative orientations of electron spins and molecular dipoles. Therefore, an eEDM couples the degenerate singlet and triplet pair states with zero total spin projections. These states constitute a decoherence-free subspace as the molecular electric and magnetic dipole moments have zero average projection on the laboratory fields and are therefore insensitive to them to first order. This is conceptually similar to the eEDM coupling in a hyperfine clock transition [41].

Similar to the single molecule case, the eEDM has little effect on the eigenstates of $H_{\mathrm{rot}}$. However, now we can switch on and off the eEDM spin precession by applying a radio-frequency (rf) magnetic field $B$ in phase with the rotating frame (this is challenging for a single molecule; see Supplemental Material). The rf magnetic field is described by $H_{B}=\Omega_{B}\widetilde{\sigma}_{z}$, with $\Omega_{B}$ the interaction strength ($\Omega_{B}\approx\mu_{B}B$ for ${}^{2}\Sigma_{1/2}$ electronic states), and it shifts $\widetilde{\ket{\uparrow\uparrow}}$ and $\widetilde{\ket{\downarrow\downarrow}}$ oppositely, as they have different orientations relative to the rf field. The couplings of $H_{\mathrm{rot}}$, $H_{B}$, and eEDM are shown in Fig. 2(c) in the Bell state basis ($\ket{\Psi^{\pm}}=\frac{1}{\sqrt{2}}(\widetilde{\ket{\uparrow\downarrow}}\pm\widetilde{\ket{\downarrow\uparrow}})$, $\ket{\Phi^{\pm}}=\frac{1}{\sqrt{2}}(\widetilde{\ket{\uparrow\uparrow}}\pm\widetilde{\ket{\downarrow\downarrow}})$).

$H_{\mathrm{rot}}$ and $H_{B}$ couple $\ket{\Psi^{+}}\leftrightarrow\ket{\Phi^{-}}$ and $\ket{\Phi^{-}}\leftrightarrow\ket{\Phi^{+}}$, respectively. The resulting eigenstates are shown in Fig. 2(d); the middle state, whose eigenenergy is not shifted, is $\ket{u}=\sin{\theta}\ket{\Psi^{+}}-\cos{\theta}\ket{\Phi^{+}}$, with the mixing angle $\theta$ given by $\tan{\theta}=\Omega_{B}/\omega_{\mathcal{P}}$. Note that these interactions do not couple to $\ket{\Psi^{-}}$. However, the eEDM interaction couples $\ket{\Psi^{-}}\leftrightarrow\ket{\Psi^{+}}$ but with coupling strength much smaller than $H_{B}$ or $H_{\mathrm{rot}}$. The eEDM therefore induces a resonant coupling $\ket{\Psi^{-}}\leftrightarrow\ket{u}$ with a reduced coupling strength of $\varepsilon_{u}=4\varepsilon_{\mathrm{CPV}}\frac{\Omega_{B}}{\sqrt{\Omega_{B}^{2}+\omega_{\mathcal{P}}^{2}}}$, which reaches $\sim 90\%$ of the maximum ($4\varepsilon_{\mathrm{CPV}}$) when $\Omega_{B}\gtrsim 2\omega_{\mathcal{P}}$. Note that this is twice the coupling of a fully polarized single molecule, thereby beating the standard quantum limit. A static magnetic field, or more generally, a magnetic field at a different frequency, causes the phase on the $\ket{\Psi^{+}}$ part of $\ket{u}$ to oscillate and thus the eEDM coupling averages to zero. Consequently, the eEDM spin precession is turned on only when the magnetic field is in-phase. The eEDM spin-precession subspace is also known as a decoherence-free subspace [42]; it is robust to noise since the total spin and dipole projections, and therefore the expectation of electric and magnetic dipole moments, is zero.

The experimental sequence for two molecules, as an example, is illustrated in Fig. 3. Molecules are initialized in $\ket{0_{\downarrow}0_{\downarrow}}$ by optical pumping. Then the spins are entangled in $\ket{\Psi^{-}}_{\mathrm{lab}}$ – this can be realized by direct dipole-dipole [17, 18] or Rydberg atom mediated interactions [27, 28], or, for trapped ions, the spin-dependent force gate [19] or the Mølmer-Sørenson interaction [43]. For more than two molecules, the entangled singlet state can be generated by a set of gate operations, adiabatic sweeping to the ground state of the many-body system [29], or extracting from cluster states [44, 45, 46, 47]. Subsequently, the molecule orientation is prepared in $\widetilde{\ket{\Uparrow\Downarrow}}$. This can be done in two sub-steps: first drive a global $\pi/2$-pulse between $\ket{0}\leftrightarrow\ket{1}$, and then apply an AC-Stark shift using a far-detuned laser focused on one of the molecules and imprint a $\pi$ phase on $\ket{1}$. By addressing different molecules, or by changing the detuning of the laser, the direction of eEDM spin precession can be controlled, thus providing “switches” to observe the eEDM [48]. Note that for multiple pairs of molecules trapped simultaneously, this could be performed in parallel across different pairs to mitigate imperfections in the laser pulses. The initial spin state $\ket{\Psi^{-}}_{\mathrm{lab}}$ is invariant under rotations and thus is equal to $\ket{\Psi^{-}}$ in the rotating frame. Next, when the rf magnetic field is turned on, eEDM spin precession $\ket{\Psi^{-}}\leftrightarrow\ket{u}$ starts in the rotating frame. After eEDM spin precession, the magnetic field is turned off and then the orientation of the molecules is rotated back to $\ket{00}$. In the lab frame, $\ket{u}$ is an rf-dressed state, which is oscillating in the triplet subspace of $\{\ket{\Psi^{+}}_{\mathrm{lab}},\ket{\Phi^{-}}_{\mathrm{lab}},\ket{\Phi^{+}}_{\mathrm{lab}}\}$. After turning off the magnetic field, the population in $\ket{u}$ is distributed in the triplet subspace but mostly mapped to $\ket{\Psi^{+}}_{\mathrm{lab}}$. Finally, the eEDM spin precession phase, i.e. the phase between $\ket{\uparrow\downarrow}$ and $\ket{\downarrow\uparrow}$ components, is measured by a projection measurement in the $\frac{1}{\sqrt{2}}(\ket{\uparrow\downarrow}\pm i\ket{\downarrow\uparrow})$ basis by the parity oscillation measurement [49, 17, 18] as described further in the Supplemental Material.

Our scheme has many advantages. First, the spin precession rate in the entangled basis is two times faster than in a fully polarized single molecule, and it scales linearly with molecule number for the anti-ferromagnetic spin states (i.e. between $\frac{1}{\sqrt{2}}(\ket{\uparrow\downarrow\uparrow...\uparrow\downarrow}+\ket{\downarrow\uparrow\downarrow...\downarrow\uparrow})\leftrightarrow\frac{1}{\sqrt{2}}(\ket{\uparrow\downarrow\uparrow...\uparrow\downarrow}-\ket{\downarrow\uparrow\downarrow...\downarrow\uparrow})$ for molecule orientation $\ket{\Uparrow\Downarrow\Uparrow...\Uparrow\Downarrow}$), thus realizing a metrological gain from entanglement. More importantly, the eEDM spin precession subspace is decoupled from various environmental noise sources, including magnetic fields, vector and tensor light shifts, etc., since the total spin and dipole projections are zero and the spin precession takes place in a rotating frame where slow noise is averaged out. This is unlike conventional eEDM protocols using polarized molecules in the lab frame, where the eEDM-enhanced entangled states, such as squeezed states or the GHZ state $\frac{1}{\sqrt{2}}(\ket{\uparrow\uparrow...\uparrow}+\ket{\downarrow\downarrow...\downarrow})$, normally require spins aligned collectively in the lab frame and thus are also increasingly sensitive to magnetic field noise, AC Stark shifts, etc. Magnetic field gradients at the same frequency may cause spin precession in the same subspace; however, this effect can be disentangled from an eEDM by switching the sign of eEDM interaction, which is controlled by the phase of the rf magnetic field and the phase of the molecule orientation. For example, the spin precession directions in $\widetilde{\ket{\Uparrow\Downarrow}}$ and $\widetilde{\ket{\Downarrow\Uparrow}}$ are opposite, and the spin does not precess in $\widetilde{\ket{\Uparrow\Uparrow}}$ or $\widetilde{\ket{\Downarrow\Downarrow}}$. Other couplings, including $H_{\mathrm{rot}}$ and $H_{B}$, are insensitive to the $\pm$ phase between $\ket{0}$ and $\ket{1}$.

Furthermore, our scheme is robust to various experimental imperfections. For example, the fidelity of entanglement generation does not have a lower threshold; the population that is not initialized in $\ket{\Psi^{-}}$ is not coupled by the eEDM and only contributes a constant background. Many possible sources may cause imperfect initialization of the molecule orientation; they include, for instance, fluctuations in the $\pi/2$-pulse power, Stark shifts, imperfect single molecule addressing light shift, or small difference in the $g$-factors of $\ket{0}$ and $\ket{1}$ states (resulting from perturbations of other electronic states), etc. If a molecule is not in equal superposition of $\ket{0}$ and $\ket{1}$ the eEDM interaction ($\Sigma_{0}$) is slightly reduced. If two molecules are not in exact opposite phases of $\ket{0}$ and $\ket{1}$ superpositions, the splitting between $\widetilde{\ket{\uparrow\downarrow}}$ and $\widetilde{\ket{\downarrow\uparrow}}$ is reduced (this can be used as a switch to tune the spin precession rate). If two molecules have different $\ket{0}$ and $\ket{1}$ populations, their eEDM interactions ($\Sigma_{0}$) are different and thus $\ket{\Psi^{-}}$ is also coupled to the $\ket{\Phi^{\pm}}$ states. However, this additional coupling does not cause spin precession since the $\ket{\Phi^{\pm}}$ states are strongly coupled by the magnetic field (see Fig. 2[c]). Importantly, all the fields are applied independently and they do not have correlation with the eEDM switch (AC Stark shift from the addressing beam). As a consequence, these imperfections do not lead to systematic effects directly, but instead to contrast reduction and increased statistical noise.

Magnetic field correlated rf electric fields, stray electric fields, and black-body radiation (BBR) have detrimental effects on the state of molecule orientation and need to be shielded. Our scheme does not require a DC electric field, and shielding electric fields is straightforward, especially without the need for electric field plates nearby. The effects of the residual fields include near-resonant couplings between $\ket{0}\leftrightarrow\ket{1}$ and off-resonant effects, such as energy shifts on $\ket{0}$ and $\ket{1}$. The coupling effect is suppressed by the dipole-dipole interaction between two molecules when the residual-field coupling strength is weaker than the dipole-dipole interaction (typically $\sim\mathrm{kHz}$ at $\sim\mathrm{\mu m}$ separation), and it can also be mitigated by applying a stronger electric field in phase with the molecule oscillation.

Stray electric fields or off-resonance BBR can cause an energy shift between $\ket{0}$ and $\ket{1}$. This alters the oscillating frequency of the rotating molecules, which may affect coherent control of the molecule orientation and may interfere with the eEDM spin precession by shifting the oscillation out of phase with the magnetic rf field. Nevertheless, stray electric fields can be actively measured and cancelled, especially since the molecules needed for this protocol will be trapped in a small volume $\sim$mm³; for example, in trapped ions a residual electric field lower than $0.1~{}\mathrm{mV/cm}$ has been achieved [50, 51]. A $0.1~{}\mathrm{mV/cm}$ fluctuation corresponds to a maximum $\sim 50~{}\mathrm{mHz}$ dephasing rate for a molecule of $d_{0}\approx 2~{}\mathrm{D}$ dipole moment and $\omega_{\mathcal{P}}\approx 100~{}\mathrm{kHz}$ parity splitting. This leads to a coherence time of $\sim 10~{}\mathrm{s}$, and the coherence time is inversely proportional to parity splitting. On the other hand, we need $\Omega_{B}\approx\mu_{B}gB\gtrsim 2\omega_{\mathcal{P}}$, where $g$ is the electron magnetic $g$-factor. To avoid using high magnetic field (a few Gauss, using a similar magnetic field coil setup in ref. [52]), our scheme is most suitable for molecules with $\omega_{\mathcal{P}}\lesssim 10~{}\mathrm{MHz}$, which is a typical range for parity doubling. In addition, for trapped ions, $\omega_{\mathcal{P}}$ needs to be much lower than the trap rf frequency ($\sim 20~{}\mathrm{MHz}$). Some examples of suitable neutral and ion species are listed in the Supplemental Material.

In summary, we have presented a quantum metrology scheme to probe T-violating effects in molecular systems. The Heisenberg scaling is particularly important for the future experiments where the molecules are well-controlled but do not necessarily have large molecule numbers, such as molecules in tweezer arrays and ion traps, as well as rare radioactive molecules [53]. The T-violating interaction causes spin precession in an entangled, decoherence-free subspace in a rotating frame, where the slow noise in the lab frame is averaged out, and the molecules do not need to be polarized by an external electric field. As a result, the scheme is compatible with stationary ion traps, such as the linear Paul trap, in which a powerful toolbox of precision spectroscopy and quantum metrology has been developed, including sympathetic cooling [54], quantum logic spectroscopy [55, 16], ion shuttling [56], micromotion compensation [57], entanglement generation, etc. Furthermore, the direction of spin precession is controlled by the phase of the applied magnetic rf field and the phase of the oscillation of the molecule orientation. In T-violation measurements, systematic effects normally arise from imperfections correlated with the switch of the sign of the T-violating interaction, such as parity state or external electric field. Our eEDM switch is an AC-Stark shift by the far-detuned addressing beam on one of the molecules, which has little correlation with other imperfections, and can be performed in parallel across multiple pairs of molecules. In addition, because of the magnetic field insensitivity, this scheme will also improve the coherence in a shot-noise limited measurement using magnetic molecules, including all laser coolable neutral molecules and certain T-sensitive molecular ions whose ground states are magnetic. These advantages will significantly improve the precision of T-violating new physics searches in the near future.