Quantum criticality and universality in the -wave paired Aubry-André-Harper model
Abstract
We investigate the quantum criticality and universality in Aubry-André-Harper (AAH) model with -wave superconducting pairing in terms of the generalized fidelity susceptibility (GFS). We show that the higher-order GFS is more efficient in spotlighting the critical points than lower-order ones, and thus the enhanced sensitivity is propitious for extracting the associated universal information from the finite-size scaling in quasiperiodic systems. The GFS obeys power-law scaling for localization transitions and thus scaling properties of the GFS provide compelling values of critical exponents. Specifically, we demonstrate that the fixed modulation phase alleviates the odd-even effect of scaling functions across the Aubry-André transition with , while the scaling functions for odd and even numbers of system sizes with a finite cannot coincide irrespective of the value of . A thorough numerical analysis with odd number of system sizes reveals the correlation-length exponent 1.000 and the dynamical exponent 1.388 for transitions from the critical phase to the localized phase, suggesting the unusual universality class of localization transitions in the AAH model with a finite -wave superconducting pairing lies in a different universality class from the Aubry-André transition. The results may be testified in near term state-of-the-art experimental settings.
I Introduction
Quantum phase transitions (QPTs) have attracted the intense interest of both theorists and experimentalists in condensed matter physics for decades. With variation of a non-thermal variable in the many-body Hamiltonian, the ground-state properties show abrupt changes as a result of competing ground-state phases Sondhi et al. (1997); Sachdev (2000); Shen et al. (2020). The Landau-Ginzburg-Wilson (LGW) paradigm has provided a well-established framework, which rests on the assumption that a continuous equilibrium phase transition can be accessed by the onset of an order parameter associated with spontaneous symmetry breaking. A broad regime of order parameter fluctuations are controlled by proximity to a quantum critical point (QCP). It has been a long time to recognize that the symmetry breaking occurs spontaneously only in infinite-size quantum many-body systems, while recently they are sometimes observed in surprisingly small systems Bayha et al. (2020) and even few-body systems Cai et al. (2021); Liu et al. (2017); Hwang et al. (2015). Despite the enormous success, the breakdown of the LGW paradigm appears in a few different situations, for example, deconfined QCPs C. Wang and Senthil (2017); Shao et al. (2016) and deconfined critical universality classes Bi et al. (2020).
In recent years, an immense effort has been expended to understand QPTs in quasiperiodic systems Goldman and Kelton (1993); Iyer et al. (2013); Kohmoto et al. (1987); Lagendijk et al. (2009); hen and Ye (2019); Gonalves et al. ; Cai et al. (2013); Gong and Tong (2005); Agrawal et al. (2020); Roy et al. (2021); Goblot et al. (2020); Wang et al. (2020). The quasiperiodic system possesses a long-range periodicity, which is intermediate between that of the clean and randomly disordered cases, offering a rich playground to study quasiperiodic QCPs and unusual characteristic features, such as hierarchical energy spectra Sutherland (1986); Hiramoto and Kohmoto (1992, 1989) and localization-delocalization transitions. A paradigmatic model of the quasiperiodic system is the Aubry-André-Harper (AAH) model Liu and Gao (2017); Zeng et al. (2018); Tong et al. (2021); Liu et al. (2015); A. Purkayastha and Kulkarni (2018); Zeng et al. (2016); Wei (2019); Roy and Sharma (2019); Fraxanet et al. (2021); Xiao et al. (2021); Wang et al. (2016); Liu et al. (2015); Mondragon-Shem and Hughes (2014); Yoo et al. (2020); Zeng et al. (2017); Zhao et al. (2017); Longhi (2019); Zeng et al. (2020); Longhi (2021); Zhang et al. (2020); Longhi (2019); Liu et al. (2020), in which the quasiperiodicity is embodied in the form of a cosine modulation incommensurate with lattice spacing. With the rapid development of experimental technologies, the AAH model can be realized in optical waveguide lattices Gredeskul and Kivshar (1989); Christodoulides and Silberberg (2003); Pertsch et al. (2004), photonic crystals Negro et al. (2003); Lahini et al. (2009); Kraus et al. (2012) and cold atom systems Roati et al. (2008). For instance, the AAH Hamiltonian has been experimentally realized by cold atomic gases in a one-dimensional optical lattice perturbed by another weak incommensurate optical lattice Roati et al. (2008). These feasible platforms allow us to explore the emerging topological states of matter with additional interactions in incommensurate systems, including modulated off-diagonal hopping Liu et al. (2015), nearest neighbor -wave superconductivity Yahyavi et al. (2019), a long-range -wave superconducting pairing Fraxanet et al. (2021), and many-body interactions Yoo et al. (2020); Štrkalj et al. (2021).
The AAH model has gained popularity since it acts as a proxy for random potentials in the study of generic disordered system. An obstacle to comprehending the critical phenomena in the disordered systems is the undecidability of local order parameters. In close proximity to QCPs, the complex and non-local entanglement between individual constituents becomes extremely prominent at all distance scales. As such, it has been recognized that the exploration of quantum critical phenomena from the perspective of quantum information science is a great privilege, such as the von Neumann entropy Gong and Tong (2008), and quantum concurrence Werlang et al. (2010). The quantum fidelity susceptibility (QFS) has proved to be particularly useful for detecting the critical points of a symmetry-knowledge unknown system Wei and Lv (2018); Garnerone et al. (2009); Chen et al. (2008); Mao et al. (2021). It was shown that the QFS can not only identify the QCPs, but also satisfy the scaling ansatz, where the universal information can be retrieved. The most significant implication is that the finite-size scaling of such a universal order parameter dictates position of QCPs and the critical exponent of the correlation length . For a quasi-periodic system with spatial complexity, the scaling theory of the QFS and the universality of localization transition have been partially understood. Notably, the finite-size scaling of the usual fidelity susceptibility is irrelevant to the dynamical exponent . However, the critical exponents obey the scaling and hyperscaling relations, implying that there are only two independent exponents. Thus, a second independent critical exponent plays a decisive role in determining the universality class, which lies at the heart of critical phenomena. In this work, we apply the generalization of fidelity susceptibility to the one-dimensional AAH model with -wave superconducting pairing, and devise a direct pathway to the determination of critical points and universal critical exponents of localization-delocalization transitions. Importantly, the theoretical predictions could be testified in state-of-the-art experiments.
The rest of the paper is organized as follows. Section II reviews the AAH model with -wave superconductivity and determines its phase diagram. In Sec. III, we introduce the concept of the generalized fidelity susceptibility (GFS) and postulate its scaling hypothesis for the universal part. Section IV is devoted to the scaling behavior of the GFS in the AAH model and identification of critical exponents. Conclusions and discussions are presented in Sec. V.
II MODEL HAMILTONIAN
The generalized AAH model with -wave superconducting pairing in a quasi-periodically modulated potential is given by the following Hamiltonian:
| (1) |
where is the fermionic creation (annihilation) operator at the -th site among total lattice sites, is the hopping strength between nearest-neighbor sites, denotes the amplitude of -wave superconducting pairing, and H.c. represents the Hermitian conjugate. The -wave pairing amplitudes can be tuned by the mixture of spin-polarized fermions with a Bose-Einstein condensate Kinnunen et al. (2018), affected by an -wave Feshbach resonance in a spin-polarized cold Fermi gas Liu et al. (2016), or induced by the proximity effect in stacking a superconducting wire on top of the normal metal. Here we focus on quasi-periodicity encoded in the chemical potential, keeping a constant hopping magnitude and pairing potential. The on-site potential terms are quasiperiodically varying according to the Aubry-André rule , where is an irrational frequency and is the strength of the incommensurate potential. The parameter shifts the origin of the modulation representing a random phase. The boundary condition is imposed as =, where = , , and corresponding to periodic, antiperiodic, and open boundary conditions, respectively. Without losing generality, can be assumed to be real [the phase can be otherwise eliminated under global U(1) transformation] and is set as energy unit throughout the paper. For , the model will be equivalent to quasiperiodic Ising model Li et al. (2021); Caneva et al. (2007). When the -wave pairing term is absent, i.e., , the AAH model in Eq.(1) becomes easily tractable as it can be written as = . The eigenvectors and the associated single-particle energies are obtained by diagonalizing the single-particle Hamiltonian matrix . In the limit when 0, Eq. (1) describes a metallic chain with all eigenstates being extended, while for the eigenmodes are localized on one site. The Aubry-André transition from being extended to being localized is known to occur at as a consequence of Aubry-André duality between the Hamiltonian in position and momentum space.
As for a finite -wave paring, i.e., , the Hamiltonian (1) can be diagonalized through a canonical Bogoliubov-de Gennes (BdG) transformation by introducing the new fermionic operators and ,
| (2) |
where and denote the two components of the wave function at site , and () is the energy band index. The eigenstates = ,,…,,,… can be determined by solving the Schrödinger equation , which can be recast into a matrix form as
| (9) |
where () is a symmetric (antisymmetric) matrix. The nonzero elements are given by =, = =, and =-=. The matrix elements for the boundary terms are ==, and =-=. The BdG Hamiltonian in Eq.(9) respects an imposed particle-hole symmetry, namely, , where the Pauli matrix acts in the Nambu space. The energy levels appear in conjugate pairs, with , except the zero energy mode, which is self-conjugate. As such, for finite lattices it is convenient to replace with , the ratio of two successive Fibonacci numbers Machida and Fujita (1986); Kohmoto (1983). Note that the irrational limit is reached as far as the numerical results are extrapolated to the scaling limit (). The period then acts like a finite length scale which controls scaling behavior. The Fibonacci-sequence quasiperiodic potential has an intimate connection with topological phase transition and Majorana modes.
While in the translational-invariant case the solution of Eq.(9) can be further reduced to the 22 matrix form with independent momenta, in the quasidisorder case one has to diagonalize the BdG matrix numerically, marking a qualitative difference between the disordered and the clean model. In terms of the new fermion operators, the Hamiltonian in Eq.(1) can be diagonalized as
| (10) |
with the single-particle eigenvalues being . The ground state of is the Bogoliubov vacuum state annihilated by all for , i.e., =0, with an energy = -. For a weak quasi-disorder strength, all the eigenstates of the system are extended, while the system becomes localized for a sufficiently strong disorder. Recently, it was found that with a nonzero superconducting pairing, a nonergodic critical phase intervenes the transition from the delocalized to localized state, and all the eigenstates are expected to be multifractal. The phase diagram shown in Fig.1 consists of the extended phase (EP), critical phase (CP), and localized phase (LP). The localized wavefunctions in the LP can be transformed into the extended ones in the EP by a Aubry-André duality occurring at across a second-order QCP. The system undergoes a continuous QPT from the EP to the CP at . One finds that Eq.(1) is invariant under the transformation as on odd -th sites and Wang et al. (2016). For the self-duality point (, ), the EP becomes unstable for arbitrarily weak disorder. The system displays a second-order QPT from CP to LP at .





In order to visually characterize the localized and extended nature of the entire energy spectrum, we evaluate the normalized inverse participation ratio (IPR) for each eigenstate of the model Evers and Mirlin (2008); Licciardello and Thouless (1978); Wegner (1980); Misguich et al. (2016), given by
| (11) |
The IPRs can quantify the extent of distribution over the preferential bases. It should be noted that IPR is erroneously employed to describe the participation ratio in many literatures reports Gong and Tong (2005); Dukesz et al. (2009), which is the reciprocal of IPR Thouless (1974). In a specific -dimensional bases , the IPR of the state reaches a maximal value when the state coincides exactly a single basis state, and attains a minimal value when the state is uniform in the selective bases. For a set of one-particle states in real space, the IPR scales inversely with the system size in the delocalized state, while appears to be independent of in the localized phase and shows intermediate behavior in the CP. Both transitions at finite strength of quasiperiodic modulation occur simultaneously for all eigenstates, as is revealed in Fig.2(a), in contrast to the presence of mobility edges in specific systems Biddle et al. (2011); Ganeshan et al. (2015); H. P. Lüschen and Bloch (2018); Guo et al. (2021). We thus further define the mean inverse participation ratio (MIPR) as
| (12) |
The evolution of MIPR is exhibited in Fig.2(b) on a logarithmic scale for different -wave pairing strength , , and . One finds the MIPR is capable of identifying the phase boundaries separating the extended, critical, and localized phases, which are captured by the turning points of the MIPR locating respectively at and . The LP is gapless for periodic boundary conditions while gapped for open boundary conditions. Note that for a pure state of the entire system, the von Neumann entropy is zero and the IPR is inversely proportional to the participation entropy of order , i.e., , which becomes the diagonal entropy for the reduced density matrix of the subsystem Polkovnikov (2011); Santos et al. (2011). As is observed in the inset of Fig.2(b), the scaling exponents extracted from the linear fittings for and with are approximately 0.98, which implies that the inverse of MIPR tends to scale extensively for extended states in the AAH model, resembling the volume-law scaling of the mean first-order Rényi entropy at infinite temperature, which is conjectured to be universal for translationally invariant quadratic fermionic Hamiltonians Vidmar et al. (2018), while declines towards a finite value close to for localized states, in analogy to the area law of the disordered averaged entanglement entropy Pastur and Slavin (2014). For critical states, the MIPR scales like Kramer and Mackinnon (1993), where the fractal dimension depends on the fractal structure of wavefunctions. The fitting lines of with respect to for and with gives rise to 0.75, implying that points in the whole CP belong to the same universality class. Remarkably, the fractal dimension and the associated IPR are proved to host intrinsic relation to the mean entanglement entropy Tomasi and Khaymovich (2020). One should be aware that a typical value of IPR can be used = , which is similar to the behavior of Eq.(12) for the AAH model (1) yet becomes more subtle when eigenstates display a single-particle mobility edge.
III Generalized fidelity susceptibility and scaling hypothesis
It is now well established that the QFS is a good measure to witness QPTs and manifest critical phenomena in translational invariant quantum systems Yang et al. (2008); Zanardi and Paunkovi (2006); You et al. (2007). The merit of the QFS in characterizing critical phenomena is the model-independent feature, which is quite suitable for quantum systems without prior knowledge of order parameters. To this end, the fidelity susceptibility is recognized as a sensitive probe of quantum criticalities in conjugate field Thesberg and Sørensen (2011), long-range interacting systems Zhu et al. (2018); Ren et al. (2020), deconfined QCP Sun et al. (2019), disordered systems, chaotic Hamiltonians Pandey et al. (2020), quantum many-body scars Surace et al. (2021), excited-state quantum phase transition Leblond et al. (2021), and holographic models Alishahiha and Astaneh (2017). Currently the investigations of the scaling of QFS in the context of quantum disordered systems are still poorly understood. In what follows, we will focus on the fidelity susceptibility and its generalization as well as the associated scaling in the AAH model.
The fidelity susceptibility provides a generic and direct approach to measure the quantum metric tensor via the transition probability of the quantum state being excited to other eigenstates during a sudden infinitesimal quench of the tuning parameter You et al. (2007). The GFS of order at the tuning parameter associated with the state is given by You and He (2015)
| (13) |
where and correspond to the th eigenstate and eigenvalue of this generic Hamiltonian , respectively. The numerator in Eq.(13) denotes the probability of exciting the system away from the state through a relevant (or marginal) perturbation . The GFS of different orders is embodied by the power of the denominator. Concretely, Eq.(13) reduces respectively to the second derivative of the ground-state energy for Chen et al. (2008) and the conventional quantum geometric tensor for You et al. (2007). We can anticipate that has a weaker divergence than at a critical point. The QFS can be also devised as the Riemannian metric tensor upon projecting the dynamics onto a single (non-degenerate) band Zanardi et al. (2007),
| (14) |
Regarding the absence of mobility edge in the energy spectrum, in the following we focus on the GFS of the lowest eigenstate . To this end, the superscript of (=, , ) is omitted for abbreviation.
We then start the description of the finite-size scaling theory by recalling its main features that hold in the vicinity of the usual continuous QPT. The sensitivity is greatly enhanced, especially for the system at the quantum criticality compared with that away from the critical region Braun et al. (2018). Single parameter scaling posits that the correlation length is the only relevant length scale in the thermodynamic limit that diverges at the transition,
| (15) |
and the single-particle spectral gap of size will vanish as
| (16) |
where is the correlation length exponent and is the dynamical critical exponent. For finite chains, the single parameter scaling hypothesis implies that the relevant physical quantities shall depend only of the ratio , at least in the vicinity of the critical point where 1 Fisher and Barber (1972). As crosses QCPs adiabatically, the GFS shows a broad peak for a finite system size, signaling the location of pseudocritical points . With increasing system sizes , the peaks of GFS become more pronounced and the maximal points of the GFS is expected that
| (17) |
where is the critical adiabatic dimension. For relevant operators on sufficiently one-dimensional large-size systems, i.e., 2, the pseudocritical points converge towards the critical points , satisfying
| (18) |
with =. Here one should be aware that the shift exponent in Eq.(18) is not necessarily equal to inverse of the correlation-length exponent Roncaglia et al. (2015), as it happens to the entanglement witness Osterloh et al. (2002); Ren et al. (2018). Accordingly, the GFS of a finite system with size in the neighborhood of a QCP shall obey the universal scaling form Albuquerque et al. (2010),
| (19) |
where is a regular universal scaling function of the GFS of order , a priori unknown. Estimates for critical parameters can thus be obtained by plotting the scaled GFS -/ versus by subtly adjusting the values of , , and until data collapse is achieved. Alternatively, taking logarithm on both sides of Eqs.(17) and (18),yields
| (20) |
where fitting parameters and can determine the critical exponents and as
| (21) |
As such, we concentrate our attention on the region close to the critical point of localization-delocalization transitions, above which the eigenstates are localized within the finite localization length Sinha et al. (2019). Unlike the Aubry-André model with , the BdG Hamiltonian (9) for a finite acts in an enlarged expanded Nambu-spinor space Altland and Zirnbauer (1997). The second-order derivative of first excitation in the neighborhood of for various odd number of system sizes with is shown in Fig.3(a). One can see that presents a divergent peak at . The linear fittings give rise to parameters = -0.994 and = 0.605 . According to Eq.(III), the fitting values imply that and . Furthermore, the single-particle spectral gap with several system sizes from = 55 up to = 4181 are considered with periodic boundary conditions for in Fig.3(b), indicating that according to Eq. (16).
IV FIDELITY SUSCEPTIBILITY IN THE AUBRY-ANDRÉ-HAPER MODEL WITH P-WAVE PAIRING
We obtain all the eigenenergies and the corresponding wave functions by diagonalizing Eq.(9). The numerical results tempt us to evaluate the GFS of the AAH model through Eq.(13). First we recapitulate the finite-size scaling hypothesis of QFS in the Aubry-André model with Mondragon-Shem and Hughes (2014). Previous work revealed the QFS near the EP-LP transition can be separately rescaled onto two different universal curves for even and odd numbers of lattice sites Wei (2019), while the retrieved critical exponents are quite close, which implies that two universal scaling functions are not necessary. The logarithm of QFS of the Aubry-André model as a function of for with different system sizes is exhibited in Fig.4(a). One can find that the fidelity susceptibility presents a maximum at . With increasing the system sizes, the peaks become more pronounced and gets closer to the critical point . The maximum value of against the system size is displayed in the log-log scale, whose linear fit shows that = -5.400, implying according to Eq.(17). This is consistent with the Harris criterion Harris (1974), which imposes that for phase transitions in the presence of incommensurate modulation. When the rescaled fidelity susceptibility -/ is plotted as a function of the proper scaling variable , all curves of distinct chain sizes in the vicinity of collapse into a single curve, as is shown in Fig.4(b), which corroborates the estimated critical parameter and the validity of the single-parameter scaling hypothesis (19). In particular the properly chosen value of much alleviates the odd-even effect.
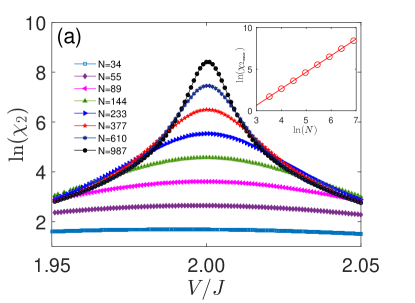
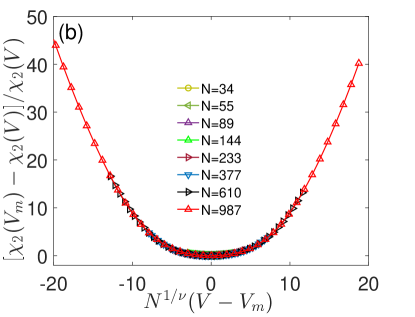
Next, the QFS in the AAH model with respect to the strength of the incommensurate potential for odd number of lattice sizes with is shown in Fig.5. The QFS exhibits an extensive scaling in the off-critical region. Therefore, the QFS per site appears to be an -independent value. Instead, the QFS shows a stronger dependence on system size around , signaling the onset of the QCP in the AAH model. The maximum values of the fidelity susceptibility near the QCP as a function of in log-log scale are plotted. The superextensive behavior at the pseudocritical point is reflected in the linear fitting (2.003 , whose slope suggests that . Meanwhile, the numerical fitting in terms of Eq.(18) yields =0.947 . The accuracy of retrieved from the algebraic law (18) is generally plagued by the precision of numerical calculation.


In order to extract the dynamical exponent of CP-LP transitions, we further study the finite-size scaling of . One can easily heed that displays much more divergent peaks than in the vicinity of QCP , as is disclosed in Fig.6. The linear fittings of the peak maxima suggests =-1.018 and . According to Eq.(21) the extracted values of critical exponents = and for the CP-LP transition with agree well with those obtained from the gap scaling Tong et al. (2021). In this vein, we continue to pick the critical exponents and via the scaling analysis of as the -wave superconducting pairing changes. The numerical results in Fig. 7(a) reveals that 1.000 and 1.388 with little variation. It turns out that there is a discontinuity of when increases from 0 to an infinitesimal value. Distinct values of for Wei (2019) and for suggest that their ground states belong to different universality classes. For all , the transitions across QCPs belong to the same universality class as the quasiperiodic Ising chain Agrawal et al. (2020).




V Discussion and summary
In this work, we investigate quantum criticality in the Aubry-André-Harper (AAH) model with -wave superconducting pairing in terms of the generalized fidelity susceptibility (GFS). This quasiperiodic fermion system is Jordan-Wigner-equivalent to the quasi-periodically modulated transverse field XY chain. The interplay of spatial modulation of potential and symmetry breaking leads to quantum critical phenomena that are different from either the commensurate potential or randomly distributed potential. In the absence of -wave pairing (=0), the AAH model hosts a phase transition from the extended state to the exponentially localized state through the self-duality point (). With a finite value of , the transition from the extended phase to the localized phase has to pass through an intermediate phase, and the critical point will develop into a critical region, which is sandwiched between the extended and localized states. Various available methods have been incorporated in identifying quantum critical points (QCPs) from numerical simulations. A useful quantity in characterizing quantum criticality of disordered systems is the inverse participation ratio (IPR), which is equivalent to the second-order participation Rényi entropy. Since there is no mobility edge in the energy spectrum, we then use the mean inverse participation ratio (MIPR) to characterize the degree of the extensivity in space of the wave function in different phases. The MIPR presents a power-law scaling in distinct phases, where =1 in the extended phase, =0 in the localized phase and the exponent in the intermediate critical phase.
We have developed accelerated methods for the location of critical points by the extrema of the universal order parameters. In this context, higher-order GFSs are more efficient in spotlighting the pseudo-critical points, even in the moderately large systems. The enhanced sensitivity is propitious for extracting the associated universal information from the finite-size scaling in quasiperiodic QCPs, whose system sizes are rapidly growing three-subsequence Fibonacci numbers Cookmeyer et al. (2020). This distinguishing feature becomes especially crucial in interacting many-body systems and higher-dimensional systems. One can see from Fig. 7(b) that has already spied on the pseudocritical point for via the visible peak. By performing a detailed numerical simulation, we find different orders of GFS obey power-law scaling in the vicinity of the localization transitions. The single parameter scaling of these macroscopic observables provide self-consistent results of critical exponents. Moreover, the generalization of fidelity susceptibility poses an efficient avenue to dynamic exponent . The determined values of correlation-length exponent 1.000 and the dynamical exponent 1.388 suggest that the quantum criticality of localization transitions in the AAH model for lies in a different universality class from the Aubry-André transition () with =1.000, and =2.375 Wei (2019); Sinha et al. (2019), where a Aubry-André-type duality may prevent the finite energy excitations from localizing. Understanding the nature of the quasiperiodic localization transition, with and without a finite -wave superconducting pairing, may thereby cut to the heart of the phenomenon. The critical properties of this fixed point are found to be intermediate to the clean and randomly disordered cases. The former case is represented by the clean transverse field Ising model in the celebrated Onsager universality class with ==1, while the latter is symbolized by the Anderson model with =2/3, =2 Cestari et al. (2011).
Last but not the least, another challenge in the study of quasiperiodic models is to separate physically measurable observables from the mathematically intriguing concepts. The quantum metric tensor has been experimentally measured with superconducting qubits Tan et al. (2019), coupled qubits in diamond Yu et al. (2020), and planar microcavity Gianfrate et al. (2020). Thus, an experimental measurement of the correlation-length exponent and the dynamical exponent becomes tractable. For instance, governs the low-temperature behavior of the specific heat and can be extracted from the density of states or through the Kibble-Zurek mechanism Sinha et al. (2019). In this respect, our results can be explored in state-of-the-art experimental settings for moderate system sizes. Our tentative approach draws a link between quantum information science and analog quasiperiodic systems without explicit order parameters, and it would be interesting to investigate whether our results can be extended to more complex disordered models.
Acknowledgements.
This work is supported by the National Natural Science Foundation of China (NSFC) under Grant No. 12174194, the startup fund of Nanjing University of Aeronautics and Astronautics under Grant No. 1008-YAH20006, Top-notch Academic Programs Project of Jiangsu Higher Education Institutions (TAPP), and stable supports for basic institute research under Grant No. 190101.References
- Sondhi et al. (1997) S. L. Sondhi, S. M. Girvin, J. P. Carini, and D. Shahar, “Continuous quantum phase transitions,” Rev. Mod. Phys. 69, 315 (1997).
- Sachdev (2000) S. Sachdev, Quantum Phase Transitions (Cambridge, UK, 2000).
- Shen et al. (2020) B. Shen, Y. Zhang, Y. Komijani, M. Nicklas, R. Borth, A. Wang, Y. Chen, Z. Nie, L. Rui, and L. Xin, “Strange-metal behaviour in a pure ferromagnetic Kondo lattice,” Nature 579, 51–55 (2020).
- Bayha et al. (2020) L. Bayha, M. Holten, R. Klemt, K. SubraAmanian, and S. Jochim, “Observing the emergence of a quantum phase transition shell by shell,” Nature 587, 583–587 (2020).
- Cai et al. (2021) M. L. Cai, Z. D. Liu, W. D. Zhao, Y. K. Wu, Q. X. Mei, Y. Jiang, L. He, X. Zhang, Z. C. Zhou, and L. M. Duan, “Observation of a quantum phase transition in the quantum Rabi model with a single trapped ion,” Nature Communications 12, 1126 (2021).
- Liu et al. (2017) M. Liu, S. Chesi, Z. J. Ying, X. Chen, H. G. Luo, and H. Q. Lin, “Universal scaling and critical exponents of the anisotropic quantum Rabi model,” Phys. Rev. Lett. 119, 220601 (2017).
- Hwang et al. (2015) M. J. Hwang, R. Puebla, and M. B. Plenio, “Quantum phase transition and universal dynamics in the Rabi model,” Phys. Rev. Lett. 115, 180404 (2015).
- C. Wang and Senthil (2017) M. A. Metlitski C. Xu C. Wang, A. Nahum and T. Senthil, “Deconfined quantum critical points: Symmetries and dualities,” Phys. Rev. X 7, 031051 (2017).
- Shao et al. (2016) H. Shao, W. Guo, and A. W. Sandvik, “Quantum criticality with two length scales,” Science 352, 213–216 (2016).
- Bi et al. (2020) Z. Bi, E. Lake, and T. Senthil, “Landau ordering phase transitions beyond the Landau paradigm,” Phys. Rev. Research 2, 023031 (2020).
- Goldman and Kelton (1993) A. I. Goldman and R. F. Kelton, “Quasicrystals and crystalline approximants,” Rev. Mod. Phys. 65, 213 (1993).
- Iyer et al. (2013) S. Iyer, V. Oganesyan, G. Refael, and D. A. Huse, “Many-body localization in a quasiperiodic system,” Phys. Rev. B 87, 134202 (2013).
- Kohmoto et al. (1987) M. Kohmoto, B. Sutherland, and C. Tang, “Critical wave functions and a cantor-set spectrum of a one-dimensional quasicrystal model,” Phys. Rev. B 35, 1020 (1987).
- Lagendijk et al. (2009) A. Lagendijk, B. V. Tiggelen, and D. S. Wiersma, “Fifty years of Anderson localization,” Phys. Today 62, 24 (2009).
- hen and Ye (2019) Y. V. Kartashov L. Torner V. V. Konotop hen, C. Huang and F. Ye, “Localization and delocalization of light in photonic moiré lattices,” Nature 577, 42–46 (2019).
- (16) M. Gonalves, B. Amorim, E. V. Castro, and P. Ribeiro, “Hidden dualities in 1D quasiperiodic lattice models,” arXiv:2103.03895 .
- Cai et al. (2013) X. Cai, L. J. Lang, S. Chen, and Y. Wang, “Topological superconductor to Anderson localization transition in one-dimensional incommensurate lattices,” Phys. Rev. Lett. 110, 176403 (2013).
- Gong and Tong (2005) L. Y. Gong and P. Q. Tong, “Von Neumann entropy of an electron in one-dimensional Determined Potentials,” Chin. Phys. Lett. 22, 2759 (2005).
- Agrawal et al. (2020) U. Agrawal, S. Gopalakrishnan, and R. Vasseur, “Universality and quantum criticality in quasiperiodic spin chains,” Nature Communications 11, 2225 (2020).
- Roy et al. (2021) S. Roy, T. Mishra, B. Tanatar, and S. Basu, “Reentrant localization transition in a quasiperiodic chain,” Phys. Rev. Lett. 126, 106803 (2021).
- Goblot et al. (2020) V. Goblot, A. Štrkalj, N. Pernet, J. L. Lado, C. Dorow, A. Lemaître, L. Le Gratiet, A. Harouri, I. Sagnes, S. Ravets, and et al, “Emergence of criticality through a cascade of delocalization transitions in quasiperiodic chains,” Nature Physics 16, 832–836 (2020).
- Wang et al. (2020) Y. Wang, X. Xia, L. Zhang, H. Yao, S. Chen, J. You, Q. Zhou, and X. J. Liu, “One-dimensional quasiperiodic mosaic lattice with exact mobility edges,” Phys. Rev. Lett. 125, 196604 (2020).
- Sutherland (1986) B. Sutherland, “Localization of electronic wave functions due to local topology,” Phys. Rev. B 34, 5208 (1986).
- Hiramoto and Kohmoto (1992) H. Hiramoto and M. Kohmoto, “Electronic spectral and wavefunction properties of one-dimensional quasiperiodic systems: a scaling approach,” Int. J. Mod Phys B 6, 281–320 (1992).
- Hiramoto and Kohmoto (1989) H. Hiramoto and M. Kohmoto, “Scaling analysis of quasiperiodic systems: Generalized Harper model,” Phys. Rev. B 40, 8225 (1989).
- Liu and Gao (2017) P. Chen S. Liu, T. Wang and X. T. Gao, “Phase diagram of a generalized off-diagonal Aubry-André model with -wave pairing,” J. Phys. B:At. Mol. Opt. Phys. 51, 025301 (2017).
- Zeng et al. (2018) Q. B. Zeng, S. Chen, and R. Lü, “Quench dynamics in the Aubry-André-Harper model with -wave superconductivity,” New J. Phys. 20, 053012 (2018).
- Tong et al. (2021) X. Tong, Y. M. Meng, X. Jiang, C. Lee, G. Dias de Moraes Neto, and X. Gao, “Dynamics of a quantum phase transition in the Aubry-André-Harper model with -wave superconductivity,” Phys. Rev. B 103, 104202 (2021).
- Liu et al. (2015) F. Liu, S. Ghosh, and Y. D. Chong, “Localization and adiabatic pumping in a generalized Aubry-André-Harper model,” Phys. Rev. B 91, 014108 (2015).
- A. Purkayastha and Kulkarni (2018) A. Dhar A. Purkayastha, S. Sanyal and M. Kulkarni, “Anomalous transport in the Aubry-André-Harper model in isolated and open systems,” Phys. Rev. B 97, 174206 (2018).
- Zeng et al. (2016) Q. B. Zeng, S. Chen, and R. Lü, “Generalized Aubry-André-Harper model with -wave superconducting pairing,” Phys. Rev. B 94, 125408 (2016).
- Wei (2019) B. B. Wei, “Fidelity susceptibility in one-dimensional disordered lattice models,” Phys. Rev. A 99, 042117 (2019).
- Roy and Sharma (2019) N. Roy and A. Sharma, “Study of counterintuitive transport properties in the Aubry-André-Harper model via entanglement entropy and persistent current,” Phys. Rev. B 100, 195143 (2019).
- Fraxanet et al. (2021) J. Fraxanet, U. Bhattacharya, T. Grass, D. Rakshit, M. Lewenstein, and A. Dauphin, “Topological properties of the long-range Kitaev chain with Aubry-André-Harper modulation,” Phys. Rev. Research 3, 013148 (2021).
- Xiao et al. (2021) T. Xiao, D. Z. Xie, Z. L. Dong, T. Chen, W. Yi, and B. Yan, “Observation of topological phase with critical localization in a quasi-periodic lattice,” Science Bulletin 66, 2175–2180 (2021).
- Wang et al. (2016) J. Wang, X. J. Liu, X. Gao, and H. Hui, “Phase diagram of a non-abelian Aubry-André-Harper model with -wave superfluidity,” Phys. Rev. B 93, 104504 (2016).
- Mondragon-Shem and Hughes (2014) I. Mondragon-Shem and T. L. Hughes, “Signatures of metal-insulator and topological phase transitions in the entanglement of one-dimensional disordered fermions,” Phys. Rev. B 90, 104204 (2014).
- Yoo et al. (2020) Y. Yoo, J. Lee, and B. Swingle, “Nonequilibrium steady state phases of the interacting Aubry-André-Harper model,” Phys. Rev. B 102, 195142 (2020).
- Zeng et al. (2017) Q. B. Zeng, S. Chen, and R. Lü, “Anderson localization in the non-Hermitian Aubry-André-Harper model with physical gain and loss,” Phys. Rev. A 95, 062118 (2017).
- Zhao et al. (2017) X. L. Zhao, Z. C. Shi, C. S. Yu, and X. X. Yi, “Effect of loss on the topological features of dimer chains described by the extended Aubry-André-Harper model,” Phys. Rev. A 95, 043837 (2017).
- Longhi (2019) S. Longhi, “Metal-insulator phase transition in a non-Hermitian Aubry-André-Harper model,” Phys. Rev. B 100, 125157 (2019).
- Zeng et al. (2020) Q. B. Zeng, Y. B. Yang, and Y. Xu, “Topological phases in non-Hermitian Aubry-André-Harper models,” Phys. Rev. B 101, 020201 (2020).
- Longhi (2021) S. Longhi, “Phase transitions in a non-Hermitian Aubry-André-Harper model,” Phys. Rev. B 103, 054203 (2021).
- Zhang et al. (2020) D. W. Zhang, Y. L. Chen, G. Q. Zhang, L. J. Lang, and S. L. Zhu, “Skin superfluid, topological Mott insulators, and asymmetric dynamics in an interacting non-Hermitian Aubry-André-Harper model,” Phys. Rev. B 101, 235150 (2020).
- Liu et al. (2020) T. Liu, H. Guo, Y. Pu, and S. Longhi, “Generalized Aubry-André self-duality and mobility edges in non-Hermitian quasiperiodic lattices,” Phys. Rev. B 102, 024205 (2020).
- Gredeskul and Kivshar (1989) S. A. Gredeskul and Yu. S. Kivshar, “Generation of dark solitons in optical fibers,” Phys. Rev. Lett. 62, 977 (1989).
- Christodoulides and Silberberg (2003) D. N. Christodoulides and Y. Silberberg, “Discretizing light behaviour in linear and nonlinear waveguide lattices,” Nature 424, 817–823 (2003).
- Pertsch et al. (2004) T. Pertsch, U. Peschel, S. Nolte, A. Tünnermann, and H. Bartelt, “Nonlinearity and Disorder in Fiber Arrays,” Phys. Rev. Lett. 93, 053901 (2004).
- Negro et al. (2003) L Dal Negro, C. J. Oton, Z. Gaburro, L. Pavesi, P. Johnson, A. Lagendijk, R. Righini, M. Colocci, and D. S. Wiersma, “Light transport through the band-edge states of Fibonacci quasicrystals,” Phys. Rev. Lett. 90, 055501 (2003).
- Lahini et al. (2009) Y. Lahini, R. Pugatch, F. Pozzi, M. Sorel, R. Morandotti, N. Davidson, and Y. Silberberg, “Observation of a localization transition in quasiperiodic photonic lattices,” Phys. Rev. Lett. 103, 013901 (2009).
- Kraus et al. (2012) Y. E. Kraus, Y. Lahini, Z. Ringel, M. Verbin, and O. Zilberberg, “Topological states and adiabatic pumping in quasicrystals,” Phys. Rev. Lett. 109, 106402 (2012).
- Roati et al. (2008) G. Roati, C D’Errico, L. Fallani, M. Fattori, C. Fort, M. Zaccanti, G. Modugno, M. Modugno, and M. Inguscio, “Anderson localization of a non-interacting Bose-Einstein condensate,” Nature 453, 895–898 (2008).
- Yahyavi et al. (2019) M. Yahyavi, B. Hetényi, and B. Tanatar, “Generalized Aubry-André-Harper model with modulated hopping and -wave pairing,” Phys. Rev. B 100, 064202 (2019).
- Štrkalj et al. (2021) A. Štrkalj, E. V. H Doggen, I. V. Gornyi, and O. Zilberberg, “Many-body localization in the interpolating Aubry-André-Fibonacci model,” Phys. Rev. Research 3, 033257 (2021).
- Gong and Tong (2008) L. Y. Gong and P. Q. Tong, “Fidelity, fidelity susceptibility, and von Neumann entropy to characterize the phase diagram of an extended Harper model,” Phys. Rev. B 78, 115114 (2008).
- Werlang et al. (2010) T. Werlang, C. Trippe, G.A.P. Ribeiro, and G. Rigolin, “Quantum correlations in spin chains at finite temperatures and quantum phase transitions,” Phys. Rev. Lett. 105, 095702 (2010).
- Wei and Lv (2018) B. B. Wei and X. C. Lv, “Fidelity susceptibility in the quantum Rabi model,” Phys. Rev. A 97, 013845 (2018).
- Garnerone et al. (2009) S. Garnerone, N. T. Jacobson, S. Haas, and P. Zanardi, “Fidelity approach to the disordered quantum model,” Phys. Rev. Lett. 102, 057205 (2009).
- Chen et al. (2008) S. Chen, L. Wang, Y. Hao, and Y. Wang, “Intrinsic relation between ground-state fidelity and the characterization of a quantum phase transition,” Phys. Rev. A 77, 032111 (2008).
- Mao et al. (2021) R. Mao, Y. W. Dai, S. Y. Cho, and H. Q. Zhou, “Quantum coherence and spin nematic to nematic quantum phase transitions in biquadratic spin-1 and spin-2 chains with rhombic single-ion anisotropy,” Phys. Rev. B 103, 014446 (2021).
- Kinnunen et al. (2018) J. J. Kinnunen, Z. Wu, and G. M. Bruun, “Induced -wave pairing in Bose-Fermi mixtures,” Phys. Rev. Lett. 121, 253402 (2018).
- Liu et al. (2016) B. Liu, X.P. Li, Randall G. Hulet, and W. Vincent Liu, “Detecting -phase superfluids with -wave symmetry in a quasi-one-dimensional optical lattice,” Phys. Rev. A 94, 031602 (2016).
- Li et al. (2021) Y. Li, Q. Y. Li, W. Li, T. Liu, and D. Adroja, “Spin dynamics and griffiths singularity in the random quantum Ising magnet prtinbo6,” npj Quantum Mater. 6, 34 (2021).
- Caneva et al. (2007) T. Caneva, R. Fazio, and G. E. Santoro, “Adiabatic quantum dynamics of a random Ising chain across its quantum critical point,” Phys. Rev. B 76, 144427 (2007).
- Machida and Fujita (1986) K. Machida and M. Fujita, “Quantum energy spectra and one-dimensional quasiperiodic systems,” Phys. Rev. B 34, 7367 (1986).
- Kohmoto (1983) M. Kohmoto, “Metal-insulator transition and scaling for incommensurate systems,” Phys. Rev. Lett. 51, 1198 (1983).
- Evers and Mirlin (2008) F. Evers and A. D. Mirlin, “Anderson transitions,” Rev. Mod. Phys. 80, 1355–1417 (2008).
- Licciardello and Thouless (1978) D. C. Licciardello and D. J. Thouless, “Conductivity and mobility edges in disordered systems. II. Further calculations for the square and diamond lattices,” J. Phys.C: Solid State Phys 11, 925–936 (1978).
- Wegner (1980) F. Wegner, “Inverse participation ratio in 2+ dimensions,” Z. Phys.B 36, 209–214 (1980).
- Misguich et al. (2016) G. Misguich, V. Pasquier, and J. M. Luck, “Inverse participation ratios in the XXZ spin chain,” Phys. Rev. B 94, 155110 (2016).
- Dukesz et al. (2009) F. Dukesz, M. Zilbergerts, and L. F. Santos, “Interplay between interaction and (un)correlated disorder in one-dimensional many-particle systems: Delocalization and global entanglement,” New J. Phys. 11, 043026 (2009).
- Thouless (1974) D. J. Thouless, “Electrons in disordered systems and the theory of localization,” Phys. Rep. 13, 93–142 (1974).
- Biddle et al. (2011) J. Biddle, D. J. Priour, B. Wang, and S. Das Sarma, “Localization in one-dimensional lattices with non-nearest-neighbor hopping: Generalized Anderson and Aubry-André models,” Phys. Rev. B 83, 075105 (2011).
- Ganeshan et al. (2015) S. Ganeshan, J. H. Pixley, and S. Das Sarma, “Nearest neighbor tight binding models with an exact mobility edge in one dimension,” Phys. Rev. Lett. 114, 146601 (2015).
- H. P. Lüschen and Bloch (2018) T. Kohlert M. Schreiber P. Bordia X. Li S. Das Sarma H. P. Lüschen, S. Scherg and I. Bloch, “Single-particle mobility edge in a one-dimensional quasiperiodic optical lattice,” Phys. Rev. Lett. 120, 160404 (2018).
- Guo et al. (2021) Q. Guo, C. Cheng, Z. H. Sun, Z. Song, H. Li, Z. Wang, W. Ren, H. Dong, D. Zheng, and Y. R. Zhang, “Observation of energy-resolved many-body localization,” Nature Physics 17, 234–239 (2021).
- Polkovnikov (2011) A. Polkovnikov, “Microscopic diagonal entropy and its connection to basic thermodynamic relations,” Ann. Phys. 326, 486–499 (2011).
- Santos et al. (2011) L. F. Santos, A. Polkovnikov, and M. Rigol, “Entropy of isolated quantum systems after a quench,” Phys. Rev. Lett. 107, 040601 (2011).
- Vidmar et al. (2018) L. Vidmar, L. Hackl, E. Bianchi, and M. Rigol, “Volume law and quantum criticality in the entanglement entropy of excited eigenstates of the quantum Ising model,” Phys. Rev. Lett. 121, 220602 (2018).
- Pastur and Slavin (2014) L. Pastur and V. Slavin, “Area Law scaling for the entropy of disordered quasifree fermions,” Phys. Rev. Lett. 113, 150404 (2014).
- Kramer and Mackinnon (1993) B. Kramer and A. Mackinnon, “Localization: Theory and experiment,” Rep.Prog.Phys 56, 1469–1564 (1993).
- Tomasi and Khaymovich (2020) G. De Tomasi and I. M. Khaymovich, “Multifractality meets entanglement: Relation for nonergodic extended states,” Phys. Rev. Lett. 124, 200602 (2020).
- Yang et al. (2008) S. Yang, S. J. Gu, C. P. Sun, and H.Q. Lin, “Fidelity susceptibility and long-range correlation in the Kitaev honeycomb model,” Phys. Rev. A 78, 012304 (2008).
- Zanardi and Paunkovi (2006) P. Zanardi and N. Paunkovi, “Ground state overlap and quantum phase transitions,” Phys. Rev. E 74, 031123 (2006).
- You et al. (2007) W. L. You, Y. W. Li, and S. J. Gu, “Fidelity, dynamic structure factor, and susceptibility in critical phenomena,” Phys. Rev. E 76, 022101 (2007).
- Thesberg and Sørensen (2011) M. Thesberg and E. S Sørensen, “General quantum fidelity susceptibilities for the - chain,” Phys. Rev. B 84, 224435 (2011).
- Zhu et al. (2018) Z. Zhu, G. Y. Sun, W. L. You, and D. N. Shi, “Fidelity and criticality of a quantum Ising chain with long-range interactions,” Phys. Rev. A 98, 023607 (2018).
- Ren et al. (2020) J. Ren, W. L. You, and X. Wang, “Entanglement and correlations in a one-dimensional quantum spin- chain with anisotropic power-law long-range interactions,” Phys. Rev. B 101, 094410 (2020).
- Sun et al. (2019) G. Y. Sun, B. B. Wei, and S. P. Kou, “Fidelity as a probe for a deconfined quantum critical point,” Phys. Rev. B 100, 064427 (2019).
- Pandey et al. (2020) M. Pandey, P. W. Claeys, D. K. Campbell, A. Polkovnikov, and D. Sels, “Adiabatic eigenstate deformations as a sensitive probe for quantum chaos,” Phys. Rev. X 10, 041017 (2020).
- Surace et al. (2021) F. M. Surace, M. Votto, E. G. Lazo, A. Silva, M. Dalmonte, and G. Giudici, “Exact many-body scars and their stability in constrained quantum chains,” Phys. Rev. B 103, 104302 (2021).
- Leblond et al. (2021) T. Leblond, D. Sels, A. Polkovnikov, and M. Rigol, “Universality in the onset of quantum chaos in many-body systems,” Phys. Rev. B 104, L201117 (2021).
- Alishahiha and Astaneh (2017) M. Alishahiha and A. F. Astaneh, “Holographic fidelity susceptibility,” Phys. Rev. D 96, 086004 (2017).
- You and He (2015) W. L. You and L. He, “Generalized fidelity susceptibility at phase transitions,” J. Phys. Condens. Matter 27, 205601 (2015).
- Zanardi et al. (2007) P. Zanardi, P. Giorda, and M. Cozzini, “Information-theoretic differential geometry of quantum phase transitions,” Phys. Rev. Lett. 99, 100603 (2007).
- Braun et al. (2018) D. Braun, G. Aerardo, F. Benatti, R. Floreanini, U. Marzolino, M. W. Mitchell, and S. Pirandola, “Quantum-enhanced measurements without entanglement,” Rev. Mod. Phys. 90, 035006 (2018).
- Fisher and Barber (1972) M. E. Fisher and M. N. Barber, “Scaling theory for finite-size effects in the critical region,” Phys. Rev. Lett. 28, 1516 (1972).
- Roncaglia et al. (2015) M. Roncaglia, L. Campos Venuti, and E. Degli, “Finding critical points using improved scaling ansätze,” J. Stat. Mech. Theory Exp. 2015, P04005 (2015).
- Osterloh et al. (2002) A. Osterloh, L. Amico, G. Falci, and R. Fazio, “Scaling of entanglement close to a quantum phase transition,” Nature 416, 608–610 (2002).
- Ren et al. (2018) J. Ren, Y. Wang, and W. L. You, “Quantum phase transitions in spin-1 XXZ chains with rhombic single-ion anisotropy,” Phys. Rev. A 97, 042318 (2018).
- Albuquerque et al. (2010) A. F. Albuquerque, F. Alet, C. Sire, and S. Capponi, “Quantum critical scaling of fidelity susceptibility,” Phys. Rev. B 81, 064418 (2010).
- Sinha et al. (2019) A. Sinha, M. M. Rams, and J. Dziarmaga, “Kibble-Zurek mechanism with a single particle: Dynamics of the localization-delocalization transition in the Aubry-André model,” Phys. Rev. B 99, 094203 (2019).
- Altland and Zirnbauer (1997) A. Altland and M. R. Zirnbauer, “Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures,” Phys. Rev. B 55, 1142 (1997).
- Harris (1974) A. B. Harris, “Effect of random defects on the critical behaviour of ising models,” J. Phys. C: Solid State Phys 7, 1671 (1974).
- Cookmeyer et al. (2020) T. Cookmeyer, J. Motruk, and J. E. Moore, “Critical properties of the ground-state localization-delocalization transition in the many-particle Aubry-André model,” Phys. Rev. B 101, 174203 (2020).
- Cestari et al. (2011) J. C. C. Cestari, A. Foerster, M. A. Gusmão, and M. Continentino, “Critical exponents of the disorder-driven superfluid-insulator transition in one-dimensional Bose-Einstein condensates,” Phys. Rev. A 84, 055601 (2011).
- Tan et al. (2019) X. Tan, D. W. Zhang, Z. Yang, J. Chu, Y. Q. Zhu, D. Li, X. Yang, S. Song, Z. Han, Z. Li, Y. Dong, H. F. Yu, H. Yan, S. L. Zhu, and Y. Yu, “Experimental measurement of the quantum metric tensor and related topological phase transition with a superconducting qubit,” Phys. Rev. Lett. 122, 210401 (2019).
- Yu et al. (2020) M. Yu, P. Yang, M. Gong, Q. Cao, Q. Lu, H. Liu, M. B. Plenio, F. Jelezko, T. Ozawa, and N. Goldman, “Experimental measurement of the quantum geometric tensor using coupled qubits in diamond,” Natl. Sci. Rev. 7, 254–260 (2020).
- Gianfrate et al. (2020) A. Gianfrate, O. Bleu, L. Dominici, V. Ardizzone, M. De Giorgi, D. Ballarini, G. Lerario, K. W. West, L. N. Pfeiffer, D. D. Solnyshkov, D. Sanvitto, and G. Malpuech, “Measurement of the quantum geometric tensor and of the anomalous Hall drift,” Nature 578, 381–385 (2020).