Quantum concentration inequalities
Abstract
We establish Transportation Cost Inequalities (TCIs) with respect to the quantum Wasserstein distance by introducing quantum extensions of well-known classical methods: First, we generalize the Dobrushin uniqueness condition to prove that Gibbs states of 1D commuting Hamiltonians satisfy a TCI at any positive temperature and provide conditions under which this first result can be extended to non-commuting Hamiltonians. Next, using a non-commutative version of Ollivier’s coarse Ricci curvature, we prove that high temperature Gibbs states of commuting Hamiltonians on arbitrary hypergraphs satisfy a TCI with constant scaling as . Third, we argue that the temperature range for which the TCI holds can be enlarged by relating it to recently established modified logarithmic Sobolev inequalities. Fourth, we prove that the inequality still holds for fixed points of arbitrary reversible local quantum Markov semigroups on regular lattices, albeit with slightly worsened constants, under a seemingly weaker condition of local indistinguishability of the fixed points. Finally, we use our framework to prove Gaussian concentration bounds for the distribution of eigenvalues of quasi-local observables and argue the usefulness of the TCI in proving the equivalence of the canonical and microcanonical ensembles and an exponential improvement over the weak Eigenstate Thermalization Hypothesis.
1 Introduction
Given a random variable of law taking values on a metric space and a function , a concentration of measure inequality quantifies the probability that the random variable deviates from its mean or its median. Since the early age of the theory, concentration inequalities have seen many new methods, refinements and exciting applications to various areas of mathematics [1, 2, 3]. Among the different classes of concentration inequalities, Gaussian concentration is arguably the most standard one: the measure is said to be sub-Gaussian if there exist constants such that, for all with we have for any
| (1) |
In her seminal work [4], Marton made the beautiful observation that the above behavior can be obtained as a consequence of a transportation cost inequality: if there exists such that, for any probability measure ,
| () |
then (1) holds with constants and for all . Here, refers to the relative entropy between the measures and , whereas the quantity in () is the Wasserstein distance between the two measures :
Later, [5] proved that transportation cost inequalities are in fact equivalent to the property of sub-Gaussianity: more precisely, () holds if and only if for all Lipschitz functions ,
One of the main advantages of transportation cost inequalities is their tensorization property: assume that satisfies , then satisfies for all , where the set is provided with the metric
Perhaps the simplest example of that sort is given by taking endowed with the Hamming distance . In the case , the corresponding Wasserstein distance reduces to the total variation, and holds for any measure , since it simply reduces to Pinsker’s inequality. For , satisfies .
While the theory of concentration inequalities for i.i.d. random variables is by now well understood, things become more challenging when the random variables are allowed to depend on each other [3, 6]. One way to extend concentration bounds to weakly dependent random variables is to assume that their joint law satisfies the so-called Dobrushin uniqueness condition [6]. Dobrushin’s uniqueness condition plays an important role in the study of Gibbs measures in the one-phase region, however it often turns out to be a very strong requirement on the measure . More recently, Marton gave an attempt at extending the i.i.d. theory beyond the mere Gibbs setting [7]. Her main result consists in a logarithmic Sobolev inequality for a generic measure - well known to imply transportation cost inequalities - under the so-called Dobrushin–Shlosman mixing condition [8], the latter condition being weaker than Dobrushin’s uniqueness condition. As mentioned in [9], such paths to establish Gaussian concentration suffer from the difficulty of deriving explicit constants. Moreover, the result of [7] also relies on the crucial assumption that the measure has full support.
Recently, concentration inequalities have attracted much attention in the communities of random matrix theory, quantum information theory and operator algebras [10, 11, 12, 13, 14, 15, 16, 17, 18]. In [14], a quantum Wasserstein distance of order 1 (or quantum distance) was defined on the set of the quantum states of qudits with the property that it strictly reduces to the classical Wasserstein distance on for states that are diagonal in the computational basis. This quantum generalization of the Wasserstein distance is based on the notion of neighboring states. Two quantum states of qudits are neighboring if they differ only in one qudit, i.e., if they coincide after that qudit is discarded. The quantum distance is then that induced by the maximum norm that assigns distance at most one to every couple of neighboring states [14, Definition 4]. Such norm is called quantum norm and is denoted with . The quantum norm proposed in Ref. [14] admits a dual formulation in terms of a quantum generalization of the Lipschitz constant. Denoting with the set of the observables of qudits, the Lipschitz constant of the observable is defined as [14, Section V]
| (2) |
Then, the quantum distance between the states and can also be expressed as [14, Section V]
| (3) |
Moreover, in [14] it was showed that holds for any tensor product of quantum states, hence extending Marton’s original inequality with the exact same constant: for any state of qudits,
where denotes Umegaki’s relative entropy between the states and .
Main results:
In this paper, we prove that any of the following conditions implies a transportation cost inequality:
Each of these methods comes with its strengths and weaknesses:
- (i)
-
(ii)
The coarse Ricci curvature bound provides TC inequalities for essentially any geometry, but it is only valid above a threshold temperature that depends on the locality of the Hamiltonian. Furthermore, such threshold temperature is in practice strictly larger than the true critical temperature (see Proposition 9).
-
(iii)
Quantum modified logarithmic Sobolev inequalities are typically more difficult to prove than their classical counterparts, and are currently only proven to hold in specific cases. However, for one-dimensional systems, a recently derived modified logarithmic Sobolev inequality [19, 20] provides us with TC (up to polylogarithmic overhead) at any positive temperature.
-
(iv)
The condition of local indistinguishability of the state for regular lattices. Although the condition can be checked for classical systems, we do not yet have a way to prove it in the quantum setting.
We conclude the article with two natural applications of our bounds. First, we derive Gaussian concentration bounds for a large class of Lipschitz observables whenever the state is that of a commuting Hamiltonian at large enough temperature (section 7). Second, we argue on the use of the transportation cost inequality in proving the equivalence between the microcanonical and the canonical ensembles and an exponential improvement over the weak Eigenstate Thermalization Hypothesis (section 8).
2 Notations and basic definitions
Given a finite set , we denote by the Hilbert space of qudits (i.e., for all ) and by the algebra of linear operators on . corresponds to the space of self-adjoint linear operators on , whereas is the subspace of traceless self-adjoint linear operators. denotes the cone of positive semidefinite linear operators on and denotes the set of quantum states. We denote by the set of probability measures on . For any subset , we use the standard notations for the corresponding objects defined on subsystem . Given a state , we denote by its marginal onto the subsystem . For any , we denote by its trace norm. The identity on , , is denoted by .
Given two states such that , their quantum relative entropy is defined as [21, 22, 23]
| (4) |
Whenever is a bipartite state and , their relative entropy reduces to the mutual information
| (5) |
In the next sections, we also utilize the measured relative entropy [24, 25, 26, 27]
| (6) |
where the supremum above is over all positive operator valued measures that map the input quantum state to a probability distribution on a finite set with probability mass function given by .
In this paper, we study inequalities relating the distance between two states to their relative entropy. More precisely, for a fixed state , we are interested in upper bounding the best constant such that, for all with ,
| (7) |
In general, given a constant , we refer to the above inequality for replaced by as a transportation cost inequality, denoted by . As mentioned in the introduction, the following holds [14, Theorem 2]:
Proposition 1.
For any product state ,
| (8) |
In the next sections, we aim at recovering the linear dependence of the constant on the size of the system under various measures of independence.
We will need the following properties of the quantum distance:
Proposition 2 ([14, Proposition 2]).
The quantum distance coincides with the trace distance for quantum states that differ in only one site, i.e., for any such that for some we have
| (9) |
Proposition 3 ([14, Proposition 5]).
The quantum distance between two quantum states that differ only in the region is at most times their trace distance, i.e., for any such that we have
| (10) |
Proposition 4 (Tensorization [14, Proposition 4]).
The quantum distance is additive with respect to the tensor product, i.e., let be disjoint subsets of . Then, for any and any we have
| (11) |
Proposition 5 ([14, Proposition 13]).
Let be a quantum channel. For any , let be the light-cone of the site , i.e., the minimum subset of such that for any such that . Then, can expand the quantum distance by at most twice the size of the largest light-cone, i.e., for any we have
| (12) |
Proposition 6 ([14, Proposition 15]).
For any and any we have
| (13) |
Proposition 7 ([14, Corollary 1]).
For any ,
| (14) |
and equality holds whenever both and are product states.
Theorem 1 ( continuity of the entropy [14, Theorem 1]).
For any we have
| (15) |
where for any
| (16) |
3 Dobrushin uniqueness condition
In this section, we consider a spin chain and prove the transportation cost inequality under a quantum generalization of Dobrushin’s uniqueness condition [6]. Such condition is formulated in terms of the conditional probability distributions of the state of a subset of conditioned on the state of a second disjoint subset of . Therefore, formulating a quantum version of Dobrushin’s uniqueness condition requires a quantum counterpart of the conditional probability distribution. In the classical setting, given two random variables and taking values in finite sets and with joint probability distribution , the conditional probability distribution of given with probability mass function
| (17) |
represents the knowledge that we have on when we know only the value of . We can associate to such conditional distribution the stochastic map that has as input a probability distribution for and as output the joint probability distribution of with probability mass function given by
| (18) |
In the quantum setting, we consider a bipartite quantum system and a joint quantum state of . The quantum counterpart of the stochastic map (18) is called quantum recovery map [28, 29] and its action on a quantum state of is
| (19) |
where is the probability distrbution on with density
| (20) |
We stress that (19) reduces to (18) whenever , and commute. If is in the state , the recovery map recovers the joint state , i.e., . The relevance of the recovery map comes from the recoverability theorem [29], which states that can recover a generic joint state from its marginal if removing the subsystem does not significantly decrease the relative entropy between and . More precisely, for any quantum state of we have
| (21) |
We consider the setting where is partitioned as
| (22) |
For any , we denote with the union . The recoverability theorem implies the following Lemma 1, which we will employ several times:
Lemma 1.
For any we have
| (23) | ||||
| (24) |
where are the recovery maps associated to .
Proof.
Eq. (19) and Pinsker’s inequality imply for any
| (25) |
Summing (25) over and using the convexity of the square function yields
| (26) |
The claim (23) follows.
With an analogous proof, applying the improved Pinsker’s inequality
| (27) |
and the convexity of the function we get
| (28) |
The claim (24) follows. ∎
The following property of the recovery map will be fundamental:
Lemma 2.
Let be a joint state of the tripartite quantum system . Let us assume that is Markovian, i.e.,
| (29) |
Then, the recovery map associated to does not act on the subsystem .
Proof.
From the characterization of the states that saturate the strong subadditivity [30], the Hilbert space of has a decomposition
| (30) |
where the Hilbert spaces and are pairwise orthogonal, and can be expressed as
| (31) |
where is a probability distribution on , and each or is a quantum state with support in the corresponding or . We have for any quantum state of
| (32) |
We have for any that
| (33) |
does not act on , and the claim follows choosing . ∎
3.1 Markovian case
In this subsection, we assume that is a one-dimensional quantum Markov state. More preciesly, let be a partition of and let . Then, we assume that
| (34) |
for any . For any , let be the recovery map (19) associated to that recovers from . From Lemma 2, acts only on , i.e., it is a map . We also define
| (35) |
We can now state the main result of this Section:
Theorem 2.
Let us assume that for any , is a contraction with respect to the trace norm for all the couples of quantum states of that differ only on the subsystem , i.e., that coincide after discarding . More precisely, we assume that there exists such that for any and any with we have
| (36) |
Then, we have
| (37) |
Furthermore, for any we have
| (38) |
Remark 1.
Condition (36) holds for some iff strictly decreases the trace distance between any two quantum states that differ only in the subsystem on which acts, i.e., that coincide after discarding . We expect this condition to hold for any strictly positive temperature.
Remark 2.
An example of quantum state satisfying (34) is a Gibbs state of a nearest-neighbor Hamiltonian on the -dimensional cubic lattice , where are neighbors iff . We can then choose and
| (41) |
with
| (42) |
and get from Theorem 2
| (43) |
We stress that, assuming that remains bounded away from , we get iff , i.e., for one-dimensional systems.
Remark 3.
We can choose
| (44) |
where is the quantum channel that replaces the input quantum state with and
| (45) |
denotes the diamond norm of the linear map on .
Proposition 8.
Let satisfy (34), and assume
| (46) |
where
| (47) |
denotes the quantum max-divergence [31] between the quantum states and . Then, we can choose in (36)
| (48) |
Proof.
From Remark 3, we can choose
| (49) |
where each is a unit vector in . We have from Pinsker’s inequality
| (50) |
(46) implies
| (51) |
From the characterization of the states that saturate the strong subadditivity [30] we get
| (52) |
therefore, (51) can be rewritten as
| (53) |
Choosing in (25) we get with the help of (53)
| (54) |
and the claim follows. ∎
3.2 Non-Markovian states
Here, we prove an alternative version of Theorem 2 where the Markov condition (34) is replaced by exponential decay of correlations.
Theorem 3.
Let be a one-dimensional lattice, and let . For any , let be the recovery map associated to that recovers the site from the sites . We assume that has exponentially decaying correlations, in the sense that there exist and such that for any , any and any ,
| (55) |
We also assume that for any , any and any
| (56) |
Then,
| (57) |
3.3 Auxiliary lemmas
Lemma 3.
Lemma 4.
For any and any ,
| (70) |
Proof.
Without loss of generality, we can assume that and for some . We have
| (71) |
where the equality follows from Proposition 2 and Proposition 4 and the last inequality follows from the triangle inequality for the trace norm and its contractivity with respect to partial traces. By induction we get
| (72) |
and the claim follows. ∎
4 Curvature bound
In the seminal paper [32], Ollivier introduced a generalization of the notion of curvature to generic, possibly discrete, metric spaces. In his framework, the curvature of a metric space endowed with a classical stochastic map acting on the probability measures on is defined as the following contraction property of the Wasserstein distance : for any two probability measures ,
| (74) |
The constant is called the coarse Ricci curvature of the triple . In particular, it is easy to verify that the existence of a positive coarse Ricci curvature induces the uniqueness of the invariant measure for the Markov kernel . Moreover, it was recently proven in [33] that Ollivier’s coarse Ricci curvature provides an upper bound on the transportation cost inequality for the measure , hence recovering the results from the smooth Riemannian setting.
Here, inspired by the works of [32] and [33], we prove that a contraction of the Lipschitz constant under a certain quantum channel constructed from the Petz recovery maps of the Gibbs state can be used to conclude that satisfies a transportation cost inequality. In particular, we do not need to assume that the underlying graph is , in contrast with section 3. Let be a hypergraph with , and let be a Hamiltonian whose local terms pairwise commute and are supported on the hyperedges . For a given site , we recall the composition of the partial trace on with the rotated Petz recovery map of :
| (75) |
for the probability density . Note that since we assumed to be the Gibbs state of a commuting Hamiltonian, the map acts non-trivially on the neighborhood of
| (76) |
We also introduce the quantum channel
| (77) |
We assume that is a contraction with respect to the norm, i.e., that
| (78) |
for some , in analogy with (74). This contraction property was already derived in Ollivier’s original article [32] as a generalization of Dobrushin’s uniqueness condition. Here, we first prove that this condition implies the transportation cost inequality for the Gibbs state :
Theorem 4.
With the conditions of the previous paragraph, we have
| (79) |
where .
Proof.
We have for any state
| (80) |
The last term can be controlled by thanks to the contraction (78):
| (81) |
On the other hand, the sum on the right-hand side of (80) can be controlled as follows:
| (82) |
where the last inequality follows by Proposition 3. Proceeding as in the proof of Lemma 1, by the joint use of Pinsker’s inequality with the recoverability bound followed by the data processing inequality we can further bound the trace distances above so that
| (83) |
Inequality (1) above uses the concavity of the entropy, so that for any state
| (84) |
It remains to prove that (78) is satisfied at high enough temperature.
Proposition 9.
There exists an inverse temperature such that for all , (78) holds for some constant . In particular, whenever , one can choose
| (85) |
where denotes the Lambert function and is defined as the inverse of .
Proof.
We have
| (86) |
Any can be expressed as [14, Section III]
| (87) |
such that for any , satisfies and
| (88) |
Therefore, we have
| (89) |
We have
| (90) |
where the equality follows from Proposition 2 and Proposition 4. Since , we have , and
| (91) |
For any we have
| (92) |
Then,
| (93) |
We have for any , recalling that ,
| (94) |
therefore,
| (95) |
and
| (96) |
Moreover,
| (97) |
Putting together (4), (91), (96) and (97), we get
| (98) |
where is the quantum channel that replaces with the state of the site . We then have
| (99) |
We have
| (100) |
Since the Hamiltonian terms commute we have that, given ,
| (101) |
Now,
| (102) |
Inequality (1) above follows from the operator convexity of as well as Lemma 6, where . Moreover,
| (103) |
Therefore,
| (104) |
and the integrand in (100) tends to zero pointwise for . On the other hand, we have for any
| (105) |
therefore the integrand in (100) is uniformly bounded. Then, we get for all that
| (106) |
Therefore, for any there exists such that condition (78) is satisfied for all . More precisely, in view of (106) and (4), it is sufficient that
| (107) |
where . Moreover, it is clear that . The result follows after choosing so that the exponentially decaying term counts for at most half the upper bound and solving (107) for , up to some numerical simplifications. ∎
Remark 5.
The lower bound (85) can be compared to that in the classical setting [32, Example 17] (see also [34]): there, the author showed that for a Hamiltonian of the form , where denotes the spin configuration at the site of a graph , i.e. ,
which shows asymptotic optimality of our result, up to numerical multiplicative constants. For comparison, the exact value of for the Ising model on the regular infinite tree with degree is known to be equal to .
4.1 Auxiliary lemma
Lemma 6.
For any positive, definite matrices and all ,
| (108) |
Proof.
It suffices to use a linear interpolation between and : . We have
| (109) |
Then,
| (110) |
by the operator convexity of where and . The result follows by operator convexity of the inverse function and further simple estimates. ∎
5 Modified logarithmic Sobolev inequalities
In this section, we pursue a different approach to prove transportation cost inequalities for , namely through the existence of a non-commutative entropic inequality known as the modified logarithmic Sobolev inequality [35, 36]. In order to introduce our main result, we need a variation of the Lipschitz constant that was introduced in [13]. This definition departs from a noncommutative differential structure, which we define below (see [37]):
Definition 1 (Differential structure).
A set of operators and constants define a differential structure for a full rank state if
-
1
;
-
2
consists of eigenvectors of the modular operator with
(111)
Such a differential structure can be used to provide the set of matrices with a Lipschitz constant that is tailored to , see e.g. [13, 37] for more on this. In order to distinguish that constant from , we refer to it as the differential Lipschitz constant and denote it by . It is defined as:
| (112) |
where . For ease of notations, we will denote the differential structure by the couple . The notion of a differential structure is also intimately connected to that of the generator of a quantum dynamical semigroup converging to [37], and properties of that semigroup immediately translate to properties of the metric. This is because the differential structure can be used to define an operator that behaves in an analogous way to the Laplacian on a smoth manifold, which in turn induces a heat semigroup. We refer to [37, 13] for more details on this connection and interpretation.
When the state is a quantum Gibbs state corresponding to a local, commuting Hamiltonian associated to a uniformly bounded interaction defined on a lattice , the differential structure can be chosen as local. This means that the operators are indexed by a site and an index of a set whose cardinality only depends on the local dimension and the locality of . Moreover, we assume that the operators are supported on a neighborhood of site of diameter and the corresponding constants are uniformly bounded: . The definition in Eq. (112) yields a metric on states by duality:
Proposition 10.
Given the Gibbs state of a local commuting Hamiltonian on with and associated local differential structure , the following bound holds for all :
for some constant independent of .
Proof.
By duality, it is equivalent to prove that for all
First, we have
| (113) | ||||
| (114) |
Now, since for each pair , is supported on a neighborhood of site ,
| (115) | ||||
| (116) |
Next, by a telescopic sum argument, we can further control the last infinity norm on the right hand side above as follows: given an arbitrary ordering of the region ,
| (117) | ||||
| (118) |
where follows from the triangle inequality whereas follows from the fact that the maps are completely positive and unital, and therefore contract the operator norm. All in all, we have derived the following bound on the differential Lipschitz constant of :
| (119) | ||||
| (120) | ||||
| (121) |
for some constant independent of , and where follows from Proposition 6. ∎
The advantage of as compared to is that it does not depend on the state . On the other hand, the bound derived in Proposition 10 can be used in conjunction with recently proved transportation cost inequalities for through the proof of the existence of a modified logarithmic Sobolev inequality in order to get analogous inequalities for (see [38] for more details):
Theorem 5.
Let be the Gibbs state of a local commuting Hamiltonian at inverse temperature on . Then, there exists a critical inverse temperature such that for some constant independent of whenever if any of the two conditions below is satisfied:
-
is classical;
-
is a nearest neighbour Hamiltonian.
Moreover, we can drop the assumption of -locality in the D case, where at the cost of getting a slightly worsened constant , so that we recover the result of Theorem 2.
Proof.
In [38, 19, 20] the existence of local differential structures associated to that satisfy the so-called modified logarithmic Sobolev inequality was proved under the conditions of the theorem. Moreover, the modified logarithmic Sobolev inequality implies the transportation cost inequality for the differential Wasserstein distance [13]: there exists a constant independent of such that
| (122) |
for all state . This fact in conjunction with Proposition 10 allows us to conclude. ∎
6 Local indistinguishability
In this section, we provide a transportation cost inequality under a condition of local indistinguishability [39, 40, 41]. In the classical setting, this condition constitues a weakening of Dobrushin Shlosman’s mixing condition [8] recently considered by Marton [7]. Moreover, as opposed to the latter, our technique has the benefit of not requiring the local specifications of the state to be uniformly lower bounded by a positive number, at the cost of getting a slightly worsened constant.
6.1 Transportation cost from local indistinguishability
We start by proving our general result in the quantum setting. Here, we assume that the qudits are arranged on a -dimensional regular lattice . Before we state our main result, we need to introduce the notion of a non-commutative conditional expectation.
Definition 2 (Conditional expectations).
Let be a von Neumann subalgebra111We recall that a finite dimensional von Neumann algebra is a matrix algebra that is close under taking the adjoint. of . A conditional expectation onto is a completely positive unital map satisfying
-
i)
for all , ;
-
ii)
for all , .
We denote by its adjoint map with respect to the trace inner product, i.e.
As a simple example, we consider a full-rank state and let be a quantum Markov semigroup. Under the following detailed balance condition, the limit is a conditional expectation onto the algebra of fixed points of the semigroup:
Next, for a state , the relative entropy with respect to is defined as follows
where the infimum is always attained by . Indeed, for any satisfying , we have the following chain rule (see [42, Lemma 3.4])
| (123) |
Hence the infimum is attained if and only if .
Definition 3 (Local indistinguishability).
Let be a set of subalgebras of such that and be a set of compatible conditional expectations acting non-trivially on region , i.e., they satisfy the property that for any , . Then, we say that satisfies local indistinguishability if there exists a fast decaying function independent of such that for every regions with , and for all states ,
For instance, take a product state and for each region , denote . One can easily verify that the maps are conditional expectations and satisfy the local indistinguishability condition with . We are now ready to state and prove the main theorem of this section. For a strictly decreasing function and a positive real number , we denote by .
Theorem 6.
Let be a set of compatible conditional expectations satisfying local indistinguishability with fast decaying function . Then for all hypercubes and all ,
| (124) |
for some fixed constant of order . In particular, whenever for all states , and assuming the exponential clustering function , the state satisfies with .
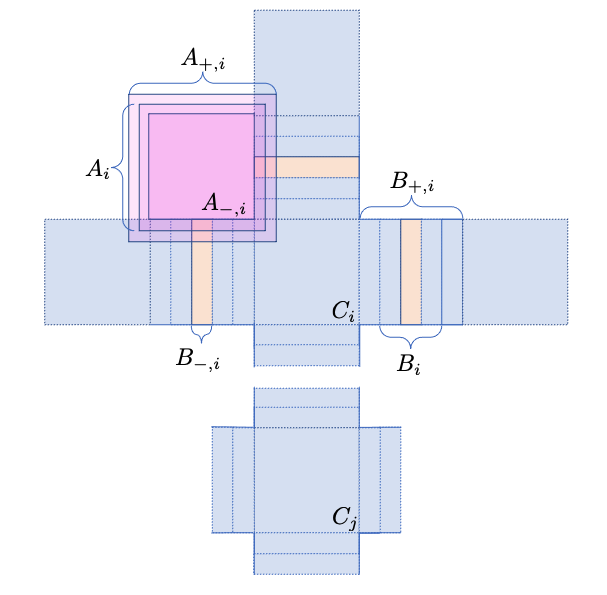
Proof.
For sake of clarity, we provide the proof for only, although the general case follows similarly. First, we partition the hypercube into regions , and in the same way as done in [41] (see also Figure 1). Then, by triangle inequality
| (125) |
where
and where the last bound in (125) follows from Proposition 5 with . Now, we control each of the norms on the right-hand side of (125) separately. First, we denote by , given an arbitrary ordering of the connected subregions in , and similarly for the other regions and . Then,
| (126) | ||||
| (127) | ||||
| (128) | ||||
| (129) |
with
where denotes the number of connected components in , and similarly for the other sets. Above, (126) follows by the triangle inequality, (127) by the triangle inequality and Proposition 3, and (128) by Pinsker’s inequality as well as Jensen’s inequality for . (129) follows from the chain rule in (123), and the fact that the regions , resp. , resp. , do not overlap, so that for instance . Next, we control the second norm on the right-hand side of (125): using Proposition 3 , we have
| (130) | ||||
| (131) | ||||
| (132) | ||||
| (133) |
Above, (130) follows form the compatibility of the conditional expectations, and (131) from and the monotonicity of the trace-distance under such CPTP map. (132) follows from the condition of local indistinguishability when taking , and , and assuming that . Finally, (133) follows from an application of Pinsker’s inequality. Similarly, we find
| (134) |
Then, by inserting (129), (133) and (134) into (125), we have
| (135) | |||
| (136) |
where (135) is another directly application of Jensen’s inequality for , whereas (136) follows from two uses of the chain rule (123) after adding the positive term to the square root and a final use of the data processing inequality. The result then follows after choosing the length so that
With this choice, and estimating the bound found in (136) can be further controlled by
| (137) | ||||
| (138) |
∎
6.2 Classical case
In this section, we restrict our analysis to classical conditional expectations and probability measures. In this setting, it is easy to see that the property of local indistinguishability is implied by the following condition. Here, with a slight abuse of notations, we will use the same symbol for a probability measure on the Borel sets of and its corresponding probability mass function.
Definition 4 (Local indistinguishability, classical case).
Let be a probability measure on , and be a set of compatible conditional probability measures acting on the sets , i.e. they satisfy the property that for any , . Then, we say that the measure satisfies local indistinguishability if there exists a fast decaying function such that for every regions such that for any and ,
where denotes the boundary of .
Corollary 1.
Let be a probability measure on satisfying local indistinguishability with fast decaying function . Then for all ,
| (139) |
Equivalently, the measure satisfies the following sub-Gaussian tail: for any function such that ,
| (140) |
7 Gaussian concentration
As mentioned before, the classical transportation cost inequalities for a measure is equivalent to the sub-Gaussian bounds on the tail probability of any Lipschitz function of a random variable drawn according to . One way to see this is by using the variational formulation of the relative entropy in order to bound the Laplace transform of . In the non-commutative setting, this leads to the following characterization of the transportation cost constant :
Proposition 11.
For any ,
| (141) |
and the can be restricted to such that .
Proof.
Let be the right-hand side of (141). On the one hand, let satisfy , and let
| (142) |
We have
| (143) |
therefore .
On the other hand, let , and let such that
| (144) |
We have
| (145) |
where the last inequality follows from the definition of , therefore , and the claim follows. ∎
In the tracial setting [10], and more generally whenever the quantity can be interpreted as the Laplace transform of in the state , and therefore the equivalence between Gaussian concentration and the transportation cost inequality holds. However, this is no longer true when and do not commute, and the following bound can turn out to be strictly stronger to the transportation cost inequality as a consequence of the Golden-Thompson inequality: for any such that ,
| (146) |
In other words, . Recently, bounds of the form of (146) were obtained for some subclasses of Lipschitz observables (typically local observables) when the is the Gibbs state of a (possibly non-commuting) quasi-local Hamiltonian [43] using cluster expansion techniques. However, the existence of the Gaussian concentration inequality for general Lipschitz observables was left open.
Here instead, we pursue a different approach using our transportation cost inequality. In particular, we prove that (146) can be approximately recovered for Gibbs states of commuting Hamiltonians for a larger class of Lipschitz observables than those considered in [43]. For this, we adapt the result of [13, Theorem 8] which was written for to the case of . In this section, we denote by , respectively the real, respectively imaginary parts of an operator . Given an observable with spectral decomposition , a state and a real number , we denote by
| (147) |
the probability of getting an eigenvalue when measuring on the state .
Theorem 7.
Assume that the full-rank state satisfies for some . Then, for any observable ,
| (148) |
Whenever the bound can be tightened into
| (149) |
Therefore, whenever corresponds to the Gibbs state of a local commuting Hamiltonian on a hypergraph at inverse temperature , the above bounds hold as long as where is defined in (85).
Proof.
Given , we denote by its decomposition onto real and imaginary parts. We also assume that and . By assumption, we have that for any
| (150) |
Then, since for any , we have that for all :
| (151) |
Next, we further upper bound the relative entropy in terms of the maximal divergence [44]. Choosing for some observable , we arrive at
| (152) |
Next, we choose , so that the previous inequality reduces to
| (153) |
The above inequality can be interpreted as a bound on the log-Laplace transform of the non-commutative variable in the state . By a use of Markov’s inequality followed by an optimization over the variable , we finally get
| (154) |
The result follows after simple rescalings. The tightening in the case of an observable commuting with can be found by following the same steps as the ones above. ∎
In general, there is no way to precisely relate the Lipschitz constants of the real and imaginary parts of to the Lipschitz constant of when . In the next result, we however prove that the constants have similar scalings in the case of a commuting Gibbs measure of a local Hamiltonian.
Lemma 7.
Let be the decomposition of an observable in , where for each subregion , is exactly supported in with , and . Let further be the Gibbs state of a geometrically -local, commuting Hamiltonian at inverse temperature . Then,
| (155) |
where denotes the -enlargement of . In particular, whenever the state satisfies with , any local observable gives rise to a sub-Gaussian random variable variance when measured in the state .
Proof.
We prove the bound for the real part of since the proof for the imaginary part follows the exact same reasoning. First, by Proposition 6, since for any , is supported in region , we have that
| (156) | ||||
| (157) | ||||
| (158) | ||||
| (159) |
The result follows. ∎
7.1 Comparison to previous tail bounds
Our main result can be compared to other recently derived concentration bounds for quantum Gibbs states: in [45, Corollary 5.4], the authors consider a product state as well as a Hamiltonian , where the set of subsets of has the following properties: for any ,
-
(i)
;
-
(ii)
.
With these conditions, he was able to prove that
where number is the number of local terms acting non-trivially on spin . A similar bound was previously derived by Kuwahara [46, Theorem 7], under a notion of -extensivity: a local Hamiltonian is said to be -extensive if for every spin , . Under this condition, he shows that
where is a constant which depends only on and . Although these results recover the Gaussian tails of our Theorem 7 (up to logarithmic overheads), they only work for tensor product states and a subclass of Lipschitz observables. In particular, the tails become trivial whenever the Hamiltonian is a sum of terms acting on non-intersecting regions of arbitrary size. In contrast, our bound is still non-trivial for this class of observables, since their Lipschitz constant is still .
More recently, Kuwahara and Saito derived new concentration bounds for Gibbs states of interacting Hamiltonians in order to study the problem of equivalence of quantum statistical ensembles [47, 43] (see section 8): in [47] first, the authors consider a Gibbs state of a local Hamiltonian on a -dimensional regular lattice . They further assume the following clustering: for any operators supported on the subsets and ,
| (160) |
whenever . Under this condition, they were able to show in Equation (S.17) (see also [45, Theorem 4.2] for a similar bound)
for some constants further depending on and , and where denotes the locality of the observable . Therefore, and although the clustering of correlations is known to hold at high enough temperature [48], the bound is suboptimal for two reasons: firstly, whenever is small enough, the exponent has the worse scaling . Secondly, the bounds baddly dependence on the locality of , and becomes trivial whenever is a sum of highly non-local terms. This second limitation also holds for the Gaussian concentration bound found in [43, Corollary 1] for high-temperature Gibbs states of Hamiltonians with long-range interactions. In comparison to the works cited above, our bound always provides better dependence of the tail on the locality of the observable, albeit under the condition that the Hamiltonian is made of local commuting terms.
8 Equivalence of statistical mechanical ensembles
The three main ensembles employed in quantum statistical mechanics to compute the equilibrium properties of quantum systems are the canonical ensemble, the microcanonical ensemble and the diagonal ensemble. The quantum state associated to the canonical ensemble is the Gibbs state, which describes the physics of a system that is at thermal equilibrium with a large bath at a given temperature. The diagonal and microcanonical ensembles both describe the physics of an isolated quantum system, and the associated states are convex combinations of the eigenstates of the Hamiltonian. The microcanonical ensemble assumes a uniform probability distribution for the energy in a given energy shell. The diagonal ensemble includes all the states that are diagonal in the eigenbasis of the Hamiltonian, and in particular it includes the eigenstates themselves.
For many quantum systems, the microcanonical and canonical ensembles give the same expectation values for local observables if the corresponding states have approximately the same average energy. A lot of effort has been devoted to determining conditions under which the two ensembles are equivalent [49, 50, 51, 52]. The most prominent among such conditions are short ranged interactions and a finite correlation length, but analytical proofs can be obtained only in the case of regular lattices [52]. The situation is more complex for the diagonal ensemble. The condition under which this ensemble is equivalent to the microcanonical and canonical ensembles is called Eigenstate Thermalization Hypothesis (ETH) [53, 54, 55, 56, 57], and states that the expectation values of local observables on the eigenstates of the Hamiltonian are a smooth function of the energy, i.e., for any given local observable, any two eigenstates with approximately the same energy yield approximately the same expectation value. The ETH is an extremely strong condition on the Hamiltonian and several quantum systems, including all integrable systems, do not satisfy it. A weak version of the ETH has been formulated [58, 47], stating that for any given local observable, most eigenstates in an energy shell yield approximately the same expectation value, or, more precisely, that the fraction of eigenstates yielding expectation values far from the Gibbs state with the same average energy vanishes in the thermodynamical limit. The weak ETH implies the equivalence between the canonical and microcanonical ensembles, but is not sufficient to prove their equivalence with the diagonal ensemble. Under the hypothesis of finite correlation length in the Gibbs state, an analytical proof of the weak ETH is available only for regular lattices [47].
A connection between a transportation cost inequality and the ETH was made by one of the authors in the case of a regular lattice and a nearest neighbour Hamiltonian [38]. Here we look at the general problem of the equivalence of the statistical mechanical ensembles and of the weak ETH from the perspective of optimal mass transport, and show that such equivalence can be formulated as closeness of the respective states in the distance. The closeness in the distance implies closeness of the expectation values of all Lipschitz observables, which constitute a significantly larger class than local observables. Therefore, the perspective of optimal mass transport can significantly extend the previous results. Moreover, we will show that the equivalence of the ensembles is intimately linked to the constant of the transportation cost inequality for the Gibbs states.
As in the rest of the paper, we consider a quantum system made by qudits located at the vertices of a graph with vertex set . Let us assume that a Gibbs state satisfies the transportation cost inequality with a constant
| (161) |
where does not depend on . This condition is satisfied under the hypotheses of Theorem 2, Theorem 4 or Theorem 5. We stress that, contrarily to the results of Refs. [52, 47], the condition does not require us to restrict to regular lattices, since Theorem 4 does not need this hypothesis. The following Proposition 12 implies that any state is close in distance to the Gibbs state with the same average energy, provided that and have approximately the same entropy, i.e.,
| (162) |
Moreover, under the same hypothesis, the average reduced states over one qudit of and are close in trace distance.
Proposition 12.
Let be a Gibbs state for the Hamiltonian . Then, any quantum state with the same average energy as satisfies
| (163) |
Moreover, let be the quantum channel that computes the average marginal state over one qudit, i.e., for any ,
| (164) |
Then,
| (165) |
Proof.
We have from the transportation cost inequality
| (166) |
where the last equality follows since .
Choosing to be diagonal in the eigenbasis of the Hamiltonian, Proposition 12 implies that any convex combination of a sufficiently large number of eigenstates is close in distance to the Gibbs state with the same average energy. Such number of eigenstates can even be an exponentially small fraction of the total number of eigenstates appearing in a microcanonical state, since the uniform superposition of a fraction of the eigenstates decreases the entropy by . Therefore, Proposition 12 constitutes an exponential improvement over the weak ETH.
A natural question is whether also the strong ETH can be captured by the distance. Unfortunately the answer is negative. Indeed, proving the strong ETH via optimal mass transport would mean to prove that all the eigenstates of the Hamiltonian are close in distance to the Gibbs states with the corresponding average energy. However, Theorem 1 implies that any state with low entropy, and in particular any pure state, is far from any state with large entropy, and in particular from a Gibbs state with temperature . More precisely, for any two states ,
| (168) |
Equation (168) also implies that any quantum state which is close in distance to the Gibbs state with the same average energy must have approximately also the same entropy, and in this sense Proposition 12 is optimal.
8.1 Comparison with previous results
To make our result more easily comparable to the literature, let us introduce more formally the microcanonical ensemble: given the decomposition , we define the microcanonical ensemble state
where corresponds to the projection onto the subspace spanned by the eigenvectors whose energy belongs to the interval .
Corollary 2.
Assume the Gibbs state satisfies . Then for any Lipschitz observable ,
Proof.
In view of Proposition 12, it suffices to control the relative entropy between the microcanonical and canonical ensemble states. Then,
| (169) |
Next, we control the ration . For this, we use an argument which was already used in [47, Equation (S.56)]: First, we have found in (149) that
Therefore, choosing the interval , we have
Next, we define
| (170) |
Choosing a slightly extended interval , we have
| (171) |
Now, for , we have
Replacing in (171), we have that
Finally, using the lower bound (170), we have that
Therefore, plugging this last bound into (169), we have found that
Therefore, whenever , and the result follows.
∎
In [47, Theorem 2], it is showed that, under the -clustering of correlations (160), for any observable where each acts on spin as well as other spins with and has ,
where , , and the constants and depend on and the locality of . Therefore, as long as the energy shell is chosen as the averages of the operator density in the canonical and microcanonical ensemble states converge to the same number as . Similar bounds were also derived in [43, Corollary 3] for larger classes of non-local Hamiltonians and observables above some threshold temperature. Corollary 2 constitutes an improvement over these results in two senses: Firstly, it applies to a more general class of Lipschitz observables. Secondly, it allows for a smaller energy shell . However, the condition is currently only known to hold for the smaller class of local commuting Hamiltonians.
Acknowledgements
The research of CR has been supported by project QTraj (ANR-20-CE40-0024-01) of the French National Research Agency (ANR) and by a Junior Researcher START Fellowship from the MCQST.
References
- [1] Maxim Raginsky and Igal Sason. Concentration of measure inequalities in information theory, communications and coding. arXiv preprint arXiv:1212.4663, 2012.
- [2] Stéphane Boucheron, Gábor Lugosi, and Pascal Massart. Concentration inequalities: A nonasymptotic theory of independence. Oxford university press, 2013.
- [3] Aryeh Kontorovich and Maxim Raginsky. Concentration of measure without independence: a unified approach via the martingale method. In Convexity and Concentration, pages 183–210. Springer, 2017.
- [4] Katalin Marton. A simple proof of the blowing-up lemma (corresp.). IEEE Transactions on Information Theory, 32(3):445–446, 1986.
- [5] Sergej G Bobkov and Friedrich Götze. Exponential integrability and transportation cost related to logarithmic sobolev inequalities. Journal of Functional Analysis, 163(1):1–28, 1999.
- [6] Roland L Dobrushin. Prescribing a system of random variables by conditional distributions. Theory of Probability & Its Applications, 15(3):458–486, 1970.
- [7] Katalin Marton. Logarithmic sobolev inequalities in discrete product spaces. Combinatorics, Probability & Computing, 28(6):919–935, 2019.
- [8] Roland L Dobrushin and Senya B Shlosman. Completely analytical interactions: constructive description. Journal of Statistical Physics, 46(5):983–1014, 1987.
- [9] Christof Külske. Concentration inequalities for functions of gibbs fields with application to diffraction and random gibbs measures. Communications in mathematical physics, 239(1):29–51, 2003.
- [10] Marius Junge and Qiang Zeng. Noncommutative martingale deviation and poincaré type inequalities with applications. Probability Theory and Related Fields, 161(3-4):449–507, February 2014.
- [11] Joel A. Tropp. An introduction to matrix concentration inequalities. Foundations and Trends® in Machine Learning, 8(1-2):1–230, 2015.
- [12] De Huang and Joel A. Tropp. From poincaré inequalities to nonlinear matrix concentration. Bernoulli, 27(3), May 2021.
- [13] Cambyse Rouzé and Nilanjana Datta. Concentration of quantum states from quantum functional and transportation cost inequalities. Journal of Mathematical Physics, 60(1):012202, January 2019.
- [14] Giacomo De Palma, Milad Marvian, Dario Trevisan, and Seth Lloyd. The Quantum Wasserstein Distance of Order 1. IEEE Transactions on Information Theory, 67(10):6627–6643, 2021.
- [15] Giacomo De Palma and Dario Trevisan. Quantum Optimal Transport with Quantum Channels. Annales Henri Poincaré, 22:3199–3234, 2021.
- [16] François Golse, Clément Mouhot, and Thierry Paul. On the mean field and classical limits of quantum mechanics. Communications in Mathematical Physics, 343(1):165–205, January 2016.
- [17] Sam Cole, Michał Eckstein, Shmuel Friedland, and Karol Życzkowski. Quantum optimal transport. arXiv preprint arXiv:2105.06922, 2021.
- [18] Eric A Carlen and Jan Maas. Gradient flow and entropy inequalities for quantum markov semigroups with detailed balance. Journal of Functional Analysis, 273(5):1810–1869, 2017.
- [19] Ivan Bardet, Ángela Capel, Li Gao, Angelo Lucia, David Pérez-García, and Cambyse Rouzé. Entropy decay for davies semigroups of a one dimensional quantum lattice, 2021.
- [20] Ivan Bardet, Ángela Capel, Li Gao, Angelo Lucia, David Pérez-García, and Cambyse Rouzé. Rapid thermalization of spin chain commuting hamiltonians, 2021.
- [21] Michael A Nielsen and Isaac Chuang. Quantum computation and quantum information, 2002.
- [22] Mark M Wilde. Quantum information theory. Cambridge University Press, 2013.
- [23] Alexander S Holevo. Quantum systems, channels, information: a mathematical introduction, volume 16. Walter de Gruyter, 2012.
- [24] Matthew J Donald. On the relative entropy. Communications in Mathematical Physics, 105(1):13–34, 1986.
- [25] Dénes Petz. Sufficient subalgebras and the relative entropy of states of a von neumann algebra. Communications in mathematical physics, 105(1):123–131, 1986.
- [26] Fumio Hiai and Dénes Petz. The proper formula for relative entropy and its asymptotics in quantum probability. Communications in mathematical physics, 143(1):99–114, 1991.
- [27] Mario Berta, Omar Fawzi, and Marco Tomamichel. On variational expressions for quantum relative entropies. Letters in Mathematical Physics, 107(12):2239–2265, 2017.
- [28] Marius Junge, Renato Renner, David Sutter, Mark M Wilde, and Andreas Winter. Universal recovery maps and approximate sufficiency of quantum relative entropy. In Annales Henri Poincaré, volume 19, pages 2955–2978. Springer, 2018.
- [29] David Sutter, Mario Berta, and Marco Tomamichel. Multivariate trace inequalities. Communications in Mathematical Physics, 352(1):37–58, October 2016.
- [30] Patrick Hayden, Richard Jozsa, Denes Petz, and Andreas Winter. Structure of states which satisfy strong subadditivity of quantum entropy with equality. Communications in mathematical physics, 246(2):359–374, 2004.
- [31] M. Tomamichel. Quantum Information Processing with Finite Resources: Mathematical Foundations. SpringerBriefs in Mathematical Physics. Springer International Publishing, 2015.
- [32] Yann Ollivier. Ricci curvature of Markov chains on metric spaces. Journal of Functional Analysis, 256(3):810–864, February 2009.
- [33] Ronen Eldan, James R. Lee, and Joseph Lehec. Transport-entropy inequalities and curvature in discrete-space markov chains. In A Journey Through Discrete Mathematics, pages 391–406. Springer International Publishing, 2017.
- [34] Robert B. Griffiths. Correlations in ising ferromagnets. III. Communications in Mathematical Physics, 6(2):121–127, June 1967.
- [35] Michael J. Kastoryano and Kristan Temme. Quantum logarithmic sobolev inequalities and rapid mixing. Journal of Mathematical Physics, 54(5):052202, May 2013.
- [36] Li Gao and Cambyse Rouzé. Complete entropic inequalities for quantum Markov chains. arXiv preprint arXiv:2102.04146, 2021.
- [37] Eric A. Carlen and Jan Maas. Non-commutative calculus, optimal transport and functional inequalities in dissipative quantum systems. Journal of Statistical Physics, 178(2):319–378, nov 2019.
- [38] Ángela Capel, Cambyse Rouzé, and Daniel Stilck França. The modified logarithmic Sobolev inequality for quantum spin systems: classical and commuting nearest neighbour interactions. arXiv preprint arXiv:2009.11817, 2020.
- [39] Toby S Cubitt, Angelo Lucia, Spyridon Michalakis, and David Perez-Garcia. Stability of local quantum dissipative systems. Communications in Mathematical Physics, 337:1275–1315, 2015.
- [40] Michael J Kastoryano and Fernando GSL Brandao. Quantum gibbs samplers: the commuting case. Communications in Mathematical Physics, 344(3):915–957, 2016.
- [41] Fernando GSL Brandão and Michael J Kastoryano. Finite correlation length implies efficient preparation of quantum thermal states. Communications in Mathematical Physics, 365(1):1–16, 2019.
- [42] Marius Junge, Nicholas LaRacuente, and Cambyse Rouzé. Stability of logarithmic sobolev inequalities under a noncommutative change of measure. arXiv preprint arXiv:1911.08533, 2019.
- [43] Tomotaka Kuwahara and Keiji Saito. Gaussian concentration bound and ensemble equivalence in generic quantum many-body systems including long-range interactions. Annals of Physics, 421:168278, October 2020.
- [44] Keiji Matsumoto. A new quantum version of f-divergence. In Nagoya Winter Workshop: Reality and Measurement in Algebraic Quantum Theory, pages 229–273. Springer, 2015.
- [45] Anurag Anshu. Concentration bounds for quantum states with finite correlation length on quantum spin lattice systems. New Journal of Physics, 18(8):083011, August 2016.
- [46] Tomotaka Kuwahara. Connecting the probability distributions of different operators and generalization of the chernoff–hoeffding inequality. Journal of Statistical Mechanics: Theory and Experiment, 2016(11):113103, November 2016.
- [47] Tomotaka Kuwahara and Keiji Saito. Eigenstate thermalization from the clustering property of correlation. Physical review letters, 124(20):200604, 2020.
- [48] M. Kliesch, C. Gogolin, M. J. Kastoryano, A. Riera, and J. Eisert. Locality of temperature. Phys. Rev. X, 4:031019, Jul 2014.
- [49] R Lima. Equivalence of ensembles in quantum lattice systems. Annales de l’IHP Physique théorique, 15(1):61–68, 1971.
- [50] R Lima et al. Equivalence of ensembles in quantum lattice systems: states. Communications in Mathematical Physics, 24(3):180–192, 1972.
- [51] Markus P Müller, Emily Adlam, Lluís Masanes, and Nathan Wiebe. Thermalization and canonical typicality in translation-invariant quantum lattice systems. Communications in Mathematical Physics, 340(2):499–561, 2015.
- [52] Fernando G. S. L. Brandão and Marcus Cramer. Equivalence of Statistical Mechanical Ensembles for Non-Critical Quantum Systems. arXiv:1502.03263 [cond-mat, physics:quant-ph], February 2015. arXiv: 1502.03263.
- [53] Josh M Deutsch. Quantum statistical mechanics in a closed system. Physical Review A, 43(4):2046, 1991.
- [54] Mark Srednicki. Chaos and quantum thermalization. Physical Review E, 50(2):888–901, August 1994.
- [55] Christian Gogolin and Jens Eisert. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Reports on Progress in Physics, 79(5):056001, 2016.
- [56] Peter Reimann. Dynamical typicality approach to eigenstate thermalization. Physical review letters, 120(23):230601, 2018.
- [57] Giacomo De Palma, Alessio Serafini, Vittorio Giovannetti, and Marcus Cramer. Necessity of eigenstate thermalization. Physical Review Letters, 115(22):220401, 2015.
- [58] Giulio Biroli, Corinna Kollath, and Andreas M Läuchli. Effect of rare fluctuations on the thermalization of isolated quantum systems. Physical review letters, 105(25):250401, 2010.