\addauthor

Jianbo [email protected] \addauthorJoão F. [email protected] \addinstitutionVisual Geometry Group
University of Oxford Quantised Transforming Auto-Encoders

Quantised Transforming Auto-Encoders:
Achieving Equivariance to Arbitrary Transformations in Deep Networks

Abstract

In this work we investigate how to achieve equivariance to input transformations in deep networks, purely from data, without being given a model of those transformations. Convolutional Neural Networks (CNNs), for example, are equivariant to image translation, a transformation that can be easily modelled (by shifting the pixels vertically or horizontally). Other transformations, such as out-of-plane rotations, do not admit a simple analytic model. We propose an auto-encoder architecture whose embedding obeys an arbitrary set of equivariance relations simultaneously, such as translation, rotation, colour changes, and many others. This means that it can take an input image, and produce versions transformed by a given amount that were not observed before (e.g\bmvaOneDota different point of view of the same object, or a colour variation). Despite extending to many (even non-geometric) transformations, our model reduces exactly to a CNN in the special case of translation-equivariance. Equivariances are important for the interpretability and robustness of deep networks, and we demonstrate results of successful re-rendering of transformed versions of input images on several synthetic and real datasets, as well as results on object pose estimation.¹¹1Project page: https://www.robots.ox.ac.uk/~vgg/research/qtae/.

1 Introduction

Deep learning has achieved impressive performance in many pattern recognition tasks, especially in the visual domain [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton, Goodfellow et al.(2016)Goodfellow, Bengio, and Courville]. A crucial factor in this success is the use of Convolutional Neural Networks (CNNs), which are highly tuned to natural images due to their natural equivariance to translations. Nevertheless, other transformations are not widely adopted as equivariances in common deep network applications in vision [Lenc and Vedaldi(2015)], with the closest equivalent being data augmentation [Goodfellow et al.(2016)Goodfellow, Bengio, and Courville], which achieves invariance instead, by randomly transforming input images during training. When we say an operator is transformation equivariant, it means that the effect of the applied transformation is detectable in the operator output, and its effect has a predictable functional form [Lenc and Vedaldi(2015)]. When considering the task of imagining what a visual scene looks like from a different point of view or with different components, which is important in computer graphics, planning and counter-factual reasoning, translation equivariance is not sufficient. There are more transformations needed to manipulate a scene freely, for instance affine transformations, out-of-plane rotation, shape, lighting, etc. While enabling in CNNs the property of equivariance to various analytical transformations has been explored in the literature (see section 2), doing so without an analytical model of the transformation is relatively under-explored. In this paper, we are interested in the question: can we make deep networks equivariant to arbitrary transformations from data alone?

An influential line of work that attempts to address this question (as well as the separate question of compositionality) is capsule networks [Hinton et al.(2011)Hinton, Krizhevsky, and Wang]. They extend auto-encoders with an equivariant latent code, and propose a simple perturbation-based training method to enforce its equivariance w.r.t. example transformations. A single capsule thus contains an embedding part with the visual entity, and another part encoding the deformations, which can then be manipulated or used for downstream tasks. Recent works [Hinton et al.(2018)Hinton, Sabour, and Frosst, Kosiorek et al.(2019)Kosiorek, Sabour, Teh, and Hinton] propose larger capsule networks, focusing on the composability aspect. However, one limitation is that they represent the transformation parameters as continuous embeddings, which are limited to simple relationships between image-space and the transformations.

In this paper, we propose to discretise the embeddings, resulting in quantised representations that are orthogonal to each other. Specifically, we use different tensor dimensions to represent different transformations, so each dimension encodes a single transformation parameter independently. Unlike capsule networks, where transformation parameters are manipulated additively, in our discretised space the embedding is rolled or shifted (depending on whether the parameter is cyclic) by a specific discrete value. Interestingly, our method encompasses convolutional neural networks as a special case – the case of translation equivariance – while extending them to more transformations, including non-geometric. We experimentally show that the proposed method can model various transformations in an equivariant manner, even for out-of-plane 3D transformations without any 3D operations such as 3D convolutions or ray-tracing. In summary, the main contributions of our work are:

1. A method to learn equivariance to arbitrary (non-geometric) transformations from data.

2. An exploration of tensor-product and tensor-sum spaces for combining transformations.

3. Experimental results across several synthetic and real datasets, demonstrating extrapolation to unseen attribute combinations and pose estimation.

2 Related Work

There are many notable examples of transformation invariance in computer vision’s history, with many consisting of linear models, such as tangent vectors centered on training images [Simard et al.(2000)Simard, Le Cun, Denker, and Victorri], and on densely-sampled transformed images [Miao and Rao(2007), Tenenbaum and Freeman(2000), Henriques et al.(2014)Henriques, Martins, Caseiro, and Batista]. Many works focus on rotation [Schmidt and Roth(2012)] or scale [Kanazawa et al.(2014)Kanazawa, Sharma, and Jacobs] alone, and most focus on geometric transformations only, as well as linear models. Building on earlier work on invariance for Boltzmann machines [Memisevic and Hinton(2010)], Hinton et al\bmvaOneDot [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] proposed “capsules”, which were meant to generalize CNN’s filters, recognizing patterns not only across translation, but also across other transformations. While this work studied capsules in isolation, more recent work focused on composing them together [Hinton et al.(2018)Hinton, Sabour, and Frosst]. They were also extended to unsupervised learning, achieving high performance in image classification [Kosiorek et al.(2019)Kosiorek, Sabour, Teh, and Hinton]. Lenc and Vedaldi [Lenc and Vedaldi(2015)] studied the emergent invariance and equivariance in networks trained for classification. Geometric transformations can be seen as forming a group, which allows analysis with tools from abstract algebra, and this has been used successfully in many works [Bruna et al.(2013)Bruna, Szlam, and LeCun, Henriques and Vedaldi(2017), Kondor and Trivedi(2018), Cohen et al.(2019)Cohen, Geiger, and Weiler, Qi et al.(2020)Qi, Zhang, Lin, and Wang, Cohen et al.(2018)Cohen, Geiger, Köhler, and Welling]; usually only geometric or rigid transformations are considered. In addition to obtaining equivariant representations, it is frequently desired that they are disentangled, which informally means that they can be manipulated independently [Higgins et al.(2018)Higgins, Amos, Pfau, Racaniere, Matthey, Rezende, and Lerchner, Kulkarni et al.(2015)Kulkarni, Whitney, Kohli, and Tenenbaum, Xiao et al.(2019)Xiao, Liu, and Lee]. Image synthesis is also extensively studied in computer vision and graphics. Some works [Chaurasia et al.(2013)Chaurasia, Duchene, Sorkine-Hornung, and Drettakis, Kopf et al.(2013)Kopf, Langguth, Scharstein, Szeliski, and Goesele, Ladicky et al.(2014)Ladicky, Shi, and Pollefeys, Penner and Zhang(2017), Rematas et al.(2016)Rematas, Nguyen, Ritschel, Fritz, and Tuytelaars, Seitz et al.(2006)Seitz, Curless, Diebel, Scharstein, and Szeliski] compute 3D representations of the scene explicitly, while others handle the 3D geometry with implicit functions [Fitzgibbon et al.(2005)Fitzgibbon, Wexler, and Zisserman, Matusik et al.(2002)Matusik, Pfister, Ngan, Beardsley, Ziegler, and McMillan]. Recent deep learning-based approaches [Flynn et al.(2019)Flynn, Broxton, Debevec, DuVall, Fyffe, Overbeck, Snavely, and Tucker, Flynn et al.(2016)Flynn, Neulander, Philbin, and Snavely, Hedman et al.(2018)Hedman, Philip, Price, Frahm, Drettakis, and Brostow, Mildenhall et al.(2019)Mildenhall, Srinivasan, Ortiz-Cayon, Kalantari, Ramamoorthi, Ng, and Kar, Srinivasan et al.(2019)Srinivasan, Tucker, Barron, Ramamoorthi, Ng, and Snavely, Eslami et al.(2018)Eslami, Rezende, Besse, Viola, Morcos, Garnelo, Ruderman, Rusu, Danihelka, Gregor, et al., Sun et al.(2018)Sun, Huh, Liao, Zhang, and Lim] can fill in missing data such as occlusions or holes, though most rely on multi-view inputs and so are more restricted. Several methods [Dosovitskiy et al.(2016)Dosovitskiy, Springenberg, Tatarchenko, and Brox, Park et al.(2017)Park, Yang, Yumer, Ceylan, and Berg, Tatarchenko et al.(2016)Tatarchenko, Dosovitskiy, and Brox, Yang et al.(2015)Yang, Reed, Yang, and Lee, Zhou et al.(2016)Zhou, Tulsiani, Sun, Malik, and Efros, Kulkarni et al.(2015)Kulkarni, Whitney, Kohli, and Tenenbaum, Sitzmann et al.(2019)Sitzmann, Zollhöfer, and Wetzstein] directly learn a mapping from a source image to the target image, purely from data, which is closer to ours. However, these methods usually need additional depth sensor as input or supervision, and do not address transformations beyond geometric ones. A recent approach is to render scenes by ray-tracing [Mildenhall et al.(2020)Mildenhall, Srinivasan, Tancik, Barron, Ramamoorthi, and Ng], though generally only viewpoint transformations are considered, as opposed to general latent spaces in auto-regressive [Van Oord et al.(2016)Van Oord, Kalchbrenner, and Kavukcuoglu] or adversarial [Goodfellow et al.(2014)Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville, and Bengio] models. Equivariance can be a complementary objective to enforce geometric structure during learning, leveraged for example by Dupont et al\bmvaOneDot [Dupont et al.(2020)Dupont, Martin, Colburn, Sankar, Susskind, and Shan] to improve neural rendering, or symmetry to reflections used to learn 3D structure [Wu et al.(2020)Wu, Rupprecht, and Vedaldi].

Refer to caption — Figure 1: Our method trains a network with pairs of images related by a transformation (which may include arbitrary non-geometric changes). An embedding tensor that encodes the image is shifted along different dimensions according to the transformed amounts, and the decoded image must match the corresponding transformed image (target). Refer to section 3.3 for a full description.

3 Method

3.1 Background

Consider training a classical auto-encoder, where the goal is to learn the two functions (or their parameters), an encoder $\phi:\,\mathcal{X}\mapsto\mathcal{Y}$ and a decoder $\psi:\,\mathcal{Y}\mapsto\mathcal{X}$ , for an input-space $\mathcal{X}$ (e.g\bmvaOneDotimages) and an embedding-space $\mathcal{Y}$ (e.g\bmvaOneDot $\mathbb{R}^{m}$ ). This is learned from a dataset $\mathcal{D}$ , so that encoding and decoding a sample results in approximately the same sample:

\min_{\phi,\psi}\mathbb{E}_{x\sim\mathcal{D}}\left\|\psi(\phi(x))-x\right\|.

(1)

The bottleneck of the embedding space encourages the auto-encoder to compress the input distribution. Many methods improve this bottleneck with regularisation terms or noise [Kingma and Welling(2014)].

3.2 Transforming auto-encoders

A transforming auto-encoder, also known as a capsule network [Hinton et al.(2011)Hinton, Krizhevsky, and Wang], is a modification of eq. 1 that additionally forces part of the embedding-space to encode a transformation $T:\,\mathcal{X}\times\mathbb{R}^{t}\mapsto\mathcal{X}$ with $t$ parameters. For example, $T$ may perform planar rotation of the image by a given angle ( $t=1$ ), or an affine transformation with $t=6$ parameters. The auto-encoder’s embedding $y\in\mathcal{Y}$ can then be written as the concatenation $y=(y_{\mathrm{t}},y_{\mathrm{e}})$ , where $y_{\mathrm{t}}\in\mathbb{R}^{t}$ expresses transformation parameters that are specific to the image (e.g\bmvaOneDothow much it is rotated away from a canonical view), and $y_{\mathrm{e}}\in\mathbb{R}^{m-t}$ encodes the rest of the image information (e.g\bmvaOneDotappearance that is not related to the transformation).

The equivariance relation that we would like to (approximately) enforce is:

\phi(T(x,u))=\phi(x)+u.

(2)

Eq. 2 establishes an equivalence between translating by $u$ in the embedding-space, and using $T$ to transform an input $x$ by the same amount $u$ . To avoid cumbersome math, $u\in\mathbb{R}^{t}$ is only added to the first $t$ elements of the embedding (i.e. to $y_{\mathrm{t}}$ , not to the full embedding $y$ ), in a slight abuse of notation.

The transforming auto-encoder is trained by minimising the reconstruction error between both sides of eq. 2, in image-space, for values of $u\in\mathbb{R}^{t}$ randomly sampled from a distribution $\mathcal{U}$ (for example, a uniform range of rotation angles):

\min_{\phi,\psi}\;\mathbb{E}_{x\sim\mathcal{D},u\sim\mathcal{U}}\left\|\psi(\phi(T(x,u))-u)-x\right\|.

(3)

In practice, $x$ and $T(x,u)$ can be two views of the same scene, with a relative transformation of $u$ (for example, the relative pose between the two views in 3D space).

Eq. 3 can be used to learn simple equivariances, however achieving the desired linearity with respect to $u$ is difficult in practice. Implicit in this objective is a regression task: setting part of the embedding to a precise value that is equal to the transformation $u$ , up to an additive constant. Since deep networks usually excel at classification tasks but are more difficult to train for regression tasks, it makes sense to replace this regression task (continuous representation of the transformation) with classification (discrete or quantised representation).

3.3 Quantised transforming auto-encoders

We do this by redefining the auto-encoder’s embedding as a tensor with one additional dimension per transformation parameter: $y\in\mathbb{R}^{d_{1}\times\cdots\times d_{t}\times m}$ , for a total of $t+1$ dimensions. They represent a quantised version of $\mathbb{R}^{t}$ , or discrete lattice, with resolution $d_{i}$ for the $i$ th dimension. Note that for the special case $y\in\mathbb{R}^{d_{1}\times d_{2}\times m}$ this reduces to a standard CNN embedding, with two spatial dimensions and $m$ channels. Similarly to eq. 2, we define an equivariance relation, but with translation in $\mathbb{R}^{t}$ replaced with translation by $u$ in the discrete lattice:

\phi(T(x,u))=S(\phi(x),u),\quad S_{v}(y,u)=y_{u+v},\forall u,v\in\mathbb{Z}^{t},

(4)

where $S(y,u)$ translates or shifts vector $y$ by an amount $u$ . For example, if $y=[y_{1},y_{2},\ldots]$ , then $S(y,1)=[y_{2},y_{3},\ldots]$ . When applied to standard CNNs, eq. 4 describes their natural equivariance: translating the input by an amount $u$ results in an equal translation of the activations.²²2A stride (subsampling) of $k$ can be taken into account by considering that $S$ translates by $ku$ . Eq. 2 does not apply to CNNs, since it only describes continuous parameter-spaces. However, our description extends this concept to more general transformations, including their combination with translation. Replacing this in eq. 3:

\min_{\phi,\psi}\;\mathbb{E}_{x\sim\mathcal{D},u\sim\mathcal{U}}\left\|\psi(S(\phi(T(x,u)),-u))-x\right\|,

(5)

which is superficially similar to eq. 3, but the intermediate operations deal with a larger embedding which has more structure (the discrete lattice). A pipeline of the proposed method when implemented as an encoding-decoding process is shown in figure 1.

Transformations with periodic and aperiodic domains.

The abstract description of the shift operator (eq. 3) ignores how boundary conditions are treated. Consider a transformation with a single parameter, a rotation angle $u\in[0,2\pi]$ . To take into account the periodicity of the angular domain, the shift operator would be defined as $S_{v}(y,u)=y_{(u+v)\textrm{ mod }2\pi},$ where mod is the modulus operation. For ease of notation, we assume that the tensor (in this example, vector) $y$ can be indexed with non-integer values, mapping the values in $[0,2\pi]$ to its $d$ elements in ascending order. This reasoning applies to all rotational parameters and the operation is more accurately described as rolling instead of shifting. Similarly, for transformation parameters that are not periodic, the shift with boundary conditions would be

S_{v}(y,u)=\begin{cases}y_{u+v}&\textrm{if }0\leq u+v<d\\ 0&\textrm{otherwise}.\end{cases}

(6)

In general, one may combine any number of transformation parameters, periodic or not, and with different discretisation size $d$ , into a composite shift $S$ that shifts or rolls each dimension independently. In standard CNNs, eq. 6 corresponds to horizontal and vertical shifts, which can be applied independently, and are zero-padded when out-of-bounds.

Combining multiple transformations.

The formulation from eq. 6 suggests a direct way to handle multiple transformations: apply $t$ shifts to different dimensions of a tensor $y\in\mathbb{R}^{d_{1}\times\ldots\times d_{t}\times m}$ , where $m$ contains channels that are not transformed. Formally,

S_{v_{1},\ldots,v_{t}}^{\otimes}(y,u)=\begin{cases}y_{u_{1}+v_{1},\ldots,u_{t}+v_{t}}&\textrm{if }0\leq u_{i}+v_{i}<d_{i}\quad\forall i\\ 0&\textrm{otherwise},\end{cases}

(7)

which is straightforward to adapt for a mix of periodic and aperiodic domains. One drawback is that the memory use grows exponentially with each transformation, which we address next.

Efficient combinations of transformations.

Rather than having a tensor product of transformations, we consider an additive product: the activations tensor is instead $y\in\mathbb{R}^{(d_{1}+\ldots+d_{t})\times m}$ , and the shift operator becomes

S^{\oplus}(y,u)=\left[S(y_{i},u_{i})\right]_{i=1}^{t},

(8)

where $\left[\cdot\right]_{i=1}^{t}$ stacks $t$ matrices vertically, and $y_{i}$ is the $i$ th block of $y$ , corresponding to the $i$ th transformation (i.e. $y=\left[y_{i}\right]_{i=1}^{t}$ ). Thus memory scales linearly with the number of transformations, but the activations $y$ can no longer model interactions between transformations.

Interpretability and theoretical justification.

Although the feature spaces of deep networks are notoriously difficult to interpret, it is natural to ask whether shift-equivariant representations (eq. 4 and eq. 7) take on a recognizable shape. Interestingly, there is one case that is well-studied: rotation and scaling, which is equivariant to shifts under a log-polar warping of the image [Reddy and Chatterji(1996)]. Concretely, eq. 4 is true for scale and rotation $T$ if $\phi$ is a log-polar warp of the input image $x$ . It has been shown [Henriques and Vedaldi(2017)] that the same result holds if $\phi$ is composed with a CNN, and that equivariance extends to different geometric transformations by considering different warps. The significance of our proposal is that non-linear operations (in the form of a deep network) can achieve arbitrary transformations (including colour and out-of-plane rotations), instead of being limited to geometric transformations of an image. One limitation of using additive or product tensor-spaces is that they are commutative (i.e. the order of transformations does not matter), so in theory they should only model commutative transformations. This property is shared with the original transforming auto-encoder [Hinton et al.(2011)Hinton, Krizhevsky, and Wang], and yet both methods cope well with affine transformations, which are not commutative (section 4.1). We speculate this is due to the $m$ non-transformation channels, which can convey arbitrary image content, and can be leveraged by the networks to overcome this difficulty.

4 Experiments

Given that the aim of our proposal is to achieve equivariance to generic transformations, and we train an auto-encoder, we focus on image re-rendering: the ability of the model to reproduce an input image but with changed transformation parameters. We test our method’s ability to extrapolate beyond the training set for several transformations: affine (including translation and rotation), colour (foreground and background), out-of-plane rotations, object identity changes, and translations in 3D space. We also assess the method’s ability to discriminate poses in these transformation spaces.

Implementation details.

We use a standard auto-encoder architecture consisting of 4 convolutional and 4 deconvolutional layers (details in supplementary material). The encoder’s embeddings are reshaped to obtain the equivariant tensor ( $d_{1}\times\ldots\times d_{t}\times m$ ), which is then shifted or rolled (eq. 7), and reshaped back to the original dimensions. An overview is in figure 1. Our method optimizes eq. 5 (with a simple L1 metric), using a product space of transformations (eq. 7) while the Transforming Auto-encoder [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] baseline uses eq. 3. All networks are trained with Adam for 100 epochs, choosing the best learning rate from $\{10^{-5},10^{-4},10^{-3}\}$ . For a self-contained description of all implementation details please refer to the supplementary material.

Metrics.

To quantitatively evaluate the performance, we report results using two metrics: 1) Peak Signal to Noise Ratio (PSNR), which describes the accuracy in pixel-space; 2) Structural SIMilarity (SSIM), which more strongly correlates with perceptual similarity.

Baselines.

We compare with several state-of-the-art view synthesis methods. The Transforming Auto-Encoder (Trans.AE) [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] is the closest work to ours (see section 3.2 for details). MV3D [Tatarchenko et al.(2016)Tatarchenko, Dosovitskiy, and Brox] proposes to encode both the input image (source view) and the transformation (rotation angle in their case) into latent codes and directly concatenate them, followed by a decoder to predict the target view together with a depth map. TVSN [Park et al.(2017)Park, Yang, Yumer, Ceylan, and Berg] instead generates a flow from the concatenated features of source view and the rotation angle, followed by a hallucination and refinement step. Similarly, Chen et al\bmvaOneDot [Chen et al.(2019)Chen, Song, and Hilliges] also generate intermediate outputs of depth and flow, via which the source view is bilinearly sampled to get the target view. Instead of concatenation, the latent code is directly multiplied with the ground-truth viewpoint transformation. Equivariant Neural Rendering (ENR) [Dupont et al.(2020)Dupont, Martin, Colburn, Sankar, Susskind, and Shan] is an auto-encoder that similarly obtains an equivariant latent-space, but focuses on viewpoint equivariance; thus it ignores other transformations in our experiments. To provide a contrast with standard generative models, we also include the $\beta$ -VAE [Higgins et al.(2016)Higgins, Matthey, Pal, Burgess, Glorot, Botvinick, Mohamed, and Lerchner] (which generalises VAEs). Note that this model is not trained to achieve equivariance, so it only reconstructs the input image after projecting it to the latent space. For a fair comparison, all methods are adapted to use the same backbone architecture as ours, and use the same optimiser and training budget.

Table 1: Quantitative evaluation (PSNR

\uparrow

and SSIM

\uparrow

) with comparison to the baseline model on four datasets. Gray colour means that the method cannot be directly applied to this scenario, and was adapted to incorporate these transformations.

\dagger

As the

\beta

-VAE model is not equivariant, we here only show its self-reconstruction performance without transformations. * indicates that the 3 colour transformations (wall, floor and object colours) are not changed.

Method	MNIST [LeCun et al.(1998)LeCun, Bottou, Bengio, and Haffner]		3D Shapes [Burgess and Kim(2018)]*		3D Shapes [Burgess and Kim(2018)]		SmallNORB [LeCun et al.(2004)LeCun, Huang, and Bottou]		RGBD-Object [Lai et al.(2011)Lai, Bo, Ren, and Fox]		KITTI [Geiger et al.(2012)Geiger, Lenz, and Urtasun]
Method	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Trans. AE [Hinton et al.(2011)Hinton, Krizhevsky, and Wang]	19.85	0.8413	28.68	0.8447	7.77	0.3142	21.21	0.6447	19.46	0.5520	10.23	0.3437
MV3D [Tatarchenko et al.(2016)Tatarchenko, Dosovitskiy, and Brox]	20.09	0.8640	26.83	0.8812	13.33	0.6406	22.79	0.7813	19.38	0.5612	8.85	0.3311
TVSN [Park et al.(2017)Park, Yang, Yumer, Ceylan, and Berg]	14.66	0.3046	28.53	0.8762	20.38	0.8283	19.11	0.7094	19.73	0.5715	7.65	0.3141
Chen et al\bmvaOneDot [Chen et al.(2019)Chen, Song, and Hilliges]	20.31	0.8731	25.10	0.8616	13.56	0.6334	17.01	0.6768	19.56	0.5406	16.76	0.5297
ENR [Dupont et al.(2020)Dupont, Martin, Colburn, Sankar, Susskind, and Shan]	-	-	14.05	0.5690	7.83	0.3884	16.67	0.6646	17.11	0.4708	6.68	0.2357
$\beta$ -VAE [Higgins et al.(2016)Higgins, Matthey, Pal, Burgess, Glorot, Botvinick, Mohamed, and Lerchner] $\dagger$	10.22	0.3437	14.19	0.6042	8.50	0.4081	16.22	0.6764	16.45	0.4411	12.45	0.2662
Ours	22.40	0.8639	30.75	0.9210	28.00	0.8845	24.99	0.8148	19.74	0.5769	16.88	0.5304

4.1 Re-rendering under novel views and transformations

Affine-transformed MNIST.

We adapted MNIST [LeCun et al.(1998)LeCun, Bottou, Bengio, and Haffner] by applying a random affine transformation to each of the 70K images, maintaining the original training-validation split and image size. The transformation ranges are $\pm 21$ for translation, $\pm 15^{\circ}$ for rotation, $[1,1/9]$ for scale, and $\pm 11$ for shear. We show the results of our method, as well as of all baselines, in figure 3. We observe that all methods are able to model the affine transformations and place the digits in the correct place, although with varying loss of quality and detail. The visualized digits “4” and “7”, in particular, have thin structures that are lost by some methods, and only our method avoids nearly transforming the “8” into a “3”. Quantitative performance is presented in table 1 (second column), confirming that our method and Chen et al\bmvaOneDot’s [Chen et al.(2019)Chen, Song, and Hilliges] perform best overall.

DeepMind 3D Shapes.

We now move to a more challenging dataset, DeepMind 3D Shapes [Burgess and Kim(2018)], which introduces non-geometric transformations (colour changes) and non-planar geometric changes (3D rotation, shape changes). It consists of 480,000 synthetic RGB images of size $64\times 64$ , generated by varying 6 factors: floor colour, wall colour, object colour, scale, shape and orientation; with 10, 10, 10, 8, 4, and 15 possible values for each factor, respectively. We consider all factors as transformations in our experiments, and training is as before. The results are shown in figure 5 (right panel). Our method is able to very accurately re-synthesize the image with the given color, shape and rotation changes, while the other methods are much less successful. For example, a standard transformation auto-encoder (Trans. AE), without our proposed discretisation, falls back to predicting a mean image in all cases. While forcing the embedding to vary linearly with each transformation is enough for simple affine-warped MNIST images (as in the original capsules proposal [Hinton et al.(2011)Hinton, Krizhevsky, and Wang]), our proposed solution of shifting the tensors instead can support much more complex image transformations. Since we realized that this difficulty may be due to the abrupt changes in colours in the dataset, we ran the same experiment again but with all colours fixed (i.e. the transformations are purely geometric, with no colour changes). The performance of the baseline methods is largely recovered in this case, as shown in figure 5 (left panel). This illustrates the fact that many state-of-the-art methods are geared towards geometric transformations, and do not model more general appearance changes correctly. Quantitative results are in table 1, and additional video results in can be found in the supplementary material.

SmallNORB.

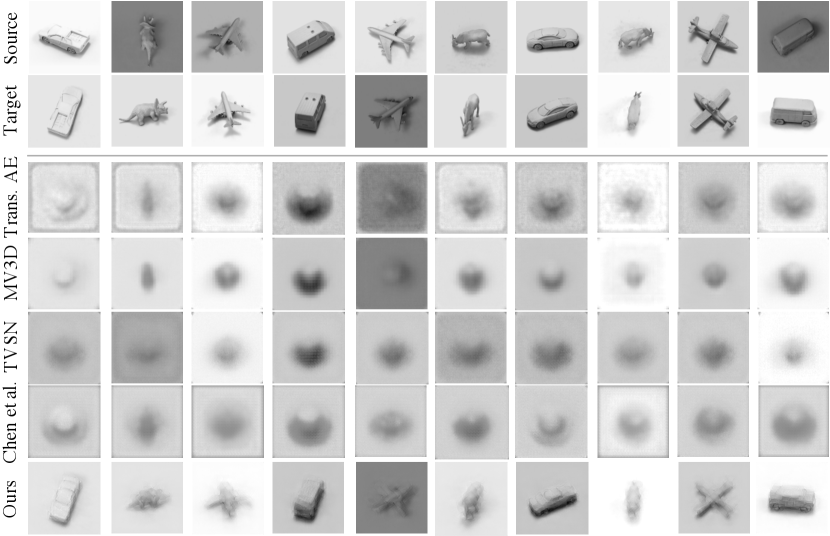
Proceeding to real images, although in a controlled environment, we also tested SmallNORB [LeCun et al.(2004)LeCun, Huang, and Bottou]. It contains grayscale images from 50 toys in 5 categories, under 6 lighting conditions, and 3D rotations (9 elevations and 18 azimuths). We therefore take these three factors as the transformation space. We use the official train/test split (5 instances of each category for training, and 5 for testing, totalling 24,300 images per set). From the results (figure 3), we see that SmallNORB is much harder to reconstruct with retargetted poses and lighting for most methods, with all but ours returning an average image, and only ours, Trans.AE and MV3D transforming the lighting correctly (which is non-geometric). The quantitative results (table 1) reflect this result. To test our method’s ability to differentiate very fine-grained transformations, we plot results varying a single transformation parameter at a time in figure 6. Note that these are novel views – only the first image is given, and it is not part of the training set. Videos with more transitions are in the supplementary material.

RGBD-Object.

To test re-rendering of unconstrained real-world objects, we used RGBD-Object [Lai et al.(2011)Lai, Bo, Ren, and Fox]. It consists of 300 objects captured with a PrimeSense RGBD camera, though we did not use the depth channel. The objects are organised into 51 semantic categories and in total have 45,000 images, each associated with a single view angle, which we use as the only transformation parameter. Since there are few instances per category, we test with one instance per category and use the remainder for training. We show quantitative results in table 1, which show that the images reconstructed by our method are closer to the ground truth. Due to lack of space the qualitative results are shown in the supplementary material, but we observe that reconstructions for all methods are less detailed than in previous datasets, which is explained by the higher complexity of the objects’ appearance, and low diversity of views available for each object. We remark that these are novel views of object instances never seen during training time, and despite this, our method recovers more accurate images than the baselines, with less noise around high-frequency textures.

Outdoor scenes.

KITTI [Geiger et al.(2012)Geiger, Lenz, and Urtasun] is a widely used standard dataset for outdoor driving scenarios, consisting of complex city scenes. The dataset contains image sequences as well as the camera poses for each frame. The transformations in this case are 3D translation and 3D rotation, for a total of 6 parameters. Following prior work [Chen et al.(2019)Chen, Song, and Hilliges], in total we have 18,560 and 4,641 images for training and testing, respectively. For each training pair, we randomly select the target view within $\pm 5$ frames of the source view. For complex scenes like KITTI, reconstructing the target images purely from the latent embedding is challenging. In order to reconstruct more details, we adapted a warping-based pipeline [Chen et al.(2019)Chen, Song, and Hilliges] that samples pixels from the source input, by inserting our shifted tensor (eq. 4) between the encoder and decoder. The corresponding results are shown in table 1 and figure 5, where we highlight some areas where our method recovers details where Chen et al.’s introduces artifacts (the other methods failed to produce meaningful images so we omit them from this figure).

Table 2: Comparison between additive and product tensor-spaces for combining transformations (section 4.2)

Space MNIST [LeCun et al.(1998)LeCun, Bottou, Bengio, and Haffner] 3D Shapes [Burgess and Kim(2018)] Efficiency PSNR SSIM PSNR SSIM Mem. #Params. Product 23.74 0.8772 30.77 0.9210 48GB 2088M Additive 21.14 0.7942 32.09 0.9064 4.4GB 205M

Table 3: Results of the compositionality experiment, with unseen concepts (section 4.4).

Test set Blue + sphere Large + cylinder Cube + red wall Metric PSNR SSIM PSNR SSIM PSNR SSIM Trans. AE [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] 18.49 0.7631 17.62 0.7025 18.34 0.7304 Ours 28.48 0.8912 24.27 0.8270 27.81 0.8354

4.2 Additive vs. product space of transformations

As discussed in section 3.3, we use a rich yet expensive product-space of transformations (eq. 7), but we also consider a more parsimonious and efficient additive space (eq. 8). We show a comparison of the two schemes in table 3 on two datasets. We can see that the additive space does not cause the performance to drop significantly, and can even improve it slightly (for PSNR on DeepMind 3D Shapes). On the other hand, the additive space is much more efficient than the product space (in memory consumption and number of parameters) when the transformation space is large (e.g\bmvaOneDotthe 6-dimensional space of the 3D Shapes).

4.3 Relative pose estimation

The equivariance property of the trained auto-encoders means that they can be used for the downstream task of relative pose estimation (between two images), although they are not directly trained on pose regression. This can be done by extracting the embedding tensors of two images, and shifting one relative to the other (eq. 4) to find the highest matching relative pose (measured with a cosine distance between the two embeddings). To test this idea, we sample image pairs from DeepMind 3D Shapes [Burgess and Kim(2018)], where the first image is sampled uniformly, and the second is the first image transformed by an out-of-plane rotation in the range $[-15^{\circ},15^{\circ}]$ . We now use the above procedure to predict the relative pose between them. This yields an average error rate over the test set (80,000 images) of just $1.077^{\circ}$ . Since the angles in the dataset are quantised to $1^{\circ}$ , this is within the expected discretisation error of our model, and represents near-perfect accuracy. As a comparison, we also test the performance of Trans.AE [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] and a direct regression baseline, with the same backbone, which despite our best efforts achieve accuracies of only $4.924^{\circ}$ and $4.968^{\circ}$ respectively.

4.4 Compositionality and out-of-distribution extrapolation

An important property of our proposal is that the transformation factors are forced to be disentangled (eq. 7 and eq. 8). This means that our method may be well equipped to compose transformations in novel ways, extrapolating beyond the training set. We test this idea by leaving one particular combination of attributes out of the training set (e.g\bmvaOneDotblue spheres are never observed), in DeepMind 3D Shapes. By training on the remaining samples, we test the network’s ability to reconstruct a concept that was never observed before. The results are in table 3, where our method successfully composes and extrapolates outside the training distribution for 3 pairs of attributes, while a transforming auto-encoder [Hinton et al.(2011)Hinton, Krizhevsky, and Wang] does not.

5 Conclusion

In this work, we propose a method to train a deep network to achieve equivariance to arbitrary transformations, entirely from data, which goes beyond the typical scenario where an analytical model of the transformations (e.g\bmvaOneDotgeometrical) is given. We demonstrate encouraging results in re-rendering images for given arbitrary transformation parameters, on both synthetic and more complex real datasets. We also experiment with extrapolating compositions beyond the training set, and a simple relative pose estimation result. Interesting avenues for future work include investigating ways to increase the visual fidelity, such as with GANs or auto-regressive models, though the simplicity of the current auto-encoder is also attractive.

Acknowledgments

We are grateful for the support of the EPSRC Programme Grant Visual AI (EP/T028572/1), and the Royal Academy of Engineering (RF\201819\18\163).

References

[Bruna et al.(2013)Bruna, Szlam, and LeCun] Joan Bruna, Arthur Szlam, and Yann LeCun. Learning stable group invariant representations with convolutional networks. In 1st International Conference on Learning Representations, ICLR, 2013.
[Burgess and Kim(2018)] Chris Burgess and Hyunjik Kim. 3D Shapes Dataset. https://github.com/deepmind/3dshapes-dataset/, 2018.
[Chaurasia et al.(2013)Chaurasia, Duchene, Sorkine-Hornung, and Drettakis] Gaurav Chaurasia, Sylvain Duchene, Olga Sorkine-Hornung, and George Drettakis. Depth synthesis and local warps for plausible image-based navigation. ACM Transactions on Graphics (TOG), 32(3):1–12, 2013.
[Chen et al.(2019)Chen, Song, and Hilliges] Xu Chen, Jie Song, and Otmar Hilliges. Monocular neural image based rendering with continuous view control. In Proceedings of the IEEE International Conference on Computer Vision, pages 4090–4100, 2019.
[Cohen et al.(2018)Cohen, Geiger, Köhler, and Welling] Taco S. Cohen, Mario Geiger, Jonas Köhler, and Max Welling. Spherical CNNs. In International Conference on Learning Representations, 2018.
[Cohen et al.(2019)Cohen, Geiger, and Weiler] Taco S Cohen, Mario Geiger, and Maurice Weiler. A general theory of equivariant cnns on homogeneous spaces. In Advances in Neural Information Processing Systems, 2019.
[Dosovitskiy et al.(2016)Dosovitskiy, Springenberg, Tatarchenko, and Brox] Alexey Dosovitskiy, Jost Tobias Springenberg, Maxim Tatarchenko, and Thomas Brox. Learning to generate chairs, tables and cars with convolutional networks. IEEE transactions on pattern analysis and machine intelligence, 39(4):692–705, 2016.
[Dupont et al.(2020)Dupont, Martin, Colburn, Sankar, Susskind, and Shan] Emilien Dupont, Miguel Bautista Martin, Alex Colburn, Aditya Sankar, Josh Susskind, and Qi Shan. Equivariant neural rendering. In International Conference on Machine Learning, pages 2761–2770. PMLR, 2020.
[Eslami et al.(2018)Eslami, Rezende, Besse, Viola, Morcos, Garnelo, Ruderman, Rusu, Danihelka, Gregor, et al.] SM Ali Eslami, Danilo Jimenez Rezende, Frederic Besse, Fabio Viola, Ari S Morcos, Marta Garnelo, Avraham Ruderman, Andrei A Rusu, Ivo Danihelka, Karol Gregor, et al. Neural scene representation and rendering. Science, 360(6394):1204–1210, 2018.
[Fitzgibbon et al.(2005)Fitzgibbon, Wexler, and Zisserman] Andrew Fitzgibbon, Yonatan Wexler, and Andrew Zisserman. Image-based rendering using image-based priors. International Journal of Computer Vision, 63(2):141–151, 2005.
[Flynn et al.(2016)Flynn, Neulander, Philbin, and Snavely] John Flynn, Ivan Neulander, James Philbin, and Noah Snavely. Deepstereo: Learning to predict new views from the world’s imagery. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 5515–5524, 2016.
[Flynn et al.(2019)Flynn, Broxton, Debevec, DuVall, Fyffe, Overbeck, Snavely, and Tucker] John Flynn, Michael Broxton, Paul Debevec, Matthew DuVall, Graham Fyffe, Ryan Overbeck, Noah Snavely, and Richard Tucker. Deepview: View synthesis with learned gradient descent. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2367–2376, 2019.
[Geiger et al.(2012)Geiger, Lenz, and Urtasun] Andreas Geiger, Philip Lenz, and Raquel Urtasun. Are we ready for autonomous driving? The KITTI Vision Benchmark Suite. In Conference on Computer Vision and Pattern Recognition (CVPR), 2012.
[Goodfellow et al.(2016)Goodfellow, Bengio, and Courville] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT Press, 2016.
[Goodfellow et al.(2014)Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville, and Bengio] Ian J Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial networks. arXiv preprint arXiv:1406.2661, 2014.
[Hedman et al.(2018)Hedman, Philip, Price, Frahm, Drettakis, and Brostow] Peter Hedman, Julien Philip, True Price, Jan-Michael Frahm, George Drettakis, and Gabriel Brostow. Deep blending for free-viewpoint image-based rendering. ACM Transactions on Graphics (TOG), 37(6):1–15, 2018.
[Henriques and Vedaldi(2017)] J. F. Henriques and A. Vedaldi. Warped convolutions: Efficient invariance to spatial transformations. In ICML, 2017.
[Henriques et al.(2014)Henriques, Martins, Caseiro, and Batista] J. F. Henriques, P. Martins, R. Caseiro, and J. Batista. Fast training of pose detectors in the fourier domain. In Advances in Neural Information Processing Systems, 2014.
[Higgins et al.(2016)Higgins, Matthey, Pal, Burgess, Glorot, Botvinick, Mohamed, and Lerchner] Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. Beta-VAE: Learning basic visual concepts with a constrained variational framework. 2016.
[Higgins et al.(2018)Higgins, Amos, Pfau, Racaniere, Matthey, Rezende, and Lerchner] Irina Higgins, David Amos, David Pfau, Sebastien Racaniere, Loic Matthey, Danilo Rezende, and Alexander Lerchner. Towards a definition of disentangled representations. arXiv preprint arXiv:1812.02230, 2018.
[Hinton et al.(2011)Hinton, Krizhevsky, and Wang] Geoffrey E Hinton, Alex Krizhevsky, and Sida D Wang. Transforming auto-encoders. In International conference on artificial neural networks, pages 44–51. Springer, 2011.
[Hinton et al.(2018)Hinton, Sabour, and Frosst] Geoffrey E Hinton, Sara Sabour, and Nicholas Frosst. Matrix capsules with EM routing. In International conference on learning representations, 2018.
[Kanazawa et al.(2014)Kanazawa, Sharma, and Jacobs] Angjoo Kanazawa, Abhishek Sharma, and David Jacobs. Locally scale-invariant convolutional neural networks. arXiv preprint arXiv:1412.5104, 2014.
[Kingma and Welling(2014)] Diederik P. Kingma and Max Welling. Auto-Encoding Variational Bayes. In ICLR, 2014.
[Kondor and Trivedi(2018)] Risi Kondor and Shubhendu Trivedi. On the generalization of equivariance and convolution in neural networks to the action of compact groups. In International Conference on Machine Learning, pages 2747–2755, 2018.
[Kopf et al.(2013)Kopf, Langguth, Scharstein, Szeliski, and Goesele] Johannes Kopf, Fabian Langguth, Daniel Scharstein, Richard Szeliski, and Michael Goesele. Image-based rendering in the gradient domain. ACM Transactions on Graphics (TOG), 32(6):1–9, 2013.
[Kosiorek et al.(2019)Kosiorek, Sabour, Teh, and Hinton] Adam Kosiorek, Sara Sabour, Yee Whye Teh, and Geoffrey E Hinton. Stacked capsule autoencoders. In Advances in Neural Information Processing Systems, pages 15512–15522, 2019.
[Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
[Kulkarni et al.(2015)Kulkarni, Whitney, Kohli, and Tenenbaum] Tejas D Kulkarni, William F Whitney, Pushmeet Kohli, and Joshua B Tenenbaum. Deep convolutional inverse graphics network. In Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2, pages 2539–2547, 2015.
[Ladicky et al.(2014)Ladicky, Shi, and Pollefeys] Lubor Ladicky, Jianbo Shi, and Marc Pollefeys. Pulling things out of perspective. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 89–96, 2014.
[Lai et al.(2011)Lai, Bo, Ren, and Fox] Kevin Lai, Liefeng Bo, Xiaofeng Ren, and Dieter Fox. A large-scale hierarchical multi-view RGB-D object dataset. In 2011 IEEE international conference on robotics and automation, pages 1817–1824. IEEE, 2011.
[LeCun et al.(1998)LeCun, Bottou, Bengio, and Haffner] Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
[LeCun et al.(2004)LeCun, Huang, and Bottou] Yann LeCun, Fu Jie Huang, and Leon Bottou. Learning methods for generic object recognition with invariance to pose and lighting. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004. CVPR 2004., volume 2, pages II–104. IEEE, 2004.
[Lenc and Vedaldi(2015)] Karel Lenc and Andrea Vedaldi. Understanding image representations by measuring their equivariance and equivalence. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 991–999, 2015.
[Matusik et al.(2002)Matusik, Pfister, Ngan, Beardsley, Ziegler, and McMillan] Wojciech Matusik, Hanspeter Pfister, Addy Ngan, Paul Beardsley, Remo Ziegler, and Leonard McMillan. Image-based 3D photography using opacity hulls. ACM Transactions on Graphics (TOG), 21(3):427–437, 2002.
[Memisevic and Hinton(2010)] Roland Memisevic and Geoffrey E Hinton. Learning to represent spatial transformations with factored higher-order Boltzmann machines. Neural computation, 22(6):1473–1492, 2010.
[Miao and Rao(2007)] Xu Miao and Rajesh PN Rao. Learning the lie groups of visual invariance. Neural computation, 19(10):2665–2693, 2007.
[Mildenhall et al.(2019)Mildenhall, Srinivasan, Ortiz-Cayon, Kalantari, Ramamoorthi, Ng, and Kar] Ben Mildenhall, Pratul P Srinivasan, Rodrigo Ortiz-Cayon, Nima Khademi Kalantari, Ravi Ramamoorthi, Ren Ng, and Abhishek Kar. Local light field fusion: Practical view synthesis with prescriptive sampling guidelines. ACM Transactions on Graphics (TOG), 38(4):1–14, 2019.
[Mildenhall et al.(2020)Mildenhall, Srinivasan, Tancik, Barron, Ramamoorthi, and Ng] Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision, pages 405–421. Springer, 2020.
[Park et al.(2017)Park, Yang, Yumer, Ceylan, and Berg] Eunbyung Park, Jimei Yang, Ersin Yumer, Duygu Ceylan, and Alexander C Berg. Transformation-grounded image generation network for novel 3D view synthesis. In Proceedings of the ieee conference on computer vision and pattern recognition, pages 3500–3509, 2017.
[Penner and Zhang(2017)] Eric Penner and Li Zhang. Soft 3d reconstruction for view synthesis. ACM Transactions on Graphics (TOG), 36(6):1–11, 2017.
[Qi et al.(2020)Qi, Zhang, Lin, and Wang] Guo-Jun Qi, Liheng Zhang, Feng Lin, and Xiao Wang. Learning generalized transformation equivariant representations via autoencoding transformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020.
[Reddy and Chatterji(1996)] B. Srinivasa Reddy and Biswanath N. Chatterji. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Transactions on Image Processing, 5(8):1266–1271, 1996.
[Rematas et al.(2016)Rematas, Nguyen, Ritschel, Fritz, and Tuytelaars] Konstantinos Rematas, Chuong H Nguyen, Tobias Ritschel, Mario Fritz, and Tinne Tuytelaars. Novel views of objects from a single image. IEEE transactions on pattern analysis and machine intelligence, 39(8):1576–1590, 2016.
[Schmidt and Roth(2012)] Uwe Schmidt and Stefan Roth. Learning rotation-aware features: From invariant priors to equivariant descriptors. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 2050–2057, 2012.
[Seitz et al.(2006)Seitz, Curless, Diebel, Scharstein, and Szeliski] Steven M Seitz, Brian Curless, James Diebel, Daniel Scharstein, and Richard Szeliski. A comparison and evaluation of multi-view stereo reconstruction algorithms. In 2006 IEEE computer society conference on computer vision and pattern recognition (CVPR’06), volume 1, pages 519–528. IEEE, 2006.
[Simard et al.(2000)Simard, Le Cun, Denker, and Victorri] Patrice Y Simard, Yann A Le Cun, John S Denker, and Bernard Victorri. Transformation invariance in pattern recognition: Tangent distance and propagation. International Journal of Imaging Systems and Technology, 11(3):181–197, 2000.
[Sitzmann et al.(2019)Sitzmann, Zollhöfer, and Wetzstein] Vincent Sitzmann, Michael Zollhöfer, and Gordon Wetzstein. Scene representation networks: Continuous 3D-structure-aware neural scene representations. In Advances in Neural Information Processing Systems, 2019.
[Srinivasan et al.(2019)Srinivasan, Tucker, Barron, Ramamoorthi, Ng, and Snavely] Pratul P Srinivasan, Richard Tucker, Jonathan T Barron, Ravi Ramamoorthi, Ren Ng, and Noah Snavely. Pushing the boundaries of view extrapolation with multiplane images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 175–184, 2019.
[Sun et al.(2018)Sun, Huh, Liao, Zhang, and Lim] Shao-Hua Sun, Minyoung Huh, Yuan-Hong Liao, Ning Zhang, and Joseph J Lim. Multi-view to novel view: Synthesizing novel views with self-learned confidence. In Proceedings of the European Conference on Computer Vision (ECCV), pages 155–171, 2018.
[Tatarchenko et al.(2016)Tatarchenko, Dosovitskiy, and Brox] Maxim Tatarchenko, Alexey Dosovitskiy, and Thomas Brox. Multi-view 3d models from single images with a convolutional network. In European Conference on Computer Vision, pages 322–337. Springer, 2016.
[Tenenbaum and Freeman(2000)] Joshua B Tenenbaum and William T Freeman. Separating style and content with bilinear models. Neural computation, 12(6):1247–1283, 2000.
[Van Oord et al.(2016)Van Oord, Kalchbrenner, and Kavukcuoglu] Aaron Van Oord, Nal Kalchbrenner, and Koray Kavukcuoglu. Pixel recurrent neural networks. In International Conference on Machine Learning, pages 1747–1756. PMLR, 2016.
[Wu et al.(2020)Wu, Rupprecht, and Vedaldi] Shangzhe Wu, Christian Rupprecht, and Andrea Vedaldi. Unsupervised learning of probably symmetric deformable 3D objects from images in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2020.
[Xiao et al.(2019)Xiao, Liu, and Lee] Fanyi Xiao, Haotian Liu, and Yong Jae Lee. Identity from here, pose from there: Self-supervised disentanglement and generation of objects using unlabeled videos. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 7013–7022, 2019.
[Yang et al.(2015)Yang, Reed, Yang, and Lee] Jimei Yang, Scott E Reed, Ming-Hsuan Yang, and Honglak Lee. Weakly-supervised disentangling with recurrent transformations for 3d view synthesis. In Advances in Neural Information Processing Systems, pages 1099–1107, 2015.
[Zhou et al.(2016)Zhou, Tulsiani, Sun, Malik, and Efros] Tinghui Zhou, Shubham Tulsiani, Weilun Sun, Jitendra Malik, and Alexei A Efros. View synthesis by appearance flow. In European conference on computer vision, pages 286–301. Springer, 2016.

Quantised Transforming Auto-Encoders: Achieving Equivariance to Arbitrary Transformations in Deep Networks