QM abelian varieties, hypergeometric character sums and modular forms
Abstract.
This is a report on recent work, with Wen-Ching Winnie Li and Ling Long. In that work explicit formulas are given, involving hypergeometric character sums, for the traces of Hecke operators acting spaces of cusp forms of weight for certain arithmetically defined Fuchsian subgroups . In particular we consider the groups attached to the quaternion division algebra over of discriminant 6.
Key words and phrases:
hypergeometric functions, motive, -adic representations, rigidity1991 Mathematics Subject Classification:
11T23, 11T24, 11S40, 11F80, 11F85, 33C05, 33C651. Introduction.
The forthcoming joint work with Wen-Ching Winnie Li and Ling Long [43] extends some investigations of Wen-Ching Winnie Li, Tong Liu, and Ling Long on 4-dimensional Galois representations with quaternion structures, [6]; see also [63]. Our main results are explicit formulas in the shape (see Section 8; terms to be explained in more detail)
| (1) |
Here is the trace of the Hecke operator acting on the space of weight- cusp forms on the arithmetic Fuchsian group . In fact, the expression will be a sum of terms for each of the local Frobenius traces on a constructible -sheaf for the étale topology on the curve . The theory of hypergeometric character sums over finite fields was developed largely by Greene [41], Katz [52], Beukers-Cohen-Mellit [12], and Fuselier-Long-Ramakrishna-Swisher-Tu [36]. The groups are certain arithmetic triangle groups.
The inspiration for this work can be found in the papers of Ahlgren, Frechette, Fuselier, Lennon, Ono, Papanikolas [1, 2, 31, 37, 61, 62], wherein formulas in terms of hypergeometric character sums for traces of Hecke operators are given, but not in terms of traces of Frobenius in étale cohomology. Rather, their approach combines (1) counting formulas for elliptic curves over finite fields due to Schoof, [79], and (2) the Selberg trace formula. In fact, formulas for the trace of Hecke operators on had already been given by Ihara, [46] by similar methods, but Ihara did not use hypergeometric character sums.
We give a different approach, which is more geometric, and applies not only to the cases treated by these authors, but also to groups arising from the units in the quaternion algebra over of discriminant 6. We will explain the geometric viewpoints on modular forms and hypergeometric functions.
2. Background.
This work weaves several major mathematical threads. On the one hand, this is part of the general Langlands program, namely that part concerned with expressing the -functions of motives in terms of -functions of automorphic forms. In the case at hand, the automorphic forms are classical modular forms on the algebraic group or its inner twist given by the quaternion algebra . The automorphic -functions are attached to local systems on modular curves. When is a congruence subgroup, these are the modular curves classifying families of elliptic curves with level structure. When comes from a quaternion algebra, these are Shimura curves. Thus, the motives involved belong to the general theory of Shimura varieties, [71].
Another major theme is that of hypergeometric functions. The term hypergeometric includes not only the classical functions, and their generalizations , Appell-Lauricella functions, etc. There are (at least) two general extensions of the theory of hypergeometric functions: (1) the -hypergeometric, or GKZ (Gelfand-Kapranov-Zelevinsky) systems, [39]; (2) the Gabber-Loeser-Sabbah hypergeometric systems, based on earlier works of M. Sato and Ore, [66, 67, 68]. See the paper of Dwork/Loeser: [24].
Generally speaking, a hypergeometric function is one that
-
1.
has power-series expansions in special form: -series;
-
2.
satisfies a (regular) holonomic system of differential equations;
-
3.
has Euler integral expressions;
-
4.
is attached to a motivic sheaf.
What the last item means is that not only are there complex-analytic functions defined by them, but also -adic and -adic versions. The -adic versions give rise to hypergeometric character sums, which are central to this paper. For the GKZ systems see [34]; for the GLS systems see [38]. The -adic versions give -adic analytic functions, first investigated by Dwork. For the GKZ systems, see [35].
Note that there are irregular differential equations of hypergeometric type, the confluent hypergeometrics. The Hodge-deRham realizations are related to irregular Hodge theory and the periods belong to exponential modules, see [25]. The character sums involve additive as well as multiplicative characters of finite fields, and hence their -adic sheaves have wild ramification at infinity. For a recent example see [33].
3. Modular forms and modular curves
3.1. Modular forms
(Reference: [85]). A Fuchsian subgroup of the first kind is a discrete subgroup such that the invariant volume is finite. This acts on the upper half-plane by
The upper half-plane is conformally equivalent to the open unit disk , via the map . This reflects the isomorphism , where
There are isomorphisms where
For a Fuchsian subgroup of first kind, let or according to whether cocompact or not. Here is the union of and the cusps of , if any. We have a finite set of points which are cusps or elliptic points, that is, their preimages in are cusps or elliptic points of , respectively. Let
the complement of the set of cusps and elliptic points, and the complement of the set of cusps, respectively. Note that is a covering space in the sense of topology. In particular, if has no elliptic points, then is the universal covering of . The action of on is via the quotient in . For the groups in this paper, . Therefore, if torsion-free, then is the universal covering of , and the fundamental group at any base-point
an isomorphism unique up to inner automorphism. In the quaternion cases this is for without torsion. In general, there is an epimorphism
If is a Fuchsian subgroup of the first kind, and is an integer, we recall that a modular form of weight is a holomorphic function for such that
which satisfies a growth condition at the cusps. For each cusp of there is a parameter such that a modular form has an expansion at : . A cusp form is one that vanishes at every cusp i.e., at every cusp of . The space of cusp forms is finite dimensional over . We assume the reader is familiar with the standard subgroups as well as the Hecke operators (the latter only defined in the case of arithmetically defined Fuchsian subgroups).
3.2. Modular curves
In our work, we consider those which are arithmetically defined subgroups. There are two cases:
-
1.
Elliptic modular case. is commensurable with . Then the cusps of is the set of rational numbers and the point .
-
2.
Quaternion case. is commensurable to the set of norm 1 elements in a maximal order of an indefinite quaternion algebra over . That is, we choose once and for all an embedding , which induces an embedding . In this case, the set of cusps is empty, so .
In both these cases, Shumura’s theory of canonical models shows that these Riemann surfaces are the -points of an algebraic curve, denoted defined over a number field . We will use the notation for the corresponding Riemann surface, if there is no ambiguity. If necessary, we use to denote the analytic space.
These curves are (in general coarse) moduli spaces. If has no torsion, then there are universal families of abelian varieties with additional structures. In the elliptic modular cases these are families of elliptic curves . In the quaternion cases, , these are families of 2-dimensional abelian varieties with an action of the quaternion algebra, that is, with a homomorphism
and additional structure.
Example 3.1.
Example 3.2.
Let
This is the moduli scheme for . The universal elliptic curve for this is
The quaternion case with will be discussed in detail in section 7.
3.3. Triangle groups
In this work, we consider those that are (or are closely related to) triangle groups. We recall the definition: Let , with . Define
and refer to as spherical, Euclidean, hyperbolic, depending on whether is , or respectively. In each of these three cases we associate a geometry
Spherical triples: , , , , for . Euclidean triples: , , , . The rest are hyperbolic. Among them, there are finitely many arithmetic triangle groups, which were enumerated by Takeuchi, see [89], [90]. To each triple we have the associated triangle group, defined as
We have representation of via isometries of the associated geometry as follows. Let be a geodesic triangle in with angles . Let , , be reflections in the three sides of . The group generated by is a discrete group with fundamental domain . The subgroup of orientation-preserving isometries is generated by
satisfies the relations of with a counterclockwise rotation at the vertex with angle . The quotient space is a Riemann orbifold of genus zero. The fundamental domain is then a union of and a reflected image of .
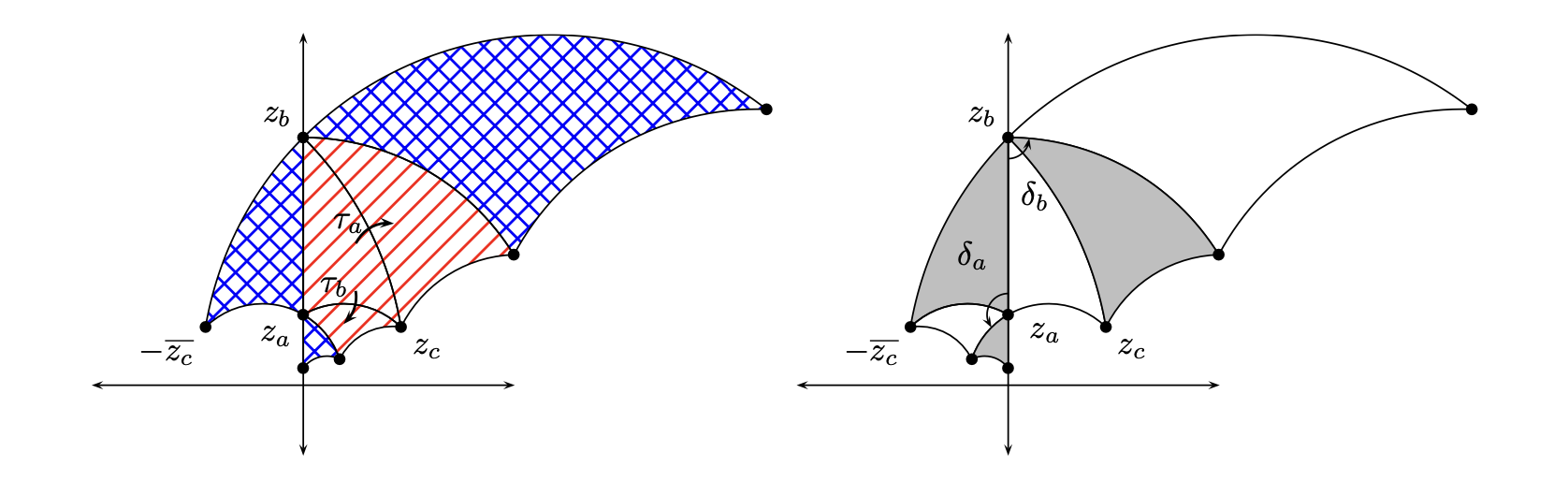
The relevance of triangle groups for hypergeometric equations arises from the fundamental theorem of H. A. Schwarz [80]. Given two independent solutions and to a hypergeometric differential equation, the ratio maps the complex upper half-plane conformally onto a region in the extended complex plane which is bounded by circular arcs. For the function
the angles are , , where , , . Schwarz observed that the monodromy of the differential equation gave rise to isometries of the associated geometry . In some cases, one obtains by analytic continuation a tessellation of . For this to extend to a tesselation we must have that are all in the shape where . We can denote the angles of this triangle by and classify the triples as above. He was especially interested in the spherical case, where the monodromy group is necessarily finite, and he managed to completely classify these.
Given a triangle group , following Theorem 9 of [92] by Y. Yang we introduce the following hypergeometric parameters:
and
Using these Yang wrote down an explicit basis for in terms of and .
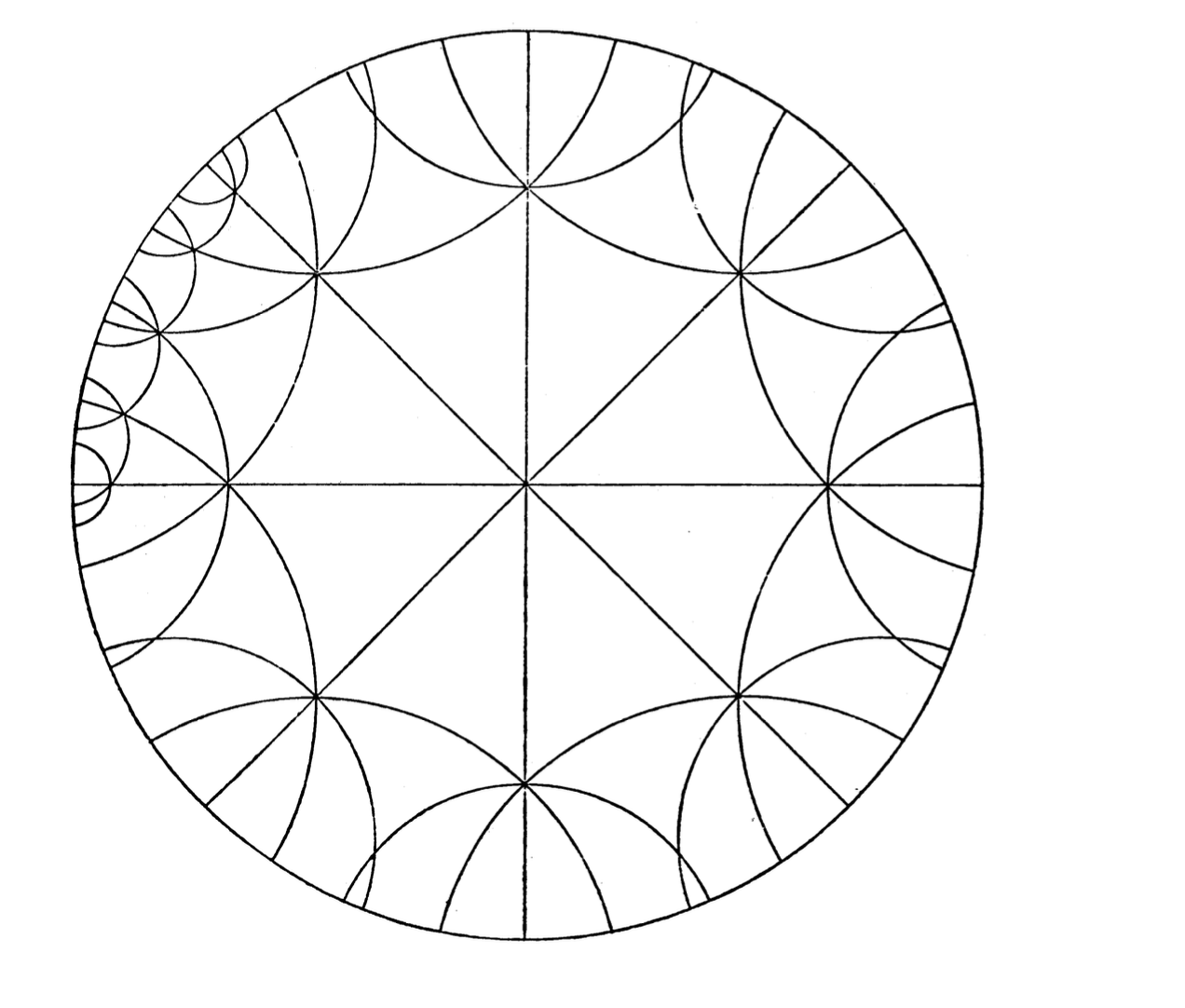
There are now extensive resources on the web for exploring hyperbolic tesselations. This had several major later developments. On the one hand, Poincaré extended this analysis to conformal maps given by second-order linear differential equations with regular singular points. The conformal image is an -gon bounded by circular arcs. By studying the transformations of these under analytic continuation, Poincaré made the link with non-Euclidean geometry and initiated the modern theories of hyperbolic geometry and automorphic forms. For hypergeometric differential equations of several variables, including those studied by Picard, and Appell and Lauricella, see the works of Deligne and Mostow, [21].
4. Local systems.
4.1. Complex analytic.
Riemann introduced the idea of monodromy into the study of analytic differential equations. Given a representation of the fundamental group
there is a unique second order rational differential equation with regular singular points with the property that if is a basis of holomorphic solutions at then analytic continuation around a loop yields the linear transformation
Since
to give the monodromy representation is equivalent to giving two-by-two matrices such that . These are well-defined up to simultaneous conjugation by an element of . As Katz observes, Riemann proved a stronger result. Namely, it suffices to give the Jordan canonical forms of to reconstruct the hypergeometric differential equation. Actually Riemann only considered the case when these were semisimple, so equivalent to diagonal matrices, with eigenvalues and ; he called the the exponents at the singular point. They are well-defined up to permutation and adding . This stronger property, that a differential equation is determined by the Jordan forms of the monodromies at the singular points, is what Katz ([53]) calls rigidity. Rigidity plays an important role in our work.
If is a connected nonsingular algebraic variety over and
is a representation, we get a local system V on the analytic space . By the Riemann-Hilbert correspondence, this is the solution sheaf to a differential equation, unique up to isomorphism,
with regular singular points at infinity ([16], [51]). If is a nonsingular algebraic variety over we let be the set of complex points with the classical topology. Assume that is quasi-projective and connected. Recall the following dictionary: The following categories are equivalent:
-
1.
Local systems of finite-dimensional -vector spaces V on .
-
2.
Representations on finite-dimensional -vector spaces .
-
3.
Holomorphic integrable connections
where is a locally free -module of finite rank.
-
4.
Integrable algebraic connections
where is a locally free -module of finite rank, and which have regular singular points “at infinity”.
4.2. -adic.
A reference: [18], [20]. Fix a prime number . In this section: scheme = a separated noetherian scheme on which is invertible. We are interested in constructible -sheaves on , in particular, those that are lisse. In this section: the étale topology is understood. An -adic representation of a profinite group on a -vector space is a homomorphism
such that there is a finite subextension and an -structure on such that factorizes in a continuous homomorphism . Recall that a geometric point of a scheme is a morphism of the spectrum of an algebraically closed field denoted to . It is localized in if its image is . If is connected and pointed by a geometric point , the functor
is an equivalence between the categories of
-
1.
lisse -sheaves on ;
-
2.
-adic continuous representations of .
Here is Grothendieck’s fundamental group. Especially if is a field, the category of lisse -sheaves on is equivalent to the category of -adic representations of .
If one is working in the category of schemes of finite type over a perfect field with algebraic closure , and is a -rational point, by convention we let be the geometric point of which is the composite .
More generally, let be an irreducible scheme of finite type over a field . Then a lisse sheaf on is equivalent to a representation
where is a geometric generic point. That is, where is the generic point of , and is the function field of .
Recall that there is a canonical exact sequence
Moreover if has characteristic and we choose an embedding , is isomorphic to the profinite completion of the Poincaré fundamental group, so this includes the geometric monodromy of .
Now let be a be a finite field of characteristic . If is a scheme of finite type, we define and recall that there is a morphism which sends a point with coordinates to the point with coordinates . The set of closed points is canonically identified with , and the Frobenius fixed points . The set of closed points is isomorphic to the set of orbits of ; for the size of the corresponding orbit is , which is also the degree of the extension field . If is a constructible -sheaf on for the étale topology, we let be deduced from by extension to the algebraic closure. If is a geometric point localized in , we define
The stalk is a -vector space of finite dimension on which acts and therefore
is defined. It is independent of the geometric point localized in , so we can simply denote it by . The coefficient of in this polynomial is the trace . The Grothendieck-Lefschetz trace formula reads:
| (2) |
where is the dimension of and is cohomology with proper support. We define the -function
The trace formula is equivalent to the factorization
4.3. Families of varieties.
Let be a proper smooth morphism of algebraic varieties. Then we get local systems:
-
1.
Over : where
is the Gauss-Manin connection on the relative deRham cohomology. Then . This has regular singular points (Griffiths; see [49]).
-
2.
-adic: is a lisse -sheaf on the étale topology of . The stalk in a geometric point , which has an action of the Galois group .
4.4. Example: Legendre curve.
Let . This is the open subset
For each we let be the projective nonsingular model of the affine curve
This is an elliptic curve with origin at infinity in the projective plane. We get a proper smooth morphism defined over with these fibers.
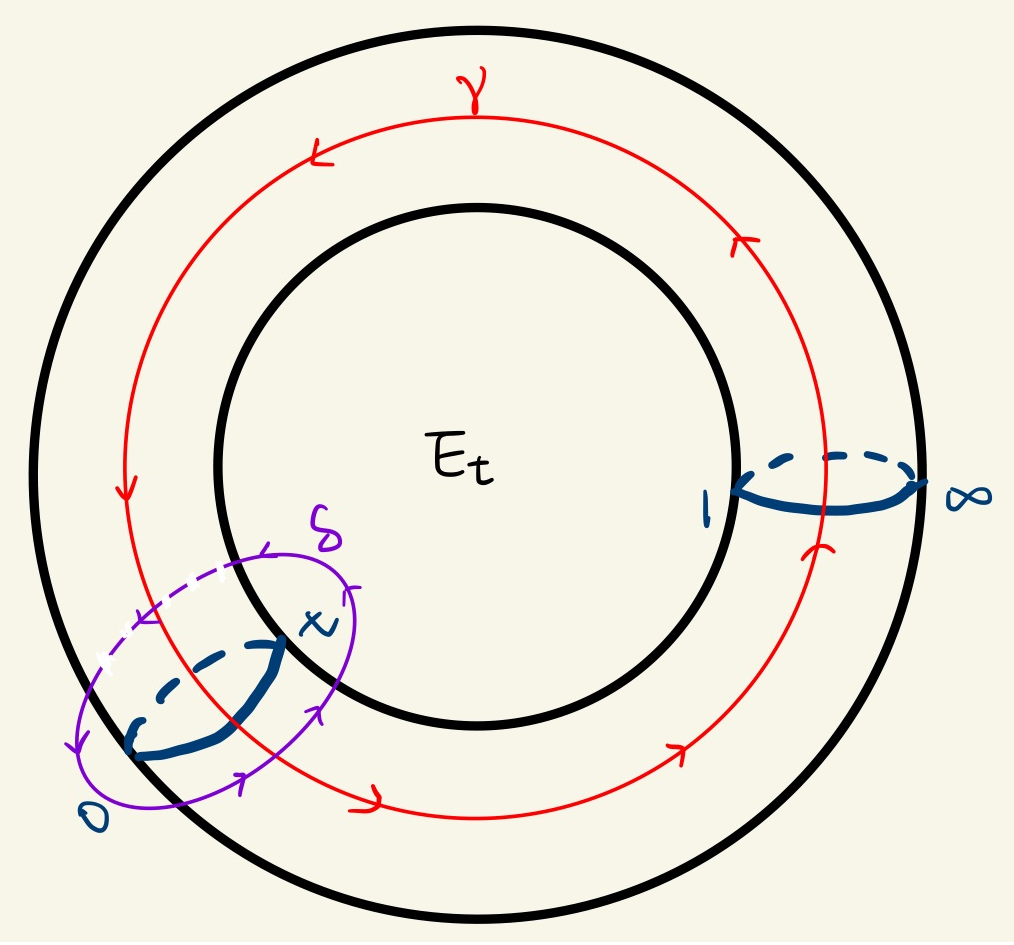
The local system over topologically is the flat bundle of for . This latter is the sphere with 3 points removed. We have
isomorphic to a free group on 2 generators. We can represent these by loops starting at the base-point and circling once around , respectively. The monodromy can be represented topologically by following the generators of as moves along these loops. This can be viewed by analytically continuing the period matrix of relative to a basis of differential forms. The deRham cohomology is a free -module of rank 2. We can take as basis
which is a basis of meromorphic 1-forms of the first and second kind modulo exact forms.
We have the following equation in :
Note that , where is a local system of free -modules of rank 2 on with a nondegenerate symplectic pairing on it. The dual local system is the homology local system: . For any local horizontal section of the dual of , it follows easily from this that the period is a solution to the differential equation
which is the differential equation satisfied by . In fact,
We view a small loop around the interval as topological cycle on the Riemann surface which is a branched cover of of degree 2.
The monodromy group of this differential equation is projectively equivalent to the principal congruence subgroup . In a suitable basis (we can take so-called vanishing cycles at and ) of the monodromy matrices are
These generate a subgroup of index 2 inside acting on the upper half plane with quotient
This map is induced by where is a generator of the field of modular functions for . The inverse of this is the multivalued function on given by the period ratio of two independent solutions to this differential equation. The above quotient space, denoted , is the coarse moduli space of elliptic curves with a level 2 structure.
The -adic local system gives zeta functions of the elliptic curves in the family. For instance, let for an odd prime , . Then this gives a geometric point of the scheme , and we can identify the fiber
which is the dual of the Tate module of the curve . Then
4.5. Example: Generalized Legendre curves.
For any ring , we denote by the coordinate on and by the open set where is invertible. Given any elements we denote by the free -module of rank 2 with basis , , and integrable -connection
Horizontal sections of the dual of over an open set can be identified with which satisfy the differential equation
These hypergeometric equations are two-dimensional factors of the the cohomology of the family of curves . In effect, the Euler integral representation
shows that the solutions to the differential equation are given by periods of those curves. Given integers greater that zero, let be the nonsingular projective model of the affine curve in -space defined by the equation . We consider this as a family of curves
We have the Gauss-Manin connection
The following theorem gives the structure of this, at least in the generic fiber . Choose an embedding . Let
This is the open affine subset where is invertible. It is affine and smooth of relative dimension one over . The map is a finite étale covering
For any root of unity there is an automorphism of given by . This gives the Galois group of the covering . Note that the defines an element in the character eigenspace where .
Proposition 4.1.
([50, 6.8.6]) Suppose that does not divide . Then for any integer which is invertible modulo the map
induces an isomorphism
This gives only the part of the cohomology belonging to primitive characters modulo . For prime to , we have . The local system on underlies a polarized variation of Hodge structures of weight 1. The modules with connection correspond to the rank 2 local system . The does not correspond to a variation of Hodge structures unless the character is real.
The eigenspaces then give the -adic realization, where is as before but now as schemes over for the étale topology.
These results are generalized to families of curves of the form
in [44]. One gets a regular holonomic system of partial differential equations in the variables .
5. Hypergeometric motives
In this paper, the word motive (really: motivic sheaf) is used informally. These concepts can be rigorously applied utilizing results of Arapura [4], [5], and Ayoub [7], [8]. For our purpose, the motives on a scheme will be viewed as giving
-
1.
a constructible sheaf of -vector spaces on the analytic space ;
-
2.
a constructible - sheaf for the étale topology on , for a fixed prime number .
In this section we will describe the motivic sheaves attached to hypergeometric data. We utilize the formalism of hypergeometric motives as developed by Roberts and Rodriguez Villegas, see [76]. A hypergeometric datum is a pair of multi-sets with . A datum with is said to be defined over if the set of column vectors mod is invariant under multiplication by all , where , called the level of , is the least common denominator of . See Definition 1 in [63, 2.2]. We mainly consider primitive hypergeometric data , namely for all .
Let . There is a motive on which forms a local system of rank and is pure of weight on .
5.1. Over .
Let denote the Gamma function. For and , define the Pochhammer symbol . Given we associate the hypergeometric function in the variable :
It satisfies the Fuchsian ordinary differential equation with three regular singular points at :
5.2. Over a finite field.
Let be a finite field of odd characteristic and use to denote the group of multiplicative characters of . We use or simply to denote the trivial character, and or to denote the quadratic character. For any , use to denote its inverse, and extend to by setting . For any characters , , with in , the -function (cf. [36]) is defined as follows:
| (5) |
where
It will be useful for us to have some notation for characters of finite fields. First we recall the th power residue symbol. Let . For every prime ideal , is a finite field with elements. Recall that is a cyclic group with elements, and since maps to an element of order modulo , we have mod . For any prime to , there is a unique th root of unity with the property
The map induces a character . Moreover, every such character is of the form for some . Given a rational number with denominator , we can identify it with an element of . Then we define a character .
We choose an isomorphism of all roots of unity with the roots of unity .
Theorem 5.1 (Katz [52, 54]).
Let be a prime. Given a primitive hypergeometric datum HD = consisting of , with and . There exists a constructible -sheaf for the étale topology on , denoted , with the following properties:
-
1.
Let be a closed point and a geometric point localized in . The residue field is a finite extension of the field . We let be the degree of this extension. Then
where and is the character
-
2.
When , the stalk has dimension and all roots of the characteristic polynomial of are algebraic numbers and have the same absolute value under all archimedean embeddings.
There is a variant of these character sums due to Beukers/Cohen/Mellit which has the important property that in many cases we can define these sheaves slightly more generally. For instance, suppose that the data is defined over , then there is a sheaf on such that
The Frobenius traces of are -valued.
5.3. Transformations
There is a huge number of identities relating different hypergeometric functions. These have parallel versions over and over finite fields. For instance:
The Clausen formula ([3] or [63, Eqn. (39)]):
| (6) |
when both sides are convergent. The finite field analog
Theorem 5.2 (Evans-Greene [30]).
For a fixed finite field , let be the quadratic character. Assume such that none of is trivial. When , we have
When , suppose for some , we have
6. Automorphic motives
There are motives on modular curves such that the cohomology is related to cusp forms on of weight . This is the content of Eichler-Shimura theory. There are two main aspects: the geometric description of modular forms, and the congruence formula relating the trace of Hecke operators to the trace of Frobenius.
6.1. Over .
The main result here due to Eichler [27] and Shimura [82] is an isomorphism
between the space of cusp forms of weight for and the parabolic cohomology group, where is the -th symmetric power of the standard representation of on . Parabolic cohomology is treated in detail in Shimura’s book, [85].
Here is a brief outline: let . For any , let be the vector whose components are ( if .) We define a representation of of dimension by the rule:
That is, . One checks, for :
We have
Let be a Fuchsian subgroup of the first kind and an integer. If we take to be even. If is a cusp-form of weight we define a vector-valued differential form
We get
the second equality holding because the representation is real. Now fix any point and define for the indefinite integral
for any path in connecting and . If they are both cusps, we can take a geodesic arc in connecting them. Then
where is a parabolic 1-cocyle of with values in the representation . This means
-
1.
.
-
2.
For each parabolic element there is a vector such that . The vector may depend on the parabolic element .
We define as the quotient of all parabolic 1-cocyles (property 1 and 2) modulo all coboundaries, that is, there is a such that for all . Similarly, taking real parts defining
the corresponding cocycle takes values in and depends only on and not on the auxiliary choices of and . Shimura proved that defines an isomorphism of real vector spaces. . This implies that . When is an arithmetically defined group, there are Hecke operators defined and the Eichler-Shimura isomorphism respects this action. Moreover in that case there is a lattice stabilized by and we have parabolic cohomology groups . One can define a complex structure and a polarization such that the torus has the structure of an abelian variety . Finally, if is a Hecke eigenform the periods of are related to the values of the -function at integer points in the critical strip for this Dirichlet series. See Manin’s papers, [69], [70] for the connection to modular symbols, -adic Hecke series and more. See Greenberg and Voight [40] for algorithms for computing Hecke eigenvalues in parabolic cohomology. See Stiller’s monograph [88] for more information on the connection to differential equations and special values of -functions. See the papers of Zagier [93] and Kontsevich/Zagier [56] for more information on differential equations and periods.
Here are examples from [93, 63]:
where is a Hauptmodul for , and is a normalized cuspidal newform expressed in LMFDB label.
Deligne [17] reinterpreted this in the following manner. Assume that has no torsion. First, we have an isomorphism
for certain coherent sheaves on the compact Riemann surface . These sheaves have the property that
In fact, over the complement of the cusps, the sheaf is the holomorphic line bundle attached to the cocycle . There are constructible sheaves of -vector spaces on for integers with the following properties:
-
1.
Over the open subset these are local systems of rank . They are thus solution sheaves to a system of regular singular differential equations on . For considered in this paper, these will be hypergeometric local systems when or 2.
-
2.
The sheaves on are extensions of the sheaves on defined above:
-
3.
We have:
which is a Hodge decomposition of type . The left-hand side is parabolic cohomology. Moreover
the image of the compactly supported cohomology. The Hecke operators act on the spaces as geometric correspondences and these isomorphisms are equivariant for the Hecke actions.
When is an arbitrary Fuchsian subgroup of the first kind, proofs of these theorems can be found in [10]. When is torsion-free, these are defined as follows. The group acts on , on the first factor by linear fractional transformations, on the second factor via , where arises from the inclusion and the canonical action of on . Then
| (7) |
When has torsion, one takes a normal subgroup of finite index and defines
This works with certain restrictions, namely if this becomes identically 0 when is odd, so one must restrict to even (this is no limitation anyway since there are no cusp forms of odd weight if ).
6.2. -adic.
Original papers: [26], [81], [83]. It is preferable to replace the group by and work with the adeles. Let be the algebraic group or according as non-cocompact or cocompact arising from an indefinite quaternion division algebra defined over . In both cases, GL which has two connected components consisting of elements with positive and negative determinants, respectively. Moreover, acts transitively on the upper half plane via fractional linear transformations so that we may identify with , where denotes the center of . Thus may be identified with , the disjoint union of upper and lower half plane. The pair satisfies the axioms of Deligne for Shimura varieties, [19]. Let . Write for the ring of adeles over , and the subring of finite adeles. Let be a compact-open subgroup of . Define
This is a finite disjoint union, indexed by , of quotients , for subgroups which are the images of under , where . Shimura’s theory of canonical models gives a curve defined over whose complex points are these. This curve is irreducible, but not absolutely irreducible. The irreducible components of are indexed by the same finite set as above, and the corresponding analytic spaces are the . These components are defined over specific abelian number fields .
We also have the spaces of cusp forms . We can describe this as
but more intrinsically as the set of functions such that
-
1.
For all , and
-
2.
For any , the function is invariant under , smooth on and satisfies
and
where
-
3.
If , then for all ,
The relation between this adelic viewpoint and classical cusp forms is explained in several places, see [47]. The above corresponds to functions which are modular with respect to subgroups as above. The second condition expresses the holomorphy of , and that it has weight . The third condition expresses the vanishing of the zeroth Fourier coefficients at the cusps and is only meaningful for us in the case .
The main theorem is
Theorem 6.1.
Let be an open compact subgroup as above, stable under the canonical involution. Let . For each rational prime there exists an -adic representation
which is unramified outside a finite set of prime numbers. For we have
where and are the standard Hecke operators.
For this is due to Deligne; for this is main result of Ohta, stated only for quaternion algebras over . For even weights and for which are sufficiently small, the -adic representation is on the -vector space
where are -adic analogs of the local systems denoted in the previous section. They have similar properties: they are constructible - sheaves, lisse of rank on the complement of cusps and elliptic points. The situation for odd weights is more complicated in general. In the quaternion case, there are sheaves but their rank is twice the corresponding . Moreover, one must exclude cases where .
The curves and sheaves all have good reduction modulo for . Using the same letters to denote them we get as a corollary that
| (8) |
Since for all , we can use the Grothendieck-Lefschetz trace formula to calculate the left-hand side. This will be explained in section 8.
7. Shimura curves.
7.1. Shimura curves in general
Let be a totally real number field of degree over . Let be an indefinite quaternion algebra over such that where is Hamilton’s quaternions. We let be a maximal order (unique up to conjugation) and the set of elements of reduced norm 1. If is commensurable with then we have a compact Riemann surface arising from , say . Shimura proved that this has a canonical model over a number field . Unless however, this has no simple moduli interpretation. Nonetheless this belongs to the general theory of Shimura varieties (but not of PEL type). When Kuga and Shimura studied these and in particular the zeta functions of the fiber spaces of abelian varieties over these curves. See [57], [58], [84]. This was extended by Ohta in a series of papers, [72], [74], [73]. Langlands also established these results by his methods. See [59], [60]. These methods are now part of the standard toolbox in the arithmetic of Shimura varieties. In our paper we follow Kuga, Shimura and Ohta.
In Takeuchi’s list of arithmetic triangle groups is the famous -tesselation. As Fricke discovered, this is related to a quaternion algebra over the cubic field . He also noted that the corresponding curve is the Klein quartic
For a modern exposition, see Elkies’ article, [29].
7.2. Shimura curves over .
References for this section: [28], [48], [77], [91]. Let be an indefinite quaternion division algebra over of discriminant . It is known that ramifies at an even number primes . We let be a maximal order in (unique up to conjugation). Define
It is known that is a normal subgroup of with quotient an elementary abelian 2-group with generators. It is also known that the elements of are the classes mod of elements of with reduced norm for some possibly empty subset . For any subset we let be the subgroup corresponding to .
Fix an isomorphism . Then the groups become isomorphic to subgroups of . For any subset we have quotient Riemann surfaces . These are compact (no cusps), but there are elliptic points. Shimura’s theory of canonical models shows that these are the sets of complex points of an algebraic curve, denoted by the same symbol if no confusion is possible, defined over a specific number field . These have interpretations as coarse moduli spaces of polarized abelian surfaces, as we briefly recall.
To define a polarization we choose an element with . This defines an anti-involution of by the rule where is the canonical involution: . This is a positive involution in that the quadratic form is positive definite. We describe the moduli space in the case , i.e., for . Namely is the coarse moduli space of triples where is an abelian surface, is a principal polarization and is an embedding such that the Rosati involution defined by on is the involution defined by . Concretely, for each we can define a triple as follows.
Then given by
is a Riemann form which defines a principal polarization on . Also, each element gives a map which maps and sends to itself, thereby inducing an endomorphism of . See [14]. We can enhance this structure by including a rigidification of the points of order for some integer , namely an isomorphism
which carries Weil pairing to the standard symplectic pairing on . The resulting moduli problem for is now representable if , so we obtain fine moduli schemes . Complex-analytically this is where .
For the case of a general , there are coarse moduli spaces that represent equivalence classes of for an equivalence relation arising from stable quadratic twisting rings . We refer to [77] for details. For each prime dividing the discriminant , there are involutions (Atkin-Lehner involutions) of the curve . In fact and viewing the as transformations of the moduli problem,
where is the set of elements whose norm is divisible by . This is a 2-sided ideal with and . Since is isotropic under the Weil pairing, inherits a principal polarization , and being a 2-sided ideal, it also inherits an action of . In other words, parametrizes up to identification of with where for .
Since these curves parametrize families of principally polarized abelian varieties of dimension 2, there are modular embeddings
inducing maps to the moduli space of principally-polarized abelian varieties of dimension 2 (see [42]). Because the Torelli map from the moduli space of genus 2 curves is a birational injection, we get algebraic coordinates on from Igusa-Clebsch invariants, [45]. The images of Shimura curves can then be described in terms of Igusa-Clebsch invariants. See [64] where Borcherds forms are used to calculate these.
7.3. The curves and modular forms
References for this section: [9], [11]. There is a unique quaternion algebra of discriminant defined over . It has generators , , , with , , . We fix the embedding
All maximal orders are conjugate and we fix the representative
The group can be identified with its image under . Then the image of this in is and is a Fuchsian group without parabolic elements. We let , for a smooth projective curve defined over , Shimura’s canonical model. This is a compact Riemann surface of genus 0. In fact, is the projective conic .
The curve sits in a Galois tower of curves, defined by Atkin-Lehner quotients with and . All these curves have genus zero and the corresponding groups have fundamental half-domains in the upper half-plane (or unit disk) which are hyperbolic polygons with either 3 or 4 sides. The angles at the vertices are where are as follows:
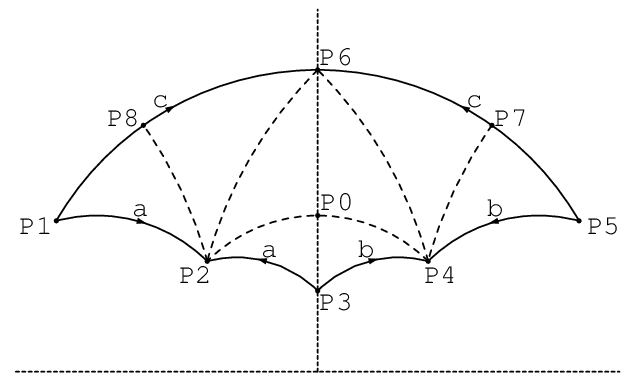
For the triangle groups listed above, we give a corresponding hypergeometric function. By suitable choices of two solutions to the corresponding differential equations (HDE), the ratios give the Schwarz conformal maps from the upper half-plane to hyperbolic triangles:
| curve | angles | HDE |
|---|---|---|
| ( 3, 4, 4) | ||
| (2, 6, 6) | ||
| (2, 4, 6) |
Let . The graded ring of modular forms is
where is the coordinate in , the subscript indicates the weight, and , are algebraically independent. The Hauptmoduln on various Atkin-Lehner quotients are expressible in terms of these modular functions. For instance the curve we have denoted by is canonically isomorphic with with a coordinate denoted .
In the canonical model of the curve as the projective plane conic the Atkin-Lehner involutions are given on by , , . The curves , , , are all isomorphic with , and the projections , , , are given by
where . See [9] for detailed discussion.
7.4. Models of the abelian varieties
If is a congruence subgroup with no torsion, then there is a universal family of abelian varieties . In fact, the groups in our paper all have torsion so that we do not have universal families. Nonetheless we do have families of abelian varieties with quaternion structure that are “sufficiently close” to universal, and these are utilized for explicit calculations. This is analogous to the situation for , where no universal family of elliptic curves exists, but there are families of elliptic curves whose -invariant = , the coordinate on the modular curve :
| (9) |
These curves are not unique, but as Ihara and Scholl [78] have shown, they can be effectively used for calculation of Hecke traces. There are three specific models of 2-dimensional abelian varieties with multiplication by the quaternion algebra relevant to this paper:
-
1.
The Jacobian of the generalized Legendre curve
decomposes according to the characters of . The part belonging to the primitive characters is 2-dimensional. It corresponds to a hypergeometric motive and has QM by . See [15].
-
2.
The subfamily of the Picard family of genus 3 curves
with has the following property: Their Jacobians factor as where is an elliptic curve with CM by and is a 2-dimensional abelian variety with endomorphisms by , [75]
-
3.
The Baba-Granath curves. In [9], Baba and Granath construct a family of genus-2 curves whose Jacobians have QM by . This family is analogous the the family of elliptic curves with -invariant = . It is defined on a quadratic covering of , not on . This is because of Mestre’s obstruction: in general you cannot define a genus 2 curve over the same field as the moduli of its Jacobian. Let , , and define , . Let be the projective nonsingular model of the curve where
We can rewrite this in terms of modular forms , , and in the previous section. Let . Then the curve where
has Jacobian isomorphic to . The Igusa-Clebsch invariant of this is
where
8. Main Theorem.
8.1. Outline.
To prove the main claim, formula (1), by combining the trace formula (2) with the result of Eichler-Shimura theory (8) we must calculate, for the groups we are considering,
The contributions are of two sorts: (1) from cusps and elliptic points and (2) the rest.
-
1.
The sheaf can be related recursively to for . This means that the traces of Frobenius at on it can be expressed as polynomial functions of the trace on . It suffices therefore to relate the Frobenius trace on to hypergeometric character sums for not a cusp or elliptic point. In fact one shows that
where is hypergeometric data attached to .
-
2.
(and ) is a rigid local system. Its local monodromies are easily computed complex-analytically, and this is the same as the local monodromy -adically. The local monodromy of the hypergeometric sheaves are also known. The Kummer twist is there to insure matching. Rigidity then shows that there is an isomorphism
for the curves/sheaves over the algebraic closure .
-
3.
To get an isomorphism over we compare both sides at (one or more) CM point. For this we need the explicit models of the curves and abelian varieties.
-
4.
The Frobenius traces of the hypergeometric sheaves at points not corresponding to cusps or elliptic points are given by hypergeometric character sums. For cusps or elliptic points, this is essentially what is done in determining the fiber at places of bad reduction for a family of abelian varieties. For elliptic curves, this is Tate’s algorithm; for abelian varieties of dimension 2 coming from genus 2 curves, this is Qing Liu’s algorithm [65]. Actually, our situation is greatly simplified and we follow the method of Scholl in [78].
8.2. Examples
For the triangle groups under consideration, we associate hypergeometric data defined over for which Beukers-Cohen-Mellit [12] introduced hypergeometric character sums for . For each integer , let be a degree- polynomial which expresses the symmetric polynomial in of degree as a polynomial in and , i.e.,
| (10) |
Theorem 8.1 ([43]).
For , the table below describes the hypergeometric datum and the choice of a generator of the field of -rational functions on by its values at each elliptic point of given order and cusp:
|
|
Given an even integer and a fixed prime , the terms on the right-hand side of (8.1) for almost all primes where has good reduction are as follows.
For not corresponding to an elliptic point or a cusp
| (11) |
where and
| (12) |
The contribution of corresponding to a cusp is . There are also explicit formulas for the contributions of the elliptic points.
Here is an example illustrating our main result. For the lowest with nontrivial is , in which case is -dimensional, where generates . By Jacquet-Langlands correspondence [47], corresponds to the normalized weight- level cuspidal newform in the LMFDB label. For primes , denote by the eigenvalue of on , which is equal to the th Fourier coefficient of . The theorem above gives
The term on the right side comes from the contribution at the elliptic point of order on ; it also equals , in terms of the th Fourier coefficient of the weight-5 CM modular form .
8.3. Future directions
Here are two:
-
1.
Ohta’s results apply to Shimura curves of quaternion algebras over any totally real number field . The triangle group, which appears in Takeuchi’s list, corresponds to a quaternion algebra over . The new part of the Jacobian of the curve
is -dimensional and has endomorphism algebra the quaternion algebra over with discriminant , the unique prime over . This is a model of the family of abelian varieties over a covering of the Shimura curve for . See [15]. The Jacquet-Langlands correspondence in this case will land in Hilbert modular forms for .
-
2.
The quaternion algebra over of discriminant 10 is also discussed in the paper of Baba-Granath. But this time, the fundamental domains are not related to triangle groups. In fact, the corresponding differential equation now has 4 regular singular points, and in particular is no longer rigid. There is an accessory parameter which was determined by Elkies in [28] using Schwarzian equations. The number theory here will be governed by Heun functions over finite fields, a theory that needs to be developed. See the entry on Heun Functions in [23].
References
- [1] Scott Ahlgren. Gaussian hypergeometric series and combinatorial congruences. In Symbolic computation, number theory, special functions, physics and combinatorics (Gainesville, FL, 1999), volume 4 of Dev. Math., pages 1–12. Kluwer Acad. Publ., Dordrecht, 2001.
- [2] Scott Ahlgren and Ken Ono. A Gaussian hypergeometric series evaluation and Apéry number congruences. J. Reine Angew. Math., 518:187–212, 2000.
- [3] George E. Andrews, Richard Askey, and Ranjan Roy. Special functions, volume 71 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 1999.
- [4] Donu Arapura. An abelian category of motivic sheaves. Adv. Math., 233:135–195, 2013.
- [5] Donu Arapura. Motivic sheaves revisited. J. Pure Appl. Algebra, 227(8):Paper No. 107125, 22, 2023.
- [6] A. O. L. Atkin, Wen-Ching Winnie Li, Tong Liu, and Ling Long. Galois representations with quaternion multiplication associated to noncongruence modular forms. Trans. Amer. Math. Soc., 365(12):6217–6242, 2013.
- [7] Joseph Ayoub. Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. I. Astérisque, (314):x+466, 2007.
- [8] Joseph Ayoub. Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. II. Astérisque, (315):vi+364, 2007.
- [9] Srinath Baba and Håkan Granath. Genus 2 curves with quaternionic multiplication. Canad. J. Math., 60(4):734–757, 2008.
- [10] Pilar Báyer and Jürgen Neukirch. On automorphic forms and Hodge theory. Math. Ann., 257(2):137–155, 1981.
- [11] Pilar Báyer and Artur Travesa. Uniformizing functions for certain Shimura curves, in the case . Acta Arith., 126(4):315–339, 2007.
- [12] Frits Beukers, Henri Cohen, and Anton Mellit. Finite hypergeometric functions. Pure Appl. Math. Q., 11(4):559–589, 2015.
- [13] Frits Beukers and Gerrit Heckman. Monodromy for the hypergeometric function . Invent. Math., 95(2):325–354, 1989.
- [14] Christina Birkenhake and Herbert Lange. Complex Abelian Varieties, volume 302 of Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, second edition, 2004.
- [15] Alyson Deines, Jenny G. Fuselier, Ling Long, Holly Swisher, and Fang-Ting Tu. Generalized Legendre curves and quaternionic multiplication. J. Number Theory, 161:175–203, 2016.
- [16] Pierre Deligne. Équations différentielles à points singuliers réguliers. Lecture Notes in Mathematics, Vol. 163. Springer-Verlag, Berlin-New York, 1970.
- [17] Pierre Deligne. Formes modulaires et représentations -adiques. In Séminaire Bourbaki. Vol. 1968/69: Exposés 347–363, volume 175 of Lecture Notes in Math., pages Exp. No. 355, 139–172. Springer, Berlin, 1971.
- [18] Pierre Deligne. La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math., (43):273–307, 1974.
- [19] Pierre Deligne. Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques. In Automorphic forms, representations and -functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proc. Sympos. Pure Math., XXXIII, pages 247–289. 1979.
- [20] Pierre Deligne. La conjecture de Weil. II. Inst. Hautes Études Sci. Publ. Math., (52):137–252, 1980.
- [21] Pierre Deligne and George D. Mostow. Monodromy of hypergeometric functions and nonlattice integral monodromy. Inst. Hautes Études Sci. Publ. Math., (63):5–89, 1986.
- [22] Pierre Deligne and Michael Rapoport. Les schémas de modules de courbes elliptiques. In Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Math., Vol. 349, pages 143–316. Springer, Berlin, 1973.
- [23] NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.1.0 of 2020-12-15. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain, eds.
- [24] Bernard Dwork and François Loeser. Hypergeometric series. Japan. J. Math. (N.S.), 19(1):81–129, 1993.
- [25] Bernard Dwork and François Loeser. Hypergeometric series and functions as periods of exponential modules. In Barsotti Symposium in Algebraic Geometry (Abano Terme, 1991), volume 15 of Perspect. Math., pages 153–174. Academic Press, San Diego, CA, 1994.
- [26] Martin Eichler. Quaternäre quadratische Formen und die Riemannsche Vermutung für die Kongruenzzetafunktion. Arch. Math., 5:355–366, 1954.
- [27] Martin Eichler. Eine Verallgemeinerung der Abelschen Integrale. Math. Z., 67:267–298, 1957.
- [28] Noam D. Elkies. Shimura curve computations. In Algorithmic number theory (Portland, OR, 1998), volume 1423 of Lecture Notes in Comput. Sci., pages 1–47. Springer, Berlin, 1998.
- [29] Noam D. Elkies. The Klein quartic in number theory. In The eightfold way, volume 35 of Math. Sci. Res. Inst. Publ., pages 51–101. Cambridge Univ. Press, Cambridge, 1999.
- [30] Ron Evans and John Greene. Clausen’s theorem and hypergeometric functions over finite fields. Finite Fields Appl., 15(1):97–109, 2009.
- [31] Sharon Frechette, Ken Ono, and Matthew Papanikolas. Gaussian hypergeometric functions and traces of Hecke operators. Int. Math. Res. Not., (60):3233–3262, 2004.
- [32] Sharon Frechette, Holly Swisher, and Fang-Ting Tu. A cubic transformation formula for Appell–Lauricella hypergeometric functions over finite fields. Res. Number Theory, 4(2):4:27, 2018.
- [33] Javier Fresán, Claude Sabbah, and Jeng-Daw Yu. Hodge theory of Kloosterman connections. Duke Math. J., 171(8):1649–1747, 2022.
- [34] Lei Fu. -adic GKZ hypergeometric sheaves and exponential sums. Adv. Math., 298:51–88, 2016.
- [35] Lei Fu, Wan Daqing, and Hao Zhang. The -adic Gelfand-Kapranov-Zelevinsky complex. arXiv:1804.05297, to appear, Mathematische Annalen.
- [36] Jenny Fuselier, Ling Long, Ravi Ramakrishna, Holly Swisher, and Fang-Ting Tu. Hypergeometric functions over finite fields. Mem. Amer. Math. Soc., 280(1382), 2022.
- [37] Jenny G. Fuselier. Hypergeometric functions over and relations to elliptic curves and modular forms. Proc. Amer. Math. Soc., 138(1):109–123, 2010.
- [38] Ofer Gabber and François Loeser. Faisceaux pervers -adiques sur un tore. Duke Math. J., 83(3):501–606, 1996.
- [39] Izrail M. Gelfand, Mikhail M. Kapranov, and Andrey V. Zelevinsky. Generalized Euler integrals and -hypergeometric functions. Adv. Math., 84(2):255–271, 1990.
- [40] Matthew Greenberg and John Voight. Computing systems of Hecke eigenvalues associated to Hilbert modular forms. Math. Comp., 80(274):1071–1092, 2011.
- [41] John Greene. Hypergeometric functions over finite fields. Trans. Amer. Math. Soc., 301(1):77–101, 1987.
- [42] Ki-ichiro Hashimoto. Explicit form of quaternion modular embeddings. Osaka J. Math., 32(3):533–546, 1995.
- [43] Jerome W. Hoffman, Wen-Ching Winnie Li, Ling Long, and Fang-Ting Tu. Traces of Hecke Operators via Hypergeometric Character Sums, 2024; arXiv: 2408.02918.
- [44] Rolf-Peter Holzapfel. Geometry and arithmetic around Euler partial differential equations, volume 11 of Mathematics and its Applications (East European Series). D. Reidel Publishing Co., Dordrecht, 1986.
- [45] Jun-ichi Igusa. Arithmetic variety of moduli for genus two. Ann. of Math. (2), 72:612–649, 1960.
- [46] Yasutaka Ihara. Hecke polynomials as congruence functions in elliptic modular case. Ann. of Math. (2), 85:267–295, 1967.
- [47] Hervé Jacquet and Robert P. Langlands. Automorphic forms on . Lecture Notes in Mathematics, Vol. 114. Springer-Verlag, Berlin-New York, 1970.
- [48] Bruce W. Jordan. On the Diophantine arithmetic of Shimura curves, thesis, Harvard University, 1981.
- [49] Nicholas M. Katz. The regularity theorem in algebraic geometry. In Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, pages 437–443. 1971.
- [50] Nicholas M. Katz. Algebraic solutions of differential equations (-curvature and the Hodge filtration). Invent. Math., 18:1–118, 1972.
- [51] Nicholas M. Katz. An overview of Deligne’s work on Hilbert’s twenty-first problem. In Mathematical developments arising from Hilbert problems (Proc. Sympos. Pure Math., Northern Illinois Univ., De Kalb, Ill., 1974), volume Vol. XXVIII of Proc. Sympos. Pure Math., pages 537–557. Amer. Math. Soc., Providence, RI, 1976.
- [52] Nicholas M. Katz. Exponential Sums and Differential Equations, volume 124 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 1990.
- [53] Nicholas M. Katz. Rigid local systems, volume 139 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 1996.
- [54] Nicholas M. Katz. Another look at the Dwork family. In Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. II, volume 270 of Progr. Math., pages 89–126. Birkhäuser Boston, Boston, MA, 2009.
- [55] Michael Klug, Michael Musty, Sam Schiavone, and John Voight. Numerical calculation of three-point branched covers of the projective line. LMS J. Comput. Math., 17(1):379–430, 2014.
- [56] Maxim Kontsevich and Don Zagier. Periods. In Mathematics unlimited—2001 and beyond, pages 771–808. Springer, Berlin, 2001.
- [57] Michio Kuga. Kuga varieties, volume 9 of CTM. Classical Topics in Mathematics. Higher Education Press, Beijing, 2018. Fiber varieties over a symmetric space whose fibers are Abelian varieties, Appendices including a letter by André Weil and an essay by I. Satake.
- [58] Michio Kuga and Goro Shimura. On the zeta function of a fibre variety whose fibres are abelian varieties. Ann. of Math. (2), 82:478–539, 1965.
- [59] Robert P. Langlands. Modular forms and -adic representations. In Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Math., Vol. 349, pages 361–500. Springer, Berlin, 1973.
- [60] Robert P. Langlands. On the zeta functions of some simple Shimura varieties. Canadian J. Math., 31(6):1121–1216, 1979.
- [61] Catherine Lennon. Gaussian hypergeometric evaluations of traces of Frobenius for elliptic curves. Proc. Amer. Math. Soc., 139(6):1931–1938, 2011.
- [62] Catherine Lennon. Trace formulas for Hecke operators, Gaussian hypergeometric functions, and the modularity of a threefold. J. Number Theory, 131(12):2320–2351, 2011.
- [63] Wen-Ching W. Li, Ling Long, and Fang-Ting Tu. A Whipple formula revisited. Matematica, 1(2):480–530, 2022.
- [64] Yi-Hsuan Lin and Yifan Yang. Quaternionic loci in Siegel’s modular threefold. Math. Z., 295(1-2):775–819, 2020.
- [65] Qing Liu. Modèles minimaux des courbes de genre deux. J. Reine Angew. Math., 453:137–164, 1994.
- [66] François Loeser and Claude Sabbah. Caractérisation des -modules hypergéométriques irréductibles sur le tore. C. R. Acad. Sci. Paris Sér. I Math., 312(10):735–738, 1991.
- [67] François Loeser and Claude Sabbah. Équations aux différences finies et déterminants d’intégrales de fonctions multiformes. Comment. Math. Helv., 66(3):458–503, 1991.
- [68] François Loeser and Claude Sabbah. Caractérisation des -modules hypergéométriques irréductibles sur le tore. II. C. R. Acad. Sci. Paris Sér. I Math., 315(12):1263–1264, 1992.
- [69] Ju. I. Manin. Parabolic points and zeta functions of modular curves. Izv. Akad. Nauk SSSR Ser. Mat., pages 19–66, 1972.
- [70] Ju. I. Manin. Periods of cusp forms, and -adic Hecke series. Mat. Sb. (N.S.), pages 378–401, 503, 1973.
- [71] James S. Milne. Introduction to Shimura varieties. In Harmonic analysis, the trace formula, and Shimura varieties, volume 4 of Clay Math. Proc., pages 265–378. Amer. Math. Soc., Providence, RI, 2005.
- [72] Masami Ohta. On -adic representations attached to automorphic forms. Japan. J. Math. (N.S.), 8(1):1–47, 1982.
- [73] Masami Ohta. On the zeta function of an abelian scheme over the Shimura curve. Japan. J. Math. (N.S.), 9(1):1–25, 1983.
- [74] Masami Ohta. On the zeta function of an abelian scheme over the Shimura curve. II. In Galois groups and their representations (Nagoya, 1981), volume 2 of Adv. Stud. Pure Math., pages 37–54. North-Holland, Amsterdam, 1983.
- [75] Maria Petkova and Hironori Shiga. A new interpretation of the Shimura curve with discriminant 6 in terms of Picard modular forms. Arch. Math. (Basel), 96(4):335–348, 2011.
- [76] David P. Roberts and Fernando Rodriguez Villegas. Hypergeometric motives. Notices Amer. Math. Soc., 69(6):914–929, 2022.
- [77] Victor Rotger. Modular Shimura varieties and forgetful maps. Trans. Amer. Math. Soc., 356(4):1535–1550, 2004.
- [78] Anthony J. Scholl. The -adic representations attached to a certain noncongruence subgroup. J. Reine Angew. Math., 392:1–15, 1988.
- [79] René Schoof. Counting points on elliptic curves over finite fields. volume 7, pages 219–254. 1995. Les Dix-huitièmes Journées Arithmétiques (Bordeaux, 1993).
- [80] Hermann A. Schwarz. Ueber diejenigen Fälle, in welchen die Gaussische hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt. J. Reine Angew. Math., 75:292–335, 1873.
- [81] Goro Shimura. Correspondances modulaires et les fonctions de courbes algébriques. J. Math. Soc. Japan, 10:1–28, 1958.
- [82] Goro Shimura. Sur les intégrales attachées aux formes automorphes. J. Math. Soc. Japan, 11:291–311, 1959.
- [83] Goro Shimura. On the zeta-functions of the algebraic curves uniformized by certain automorphic functions. J. Math. Soc. Japan, 13:275–331, 1961.
- [84] Goro Shimura. An -adic method in the theory of automorphic forms. Collected Papers, II:237–272, 1968.
- [85] Goro Shimura. Introduction to the arithmetic theory of automorphic functions, volume 11 of Publications of the Mathematical Society of Japan. Princeton University Press, Princeton, NJ, 1994. Reprint of the 1971 original, Kanô Memorial Lectures, 1.
- [86] Tetsuji Shioda. On rational points of the generic elliptic curve with level structure over the field of modular functions of level . J. Math. Soc. Japan, 25:144–157, 1973.
- [87] Lucy Joan Slater. Generalized hypergeometric functions. Cambridge University Press, Cambridge, 1966.
- [88] Peter Stiller. Special values of Dirichlet series, monodromy, and the periods of automorphic forms. Mem. Amer. Math. Soc., 49(299):iv+116, 1984.
- [89] Kisao Takeuchi. Arithmetic triangle groups. J. Math. Soc. Japan, 29(1):91–106, 1977.
- [90] Kisao Takeuchi. Commensurability classes of arithmetic triangle groups. J. Fac. Sci. Univ. Tokyo Sect. IA Math., 24(1):201–212, 1977.
- [91] John Voight. Quaternion algebras, volume 288 of Graduate Texts in Mathematics. Springer, Cham, [2021] ©2021.
- [92] Yifan Yang. Schwarzian differential equations and Hecke eigenforms on Shimura curves. Compos. Math., 149(1):1–31, 2013.
- [93] Don Zagier. The arithmetic and topology of differential equations. In European Congress of Mathematics, pages 717–776. Eur. Math. Soc., Zürich, 2018.