Pure momentum-shift bulk photovoltaic effect in ferroelectric flat-band Mott insulators
Abstract
The shift current photovoltaic effect is conventionally understood as the real-space displacement of a wave packet induced by photoexcitation. However, this interpretation becomes insufficient in flat-band systems, where quasiparticles are too massive to accelerate in real space under the optical electric field. Here, we developed a physically consistent method to decompose the shift current into real-space and momentum-space components. A surprising pure momentum-space shift current is found theoretically in flat-band Mott insulator Nb3X8 (X = Cl, Br, I) monolayers. This work underscores that significant shift current responses can emerge even in systems with minimal interband polarization differences, highlighting the potential for exploring novel bulk photovoltaic effects in flat-band Mott insulators.
Introduction.—Under monochromatic light irradiation, a direct current (DC) photocurrent, known as the bulk photovoltaic effect, arises in systems with broken spatial inversion symmetry. Initially, the bulk photovoltaic effect garnered attention for its potential to achieve high energy conversion efficiency beyond the Shockley-Queisser limit, which restricts the traditional photovoltaic effect [1, 2]. More recently, this effect has become a focus of research due to its connection to fundamental properties of quantum materials, including symmetry, order parameters (such as ferroelectricity and ferromagnetism), topology, and many-body interactions [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. This connection holds promise for applications in material characterization and the development of devices based on novel quantum transport and optical phenomena.
In intrinsic semiconductors, when photon energy exceeds the bandgap, shift current becomes one of the primary mechanisms driving the bulk photovoltaic effect [16, 17]. Shift current refers to the photocurrent generated by the displacement between the centers of electron wavefunctions in the conduction and valence bands during photoexcitation, traditionally interpreted as a real-space phenomenon. Based on recent studies employing an anomalous acceleration framework, it has been shown that the shift current arises from contributions in both real and momentum spaces [18, 17]. Within this framework, for dispersive-band systems, the extended nature of the wavefunctions combined with their small effective masses leads to a significant real-space displacement upon photoexcitation. In contrast, in flat-band systems, where wavefunctions are highly localized in real space, the framework indicates that real-space displacement is minimal, making momentum-space displacement the dominant contributor.
However, the previous treatment of the real-space shift as the difference in the gauge-dependent Berry connections between the conduction and valence bands results in an ambiguous interpretation of both real-space and momentum-space shifts, and limits discussions to model Hamiltonians [17]. A prototypical topological flat-band system, e.g. twisted bilayer graphene [19, 20, 21, 22, 23], has been considered an ideal candidate for realizing such photovoltaic effect [17]. Nonetheless, its experimental realization is hindered by graphene’s zero bandgap and precise control required for twisted angles.
To address these challenges, this work aims to develop a physically consistent theory to decompose the real-space and momentum-space contributions to the shift current, enabling first-principles studies of this phenomenon in flat-band systems. Moreover, we focus on Nb3X8 monolayers, which provide an ideal platform for investigating the impact of correlations and topological flat bands on nonlinear optical responses [24, 25, 26, 27, 28]. In these systems, the topological flat bands arise from the destructive interference of wavefunctions in a breathing Kagome lattice. Recent studies have further identified Nb3X8 monolayers as long-sought single-band Mott insulators, simplifying the low-energy physics to intrinsically correlated systems[29, 26, 28].
In this work, we develop a comprehensive theory about pure momentum-shift current in flat-band Mott insulator to decompose the shift current into real-space and momentum-space contributions, establishing a physically consistent approach to understanding the bulk photovoltaic effect in topological flat-band systems. We begin by introducing the microscopic expression for shift current, which is proportional to the sum of the products of the shift vector and the absorption strength across all -points. We propose that the real-space shift is described by the difference between the Wannier centers of the conduction and valence bands. By subtracting the real-space shift from the shift vector, we obtain the momentum-space shift. This decomposition allows us to isolate the real-space and momentum-space contributions to the shift current during photoexcitation. With this framework, we perform first-principles calculations on monolayers and analyze the characteristics of their shift current. Our results reveal that their maximum peaks in shift current spectra are entirely driven by the momentum-space shift, with minimal real-space contribution. Additionally, we examine the relationship between the shift current, collective shift vector and the imaginary part of the dielectric function, finding that their magnitudes are generally correlated.
Comprehensive theory of shift current.—For a system illuminated by linearly polarized light , the shift current can be formulated as
| (1) |
where is the current density arising from the shift mechanism, and is the shift current photoconductivity, with the frequency dependence omitted here for simplicity. According to nonlinear optical theory, this photoconductivity can be expressed as [30, 16, 11]:
| (2) |
where is the electron charge, , is the well-known shift vector describing the extent of wavepacket displacement, and characterizes the absorption strength during photoexcitation. Specifically, , where is the intraband Berry connection, and is the phase of the interband Berry connection . Additionally, , where denotes the joint density of states, and represents the transition probability. Here, is the Fermi-Dirac distribution with , and is the Dirac delta function enforcing energy conservation during photoexcitation.
Building on this understanding, we aim to decompose the shift current into real-space and momentum-space components in a physically meaningful way. First, we recognize that the wavepacket shift in real space during photoexcitation is described by the change in the Wannier center, , where . Next, we obtain the wavepacket’s shift in momentum space by subtracting the shift vector from the real-space shift :
| (3) |
This decomposition remains invariant provided a specific unit cell is chosen to resolve the ambiguity in the Wannier center difference, . As illustrated in Fig. 1(a), the shift current photoconductivity can be decomposed into two components, , where and represent contributions from the real-space shift () and momentum-space shift (), respectively. The decomposition of shift current in dispersive-band and flat-band systems is schematically illustrated in Fig. 1(b) 111We observe that a divergent shift vector and zero absorption result in a finite shift current in the SnTe monolayer [npj Comput. Mater. 10, 23 (2024)]. Therefore, while optical transitions induce a large real-space shift due to the dispersive nature of the bands, the momentum-space shift current dominates. However, in most cases, the bulk photovoltaic effect is correlated with a finite optical absorption process. We will restrict our discussion to this scenario..
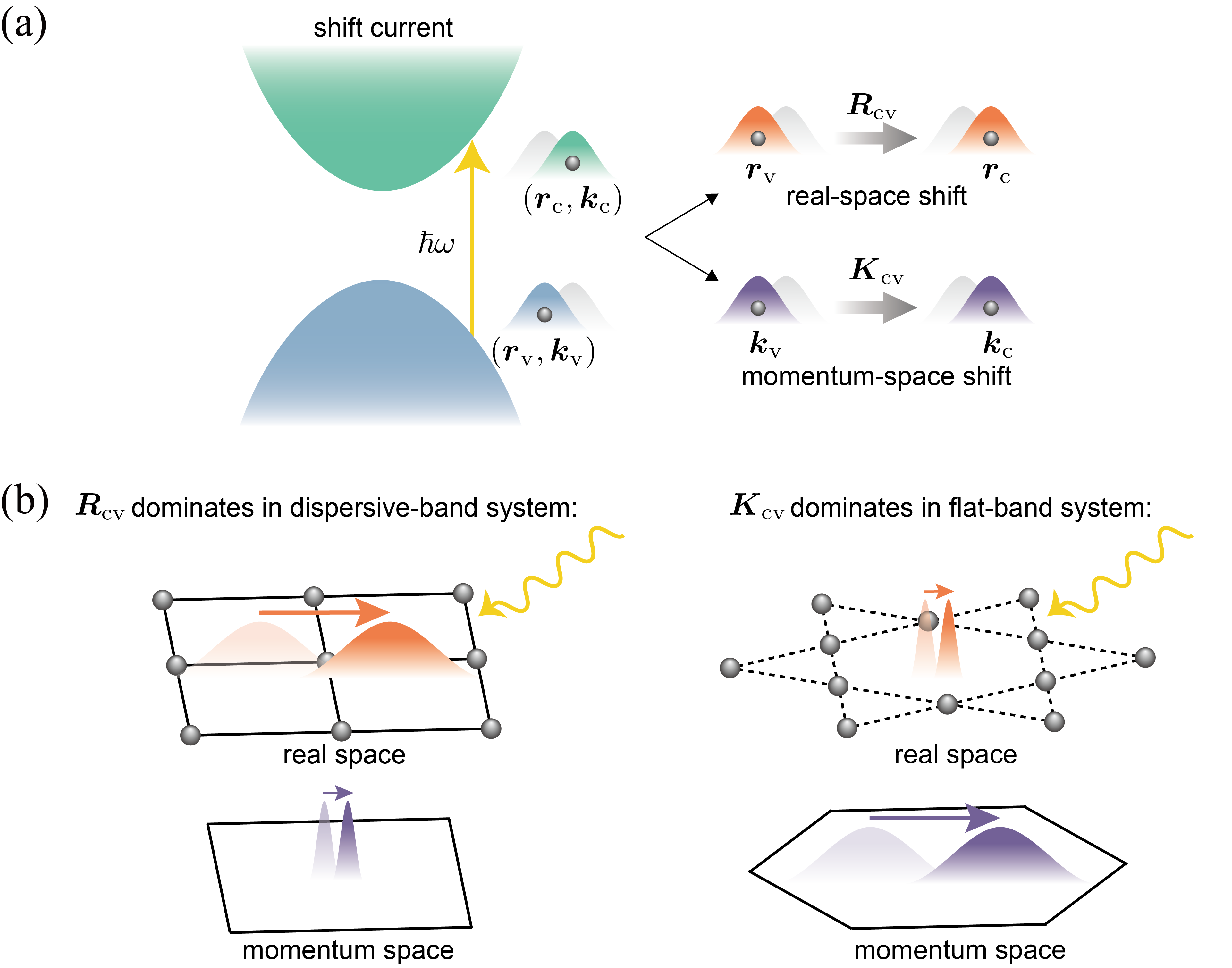
According to Eq. (3), we can obtain the decomposition of the shift current. However, the interpretation of the momentum-space shift remains unclear. To address this issue, we consider the integration of photoconductivity over frequency, a quantity more relevant to real-world applications [32], and directly related to the integral of the shift vector, which can be expressed as follows:
| (4) |
where transition probability is approximated by an averaged value , is the interband polarization difference with according to the modern theory of polarization [33], is the winding of the phase [34]. From our previous discussion, it is evident that and correspond to the real-space and momentum-space shifts, respectively. If optical zeros ( at certain points in the Brillouin zone) are absent, the total response will arise solely from the real-space shift current, as the momentum-space shift current can be eliminated by explicitly choosing the optical gauge where . However, optical zeros are commonly present in real materials, leading to a discontinuity in and causing to affect the total response. As a result, the momentum-space shift current can be attributed to these singular optical zeros in the Brillouin zone, which can significantly contribute to the shift current.
Before concluding this section, we want to discuss the feasibility of distinguishing between the real-space shift current and the momentum-space shift current. We note that for a system describable within the two-band approximation, simplifies to
| (5) |
where , with and denoting the conduction and valence bands, respectively. Here, is the imaginary part of the dielectric function [16, 35]. The change in the Wannier center, , is factored out of the integral since it is independent of , and the summation over band indices is omitted in the two-band case. In Eq. (5), has been expressed as the product of two measurable quantities. This implies that our discussion of the real-space and momentum-space shift currents could potentially be verified.
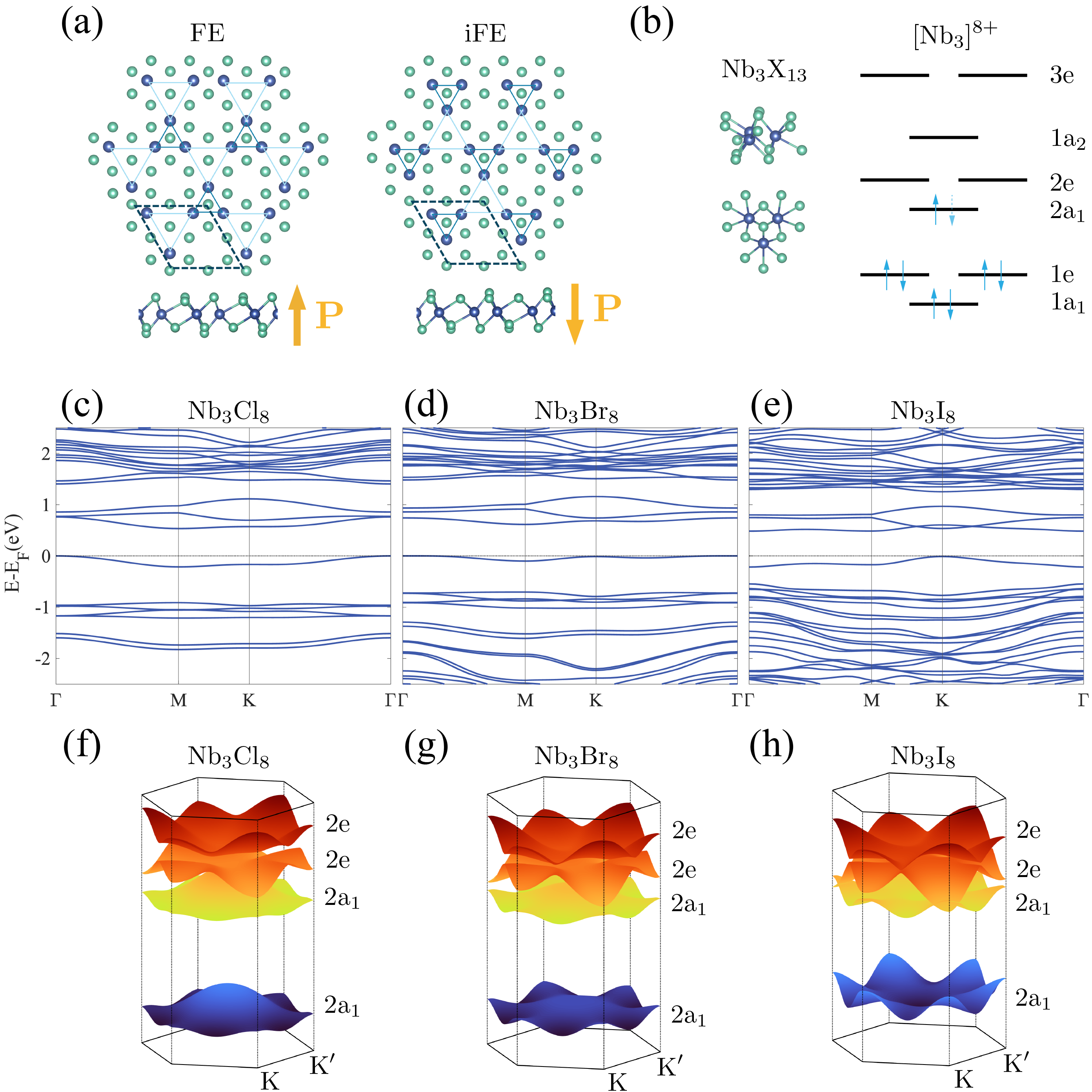
Shift current in monolayers.—To validate our shift current theory, we performed first-principle calculations of shift current and its decomposition in the topological flat-band system monolayers. monolayers belong to space group P3m1. The ferroelectricity in these systems arise from inversion symmetry breaking induced by Nb trimerization. Two ferroelectric configurations with opposite out-of-plane polarizations are depicted in Fig. 2(a). As schematically illustrated in Fig. 2(b), the electrons in monolayers resemble the molecular orbitals of Nb-Nb metal bonds within a cluster, as the monolayers can be considered to form through the interconnection of clusters [36, 37, 38, 39, 40, 26]. For concreteness, we focus on the FE configurations and assume that the magnetic moment of the Nb trimer is oriented along the positive direction. This assumption is reasonable because the shift current is even under time-reversal symmetry and is thus insensitive to the direction of the magnetic moment. The details of our first-principles calculations for monolayers are provided in Supplementary. As shown in Fig. 2(c-e), the low-energy physics of these monolayers is dominated by four isolated bands directly associated with the molecular orbitals. The 2D plots of these four bands are presented in Fig. 2(f-h).
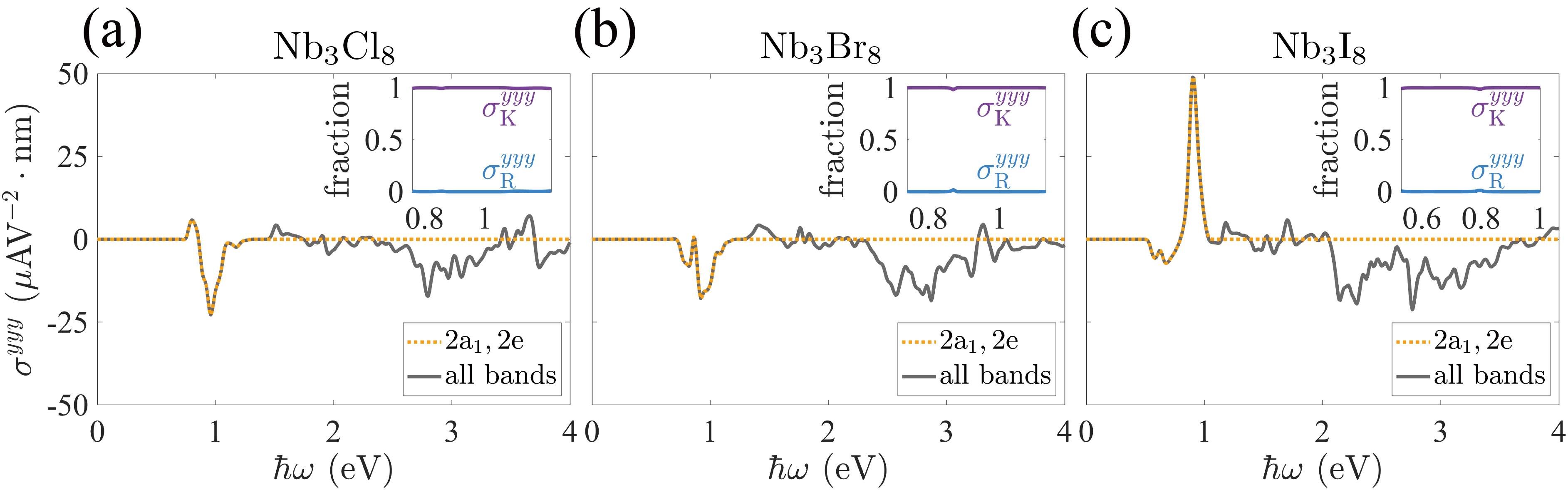
Shift current spectra of Nb3X8 monolayers are calculated and plotted as the gray lines in Fig. 3. Here, we only present the results of component. Because the shift current photoconductivity of Nb3X8 monolayers has only one independent non-zero component according to symmetry analysis, specifically . Based on the discussion in the previous section, we further calculated the contributions of the real-space shift and momentum-space shift to the total response and plotted their fractions in the inset of Fig. 3. We were surprised to find that the maximum peaks of shift current spectra in Nb3X8 monolayers originate entirely from the momentum-space shift. To illustrate its origin, we separately calculated the contributions of excitations from the occupied 2a1 molecular orbital to the unoccupied 2a1 and 2e molecular orbitals for the shift current, and plotted these contributions as orange lines in Fig. 3. We observed that this contribution completely overlaps with the total response at these peaks, indicating that these molecular orbitals are responsible for both the peaks and the pure momentum-space shift. Further symmetry analysis revealed it is the C3z symmetry that enforces these molecular orbitals to be located at the center of the Nb trimer, which results in a zero real-space shift during photoexcitation. Therefore, this pure momentum-space shift current is robust to deformation and disorder, as long as the C3z symmetry is preserved. Despite we did not present the decomposition of the shift current at higher energies, it can be anticipated that as more bands participate in photoexcitation, the real-space shift current will become non-zero and may even dominate.
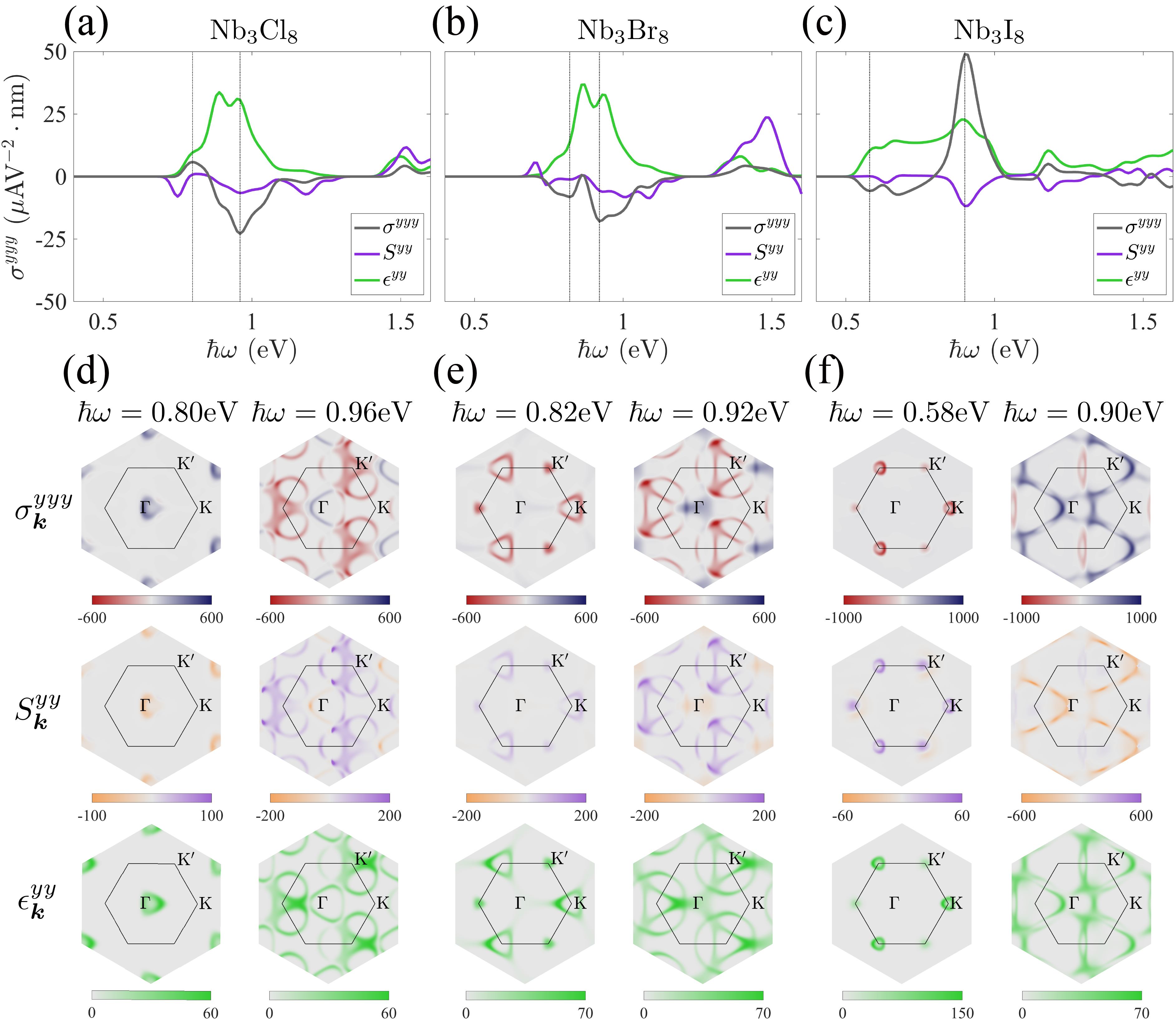
To clarify the influence of the shift vector and the imaginary part of the dielectric function on the magnitude of the shift current photoconductivity, we further studied the relationship between the spectra of , and and plotted them in Fig. 4(a-c), where the collective shift vector , defined as
| (6) |
characterizes the displacement strength of wavepacket centers in real space and momentum space during photoexcitation. Since and have different units, they are scaled by a constant factor for easier comparison. While the maximum peak of in the monolayer is slightly lower than that in and monolayers, the notably larger in results in the highest among the monolayers. This indicates that the magnitude of is roughly proportional to the product of and . In Fig. 4(d-f), we show the -resolved , and corresponding to the first and maximum peaks in the shift current spectra of monolayers. We can see that the first peaks arise from photoexcitations near the band edges, while the maximum peaks involve contributions from photoexcitations distributed across the entire Brillouin zone. Therefore, the maximum peaks in the shift current spectra can be attributed to the enhancement of large joint density of states in flat-band systems.
Discussion and conclusion.—In summary, we propose a physically consistent theory that decomposes the shift current into two contributions: real-space and momentum-space shifts. Using this theory, we investigated the shift current in the flat-band systems monolayers. We found that the maximum peak of the shift current spectra is driven by photoexcitation between the molecular orbitals of the Nb trimers, originating entirely from the momentum-space shift contribution. This pure momentum-space shift current remains robust as long as the C3z symmetry is preserved. Additionally, we discussed the connections between the shift current photoconductivity, collective shift vector, and imaginary part of the dielectric function. As detailed in Supplementary, we also studied the injection current spectra of monolayers. We found that the magnitude of the injection current is negligible compared to that of the shift current. This characteristic can be attributed to the weakly broken time-reversal symmetry and the flatness of the bands in monolayers. Our research provides a crucial distinction between the bulk photovoltaic effects observed in topological flat-band systems and conventional systems, expanding the search for materials that exhibit a large bulk photovoltaic effect.
Acknowledgments.—H.W. acknowledges the support from the NSFC under Grants Nos. 12304049 and 12474240, as well as the support provided by the Zhejiang Provincial Natural Science Foundation of China under grant number LDT23F04014F01. K. C. acknowledges the support from the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants Nos. XDB28000000 and XDB0460000), the NSFC under Grants Nos. 92265203 and 12488101, and the Innovation Program for Quantum Science and Technology under Grant No. 2024ZD0300104.
References
- Spanier et al. [2016] J. E. Spanier, V. M. Fridkin, A. M. Rappe, A. R. Akbashev, A. Polemi, Y. Qi, Z. Gu, S. M. Young, C. J. Hawley, D. Imbrenda, G. Xiao, A. L. Bennett-Jackson, and C. L. Johnson, Power conversion efficiency exceeding the Shockley–Queisser limit in a ferroelectric insulator, Nat. Photonics 10, 611 (2016).
- Dai and Rappe [2023] Z. Dai and A. M. Rappe, Recent progress in the theory of bulk photovoltaic effect, Chem. Phys. Rev. 4, 011303 (2023).
- Hosur [2011] P. Hosur, Circular photogalvanic effect on topological insulator surfaces: Berry-curvature-dependent response, Phys. Rev. B 83, 035309 (2011).
- Young and Rappe [2012] S. M. Young and A. M. Rappe, First principles calculation of the shift current photovoltaic effect in ferroelectrics, Phys. Rev. Lett. 109, 116601 (2012).
- Morimoto and Nagaosa [2016] T. Morimoto and N. Nagaosa, Topological nature of nonlinear optical effects in solids, Sci. Adv. 2, e1501524 (2016).
- Nakamura et al. [2017] M. Nakamura, S. Horiuchi, F. Kagawa, N. Ogawa, T. Kurumaji, Y. Tokura, and M. Kawasaki, Shift current photovoltaic effect in a ferroelectric charge-transfer complex, Nat. Commun. 8, 281 (2017).
- Chan et al. [2017] C.-K. Chan, N. H. Lindner, G. Refael, and P. A. Lee, Photocurrents in Weyl semimetals, Phys. Rev. B 95, 041104 (2017).
- Ma et al. [2019] J. Ma, Q. Gu, Y. Liu, J. Lai, P. Yu, X. Zhuo, Z. Liu, J.-H. Chen, J. Feng, and D. Sun, Nonlinear photoresponse of type-II Weyl semimetals, Nat. Mater. 18, 476 (2019).
- Zhang et al. [2019] Y. Zhang, T. Holder, H. Ishizuka, F. De Juan, N. Nagaosa, C. Felser, and B. Yan, Switchable magnetic bulk photovoltaic effect in the two-dimensional magnet CrI3, Nat. Commun. 10, 3783 (2019).
- Gao et al. [2020] Y. Gao, Y. Zhang, and D. Xiao, Tunable layer circular photogalvanic effect in twisted bilayers, Phys. Rev. Lett. 124, 077401 (2020).
- Wang and Qian [2020] H. Wang and X. Qian, Electrically and magnetically switchable nonlinear photocurrent in PT-symmetric magnetic topological quantum materials, npj Comput. Mater. 6, 199 (2020).
- Rees et al. [2020] D. Rees, K. Manna, B. Lu, T. Morimoto, H. Borrmann, C. Felser, J. E. Moore, D. H. Torchinsky, and J. Orenstein, Helicity-dependent photocurrents in the chiral Weyl semimetal RhSi, Sci. Adv. 6, eaba0509 (2020).
- de Juan et al. [2017] F. de Juan, A. G. Grushin, T. Morimoto, and J. E. Moore, Quantized circular photogalvanic effect in Weyl semimetals, Nat. Commun. 8, 15995 (2017).
- Ahn et al. [2020] J. Ahn, G.-Y. Guo, and N. Nagaosa, Low-frequency divergence and quantum geometry of the bulk photovoltaic effect in topological semimetals, Phys. Rev. X 10, 041041 (2020).
- Chaudhary et al. [2022] S. Chaudhary, C. Lewandowski, and G. Refael, Shift-current response as a probe of quantum geometry and electron-electron interactions in twisted bilayer graphene, Phys. Rev. Research 4, 013164 (2022).
- Sipe and Shkrebtii [2000] J. E. Sipe and A. I. Shkrebtii, Second-order optical response in semiconductors, Phys. Rev. B 61, 5337 (2000).
- Kaplan et al. [2022] D. Kaplan, T. Holder, and B. Yan, Twisted photovoltaics at terahertz frequencies from momentum shift current, Phys. Rev. Research 4, 013209 (2022).
- Holder et al. [2020] T. Holder, D. Kaplan, and B. Yan, Consequences of time-reversal-symmetry breaking in the light-matter interaction: Berry curvature, quantum metric, and diabatic motion, Phys. Rev. Research 2, 033100 (2020).
- Cao et al. [2018a] Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Unconventional superconductivity in magic-angle graphene superlattices, Nature 556, 43 (2018a).
- Cao et al. [2018b] Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, Correlated insulator behaviour at half-filling in magic-angle graphene superlattices, Nature 556, 80 (2018b).
- Lu et al. [2019] X. Lu, P. Stepanov, W. Yang, M. Xie, M. A. Aamir, I. Das, C. Urgell, K. Watanabe, T. Taniguchi, G. Zhang, A. Bachtold, A. H. MacDonald, and D. K. Efetov, Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene, Nature 574, 653 (2019).
- Yankowitz et al. [2019] M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young, and C. R. Dean, Tuning superconductivity in twisted bilayer graphene, Science 363, 1059 (2019).
- Cao et al. [2020] Y. Cao, D. Rodan-Legrain, O. Rubies-Bigorda, J. M. Park, K. Watanabe, T. Taniguchi, and P. Jarillo-Herrero, Tunable correlated states and spin-polarized phases in twisted bilayer–bilayer graphene, Nature 583, 215 (2020).
- Sun et al. [2022] Z. Sun, H. Zhou, C. Wang, S. Kumar, D. Geng, S. Yue, X. Han, Y. Haraguchi, K. Shimada, P. Cheng, L. Chen, Y. Shi, K. Wu, S. Meng, and B. Feng, Observation of topological flat bands in the kagome semiconductor Nb3Cl8, Nano Lett. 22, 4596 (2022).
- Regmi et al. [2022] S. Regmi, T. Fernando, Y. Zhao, A. P. Sakhya, G. Dhakal, I. Bin Elius, H. Vazquez, J. D. Denlinger, J. Yang, J.-H. Chu, X. Xu, T. Cao, and M. Neupane, Spectroscopic evidence of flat bands in breathing kagome semiconductor Nb3I8, Commun. Mater. 3, 100 (2022).
- Gao et al. [2023] S. Gao, S. Zhang, C. Wang, S. Yan, X. Han, X. Ji, W. Tao, J. Liu, T. Wang, S. Yuan, G. Qu, Z. Chen, Y. Zhang, J. Huang, M. Pan, S. Peng, Y. Hu, H. Li, Y. Huang, H. Zhou, S. Meng, L. Yang, Z. Wang, Y. Yao, Z. Chen, M. Shi, H. Ding, H. Yang, K. Jiang, Y. Li, H. Lei, Y. Shi, H. Weng, and T. Qian, Discovery of a single-band mott insulator in a van der Waals flat-band compound, Phys. Rev. X 13, 041049 (2023).
- Feng et al. [2023] L. Feng, X. Chen, and J. Qi, Nonvolatile electric field control of spin-valley-layer polarized anomalous Hall effect in a two-dimensional multiferroic semiconductor bilayer, Phys. Rev. B 108, 115407 (2023).
- Grytsiuk et al. [2024] S. Grytsiuk, M. I. Katsnelson, E. G. V. Loon, and M. Rösner, Nb3Cl8: A prototypical layered mott-hubbard insulator, npj Quantum Materials 9, 8 (2024).
- Lee et al. [2006] P. A. Lee, N. Nagaosa, and X.-G. Wen, Doping a mott insulator: Physics of high-temperature superconductivity, Rev. Mod. Phys. 78, 17 (2006).
- Aversa and Sipe [1995] C. Aversa and J. E. Sipe, Nonlinear optical susceptibilities of semiconductors: Results with a length-gauge analysis, Phys. Rev. B 52, 14636 (1995).
- Note [1] We observe that a divergent shift vector and zero absorption result in a finite shift current in the SnTe monolayer [npj Comput. Mater. 10, 23 (2024)]. Therefore, while optical transitions induce a large real-space shift due to the dispersive nature of the bands, the momentum-space shift current dominates. However, in most cases, the bulk photovoltaic effect is correlated with a finite optical absorption process. We will restrict our discussion to this scenario.
- Rangel et al. [2017] T. Rangel, B. M. Fregoso, B. S. Mendoza, T. Morimoto, J. E. Moore, and J. B. Neaton, Large bulk photovoltaic effect and spontaneous polarization of single-layer monochalcogenides, Phys. Rev. Lett. 119, 067402 (2017).
- King-Smith and Vanderbilt [1993] R. D. King-Smith and D. Vanderbilt, Theory of polarization of crystalline solids, Phys. Rev. B 47, 1651 (1993).
- Fregoso et al. [2017] B. M. Fregoso, T. Morimoto, and J. E. Moore, Quantitative relationship between polarization differences and the zone-averaged shift photocurrent, Phys. Rev. B 96, 075421 (2017).
- Ibañez-Azpiroz et al. [2018] J. Ibañez-Azpiroz, S. S. Tsirkin, and I. Souza, Ab Initio calculation of the shift photocurrent by Wannier interpolation, Phys. Rev. B 97, 245143 (2018).
- Cotton [1964] F. A. Cotton, Metal atom clusters in oxide systems, Inorg. Chem. 3, 1217 (1964).
- Bursten et al. [1982] B. E. Bursten, F. A. Cotton, M. B. Hall, and R. C. Najjar, Survey of the bonding in several structural types of trinuclear molybdenum and tungsten cluster compounds, Inorg. Chem. 21, 302 (1982).
- Kennedy et al. [1996] J. R. Kennedy, P. Adler, R. Dronskowski, and A. Simon, Experimental and theoretical electronic structure investigations on -Nb3Cl8 and the intercalated phase -NaNb3Cl8, Inorg. Chem. 35, 2276 (1996).
- Sheckelton et al. [2017] J. P. Sheckelton, K. W. Plumb, B. A. Trump, C. L. Broholm, and T. M. McQueen, Rearrangement of van der waals stacking and formation of a singlet state at T = 90 K in a cluster magnet, Inorg. Chem. Front. 4, 481 (2017).
- Haraguchi et al. [2017] Y. Haraguchi, C. Michioka, M. Ishikawa, Y. Nakano, H. Yamochi, H. Ueda, and K. Yoshimura, Magnetic–nonmagnetic phase transition with interlayer charge disproportionation of Nb3 trimers in the cluster compound Nb3Cl8, Inorg. Chem. 56, 3483 (2017).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Jiang et al. [2017] J. Jiang, Q. Liang, R. Meng, Q. Yang, C. Tan, X. Sun, and X. Chen, Exploration of new ferromagnetic, semiconducting and biocompatible Nb3X8 (X = Cl, Br or I) monolayers with considerable visible and infrared light absorption, Nanoscale 9, 2992 (2017).
- Hu et al. [2023] J. Hu, X. Zhang, C. Hu, J. Sun, X. Wang, H.-Q. Lin, and G. Li, Correlated flat bands and quantum spin liquid state in a cluster Mott insulator, Commun Phys 6, 172 (2023).
- Pizzi et al. [2020] G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J.-M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi, and J. R. Yates, Wannier90 as a community code: New features and applications, J. Phys.: Condens. Matter 32, 165902 (2020).
Supplementary
.1 A. Numerical calculation details
To access the electronic structures of Nb3X8 monolayers, first-principles calculations were performed using the Vienna ab initio Simulation Package (VASP) equipped with the projector-augmented-wave potentials [41]. The exchange-correlation interactions were considered in the generalized gradient approximation (GGA) with Perdew-Burke-Ernzerhof scheme [42]. A 400 eV cutoff energy and -point sampling were considered for relaxation and self-consistent calculations. The structures were optimized until the force on each atom is reduced to below 0.01 eV/Å. The correlation of orbitals of Nb was treated with GGA+ method, with an isotropic eV [43, 25, 44]. Spin-orbit coupling (SOC) was included in all calculations. To calculate the photoconductivities of the shift current and injection current, as well as the -resolved quantities, we constructed a Wannier tight-binding model using the wannier90 package and utilized a modified postw90 program [45]. To calculate the injection current conductivity, we used a moderate relaxation time of s.
.2 B. Effects of Hubbard
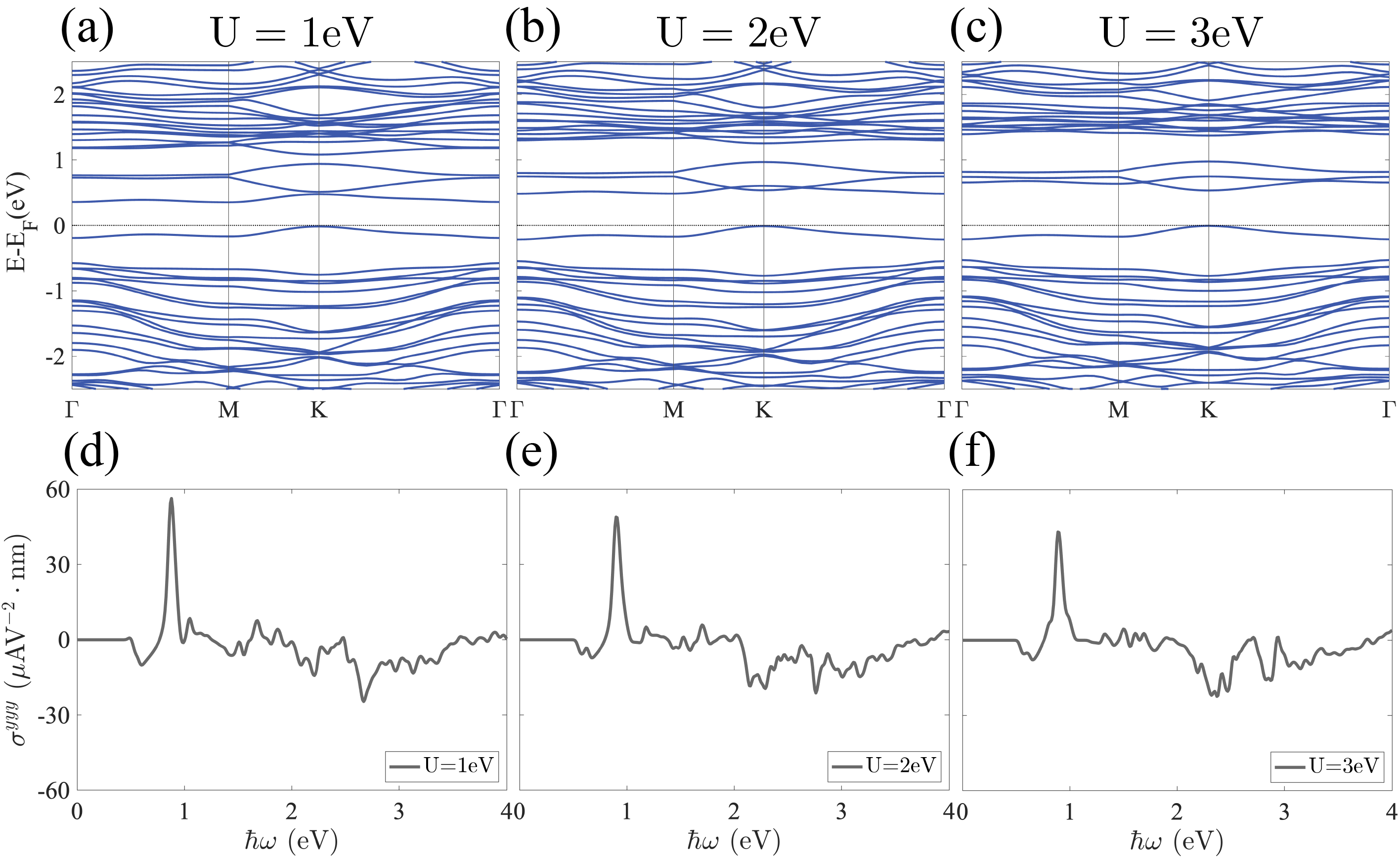
As discussed in the Section A of Supplementary, we used a widely adopted Hubbard eV to describe the correlation effects in monolayers [43, 25, 44]. However, since the strength of Hubbard can significantly affect the electronic structure and transport properties in correlated systems, it is crucial to access the impact of the choice of . In this section, we perform first-principles calculations for the monolayer, which exhibits the highest response among the monolayers, using Hubbard , 2, and 3 eV to investigate its influence on the numerical results. In Fig. 5(a-c), we show the band structures for Hubbard , 2, and 3 eV, respectively. As shown, four bands near the Fermi level remain distinct and are separated from other bands. Additionally, as increases from 1 eV to 3 eV, the overlap between the unoccupied 2 and 2 orbitals becomes stronger. In Fig. 5(d-f), we present the shift current spectra for monolayer with Hubbard , 2, and 3 eV, respectively. While the maximum peak slightly decreases as increases, the shift current spectra for different values of remain similar, with the peak in the low energy region consistently being the highest. Therefore, the conclusions in the main text are robust to variations in Hubbard across this range.
.3 C. Injection current in monolayers
Besides the shift current, another primary mechanism contributing to the bulk photovoltaic effect is the injection current [16], with a schematic illustration of the injection mechanism shown in Fig. 6(a). The term ”injection current” originates from the fact that the magnitude of this photocurrent is proportional to the illumination time when scattering mechanisms are neglected. Microscopically, injection current can be interpreted as the photocurrent generated by the difference in group velocities of electrons in the conduction and valence bands during photoexcitation. Driven by linearly polarized light, the microscopic expression for the injection current photoconductivity is given by:
| (C1) |
where is the relaxation time, and is the difference of group velocity between band and band along the -direction. Other quantities are defined in the discussion of shift current photoconductivity in Section II. In contrast to , which is even under time-reversal symmetry, is odd under time-reversal symmetry. Thus, this contribution only exists in magnetic systems where time-reversal symmetry is broken.
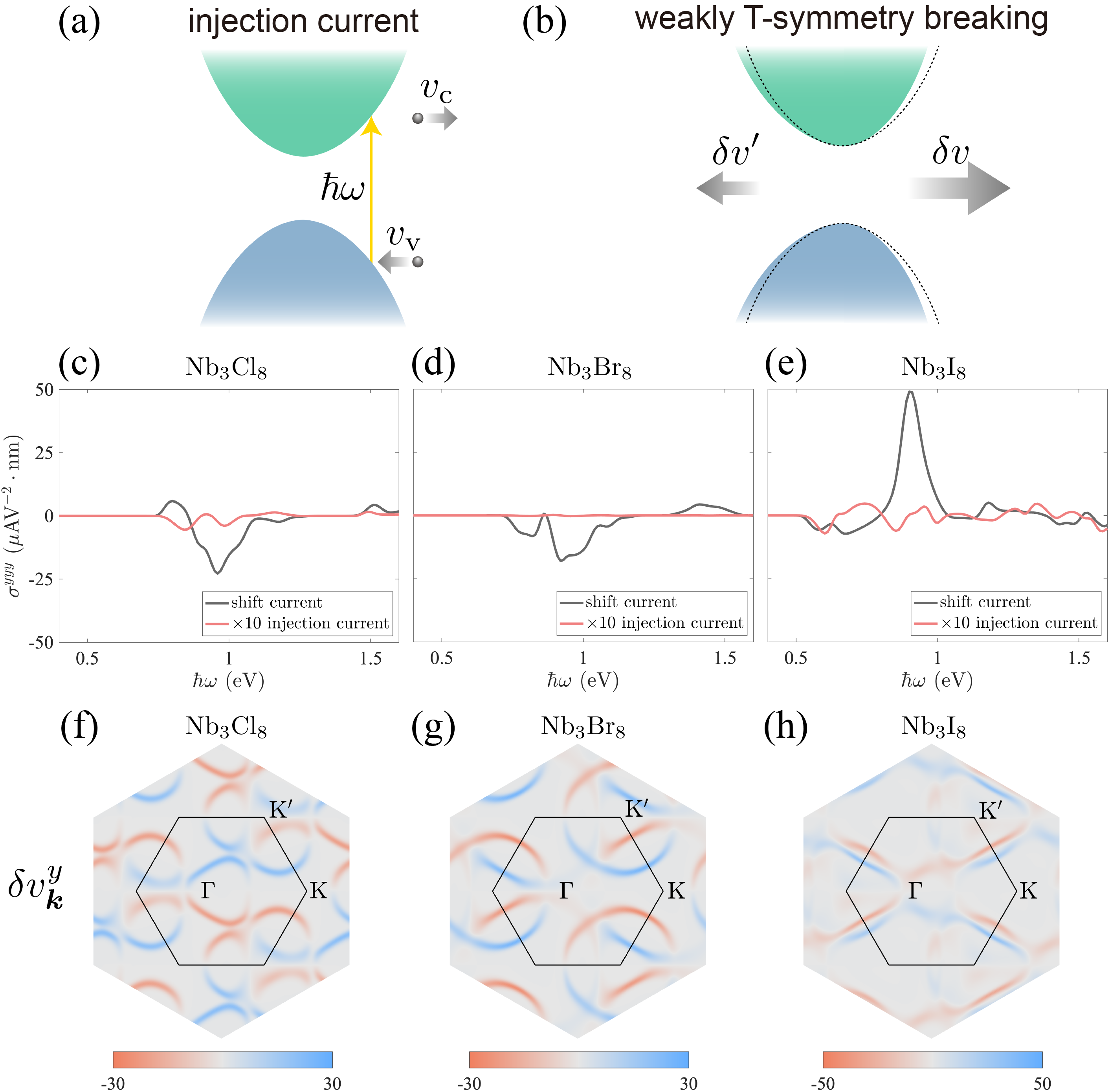
We calculated the injection current spectra in monolayers, as shown in Fig. 6(c-e). The injection current photoconductivity remains significantly smaller than that of the shift current, even when scaled by a factor of ten. This characteristic of the bulk photovoltaic effect in monolayers can be explained as follows. First, as shown in the schematic in Fig. 6(b), in systems with slightly broken time-reversal symmetry, contributions to the injection current from pairs of -points related by time-reversal symmetry tend to cancel each other. Thus, only systems with sufficiently strong magnetism can exhibit a significant injection current. In monolayers, the magnetic moment of 1 per Nb trimer induces only a relatively weak breaking of time-reversal symmetry. Therefore, the injection current in monolayers is expected to be correspondingly small. Additionally, the bands near the Fermi level in monolayers show minimal energy dispersion, leading to a small difference in group velocities between the conduction and valence bands during photoexcitation. This can help explain why the monolayer, which has the narrowest bandwidth among the monolayers, exhibits the smallest injection current within this family. We attribute the significantly smaller injection current relative to the shift current in monolayers to the factors discussed above. To provide further insight into the extremely weak injection current in monolayers, we define a collective velocity difference, analogous to the collective shift vector, as follows:
| (C2) |
which characterizes the magnitude of the velocity difference during photoexcitation. The distribution of across the Brillouin zone is shown in Fig. 6(f-h). As expected, contributions in the Brillouin zone exhibit significant cancellation.