$p\to\infty$ limit of tachyon correlators in $(2,2p+1)$ minimal Liouville gravity from classical Liouville theory

Liouville conformal filed theory is a 2-dimensional CFT which has the action of the form

$\hat{g}$ is a reference metric that we introduce to give theory a covariant form. We will only consider Liouville theory on the sphere in this paper. Parameter $Q=b+b^{-1}$; the Virasoro central charge of the theory is then given by $c_{L}=1+6Q^{2}$. $\mu$ is the parameter of the theory called the ‘‘cosmological constant’’ in this context; dependence of the correlators on $\mu$ is fixed, e.g. by noticing that $\mu$ can be put to one by shifting $\phi\to\phi-\frac{1}{2b}\log\mu$.

Holomorphic stress-energy tensor of the theory is $T=-(\partial\phi)^{2}+Q\,\partial^{2}\phi$. Exponential operators $V_{a}=e^{2a\phi}$ are primary fields of the model of dimension $\Delta^{L}_{a}=a(Q-a)$. Operators $V_{a}$ and $V_{Q-a}$ are identified up to a factor $R_{L}(a)$ called the ‘‘reflection coefficient’’.

As usually the case in CFT, in Liouville theory there are the so-called ‘‘degenerate’’ fields. They correspond to fields $V_{m,n}\equiv V_{a_{m,n}}$ with

These are the primary fields (Virasoro highest vectors) with a descendant on level $mn$ which is annihilated by positive part of the Virasoro algebra and is a highest vector by itself (in other words, the corresponding Vermat module has a submodule). To work only with irreducible representations, in CFT such submodules are usually decoupled by putting its highest vector to zero. Decoupling conditions can be written as $D_{m,n}V_{m,n}=0$, where $D_{m,n}$ is a polynomial of Virasoro generators $L_{-k}$ of degree $mn$; in particular, $D_{1,2}=L_{-1}^{2}+b^{2}L_{-2}$. From this follows the celebrated BPZ equation bpz for a 4-point correlator with degenerate field:

An expression for the three-point functions (or structure constants) of Liouville theory $C_{L}(a_{1},a_{2},a_{3})$ was first proposed by two groups of authors dornotto1994 and zamzam1996 . It is called Dorn-Otto-Zamolodchikov-Zamolodchikov (DOZZ) three-point function. The formula is

where $\Upsilon_{b}(x)$ is a certain special function that we will not be discussing in detail. We cite two important properties of it: the shift relations

with $\gamma(z)=\frac{\Gamma(z)}{\Gamma(1-z)}$ and the fact that this function has zeroes for $x=-mb-\frac{n}{b}$ and $x=Q+\frac{m}{b}+nb$ for $m,n$ non-negative.

The OPE $V_{a_{1}}(x)V_{a_{2}}(0)$ in Liouville CFT is most simply written when $a_{1},a_{2}$ lie in the so-called ‘‘basic domain’’ defined by

In this case we write

The fields that appear here are parametrized by one real number $P$ instead of complex $a$ — only operators with $a=\frac{Q}{2}+iP,\,P\in\mathbb{R}$, correspond to normalizable, or ‘‘physical’’, states of the theory seibergnotes . This is why we sum over these states only in the OPE. When parameters of the correlators are not in this domain, some poles of the structure constants may cross the contour over which we integrate. In order to keep the analyticity in parameters, in such case we should either deform the contour of integration over $P$ or (equivalently) keep the contour the same but explicitly add contributions from these poles which are referred to as ‘‘discrete terms’’.

Liouville theory has a nice semiclassical limit which is obtained when $b\to 0$ (or $c\to\infty$). After rescaling the field $b\phi(x)=\varphi(x)$, in terms of $\varphi$ the action has a large prefactor $\sim 1/b^{2}$. Functional integral is then saturated by a saddle point — solution of classical Liouville equation

Function $\varphi_{cl}$ can be interpreted as the Weyl factor of constant curvature metrics on the surface that we consider. We will put $\Lambda=1$ in what follows for simplicity. Classical limit of correlator of primary operators $\exp(2a_{k}\phi(x))=\exp(2\frac{a_{k}}{b}\varphi(x))$ depends on how their dimension scale with $b$: if $a=\eta/b\to\infty,\,b\to 0$ with $\eta$ finite (‘‘heavy’’ fields), such operators affect the equations of motion and the saddle solution, adding delta-functional terms to the RHS:

Leading approximation to correlation functions is then $\exp(-\frac{1}{b^{2}}S^{cl})$, where $S^{cl}$ is the action evaluated on the solution of (8). This modification of EOMs can be interpreted as adding conical singularities (for real $0<\eta<1/2$) of angle deficit $4\pi\eta$ on the surface. For $\eta=1/2+ip$ these are rather macroscopic holes with geodesic boundaries of length $\sim p$. If dimensions $\Delta$ of fields stay of order $1$ when $b\to\infty$, we refer to such fields as ‘‘light’’. They do not affect the saddle point and are just evaluated on the solution, contributing the factor $\exp(2a\varphi_{cl}/b)$ to the correlator.

After proper regularization, in simple cases we can explicitly evaluate the classical action. For the case of three-point function it is easily verified (both for conical defects zamzam1996 and geodesic boundaries Hadasz_2004 ) that the classical action coincides with the straightforward $b\to 0$ limit of the logarithm of DOZZ structure constant (4); assuming $\sum\limits_{i=1}^{3}\eta_{i}>1$, the formula is

where

and $\psi^{(n)}$ is a polygamma function.

An important ingredient in the study of classical Liouville theory is the $b\to 0$ limit of the BPZ equation (3). Since degenerate field $V_{1,2}(z)=e^{-\varphi(z)}$ is light, $z$-dependence factorizes out of the correlator; if the other 3 fields are heavy, we have

We can then write the BPZ equation as follows:

In this form, it is just a consequence of Liouville EOMs and is not very helpful. However, the form of $t(z)$ can be understood even without knowing the solution, based on its singularities at $x_{i}$ (determined by contact terms in (8)), behaviour at $\infty$ and the fact that it is holomorphic (which also follows from EOM). E.g. for correlator of 4 heavy fields $\eta_{1},\dots,\eta_{4}$ at $x,0,1,\infty$ $t(z)$ looks like

Parameter $c$ is called ‘‘accessory parameter’’ and cannot be determined from the requirements above (there would be more than one such parameter for $n$-point correlators, one for each of $n-3$ complex coordinates on $n$-punctured sphere moduli space $\mathcal{M}_{0,n}$). If $\psi$ is built from the physical solution $\varphi_{cl}$ of Liouville equation, from previous factorization arguments (11) one expects that

which is a so-called Polyakov conjecture. This statement (at least for the case of the sphere) can be rigorously proven for properly regularized Liouville action (Zograf_1988 , Hadasz_2003 , Cantini_2001 ). One can build from $\psi_{1,2}$ (2 independent solutions of equation (12)) a solution of Liouville equation: the function

formally solves it if $\text{det }\Lambda_{ij}=-1$. For $\tilde{\varphi}_{cl}$ to be single-valued, one needs the monodromy of solutions $\psi$ to lie in the subgroup preserving the bilinear form $\Lambda$, i.e. in some real subgroup of $SL(2,\mathbb{C})$ isomorphic to either $SU(2)$ or $SU(1,1)$, depending on the sign of the curvature. This condition determines the accessory parameter $c$, for which solutions of (12) determine $\varphi_{cl}$ that solves (8).

As already mentioned, we will be interested in classical Liouville action’s interpretation as a Kähler potential for certain metrics on moduli space of punctured spheres, proposed by Zograf and Takhtajan in (Zograf_1988 ,takhtajan2001hyperbolic ): $g^{ZT}_{i{\overline{j}}}\sim\partial_{i}{\overline{\partial}}_{j}S^{(cl)}$. Here $i\in 1\dots n-3$ enumerate complex coordinates on the moduli space $\mathcal{M}_{0,n}$; a standard choice for these are $n-3$ independent cross-ratios of defects’ coordinates $x_{i}$.

A CFT of total central charge 0 that consists of Liouville theory, CFT minimal model $M_{r,r^{\prime}}$ and fermionic $BC$-system of central charge $-26$ (BRST ghosts) is referred to as $(r,r^{\prime})$ minimal Liouville gravity (MLG):

From requirement of zero total central charge it follows that Liouville parameter $b=\sqrt{r/r^{\prime}}$. We will not review the properties of $BC$-CFT and minimal models in detail here; we just want to define the objects that we study in what follows. More details can be found e.g. in Zamolodchikov:2005fy .

An important class of operators in this theory are the ‘‘tachyons’’, obtained by dressing minimal model primaries $\Phi_{m,n}$ with Liouville operators $V_{a}$ and ghosts $C{\overline{C}}$ so that their total conformal dimension is $0$: in previously defined Liouville parametrization they read $W_{m,n}\equiv C{\overline{C}}V_{m,-n}\Phi_{m,n}$. These are representatives of cohomology classes for nilpotent BRST-operator $\mathcal{Q}=C(T_{L}+T_{M})+C\partial CB$ in this theory. Instead of adding ghosts, one can also integrate the operators $U_{m,n}\equiv V_{m,-n}\Phi_{m,n}$ of dimension $(1,1)$ over the surface to obtained BRST-invariant objects.

Correlators of multiple tachyon operators $\int d^{2}x\,U_{a}(x)$ and $W_{a}(x)$ on a sphere (in fact, due to ghost number anomaly the number of $C$-ghosts in such correlator needs to be equal to three; so, three fields are $W$ and all the others are integrated operators $\int d^{2}x\,U_{a}$) are what we consider in this paper. Such correlators do not depend on any insertion points $x_{i}$ and are just numbers. Moreover, in certain normalization, they turn out to simplify greatly compared to the constituents (Liouville and minimal model correlators) and become piecewise-polynomial in $m_{i}$ and $n_{i}$.

A long-standing conjecture is that these correlation numbers can be equivalently obtained from double-scaling limit of matrix models (in fact, calculations in this approach are significantly simpler than in Liouville gravity); see e.g. franc1995 , Moore:1991ir for early studies of the problem. Identification of matrix model and LG generating functionals is complicated by the necessity to do an analytic redefinition of coupling constants, which is referred to as ‘‘resonance transformations’’; their form is most fully understood for the case of $(2,2p+1)$ MLG, corresponding to one-matrix model belzam2009 . Solidifying the connection betweeen two approaches in general case is a subject of separate line of research; in this paper we will mostly examine $4$-point correlation numbers on the sphere in $(2,2p+1)$ minimal gravity, for which calculation in continuous approach can be done and the agreement with matrix model is proven (Belavin:2005jy , alesh2016 ). In other cases, where only matrix model answers are available, we will be assuming the equivalence of two approaches and call matrix model results MLG correlation numbers.

Let us order the parameters of the tachyon correlator $\langle W_{1,k_{1}+1}\dots\int d^{2}x\,U_{1,k_{n}+1}\rangle$ in $(2,2p+1)$ MLG as $0\leq k_{1}\leq k_{2}\leq k_{3}\leq\dots\leq k_{n}\leq p-1$. Then the four-point correlation number, as obtained from the matrix model, reads belzam2009

where $k_{ij|lm}$ and the function $F_{\theta}$ are defined as

There are corrections to this answer that are nonzero only if the so called ‘‘fusion rules’’

are not satisfied; they nullify the correlation number in this case. The $p\to\infty$ limit of this correlator when all operators are ‘‘heavy’’ (as before, it means that parameter of the dressing Liouville fields for tachyons $\eta_{1,-k_{i}-1}=ba_{1,-k_{i}-1}=b^{2}\frac{k_{i}+2}{2}$ or, equivalently, $\kappa_{i}=\frac{k_{i}}{p}\approx k_{i}b^{2}$ stays finite in the limit $b\to 0$) is taken using the asymptotic for function $F_{\theta}$:

We also can say a bit more about the meaning of fusion rules (19) in semiclassical limit. The odd-sector one becomes $\kappa_{1}+\dots+\kappa_{4}>2$ and is nothing but Gauss-Bonnet theorem, which is a necessary condition for the metric on the sphere with given defects to be hyperbolic. If this inequality is not satisfied, only metric with constant positive curvature may exist; in this case, a known necessary condition for existence of such metric is the inequality $\kappa_{1}+\kappa_{2}+\kappa_{3}>\kappa_{4}$, coinciding with even sector fusion rules. This inequality is referred to as Troyanov condition in the literature mazzeo2015teichmuller .

For further reference in section 4, we also note the following property of these numbers: assume that sum of any two numbers $k_{i}+k_{j},\,i\neq j$ is less than $p$ for the four-point function, the same is valid for the sum of any three numbers for five-point function and so on. Then the expression for correlation number factorizes and, up to a factor dependent only on $\sum k_{i}$, counts the number of conformal blocks in minimal model part of the correlator. E.g. for four-point number we have

This property was noted in Artemev_2022 for four- and five-point correlation numbers based on the results of belzam2009 , tarn2011 . For higher than 5-point correlators, this behaviour can be anticipated from calculations of Fateev_2008 (although these results, relying on analytic continuation of expressions obtained from Coulomb integrals, have limited applicability in MLG, where correlators are non-analytic).

We start with the known decomposition of Liouville four-point correlator

Here the conformal block is normalized so that its series expansion in $x$ starts with $x^{\Delta-\Delta_{1}-\Delta_{2}}$. If we assume that all the external and intermediate dimensions are ‘‘heavy’’ (with the parameters scaling with $b\to 0$ as before), the structure constants, as well as conformal blocks, are known to exponentiate in the $b\to 0$ limit. The integral then takes the form

Semiclassical structure constant $S^{(3)}_{cl}$ is given in (9). Then, by the usual saddle point arguments, we expect that in the semiclassical limit the integral is approximately given by $\exp\left(-\frac{1}{b^{2}}S^{(4)}(p_{\text{saddle}}(x,{\overline{x}}),x,{\overline{x}})\right)$ at the extremum of the expression in exponent, i.e. $p_{\text{saddle}}$ is such that $\frac{\partial S^{(4)}}{\partial p}\mid_{p=p_{\text{saddle}}}=0$. It is reasonable to assume (although not proven rigorously), that at least in a certain region of parameter space $S^{(4)}(p_{\text{saddle}},x,{\overline{x}})$, computed by this method from CFT, coincides with the usual regularized classical Liouville action. It turns out that for some values of parameters $\eta$ this is not quite true (e.g. because the nontrivial real saddle disappears). We will comment on this in the following sections.

We note in passing that real $p_{\text{saddle}}$, when it exists, has a simple geometrical meaning, being proportional to the length of the (unique) simple closed geodesic separating pairs of points $(0,x)$ and $(1,\infty)$, i.e. one of the Fenchel-Nielsen coordinates $l$. On the other hand, derivative with respect to $p$ of the holomorphic part of the action (which includes holomorphic classical conformal block and half of classical structure constants) is proportional to $i\theta$ teschner2014supersymmetric , where $\theta$ is a conjugate twist coordinate; a saddle point condition for the integral then means that for real $p$ $\theta$ is real as well.

One can develop an expansion for $p_{\text{saddle}}$ on the boundary of moduli space (when $x\to 0$). Consider the first few terms of the expansion of $S^{(4)}$ in $p$; from explicit expressions one can see that part of $S^{(4)}(p,x,{\overline{x}})$ coming from the structure constants is an even function of $p$, but non-analytic at $p=0$ in such a way so we have

Then in leading approximation the saddle point equation reads

It confirms that $p_{\text{saddle}}$ is small for small $x$ (note that solution exists only for $A>0$). However, all the terms that we ignored in the expansion of classical conformal blocks are ‘‘nonperturbatively’’ smaller than $p$ to any power, being proportional to powers of $q=\exp(-\#/p_{\text{saddle}})$. Ignoring them, we can first find a ‘‘perturbative’’ expansion for $p_{\text{saddle}}$ in $\frac{1}{\log(x{\overline{x}})}$, by restoring other terms in the series for $(\partial S^{(3)}_{cl}/\partial p)$ in $p$ and solving the ‘‘corrected’’ saddle-point equation order by order.

Instead of $x$, we will parametrize the moduli space with ‘‘elliptic’’ $q$ variable, defined as

where $K(x)$ is the complete elliptic integral of the first kind. To rewrite the expansion in terms of $q$ one can use that $x=16q(1+\dots)$. Terms denoted by $\dots$ in brackets do not matter for ‘‘perturbative’’ expansion. We prefer ‘‘elliptic’’ parametrization because convergence of series in $q$ is generically better; also, ‘‘non-perturbative’’ corrections would be easier to construct systematically — one can write subleading terms in the $q$-expansion of conformal block order by order using Zamolodchikov’s recursion relation Zamolodchikov1987ConformalSI (this approach was successfully used in harrison2022liouville ). Also, we note that in principle we can expand in $\epsilon=(\log a(\eta_{i})/q{\overline{q}})^{-1}$ for any function $a(\eta)$; for a specific choice $a=e^{B}/2^{8}$ quadratic in $p$ terms in the expansion have the most simple form.

After the series for $p_{\text{saddle}}$ is found, we can compute the ‘‘classical action’’ $S^{(4)}$ and the associated Kähler metric on the moduli space: $g_{q{\overline{q}}}=-4\pi\partial_{q}\partial_{{\overline{q}}}S^{(4)}(q,{\overline{q}})$ (as a series expansion in $\epsilon$). Up to this step, obtaining analytic expressions is possible; the only thing left to compute the volumes is to integrate $\sqrt{\text{det }g}$ over the moduli space $\mathcal{M}_{0,4}$. The discrete group $S_{3}=S_{4}/(S_{2}\times S_{2})$ of order 6 permutes the conical defects and, nontrivially acting on cross-ratio $x$, acts on $\mathcal{M}_{0,n}$. A convenient choice of fundamental domain of this action is

It is depicted on Fig. 1, but it is easier to understand how this domain looks in $\tau$ coordinate, where it is just the usual fundamental domain for $SL(2,\mathbb{Z})$ action on the upper half-plane. Integration over this domain of the terms in the series for $g_{q{\overline{q}}}$ can be carried out numerically.

Let us now specify previous results for an example that we introduced in the beginning of this section: the four-point function $\langle V_{\kappa/2b}(0)V_{\kappa/2b}(x)V_{1/2b}(1)V_{1/2b}(\infty)\rangle$. The moduli space $\mathcal{M}_{0,4}$ is decomposed into a fundamental domain $\mathcal{F}$ and $5$ its images under the action of the aforementioned $S^{3}$ group; in 2 of these 6 domains, $V_{\kappa/2b}(x)$ is closer to the operator $V_{\kappa/2b}(0)$ and should be fused with it, while in the other 4 it should be fused with $V_{1/2b}$. To calculate the integral over the whole moduli space, in each domain we should use decomposition like the formula (23) in a corresponding channel.

First, we need to understand when the real saddle point, that we need to evaluate the integral, exists. Using the formula (9) for classical structure constants, we get that for $(1/2,\kappa/2)$ fusion channel for all $0<\kappa<1$ the coefficient $A$ in (26) is equal to $2\pi>0$. Thus, the real saddle exists and in the corresponding domains the calculation procedure is reliable. However, for the $(\kappa/2,\kappa/2)$ channel this is not the case — the coefficient $A$ is equal to $2\pi$ for $\kappa>1/2$ and otherwise is zero. For more general values of parameters of the correlator, real saddle in the integral (23) would disappear if the parameters $\eta_{1},\eta_{2}$ of fused fields are such that $\eta_{1}+\eta_{2}<1/2$.

The formal reason for such behaviour is the following — functions $F(\eta_{1}+\eta_{2}-1/2-ip)$ and $F(\eta_{1}+\eta_{2}-1/2+ip)$, entering the classical structure constants (9) and defined by integral representation (10), develop an additional linear in $p$ contribution to the Maclaurin series in $p$ when $\text{Re }(\eta_{1}+\eta_{2}-1/2)<0$. Indeed, the integrand $\log\gamma(z)$ in (10) obtains an additional imaginary part $\pm i\pi$; from this the proposed behaviour of $F(\eta)$ follows. These additional linear terms from two $F$-functions above then cancel the term $-2\pi|p|$ that series for $S^{(4)}$ had when $\kappa>1/2$.

We were a little bit inaccurate in the arguments of the previous paragraph, using naive analytic continuation for classical structure constants (9) in the domain $\eta_{1}+\eta_{2}<1/2$. In fact, as noted before in Harlow_2011 , in this case classical limit of the three-point function changes less trivially: if real part of the argument of some $F$-function in (9) is $-1<\eta<0$, to get the asymptotic coinciding with the logarithm of DOZZ formula one needs to replace

For $\text{Im }\eta=\pm p$ the denominator can be expanded in series in $\exp(-\pi|p|/b^{2})$. This expansion can be interpreted as sum over certain complex saddle points in the functional integral. Performing the replacement above for 2 $F$-functions with negative real part of their argument and proceeding with the expansion, it is easy to see that there is no nontrivial real saddle for integral over $p$ in any of the terms in the obtained series.

Recalling that $p_{\text{saddle}}$ is proportional to the length of separating geodesic, we can understand the geometric meaning of why the saddle point disappears: on a hyperbolic surface such geodesic does not exist if conical defects are not sharp enough. Indeed, consider Fig. 1; suppose that geodesic $AEBE^{\prime}A$ that separates two pairs of points exist. Then, together with the parts of geodesics that connect the defects, we obtain 2 hyperbolic tetragons $AEBCD$ and $AE^{\prime}BCD$. The sum of all their angles is equal to $2\pi(2-2\eta_{1}-2\eta_{2})+2\pi$ and by Gauss-Bonnet theorem should be less than $4\pi$, which leads necessarily to $\eta_{1}+\eta_{2}>1/2$.

Summarising this discussion, we see that the procedure that we use is only reliable for $\kappa>1/2$. Thus, we will only restrict to such values of the parameter in the next section.

For brevity we will call $(\kappa/2,\kappa/2)$ and $(1/2,\kappa/2)$ channels ‘‘channel 1’’ and ‘‘channel 2’’ respectively. We introduce the ‘‘perturbative’’ expansion parameter $\epsilon$ as

where $\delta\equiv\kappa-\frac{1}{2}$ and $f$ is some function of $\delta$, independent of $x$. Then, the saddle point equation in ‘‘perturbative’’ approximation becomes

and can be solved order by order in $\epsilon$, putting $p_{\text{saddle}}=\sum\limits_{n=1}^{n_{max}}p_{n}\epsilon^{n}$. For the following choice of $f$ for channels $1$ and $2$ respectively

expansion coefficients look the simplest; e.g. up to 6th order in $\epsilon$ the saddle point momentum is

in channel 1 and

in channel 2. We can now substitute that in the action/Kähler potential, obtaining the series in $\epsilon$, differentiate it termwise using

and obtain the series expansion for the metric in 2 channels (again, for simplicity we write the formulas for the choice of $f$ as in (32))

Then, we integrate each term over the fundamental domain $\mathcal{F}$. Radial integration can be performed exactly

and integration over the angle $\psi$ — only numerically. Expanding to 25th order in $\epsilon$, integrating over the fundamental domain in two channels, we obtain the following plots (Fig. 2).

When $\kappa$ is close enough to 1, agreement is very good. However, expansion coefficients for the metric start growing too quickly if we change $\kappa$. The final numeric sum doesn’t seem to converge when truncated to the order that we consider (the highest one we considered was 50th order in $\epsilon$). E.g. on Fig. 3 we have the results of integration of different terms in the series for the metricin channel 1 for $\delta=0.25$:

However, it turns out that this problem can be tamed by tuning $f(\delta)$ and the expansion parameter $\epsilon$. In Table 4 and Figure 5 for each data point we fitted $f(\delta)$ to obtain optimal convergence (also, for some points it was necessary to extend the expansion from 25th to 40th order in $\epsilon$).

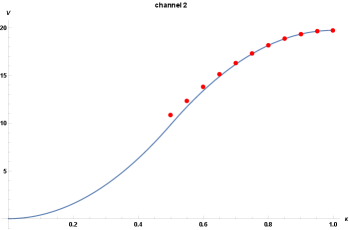
Contributions in 2 different channels start to look different from each other and the analytic prediction (22) when $\kappa$ is small enough. However, the appropriate sum over all 6 images of fundamental domain is in quite good agreement (accuracy $\sim 1\%$) with the analytic answer for all considered values of parameter $\kappa$ (see Fig. 6).

The simplification of MLG answers when $p>k_{i}+k_{j}$ mentioned near (21) is suggestive of how the moduli space metric behaves for these values of parameters. Consider e.g. the sphere 4-point function in the case when $k_{1}+k_{4}<k_{2}+k_{3}$, which means that the number of conformal blocks is maximal and equal to $(1+k_{1})$ (as before we assume $k_{1}\leq k_{2}\leq k_{3}\leq k_{4}\leq p-1$), MLG correlator and its semiclassical limit are (21)

For general $n$-point correlator on the sphere under the same conditions apparently we would have (see the discussion at the end of 2.3)

Before semiclassical limit, formula is a bit more complicated: the factor other than the number of conformal blocks is most easily expressed via number of screenings, see Fateev_2008 . Note that this factor is just the RHS of Gauss-Bonnet theorem