Pseudo links and singular links in the Solid Torus
Abstract
In this paper we introduce and study the theories of pseudo links and singular links in the Solid Torus, ST. Pseudo links are links with some missing crossing information that naturally generalize the notion of knot diagrams, and that have potential use in molecular biology, while singular links are links that contain a finite number of self-intersections. We consider pseudo links and singular links in ST and we set up the appropriate topological theory in order to construct invariants for these types of links in ST. In particular, we formulate and prove the analogue of the Alexander theorem for pseudo links and for singular links in ST. We then introduce the mixed pseudo braid monoid and the mixed singular braid monoid, with the use of which, we formulate and prove the analogue of the Markov theorem for pseudo links and for singular links in ST.
Moreover, we introduce the pseudo Hecke algebra of type A, , the cyclotomic and generalized pseudo Hecke algebras of type B, , and discuss how the pseudo braid monoid (cor. the mixed pseudo braid monoid) can be represented by (cor. by ). This is the first step toward the construction of HOMFLYPT-type invariants for pseudo links in and in ST. We also introduce the cyclotomic and generalized singular Hecke algebras of type B, , and we present two sets that we conjecture they form linear bases for . Finally, we generalize the Kauffman bracket polynomial for pseudo links in ST.
keywords:
solid torus, pseudo knots, pseudo links, singular knots, mixed pseudo links, mixed singular links, mixed pseudo braids, mixed pseudo braid monoid, mixed singular braids, pseudo braid monoid of type B, mixed singular braid monoid, pseudo Hecke algebra of type A, pseudo Hecke algebras of type A and of type B, cyclotomic and generalized singular Hecke algebras of type B, pseudo bracket polynomial.57K10, 57K12, 57K14, 57K31, 57K35, 57K45, 57K99, 20F36, 20F38, 20C08. \VOLUME31 \YEAR2023 \NUMBER1 \DOIhttps://doi.org/10.46298/cm.10438 {paper}
1 Introduction
Pseudo diagrams of knots were introduce by Hanaki in [H] as projections on the 2-sphere with over/under information at some of the double points missing. They comprise a relatively new and important model for DNA knots, since there exist DNA knots that is impossible to distinguish a positive from a negative crossing, even when studying them by electron microscopes. By considering equivalence classes of pseudo diagrams under equivalence relations generated by a specific set of Reidemeister moves, we obtain the theory of pseudo knots, that is, standard knots whose projections contain crossings with missing information (see [HJMR] for more details). In [BJW], the pseudo braid monoid is introduced, which is related to the singular braid monoid, and with the use of which, the authors present the analogues of the Alexander and the Markov theorems for pseudo knots in . From now on and throughout the paper, by pseudo links we shall mean both pseudo links and pseudo knots. In [D], the author introduces the -moves for pseudo links and formulates and proves a sharpened version of the analogue of the Markov theorem for pseudo links, as well as an alternative proof of the analogue of the Alexander theorem for pseudo links in . In this paper we extend these results for pseudo links in the solid torus ST. Our aim is the construction of pseudo knot invariants in and ST, and toward that end we present the pseudo bracket polynomial for pseudo links in ST and discuss HOMFLYPT-type invariants for pseudo links in and ST via appropriate Hecke type algebras, following [Jo] [La1] and [PR]. Singular knots are knots with finite many rigid self-intersections, and as shown in [BJW], the theory of singular links in is closely related to the theory of pseudo links in . In this paper, we establish this correspondence for the case of ST, and through this correspondence we formulate the analogues of the Alexander and Markov theorems for singular links in ST. Then, following [PR], we define the generalized (and cyclotomic) singular Hecke algebras of type B and discuss further research needed toward the construction of HOMFLYPT-type invariants for singular links in ST, which in turn relate to invariants of pseudo links in ST. This is the subject of a sequel paper. The paper is organized as follows: In § 2 we recall results on pseudo links, on singular links and on knots in the solid torus from [BJW], [HJMR], [D], [La] and [La2]. In § 3 we present a braiding algorithm for pseudo and singular links in ST and we introduce the mixed pseudo braid monoid and the mixed singular braid monoid. We then formulate and prove the analogue of the Markov theorem for pseudo links and for singular links in ST. In § 4 we introduce the pseudo Hecke algebras of type A, related to the pseudo knot theory of , and we present some results toward the construction of HOMFLYPT-type invariants for pseudo links in . In particular, we present a spanning set for the pseudo Hecke algebra of type A. We introduce the cyclotomic and the generalized pseudo Hecke algebras of type B, which are related to the pseudo knot theory of ST, and we discuss further steps toward the construction of HOMFLYPT-type invariants for pseudo links in ST. We conclude by presenting potential bases for these algebras. In a similar way, we also introduce the cyclotomic and generalized singular Hecke algebras of type B, through which, HOMFLYPT-type invariants for singular links in ST may be constructed. Finally, in § 5 we generalize the (Kauffman) bracket polynomial for pseudo links in ST. The results of this paper will be used for the construction of HOMFLYPT-type invariants for these type of knots in the solid torus in the same sense as in [La1] for the case of classical knots in the solid torus and in [PR] for the case of singular knots in . Our aim is to extend these invariants for the case of lens spaces following [DL3], [DL4] and [DLP].
2 Preliminaries
2.1 The theories of pseudo links and singular links in
In this subsection we recall results on pseudo links and on singular links in . In particular, we recall the pseudo braid monoid , introduced in [BJW], that is related to the singular braid monoid ([Ba], [Bi]), and we recall all necessary results in order to present the analogues of the Alexander and the Markov theorems for pseudo links and singular links in . A pseudo diagram of a knot consists of a regular knot diagram with some missing crossing information, that is, there is no information about which strand passes over and which strand passes under the other. These undetermined crossings are called pre-crossings (for an illustration see Figure 1).

Definition 2.1.
Pseudo knots are defined as equivalence classes of pseudo diagrams under an appropriate choice of Reidemeister moves that are illustrated in Figure 2.

As explained in [BJW], pseudo knots are closed related to singular knots, that is, knots that contain a finite number of self-intersections. In particular, there exists a bijection from the singular knot diagrams to the set of pseudo knot diagrams where singular crossings are mapped to pre-crossings. In that way we may also recover all of the pseudo knot Reidemeister moves, with the exception of the pseudo-Reidemeister I (PR1) move (see Figure 2). Moreover, induces an onto map from singular knots to pseudo knots, since the image of two isotopic singular knot diagrams are also isotopic pseudo knot diagrams with exactly the same sequence of Reidemeister moves. We now introduce the pseudo braid monoid, , following [BJW].
Definition 2.2.
The monoid of pseudo braids, , is the monoid generated by the elements (), illustrated in Figure 3, where generate the braid group and satisfy the following relations:

Note that corresponds to a standard crossing and not to a singular crossing. We denote a singular crossing by and we have that if we replace the pre-crossings of Definition 2.2 by singular crossings , we obtain the singular braid monoid, , defined in [Ba] and [Bi]. Thus, we obtain the following result:
Proposition 2.3 (Proposition 2.3 [BJW]).
The monoid of pseudo braids is isomorphic to the singular braid monoid, .
Remark 2.4.
In [FKR] it is shown that , the singular braid monoid, embeds in a group, the singular braid group . It follows that embeds in a group also, the pseudo braid group , generated by and , , satisfying the same relations as . Obviously, is isomorphic to (recall Proposition 2.3 [BJW]).
Define now the closure of a pseudo braid (cor. of a singular braid) as in the standard case (for an illustration of the closure of a pseudo braid see Figure 8). By considering , we can consider the inductive limit . Using the analogue of the Alexander theorem for singular knots ([Bi]), in [BJW] the analogue of the Alexander theorem for (oriented) pseudo links is presented. In particular:
Theorem 2.5 (Alexander’s theorem for pseudo links).
Every pseudo link can be obtained by closing a pseudo braid.
We now recall the notion of -moves for pseudo knots and results from [D] and [La]. -moves make up an important tool for braid equivalence in any topological setting and they allow us to formulate sharpened versions of the analogues of the Markov theorems. For more details the reader is referred to [La] and references therein.
Definition 2.6.
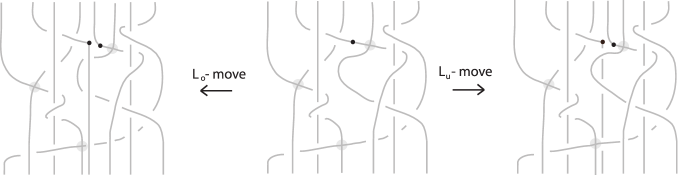
An -move on a braid , consists in cutting an arc of open and pulling the upper cut-point downward and the lower upward, so as to create a new pair of braid strands with corresponding endpoints (on the vertical line of the cut-point), and such that both strands cross entirely over or under with the rest of the braid. Stretching the new strands over will give rise to an -move and under to an -move as shown in Figure 4 by ignoring all pre-crossings.
-moves for pseudo braids are defined in the same way as in the singular case, that is, the two strands that appear after the performance of an -move should cross the rest of the braid only with real crossings (all over in the case of an -move or all under in the case of an -move). For an illustration see Figure 4 for the case of an -move performed on a pseudo braid.
As explained in [D], -moves on pseudo knots can be used in order to obtain the analogue of the Alexander theorem for pseudo knots following the braiding algorithm in [Bi], [A] and [LR1]. The main idea of this algorithm is to keep the arcs of the oriented links diagram that go downwards with respect to the height function unaffected and replace arcs that go upwards with braid strands. We first isotope the pre-crossings in such a way that the braiding algorithm will not affect them (see Figure 10), and we may then apply the braiding algorithm of [Bi] or [LR1] by ignoring the pre-crossings. The same is true for the case of singular links in (for a detailed proof for the case of singular links in see [PR] Theorem 2.3). In § 3.2 we recall the braiding algorithm from [LR1] and we modify it in order to obtain the analogue of the Alexander theorem for pseudo links and singular links in ST (see also [La2]). We now state the analogue of the Markov theorem for oriented pseudo links and for oriented singular links in ([G], [La], [BJW] and [D]).
Theorem 2.7 (The analogue of the Markov Theorem for singular links).
Two oriented singular links are isotopic if and only if any two corresponding singular braids differ by braid relations in and a finite sequence of the following moves:
where , the singular braid group, and a singular crossing.
Theorem 2.8 (The analogue of the Markov Theorem for pseudo links).
Two pseudo braids have isotopic closures if and only if one can be obtained from the other by a finite sequence of the following moves:
Equivalently, two pseudo braids have isotopic closures if and only if one can be obtained from the other by a finite sequence of the following moves:
2.2 The knot theory of ST
We now view ST as the complement of a solid torus in and we present results from [LR1]. An oriented link in ST can be represented by an oriented mixed link in , that is, a link in consisting of the unknotted fixed part representing the complementary solid torus in and the moving part that links with . A mixed link diagram is a diagram of on the plane of , where this plane is equipped with the top-to-bottom direction of . For an illustration see Figure 6 by ignoring the pre-crossings. Consider now an isotopy of an oriented link in ST. As the link moves in ST, its corresponding mixed link will change in by a sequence of moves that keep the oriented pointwise fixed. This sequence of moves consists in isotopy in and the mixed Reidemeister moves. In terms of diagrams we have the following result for isotopy in ST: The mixed link equivalence in includes the classical Reidemeister moves and the mixed Reidemeister moves, which involve the fixed and the standard part of the mixed link, keeping pointwise fixed. By the Alexander theorem for knots in solid torus ([La2]), a mixed link diagram of may be turned into a mixed braid with isotopic closure. This is a braid in where, without loss of generality, its first strand represents , the fixed part, and the other strands, , represent the moving part . The subbraid is called the moving part of . For an illustration see Figure 8 by ignoring the pre-crossings. The sets of braids related to ST form groups, the Artin braid groups type B, denoted , with presentation:
where the generators and are illustrated in Figure 5.

We finally have that isotopy in ST is translated on the level of mixed braids by means of the following theorem.
Theorem 2.9 (The analogue of the Markov Theorem for mixed braids, Theorem 3 [La1]).
Let be two oriented links in ST and let be two corresponding mixed braids in . Then is isotopic to in ST if and only if is equivalent to in by the following moves:
3 Pseudo Links & Singular Links in ST
In this section we introduce and study pseudo links and singular links in ST, through mixed pseudo (cor. singular) braids and the mixed pseudo (cor. singular) braid monoid of type B. We conclude this section by formulating and proving the analogues of the Alexander and the Markov theorems for pseudo links and singular links in ST.
3.1 Mixed pseudo links and mixed singular links
As explained in § 2.2 we view ST as the complement of another ST in and thus, pseudo links in ST can be seen as mixed pseudo links in containing the complementary ST. Similarly, singular links in ST can be viewed as mixed singular links in . For an illustration of a mixed pseudo link see Figure 6, where by changing pre-crossings to singular crossings, one obtains a singular mixed link.

Isotopy for pseudo links in ST is now translated on the level of mixed pseudo links in by means of the following theorem:
Theorem 3.1 (The analogue of the Reidemeister theorem for mixed pseudo links).
Two mixed pseudo links in are isotopic if and only if they differ by a finite sequence of the classical and the pseudo Reidemeister moves illustrated in Figure 2 for the standard part of the mixed pseudo links, and moves that involve the fixed and the standard part of the mixed pseudo links, called mixed Reidemeister moves, and are illustrated in Figure 7.

Remark 3.2.
It is worth mentioning that we do not allow special crossings, i.e. pre-crossings for the case of pseudo links and singular crossings for the case of singular links, between the fixed and the moving part of the mixed pseudo (cor. singular) braid.
3.2 Mixed pseudo braids, mixed singular braids and a braiding algorithm
We now define the mixed pseudo braids, which are related to mixed pseudo links, and the mixed singular braids, related to the mixed singular links.
Definition 3.3.
A mixed pseudo braid (cor. mixed singular braid) on strands, denoted by , is an element of the pseudo braid monoid (cor. singular braid monoid ) consisting of two disjoint sets of strands, one of which is the identity braid representing the complementary solid torus in , and strands form the moving subbraid representing the pseudo (cor. singular) link in ST. For an illustration see the left hand side of of Figure 8. Moreover, a diagram of a mixed pseudo braid is a braid diagram projected on the plane of .
Without loss of generality, we assume that the first strand of the mixed pseudo braid represents the complementary solid torus in . This can be realized by performing the technique of (standard) parting, in order to separate the endpoints of the mixed braids into two different sets, the first represents the complementary solid torus in (i.e. the fixed part ), and the last strands represent the moving part of the mixed braid, i.e. the link in ST, and so that the resulting braids have isotopic closures. This can be realized by pulling each pair of corresponding moving strands to the right and over or under the strand of that lies on their right according to its label. We start from the rightmost pair respecting the position of the endpoints. For more details the reader is referred to [LR1] and [DL1]. We also define the closure of a mixed pseudo (cor. singular) braid as follows:
Definition 3.4.
The closure of a mixed pseudo braid (cor. mixed singular braid) in ST is defined as in the case of classical braids in . See Figure 8 for the case of a mixed pseudo braid.

We now present a braiding algorithm for mixed pseudo links in ST and for mixed singular links in ST. By “mixed links” in the braiding algorithm that follows, we shall mean both mixed pseudo links and mixed singular links, and by special crossings we shall mean pre-crossings or singular crossings. The main idea of the braiding algorithm is to keep the arcs of the oriented mixed link diagrams that go downwards with respect to the height function unaffected, and replace arcs that go upwards with braid strands. These arcs are called up-arcs (see Figure 9).

Note that the braiding algorithm should keep the fixed part of the mixed link unaffected and should also ”take care“ of the special crossings in the mixed diagram which contain at least one up-arc. For this we apply the idea used in [Bi] for the case of singular knots, (see also [KL] for the case of virtual knots). Namely, before we apply the braiding algorithm we have to isotope the mixed link in such a way that the special crossings will only contain down-arcs, so that the braiding algorithm will not affect them. This is achieved by rotating all special crossings that contain at least one up-arc, so that the two arcs are now directed downward. This is illustrated in Figure 10 for the case of pre-crossings. Then we may apply the braiding algorithm of [La2], which is a modification of the braiding algorithm for oriented mixed links presented in [LR1], for the mixed link (ignoring the special crossings). In particular:
-
•
We first ”take care“ of the special crossings by isotoping the mixed link in such a way that the braiding algorithm will not affect them. For an illustration see Figure 10.

Figure 10: Rotating pre-crossings. We now recall the braiding algorithm of [La2] (for more details the reader is referred to [La2] and references therein).
-
•
Consider now a vertical line that passes through the maximum and minimum of as illustrated in Figure 11. By small perturbations we can assume that does not pass through any crossings of the link.

Figure 11: -
•
We now apply the following braiding algorithm to the part of the link that lies to the left of the vertical line , keeping fixed:
-
–
Chose a base-point and we run along the diagram of the link according to its orientation.
-
–
When/If we run along an opposite arc, we subdivide it into smaller arcs, each containing crossings of one type only as shown in Figure 9.
-
–
Label now every up-arc with an “o”or a “u”, according to the crossings it contains. If it contains no crossings, then the choice is arbitrary.
-
–
Perform an -braiding moves on all up-arcs which were labeled with an “o” and -braiding moves on all up-arcs which were labeled with an “u” (see Figure 12).

Figure 12: Braiding moves for up-arcs.
-
–
-
•
Close the braided part of the link that lies to the left of and consider this operation to be enclosed in a tube (see left hand side of Figure 13).
-
•
Apply once again the braiding algorithm on the right hand side of keeping fixed, and we close now this braided portion of the link and enclose the strings participating in this operation in a tube (see right hand side of Figure 13).
-
•
Rotate now around the back of the diagram in order to bring the tube to the very right of the diagram and to the very left of the diagram, and so that the resulting diagram goes around a central point, say on .
-
•
Local maxima and minima in the diagram, if any, would lie on the vertical line . We isolate each one in neighborhoods that do not contain other parts of the diagram, and we stretch the arcs above and below a point of symmetry , so that the extrema would lie on again but in reverse order. Note also that we numerate the extrema with integers with respect to the point . For an illustration see right hand side of Figure 13.

Figure 13: -
•
Open the braided diagram by cutting through a half-line starting from and we isotope in ST.
-
•
The result is a mixed pseudo braid (cor. a mixed singular braid) whose closure is isotopic to the initial mixed link.
This braiding algorithm provides a proof of the following theorem:
Theorem 3.5 (The analogue of the Alexander theorem for oriented pseudo links and for oriented singular links in ST).
Every oriented mixed pseudo link is isotopic to the closure of a mixed pseudo braid and very oriented mixed singular link is isotopic to the closure of a mixed singular braid.
Remark 3.6.
-
i.
The braiding algorithm described above can be also applied for the case of orientedtied pseudo links in ST, that is, pseudo links in ST equipped with some non-embedded arcs called ties. The reader is referred to [D] for a treatment of tied pseudo links in . Note that tied links in were introduced in [AJ] and that in [F] the author generalized the notion of tied links in ST. Finally, in [D1] the author studies tied links in various 3-manifolds.
-
ii.
It is also worth mentioning that the [La2]-braiding algorithm with the modifications described above, can be applied for braiding pseudo singular links in and ST. Pseudo singular links are defined as links with finitely many self-intersections and with some missing crossing information. This theory will be studied in a sequel paper for both and ST.
3.3 The mixed pseudo braid monoid & the mixed singular braid monoid of type B
We now study algebraic structures related to mixed pseudo braids and mixed singular braids. Our aim is to formulate the analogue of the Markov theorem algebraically. We start by defining the mixed pseudo braid monoid , the counterpart of the Artin’s braid group of type B for pseudo links, and also derive the mixed singular braid monoid. In order to define the mixed pseudo braid monoid , we need to find the defining relations of this monoid. We analyze the moves of Theorem 3.1 and this leads to the following definition:
Definition 3.7.
The mixed pseudo braid monoid of type B is defined as the monoid generated by the standard braid generators ’s of , the pseudo generators ’s of and the looping generator ’s of , satisfying the following relations:
Note that every isotopy can be decomposed in a sequence of elementary isotopies which correspond to the relations in Definition 3.7, and that means that we have obtained a complete set of relations. It is also worth mentioning that by replacing the pre-crossings in Definition 3.7, we obtain the singular braid monoid of type B, , presented in Theorem 4.4 [V]. Note also that in [V], the singular braid monoid of type B is called singular braid monoid of the Annulus. Thus, we have the following result:
Theorem 3.8.
There exists an isomorphism from the singular braid monoid of type B to the pseudo braid monoid of type B, defined as follows:
| (1) |
Moreover, by considering the natural inclusion (see Figure 14), we can define the inductive limit , and similarly, by considering the natural inclusion , we may define the inductive limit .

3.4 The analogue of the Markov theorem for mixed pseudo braids and mixed singular braids
Using the braiding algorithm presented in § 3.2 for pseudo links in , we have a stronger version of the analogue of the Markov theorem for pseudo knots, similar to Theorem 2 in [La2]. In particular, we have the following:
Theorem 3.9 (Relative version of the analogue of the Markov theorem for pseudo links).
Two pseudo links containing the same braided part are isotopic if and only if any two corresponding pseudo braids, both containing the same braided part, differ by conjugation, commuting, stabilization and pseudo-stabilization moves that do not affect the already braided part.
Since all pseudo links related to the solid torus contain the same braided part , we have that corresponding pseudo braids contain the same braided part . Therefore, we obtain the following:
Corollary 3.10.
Two pseudo links in ST are isotopic if and only if any two corresponding pseudo braids of theirs, differ by conjugation, commuting, stabilization and pseudo-stabilization moves that do not affect .
Theorem 3.11 (The analogue of the Markov Theorem for mixed pseudo braids).
Two mixed pseudo braids have equivalent closures if and only if one can obtained from the other by a finite sequence of the following moves:
Note that from the discussion in § 2.1 and Theorem 2.8 it follows that conjugation and stabilization moves can be replaced by the -moves. Hence, we obtained a sharpened version of Theorem 3.11. More precisely, we have the following:
Theorem 3.12 (-move Markov’s Theorem for mixed pseudo braids).
Two mixed pseudo braids have isotopic closures if and only if one can obtained from the other by a finite sequence of the following moves:
Similarly, by Theorem 3.8, we have the following result for mixed singular braids:
Theorem 3.13 (The analogue of the Markov Theorem for mixed singular braids).
Two mixed singular braids have equivalent closures if and only if one can obtained from the other by a finite sequence of the following moves:
Equivalently, by a finite sequence of the following moves:
4 Pseudo Hecke and singular Hecke algebras of type A and of type B
In [PR] the authors define the singular Hecke algebra of type A, , and through a universal Markov trace constructed in , they present a HOMFLYPT-type invariant for singular links in . In this section we discuss techniques from [Jo], [PR] and [La1] toward the construction of HOMFLYPT-type invariants for pseudo links in and ST, and for singular links in ST. The construction of these type of invariants will be the subject of a sequel paper.
4.1 The pseudo Hecke algebra of type A
The technique of [PR] can be applied for the case of pseudo knots in , since, as mentioned before, pseudo knot theory of can be realized as the quotient of the theory of singular knots in , modulo the pseudo-Reidemeister move 1. In that sense, we present here results from [PR] which are adapted accordingly. Recall that the Hecke algebra of type A, , has presentation obtained from the classical braid group by corresponding the braiding generators to and by adding the quadratic relations:
| (2) |
That is, . We define the pseudo Hecke algebra of type A in a similar way. More precisely:
Definition 4.1.
Define the pseudo Hecke algebra of type A, , as the quotient of the pseudo braid monoid by the quadratic relations (2). That is,
Note that the embedding induces a homomorphism . Moreover, each has a natural grading with respect to the pre-crossings, namely, , where denote the set of mixed pseudo braids with pre-crossings. This grading induces a grading on , since the quadratic relations affect only the ’s. In particular, we have that:
Recall now the following linear basis for the Hecke algebra of type A [Jo]:
for . The basis yields directly an inductive basis for , which is used in the construction of the Ocneanu trace, leading to the HOMFLYPT or -variable Jones polynomial. Similarly, we want to find a basis for . Although is not of finite dimension, each subspace of the graduation is of finite dimension. Indeed we have the following (compare to Proposition 3.1 [PR]):
Proposition 4.2.
The set
spans .
The proof is similar to that of Proposition 3.1 [PR] by replacing the singular crossings ’s by the pre-crossings ’s. In order now to define HOMFLYPT-type invariants for pseudo links in , one should construct a family of Markov traces on and . Note that the difference between the family of traces we have to define in to that defined in [PR], is the relation that comes from the pseudo-Reidemeister move 1, and which is not allowed in the theory of singular knots. In a sequel paper we shall work toward the construction of such Markov traces. Note that the construction of a Markov trace leads naturally to a HOMFLYPT-type invariant for pseudo links in . As shown in [PR], one would have to fix a Markov trace on , and then follow [Jo] in order to define an invariant for pseudo knots in .
4.2 On the pseudo Hecke algebras and the singular Hecke algebras of type B
In this subsection we define the generalized pseudo Hecke algebra of type B and the cyclotomic pseudo Hecke algebras of type B, related to pseudo links in ST, and similarly, we define the cyclotomic and the generalized singular Hecke algebra of type B, related to the theory of singular links in ST, following [La1]. Our aim is to apply similar techniques from [La1], [PR] and [Jo] toward the construction of HOMFLYPT-type invariants for pseudo links and singular links in the Solid Torus, ST, which is the subject of a sequel paper. It has been established that Hecke algebras of type B form a tower of B-type algebras that are related to the knot theory of ST. A presentation for the basic one is obtained from the presentation of the Artin group by adding the quadratic relation (2) and , where are seen as fixed variables. The middle B-type algebras are the cyclotomic Hecke algebras of type B, whose presentations are obtained by the quadratic relation (2) and . The topmost Hecke-like algebra in the tower is the generalized Hecke algebra of type B, , which has the following presentation:
That is:
Note that in the generator satisfies no polynomial relation, making the algebra infinite dimensional. Also that in [La1] the algebra is denoted as . Following [La1] and [PR], we now define the generalized pseudo Hecke algebra of type B and the cyclotomic pseudo Hecke algebras of type B.
Definition 4.3.
Define the generalized pseudo Hecke algebra of type B, , as the quotient of the mixed pseudo braid monoid by the quadratic relations (2). That is,
The cyclotomic pseudo Hecke algebras of type B, is defined as the quotient of the mixed pseudo braid monoid by the quadratic relations (2) and the relations:
As in the case of pseudo Hecke algebras of type A, the embedding induces a homomorphism , and moreover, also has a natural grading with respect to the pre-crossings, i.e. , where denotes the set of mixed pseudo braids with pre-crossings. This grading induces a grading on :
Consider now the elements illustrated in Figure 15 and recall the following linear bases for the generalized Hecke algebra of type B [La1]:
where and a basic element in .

The basis yields an inductive basis for the generalized Hecke algebra of type B, which is used in the construction of the Ocneanu trace, leading to the HOMFLYPT or -variable Jones polynomial (the reader is referred to [La1] for more details). Similarly, we want to find a basis for , with the use of which we will construct HOMFLYPT-type invariants for pseudo links in ST. This is more complicated (compared to the type A case) and further research is required. We conclude this discussion with a conjecture:
Conjecture 4.4.
For , the following sets span :
Remark 4.5.
For singular links in ST, we define the generalized singular Hecke algebra of type B, , as
and the cyclotomic singular Hecke algebras of type B, , as the following quotient:
Similarly to Conjecture 4.4, the sets
where , are potential spanning sets of .
Remark 4.6.
It is worth mentioning that, as shown in [DL3], [DL4], [DLP] and [D4], the generalized Hecke algebra of type B is related to the knot theory of lens spaces . This can be realized by the fact that one may generalize a HOMFLYPT-type invariant for links in ST to an invariant for links in by imposing relations coming from the braid band moves, that is, moves that reflect isotopy in and which are similar to the second Kirby move ([LR1], [DL1]).
5 The pseudo bracket polynomial for pseudo links in ST
In this section we recall results from [LK] and [HD] on the pseudo bracket polynomial for pseudo links in and we extend this polynomial for the case of pseudo links in ST. For that reason, we view ST as a punctured disk, that is, a disk with a hole in its center, representing the complementary solid torus in (for an illustration see Figure 16).
5.1 The pseudo bracket polynomial for pseudo links in
In [HD] the pseudo bracket polynomial, , is defined for pseudo links in extending the Kauffman bracket polynomial for classical knots presented in [LK]. Note that the orientation of a diagram in the case of pseudo links is needed in order to define a skein relation on pre-crossings. More precisely, we have the following:
Definition 5.1.
Let be an oriented pseudo link in . The pseudo bracket polynomial of is defined by means of the following relations:
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/951913fc-241c-4469-ba81-7729d597419f/x16.png)
It can be easily seen that the pseudo bracket is invariant under Reidemeister moves 2 and 3 and the pseudo moves PR1, PR2 and PR3 ([HD] Theorem 1). As in [LK], by normalizing the pseudo bracket polynomial using the writhe, we obtain the normalized pseudo bracket polynomial, which is an invariant of pseudo knots in ([HD], Corollary 2). In particular:
Theorem 5.2.
Let be a pseudo diagram of a pseudo knot. The polynomial
where , the set of classical crossings of and the pseudo bracket polynomial of , is an invariant of pseudo knots in .
Remark 5.3.
For the case of singular links in the reader is referred to [CCC], where three different approaches to the bracket polynomial for singular links in are presented.
5.2 The pseudo bracket polynomial for pseudo knots in ST
We now generalize the pseudo bracket polynomial for pseudo links in ST. Note that we now view ST as a punctured disc (for an illustration of the looping generator in this set up see Figure 16).

We have the following:
Definition 5.4.
Let be an oriented pseudo link in ST. The pseudo bracket polynomial of is defined by means of the relations in Definition 5.1 together with the following relations:
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/951913fc-241c-4469-ba81-7729d597419f/x18.png)
An immediate result of Theorem 1 [HD] is the following:
Proposition 5.5.
The pseudo bracket polynomial for pseudo knots in ST is invariant under Reidemeister moves 2 and 3 and all pseudo moves.
As in the case of pseudo links in we obtain the following result:
Corollary 5.6.
Let be a pseudo diagram of a pseudo knot in ST. The polynomial
where is the writhe of the pseudo knots and the pseudo bracket polynomial of , is an invariant of pseudo knots in ST.
Remark 5.7.
-
i.
For the case of the bracket polynomial for singular knots in ST the reader is referred to [BRA].
-
ii.
For a generalization of Corollary 2 to a more general setting with an arbitrary handlebody and not just the solid torus, the reader is referred to [D6].
-
iii.
It is well known that the Temperley-Lieb algebras are related to the Kauffman bracket polynomial (see [LK1]). In [D2], and with the use of the Tempereley–Lieb algebra of type B, an alternative basis for the Kauffman bracket skein module of the solid torus is presented. It would be interesting to construct Kauffman-type invariants for pseudo links in ST using a generalized pseudo Temperley-Lieb algebra, and then extend this invariant to and invariant for pseudo links in the lens spaces . Note that one may also use the diagrammatic braid approach for computing Kauffman bracket skein modules (see for example [D3] and [D7]).
6 Conclusions
In this paper we introduce and study pseudo links in ST via the mixed pseudo braid monoid. In particular, we present the appropriate topological set up toward the construction of HOMFLYPT-type invariants for pseudo links in and in ST. We believe that pseudo knots can be used in various aspects of molecular biology, and in particular, they could serve as a model to biological objects related to DNA. We also introduce and study singular links in ST and we relate the singular knot theory of ST to that of pseudo knot theory of ST. In a sequel paper we shall adopt these results in order to construct HOMFLYPT-type invariants of pseudo links in and ST (cor. for singular links in ST) via the generalized pseudo Hecke algebra of type B (cor. the generalized singular Hecke algebras of type B). Finally, it is worth mentioning that in [D6] we study pseudo links in handlebodies and in [D8] we work toward formulating the analogues of the Alexander and the Markov theorems for pseudo links in various 3-manifolds.
References
- [1] \referPaperA \RauthorAlexander J. W. \RtitleA lemma on systems of knotted curves \RjournalProc. Nat. Acad. Sei. U.S.A. \Ryear1923 \Rnumber09 \Rpages93-95
- [2] \referPaperAJ \RauthorAicardi F., Juyumaya J. \RtitleTied Links \RjournalJ. Knot Theory and Ramifications \Rvolume25 \Ryear2016 \Rnumber09 \Rpages1641001
- [3] \referPaperBa \RauthorBaez J. C. \RtitleLink invariants of finite type and perturbation theory \RjournalLett. Math. Phys. \Rvolume26 \Ryear1992 \Rnumber01 \Rpages43–51
- [4] \referPaperBi \RauthorBirman J. S. \RtitleNew points of view in knot theory \RjournalBull. Amer. Math. Soc. (New Series) \Rvolume28 \Ryear1993 \Rpages253–287
- [5] \referPaperBRA \RauthorBataineh K., Abudriei R. \RtitleOn Jones polynomial for singular knots and links \RjournalCommunications in Mathematics and Applications \Rvolume7 \Ryear2016 \Rnumber4 \Rpages291-302
- [6] \referPaperBJW \RauthorBardakov V., Jablan S., Wang H. \RtitleMonoid and group of pseudo braids \RjournalJ. Knot Theory and Ramifications \Rvolume25 \Ryear2016 \Rnumber9 \Rpages1641002
- [7] \referPaperCCC \RauthorCaprau C., Chichester A., Chu P. \RtitleThree approaches to a bracket polynomial for singular links \RjournalInvolve \Rvolume10 \Ryear2017 \Rnumber2
- [8] \referPaperD \RauthorDiamantis I. \RtitleTied pseudo links & pseudo knotoids \RjournalMediterr. J. Math. \Rvolume18 \Ryear2021 \Rpages201
- [9] \referPaperD1 \RauthorDiamantis I. \RtitleTied links in various topological settings \RjournalJ. Knot Theory and Ramifications \Rvolume30 \Ryear2021 \Rnumber07 \Rpages2150046
- [10] \referProceedingsD2 \RauthorDiamantis I. \RtitleAn Alternative Basis for the Kauffman Bracket Skein Module of the Solid Torus via Braids \ReditorAdams C. et al. \RjournalKnots, Low-Dimensional Topology and Applications. KNOTS16 2016 \RpublisherSpringer Proceedings in Mathematics & Statistics \Rpages329–345
- [11] \referPaperD3 \RauthorDiamantis I. \RtitleThe Kauffman bracket skein module of the handlebody of genus 2 via braids \RjournalJ. Knot Theory and Ramifications \Rvolume28 \Ryear2019 \Rnumber13 \Rpages1940020
- [12] \referPaperD4 \RauthorDiamantis I. \RtitleHOMFLYPT skein sub-modules of the lens spaces via braids \RjournalTopology and its Applications \Rvolume301 \Ryear2021 \Rpages107500
- [13] \referPaperD6 \RauthorDiamantis I. \RtitlePseudo links in handlebodies \RjournalBulletin of the Hellenic Mathematical Society \Rvolume65 \Ryear2021 \Rpages17-34
- [14] \referArxivD7 \RauthorDiamantis I. \RtitleThe Kauffman bracket skein module of the complement of -torus knots via braids \Rarxivid2106.04965[math.GT]
- [15] \referOtherD8 \RauthorDiamantis I. \RtitlePseudo links in 3-manifolds \Ryearwork in progress
- [16] \referPaperDL1 \RauthorDiamantis I., Lambropoulou S. \RtitleBraid equivalences in 3-manifolds with rational surgery description \RjournalTopology and its Applications \Rvolume194 \Ryear2015 \Rpages269-295
- [17] \referPaperDL2 \RauthorDiamantis I., Lambropoulou S. \RtitleA new basis for the HOMFLYPT skein module of the solid torus \RjournalJ. Pure Appl. Algebra \Rvolume220 \Ryear2016 \Rnumber2 \Rpages577-605
- [18] \referProceedingsDL3 \RauthorDiamantis I., Lambropoulou S. \RtitleThe braid approach to the HOMFLYPT skein module of the lens spaces \ReditorLambropoulou, S., Theodorou, D., Stefaneas, P., Kauffman, L. \RjournalAlgebraic Modeling of Topological and Computational Structures and Application, 2017 \RpublisherSpringer Proceedings in Mathematics & Statistics \Rpages143–176
- [19] \referPaperDL4 \RauthorDiamantis I., Lambropoulou S. \RtitleAn important step for the computation of the HOMFLYPT skein module of the lens spaces via braids \RjournalJ. Knot Theory and Ramifications \Rvolume28 \Ryear2019 \Rnumber11 \Rpages1940007
- [20] \referPaperDLP \RauthorDiamantis I., Lambropoulou S., Przytycki J. H. \RtitleTopological steps on the HOMFLYPT skein module of the lens spaces via braids \RjournalJ. Knot Theory and Ramifications \Rvolume25 \Ryear2016 \Rnumber14 \Rpages1650084
- [21] \referPaperF \RauthorFlores M. \RtitleTied Links in the Solid Torus \RjournalJ. Knot Theory and Ramifications \Rvolume30 \Ryear2021 \Rnumber1 \Rpages2150006
- [22] \referPaperFKR \RauthorFenn R., Keyman E., Rourke C. P. \RtitleThe singular braid monoid embeds in a group \RjournalJ. Knot Theory and Ramifications \Rvolume7 \Ryear1998 \Rnumber7 \Rpages881–892
- [23] \referPaperG \RauthorGemein B. \RtitleSingular braids and Markov’s theorem \RjournalJ. Knot Theory and Ramifications \Rvolume6 \Ryear1996 \Rnumber04 \Rpages441–454
- [24] \referPaperH \RauthorHanaki R. \RtitlePseudo diagrams of links, links and spatial graphs \RjournalOsaka J. Math. \Rvolume47 \Ryear2010 \Rpages863-883
- [25] \referPaperHJMR \RauthorHenrich A., Hoberg R., Jablan S., Johnson L., Minten E., Radovic L. \RtitleThe theory of pseudoknots \RjournalJ. Knot Theory and Ramifications \Rvolume22 \Ryear2013 \Rnumber07 \Rpages1350032
- [26] \referPaperHD \RauthorDye H. A. \RtitlePseudo knots and an obstruction to cosmetic crossings \RjournalJ. Knot Theory and Ramifications \Rvolume26 \Ryear2017 \Rnumber04 \Rpages1750022
- [27] \referPaperJo \RauthorJones V. F. R. \RtitleHecke algebra representations of braid groups and link polynomials \RjournalAnn. Math. \Rvolume126 \Ryear1987 \Rpages335-388
- [28] \referPaperKL \RauthorKauffman L. H., Lambropoulou S. \RtitleVirtual braids and the -move \RjournalJ. Knot Theory and Ramifications \Rvolume15 \Ryear2006 \Rnumber06 \Rpages773-811
- [29] \referPaperLa \RauthorLambropoulou S. \RtitleL-Moves and Markov theorems \RjournalJ. Knot Theory and Ramifications \Rvolume16 \Ryear2007 \Rnumber10 \Rpages1459-1468
- [30] \referPaperLa1 \RauthorLambropoulou S. \RtitleKnot theory related to generalized and cyclotomic Hecke algebras of type B \RjournalJ. Knot Theory and Ramifications \Rvolume8 \Ryear1999 \Rnumber05 \Rpages621-658
- [31] \referProceedingsLa2 \RauthorLambropoulou S. \RtitleSolid torus links and Hecke algebras of B-type \ReditorYetter D. N. \RjournalQuantum Topology \RpublisherWorld Scientific Press \Rpages225-245
- [32] \referPaperLR1 \RauthorLambropoulou S., Rourke C. P. \RtitleMarkov’s theorem in -manifolds \RjournalTopology and its Applications \Rvolume78 \Ryear1997 \Rpages95-122
- [33] \referPaperLK \RauthorKauffman L. H. \RtitleNew invariants in the theory of knots \RjournalAmer. Math. Monthly \Rvolume95 \Ryear1988 \Rnumber3 \Rpages195-242
- [34] \referBookLK1 \RauthorKauffman L. H. \RtitleKnots in Physics \RpublisherWorld Scientific Press \Ryear1994
- [35] \referPaperPR \RauthorParis L., Rabenda L. \RtitleSingular Hecke algebras, Markov traces, and HOMFLY-type invariants \RjournalAnnales de l’Institut Fourier \Rvolume58 \Ryear2008 \Rnumber7 \Rpages2413-2443
- [36] \referPaperV \RauthorVershinin V. V. \RtitleAbout presentations of braid groups and their generalizations \RjournalBanach Center Publications \Rvolume100 \Ryear2014 \Rpages235-271
- [37]
June 28, 2021February 08, 2022Ivan Kaygorodov