Pruning Early Exit Networks

Alperen Görmez and Erdem Koyuncu
Department of Electrical and Computer Engineering
University of Illinois Chicago
Chicago, IL
{agorme2, ekoyuncu}@uic.edu

Abstract

Deep learning models that perform well often have high computational costs. In this paper, we combine two approaches that try to reduce the computational cost while keeping the model performance high: pruning and early exit networks. We evaluate two approaches of pruning early exit networks: (1) pruning the entire network at once, (2) pruning the base network and additional linear classifiers in an ordered fashion. Experimental results show that pruning the entire network at once is a better strategy in general. However, at high accuracy rates, the two approaches have a similar performance, which implies that the processes of pruning and early exit can be separated without loss of optimality.

1 Introduction

Modern deep learning models require large amount of computation to achieve good performance Howard (2022); Brown et al. (2020). This is undesirable for scenarios in which the model will run on power limited devices such as mobile phones, drones and IoT devices.

The problem of reducing the amount of computation while keeping the model performance high have been tackled from many different angles. Knowledge distillation approach aims to train a smaller model to mimic the output of a larger model Hinton et al. (2015). Quantization assigns less bits to the model weights to reduce the computational cost Shen et al. (2020); Han et al. (2015). Adaptive computation methods propose skipping some parts of the model based on the input Figurnov et al. (2017); Veit and Belongie (2018); Wang et al. (2018). Pruning methods remove redundant weights in the network Li et al. (2016); Blalock et al. (2020); Liu et al. (2018). Early exit networks have additional exit points so that not every sample will have to go through the entire network Gormez et al. (2022); Kaya et al. (2019); Teerapittayanon et al. (2016).

Most early exit networks have two components: an off-the-shelf base network, and additional small classifiers Gormez et al. (2022); Kaya et al. (2019); Teerapittayanon et al. (2016). Until now, no work has been done to prune early exit networks. This paper aims to fill this gap. In particular, we evaluate the performance of two strategies. In the first strategy, we prune and train the additional internal classifiers that enable early exit jointly with the base network. In the second strategy, we first prune and train the base network, and then the classifiers. The significance of the second strategy is that its optimality implies one can separate the processes of early exit and pruning without loss of optimality.

2 Experiment

We compare the following two approaches using a ResNet-56 and CIFAR-10 He et al. (2016); Krizhevsky et al. (2009):

1.

Multiple linear layers are added to a ResNet-56 (the resulting network is a Shallow-Deep Network Kaya et al. (2019)) and the entire model is pruned.
2.

A ResNet-56 is pruned, multiple linear layers are added to the resulting network and then these linear layers are pruned.

The number, locations, and the architectures of the additional linear layers are as described in Kaya et al. (2019). For both approaches, pruning is followed by fine tuning. The procedure of pruning and fine tuning is repeated 20 times. At each pruning phase, $10\%$ of the weights are pruned using global unstructured $l_{1}$ norm based pruning. At each fine tuning phase, the model is trained for 10 epochs. Accuracy vs. FLOPs graphs are obtained using different confidence thresholds and applying time sharing as in Gormez et al. (2022); Kaya et al. (2019).

Refer to caption — (a) Sparsity rates of the weights of each layer after 20 iterations of pruning and fine tuning.

3 Results

3.1 Approach 1

The sparsity rate of each layer’s weights and the exit performances after 20 iterations of pruning and fine tuning are shown in Fig. 1. We can make the following observations:

1.

Deeper layers are pruned slightly more than earlier layers, and final exit is pruned much less than earlier exits as seen from Fig. 1a.
2.

Despite extensive pruning, exit performances at earlier exits are comparable with the unpruned baseline, and even better at the first and second exit points as seen from Fig. 1b. This suggests pruning can improve model performance.
3.

Performance at the last exit is most likely hurt by the joint training of all linear classifiers.
4.

Pruning reduces the computational cost up to around $20\%$ without loss of performance. Best accuracy obtained with pruning is around $4\%$ less than the unpruned baseline, but the computational cost is reduced to half as seen from Fig. 1c.

3.2 Approach 2

In this approach, the ResNet-56 is pruned and fine tuned first. Then, linear layers are added to the model and these layers are pruned and fine tuned. The sparsity rate of each layer’s weights and the exit performances after 20 iterations of pruning and fine tuning are shown in Fig. 2. We can make the following observations:

1.

Fig. 2a and Fig. 2b shows that although the final exit went through two pruning phases (one with base network, one with additional linear classifiers), it is not pruned much.
2.

Except the last exit, deeper exits are pruned more than earlier exits as seen from Fig. 2a and Fig. 2b.
3.

Compared to Fig. 1, linear layers become more sparse as seen from Fig. 2b.
4.

Unpruned baseline in Fig. 2c has high accuracy only at the last exit because earlier exits are attached after the base network was pruned and fine tuned. The additional linear classifiers were not trained at this point.
5.

Fine tuning linear layers pushes the computational cost up as seen in Fig. 2d, which is interesting.

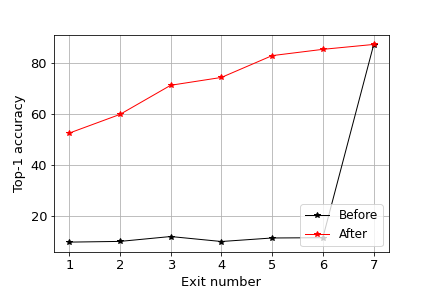
3.3 Comparison

The exit performances of the two approaches are shown in Fig. 3. From Fig. 3a, it can be seen that that pruning all layers at the same time performs better at earlier exit points compared to pruning the layers in an ordered fashion. However, ordered pruning approach performs better at deeper exit points which give the best performance.

In terms of computational cost, pruning all layers at once reduces the computational cost by up to $15\%$ compared to ordered pruning, but the performances are close at high accuracy rates as seen from Fig. 3b. Both approaches are able to reduce the computational cost by half at the cost of $4\%$ decrease in the accuracy.

4 Conclusion

In this paper, we considered the problem of pruning early exit architectures. We evaluated the performance of two strategies in particular. First, intermediate classifiers are pruned jointly with the base network. Second, the base network is pruned first, followed by the intermediate classifiers. Although the former strategy outperforms the latter in general, the performance of the two strategies are close at high accuracy rates. Therefore, the processes of pruning and early exit can potentially be separated without significant penalty in performance.

Acknowledgments and Disclosure of Funding

This work was supported in part by Army Research Lab (ARL) under Grant W911NF-21-2-0272, National Science Foundation (NSF) under Grant CNS-2148182, and by an award from the University of Illinois at Chicago Discovery Partners Institute Seed Funding Program.

References

Blalock et al. (2020) Davis Blalock, Jose Javier Gonzalez Ortiz, Jonathan Frankle, and John Guttag. What is the state of neural network pruning? Proceedings of machine learning and systems, 2:129–146, 2020.
Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901, 2020.
Figurnov et al. (2017) Michael Figurnov, Maxwell D Collins, Yukun Zhu, Li Zhang, Jonathan Huang, Dmitry Vetrov, and Ruslan Salakhutdinov. Spatially adaptive computation time for residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1039–1048, 2017.
Gormez et al. (2022) Alperen Gormez, Venkat Dasari, and Erdem Koyuncu. E2cm: Early exit via class means for efficient supervised and unsupervised learning. In IEEE World Congress on Computational Intelligence (WCCI): International Joint Conference on Neural Networks (IJCNN), 2022.
Han et al. (2015) Song Han, Huizi Mao, and William J Dally. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149, 2015.
He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
Hinton et al. (2015) Geoffrey Hinton, Oriol Vinyals, Jeff Dean, et al. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2(7), 2015.
Howard (2022) J. Howard. Which image models are best? Kaggle, 2022. URL https://www.kaggle.com/code/jhoward/which-image-models-are-best.
Kaya et al. (2019) Yigitcan Kaya, Sanghyun Hong, and Tudor Dumitras. Shallow-deep networks: Understanding and mitigating network overthinking. In International conference on machine learning, pages 3301–3310. PMLR, 2019.
Krizhevsky et al. (2009) Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
Li et al. (2016) Hao Li, Asim Kadav, Igor Durdanovic, Hanan Samet, and Hans Peter Graf. Pruning filters for efficient convnets. arXiv preprint arXiv:1608.08710, 2016.
Liu et al. (2018) Zhuang Liu, Mingjie Sun, Tinghui Zhou, Gao Huang, and Trevor Darrell. Rethinking the value of network pruning. arXiv preprint arXiv:1810.05270, 2018.
Shen et al. (2020) Jianghao Shen, Yue Wang, Pengfei Xu, Yonggan Fu, Zhangyang Wang, and Yingyan Lin. Fractional skipping: Towards finer-grained dynamic cnn inference. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 5700–5708, 2020.
Teerapittayanon et al. (2016) Surat Teerapittayanon, Bradley McDanel, and Hsiang-Tsung Kung. Branchynet: Fast inference via early exiting from deep neural networks. In 2016 23rd International Conference on Pattern Recognition (ICPR), pages 2464–2469. IEEE, 2016.
Veit and Belongie (2018) Andreas Veit and Serge Belongie. Convolutional networks with adaptive inference graphs. In Proceedings of the European Conference on Computer Vision (ECCV), pages 3–18, 2018.
Wang et al. (2018) Xin Wang, Fisher Yu, Zi-Yi Dou, Trevor Darrell, and Joseph E Gonzalez. Skipnet: Learning dynamic routing in convolutional networks. In Proceedings of the European Conference on Computer Vision (ECCV), pages 409–424, 2018.