Proton induced deuteron knockout reaction as a probe of an isoscalar proton-neutron pair in nuclei

We consider the ¹⁶O($p,pd$)¹⁴N^∗ reaction in normal kinematics; in the final channel ¹⁴N is assumed to be in the second $1^{+}$ excited state. The incoming proton is labeled as particle 0, and the outgoing proton and deuteron are labeled as particles 1 and 2, respectively. We denote the target (residual) nucleus ¹⁶O (¹⁴N^∗) by A (B) and its mass number by $A$ ($B$). In what follows, $\hbar\bm{K}_{i}$, $E_{i}$, and $T_{i}$ represent the momentum, the total energy, and the kinetic energy of particle $i$ ($=0,1,2,\textrm{A},\textrm{or B}$), respectively. The solid angle of the outgoing particle $j$ ($=1\textrm{ or }2$) is denoted by $\Omega_{j}$. The quantities with and without the superscript L represent that we evaluate these in the laboratory (L) and $p$-A center-of-mass (c.m.) frames, respectively.

In the distorted wave impulse approximation (DWIA) framework, the transition amplitude of the A($p,pd$)B reaction is given by

	$\displaystyle T$	$\displaystyle=\left\langle\chi^{(-)}_{1,\bm{K}_{1}}(\bm{R}_{1})\phi_{d}(\bm{r})\chi^{(-)}_{2,\bm{K}_{2}}(\bm{R}_{2})\right|$
		$\displaystyle\qquad\times t_{pd}(\bm{s})\left|\chi^{(+)}_{0,\bm{K}_{0}}(\bm{R}_{0})\phi_{d}(\bm{r})\varphi_{pn}(\bm{R}_{2})\right\rangle,$		(1)

where $\chi_{i,\bm{K}_{i}}$ with $i=0,1,\textrm{ and }2$ are the distorted waves of the $p$-A, $p$-B, and $d$-B systems, respectively. The coordinate between the incoming (outgoing) proton and A (B) is denoted by $\bm{R}_{0}$ ($\bm{R}_{1}$) and that between the outgoing deuteron and B by $\bm{R}_{2}$. As seen from Fig. 1, $\bm{R}_{2}$ also means the coordinate of the c.m. of the isoscalar ($T=0$) spin-triplet ($S=1$) $pn$ pair relative to B inside A. The scattering waves with the superscripts $(+)$ and $(-)$ satisfy the outgoing and incoming boundary conditions, respectively. $\phi_{d}$ is the $pn$ relative wave function in the ground state of deuteron and $t_{pd}$ is the effective interaction between $p$ and $d$. The coordinates relevant to $\phi_{d}$ and $t_{pd}$ are denoted by $\bm{r}$ and $\bm{s}$, respectively. $\varphi_{pn}$ defined by

$\displaystyle\varphi_{pn}(\bm{R}_{2})=\left\langle\Psi_{\textrm{B}}\right|\left.\Psi_{\textrm{A}}\right\rangle_{\xi_{\textrm{B}}}$

(2)

is the wave function between the c.m. of the $pn$ pair and B inside A; $\Psi_{\textrm{C}}$ ($\textrm{C}=\textrm{A or B}$) is the many-body wave function of C. In Eq. (2), it is understood that the integration is taken over all the intrinsic coordinates $\xi_{\textrm{B}}$ of B. A detailed description of $\varphi_{pn}$ is given in Sec. II.2.

We apply the asymptotic momentum approximation KazuYoshi16 to the distorted waves in Eq. (1) and obtain

$\displaystyle T\approx\tilde{t}_{pd}(\bm{\kappa}^{\prime},\bm{\kappa})\int d\bm{R}~{}F(\bm{R})\varphi_{pn}(\bm{R}).$

(3)

Here, $\bm{\kappa}$ ($\bm{\kappa}^{\prime}$) indicates the relative momentum between $p$ and $d$ in the initial (final) state, and we define $\tilde{t}_{pd}$ and $F$ as follows:

$\displaystyle\tilde{t}_{pd}(\bm{\kappa}^{\prime},\bm{\kappa})\equiv\left\langle\phi_{d}(\bm{r})e^{i\bm{\kappa}^{\prime}\cdot\bm{s}}\right|t_{pd}(\bm{s})\left|\phi_{d}(\bm{r})e^{i\bm{\kappa}\cdot\bm{s}}\right\rangle,$

(4)

$\displaystyle F(\bm{R})\equiv\chi^{*(-)}_{1,\bm{K}_{1}}(\bm{R})\chi^{*(-)}_{2,\bm{K}_{2}}(\bm{R})\chi^{(+)}_{0,\bm{K}_{0}}(\bm{R})e^{-2i\bm{K}_{0}\cdot\bm{R}/A}.$

(5)

Using the final-state on-the-energy-shell prescription, i.e.,

$\displaystyle\bm{\kappa}\approx\kappa^{\prime}\hat{\bm{\kappa}},$

(6)

in the evaluation of $\tilde{t}_{pd}$, we find

$\displaystyle\frac{\mu^{2}_{pd}}{(2\pi\hbar^{2})^{2}}\frac{1}{6}\left|\tilde{t}_{pd}(\bm{\kappa}^{\prime},\bm{\kappa})\right|^{2}\approx\frac{d\sigma_{pd}}{d\Omega_{pd}}(\theta_{pd},E_{pd}),$

(7)

where $d\sigma_{pd}/d\Omega_{pd}$ is the $p$-$d$ elastic differential cross section in free space with $\theta_{pd}$ and $E_{pd}$ being the c.m. scattering angle and the scattering energy, respectively. $\mu_{pd}$ is the reduced mass of the $p$-$d$ system.

The triple differential cross section (TDX) for the A($p,pd$)B reaction is then given by

$\displaystyle\frac{d^{3}\sigma}{dE^{\textrm{L}}_{1}d\Omega^{\textrm{L}}_{1}d\Omega^{\textrm{L}}_{2}}=F_{\textrm{kin}}C_{0}\frac{d\sigma_{pd}}{d\Omega_{pd}}(\theta_{pd},E_{pd})\left|\bar{T}\right|^{2},$

(8)

where

$\displaystyle F_{\rm kin}\equiv J_{\textrm{L}}\frac{K_{1}K_{2}E_{1}E_{2}}{(\hbar c)^{2}}\left[1+\frac{E_{2}}{E_{\textrm{B}}}+\frac{E_{2}}{E_{\textrm{B}}}\frac{\bm{K}_{1}\cdot\bm{K}_{2}}{K_{2}}\right]^{-1},$

(9)

$\displaystyle C_{0}\equiv\frac{E_{0}}{(\hbar c)^{2}K_{0}}\frac{\hbar^{4}}{(2\pi)^{3}\mu^{2}_{pd}},$

(10)

and

$\displaystyle\bar{T}\equiv\int d\bm{R}~{}F(\bm{R})\varphi_{pn}(\bm{R}).$

(11)

In Eq. (9), $J_{\textrm{L}}$ is the Jacobian from the $p$-A c.m. frame to the L frame.

Once all the distorting potentials are switched off, i.e., the plane wave impulse approximation (PWIA) is adopted, $\bar{T}$ turns out to be the Fourier transform of $\varphi_{pn}(\bm{R})$:

$\displaystyle\bar{T}\approx\int d\bm{R}~{}e^{-i\bm{K}_{pn}\cdot\bm{R}}\varphi_{pn}(\bm{R}),$

(12)

where $\bm{K}_{pn}$ is given by

$\displaystyle\bm{K}_{pn}=\bm{K}_{1}+\bm{K}_{2}-\left(1-\frac{2}{A}\right)\bm{K}_{0}.$

(13)

By assuming the residual nucleus B is a spectator, one can interpret $\bm{K}_{pn}$ as the momentum of the c.m. of the $pn$ pair.

In the recoilless (RL) condition, which is characterized by $K_{pn}=0$, one finds

$\displaystyle\bar{T}\approx\int d\bm{R}~{}\varphi_{pn}(\bm{R})\equiv\mathcal{A}_{pn}.$

(14)

This clearly shows that the TDX in the RL condition reflects the total amplitude $\mathcal{A}_{pn}$ of the $pn$ pair.

We apply the nuclear energy-density functional (EDF) method to describing microscopically the wave function of the $pn$ pair. In a framework of the nuclear EDF, the $pn$-pair-removed excited states in ¹⁴N are described in the proton-neutron hole-hole Random-Phase Approximation (pn-hhRPA) KenYoshi14 considering the ground-state of ¹⁶O as an RPA vacuum; $\displaystyle|\Psi_{\textrm{B}}\rangle=\Gamma^{\dagger}|\Psi_{\textrm{A}}\rangle$, where $\hat{\Gamma}^{\dagger}$ represents the RPA phonon operator;

$\displaystyle\hat{\Gamma}^{\dagger}=\sum_{ii^{\prime}}X_{ii^{\prime}}\hat{b}^{\dagger}_{p,i}\hat{b}^{\dagger}_{n,i^{\prime}}-\sum_{mm^{\prime}}Y_{mm^{\prime}}\hat{b}^{\dagger}_{n,m^{\prime}}\hat{b}^{\dagger}_{p,m}.$

(15)

Here, $\hat{b}^{\dagger}_{p,i}$ ($\hat{b}^{\dagger}_{n,i^{\prime}}$) create a proton (neutron) hole in the single-particle level $i$ ($i^{\prime}$) below the Fermi level, and $\hat{b}^{\dagger}_{p,m}$ ($\hat{b}^{\dagger}_{n,m^{\prime}}$) create a proton (neutron) hole above the Fermi level. Note that the backward-going amplitudes $Y$ vanish if the ground-state correlation in ¹⁶O is neglected. The single-particle basis is obtained as a self-consistent solution of the Skyrme-Hartree-Fock (SHF) equation.

The $S=1$ $pn$-pair-removal transition density that we need for the transition amplitude is given as

$\displaystyle\delta\bar{\rho}_{\mu}(\bm{r}_{n},\bm{r}_{p})=\frac{1}{2}\sum_{\sigma\sigma^{\prime}}(-2\sigma^{\prime})\left\langle\sigma^{\prime}|\bm{\sigma}_{\mu}|\sigma\right\rangle\left\langle\Psi_{\textrm{B}}|\hat{\psi}_{n}(\bm{r}_{n}-\!\sigma^{\prime})\hat{\psi}_{p}(\bm{r}_{p}\sigma)-\hat{\psi}_{p}(\bm{r}_{p}-\!\sigma^{\prime})\hat{\psi}_{n}(\bm{r}_{n}\sigma)|\Psi_{\textrm{A}}\right\rangle,$

(16)

where $\bm{\sigma}=(\sigma_{-1},\sigma_{0},\sigma_{+1})$ denotes the spherical components of the Pauli spin matrices, and $\hat{\psi}_{q}(\bm{r}\sigma)$ the nucleon annihilation operator at the position $\bm{r}$ with the spin direction $\sigma=\pm 1/2$ expanded in the single-particle basis with $q=n$ or $p$. Since the transition density is spherical in spin space, we have only to consider one of the components for $\mu$. Here, we take the $\mu=0$ component of the wave function.

From Eqs. (1), (2), and (16), we can regard the transition density $\delta\bar{\rho}_{0}$ as

$\displaystyle\delta\bar{\rho}_{0}(\bar{\bm{R}},\bm{r})\approx\varphi_{pn}(\bm{R})\phi_{d}(\bm{r}),$

(17)

where $\bar{\bm{R}}=(\bm{r}_{n}+\bm{r}_{p})/2$ and $\bm{r}=\bm{r}_{p}-\bm{r}_{n}$ and

$\displaystyle\varphi_{pn}(\bm{R})\equiv\frac{\delta\bar{\rho}_{0}(\bm{R},0)}{\phi_{d}(0)}=\hat{\varphi}_{pn}(R)Y_{00}(\Omega_{\bm{R}}).$

(18)

Thus, in evaluating $\varphi_{pn}$, we consider the $pn$ pair is $S$-wave and a point particle, namely $\bm{r}=0$. The use of Eqs. (17) and (18) means that the component of the ¹⁶O wave function that contains a deuteron is selected out. This treatment is consistent with the DWIA framework described in Sec. II.1.

With this, the $pn$-pair-removal transition strength is given by

$\displaystyle 3\left|4\pi\int^{\infty}_{0}dR~{}R^{2}\hat{\varphi}_{pn}(R)\phi_{d}(0)\right|^{2},$

(19)

where the factor three comes from the sum of $\mu=-1$, 0, and 1 components.

To obtain the single-particle basis used in the pn-hhRPA calculation, the SHF equation is solved in cylindrical coordinates $\bm{r}=(r,z,\phi)$ with a mesh size of $\Delta r=\Delta z=0.6$ fm and with a box boundary condition at $(r_{\textrm{max}},z_{\textrm{max}})=(14.7,14.4)$ fm. The axial and reflection symmetries are assumed in the ground state, and the ground-state of ¹⁶O is calculated to be spherical. More details of the calculation scheme are given in Ref. KenYoshi13 . The SGII interaction NVGiai81 is used for the particle-hole (ph) channel, and the density-dependent contact interaction defined by

	$\displaystyle v_{\textrm{pp}}$	$\displaystyle(\bm{r}\sigma\tau,\bm{r}^{\prime}\sigma^{\prime}\tau^{\prime})=$
		$\displaystyle V_{0}\frac{1+P_{\sigma}}{2}\frac{1-P_{\tau}}{2}\left[1-\frac{\rho(\bm{r})}{\rho_{0}}\right]\delta(\bm{r}-\bm{r}^{\prime})$		(20)

is employed for the particle-particle (pp) channel. Here, $\rho_{0}$ is $0.16$ fm^-3 and $\rho(\bm{r})=\rho_{p}(\bm{r})+\rho_{n}(\bm{r})$. We adopt three values $-100$, $-490$, and $-600$ MeV fm³ for the pairing strength $V_{0}$.

For the distorting potentials of proton, the EDAD1 parameter set of the Dirac phenomenology SHama90 ; EDCoop93 is used, whereas we employ the global optical potential by An and Cai HAn06 for deuteron. We construct the Coulomb potential in each distorting potential by assuming a uniformly charged sphere with the radii of $r_{0}C^{1/3}~{}(C=A\textrm{ or }B)$ with $r_{0}$ being $1.41$ fm. Nonlocality corrections to the distorted waves of deuteron and proton are made by multiplying the wave functions by the Perey factor Per63 with the 0.54 fm of the range of nonlocality and the Darwin factor SHama90 ; Arn81 , respectively. For the $p$-$d$ elastic cross section in Eq. (8), we take the experimental data from Refs. MDavi63 ; CCKim64 ; KKuro64 ; FHin68 ; SNBun68 ; TACahi71 ; NEBooth71 ; HShimi82 ; KSaga94 ; KSeki02 ; KHata02 ; KErm05 with the Lagrange interpolation with respect to the scattering angle and energy. The kinematics of all the particles are treated relativistically. The Møller factor Mol45 ; Ker59 is taken into account to describe the transformation of the $p$-$d$ transition matrix from the $p$-$d$ c.m. frame to the $p$-A c.m. frame.

We briefly mention the structure of the calculated low-lying $1^{+}$ states in ¹⁴N in the present framework before discussing the TDX. Figure 2 shows the $S=1$ $pn$-pair-removal transition-strength distributions. The excitation energy is defined with respect to the excitation energy of the simplest configuration of $(p_{1/2})^{-2}$ coupled to $T=0,S=1$ in ¹⁶O. The lowest state and the second lowest state for each pairing strength correspond to the ground $1^{+}$ state and the $1^{+}_{2}$ state that we are interested in, respectively. They are constructed by mainly the $(\nu p_{1/2})^{-1}(\pi p_{1/2})^{-1}$ configuration, and the superposition of the $(\nu p_{1/2})^{-1}(\pi p_{3/2})^{-1}$ and $(\nu p_{3/2})^{-1}(\pi p_{1/2})^{-1}$ configurations, respectively. With an increase of the pairing strength, the energies become lower and the strengths get enhanced for both states. For the case of $V_{0}=-600$ MeV fm³, the $(p_{3/2})^{-2}$ configuration is not negligible for enhancing the transition strength to the $1^{+}_{2}$ state. Therefore, the collectivity of the $1^{+}_{2}$ state becomes stronger with an increased pairing strength.

The question arisen here is how much of the pairing strength we should employ. We are going to look at the energy difference of the $1^{+}$ states; $\Delta E=E_{1^{+}_{2}}-E_{1^{+}_{1}}$. For the case of $V_{0}=-100$, $-490$, and $-600$ MeV fm³, the calculated $\Delta E$ is $5.41$, $4.12$, and $3.48$ MeV, respectively, while $\Delta E=3.95$ MeV experimentally. We can thus say that the pairing strengths $V_{0}=-490$ and $-600$ MeV fm³ are a reasonable choice in the present study.

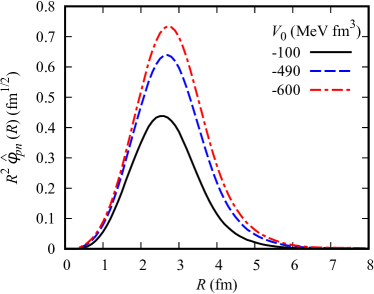
Next, we check the behavior of $\varphi_{pn}(\bm{R})$. The radial components of $\varphi_{pn}(\bm{R})$ with $V_{0}=-100$ MeV fm³ (solid line), $-490$ MeV fm³ (dashed line), and $-600$ MeV fm³ (dot-dashed line), respectively, are shown in Fig. 3. It should be noted that each line is multiplied by $R^{2}$. One can clearly find that the stronger the pair interaction is, the larger the amplitude of $R^{2}\hat{\varphi}_{pn}(R)$ is, i.e., the stronger collectivity the $pn$ pair has. Note that in the $V_{0}\rightarrow 0$ limit, the independent-particle picture of ¹⁶O is realized. Then, the peak of the $R^{2}\hat{\varphi}_{pn}(R)$ will almost disappear.

In Fig. 4 we show the TDX for the ¹⁶O($p,pd$)¹⁴N^∗ reaction at $101.3$ MeV as a function of $T^{\textrm{L}}_{1}$. The emission angle of particle 1 is fixed at $(\theta^{\textrm{L}}_{1},\phi^{\textrm{L}}_{1})=(40.1^{\circ},0^{\circ})$ and that for particle 2 at $(\theta^{\textrm{L}}_{2},\phi^{\textrm{L}}_{2})=(40.0^{\circ},180^{\circ})$; we follow the Madison convention. At $T^{\textrm{L}}_{1}\sim 52$ MeV, the RL condition is almost satisfied. This kinematical condition corresponds to $E_{pd}\sim 56$ MeV and $\theta_{pd}\sim 68^{\circ}$ for the $p$-$d$ scattering. The results using $\hat{\varphi}_{pn}$ calculated with $V_{0}=-100$, $-490$, and $-600$ MeV fm³ are shown by the solid, dashed, and dot-dashed lines, respectively. One sees a clear correspondence between $V_{0}$ and the TDX. In other words, the height of the TDX reflects the collectivity of the $pn$ pair that forms deuteron in ¹⁶O. Unfortunately, however, it is difficult to make a quantitative comparison of the current results with experimental data. This is mainly because of the approximate treatment of $\varphi_{pn}$ in Eq. (18); the TDX of knockout reactions is known to be quite sensitive to the radial distribution of the wave function of the particle to be knocked out, which may be affected by the approximation of Eq. (18) in the present case. A sensitivity test of the TDX on $\varphi_{pn}$ is given in Appendix. Besides, there may exist other reaction mechanisms that are not considered in this study; we come to this point in Sec. IV. Nevertheless, the $V_{0}$ dependence of the TDX can safely be investigated, which is our primary objective of this study.

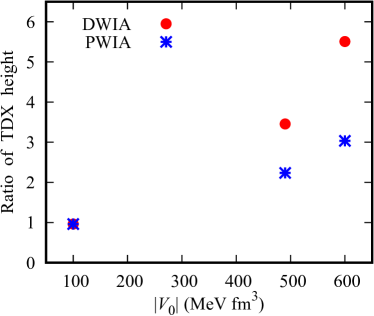
To see the $V_{0}$-TDX correspondence more clearly, in Fig. 5 we show the values of the TDX at $T^{\textrm{L}}_{1}=52$ MeV, the TDX height, in ratio to the value calculated with $V_{0}=-100$ MeV fm³. The result of the DWIA (PWIA) is represented by the circles (asterisks). As mentioned above, $T^{\textrm{L}}_{1}=52$ MeV corresponds to the RL condition. In the PWIA limit, one expects from Eqs. (8) and (14) a clear relation between the TDX height and $|\mathcal{A}_{pn}|^{2}$, as shown by the asterisks. When the distortion is included, the ratio is found to increase further. This indicates that the TDX height observed in the ¹⁶O($p,pd$)¹⁴N^∗ reaction at $101.3$ MeV is more sensitive to the $pn$ pair amplitude $\hat{\varphi}_{pn}$ than naively expected in the PWIA limit. Quantitative extraction of the collectivity through a comparison with experimental data, however, requires a more accurate description of the ($p,pd$) process as mentioned in Sec. I.

Figure 6 shows the transition matrix density (TMD) $\delta(R)$, which was originally introduced as a weighting function for the mean density of the ($p,2p$) reaction in Ref. KHata97 . The definition of the TMD is given by

$\displaystyle\delta(R)=T^{*}I(R),$

(21)

where $I(R)$ is the complex radial amplitude of $T$ of Eq. (1), i.e.,

$\displaystyle T=\int^{\infty}_{0}dR~{}I(R).$

(22)

The solid lines denotes the real part of the TMD, which can be interpreted as a radial distribution of the TDX as discussed in Refs. KHata97 ; TNoro99 ; TWaka17 . To make this interpretation plausible, however, the real part of the TMD should not have a large negative value. Another condition is that the imaginary part of the TMD is nearly equal to 0 for all $R$. As one sees from Fig. 6, neither of the two conditions is satisfied well. This indicates that the interference between amplitudes at different $R$ is strong. Furthermore, the TMD is finite even at small $R$, which means the nuclear absorption is not enough to mask the interior region in the evaluation of the transition matrix. These features are completely different from for ($p,p\alpha$) reactions discussed in Refs. MLyu18 ; KazuYoshi18 . In other words, the distortion effect in the ($p,pd$) reaction investigated in this study is found to be rather complicated and the mechanism for the increase in the relative TDX height due to the distortion is still unclear.