Proton and deuteron mass radii from near-threshold -meson photoproduction
Abstract
We analyze the exclusive -meson photoproduction on both hydrogen and deuterium targets based on the published data of CLAS, SAPHIR and LEPS collaborations. A dipole-form scalar gravitational form factor is applied to describe the -dependence of the differential cross section. Based on the average of all the near-threshold data from CLAS, SAPHIR and LEPS, we find that the proton and deuteron mass radii are fm and fm respectively. The coherent and near-threshold quarkonium photoproduction seems to be sensitive to the radius of the hadronic system. The vector-meson-dominance model together with a low-energy QCD theorem well describe the data of near-threshold photoproduction on the hadronic systems.
pacs:
12.38.-t, 14.20.DhHadronic matter accounts for nearly all the mass of the visible universe. However many mysteries remain concerning hadron structure, such as how the hadron mass, spin and pressure are fixed by strong interactions of the quarks and gluons inside Ji (1995a, b); Ji and Liu (2021); Ji (1997a, 1998, b); Teryaev (2016); Polyakov (2003); Polyakov and Schweitzer (2018); Burkert et al. (2018). The inside of a hadron is governed by quantum chromodynamics (QCD) theory. In particular, the strong force carrier in QCD, the gluon, is believed to play a dominant role in determining the basic properties of the proton, such as its mass. X. Ji found that the proton mass scale is fixed by the QCD quantum trace anomaly Ji (1995a, b); Ji and Liu (2021); Yang et al. (2018); Wang et al. (2020); Rodini et al. (2020); Metz et al. (2020).
The mechanical properties of the hadronic system are well encoded in the energy-momentum tensor (EMT) , and the gravitational form factors (GFF) are the EMT matrix elements in the hadron state Kobzarev and Okun (1962); Pagels (1966); Ji (1997a); Teryaev (2016); Polyakov (2003); Polyakov and Schweitzer (2018). The EMT characterizes the response of the hadronic system to the change of the space-time metric, hence the GFF could be directly accessed via the graviton scattering but with almost zero hope in reality. GFF contains three fundamental properties of the hadron: mass, spin and D-term (pressure and shear) Pagels (1966); Ji (1997a, 1998); Teryaev (2016); Polyakov (2003); Polyakov and Schweitzer (2018). Due to the significance of GFF, searching for the experimental ways of constraining GFF is of high interests.
Now the proton mass radius is the subject of heated discussions. This mass radius characterizes how the mass is distributed inside the proton, namely the mass density distribution. Experimentally, the form factors as a function of momentum transfer () are measured in elastic scattering processes, which correspond to the Fourier transforms of the various density distributions. Theoretically, the mass radius of a hadron can be defined in terms of the scalar GFF , the form factor of the trace of the QCD EMT, in a nonrelativistic and weak gravitational field approximation Kharzeev (2021). Similar to the definition of the charge radius, the mass radius is defined as the derivative of the form factor at zero momentum transfer Kharzeev (2021); Miller (2019),
| (1) |
with . Theoretically, the density distribution inside the proton is the expectation value of the component of EMT. Assuming local equilibrium, the EMT can be expanded in a gradient expansion, and it is entirely characterized by the density and the pressure at leading order of the expansion. For the stable system, the pressure-volume work vanishes. In this case, in the Landau frame, is equal to the trace of EMT. Therefore it is not surprising that, at small momentum transfer, the density distribution may be constrained by an experimental determination of the scalar form factor .
Following the proposal by D. Kharzeev Kharzeev (2021, 1996); Kharzeev et al. (1999); Fujii and Kharzeev (1999), we describe the near-threshold cross section for heavy quarkonium photoproduction using the QCD Van der Waals force of leading-twist gluon operators derived from a QCD low energy theorem and a vector-meson-dominance (VMD) model. The theoretical uncertainties are argued to be under control in the nonrelativistic limit. The differential cross section for quarkonium photoproduction in the small- region and near the production threshold can be described with the scalar GFF Kharzeev (2021), which is written as,
| (2) |
Therefore the near-threshold quarkonium photoproduction data is sensitive to the GFF and the mass distribution. With this theoretical framework and the dipole form of GFF, , the mass radius of the proton has been extracted from vector meson production data on the hydrogen targets Kharzeev (2021); Wang et al. (2021). By analyzing the GlueX data of J/ photoproduction near the threshold Ali et al. (2019), Kharzeev extracted the mass radius of the proton to be fm Kharzeev (2021).
The VMD model is successful in describing the vector meson photoproduction process, at least as the first step of more extensive theoretical studies. In the VMD model, a real photon fluctuates into a virtual vector meson, which subsequently scatters off the proton target. This model assumption is based on the fact that the vector meson has the same quantum numbers of the photon. Recently, the VMD model was used for determining the , and J/ scattering lengths Strakovsky et al. (2015, 2020a, 2020b). These analyses show that the J/ scattering length is much smaller than that of and . This suppressed interaction in system can be explained with the “young” vector meson effect Strakovsky et al. (2021); Feinberg (1980). If the mass of the quark pair is far from the photon mass, then the vector meson - proton interaction is strongly suppressed due to the small size of the “young” vector meson just created by the photon. The pair lacks sufficient time to form the complete wave function of J/, and its radius is much smaller than that of J/. To avoid the influence that may associated with the “young” vector meson effect, it is necessary and worthy trying to look at the light vector meson photoproduction.
The vector meson is a typical quarkonium which do not has the same type of quark of the proton valence components. Thus the meson interacts with the proton via the gluon exchanges which is argued to be sensitive to the scalar GFF of the proton. Moreover, the minimum momentum transfer square is around 0.2 GeV2, for the current available -photoproduction data near threshold. The large makes the use of VMD model questionable. Hence the data of small is better for the study of the interaction between the vector meson and the proton, applying the VMD model.
An interesting question is whether or not the scalar GFF is also applicable to the near-threshold quarkonium production on the atomic nucleus (such as the deuteron). The CLAS and LEPS collaborations have measured the coherent -photoproduction cross sections on hydrogen and deuterium targets Seraydaryan et al. (2014); Mibe et al. (2007, 2005); Chang et al. (2008). Due to the high luminosity of the accelerator and the large acceptance of the CLAS spectrometer, the CLAS data is of high precision over a wide range Seraydaryan et al. (2014); Mibe et al. (2007). SAPHIR collaboration also has measured the -photoproduction on the hydrogen target near the reaction threshold Barth et al. (2003). These exclusive -photoproduction data provide an excellent opportunity to determine the mass radii of the proton and the deuteron, and to examine the scalar GFF interpretation of the quarkonium production mechanism in the nonperturbative region.
In this paper, we present simultaneous analyses of the proton mass radius and the deuteron mass radius using CLAS, SAPHIR and LEPS data, following the previous studies on the proton mass radius Kharzeev (2021); Wang et al. (2021). The systematic uncertainty from varying the range of the fit is also investigated, thanks to the wide range of CLAS data.
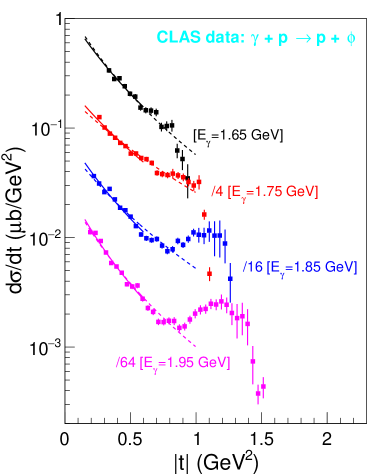
| (GeV) | 1.65 | 1.75 | 1.85 | 1.95 |
|---|---|---|---|---|
| (fm) |
Fig. 1 shows the CLAS collaboration’s near-threshold differential cross section data for photoproduction on the proton. It has been suggested that the -dependence of the differential cross section is described by the scalar GFF of the proton. Some fits based on Eq. (2) are shown in the figure. The differential cross section data are well reproduced by the dipole form of the scalar GFF. However in the large- region, approaching , we see the cross section rising with . This behavior in the large- region may be due to the direct -radiation contributions from -channel and -channel with coupling or coupling Anciant et al. (2000); Laget (2000); Zhao et al. (2001); Titov and Lee (2003); Williams (1998); Titov et al. (1999a, b); Oh and Bhang (2001).
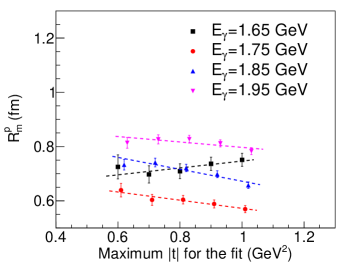
In order to avoid such -channel or -channel contamination, we narrow the fitting range of towards the small- region. We studied the fits restricted in quite different ranges carefully, as the CLAS data covers a wide range and of high precision. To understand the effect of the large- data on the extraction of the scalar GFF, we perform a series of fits excluding the large- data requiring GeV2, GeV2, GeV2, GeV2, and GeV2 respectively. With each fit, we extract the parameterized scalar GFF and by calculating the derivative at GeV2 we find the mass radius. The obtained proton mass radii from these fits are shown in Fig. 2, as a function of the cut at large . We find that, beneath 1 GeV2, the extracted mass radius does not depend strongly on the choice of large- cut. This is probably because the -channel or -channel contribution only dominates in the large- region where the error bars are comparatively large Laget (2000); Zhao et al. (2001); Titov and Lee (2003); Williams (1998); Titov et al. (1999a, b); Oh and Bhang (2001). Therefore the large- data hardly affects the fits. The uncertainty from varying the fitting range of is of the same order as the statistical uncertainty in the data.
With the linear extrapolations of the dependence on the fitting range shown in Fig. 2, we provide the mass radii in Table 1. We see that the extracted mass radius depends weakly on the energy of the incident photon. Since the formulism based on the GFF works mainly in the low energy limit, the reliable mass radius should be given by the data closest to the production threshold. Hence, from the CLAS data, the mass radius of the proton should be fm, as determined from the photoproduction data at GeV (the most near-threshold photon energy of CLAS data).
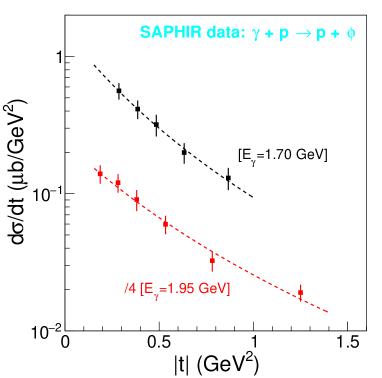
The proton mass radius from the proton data of LEPS collaboration is provided in the previous analysis, which is in average Wang et al. (2021). Though with fewer data points and larger statistical uncertainties, SAPHIR collaboration has also measured the near-threshold photoproduction on the proton two decades ago Barth et al. (2003). The differential cross section data of SAPHIR are shown in Fig. 3. From the fits of dipole GFF, the SAPHIR data give the proton mass radii to be fm and fm at GeV and GeV, respectively (summarized in Table 2). The CLAS, LEPS and SAPHIR data are more or less consistent with each other.
By looking at the average of all the near-threshold data of CLAS, LEPS and SAPHIR, the proton mass radius is combined to be fm. Compared to the analysis of the J/-photoproduction data Kharzeev (2021), the extracted proton mass radius from -photoproduction data is much smaller. This discrepancy is maybe due to the different strengths of the “young” vector meson effect for J/ and , or that the VMD model is no longer effective in the large region. More theoretical studies are needed to understand the dependence on the size of the vector meson probe and the validity of applying VMD model in case of J/.
| (GeV) | ||
|---|---|---|
| (fm) |
| (GeV) | ||
|---|---|---|
| (fm) |
| (GeV) | |||
|---|---|---|---|
| (fm) |
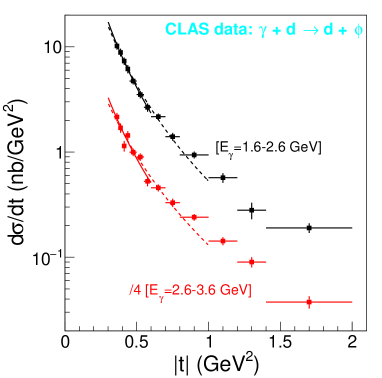
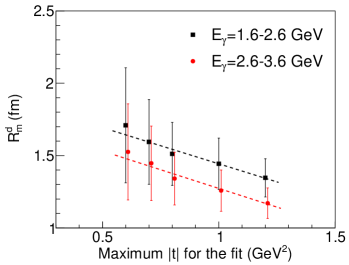
In the following, we perform a similar analysis on the deuteron data. First, we fit the differential cross section data on the deuteron of CLAS collaboration, applying the VMD model and the scalar GFF. Still surprisingly, the dipole form GFF describes well the coherent photoproduction data on the deuterium target, which is shown in Fig. 4. Second, we study the mass radii of the deuteron extracted from the fits of different ranges (see Fig. 5). In Fig. 5, we see a relatively stronger dependence on the -maximum boundary of the fitting range, in comparison to the proton data. One reason is probably that there is a stronger contribution from baryonic or nuclear resonances for the deuteron data at the relatively higher photon energy. By linearly extrapolating the fitting range to 0 GeV2, the mass radii of the deuteron at zero momentum transfer are obtained, which are listed in Table 3. Finally, as suggested by the most near-threshold data of CLAS ( GeV), the mass radius of the deuteron is estimated to be fm.
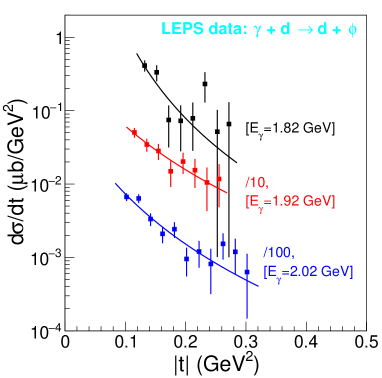
LEPS collaboration also measured the near-threshold photoproduction on the deuteron Chang et al. (2008). The statistical errors are much larger compared to the CLAS data. The range of the variable is also much narrower, which is not good for the extraction of the slope of the differential cross section as a function of . Nevertheless, the -dependence of LEPS data also can be described with the dipole form factor. Fig. 6 shows the fits compared to the cross-section data from LEPS. The extracted mass radii of the deuteron at different energies are listed in Table 4. The LEPS data is closer to GeV2, and the obtained deuteron mass radius is consistent with the values extracted from CLAS data.
By looking at the average of all the near-threshold data of CLAS and LEPS, the deuteron mass radius is combined to be fm. Strikingly and similar to the proton case, the mass radius of the deuteron is also smaller than the world average of the charge radius of the deuteron (CODATA-2010 average is fm). The high precision data of the deuteron charge radius is from the Lamb shift in the spectrum of the muonic deuterium, which gives a value of fm Pohl et al. (2016). For both the proton and the deuteron, the mass radii are about fm smaller than the charge radii.
In summary, first, we verified that the VMD model and low-energy QCD theorem suggested by D. Kharzeev accurately describes the near-threshold quarkonium photoproduction. We find that the VMD model and the dipole-form GFF reproduce well the -dependence of the differential cross section of photoproduction on both the proton and the deuteron. Nevertheless, there should be more studies on the GFF and the mechanical properties of the hadronic system encompassing more experimental data in the future. Second, the mass radii of the proton and the deuteron are determined from the parameterized GFF extracted from the coherent and near-threshold photoproduction data from CLAS and LEPS collaborations. The mass radii are found to be smaller than the charge radii for both the proton and the deuteron. Third, the systematic uncertainty of the analysis is briefly investigated. The mass radius extracted from the -dependence of the cross section is not sensitive to the size of the fitting range as long as GeV2. The dependence of the extracted mass radius on the photon energy is not big. Judged by the CLAS data at several near-threshold energies, the model uncertainty from not-at-threshold effects is of the same order as the current statistical uncertainty for both the proton and the deuteron. Last, the systematic uncertainty related to the size of the vector meson probe needs more future theoretical investigations. The near threshold -photoproduction data gives larger mass radius compared to the J/-photoproduction data Kharzeev (2021).
To further check the GFFs and the mass distributions of the proton and the nuclei, the measurements of near-threshold photoproduction of J/ and will be performed at future Electron-Ion Colliders Abdul Khalek et al. (2021); Accardi et al. (2016); Chen (2018); Chen et al. (2020); Anderle et al. (2021).
Acknowledgements.
This work is supported by the Strategic Priority Research Program of Chinese Academy of Sciences under the Grant Number XDB34030301, the CAS Key Research Program of Frontier Sciences QYZDY-SSW-SLH006 and the National Natural Science Foundation of China under the Grant Numbers: 12005266, 11875296 and 11675223.References
- Ji (1995a) X.-D. Ji, Phys. Rev. Lett. 74, 1071 (1995a), arXiv:hep-ph/9410274 .
- Ji (1995b) X.-D. Ji, Phys. Rev. D 52, 271 (1995b), arXiv:hep-ph/9502213 .
- Ji and Liu (2021) X. Ji and Y. Liu, (2021), arXiv:2101.04483 [hep-ph] .
- Ji (1997a) X.-D. Ji, Phys. Rev. D 55, 7114 (1997a), arXiv:hep-ph/9609381 .
- Ji (1998) X.-D. Ji, Phys. Rev. D 58, 056003 (1998), arXiv:hep-ph/9710290 .
- Ji (1997b) X.-D. Ji, Phys. Rev. Lett. 78, 610 (1997b), arXiv:hep-ph/9603249 .
- Teryaev (2016) O. V. Teryaev, Front. Phys. (Beijing) 11, 111207 (2016).
- Polyakov (2003) M. V. Polyakov, Phys. Lett. B 555, 57 (2003), arXiv:hep-ph/0210165 .
- Polyakov and Schweitzer (2018) M. V. Polyakov and P. Schweitzer, Int. J. Mod. Phys. A 33, 1830025 (2018), arXiv:1805.06596 [hep-ph] .
- Burkert et al. (2018) V. D. Burkert, L. Elouadrhiri, and F. X. Girod, Nature 557, 396 (2018).
- Yang et al. (2018) Y.-B. Yang, J. Liang, Y.-J. Bi, Y. Chen, T. Draper, K.-F. Liu, and Z. Liu, Phys. Rev. Lett. 121, 212001 (2018), arXiv:1808.08677 [hep-lat] .
- Wang et al. (2020) R. Wang, J. Evslin, and X. Chen, Eur. Phys. J. C 80, 507 (2020), arXiv:1912.12040 [hep-ph] .
- Rodini et al. (2020) S. Rodini, A. Metz, and B. Pasquini, JHEP 09, 067 (2020), arXiv:2004.03704 [hep-ph] .
- Metz et al. (2020) A. Metz, B. Pasquini, and S. Rodini, Phys. Rev. D 102, 114042 (2020), arXiv:2006.11171 [hep-ph] .
- Kobzarev and Okun (1962) I. Y. Kobzarev and L. B. Okun, Zh. Eksp. Teor. Fiz. 43, 1904 (1962).
- Pagels (1966) H. Pagels, Phys. Rev. 144, 1250 (1966).
- Kharzeev (2021) D. E. Kharzeev, Phys. Rev. D 104, 054015 (2021), arXiv:2102.00110 [hep-ph] .
- Miller (2019) G. A. Miller, Phys. Rev. C 99, 035202 (2019), arXiv:1812.02714 [nucl-th] .
- Kharzeev (1996) D. Kharzeev, Proc. Int. Sch. Phys. Fermi 130, 105 (1996), arXiv:nucl-th/9601029 .
- Kharzeev et al. (1999) D. Kharzeev, H. Satz, A. Syamtomov, and G. Zinovjev, Eur. Phys. J. C 9, 459 (1999), arXiv:hep-ph/9901375 .
- Fujii and Kharzeev (1999) H. Fujii and D. Kharzeev, Phys. Rev. D 60, 114039 (1999), arXiv:hep-ph/9903495 .
- Wang et al. (2021) R. Wang, W. Kou, Y.-P. Xie, and X. Chen, Phys. Rev. D 103, L091501 (2021), arXiv:2102.01610 [hep-ph] .
- Ali et al. (2019) A. Ali et al. (GlueX), Phys. Rev. Lett. 123, 072001 (2019), arXiv:1905.10811 [nucl-ex] .
- Strakovsky et al. (2015) I. I. Strakovsky et al., Phys. Rev. C 91, 045207 (2015), arXiv:1407.3465 [nucl-ex] .
- Strakovsky et al. (2020a) I. I. Strakovsky, L. Pentchev, and A. Titov, Phys. Rev. C 101, 045201 (2020a), arXiv:2001.08851 [hep-ph] .
- Strakovsky et al. (2020b) I. Strakovsky, D. Epifanov, and L. Pentchev, Phys. Rev. C 101, 042201 (2020b), arXiv:1911.12686 [hep-ph] .
- Strakovsky et al. (2021) I. I. Strakovsky, W. J. Briscoe, L. Pentchev, and A. Schmidt, (2021), arXiv:2108.02871 [hep-ph] .
- Feinberg (1980) E. L. Feinberg, Sov. Phys. Usp. 23, 629 (1980).
- Seraydaryan et al. (2014) H. Seraydaryan et al. (CLAS), Phys. Rev. C 89, 055206 (2014), arXiv:1308.1363 [hep-ex] .
- Mibe et al. (2007) T. Mibe et al. (CLAS), Phys. Rev. C 76, 052202 (2007), arXiv:nucl-ex/0703013 .
- Mibe et al. (2005) T. Mibe et al. (LEPS), Phys. Rev. Lett. 95, 182001 (2005), arXiv:nucl-ex/0506015 .
- Chang et al. (2008) W. C. Chang et al., Phys. Lett. B 658, 209 (2008), arXiv:nucl-ex/0703034 .
- Barth et al. (2003) J. Barth et al., Eur. Phys. J. A 17, 269 (2003).
- Anciant et al. (2000) E. Anciant et al. (CLAS), Phys. Rev. Lett. 85, 4682 (2000), arXiv:hep-ex/0006022 .
- Laget (2000) J. M. Laget, Phys. Lett. B 489, 313 (2000), arXiv:hep-ph/0003213 .
- Zhao et al. (2001) Q. Zhao, B. Saghai, and J. S. Al-Khalili, Phys. Lett. B 509, 231 (2001), arXiv:nucl-th/0102025 .
- Titov and Lee (2003) A. I. Titov and T. S. H. Lee, Phys. Rev. C 67, 065205 (2003), arXiv:nucl-th/0305002 .
- Williams (1998) R. A. Williams, Phys. Rev. C 57, 223 (1998).
- Titov et al. (1999a) A. I. Titov, T. S. H. Lee, and H. Toki, Phys. Rev. C 59, R2993 (1999a), arXiv:nucl-th/9812074 .
- Titov et al. (1999b) A. I. Titov, T. S. H. Lee, H. Toki, and O. Streltsova, Phys. Rev. C 60, 035205 (1999b).
- Oh and Bhang (2001) Y.-s. Oh and H. C. Bhang, Phys. Rev. C 64, 055207 (2001), arXiv:nucl-th/0104068 .
- Pohl et al. (2016) R. Pohl et al. (CREMA), Science 353, 669 (2016).
- Abdul Khalek et al. (2021) R. Abdul Khalek et al., (2021), arXiv:2103.05419 [physics.ins-det] .
- Accardi et al. (2016) A. Accardi et al., Eur. Phys. J. A 52, 268 (2016), arXiv:1212.1701 [nucl-ex] .
- Chen (2018) X. Chen, PoS DIS2018, 170 (2018), arXiv:1809.00448 [nucl-ex] .
- Chen et al. (2020) X. Chen, F.-K. Guo, C. D. Roberts, and R. Wang, Few Body Syst. 61, 43 (2020), arXiv:2008.00102 [hep-ph] .
- Anderle et al. (2021) D. P. Anderle et al., Front. Phys. (Beijing) 16, 64701 (2021), arXiv:2102.09222 [nucl-ex] .