Also at ]Key Laboratory of Artificial Structures and Quantum Control (Ministry of Education), School of Physics and Astronomy, Shanghai Jiao Tong University, 800 Dong Chuan Road, Shanghai 200240, China Also at ]Key Laboratory of Artificial Structures and Quantum Control (Ministry of Education), School of Physics and Astronomy, Shanghai Jiao Tong University, 800 Dong Chuan Road, Shanghai 200240, China
Proposal for measuring Newtonian constant of gravitation at an exceptional point in an optomechanical system
Abstract
We develop a quantum mechanical method of measuring the Newtonian constant of gravitation, . In this method, an optomechanical system consisting of two cavities and two membrane resonators is used. The added source mass would induce the shifts of the eigenfrequencies of the supermodes. Via detecting the shifts, we can perform our measurement of . Furthermore, our system can features exceptional point (EP) which are branch point singularities of the spectrum and eigenfunctions. In the paper, we demonstrate that operating the system at EP can enhance our measurement of . In addition, we derive the relationship between EP enlarged eigenfrequency shift and the Newtonian constant. This work provides a way to engineer EP-assisted optomechanical devices for applications in the field of precision measurement of
I Introduction
Newton’s law of gravitation is often written as
| (1) |
where and are the masses of two particles, is the distance between them and is the gravitational constant. Though the absolute value of has been measured by many experiments [1, 2, 3], two big puzzles still exist nowadays. One is the value of G ramains the least preciously known of the fundamental constants [4]. The Committee on Data for Science and Technology (CODATA) recommended value of based on the 2014 adjustment is , and the relative measurement uncertainty is as high as [5]. The other puzzle is the experimental values of are not consistent with each other[6]. To resolve these puzzles strongly motivates us to develop different measurement methods [7].
In this paper, we develop a new method for determining . In our method, a quantum system consisting of two cavities and two membranes is considered. Gravitational force gradient originating from the source mass causes shifts of the resonant frequencies of two membranes, resulting the shifts of the eigenfrequencies of the supermodes emerging in our system. Based on this, we establish our measurement principles. Exceptional points are branch point singularities of the spectrum and eigenfunctions [8] which occur generically in eigenvalue problems that depend on a parameter[9]. Because EPs in open quantum and wave systems can exhibit a strong spectral response to perturbations[10], their potential applications in precision measurement have been investigated both theoretically[11, 12] and experimentally[13, 14]. In this paper, EP effect is investigated numerically. The relating results indicate that this effect can enhance the detection of the eigenfrequency shift. Furthermore, the relationship between eigenfrequency shift and Newtonian constant is established provided that our system is operated at EP. In summary, we propose an EP-based quantum mechanical method for measuring . Finally we expect our work can enrich the experimental approaches of determining .
The remainder of the paper is organized as follows: In Sec. II we demonstrate the theoretical framework, in Sec. III we present the measurement principles, in Sec. IV we summarize the paper and provide an outlook.
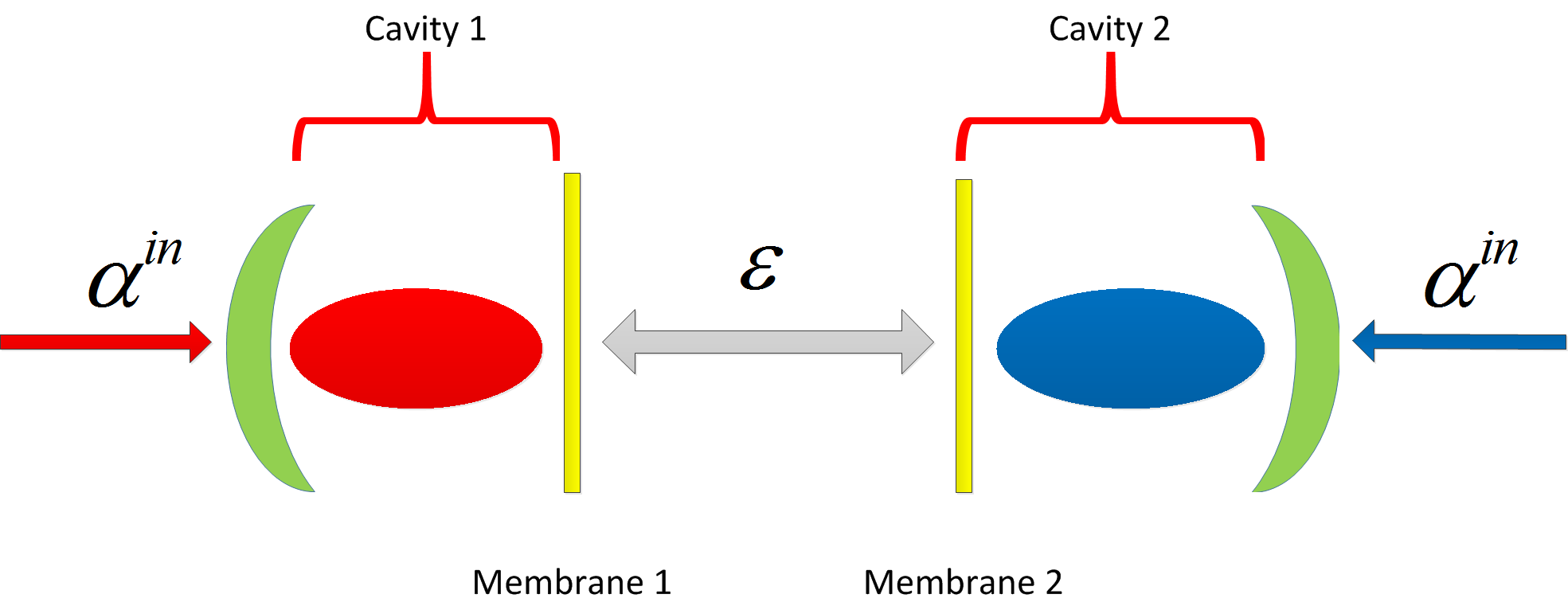
II Theoretical framework
We consider a system composed of two optomechanical cavities the two end-mirrors of which are two nanosized membrane resonators [15]. Cavity 1(2) is driven with a red (blue) detuned laser. By symmetrically driving the cavities we can engineer either mechanical gain or mechanical loss [16]. Note that at the gain and loss balance the system features EP. In the rotating frame of the driving fields, the Hamiltonian of the system could be written as ()
| (2) |
where
| (3) |
Here and are the annihilation bosonic field operators describing the optical and mechanical resonators. is the mechanical frequency of the resonator and is the optical detuning between the optical () and the cavity () frequencies. is the coupling strength between the two mechanical resonators, is the vacuum optomechanical coupling strength. The amplitude of the driving pump is .
The quantum Langevin equations (QLEs) for the operations of the optical and the mechanical modes are derived from Eq. (3) as
| (4) |
where optical () and mechanical () dissipations have been added, is defined as , and the amplitude of the driving pump has been substituted as in order to account for losses. The term () denotes the optical (thermal) Langevin noise at room temperature. We seek to investigate in the classical limit, where photon and phonon numbers are assumed large in the system, and noise terms can be neglected in our analysis. Then we can derive the following set of nonlinear equations:
| (5) |
Here and .
To identify the EP feature, we approach the limit cycle oscillations by the ansatz, . is a constant shift in the origin of the movement, is taken to be a slowly varying function of time, and is the mechanical locked frequency. According to [17], we can derive
| (6) |
where is the state vector and the effective Hamiltonian is
. Here and define the effective frequencies and the effective damping respectively. The optical spring effect and the optical damping are given by
| (7) |
and
| (8) |
,, , and is the Bessel function of the first kind of order . The eigenvalues of the effective Hamiltonian can be described as
| (9) |
with
| (10) |
The EP of our system appears if . The eigenfrequencies and the dissipations of the supermodes are defined as the real and imaginary parts of the eigenvalues, i.e.,, and . At the EP, both pairs of eigenfrequencies and dissipations coalesce, i.e., and .
For simplicity, we assume the two resonators are degenerated, causing . We adopt a weak driving regime, resulting . We further assume with . Then the eigenvalues of the Hamiltonian can be written as
| (11) |
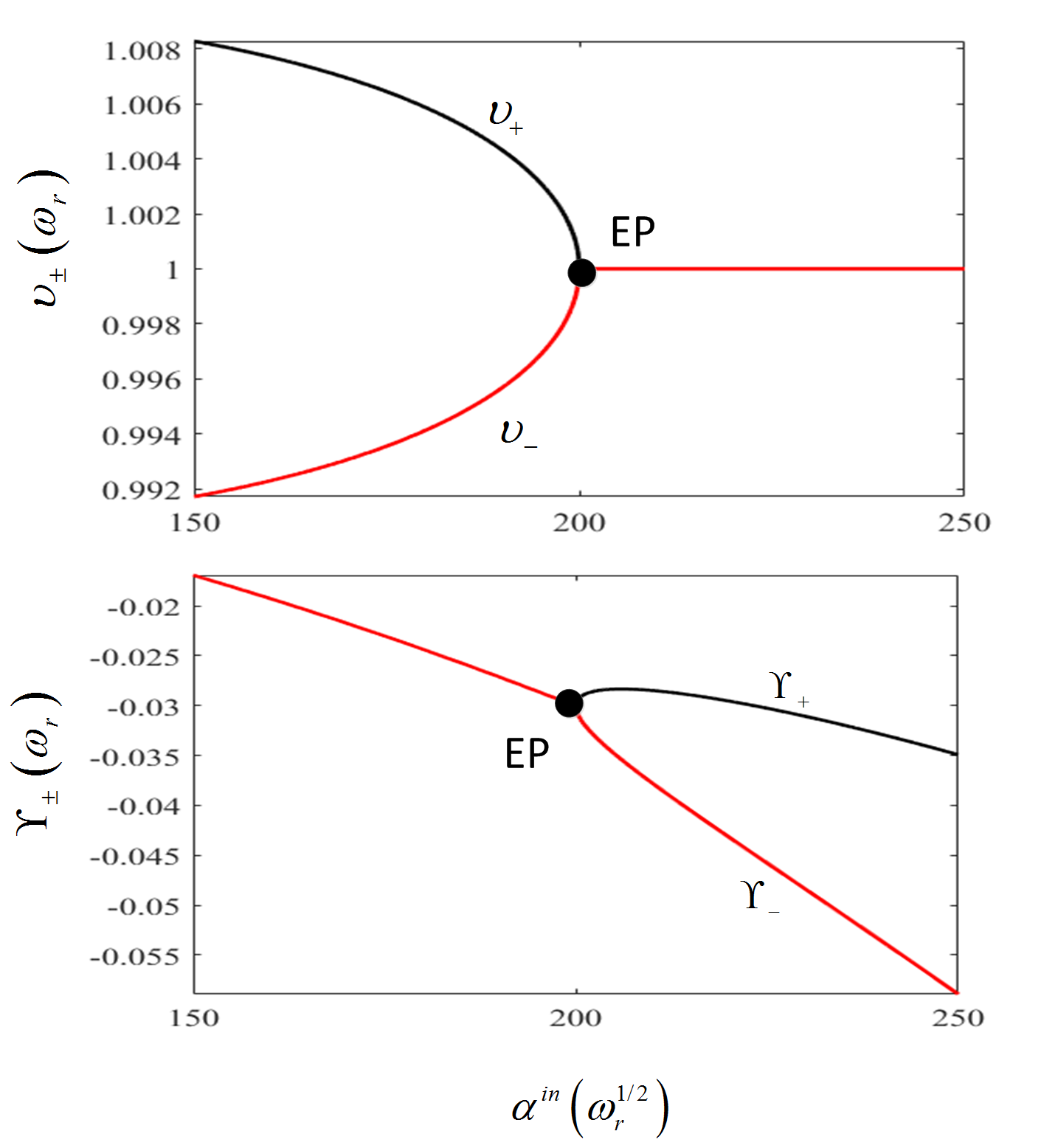
As a result, the EP condition is tranformed into , from which we derive that . Now we use an example to illustrate the EP feature (see Fig. 2). In this example, the parameters used are The corresponding EP is . From the figure, it is seen that two eigenfrequencies coalesce at the EP as well as two dissipations. Based on the above analysis about our system, we present the principles of measurement in the next section.
III Principles of measurement
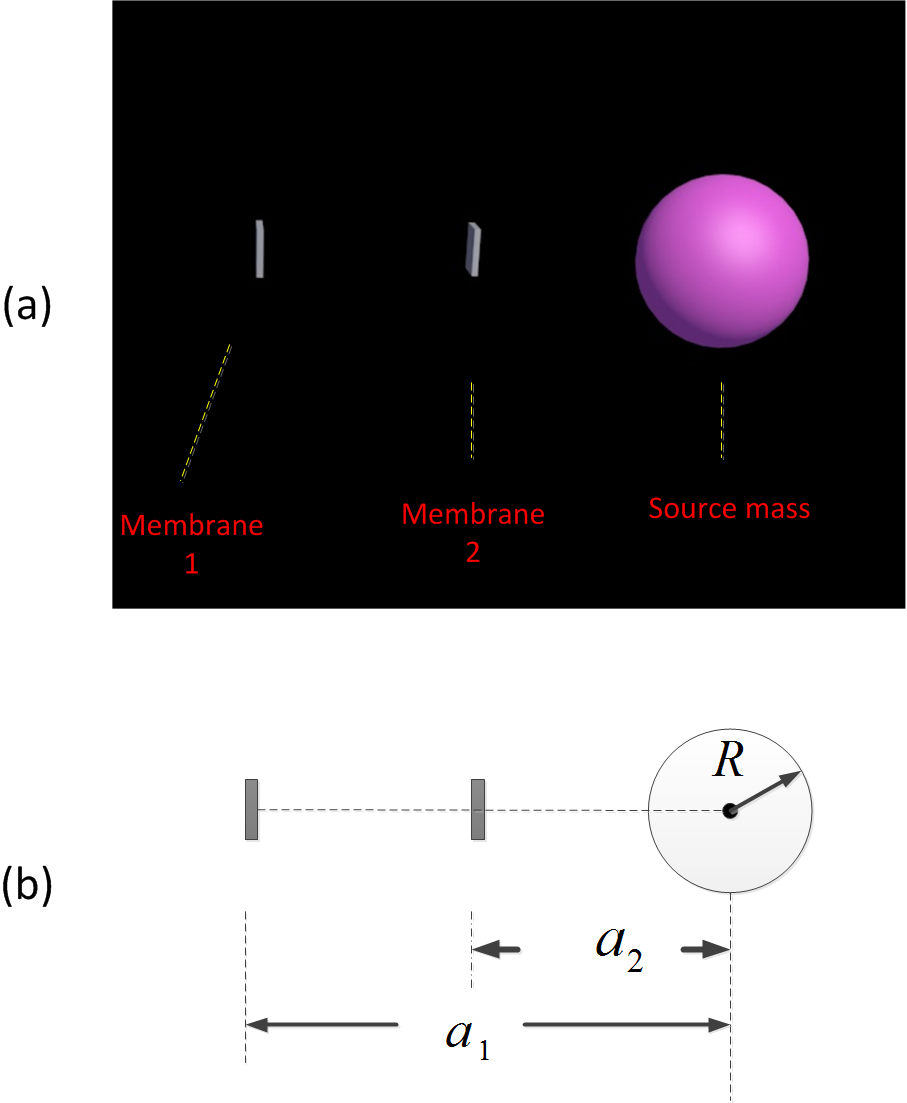
In our proposed method, a sphere with uniformly distributed mass , radius and density is utilized. This sphere and two membranes of our system are placed as shown in Fig. 3(a) Note that the sizes of two membrane resonators are much smaller than . The distances between two membranes and the center of the sphere are and respectively, which is shown in Fig. 3(b). We assume that exotic forces such as non-Newtonian gravitylike forces applied to the two membranes can be neglected. Because of the gravitational forces generated by the source mass, the resonant frequencies of two resonators are modified by and respectively. Here and are defined as , where is the perturbed resonant frequency. From [18] we obtain
| (12) |
where is the mass of th membrane, and the gravitational force acting on th membrane is
| (13) |
From the above two equations, we derive
| (14) |
From section 2 we know . Then we assume that , resulting .
As a result of resonant frequency modification of two membranes, the eigenvalues of the Hamiltonian can be rewritten as
| (15) |
For convenience, we substitute for in the remaining section. The shifts of the eigenfrequencies of the supermodes caused by the source mass can be described as
| (16) |
Then from Eqs. (11), (15)-(16) we derive that
| (17) |
In the following, we consider three cases denoted by X, Y, and Z where we operate our system near the EP.
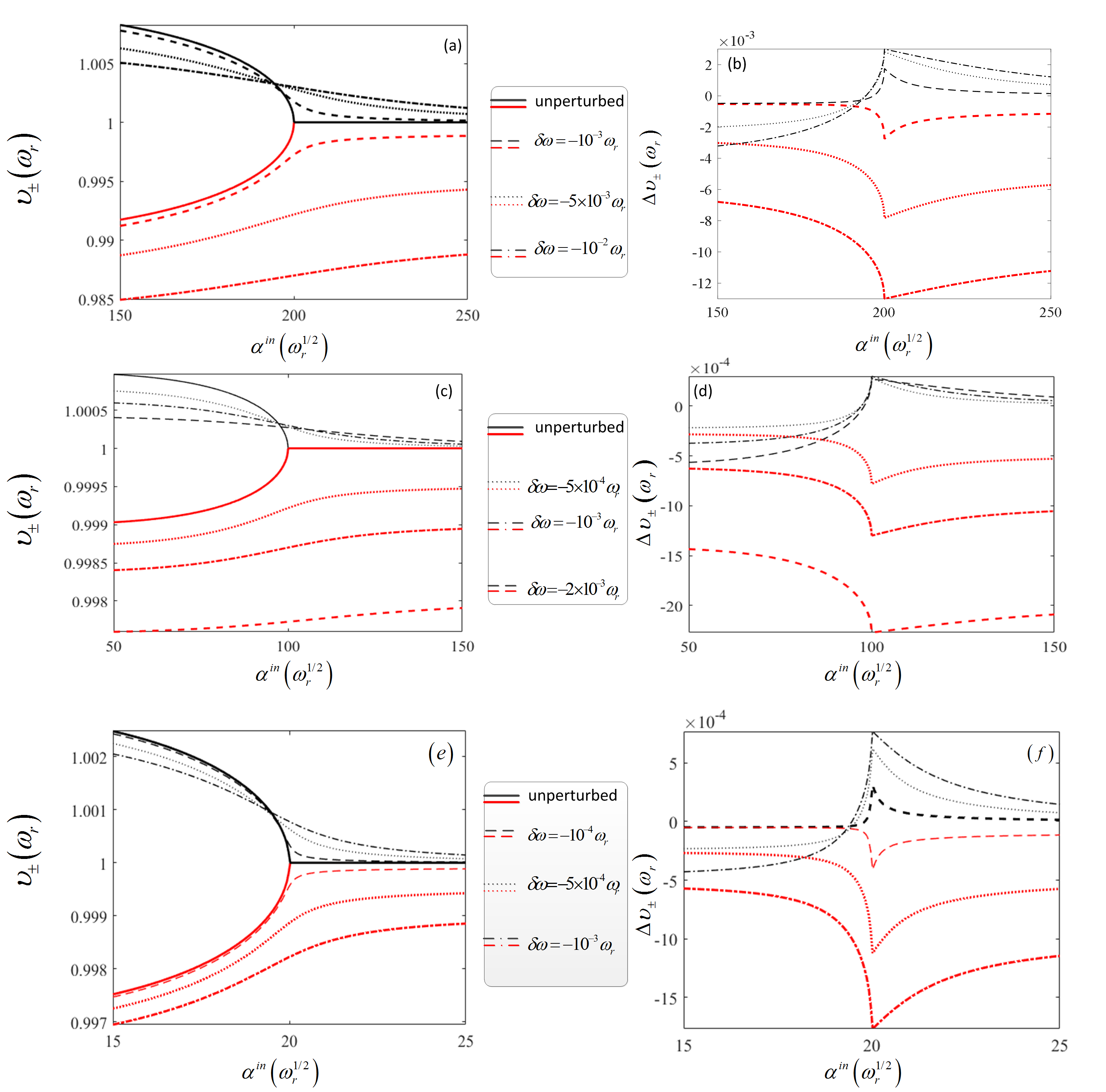
In the case of X, the parameters used are and the corresponding EP is . In Y, In Z, Figure 4 illustrates how eigenfrequencies () and eigenfrequencies shifts () undergo the EP corresponding to different perturbation. (a)-(b), (c)-(d) and (e)-(f) are for X, Y, Z respectively. The black curves are for and , while red ones for and . From this figure, we find that in all nine situations (different perturbation and different three cases) we would obtain a relative bigger positive frequency shift () and a maximum negative eigenfrequency shift () at EPs.
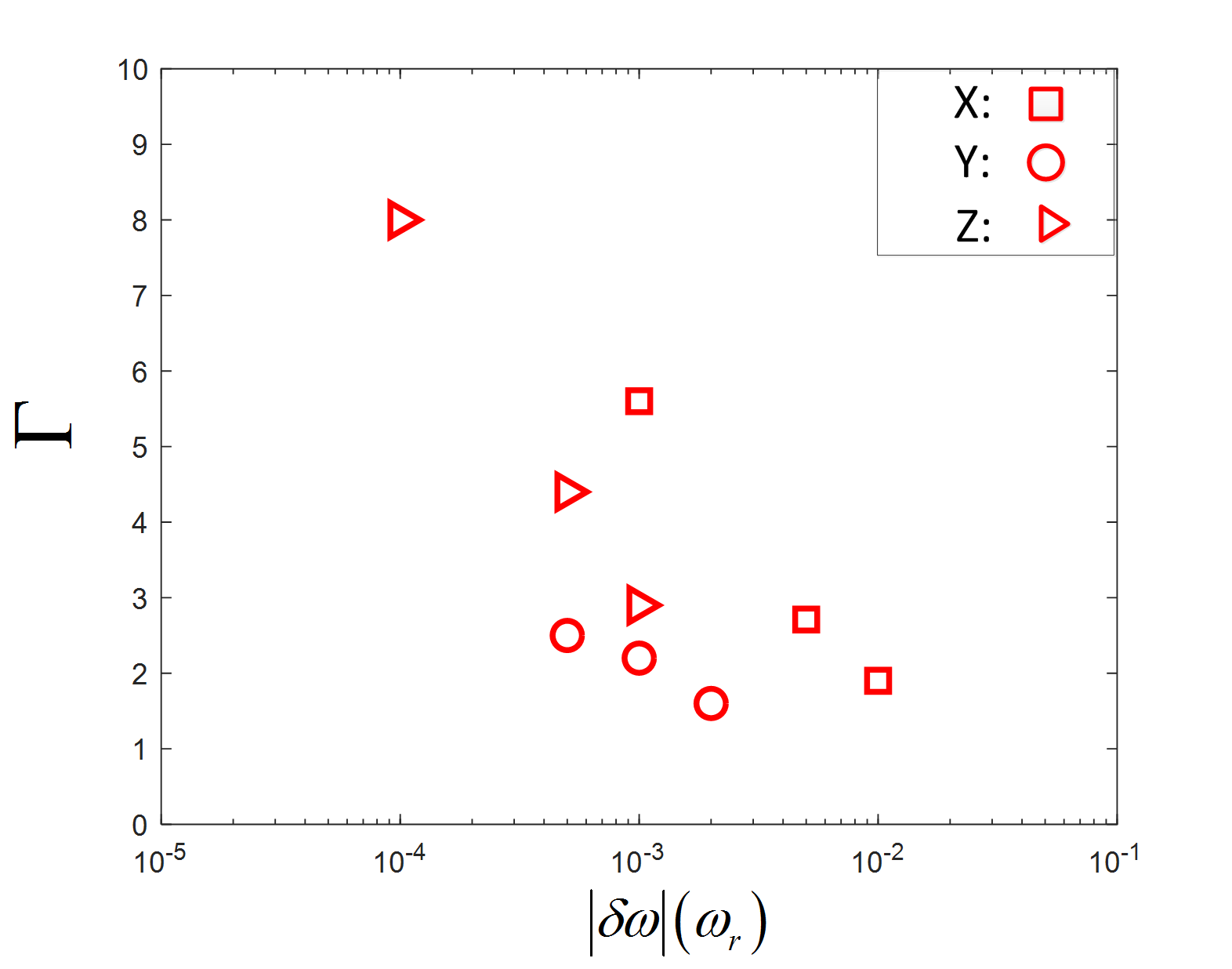
To further demonstrate the EP effect, we define ratio as , where is the value of related to and is the minimum value of . Nine values of correspond to three cases(X, Y, and Z) and different perturbation () are shown in Fig. 5. where square, circles and triangle correspond to X, Y and Z respectively. We can find that in any of three cases a smaller corresponds to a bigger . Since in practical experiments would be very tiny, we conclude that operating the system at EP may make a large contribution to our measurement.
We assume our system is operated at EP and investigate the relationship between EP enlarged eigenfrequency shift and the Newtonian constant. Accordingly there is . With the assumption , according to Eq. (17) we derive that
| (18) |
Then, from Eq. (18) we derive
| (19) |
Next we focus on . From the above, we obtain
| (20) |
From Eqs. (19)-(20), we derive
| (21) |
We assume . Consequently there is . Since , equation (21) can be rewritten as
| (22) |
Then we obtain
| (23) |
Till now, we have derived the relationship between eigenfrequency shift and the Newtonian constant. Then we can determine the value of and the relative uncertainty via the detection of .
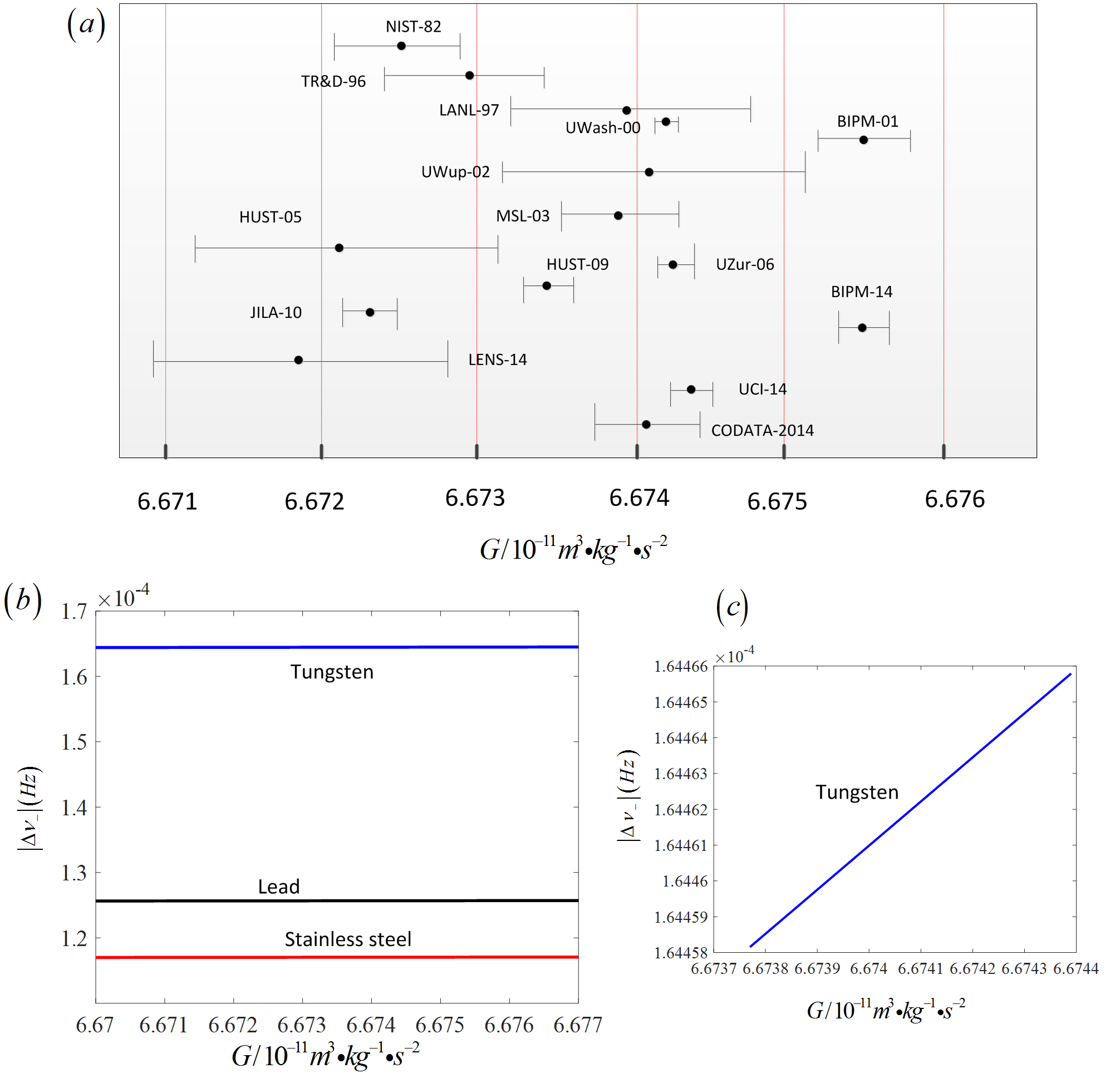
In Fig.6(a), the adopted values of in CODATA-2014 adjustment [5, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33] are illustrated according to [2]. To visualize our result (Eq.(23)), we plot as a function of in Fig.6(b)-(c), where the parameters used are , and . In (b), we utilize a Stainless steel sphere with , a Lead one with and a Tungsten one with . On the contrary, only a Tungsten sphere is considered in (c), where takes values of which is the 2014 CODATA recommended value of .
IV Summary and outlook
In sum, this paper presents a novel method which can be considered in the field of precision measurement of . In this method, two cavities and two membrane resonators constitute an optomechanical system. Gravitational force gradient perturbs the resonant frequencies of two membranes, resulting the shifts of the eigenfrequencies of the supermodes. Based on EP enhanced shifts, we can perform the measurement of . Compared to traditional measurements methods [34, 35] such as torsion balance, atom interferometry, etc., our method possesses two distinct characters. They are: a. The proposed setup is a minute-sized optomechanical system. b. EP effect plays an important role in the measurement of .
Based on this work where a second-order EP feature emerges in the proposed system, we can attempt to construct a new system which can be operated at higher-order EP, and a higher sensitivity may be achieved [36, 13, 37]. So far, EP effect in optomechanical systems have been observed [38, 39], indicating that our method can be put into consideration. Moreover, [40] can be referred to for the detection of the shift of the supermode eigenfrequency. Finally, we expect our proposal can promote the application of EP-based sensors to the measurement of .
Acknowledgements.
This work was supported by Natural Science Foundation of Shanghai (No. 20ZR1429900).References
- Xue et al. [2020] C. Xue, J. P. Liu, Q. Li, J. F. Wu, S. Q. Yang, Q. Liu, C. G. Shao, L. C. Tu, Z. K. Hu, and J. Luo, Precision measurement of the newtonian gravitational constant, National Science Review (2020).
- Liu et al. [2018] J.-P. Liu, J.-F. Wu, Q. Li, C. Xue, D.-K. Mao, S.-Q. Yang, C.-G. Shao, L.-C. Tu, Z.-K. Hu, and J. Luo, Experimental progresses on precision measurement of gravitational constant g, Acta Physica Sinica 67, 160603 (2018).
- Gillies [1987] G. T. Gillies, The newtonian gravitational constant: an index of measurements, Metrologia 24, 1 (1987).
- Li et al. [2018] Q. Li, C. Xue, J.-P. Liu, J.-F. Wu, S.-Q. Yang, C.-G. Shao, L.-D. Quan, W.-H. Tan, L.-C. Tu, Q. Liu, et al., Measurements of the gravitational constant using two independent methods, Nature 560, 582 (2018).
- Mohr et al. [2016] P. J. Mohr, D. B. Newell, and B. N. Taylor, Codata recommended values of the fundamental physical constants: 2014, Rev. Mod. Phys. 88, 035009 (2016).
- Křen [2019] P. Křen, On the inconsistency in experimental results of the gravitational constant, Measurement 136, 622 (2019).
- Quinn [2014] T. Quinn, Don’t stop the quest to measure big g, Nature 505, 455 (2014).
- Heiss [2004] W. D. Heiss, Exceptional points of non-hermitian operators, Journal of Physics A: Mathematical and General 37, 2455 (2004).
- Heiss [2012] W. D. Heiss, The physics of exceptional points, JPhA 45 (2012).
- Wiersig [2020] J. Wiersig, Review of exceptional point-based sensors, Photon. Res. 8, 1457 (2020).
- Wiersig [2016] J. Wiersig, Sensors operating at exceptional points: General theory, Phys. Rev. A 93, 033809 (2016).
- Wiersig [2014] J. Wiersig, Enhancing the sensitivity of frequency and energy splitting detection by using exceptional points: Application to microcavity sensors for single-particle detection, Phys. Rev. Lett. 112, 203901 (2014).
- Hodaei et al. [2017] H. Hodaei, A. U. Hassan, S. Wittek, H. Garcia-Gracia, R. El-Ganainy, D. N. Christodoulides, and M. Khajavikhan, Enhanced sensitivity at higher-order exceptional points, Nature 548, 187 (2017).
- Chen et al. [2017] W. Chen, S. K. Ozdemir, G. Zhao, J. Wiersig, and L. Yang, Exceptional points enhance sensing in an optical microcavity, Nature 548, 192 (2017).
- Aspelmeyer et al. [2014] M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, Cavity optomechanics, Reviews of Modern Physics 86, 1391 (2014).
- Djorwe et al. [2019] P. Djorwe, Y. Pennec, and B. Djafari-Rouhani, Exceptional point enhances sensitivity of optomechanical mass sensors, Physical Review Applied 12, 024002 (2019).
- Djorwe et al. [2018] P. Djorwe, Y. Pennec, and B. Djafari-Rouhani, Frequency locking and controllable chaos through exceptional points in optomechanics, Physical Review E 98, 032201 (2018).
- Harber et al. [2005] D. M. Harber, J. M. Obrecht, J. M. McGuirk, and E. A. Cornell, Measurement of the casimir-polder force through center-of-mass oscillations of a bose-einstein condensate, Phys. Rev. A 72, 033610 (2005).
- Luther and Towler [1982] G. G. Luther and W. R. Towler, Redetermination of the newtonian gravitational constant g, Physical Review Letters 48, 121 (1982).
- Karagioz and Izmailov [1996] O. Karagioz and V. Izmailov, Measurement of the gravitational constant with a torsion balance, Measurement Techniques 39, 979 (1996).
- Bagley and Luther [1997] C. H. Bagley and G. G. Luther, Preliminary results of a determination of the newtonian constant of gravitation: a test of the kuroda hypothesis, Physical Review Letters 78, 3047 (1997).
- Gundlach and Merkowitz [2000] J. H. Gundlach and S. M. Merkowitz, Measurement of newton’s constant using a torsion balance with angular acceleration feedback, Physical Review Letters 85, 2869 (2000).
- Quinn et al. [2001] T. Quinn, C. Speake, S. Richman, R. Davis, and A. Picard, A new determination of g using two methods, Physical Review Letters 87, 111101 (2001).
- Kleinevoß [2002] U. Kleinevoß, Bestimmung der Newtonschen gravitationskonstanten G, Ph.D. thesis, Universität Wuppertal, Fakultät für Mathematik und Naturwissenschaften … (2002).
- Armstrong and Fitzgerald [2003] T. Armstrong and M. Fitzgerald, New measurements of g using the measurement standards laboratory torsion balance, Physical review letters 91, 201101 (2003).
- Hu et al. [2005] Z.-K. Hu, J.-Q. Guo, and J. Luo, Correction of source mass effects in the hust-99 measurement of g, Physical Review D 71, 127505 (2005).
- Holzschuh et al. [2006] E. Holzschuh, W. Kündig, F. Nolting, R. Pixley, J. Schurr, U. Straumann, et al., Measurement of newton’s gravitational constant, Physical Review D 74, 082001 (2006).
- Luo et al. [2009] J. Luo, Q. Liu, L.-C. Tu, C.-G. Shao, L.-X. Liu, S.-Q. Yang, Q. Li, and Y.-T. Zhang, Determination of the newtonian gravitational constant g with time-of-swing method, Physical Review Letters 102, 240801 (2009).
- Tu et al. [2010] L.-C. Tu, Q. Li, Q.-L. Wang, C.-G. Shao, S.-Q. Yang, L.-X. Liu, Q. Liu, and J. Luo, New determination of the gravitational constant g with time-of-swing method, Physical Review D 82, 022001 (2010).
- Parks and Faller [2010] H. V. Parks and J. E. Faller, Simple pendulum determination of the gravitational constant, Physical Review Letters 105, 110801 (2010).
- Quinn et al. [2013] T. Quinn, H. Parks, C. Speake, and R. Davis, Improved determination of g using two methods, Physical Review Letters 111, 101102 (2013).
- Rosi et al. [2014] G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, and G. Tino, Precision measurement of the newtonian gravitational constant using cold atoms, Nature 510, 518 (2014).
- Newman et al. [2014] R. Newman, M. Bantel, E. Berg, and W. Cross, A measurement of g with a cryogenic torsion pendulum, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372, 20140025 (2014).
- Rothleitner and Schlamminger [2017] C. Rothleitner and S. Schlamminger, Invited review article: Measurements of the newtonian constant of gravitation, g, Review of Scientific Instruments 88, 111101 (2017).
- Rosi [2016] G. Rosi, Challenging the ‘big g’measurement with atoms and light, Journal of Physics B: Atomic, Molecular and Optical Physics 49, 202002 (2016).
- Jing et al. [2017] H. Jing, Ş. Özdemir, H. Lü, and F. Nori, High-order exceptional points in optomechanics, Scientific reports 7, 1 (2017).
- Miri and Alù [2019] M.-A. Miri and A. Alù, Exceptional points in optics and photonics, Science 363, eaar7709 (2019).
- Zhang et al. [2018] J. Zhang, B. Peng, s. K. özdemir, K. Pichler, D. O. Krimer, G. Zhao, F. Nori, Y.-x. Liu, S. Rotter, and L. Yang, A phonon laser operating at an exceptional point, Nature Photonics 12, 479 (2018).
- Xu et al. [2016] H. Xu, D. Mason, L. Jiang, and J. Harris, Topological energy transfer in an optomechanical system with exceptional points, Nature 537, 80 (2016).
- Peng et al. [2014] B. Peng, A. K. Zdemir, F. Lei, F. Monifi, M. Gianfreda, G. L. Long, S. Fan, F. Nori, C. M. Bender, and L. Yang, Parity-time-symmetric whispering-gallery microcavities, Nature Physics 10, 394 (2014).