Properties of the mixed phase core in maximum mass neutron stars
Abstract
In the context of observed massive neutron stars (NSs), we examine the internal structure, phase transitions, and the impacts of the equation of state (EOS) in maximum NSs. We investigate the stiffness changes in the EOS during the hadron-quark phase transition within the NSs. The relativistic mean-field (RMF) model and RMF model with a density-dependent isovector coupling, known as the RMFL model, are used to describe hadronic matter, while to the represent quark matter, the Nambu-Jona-Lasinio (NJL) model is applied. We explore the strength of vector coupling in quark matter, which delayed the onset density and reduced the maximum mass of NS, but does not exhibit a clear correlation with the NS central density. A considerable size of the mixed phase core could exist in the maximum mass NS but with corresponding small mixed phase mass.
I Introduction
The equation of state (EOS) plays a crucial role in the fields of nuclear physics and astrophysics Baym2018 , as it determines the composition and properties of compact stars. It also sheds light on the nature of strong interactions within these stars. The quantum chromodynamics (QCD) phase transition at finite temperature and low baryon density support the hot dense quark matter exist, while cold dense quark matter may only can found in neutron stars (NS). The question of whether quark matter can exist in NSs has been a topic of interest for researchers for several decades Baym1976 ; Glendenning1992 , yet it remains an open question. At high density, there is a Bodmer–Witten assumption that strange quark matter composed of quarks may actually be the true ground state of matter Witten1984 , exhibiting a lower energy per baryon compared to both quark matter and nucleon matter. Whether strange quark matter is absolutely stable is model dependent Liu2023 . Overall, it is possible that a first-order hadron-quark phase transition occurs within the core of massive NS Glendenning2001 ; Weber2005 ; Brandes2023 , where the density could reach times saturation density .
In the past decade, significant progress in astronomical observations has provided abundant data on neutron star mass, radius, and tidal deformabilities. These constraints have spurred explorations into theories of dense matter, narrowing down the range of plausible strong interaction theories. Recent Shapiro delay measurements of massive neutron star PSR J0740+6620 Cromartie2020 ; Fonseca2021 , gives a lower limit of (68.3% credibility interval), similar restrictions are also imposed by PSR J1614-2230 () Arzoumanian2018 and PSR J0348+0432 () Antoniadis2013 , respectively. These results provides constraints on the EOSs, that disallow configurations unable to support twice the solar mass. Additionally, the black-widow pulsar, PSR J0952-0607, reports a mass of Romani2022 (68.3% credibility interval), which is the heaviest NS observed. The inferred mass and equatorial radius from x-ray data detected with the Neutron Star Interior Composition Explorer (NICER) view of PSR J0030+0451 suggested estimation are (68% credible interval) , Riley2019 as well as , Miller2019 , respectively. Moreover, NICER view observations of PSR J0740+6620 (68.3% credibility interval) suggest a mass of , Riley2021 and , Miller2021 . These massive NS ruled out the soft EOSs. The possibility that the secondary component of the gravitational wave event GW190814 may be the most massive NS Abbott2020 or a black hole. The GW170817 event provided constraints on tidal deformations Abbott2017 . A roughly NS radius, consistent with the tidal deformability up limit, refers Annala2018 . The NICER and gravitational wave detection have opened new avenues for exploration.
On one hand, the massive NS mass constraints need stiff EOS, on the other hand, the radius or tidal deformability limit need relative soft EOS in low-density range. To fulfil these constraints above, many works contain quark degree of freedom in NS have been done Alford2019 ; Bauswein2019 ; Annala2020 ; Ferreira2021 ; Huang2022 ; Liu2023 ; Liu2023b . A relative large pure quark core in the massive NS is expected in Ref. Annala2020 using speed-of-sound interpolation between chiral effective field theory (CET) and perturbative-QCD (pQCD) EOSs. This conclusion is supported in Ref. Liu2023b ; Ferreira2021 with additional quark interactions, in which the eight-quark vector interaction and the four-quark isovector-vector interaction play very different roles in determining the size of the quark core. The framework of hybrid star with twin star under Maxwell construction is discussed in Ref. Li2021 ; Podder2024 . Ref. Li2023apj raised a model contain sequential phase transitions from hadronic matter to low- and then to high-density quark matter phases. Usually hadron-quark phase transition will not affect the properties of NS properties, since the onset density beyond the central density of NS. But twin star could give another counterpart with smaller radius.
The purpose of this study is explore the stiffness changes in the EOS during the transition from hadronic matter to quark matter, and to investigate the properties of the maximum mass NS containing quark degree of freedom, taking into account the recent observational constraints listed above. Describing both hadronic and quark matter within a unified framework presents challenges, as these phases typically involve different particles. Usually distinct models are required, then select the phase with the lower energy density at given baryon number density. To describe hadronic matter, we employ the relativistic mean-field (RMF) model and RMF model with a density-dependent isovector coupling, like the way in the density-dependent relativistic mean-field (DDRMF) model, refereed as RMFL mdoel Spinella2017 ; Wu2021 . For the representation of quark matter, We apply the Nambu-Jona-Lasinio (NJL) model. The Gibbs construction Glendenning1992 is adopted for modeling the hadron-quark mixed phase, different from Maxwell construction, which could be considered as a extremely high surface tension that Gibbs construction becomes unstable Maruyama2008 ; Wu2019 . In the Gibbs construction both hadronic matter and quark matter could coexist within a density region characterized by dynamic equilibrium, baryon chemical potential equilibrium and global charge neutrality. The transition from the hadronic phase to the quark phase results in a softening of the EOS, leading to a lower maximum mass of NS compared to their pure hadronic counterparts, due to the increase in degrees of freedom. By analyzing these aspects, the study could enhance our understanding of the EOS behavior and characteristics of maximum mass NS with quark matter. In this study, hyperons in the hadronic matter are neglected due to the lack of experimental or observational evidence supporting their presence in compact star cores. Furthermore, the onset density of quarks and hyperons are close which make it complicated to distinguish the effect of hyperons or quarks degree of freedom on EOS and NS properties.
This article is structured as follows. In Section II, we provide a concise overview of the NJL model, which describes quark matter, as well as the RMF/RMFL model, which characterizes hadronic matter. Additionally, the hadron-quark phase transition under Gibbs equilibrium is discussed. In Sec. III, we present the numerical results of the hadron-quark phase transition, and provide a detailed analysis of the events occurring during this process, including its effect on the properties of the maximum mass HS. Finally, Section IV offers a summary of our findings.
II The theoretical model
II.1 Hadronic matter phase
The RMF/RMFL model is employed to describe the hadronic matter, where nucleons interact through the exchange of isoscalar-scalar meson , isoscalar-vector meson , and isovector-vector meson . In the RMF model, the isovector-vector meson coupling is a constant, whereas in the RMFL model, it varies with the change of number density . The Lagrangian density for the hadronic matter, comprising nucleons ( and ) and leptons ( and ) is written as
| (1) | |||||
where and denote the antisymmetric field tensors associated with and , respectively. Within the RMF/RMFL approach, the meson fields are considered classical fields, and the field operators are substituted with their corresponding expectation values. For a static system, the non-vanishing expectation values are , , and .
In uniform hadronic matter, the equations of motion for meson mean fields can be expressed as
| (2) | |||||
| (3) | |||||
| (4) |
where and denote the scalar and number densities of species , respectively. In the context of hadronic matter under equilibrium, the chemical potentials satisfy the relations and . At zero temperature approximation, the chemical potentials are given by
| (5) | |||||
| (6) |
where denotes the effective nucleon mass. The energy density of hadronic phase (HP) is expressed as
| (7) | |||||
and the pressure is calculated as
| (8) | |||||
In the RMFL model, varies with the change in baryon number density ,
| (9) |
where is the saturation density. This difference from the constant in the RMF model results in a rearrangement item for nucleons in the RMFL model,
| (10) |
and contributes to the formulation of the chemical potential
| (11) | |||||
| (12) |
The pressure also affected by the rearrangement item ,
| (13) | |||||
while the energy density remains unaffected. When in Eq. 9 equals zero, the rearrangement term vanished, and Eqs. (11-12) simplifies to Eq. (5), the pressure Eq. (13) simplifies to Eq. (8).
In order to investigate the impact of EOS on NS structures and the hadron-quark phase transition, we adopt the successful RMF/RMFL models, including BigApple Fattoyev2020 , NL3L-50 Wu2021 , TM1e Bao2014 ; Wu2018 and NL3 Lalazissis1997 to characterize nuclear interactions. The details of NL3L-50 is comprehensively outlined in Ref. Wu2021 . For the sake of completeness, we present the parameter sets and saturation properties of these models in Tables LABEL:tab:para and LABEL:tab:sat, respectively.
It is well known that nuclear symmetry energy and its slope play a crucial role in determining the properties of neutron stars. Within the Ref. Tews2017 ; LiBA2021 , there are commonly used constraints for these quantities: the symmetry energy lies within the range of , while the slope about . The parameters adopted in this study fall within the aforementioned range, except NL3, which is concluded as a comparison.
| Parameters | BigApple | NL3L-50 | TM1e | NL3 |
|---|---|---|---|---|
| 939.0 | 939.0 | 938.0 | 939.0 | |
| 492.730 | 508.194 | 511.198 | 508.194 | |
| 782.500 | 782.501 | 783.000 | 782.501 | |
| 763.0 | 763.0 | 770.0 | 763.0 | |
| 9.6699 | 10.217 | 10.0289 | 10.217 | |
| 12.316 | 12.868 | 12.6139 | 12.868 | |
| 14.1618 | 8.948 | 12.2413 | 8.948 | |
| 11.9214 | 10.431 | 7.2325 | 10.431 | |
| -31.6796 | -28.885 | 0.6183 | -28.885 | |
| 2.6843 | 0 | 71.3075 | 0 | |
| 0.0475 | 0 | 0.0327 | 0 | |
| 0 | 0.583455 | 0 | 0 |
| Model | (fm-3) | (MeV) | (MeV) | (MeV) | (MeV) |
|---|---|---|---|---|---|
| BigApple | 0.155 | 16.34 | 227.0 | 31.3 | 39.8 |
| NL3L-50 | 0.148 | 16.24 | 272.3 | 37.4 | 50 |
| TM1e | 0.145 | 16.26 | 281.0 | 32.4 | 50 |
| NL3 | 0.148 | 16.24 | 272.3 | 37.4 | 118.5 |
II.2 Quark matter phase
To describe the quark matter, we chose to utilize the SU(3) NJL model, which incorporates three flavors of quarks . The Lagrangian density of the NJL model is give by
| (14) | |||||
where refers to the quark field, which contains three flavors () and three colors (). The current quark mass matrix is given by . In this study, we take into account chirally symmetric four-quark interaction characterized by the coupling constant , Kobayashi–Maskawa–’t Hooft (KMT) six-quark interaction represented by the coupling constant , and repulsive vector interaction governed by the coupling constant . The inclusion of the vector coupling is essential in describing massive stars, as shown in Refs. Yasutake2014 ; Masuda2013 ; Chu2015 ; Pereiar2016 ; Liu2023 . In our current study, we adopt the parameters provided in Ref. Rehberg1996 , , , , , and . The vector coupling is treated as a free parameter in our analysis, following the approach adopted in Refs. Yasutake2014 ; Pereiar2016 . This is because there is currently no well-constrained value for at finite density. By treating as a free parameter, we aim to explore its influence on the properties and behavior of quark matter within our study. Since the vector coupling only serves to stiffen the EOS of quark matter, its effects on the hadron-quark phase transition are expected to be qualitatively similar across different models. By including , the EOS would become more resistant to compression, resulting in increased pressure for a given density.
At the mean-field level, the constituent quark masses arise from spontaneous chiral symmetry breaking. In vacuum, the constituent quark mass is much larger than the current quark mass . The determination of constituent quark masses in quark matter involves solving the relevant gap equations,
| (15) |
with () being any permutation of (). The energy density of quark matter is given by
| (16) | |||||
where denotes the quark condensate of flavor . The constant is introduced to ensure that the energy density in the physical vacuum is zero. In our current study, the choice of lead the pressure also vanishes in the vacuum.
In quark matter, the chemical potentials of quarks and leptons satisfy the equilibrium condition, which is expressed as and . The chemical potential of quark flavor is given by
| (17) |
The total energy density and pressure in quark phase (QP) are written as
| (18) | |||||
| (19) |
II.3 Hadron-quark mixed phase
In our study, we employ the Gibbs construction to describe the hadron-quark mixed phase. Within this construction, the system satisfies the equilibrium is satisfied. Both hadronic matter and quark matter are allowed to be charged separately, but the total charge remains zero. The energy density of the mixed phase (MP) is
| (20) |
where is the volume fraction of quark matter. The pressure equilibrium and the chemical potential equilibrium between two phases are shown below,
| (21) | |||||
| (22) |
At a given baryon density , there are two independent chemical potentials, and , which can be determined by the constraints of global charge neutrality and baryon number conservation given in
| (23) | |||||
| (24) |
All properties of the mixed phase can be calculated, under the equilibrium state with given .
III Results and Discussion







The presence of deconfined quarks in the core of massive NSs is an intriguing possibility. In this section, we thoroughly investigate the EOS and its impact on the internal structure of the most massive NSs. To describe the hadronic matter, we employ the RMF/RMFL models, while the NJL model with repulsive vector coupling is utilized for quark matter. The hadron-quark mixed phase is treated under the Gibbs equilibrium condition. For the representation of larger mass NSs, we employ the stiff parameter sets BigApple and NL3L-50, while the TM1e parameter set is used to illustrate the results for NSs with a mass around . The results obtained from the NL3 parameter set are included in select figures for comparison purposes, as this set tends to predict excessively large radii and tidal deformability compared to observational data.






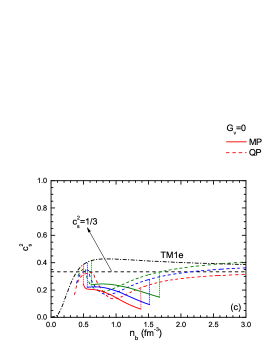
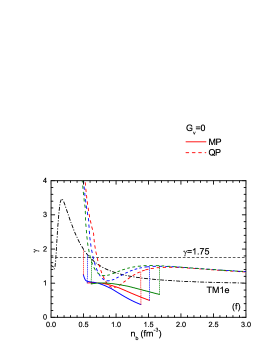
In Figure 1, we illustrate the EOSs for the hadronic phase, mixed phase, and quark phase using the BigApple, NL3L-50, and TM1e parameter sets, considering various strengths of vector couplings, . Before a density of , the EOS lines for the hadronic phase using the BigApple and NL3L-50 parameter sets exhibit similarities, with BigApple being slightly softer. This shortly delay in the onset of the mixed phase, combined with an enlarged range of the mixed phase for all values of . The softer parameter set, TM1e, further enhances this trend. However, it is noteworthy that the mixed phase EOS derived from TM1e is stiffer compared to that of BigApple and NL3L-50. This observation is counter-intuitive since, despite the hadron-quark phase transition being delayed for a softer EOS (TM1e), the stiffness of soft EOS (TM1e) at the onset density of the mixed phase is still lower than that of the stiff EOS (BigApple and NL3L-50). This is illustrated in Figure 2. One plausible hypothesis is that a stiffer hadronic EOS results in higher energy within the mixed phase, causing nucleons to dissociate into quarks more rapidly than in a softer hadronic EOS. Consequently, the rate of soft EOS stiffness change becomes smoother, as evident in Figure 2. With increasing , the onset of the mixed phase shifts to higher densities, accompanied by an increase in the pressure of the mixed phase. The degrees of freedom of the mixed phase encompass those of both the hadronic and quark phases, contributing to the gentlest pressure change among the phases. We utilize the squared sound velocity and the polytropic index to quantify the stiffness of EOSs as illustrated in Fig. 1. The sound velocity is defined as , which asymptotically approaches in the conformal limit corresponding to free mass-less quarks. The conformal limit usually requires . On the other hand, the polytropic index is defined as , and has a value in conformal limit matter. The squared sound speed (upper panel) and the polytropic index (lower panel) as functions of the baryon number density are depicted in Fig. 2. We show the results that stretched up to only for comparison purpose where the hadronic matter models used in this study should not applicable at such high densities. Both sound velocity and the polytropic index could characterize the stiffness change of the EOS, but sound velocity is the better choice in low densities because of it without a fluctuation . The decrease of sound velocity of BigApple and TM1e may be related to the effect of parameter in RMF models. The sudden decrease in the squared sound velocity or the polytropic index at the onset of the mixed phase corresponds to an increase in degrees of freedom. That values of and for the mixed phase are the lowest among three phases. Towards the end of the mixed phase, the change trend of close to zero (especially for BigApple and NL3L-50), resembling the results of the Maxwell construction (where ). This is due to the fact that at the end of the mixed phase in the Gibbs construction, the number density of leptons approaches zero, resulting in the hadronic and quark parts approaching local charge neutrality, similar to the Maxwell construction. The value , from Ref. Annala2020 , splits the pure nucleon part and non-nucleon part: all the hadronic matter EOS have except the case TM1e-, and all the mixed phase and quark phase EOSs have .
In Fig. 3, we display the mass-radius relations (left panel) and mass-central density relations (right panel) for BigApple, NL3L-50 and TM1e EOSs with different strength of vector coupling . Several constraints from astrophysical observations are also displayed in different color regions. The predicted maximum mass of HS depends on . Due to the stiff enough EOS of hadronic matter, even with BigApple and NL3L-50 could support a maximum mass of , while TM1e requires . The maximum mass could reach with using the NL3L-50 parameter set. The appearance of quark degrees of freedom in the mixed phase leads to an obvious reduction of the maximum mass of NS, but larger values of make the reduction of maximum mass smaller. Compared with stiffer EOSs (BigAllpe and NL3L-50), the effect of different values of on TM1e is smaller. The normal NS properties are determined by the EOS around 2 , where quarks have not appeared. Therefore, the mixed phase does not affect mass-radius line through PSR J0030+0451 constraints Riley2019 ; Miller2019 . Even when considering the hadron-quark phase transition, the radius and mass of NSs are still mainly effected by the hadronic part. A large enough mixed phase core in the maximum mass NS is expected, but with the mixed phase core is not supported by these parameter sets in this study, except for TM1e-.




To better examine the properties of the maximum mass NS, we present the relations of mass and radius of the maximum mass NS in Fig. 4. The solid square indicates where the deconfined quarks appear. On the left side of the solid square are the mixed phase core, which could close to and around for . With larger , stiffer quark matter EOS, leading the size and mass of the mixed-phase core of the maximum mass NS decrease. A relative softer hadronic phase EOS (TM1e) could have relative large size and mass of the mixed phase core compared with stiffer hadronic phase EOS (BigApple and NL3L-50), though offers relative small maximum mass. No pure quark core is observed under the framework in this study, as the pure quark phase onset density is beyond the maximum mass NS center density, as seen in Fig. 3 (right panel). Fig. 5 shows the central density-radius relation of maximum mass NS, including the NL3 parameter set, which offers a larger mixed phase radius that others. This is because the NL3 parameter set predicts larger radius than other parameter sets for all mass values, but beyond the observation constraints. With , around radius of the maximum mass NS are the mixed phase.

The relation between maximum value of squared speed of sound and the radius of the mixed phase of the maximum mass NS is exhibited in Fig. 6. The is actually corresponds to the at density for hadronic matter, , as shown in Fig. 2. But the extreme case where , with no mixed phase core, , as shown in 7, where the central density of the maximum mass NS little than the onset density of the mixed phase. Because is affected by , within the same model, and both increase with increase, together with decrease, leading to a smaller proportion of the mixed phase radius in the maximum mass NS. This trend is consistent with the findings in Ref Annala2020 .



We examined the effect of vector coupling on the phase transition density and maximum mass NS central density , as shown in Fig. 7. With increase, the mixed phase is delayed to higher densities, affecting both and , but leaving the central density relatively stable. If , it indicates that the maximum stable density occurs in the pure hadronic matter without deconfined quarks. The maximum mass is primarily determined by the stiffness EOS of the hadronic phase, whose range is influenced by vector coupling. However, a strong enough can prevent the hadron-quark phase transition, and the threshold value of c is determined by the EOS of hadronic phase. BigApple and NL3L-50 support a maximum value of about and , respectively. Through this idea, TM1e supports a maximum value about , however, with , is larger than , which is over 15 times the saturation density . Therefore, could consider as the threshold value. The relatively large upper limit derived here benefits the stiffness of the EOS. This, coupled with the results from Fig. 2 showing that larger values of lead to larger , which should not exceed at high densities, leads to the universal conclusion that non-zero should be density-dependent. The decrease in the range between and as increase indicates a reduction in the mixed phase range. Beyond the threshold value of , though the hadron-quark phase transition could occur, the mixed phase is not supported in a NS. With given , compared with results of NL3L-50, derived from BigApple slightly moves to higher density, but shifts more. This can also explained by the nucleons dissociation rate hypothesis above that nucleons with NL3L-50 dissociate faster to quarks than with BigApple interaction.
IV Summary
In this work, we focus on exploring the properties of maximum mass neutron stars with quark degrees of freedom. We have conducted an investigation of the EOS with the hadron-quark phase transition under Gibbs equilibrium. To achieve this, we have employed the RMF/RMFL model to characterize hadronic matter, while the NJL model with repulsive vector coupling has been utilized for the representation of quark matter. Our findings indicate that the properties of maximum mass NSs are significantly influenced by the model parameters used, including the strength of the vector coupling. Specifically, a stiffer hadronic matter EOS and a larger vector coupling are shown to potentially support more massive NSs. The presence of vector coupling has the capacity to increase the maximum mass of neutron stars, mitigating the reduction in maximum mass caused by the appearance of quarks to a certain extent. However, no clear correlation has been observed between the central density of maximum mass NSs and the vector coupling. Under the condition of the same vector coupling strength , a relatively softer hadronic matter EOS has the potential to support a relatively larger mixed phase core. This core could occupy nearly half of the entire neutron star when , but the corresponding mass of the mixed phase core is comparatively small in relation to the total mass.
In summary, our study reveals that the global properties of maximum mass NSs are sensitive to the strength of the maximum sound velocity of the EOS. Furthermore, it is possible for a relatively large radius of the mixed phase to exist in the core of maximum mass NSs when there is a small vector coupling in the quark matter. But for NSs have , only tiny mixed phase core is possible in this study (with TM1e-). If the vector coupling is sufficiently large to exceed a certain threshold, it can prevent the occurrence of the hadron-quark phase transition in NSs. Besides, a non-zero should be density dependent to fulfil the sound speed conformal limit.
Acknowledgment
This work is supported by the National Natural Science Foundation of China under Grants No. 12305148, No. 11975132, No. 12205158, Hebei Natural Science Foundation No. A2023203055, and the Shandong Provincial Natural Science Foundation, China under Grants No. ZR2023QA112, No. ZR2022JQ04, No. ZR2021QA037, and No. ZR2019YQ01.
References
- (1) G. Baym, T. Hatsuda, T. Kojo, P. D. Powell, Y. Song and T. Takatsuka, Rep. Prog. Phys. 81, 056902 (2018).
- (2) G. Baym and S. A. Chin, Phys. Lett. B 62, 241–4 (1976).
- (3) N. K. Glendenning, Phys. Rev. D 46, 1274 (1992).
- (4) Witten E., Phys. Rev. D, 30, 272 (1984).
- (5) H. Liu, Y.-H. Yang, Y. Han, and P.-C. Chu, Phys. Rev. D 108, 034004 (2023).
- (6) N. K. Glendenning, Phys. Rep. 342, 393 (2001).
- (7) F. Weber, Prog. Part. Nucl. Phys. 54, 193 (2005).
- (8) L. Brandes, W. Weise, and N. Kaiser, Phys. Rev. D 108, 094014 (2023).
- (9) E. Fonseca, H.T. Cromartie, T.T. Pennucci, et al., Astrophys. J. Lett. 915 L12 (2021).
- (10) H. T. Cromartie, E. Fonseca, S. M. Ransom, et al., Nat. Astron. 4, 72 (2020).
- (11) Z. Arzoumanian et al., Astrophys. J. Suppl. 235, 37 (2018).
- (12) J. Antoniadis, P. C. C. Freire, N. Wex, et al., Sci, 340, 448 (2013).
- (13) R.W. Romani, D. Kandel, A.V. Filippenko, T.G. Brink, W. Zheng, Astrophys. J. Lett. 934, L18 (2022).
- (14) T. E. Riley et al., Astrophys. J. Lett. 887, L21 (2019).
- (15) M. C. Miller et al., Astrophys. J. Lett. 887, L24 (2019).
- (16) T. E. Riley, A. L. Watts, P. S. Ray, et al., Astrophys. J. Lett. 918, L27 (2021).
- (17) M. C. Miller, F. K. Lamb, A. J. Dittmann, et al., Astrophys. J. Lett. 918, L28 (2021).
- (18) R. Abbott et al. (LIGO Scientific and Virgo Collabora- tions), Astrophys. J. Lett. 896, L44 (2020).
- (19) B. P. Abbott, et al.(The LIGO Scientific Collaboration and the Virgo Collaboration) Phys. Rev. Lett. 119, 161101 (2017).
- (20) E. Annala, T. Gorda, A. Kurkela, A. Vuorinen, Phys. Rev. Lett. 120, 172703 (2018).
- (21) M. Ferreira, R. C. Pereira , and C. Providncia, Phys. Rev. D 103, 123020 (2021).
- (22) H. Liu, X. -M. Zhang and P.-C. Chu, Phys. Rev. D 107, 094032 (2023).
- (23) E. Annala, T. Gorda, A. Kurkela, J. Nttil, A. Vuorinen, Nat. Phys. 16, 907 (2020).
- (24) M. G. Alford, S. Han, and K. Schwenzer, J. Phys. G 46, 114001 (2019).
- (25) A. Bauswein, N. F. Bastian, D. B. Blaschke, K. Chatziioannou, J. A. Clark, T. Fischer, and M. Oertel, Phys. Rev. Lett. 122, 061102 (2019).
- (26) Y. J. Huang, L. Baiotti, T. Kojo, K. Takami, H. Sotani, H. Togashi, T. Hatsuda, S. Nagataki, and Y. Z. Fan, Phys. Rev. Lett. 129, 181101 (2022).
- (27) J. J. Li, A. Sedrakian, and M. Alford, Phys. Rev. D 104, L121302 (2021).
- (28) S. Podder, S. Pal, D. Sen, G. Chaudhuri, Nucl. Phys. A 1042, 122796 (2024).
- (29) J. J. Li, A. Sedrakian, and M. Alford Astrophys. J. 944, 206 (2023).
- (30) W. M. Spinella, A Systematic Investigation of Exotic Matter in Neutron Stars, Ph.D. thesis, Claremont Graduate University & San Diego State University (2017).
- (31) X. H. Wu, S. S. Bao, H. Shen, and R. X. Xu, Phys. Rev. C 104, 015802 (2021).
- (32) T. Maruyama, S. Chiba, H.J. Schulze, T. Tatsumi, Phys. Lett. B 659, 192 (2008).
- (33) X. H. Wu and H. Shen, Phys. Rev. C 99, 065802 (2019).
- (34) F. J. Fattoyev, C. J. Horowitz, J. Piekarewicz, and B. Reed, Phys. Rev. C 102, 065805 (2020).
- (35) S. S. Bao, J. N. Hu, Z. W. Zhang, and H. Shen, Phys. Rev. C 90, 045802 (2014).
- (36) X. H. Wu, A. Ohnishi, and H. Shen, Phys. Rev. C 98, 065801 (2018).
- (37) G. A. Lalazissis, J. Knig and P. Ring, Phys. Rev. C 55, 540 (1997).
- (38) I. Tews, J. M. Lattimer, A. Ohnishi, and E. E. Kolomeitsev, Astrophys. J. 848, 105 (2017).
- (39) B. A. Li, B. J. Cai, W. J. Xie, and N. B. Zhang, Universe 7, 182 (2021).
- (40) N. Yasutake, R. Łastowiecki, S. Benić, D. Blaschke, T. Maruyama, and T. Tatsumi, Phys. Rev. C 89, 065803 (2014).
- (41) K. Masuda, T. Hatsuda, and T. Takatsuka, Astrophys. J. 764, 12 (2013); Prog. Theor. Exp. Phys. 7, 073D01 (2013).
- (42) P. C. Chu, X. Wang, L. W. Chen, and M. Huang, Phys. Rev. D 91, 023003 (2015).
- (43) R. C. Pereira, P. Costa, and C. Providência, Phys. Rev. D 94, 094001 (2016).
- (44) P. Rehberg, S. P. Klevansky, and J. Hüfner, Phys. Rev. C 53, 410 (1996).