Properties of spin-1/2 heavy baryons at nonzero temperature
Abstract
The spectroscopic properties of single heavy spin-1/2 , , and baryons are investigated at finite temperature in the framework of the thermal QCD sum rule. We discuss the behavior of the mass and residue of these baryons with respect to temperature taking into account contributions of non-perturbative operators up to dimension eight. We include additional operators coming from the Wilson expansion due to breaking the Lorentz invariance at nonzero temperature. The obtained results show that the mass of these baryons remain stable up to roughly MeV while their residue is unchanged up to MeV. After these points, the mass and residue start to diminish by increasing the temperature. The shifts in the mass and residue for both the bottom and charm channels are considerably large and we observe the melting of these baryons near to thepseudocritical temperature determined by recent lattice QCD calculations. We present our results for the mass of these baryons with both the positive and negative parity at the limit, which are consistent with the existing theoretical predictions as well as experimental data.
I Introduction
One of the most attractive subjects in particle physics is to investigate the spectroscopic properties of hadrons at finite temperatures. Such studies provide us with a better understanding of the perturbative and non-perturbative natures of QCD at hot mediums. They will also help us in analyses of data provided by future heavy ion collision experiments aiming to investigate the hadronic properties and possible phase transitions to quark gluon plasma (QGP) at finite temperatures and densities. In the last two decades, there have been significant experimental and theoretical studies on single heavy baryons in vacuum. Roughly, all single heavy baryons containing a heavy or quark have been successfully observed PDG . The investigation of these baryons at a medium with nonzero temperature is a very prominent research subject now and it will be in agenda of different experimental and theoretical studies.
Single heavy baryons are composite particles made of one heavy ( or ) and two light quarks ( or ). These particles belong to either antitriplet of flavor antisymmetric state or sextet of flavor symmetric state 6. It is well known that total spin-parity of the ground state single heavy baryons in sextet state is either or while spin-parity of the single heavy baryons in antitriplet state is only . In this paper, we study the spectroscopic parameters of the spin-1/2 heavy bottom/charmed baryons both in antitriplet and sextet representations, whose members are shown in Table 1.
| Baryon | SU(3) | ||
|---|---|---|---|
In the literature, a lot of theoretical studies on the investigation of the spin-1/2 heavy baryons in vacuum have been performed using different phenomenological approaches such as the quark model Roberts ; Karliner , quark potential model Capstick , heavy quark effective theory (HQET) Dai ; Liu ; Korner , chiral perturbation theory Savage , Feynman-Hellman theorem Roncaglia , hypercentral approach Ghalenovi1 ; Ghalenovi2 ; Patel1 ; Patel2 , lattice QCD simulation Brown ; Mathur ; Lewis ; Bahtiyar , relativistic (constituent) quark model Ebert1 ; Ebert2 ; Ebert3 ; Migura ; Gerasyuta1 ; Gerasyuta2 ; Gerasyuta3 ; Garcilazo , chiral quark-soliton model Kim , symmetry-preserving treatment of a vectorvector contact interaction model Yin , QCD sum rules Shuryak ; Bagan ; Azizi ; Wang1 ; Wang2 ; Wang3 ; Zhang1 ; Zhang2 ; Agaev1 ; Agaev2 ; Agaev3 ; Agaev4 , etc. As we also previously mentioned, to better understand the hot and dense QCD matter created in relativistic heavy-ion collision experiments such as Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory’s (BNL) and the Large Hadron Collider (LHC) at the European Organization for Nuclear Research’s (CERN), the investigation of effects of temperature on spectroscopic properties of hadrons at nonzero temperature is needed. Such investigations can also help us to improve our understanding of phase transition, quark-gluon deconfinement and chiral symmetry restoration. By increasing in the temperature, a transition or chiral crossover Aoki ; MCheng from the hadronic phase to QGP phase may be occurred. Lattice QCD calculations show that thepseudocritical temperature is for chiral crossover Bhattacharya ; Bazavov2 to QGP.
One of the most applicable and powerful phenomenological tools that can be used to analyze the spectroscopic properties of hadrons at nonzero temperature is the thermal QCD sum rule method (TQCDSR). This method is the thermal version Bochkarev of the QCD sum rule, firstly introduced by Shifman, Vainshtein and Zakharov for mesons at zero temperature Shifman and then applied to baryons in vacuum by Ioffe Ioffe . In thermal version, some additional operators appear in the operator product expansion (OPE/Wilson expansion) due to the breaking of the Lorentz invariance and vacuum expectation values are replaced by their thermal forms at finite temperature. The essential objective of this study is to extend our previous work on the thermal properties of the spin-3/2 heavy baryons at nonzero temperature AziziTurkan and investigate the shifts on the mass and residue of the spin-1/2 heavy , , , and baryons with respect to temperature using TQCDSR. In our calculations, we take account the extra operators arising from the OPE at nonzero temperature and use the thermal quark, gluon and mixed condensates up to dimension eight as well as the temperature-dependent energy-momentum tensor.
This study is structured as follows: In Sec. II, we derive the TQCDSR for masses and residues of the spin-1/2 heavy baryons at nonzero temperature. In Sec. III, we present the numerical analysis of the obtained sum rules for the physical parameters and a comparison of our results at zero temperature with those existing in the literature. The last section is devoted to both the summary of the results and our concluding remarks.
II Thermal QCD Sum Rule Calculations
The aim of this section is to obtain TQCDSR for the masses and residues of the spin-1/2 heavy , , , and baryons at nonzero temperature. For this purpose, we start our calculations by considering the following two-point thermal correlation function:
| (1) |
where denotes the four-momentum of the considered spin-1/2 heavy baryon (), indicates the ground state of the hot medium and is the time-ordering operator. is the interpolating current of baryon, which couples to both the positive and negative parities. It is represented by the following expressions for anti-triplet () and sextet (6) baryons Bagan :
| (2) | |||||
| (3) | |||||
where is the Levi-Civita tensor with color indices , is the charge conjugation operator, , , and in which denotes an arbitrary mixing parameter with corresponds to the famous Ioffe currents that we consider in the present study. As we previously noted, and stand for light quarks and for heavy quark field and they are given in Table 1 for all considered baryons. Thus, considering Eq. (2) and Eq. (3), the interpolating currents for each state can be written as
| (4) |
According to the standard philosophy of the QCD sum rule method, the aforementioned thermal correlation function is evaluated in two basic ways: i) On the hadronic side, it is calculated in terms of hadronic parameters such as the temperature-dependent mass and residue of hadron. ii) On the QCD side, it is calculated in terms of temperature-dependent QCD degrees of freedom in the deep Euclidean region with the help of OPE. Then, matching the coefficients of the selected structures from both sides in momentum space, via the dispersion relation, the QCD sum rules for the spectroscopic parameters of the at nonzero temperature are obtained. In the final step, to suppress the contributions of the higher states and continuum in obtained sum rules, Borel transformation and continuum subtraction are applied to both sides of these equalities. One may first apply the Borel transformation and continuum subtraction, then match the coefficients of the selected structures from both sides.
The thermal correlation function in the hadronic side is obtained by inserting the full set of hadronic states having the same quantum numbers as the related interpolating current into Eq. (1). After performing the integration over four-, the thermal correlation function for the hadronic side can be written as
where and are spin-1/2 single heavy baryon states with the positive and negative parity, respectively, dots stand for the contributions of the higher states and continuum and is the temperature-dependent mass of . The matrix elements for are defined as
| (6) |
where is the temperature-dependent residue of and is Dirac spinor of spin and the four-momentum . To proceed, we insert Eq. (II) into Eq. (II) and perform summation over spins of . The hadronic side of thermal correlation function in its final form is decomposed in terms of different structures as
| (7) | |||||
This correlation function can be written in terms of the structures and as
where , as the coefficients of the selected Lorentz structures, in Borel scheme are obtained as
| (9) | |||||
and
| (10) | |||||
where is the Borel parameter to be determined in next section.
Now, we have to evaluate the QCD side of the thermal correlation function in terms of the quark-gluon degrees of freedom in the deep Euclidean region. For this aim, we insert the related interpolating current of given in Eq. (II) into Eq. (1) and contract all light and heavy quark fields using the Wick theorem. Thus, the most general form of the thermal correlation function on the QCD side in terms of thermal light (heavy) quark propagators for and 6 baryons are obtained as
| (11) | |||||
| (12) | |||||
where . To proceed, thermal light (heavy) quark propagators in coordinate space are needed, which are used as (see also Azizi1 ; Azizi2 ; Prop_C )
| (14) | |||||
Here, is the light (heavy) quark mass, is the thermal quark condensate, is thermal gluon condensate, is the thermal mixed condensate. The new operators, emerging in OPE, appear to restore the Lorentz invariance broken out by the choice of the thermal rest frame at nonzero temperature. They are expressed in terms of fermionic and gluonic parts of the energy momentum tensor and the four-vector velocity of the medium, . To this end, is chosen which leads to . In the rest frame of the heat bath, , with being the energy of quasi particle, , in the mass-shell condition. At limit it is the mass of the particle. In the light quark propagator, the fermionic part of the energy momentum tensor, , is seen explicitly whereas the gluonic part, , appears in the trace of two-gluon field strength tensor in the heat bath Mallik , i.e.
| (15) | |||||
The QCD side of the correlation function can be written similar to hadronic side in terms of different Lorentz structures as
where are the coefficients of the selected Lorentz structures and they contain both the perturbative and non-perturbative contributions. The perturbative and some non-perturbative parts are written in terms of the dispersion integrals in the present study. Thus,
| (17) |
where , are the spectral densities and stand for the remaining non-perturbative contributions that are calculated directly by applying the Borel transformation. The related spectral densities are defined as
| (18) |
After Borel transformation and continuum subtraction we get
where is the temperature-dependent continuum threshold. The main task in this part is to find the expressions for and . They are obtained after inserting the explicit forms of the heavy and light quark propagators into the QCD side of the thermal correlation function given in Eqs. (11) and (12) for and 6 baryons with spin-1/2, performing the Fourier integral to go to the momentum space and applying the steps above to get the perturbative and non-perturbative parts. As a result, the explicit forms of the functions and are obtained. Because of obtained expressions are quite lengthy, we present the expressions of and for only baryon as an example in the Appendix.
Finally, we match the coefficients of the selected structures from the hadronic and QCD sides of the correlation function and find the sum rules:
| (20) | |||||
and
| (21) | |||||
In order to obtain the four unknowns, , , and , two more equations which can be achieved by applying derivatives with respect to to both sides of Eqs. (20) and (21) are needed. Therefore, we get
| (22) | |||||
| (23) | |||||
By simultaneously solving the above four equations, the temperature-dependent masses and residues for the positive and negative parity spin-1/2 heavy baryons are obtained in terms of , , QCD degrees of freedom and other inputs. For the masses, as examples, we get
| (24) |
| (25) |
where
| (26) |
Similar results are obtained for the temperature-dependent residues.
III Numerical results
In this section, we perform the numerical analyses of the sum rules for the masses and residues of the spin-1/2 heavy , , , and baryons at nonzero temperature. For this aim, firstly we use the numerical values of some input parameters collected in Table 2 in our calculations.
| Parameters | Values |
|---|---|
| ; | ; |
| ; | ; |
| ; | ; |
| ; | ; |
| ; | ; |
| ; | ; |
| ; | ; |
To go further in the analyses, we also need to know the thermal quark condensates (for and ), parametrized in terms of vacuum condensates and temperature. For this purpose, we use the following parametrization, which are based on lattice QCD results presented in Ref. Gubler
| (27) |
where the coefficients A, B and C for the corresponding and are given in Table 3. Note, that the lattice results in Ref. Gubler are given in a wide range of the temperature, however, we find their fit functions up to the critical temperature under consideration in the present study (see also AziziTurkan ). The above fit together with the parameters in the Table 3 exactly reproduce the graphics for the temperature-dependent quark condensates in Ref. Gubler .
| A | B [GeV] | C | |
|---|---|---|---|
| for | 0.025 | 1.015 | |
| for | 0.019 | 1.002 |
The temperature-dependent gluon condensate is given as Gubler :
| (28) | |||||
where
| (29) |
and is defined as
| (30) |
with being the energy density and is the pressure. Using the recent Lattice calculations given in Bazavov1 ; Borsanyi , we obtain the following fit function for (see also AziziTurkan ):
| (31) |
Note that this function, obtained in the present study, exactly reproduces the lattice QCD graphics for with respect to temperature presented in Refs. Bazavov1 ; Borsanyi . The temperature-dependent strong coupling is also given as Kaczmarek ; Morita
where, .
We use results on the thermal behavior of the energy-momentum tensor given by lattice QCD in Ref. Bazavov1 and parametrize the gluonic and fermionic parts of the energy density up to thepseudocritical temperature. Hence, we use:
| (33) |
with the related coefficients defined in Table 4. This function, obtained in the present study, reproduces the temperature-dependent energy densities presented in Ref. Bazavov1 by graphics.
| D | E [Gev] | F | |
|---|---|---|---|
| for | 0.040 | 0.024 | |
| for | 0.047 | -0.731 |
In the next step, we have to obtain the temperature-dependent continuum threshold . For this purpose, we use the following parametrization:
| (34) |
where is continuum threshold at zero temperature. It is not totally arbitrary and depends on the energy of the first excited state lies just above the considered positive and negative parity states with the same quantum numbers. should reduce to at limit and must obey at this limit. As we mentioned in the previous section, the four unknowns (masses of the positive and negative parity baryons as well as their residues) at each channel are obtained in terms of Borel parameter, QCD degrees of freedom and . As it is seen the temperature-dependent continuum threshold, , contains the vacuum continuum threshold and . The together with are determined considering the standard prescriptions of the method and will be discussed below. One of the main tasks is to determine the function , which plays an important role in determination of the behavior of the physical quantities with respect to the temperature. To determine we apply another derivative with respect to to both sides of Eq. (22) and use the expressions of the masses and residues, obtained in the previous section that also contain though , in the resultant equation . By numerical solving of the obtained equation at different temperature (up to thepseudocritical temperature used in the present study), we find the following fit function for :
| (35) |
Let us now discuss how we determine the working windows for the Borel parameter and vacuum continuum threshold . They are fixed using the standard criteria of the method. Namely, the pole dominance, OPE convergence and weak dependence of the physical quantities on these parameters. All of these requirements lead to the following working intervals for different members of the baryons under study:
| (36) |
for bottom and
| (37) |
for charmed baryons. To check the stability of the results with respect to the changes in and in their working intervals, as an example, we plot a 3D graphic of the mass of positive parity baryon as functions of these auxiliary parameters at in Figure 1. We see that the dependence of the mass on both and is weak and the changes remain within the acceptable limits of the method. The parameters of other members show similar behavior.

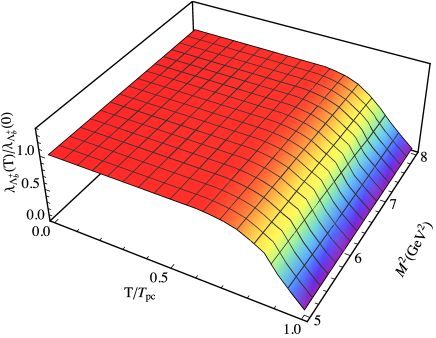
Now, we proceed to investigate the temperature dependence of the masses and residues of the baryons. As examples, we only present the results on the temperature-dependent masses and residues for the positive parity baryons. They reflects behavior of the OPE sides, which are common for both the positive and negative parity baryons, i.e., the masses and residues of both parities are obtained in terms of the functions in OPE sides as presented in the previous section. To this end, we plot the ratio of the temperature-dependent mass (residue) to its vacuum value, (), for the positive parity baryons as functions of and ratio in 3D at average values of for , , , and baryons in Figs. 2 and 3. From these figures, we see that the spectroscopic parameters of these baryons remain approximately unchanged with respect to the changes in up to for masses and for residues. After these points, they start to decrease rapidly with increasing the temperature and we are witness of melting of these baryons. We realize that similar situation is valid for the charmed , , , and baryons. The amount of negative shifts in masses and residues near to the critical point are shown in Tables 5 and 6. In the case of mass, the order of shifts roughly are comparable between the bottom and charmed baryons of each channel. Among the results, the order of negative shifts for all channels in bottom case is roughly the same but shows some differences among the charmed baryons. The sum rules for masses give reliable predictions up to thepseudocritical point considered in the present study. As far as the residues are concerned, the amount of shifts are roughly the same for b- and c-baryons and they are very large. Thus, at limit, the residues approaches to zero and we see the melting of the baryons.
| Negative shift |
|---|
| Negative shift |
|---|









Our final task in this section is to discuss the results at limit. In this limit, the values of masses for the spin-1/2 heavy baryons containing a bottom quark with both the positive and negative parities are presented in Tables 7 and 8, respectively. Similarly, the vacuum masses for the spin-1/2 heavy baryons containing a charm quark with both the positive and negative parities are presented in Tables 9 and 10, respectively. From these tables, we see that our results are in good consistency with existing experimental data and other theoretical predictions within the presented uncertainties. These consistency lead us to hope that, the obtained results at nonzero temperature in the present study can shed light on the future heavy ion collision experiments and can be used in analyses of the related data. The uncertainties in our predictions belong to those related to the working intervals of the auxiliary parameters as well as the uncertainties of all the presented input parameters.
| present work | |||||
|---|---|---|---|---|---|
| ExpPDG | |||||
| Roberts | 5.612 | 5.844 | 5.833 | 6.081 | |
| Karliner | 5.790-5800 | ||||
| Capstick | 5.585 | 5.795 | |||
| Dai | |||||
| Liu | |||||
| Korner | 5.80 | 5.82 | 5.94 | 6.04 | |
| Roncaglia | |||||
| Ghalenovi1 | 5.833 | 5.815 | 5.948 | ||
| Ghalenovi2 | 5.683 | 5.833 | 5.708 | 5.967 | |
| Brown | 5.626 | 5.771 | 5.856 | 5.933 | 6.056 |
| Mathur | 5.664 | 5.762 | 6.021 | ||
| Ebert1 | 5.622 | 5.812 | 5.805 | 5.937 | 6.065 |
| Ebert2 | 5.622 | 5.812 | 5.805 | 6.065 | |
| Ebert3 | 5.620 | 5.803 | 5.808 | 6.064 | |
| Kim | 5.609 | 5.8036 | 5.8055 | 5.9338 | 6.0571 |
| Yin | 5.62 | 5.75 | 5.75 | 5.88 | 6.00 |
| Azizi | |||||
| Wang1 ; Wang2 | |||||
| Wang3 | |||||
| Zhang1 ; Zhang2 | |||||
| Agaev2 | 6.487 | ||||
| Agaev4 |
| present work | |||||
|---|---|---|---|---|---|
| ExpPDG | |||||
| Roberts | 5.939 | 6.108 | 6.099 | 6.301 | |
| Capstick | 5.912 | 6.070 | |||
| Ebert2 | 5.930 | 6.119 | 6.352 | ||
| Ebert3 | |||||
| Garcilazo | 6.076 | 6.039 | 6.278 | ||
| Yin | |||||
| Wang3 | |||||
| Zhang1 ; Zhang2 | |||||
| Agaev2 |
| present work | |||||
|---|---|---|---|---|---|
| ExpPDG | |||||
| Roberts | 2.268 | 2.492 | 2.455 | 2.718 | |
| Capstick | 2.265 | 2.440 | |||
| Dai | |||||
| Liu | |||||
| Korner | 2.57 | ||||
| Roncaglia | |||||
| Ghalenovi1 | 2.473 | 2.455 | 2.588 | ||
| Ghalenovi2 | 2.303 | 2.453 | 2.328 | 2.587 | |
| Patel1 | 2.653 | 2.586 | 2.720 | ||
| Patel2 | 2.648 | 2.575 | 2.723 | ||
| Brown | 2.254 | 2.433 | 2.474 | 2.574 | 2.679 |
| Mathur | 2.440 | 2.407 | 2.652 | ||
| Lewis | 2.295 | 2.462 | 2.490 | 2.594 | 2.699 |
| Bahtiyar | 2.343(23) | 2.474(11) | 2.711(16) | ||
| Ebert1 ; Ebert2 | 2.297 | 2.481 | 2.439 | 2.578 | 2.698 |
| Ebert3 | 2.286 | 2.476 | 2.443 | 2.698 | |
| Kim | 2.2807 | 2.4752 | 2.4485 | 2.5768 | 2.7001 |
| Yin | 2.40 | 2.55 | 2.45 | 2.59 | 2.73 |
| Azizi | |||||
| Wang1 ; Wang2 | |||||
| Wang3 | |||||
| Zhang1 ; Zhang2 | |||||
| Agaev1 | |||||
| Agaev3 ; Agaev4 |
| present work | |||||
|---|---|---|---|---|---|
| ExpPDG | |||||
| Roberts | 2.625 | 2.763 | 2.748 | 2.977 | |
| Capstick | 2.630 | 2.795 | |||
| Bahtiyar | 2.668(16) | 2.770(67) | 3.044(15) | ||
| Ebert2 | 2.598 | 2.801 | 3.020 | ||
| Ebert3 | |||||
| Migura | 2.769 | 2.769 | |||
| Gerasyuta1 ; Gerasyuta2 ; Gerasyuta3 | 2.700 | ||||
| Garcilazo | 2.749 | 2.706 | 2.959 | ||
| Yin | 2.79 | 2.84 | 3.03 | ||
| Wang3 | |||||
| Zhang1 ; Zhang2 | |||||
| Agaev1 | |||||
| Agaev3 ; Agaev4 |
IV Summary and Conclusions
We investigated the mass and residue of the spin-1/2 single heavy , , , and baryons as functions of temperature in the framework of thermal QCD sum rule. In our calculations, we took into account the non-perturbative operators up to mass dimension 8 including those arising from the Wilson expansion at finite temperature due to breaking the Lorentz invariance. The obtained results indicate that the mass of these baryons in both the bottom and charm channels remain stable up to roughly MeV while their residue are unchanged up to MeV. After these points, the masses and residues start to diminish by increasing in the temperature. The shifts in the mass and residue for both the bottom and charm channels are considerably large and we observe the melting of these baryons near to thepseudocritical temperature determined by recent lattice QCD calculations. The amount of negative shifts near to thepseudocritical point have been shown in Tables 5 and 6. The order of shifts in masses are roughly the same between the bottom and charmed baryons of each channel. Among the results, the order of shifts for all channels for bottom baryons is roughly the same but shows some differences among the charmed members. The sum rules for masses give reliable predictions up to thepseudocritical point considered in the present study (roughly MeV). As far as the residues are concerned, the amounts of shifts in bottom and charmed cases of each channel are the same. The negative shifts near to the end point are very large for all baryons and the residues approach to zero atpseudocritical point.
We presented our results for the mass of the single heavy baryons with both the positive and negative parities at limit in Tables 7, 8, 9 and 10. We observed that the obtained results for the single heavy bottom and charmed baryons of spin-1/2 with both the positive and negative parities in the present study are in good consistencies with the experimental data presented in Ref. PDG as well as with other theoretical predictions made via different phenomenological approaches. Our results on the behavior of the physical quantities considered in the present study with respect to temperature and the amount of shifts in these quantities near to the pseudocritical point may be checked via other phenomenological approaches. The obtained results in the present study may shed light on analyses of the data provided by the future heavy ion collision experiments.
V Appendix
In this appendix, we present the explicit forms of the spectral density (for perturbative and some non-perturbative parts) and the function defining other non-perturbative contributions for baryon as examples. They are obtained as
| (38) |
| (39) |
| (40) |
Here, is Feynman parameter, indicates the unit-step function, and . The explicit form of the function for the baryon is obtained as
| (41) | |||||
where the dimensions of some operators included in the formulas are given in Table 11.
| Dimension | Operator |
|---|---|
| 1 | |
| 3 | |
| 4 | |
| 4 | |
| 5 | |
| 6 | |
| 6 | |
| 7 | |
| 7 | |
| 8 | |
| 8 | |
| 8 |
References
- (1) P.A. Zyla et al. (Particle Data Group), “Review of Particle Physics,” Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
- (2) W. Roberts and M. Pervin, “Heavy Baryons in a Quark Model,” Int. J. Mod. Phys. A 23, 2817 (2008).
- (3) M. Karliner, B. Keren-Zura, H. J. Lipkin, and J. L.Rosner, “The quark model and b baryons,” Annals Phys. 324, 2 (2009).
- (4) S. Capstick and N. Isgur, “Baryons in a relativized quark model with chromodynamics,” Phys. Rev. D 34, 2809 (1986).
- (5) Y. B. Dai, C. S. Huang, C. Liu and C. D. Lu, “1m corrections to heavy baryon masses in the heavy quark effective theory sum rules,” Phys. Lett. B 371, 99 (1996).
- (6) X. Liu, H. X. Chen, Y. R. Liu, A. Hosaka, and S. L. Zhu, “Bottom baryons,” Phys. Rev. D 77, 014031 (2008).
- (7) J. G. Körner, M. Krämer, and D. Pirjol, “Heavy baryons,” Prog. Part. Nucl. Phys., 33, 787 (1994).
- (8) M. J. Savage, “Charmed baryon masses in chiral perturbation theory,” Phys. Lett. B 359, 189 (1995).
- (9) R. Roncaglia, D. B. Lichtenberg, and E. Predazzi, “Predicting the masses of baryons containing one or two heavy quarks,” Phys. Rev. D 52, 1722 (1995); R. Roncaglia, A. Dzierba, D. B. Lichtenberg, and E. Predazzi, “Predicting the masses of heavy hadrons without an explicit Hamiltonian,” Phys. Rev. D 51, 1248 (1995).
- (10) Z. Ghalenovi, A.A. Rajabi and A. Tavakolinezhad, “The Heavy Baryon Masses and Spin-Isospin Dependence,” J.Phys.Conf.Ser. 347, 012015 (2012).
- (11) Z. Ghalenovi, A.A. Rajabi, M. Hamzavi, “The heavy baryon masses in variational approach and spin-isospin dependence,” Acta Phys.Polon.B 42, 1849 (2011).
- (12) B. Patel, A.K. Rai, P.C. Vinodkumar, “Masses and Magnetic Moments of Charmed Baryons Using Hyper Central Model,” arXiv:0803.0221 [hep-ph].
- (13) B. Patel, A.K. Rai, P.C. Vinodkumar, “Heavy flavor baryons in hypercentral model,” Pramana 70, 797 (2008) arXiv:0802.4408v1 [hep-ph].
- (14) Z. S. Brown, W. Detmold, S. Meinel, K. Orginos, “Charmed bottom baryon spectroscopy from lattice QCD,” Phys. Rev. D 90, 094507 (2014).
- (15) N. Mathur, R. Lewis, R. M. Woloshyn, “Charmed and bottom baryons from lattice nonrelativistic QCD,” Phys.Rev.D 66, 014502 (2002).
- (16) R. Lewis, N. Mathur, R.M. Woloshyn, “Charmed baryons in lattice QCD,” Phys.Rev.D 64, 094509 (2001).
- (17) H. Bahtiyar,K. U. Can ,G. Erkol,P. Gubler, M. Oka and T. T. Takahashi, “Charmed baryon spectrum from lattice QCD near the physical point,” Phys.Rev.D 102, 054513 (2020).
- (18) D. Ebert, R. N. Faustov, and V. O. Galkin, “Masses of heavy baryons in the relativistic quark model,” Phys. Rev. D 72, 034026 (2005).
- (19) D. Ebert, R. N. Faustov and V. O. Galkin, “Masses of excited heavy baryons in the relativistic quark-diquark picture,” Phys.Lett.B 659, 612 (2008).
- (20) D. Ebert, R. N. Faustov and V. O. Galkin, “Spectroscopy and Regge trajectories of heavy baryons in the relativistic quark-diquark picture,” Phys. Rev. D 84, 014025 (2011).
- (21) S. Migura, D. Merten, B. Metsch and H. R. Petry, “Charmed baryons in a relativistic quark model,” Eur. Phys. J. A 28, 41 (2006).
- (22) S. M. Gerasyuta and D. V. Ivanov, “Charmed baryons in bootstrap quark model,” Nuovo Cim. A 112, 261 (1999).
- (23) S. M. Gerasyuta and E. E. Matskevich, “Charmed baryon multiplet,” Int.J.Mod.Phys.E 17, 585 (2008).
- (24) S. M. Gerasyuta and E. E. Matskevich, “S-wave bottom baryons,” Int.J.Mod.Phys.E 18, 1785 (2009).
- (25) H. Garcilazo, J. Vijande and A. Valcarce, “Faddeev study of heavy-baryon spectroscopy,” J. Phys. G Nucl. Part. Phys. 34, 961 (2007).
- (26) J.Y. Kim, H. C. Kim, G.S. Yang, “Mass spectra of singly heavy baryons in a self-consistent chiral quark-soliton model,” Phys. Rev. D 98, 054004 (2018).
- (27) P.-L. Yin, Z.-F. Cui, C. D. Roberts, J. Segovia, “Masses of positive- and negative-parity hadron ground-states, including those with heavy quarks,” Eur.Phys.J.C 81, 327 (2021).
- (28) E. V. Shuryak, “Hadrons containing a heavy quark and QCD sum rules,” Nucl. Phys. B 198, 83 (1982).
- (29) E. Bagan, M. Chabab, H. G. Dosch, and S. Narison, “The Heavy baryons from QCD spectral sum rules,” Phys. Lett. B 278, 367 (1992).
- (30) K. Azizi, N. Er, H. Sundu, “Scalar and vector self-energies of heavy baryons in nuclear medium,” Nucl.Phys. A 960, 147 (2017).
- (31) Z. G. Wang, “Analysis of baryons in nuclear matter with QCD sum rules,” Phys. Rev. C 85, 045204 (2012).
- (32) Z. G. Wang, “Analysis of the baryons in the nuclear matter with the QCD sum rules,” Eur.Phys.J.C 71, 1816 (2011).
- (33) Z. G. Wang, “Analysis of the flavor antitriplet heavy baryon states with QCD sum rules,” Eur.Phys.J.C 68, 479 (2010).
- (34) J. R. Zhang and M. Q. Huang, “Mass spectra of the heavy baryons and from QCD sum rules,” Phys. Rev. D 77, 094002 (2008).
- (35) J. R. Zhang and M. Q. Huang,“Heavy baryon spectroscopy in QCD,” Phys. Rev. D 78, 094015 (2008).
- (36) S. S. Agaev, K. Azizi, H. Sundu, “Newly discovered resonances and their parameters,” Eur.Phys.J. A 57, 201 (2021).
- (37) S. S. Agaev, K. Azizi, H. Sundu, “Decay widths of the excited baryons,” Phys.Rev.D 96, 094011 (2017).
- (38) S. S. Agaev, K. Azizi, H. Sundu, “Interpretation of the new states via their mass and width,” Eur.Phys.J.C 77, 395 (2017).
- (39) S. S. Agaev, K. Azizi, H. Sundu, “On the nature of the newly discovered states,” EPL 118, 61001 (2017).
- (40) Y. Aoki, G. Endrődi, Z. Fodor, S.D. Katz, K.K. Szabó, “The order of the quantum chromodynamics transition predicted by the standard model of particle physics,” Nature 443, 675-678, (2006).
- (41) M. Cheng et al., “Transition temperature in QCD,” Phys. Rev. D 74, 054507 (2006).
- (42) T. Bhattacharya et al., “QCD Phase Transition with Chiral Quarks and Physical Quark Masses,” Phys. Rev. Let. (PRL) 113, 082001 (2014).
- (43) A. Bazavov et al., “QCD equation of state to from lattice QCD,” Phys. Rev. D 95, 054504 (2017).
- (44) A. I. Bochkarev, M. E. Shaposhnikov, “The spectrum of hot hadronic matter and finite-temperature QCD sum rules,” Nucl. Phys. B 268, 220 (1986).
- (45) M. A. Shifman, A. I. Vainstein, V. I. Zakharov, “QCD and resonance physics. theoretical foundations,” Nucl. Phys. B 147, 385 (1979); M. A. Shifman, A. I. Vainstein, V. I. Zakharov, “QCD and resonance physics. applications,” Nucl. Phys. B 147, 448 (1979).
- (46) B. L. Ioffe, “Calculation of baryon masses in quantum chromodynamics,” Nucl. Phys. B 188, 317 (1981).
- (47) K. Azizi, A.Türkan, “S-wave single heavy baryons with spin-3/2 at finite temperature,” Eur. Phys. J. C 80, 425 (2020).
- (48) K. Azizi, G. Kaya, “Thermal behavior of the mass and residue of hyperons,” J. Phys. G: Nucl. Part. Phys. 43, 055002 (2016).
- (49) K. Azizi, A. Türkan, E. Veli Veliev, H. Sundu, “Thermal Properties of Light Tensor Mesons via QCD Sum Rules,” Adv. High Energy Phys. 2015, 794243 (2015).
- (50) L. J. Reinders, H. Rubinstein and S. Yazaki, “Hadron properties from QCD sum rules,” Phys. Rept. 127, 1 (1985).
- (51) S. Mallik, “Operator product expansion at finite temperature,” Phys. Lett. B 416, 373 (1998).
- (52) P. Gubler, D. Satow, “Recent Progress in QCD Condensate Evaluations and Sum Rules,” Prog. Part. Nucl. Phys. 106, 1 (2019) arXiv:1812.00385 [hep-ph].
- (53) V. M. Belyaev, B. L. Ioffe, “ Determination of the baryon mass and baryon resonances from the quantum-chromodynamics sum rule. Strange baryons,” Sov. Phys. JETP, 57, 716 (1983).
- (54) H. G. Dosch, M. Jamin and S. Narison, “Baryon masses and flavour symmetry breaking of chiral condensates,” Phys. Lett. B 220, 251 (1989).
- (55) B. L. Ioffe, “QCD (Quantum chromodynamics) at low energies,” Prog. Part. Nucl. Phys. 56, 232 (2006).
- (56) A. Bazavov et al., “Equation of state in -flavor QCD,” Phys. Rev., D 90, 094503 (2014).
- (57) S. Borsanyiet al., “Full result for the QCD equation of state with flavors,” Phys. Lett. B 730, 99 (2014).
- (58) O. Kaczmarek, F. Karsch, F. Zantow, P. Petreczky, “Static quark-antiquark free energy and the running coupling at finite temperature,” Phys. Rev. D 70, 074505 (2004).
- (59) K. Morita, S. H. Lee , “Critical behavior of charmonia across the phase transition: A QCD sum rule approach,” Phys. Rev. C 77, 064904 (2008).