Projection based adiabatic elimination of bipartite open quantum systems

Let $\rho(t)$ be the density operator on the Hilbert space $\mathcal{H}$ describing the quantum state of the system at time $t$. We suppose that the evolution of $\rho(t)$ is generated by a Lindblad operator $\mathcal{L}$: $\dot{\rho}(t)=\mathcal{L}\rho(t)$. We define the Hilbert space $\mathbfcal{H}$ of operator $O$ on $\mathcal{H}$, equipped with the scalar product $\text{tr}\left[O_{1}^{\dagger}O_{2}\right]$. We first recall the main results presented in Ref Finkelstein-Shapiro et al. (2020) related to projector techniques. Let $\mathcal{P}$ the projector such that $\rho_{s}(t)=\mathcal{P}\rho(t)$ is the the slow part of the system and write $\mathcal{Q}=\openone-\mathcal{P}$, where $\openone$ is the identity operator on $\mathbfcal{H}$. Let $\mathcal{G}(z)=(z-\mathcal{L})^{-1}$ be the resolvent of the Lindblad operator $\mathcal{L}$. Operators like $\mathcal{P},\mathcal{Q},\mathcal{L}$ or $\mathcal{G}$ are operators on $\mathbfcal{H}$. They are sometimes called super-operators. They are here denoted with calligraphic letter, to distinguish them from operators on $\mathcal{H}$ (belonging to $\mathbfcal{H}$), like the density matrix $\rho$.

We define the effective Lindblad operator $\mathcal{L}_{\text{eff}}(z)$, such that $\mathcal{P}\mathcal{G}(z)\mathcal{P}=(z-\mathcal{L}_{\text{eff}}(z))^{-1}$. The effective Lindblad operator $\mathcal{L}_{\text{eff}}(z)$ can be written as :

where

For any $\rho(t=0)$, such that $\mathcal{Q}\rho(t=0)=0$, the slow dynamics inside $\mathcal{P}\mathbfcal{H}$ can be obtained with the inverse Laplace transform as:

where $\rho_{s}(t=0)=\mathcal{P}\rho(t=0)$ and the integral on the complex plane is performed on a straight line $D=\left\{z\in\mathbb{C};\Re{z}=a>0\right\}$. At this point no approximation has been made. Eq. (3) gives the exact dynamics inside $\mathcal{P}\mathbfcal{H}$, as long as the initial condition is also inside $\mathcal{P}\mathbfcal{H}$, that is $\mathcal{Q}\rho(t=0)=0$. Because $\mathcal{L}_{\text{eff}}(z)$ captures the effect of the dynamics in $\mathcal{Q}\mathbfcal{H}$, it is a nonlinear superoperator, in the sense that $(z-\mathcal{L}_{\text{eff}}(z))\vec{\nu}=0$ is a nonlinear eigenvalue problem.

The approximation of a slow dynamics of $\mathcal{P}\rho(t)$, with respect to the fast dynamics of $\mathcal{Q}\rho(t)$ is equivalent to considering the dynamics inside $\mathcal{P}\mathbfcal{H}$ in the vicinity of the stationary state reached in the limit $t\rightarrow\infty$. In this long time limit only the $z\rightarrow 0$ limit will contribute to the inverse Laplace transform of Eq. (3). We thus approximate $\mathcal{L}_{\text{eff}}(z)$ to the lowest relevant order:

where $\mathcal{L}_{0}=\mathcal{L}_{\text{eff}}(z=0)$ and $\mathcal{L}_{n}=\frac{1}{n!}\left.\frac{\mathrm{d}}{\mathrm{d}z}\mathcal{L}_{\text{eff}}(z)\right|_{z=0}$. Using the expression of $\mathcal{L}_{\text{eff}}(z)$ given by Eq. (1) allows to express $\mathcal{L}_{0}$ and $\mathcal{L}_{n}$ as:

In this work, we consider the approximation given by Eq. (4) with $n\leq 1$ only, which is a standard approximation for most of the effective operators that are calculated explicitly. The systematic study of higher order approximations ($n>1$) will be considered in a future work. Within the approximation given by Eq. (4), with $n=1$, the inverse Laplace transform of Eq. (3) can be computed explicitly. We obtain:

The stationary state $\rho_{f}$ of this dynamics, reached at $t\rightarrow+\infty$, is in the kernel of $\mathcal{L}_{0}$. We note that although the dynamics described by Eq. (6) is an approximation, the final reached stationary state $\rho_{f}$ is the exact one.

To conclude, after the adiabatic elimination of the fast part, the generator of the slow dynamics is approximatively given by $(1-\mathcal{L}_{1})^{-1}\mathcal{L}_{0}$, $\dot{\rho}(t)=(1-\mathcal{L}_{1})^{-1}\mathcal{L}_{0}\rho(t)$, where $\mathcal{L}_{0}$ and $\mathcal{L}_{1}$ can in principle be computed using Eq. (5). The hard part in these equations is the evaluation of the inverse $(\mathcal{Q}\mathcal{L}\mathcal{Q})^{-1}$, which in the most general case, as we will see later, can only be achieved through a perturbative expansion.

Theses results are very general, and require only the definition of a projector $\mathcal{P}$ and that the initial state fulfills the condition $\mathcal{Q}\rho(t=0)=0$. We note that $\mathcal{P}$ doesn’t have to be hermitian, that is the projection does not need to be orthogonal.

In Ref. Finkelstein-Shapiro et al. (2020), this formalism was applied to the case where the slow and fast degrees of freedom correspond to a partition of the underlying Hilbert space in two complementary sub-spaces, that is $\mathcal{H}=\mathcal{H}^{(A)}\oplus\mathcal{H}^{(B)}$. In the next section we will adapt this general formalism to the bipartite case where $\mathcal{H}=\mathcal{H}^{(A)}\otimes\mathcal{H}^{(B)}$.

We suppose that the state of the bipartite system at time $t$ is described by a density operator $\rho^{(AB)}(t)$ acting on the Hilbert space $\mathcal{H}=\mathcal{H}^{(A)}\otimes\mathcal{H}^{(B)}$. We consider that the dynamics of subsystem $A$ is very slow compared to the dynamics of subsystem $B$. We suppose that the exact stationary state in $\mathbfcal{H}$ is unique and that it is a product state $\rho_{f}=\rho_{a}\otimes\rho_{b}$, where $\rho_{a}\in\mathbfcal{H}^{(A)}$ and $\rho_{b}\in\mathbfcal{H}^{(B)}$ with $\mathbfcal{H}^{(i)},i=A,B$, the Hilbert space of operators on $\mathcal{H}^{(i)}$. As the the dynamics of $B$ subsystem is very fast, we suppose that it is a good approximation to consider that at $t=0$, $\rho^{(AB)}(t=0)=\rho^{(A)}_{0}\otimes\rho_{b}$. In other word, we consider that $B$ reaches its steady state instantaneously in the time scale of the subsystem $A$. We thus define $\mathcal{P}$ as

where $\text{tr}_{B}\left[\right]$ denotes the partial trace over $B$. The reduced density operator $\rho^{(A)}(t)$ in $\mathbfcal{H}^{(A)}$ can then be obtained as $\rho^{(A)}(t)=\text{tr}_{B}\left[\mathcal{P}\rho^{(AB)}(t)\right]$.

For the purpose of simplifying some expressions and calculations, it will be useful to use the operator-vector isomorphism Havel (2003) which maps each element of $\mathbfcal{H}$ to a vector in $\mathcal{H}\otimes\mathcal{H}$ as follows. An operators such as $\lvert a\rangle\langle b\rvert\in\mathbfcal{H}$ is mapped to the vector $\lvert\overline{b}\rangle\otimes\lvert a\rangle$ in the $\mathcal{H}\otimes\mathcal{H}$ Hilbert space, where $\lvert\overline{b}\rangle$ is the complex conjugate of $\lvert b\rangle$. Consequently, any $n\times n$ density matrix $\rho\in\mathbfcal{H}$ is mapped to a column vector $\lvert\lvert\rho\rangle\rangle\in\mathcal{H}\otimes\mathcal{H}$, with $n^{2}$ elements, by stacking the columns of the $\rho$ matrix. Under this isomorphism, super-operators on $\mathbfcal{H}$ are mapped to operators on $\mathcal{H}\otimes\mathcal{H}$. In particular, the super-operator $\mathcal{O}$ performing the operation $\rho\rightarrow O_{1}\rho O_{2}^{\dagger}$, with $O_{1}$ and $O_{2}$ operators in $\mathbfcal{H}$, is mapped to $\lvert\lvert\rho\rangle\rangle\rightarrow\overline{O}_{2}\otimes O_{1}\lvert\lvert\rho\rangle\rangle$, where $\overline{O}$ denotes the complex conjugate of $O$; that is $\overline{O}=\left(O^{\dagger}\right)^{T}$, where $O^{\dagger}$ is the adjoint and $O^{T}$ is the transpose of $O$. In this way, the scalar product $\text{tr}\left[\rho_{1}^{\dagger}\rho_{2}\right]$ between two operators $\rho_{1}$ and $\rho_{2}$ in $\mathbfcal{H}$ is equal to the usual scalar product $\langle\langle\rho_{1}\rvert\rho_{2}\rangle\rangle$ in $\mathcal{H}\otimes\mathcal{H}$. Some useful remarks can be made. The identity operator $\openone$ in $\mathbfcal{H}$ is mapped to the maximally entangled state

in $\mathcal{H}\otimes\mathcal{H}$, where $\left\{\lvert k\rangle\right\}$ is an orthonormal basis of $\mathcal{H}$. We also note that the usual density matrix normalization $\text{tr}\left[\rho\right]=1$ does not correspond to the normalization induced by the scalar product $\text{tr}\left[\rho^{2}\right]=1$ (except in the case of a pure state). Using the previous remark, we have that $\text{tr}\left[\rho\right]=\text{tr}\left[\openone\rho\right]=1$ is mapped to $\langle\langle\openone\rvert\rho\rangle\rangle=1$. For our bipartite case, $\mathcal{H}=\mathcal{H}^{(A)}\otimes\mathcal{H}^{(B)}$. Therefore, an operator in $\mathbfcal{H}$ as $\lvert a_{1}\rangle\langle a_{2}\rvert\otimes\lvert b_{1}\rangle\langle b_{2}\rvert$, where $\lvert a_{i}(b_{i})\rangle\in\mathcal{H}^{(A)}(\mathcal{H}^{(B)})(i=1,2)$, is mapped to $\lvert\overline{a_{2}}\rangle\otimes\lvert a_{1}\rangle\otimes\lvert\overline{b_{2}}\rangle\otimes\lvert b_{1}\rangle$. The partial trace over $\mathcal{H}^{(B)}$, $\text{tr}_{B}\left[\rho\right]\in\mathbfcal{H}^{(A)}$ is mapped to $\langle\langle\openone^{(B)}\rvert\rho\rangle\rangle\in\mathcal{H}^{(A)}\otimes\mathcal{H}^{(A)}$, where $\lvert\openone^{(B)}\rangle=\sum_{k}\lvert k\rangle\otimes\lvert k\rangle$ in $\mathcal{H}^{(B)}\otimes\mathcal{H}^{(B)}$, where $\left\{\lvert k\rangle\right\}$ is now an orthonormal basis of $\mathcal{H}^{(B)}$.

Consequently, the operator $\mathcal{P}\rho^{(AB)}\in\mathbfcal{H}$ is mapped to the vector $\langle\langle\openone^{(B)}\rvert\rho^{(AB)}\rangle\rangle\otimes\lvert\lvert\rho_{b}\rangle\rangle\in\mathcal{H}\otimes\mathcal{H}$. The projector $\mathcal{P}$ acting on $\mathcal{H}\otimes\mathcal{H}$ can thus be written as:

where $\openone^{(2A)}$ is the identity operator on $\mathcal{H}^{(A)}\otimes\mathcal{H}^{(A)}$. The operator $\mathcal{Q}=\openone-\mathcal{P}$ simply reads as:

where $\openone^{(2B)}$ is the identity operator on $\mathcal{H}^{(B)}\otimes\mathcal{H}^{(B)}$.

In general, the Lindblad operator of the system can be split in 3 terms as follows:

where $\mathcal{L}_{A(B)}$ is a Lindblad operator acting on the $A(B)$ part only. The decomposition of $\mathcal{L}$ with the help of $\mathcal{P}$ and $\mathcal{Q}$ reads:

Where we have used the fact that $\langle\langle\openone^{(B)}\rvert\rvert\mathcal{L}_{B}=0$, as $\mathcal{L}_{B}$ is a trace preserving operator. In some specific cases, it can be a good approximation to take as $\rho_{B}$, a stationary state of $\mathcal{L}_{B}$. In that case $\mathcal{L}_{B}\mathcal{P}_{B}=0$ and $\mathcal{Q}\mathcal{L}\mathcal{P}$ in Eq. (14) can be simplified as

For computing $\mathcal{L}_{0}$ using Eq. (6), the main difficulty resides in the inversion of $\mathcal{Q}\mathcal{L}\mathcal{Q}$. In general this inversion can not be done explicitly, but a perturbative expansion can give a good approximation. In many cases $\mathcal{Q}\mathcal{L}\mathcal{Q}$ can be divided into two terms, $\mathcal{Q}\mathcal{L}\mathcal{Q}=\mathcal{D}+\mathcal{V}$, where the computation of $\mathcal{D}^{-1}$ is easy, and $\mathcal{V}$ is small compared to $\mathcal{D}$. In that case we can write

Retaining the terms up to $n=0$ or $n=1$ may give a good approximation.

In some cases, the term $\openone^{(2A)}\otimes\mathcal{Q}_{B}\mathcal{L}_{B}\mathcal{Q}_{B}$ in Eq. (15) is dominant over the two other terms. In that case, approximating the inverse of $\mathcal{Q}\mathcal{L}\mathcal{Q}$ by

can be sufficient as we will see in the examples in the next section. So, $\mathcal{L}_{0}$ can be approximated by the following expression:

This is the main result of this work.

This two qubits system has been considered previously by Azouit et in Ref. Azouit et al. (2017a) to test another method of bipartite adiabatic elimination (note that in their work, it is the $A$ spin which is the strongly dissipative spin). It consists in a strongly dissipative driven qubit $B$ dispersively coupled to a target qubit $A$. This model is used in Ref. Sarlette et al. (2020) to describe the continuous measurement of a harmonic oscillator excitation number (corresponding to system $A$) by a spin (corresponding system $B$). The Lindblad equation for the bipartite system can be written as:

where $\sigma_{+}=\lvert 1\rangle\langle 0\rvert$, $\sigma_{-}=\sigma_{+}^{\dagger}$ and $\lvert 0\rangle,\lvert 1\rangle$ are the eignvectors of the Pauli matrix $\sigma_{z}$ with eigenvalues $-1,1$ respectively. Defining the new parameters $\tau=ut$, $\chi^{\prime}=\dfrac{\chi}{u}$, and $\gamma^{\prime}=\dfrac{\gamma}{u}$ and using the column-vector isomorphism, we write the superoperator form of the Liouvillian as:

where we have used the relations

From now on, we will drop the prime in all the parameters $\gamma^{\prime}$, $\chi^{\prime}$. As the qubit $A$ only comes into play through the Hamiltonian term $-i\chi[\sigma_{z}^{A}\otimes\sigma_{z}^{B},\rho]$ (see Eq. (20)), the kernel of the Lindblad operator is two dimensional, according to the two eigenvectors $\sigma_{z}^{A}$. Hence the kernel can be considered as the span of $\{\rho_{s0}^{(A)}\otimes\rho_{s0}^{(B)},\rho_{s1}^{(A)}\otimes\rho_{s1}^{(B)}\}$, where $\rho_{s0}^{(A)}=\lvert 0\rangle\langle 0\rvert$, $\rho_{s1}^{(A)}=\lvert 1\rangle\langle 1\rvert$ and (see Appendix for details):

In order to avoid any unnecessary complications, we will assume that the qubit $A$ has an extremely slow dissipation rate that we will omit from our calculations, but will ensure the uniqueness of the steady state. In other words, the steady state of the considered system will be $\rho_{ss}=\rho_{s_{0}}^{(A)}\otimes\rho_{s_{0}}^{(B)}$. We thus assume that the initial state is of the form $\rho_{0}=\rho^{(A)}_{0}\otimes\rho_{s_{0}}^{(B)}$, and we define the projector $\mathcal{P}$ (see Eq. (9)):

where according to Eq. (8), $\lvert\lvert\openone^{(B)}\rangle\rangle=\lvert 0\rangle\otimes\lvert 0\rangle+\lvert 1\rangle\otimes\lvert 1\rangle$. This ensures that $\mathcal{Q}=\openone-\mathcal{P}$ verifies $\mathcal{Q}\lvert\rho_{0}\rangle=0$ as it should be. In Appendix A, we calculate in detail all the quantities necessary to compute $\mathcal{L}_{0}$ and $\mathcal{L}_{1}$ as given by Eq. (5) :

where $\mathcal{X}_{i,j}$, $\mathcal{X}\in\{\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D}\},\;\text{and}\;i,j\in{0,1}$, are operators acting on $\mathbfcal{H}^{(B)}$ and we have simplified the notation as $\lvert i,j\rangle=\lvert i\rangle\otimes\lvert j\rangle\in\mathcal{H}^{(A)}\otimes\mathcal{H}^{(A)}\quad(i,j=0,1)$, see Appendix. A. From the block diagonal form of Eq. (28), it is relatively easy to invert $\mathcal{Q}\mathcal{L}\mathcal{Q}$ exactly. In addition, we are only interested in quantities of the form $\mathcal{P}\mathcal{L}\mathcal{Q}(\mathcal{Q}\mathcal{L}\mathcal{Q})^{-n}\mathcal{Q}\mathcal{L}\mathcal{P}$. Hence, from the form of $\mathcal{P}\mathcal{L}\mathcal{Q}$ in Eqs.(26), we only need to calculate $\mathcal{B}_{0,1}^{-1}$ and $\mathcal{B}_{1,0}^{-1}$.

Using Eqs. (25) to (28) in Eq. (5), we can write $\mathcal{L}_{0}$ and $\mathcal{L}_{1}$ as:

Since $\mathcal{P}^{(B)}$ is a projector of rank $1$, we can write:

where (see Appendix. A):

and, see Appendix A:

With these variables and truncating (4) to the zeroth order, the effective Liouville equation can be written in operator space as:

Note that approximating the expression of $\xi$ and $\zeta$ (given in Appendix. A) by their lowest order in $\chi$ gives for Eq. (34) the same result as the one obtained by Azouit et al. Azouit et al. (2017a) using a completely different method. Finally, it is straightforward to calculate $\left(\openone-\mathcal{L}_{1}\right)^{-1}$ exactly , given that $\mathcal{L}_{1}$ (Eq. (30)) is block diagonal:

Let us define the modified initial state of the qubit $A$ as $\lvert\tilde{\rho}^{(A)}_{0}\rangle=(1-\mathcal{L}_{1})^{-1}{\rho}^{(A)}_{0}$:

where $\rho_{0,0},\rho_{1,1}$ represent population in the state $\rho^{(A)}_{0}$ while $\rho_{0,1},\rho_{1,0}$ represent initial coherences. The physical meaning of this redefined initial density matrix is the state of qubit $A$ immediately after qubit $B$ has reached its steady-state. In this case this corresponds to a rescaling of the coherences. Using $\mathcal{Q}_{B}\rho^{(B)}_{s_{0}}=0$, we can rewrite Eq. (6) to describe the dynamics of the slow qubit as:

where $\tilde{\mathcal{L}}_{0}=(1-\mathcal{L}_{1})^{-1}\mathcal{L}_{0}=\frac{\alpha}{1+\beta}\left|{0,1}\right\rangle\left\langle{0,1}\right|+\frac{\overline{\alpha}}{1+\overline{\beta}}\left|{1,0}\right\rangle\left\langle{1,0}\right|$. The evolution operator $U(t)=e^{\tilde{L}_{0}t}$ is simple to calculate:

where we have defined

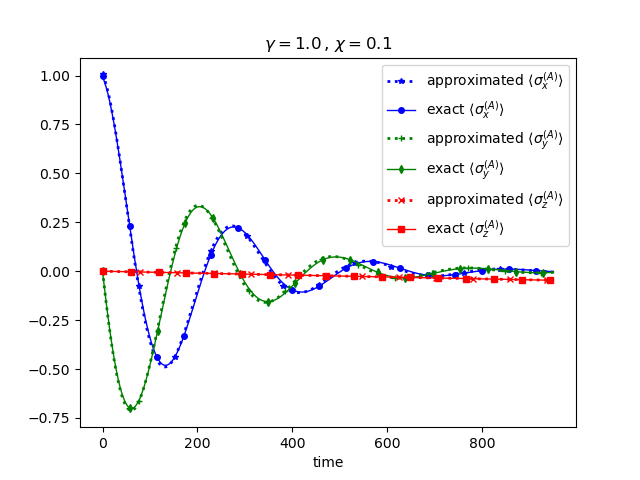
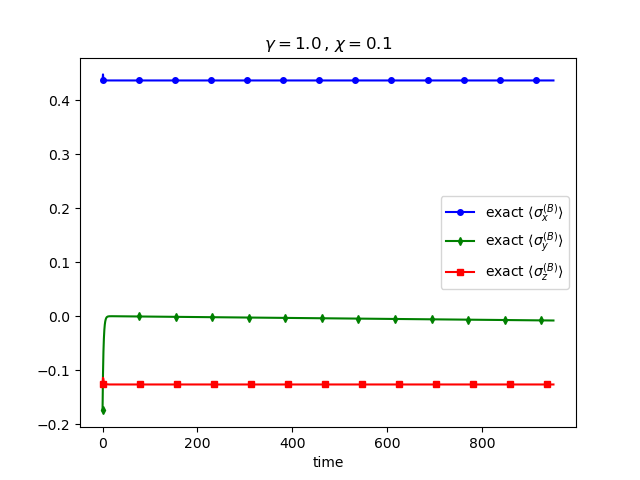
The evolution of the approximated expectation value of the Pauli matrices for qubit $A$ and $B$ for $\gamma=1$ and $\chi=0.1$ and with the initial state taken as

are compared in Figure 1 to the ones obtained through an exact full numerical propagation. We see that the adiabatic elimination captures the exact dynamics faithfully and that indeed qubit $B$ reaches its steady-state before any appreciable dynamics in $A$ has taken place.

It is worth mentioning that when adiabatic elimination is valid, i.e. $\chi\ll\gamma$, the exact final state of the fast qubit $B$ is very close to the steady state of $\mathcal{L}_{B}$:

Defining the projector $\mathcal{P}_{B}=\lvert\lvert\rho_{ss}^{(B)}\rangle\rangle\langle\langle\openone^{(2B)}\rvert\rvert$ leads to considerable simplifications in Eq. (14) where the first term becomes zero. Thus, taking the interaction $\mathcal{Q}\mathcal{L}_{AB}\mathcal{Q}$ to be small, we only need the term $n=0$ in Eq. (17) and taking the zero order only in (4), one can check that it leads to the same Lindblad operator derived in Azouit et al. (2017a) which is enough to obtain a very good approximation in the adiabatic limit.

The open Rabi model has been considered recently by Garbe et al. Garbe et al. (2020) in a quantum metrology context. It consist in a spin-$\frac{1}{2}$ (with frequency $\Omega$) interacting with one bosonic mode (frequency $\omega_{0}$) of a cavity described by the following Hamiltonian:

where $a$ ($a^{\dagger}$) is the annihilation (creation) operator of the bosonic mode. The dynamics of the open Rabi model where the relaxation of the spin (at a rate $\Gamma^{\prime}$) and the photon losses from the cavity (at a rate $\kappa^{\prime}$) are taken into account is generated by the following Lindblad operator:

where we have used the notation

We also assume that $\Gamma^{\prime}\thicksim\Omega$ and $\kappa^{\prime}\thicksim\omega_{0}$. If we rescale the time by dividing the above equation by $\sqrt{\Omega\omega_{0}}$, and define:

we rewrite the Lindbladian:

with :

It has been shown that, in the limit where $\omega_{0}\ll\Omega$, this model exhibits a quantum phase transition when $g$ increases Hwang et al. (2015); Puebla et al. (2017); Hwang et al. (2018); Garbe et al. (2020). The critical point corresponding to $g=1$ separates a normal phase ($g<1$) from a superadiant phase ($g>1$). Here we show that our method can be used to obtain an effective Lindblad operator for the boson in the normal phase after the elimination of the fast spin. After rescaling, the adiabatic limit $\omega_{0}\ll\Omega$ corresponds to $\eta\rightarrow 0$.

In the normal phase ($g<1$), the steady state of the system, which is the kernel of the Lindblad operator given by Eq. (42), is separable and unique Garbe et al. (2020). It is straight forward to verify that the steady state of $\mathcal{L}_{B}$ is:

Following the same steps of the last example, see Appendix. B, we define the projector $\mathcal{P}_{B}=\lvert\lvert\rho^{(B)}_{ss}\rangle\rangle\langle\langle\openone^{(2B)}\rvert\rvert$ and we only calculate the term $\mathcal{Q}\mathcal{L}_{B}\mathcal{Q}$, the inverse of which corresponds to $\mathcal{Q}\mathcal{L}\mathcal{Q}^{-1}$ up to zeroth order in Eq. (17). Simple and straightforward calculations lead to the following Lindbladian evolution of the boson:

which is exactly the formula derived in Garbe et al. (2020) using a completely different method, where one should take into consideration that the parameters in (42) are double those considered in Garbe et al. (2020).