Progress in Higgs inflation
Abstract
We review the recent progress in Higgs inflation focusing on Higgs- inflation, primordial black hole production and the term.
I Introduction
Among many models, Higgs inflation Bezrukov and Shaposhnikov (2008), equivalently Starobinsky’s inflation with a term Starobinsky (1980), 111Neglecting the kinetic term during the inflation, both theories are equivalent since is mapped to by solving the field equation for . attracts special attention as it provides the best fit to the astrophysical and cosmological observations Aghanim et al. (2018); Akrami et al. (2018). The success of Higgs inflation can be generalized to a broader perspective Park and Yamaguchi (2008). However, Higgs inflation is not free from theoretical issues: most notably, its original setup requires a large nonminimal coupling that leads to a low cutoff Burgess et al. (2009); Barbon and Espinosa (2009); Burgess et al. (2010); Lerner and McDonald (2010); Park and Shin (2019). Several proposed solutions include considering a field-dependent vacuum expectation value Bezrukov et al. (2011), introducing the Higgs near-criticality Hamada et al. (2014); Bezrukov and Shaposhnikov (2014); Hamada et al. (2015) or adding new degrees of freedom Giudice and Lee (2011); Barbon et al. (2015); Giudice and Lee (2014); Ema (2017); Gorbunov and Tokareva (2019).
The addition of a term to the gravity sector proved to be a novel setup that resolves these issues during inflation and reheating. The term, which may dynamically arise from radiative corrections of the nonminimal interactions Salvio and Mazumdar (2015); Calmet and Kuntz (2016); Wang and Wang (2017); Ema (2017); Ghilencea (2018); Ema (2019); Canko et al. (2019), then pushes the theory’s cutoff scale beyond the Planck scale: the new scalar field, , called the scalaron emerges in association with the term and unitarizes the theory Gorbunov and Tokareva (2019); He et al. (2019, 2018); Gundhi and Steinwachs (2018) just like the Higgs field does for the electroweak theory. The violent preheating in pure Higgs inflation Ema et al. (2017) is also resolved by the term He et al. (2018, 2019). Therefore, the most realistic approach is to consider both scalars in our setup. We refer this setup as ‘Higgs-’ inflation. More theoretical discussions include Palatini formulation of gravity Jinno et al. (2020) and swampland conjectures Cheong et al. (2019a); Park (2019).
II Pure Higgs inflation
II.1 Model
As inflation has been regarded as a standard paradigm describing the early universe, it also has become important to understanding how inflation is actually realized in particle physics models. In the Standard Model(SM), there is an unique candidate, which is the Higgs boson.
Unfortunately, the chaotic inflation type of potential is known to be inconsistent with cosmological measurements because it predicts a large tensor-to-scalar ratio . However, an additional non-minimal coupling between the Higgs scalar and the Ricci scalar in the gravity sector flattens the potential in the large field regime in the Einstein frame and suppresses Bezrukov and Shaposhnikov (2008).
The Lagrangian for the relevant inflaton and gravity sectors is
| (1) |
where with and stands for the Jordan frame. To eliminate the non-minimal coupling, we redefine the metric as
| (2) |
where
| (3) |
and we canonicalize the kinetic term with the relation
| (4) |
Then, the action in the canonical Einstein frame is 222In fact, the form of the action is different when the Palatini formalism is used, which regard the metrics and affine connection independently. In this review, we take the standard metric formalism.
| (5) |
where
| (6) |
Approximately, the potential takes the form
| (7) |
Note that we neglected and that the potential becomes asymptotically constant at large field values. The e-folding number , with ‘end’ meaning the time at the end of the inflation and meaning CMB pivot scale/time, is
| (8) | ||||
| (9) |
Here, we use during slow-roll inflation and . Normally, the number of e-foldings required to solve the horizon and flatness problems is assumed to be .
From the potential in the Einstein frame, we can calculate the slow roll parameters as
| (10) | ||||
| (11) |
where denotes the derivative with respect to .
By parameterizing the scalar and tensor power spectrum as
| (12) |
respectively, cosmological observables such as the spectral index and the tensor-to-scalar ratio are approximated with the slow-roll parameters:
| (13) | ||||
| (14) |
which are perfectly consistent with current Planck 2018 measurement Akrami et al. (2018). To satisfy the amplitude of the curvature power spectrum , one needs other constraints for and .
| (15) |
Therefore, by assuming , for example, we have to assume very large non-minimal coupling . Such a large non-minimal coupling causes theoretical issues including naturalness, and more seriously, the unitarity problem Barbon and Espinosa (2009); Burgess et al. (2009, 2010); Lerner and McDonald (2010). We will come back to this issue later in this review.
Note that we assumed constant and without considering the quantum corrections. In the Higgs inflation case, however, quantum corrections give non-trivial modifications not only to the inflaton dynamics, but also to cosmological observables.
II.2 Critical Higgs Inflation
For the currently known Higgs masses and top quark masses, the EW Higgs potential is known to be metastable as becomes negative when the renormalization scale is Degrassi et al. (2012). This fact may not be a big problem as long as the lifetime of the EW vacuum is longer than the age of the universe. However, if this is the case, the validity of the Higgs inflation scenario may be questioned Bezrukov et al. (2015). 333Even in non-Higgs inflation cases, large quantum fluctuation in de Sitter bachground during inflation may cause a problem. See the Ref. Markkanen et al. (2018a).
However, this result sensitively depends on the top quark mass measurement. In fact, the usually referred to top quark mass is the so-called ‘Monte-Carlo (MC) mass’. This is a mere parameter in MC simulations and the theoretical uncertainties on being identifed as the pole mass are large, up to Corcella (2019). Instead, by taking the latest pole mass from cross-section measurements Zyla et al. (2020)
| (16) |
the top quark mass which guarantees the Higgs potential stability is within the bound. In this review, we will assume absolute stability of the Higgs potential.
On the other hand, considering the effects of the running of the coupling to Higgs inflation cases is still important Hamada et al. (2014); Bezrukov and Shaposhnikov (2014); Hamada et al. (2015). The quartic coupling can be parameterized as
| (17) |
with , as denoted in Degrassi et al. (2012); Buttazzo et al. (2013).444In fact, due to the non-renormalizability of the theory, there exists a dependence on the way to choose the renormalization scale, which is also called ‘prescription’. In this review, we choose , where is the Jordan frame Higgs field value. For the meaning of the prescription dependence in detail, see Ref. Hamada et al. (2017).
One of the major consequences is that small non-minimal couplings, , are allowed, assuming . Another possible result is that the form of the potential could have an inflection point when the values of are tuned to be nearly zero, and this type of inflation is referred to as ‘critical Higgs inflation (CHI)’. This fact has motivated efforts to look into the possibilities of generating primordial black holes (PBH) on the model, as the inflection shape potential is a well-known class of models to induce large curvature power spectrum on small scales producing a significant amount of PBHs.
II.3 Unitarity Problem
One should be careful when dealing with the cut-off scale of the Higgs inflation due to the existence of large non-minimal coupling Burgess et al. (2009, 2010); Barbon and Espinosa (2009).
For the small field region , from Eq. (5), fields in each frames are related by
| (18) |
This means that the kinetic term of the field in the Einstein frame contains derivative couplings
| (19) |
From the second term, one concludes that the theory becomes strongly coupled at .
During inflation, the fluctuation is defined with respect to the classical background field value (denoted with ‘bar’) as
| (20) |
Therefore, in the region where corresponding to the inflationary region,
| (21) |
implying
| (22) |
Therefore, the cut-off scale during inflation is safely higher than the energy scale of inflation Bezrukov et al. (2011).
However, after inflation, the inflaton rolls down to the minimum of the potential and starts to oscillate coherently. Lastly, the Higgs field decays to SM particles and loses its energy. These procedures are called ‘reheating’. During the reheating phase, the decay of the longitudinal gauge boson is violent and the momentum of the produced particles is , which is larger than the cut-off scale during the reheating, 555In fact, the Higgs boson decay to the longitudinal mode of the gauge boson may depend sensitively on higher order operators. See the Ref. Hamada et al. (2020). Ema et al. (2017). Above the cut-off scale, decay processes violate unitarity, becoming strongly coupled, and lose its predictivity.
To unitarize the Higgs inflation during reheating, there has been a lot of attempts to raise the cut-off scale of the Higgs inflation by introducing additional degrees of freedom Giudice and Lee (2011); Barbon et al. (2015); Giudice and Lee (2014). One of the simplest and minimal ways is to consider the corrections Ema (2017); Gorbunov and Tokareva (2019); He et al. (2019, 2018); Gundhi and Steinwachs (2018), as described in the next section.
III Higgs- inflation
III.1 Model
The Higgs- inflation is a simple UV extension that cures the theoretical/phenomenological issues of single-field Higgs inflation Ema (2017); Gorbunov and Tokareva (2019). The action takes the following form.
| (23) |
where is the scalaron mass, is a scalar that stands for the Standard Model Higgs in the unitary gauge, and a conveniently defined function and its derivative with respect to
| (24) | ||||
| (25) |
The scalaron field is defined as
| (26) | ||||
| (27) |
Through a Weyl transformation, , we can get the action in the Einstein frame as
| (28) |
where the scalar potential is
| (29) |
As noted in the potential Eq. (29), higher order operators are induced in the analysis; therefore, the perturbativity of the system is guaranteed for a specific cutoff scale. Expanding the potential around yields a cutoff scale
| (30) |
for scalaron masses within the following range . This cutoff scale guarantees the perturbative analysis of this model throughout inflation and preheating, alleviating the unitarity problem of single-field Higgs inflation Gorbunov and Tokareva (2019); He et al. (2019, 2018); Gundhi and Steinwachs (2018) .
This additional term can also be induced through quantum loop corrections in the large- limit. Renormalization group equations of the system imply a new scalar degree at the mass scale , which in turn corresponds to the strong coupling scale of Higgs inflation Salvio and Mazumdar (2015); Calmet and Kuntz (2016); Wang and Wang (2017); Ema (2017); Ghilencea (2018); Ema (2019); Canko et al. (2019); Ema et al. (2020). Therefore, the addition of the term is a natural aspect in terms of both perturbative unitarity and renormalizability.
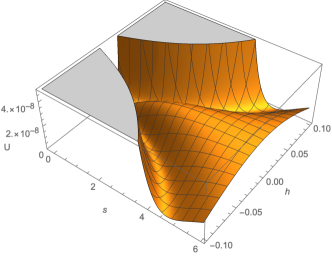
III.2 Inflation
The additional scalar degree of freedom in the action yields a multifield inflationary potential. For a non-critical case with , the potential takes a valley form as in Fig. 1. Re-formulating the action, we obtain the equation of motion
| (31) |
with
| (32) |
where is the curved field space metric, , , and . The inflaton will approximately roll down the valley, resulting in successful slow-roll inflation. This particular valley structure exhibits an isocurvature mass , leading to exponentially decaying isocurvature perturbations and allowing for an effective single-field description of the system. The potential along the direction is locally minimized at
| (33) |
Inserting this into the potential and taking the large limit, we find that the inflationary potential at the plateau becomes
| (34) |
yielding the cross-correlation between parameters , and .
| (35) |
III.3 Preheating
After the inflationary stage, the inflaton rolls down to the minimum at . Depending on the parameters, the inflaton oscillates in both the and the directions, making the effective single-field analysis insufficient. In this period, the quantum creation of the NG boson mode from is important. This direction arises from the following terms in the Lagrangian He et al. (2019):
| (36) |
where and is the scale factor in the FRW metric. By computing the effective NG mode mass, the peak value takes the form
| (37) |
with and . This quantity is noticeably lower than the cutoff scale of the theory. Therefore, the violent preheating behavior is present and physical, albeit it is not as violent as it would be in the single field Higgs inflation case and does not violate the unitarity problem Ema et al. (2017).
For specific parameters, the inflaton may climb up the hill of the potential at , giving a negative and inducing a tachyonic preheating phase Bezrukov et al. (2019); He et al. (2020); Bezrukov and Shepherd (2020). This in turn gives an exponential enhancement to the particle production, rapidly completing the preheating process. The criticality of the Standard Model Higgs quartic coupling may also lead to interesting and unique phenomena in the preheating procedure. We will do a detailed analysis in future works.
IV PBH production
As no strong signals of standard particle types of dark matter including WIMPs or axions have been found, PBHs are obtaining more attention again as a candidate for dark matter. Different from the astrophysical BH, PBHs originate from the large quantum fluctuations during the inflation.
Large efforts have been made on searching/constraning mass windows for MACHO types of dark matter and now a narrow mass range is left for PBHs to explain the whole of dark matter: , as depicted in Fig. 2. denotes the solar mass. Indeed, numerous models and scenarios of inflation have been suggested to produce enough PBHs with appropriate mass ranges to explain dark matter. Future experiments, including femtolensing and gravitational waves experiments, are planned or suggested to cover these mass ranges Katz et al. (2018); Jung and Kim (2019); Dasgupta et al. (2019). Those experiments are expected to give hints to the validity of the scenarios to explain the origin of dark matter with PBHs.
One of the most realistic and minimal possibility is to consider the critical Higgs inflation model, which was motivated by the fact that the power spectrum is enhanced in ultra-slow-roll inflation and can cause large fluctuations at small scales. Unfortunately, single-field CHI turns out to generate PBHs away from the desired mass range, and its predictions itself are questioned in many studies Ezquiaga et al. (2018); Kannike et al. (2017); Germani and Prokopec (2017); Bezrukov et al. (2018); Motohashi and Hu (2017); Masina (2018); Drees and Xu (2019). In this review, we summarize the recent progress on Higgs inflation providing a new possibility of PBH generation as dark matter from the Higgs- model Cheong et al. (2019b).
IV.1 Primordial Black Hole
In this subsection, we briefly summarize the formulas to obtain the PBH mass spectrum given a curvature power spectrum from inflation.
When the energy density perturbation 666At linear order, there is a simple relation between the energy density fluctuation and the curvature perturbation: (38) exceeds a critical values Green et al. (2004); Harada et al. (2013); Musco (2019), the matter in the Hubble sphere with radius starts to collapes to a black hole when the corresponding mode re-enters to the horizon during the radiation dominated (RD) era Carr (1975); Carr et al. (2010). The energy density of the background is also determined by the Hubble parameter. Therefore, the mass of the primordial black hole is determined solely by the Hubble scale at the time of its formation Green et al. (2004),
| (39) |
where represents the efficiency of the collapsing processes and is the comoving momentum scale on which the primordial black hole is generated. The variance of the density contrast is calculated from the curvature power spectrum and the window function smoothing over the comoving scale :
| (40) |
We follow the ‘peaks theory’ method Green et al. (2004); Young et al. (2014) to compute the PBH abundance and the mass spectrum. We use the variable . The energy density fraction of PBHs at formation, denoted by can be calculated using
| (41) |
with
| (42) |
Finally, the fraction of PBHs against the total dark matter energy density is
| (43) |
where is the effective relativistic degree of freedom at the time of formation.
IV.2 PBH Production from Higgs- Inflation
As a minimal extension of Higgs inflation, it is highly motivated to consider the role of the term with criticality of the self quartic coupling in generating PBHs as dark matter.
In the Higgs- model, three relevant running parameters exist. The 1-loop beta functions are Codello and Jain (2016); Markkanen et al. (2018b); Gorbunov and Tokareva (2019); Ema (2019)
| (44) | ||||
| (45) | ||||
| (46) |
where . stands for the other terms from the SM De Simone et al. (2009). Among those, as in the original critical Higgs inflation case, the running of is most important in our analysis.
During inflation, including the inflection point, the Higgs field value is comparable to the Planck scale . On the other hand, the effects of the Ricci scalar in the de Sitter background on determining the renormalization scale is negligible due to the small Hubble parameter . Therefore, we choose our prescription and express as Eq. (17). Note that the Higgs field values are independent of the frame used for Higgs- inflation.
The field values and the corresponding value for the potential to have an inflection point can be determined by using the conditions
| (47) |
We then compute the value777In fact, to generate a large enough power spectrum, , with at the corresponding scale, the must be smaller than the pure inflection value by as much as so that the potential should deviate from a true inflection point., which we assumed to include all the information from the SM parameters.

Fig. 2 shows the new possibility of the Higgs- inflation model generating a sufficient number of PBHs with , in appropriate mass ranges without any strong astronomical bound. From the multi-field nature of the model with an additional scalaron direction, the inflection point is located on a relatively low scale along the inflationary trajectory.
A correlation also exists between the spectral index and the PBH mass . Without additional higher order corrections such as , the constraint on narrows the possible mass ranges of PBHs from Higgs- inflation as Cheong et al. (2019b), with a compatibility with Planck and LHC data.
V term
In this section, we discuss the recent progress with additional higher order gravity terms in Higgs inflation focusing on the term, and analyzing the inflationary predictions and their implications on PBH production. These additional Ricci scalar terms are characterized in the gravity class, which in turn is formulated in a scalar tensor theory as Huang (2014); Sebastiani et al. (2014); Kamada and Yokoyama (2014); Artymowski et al. (2015); Cheong et al. (2020)
| (48) | ||||
| (49) | ||||
| (50) |
with being taken for simplicity. The factors and can be expressed as
| (51) | ||||
| (52) |
When transformed to the Einstein frame, the dimension cutoff scale for becomes
| (53) |
where . This value is generically larger than , which guarantees that the perturbative analysis holds for generic polynomial gravity theories.
The extension with parameters , and yields a dual scalar theory with
| (54) |
for which the solution takes the form
| (55) | |||||
| (56) |
where on the last line the conditions and are implied. This perturbative expansion gives additional terms in the Einstein potential, when expanded in powers of :
| (57) |
with being the potential for the pure Starobinsky inflation scenario . These additional terms alter the predictions of the slow-roll parameters and CMB observables in powers of . In particular, the spectral index and the tensor-to-scalar ratio can be expressed as
| (58) | ||||
| (59) |
and
| (60) |
with and being the inflation duration’s e-fold number. Current Planck CMB data Akrami et al. (2018) give a rough constraint of , which indicates that the large-scale predictions of this model are highly sensitive to the term.
As this additional term modifies the large-scale predictions, the presence of this operator can also effect CMB predictions for PBH-compatible critical Higgs- inflationary scenarios. The gravitational part of the action contains the following expression:
| (61) |
for which the Einstein frame potential is
| (62) |
By taking the running of and inducing an inflection point, one can plot the contribution to the potential
| (63) |
along with the trajectory, as shown in Fig. 3. Notice that the inflection point lies on the zero contour of the potential variance, indicating that the curvature power spectrum is effectively identical to the Higgs- scenario while the CMB large scale predictions shift accordingly.


Fig. 4 presents this shift of CMB/PBH observable values. As mentioned in the previous sections, the pure critical Higgs- scenario can give both CMB- and PBH-compatible scenarios; however its compatibility is within the range, slightly shifting its predictions from the Planck central values. The addition of higher order terms, i.e., , shifts the CMB large-scale observables in the form of Eq. (59) and Eq. (60), whereas the peak profile remains effectively identical to that for the corresponding Higgs- case. The tune of parameters therefore widens the allowed parameter region, which gives a better CMB compatibility for the Higgs- PBH scenario.
VI Conclusion
The only scalar field in the standard model of particle physics, the Higgs field, has been known to be responsible for electroweak symmetry breaking and the masses of elementary particles for several decades. However, its irreplaceable roles in the early Universe have relatively recently been realized and appreciated. In this selective review, we focus on the inflationary era starting from how the Higgs field provides the exponential expansion of the universe and produces the primordial density fluctuations. We also review the possible production of primordial black holes, which may be responsible for all dark matter in the universe. Probably this is not the end of the story. We strongly believe that the full power of the Higgs field in particle physics and cosmology still needs further understanding.
Acknowledgements.
We thank Kazunori Kohri, Misao Sasaki, Hyun Min Lee, Shi Pi, and Fedor Bezrukov for helpful discussions and Alexei Starobinski, Minxi He, Jun’ichi Yokoyama, Ryusuke Jinno, Kohei Kamada, Kin-ya Oda, and Mio Kubota for valuable collaborations. This work was supported by National Research Foundation grants funded by the Korean government (MSIT) (NRF-2018R1A4A1025334),(NRF-2019R1A2C1089334) (SCP) and (MOE) (NRF-2020R1A6A3A13076216) (SML). The work of SML is supported by the Hyundai Motor Chung Mong-Koo Foundation.References
- Bezrukov and Shaposhnikov (2008) F. L. Bezrukov and M. Shaposhnikov, Phys. Lett. B659, 703 (2008), arXiv:0710.3755 [hep-th] .
- Starobinsky (1980) A. A. Starobinsky, Phys. Lett. 91B, 99 (1980), [,771(1980)].
- Aghanim et al. (2018) N. Aghanim et al. (Planck), (2018), arXiv:1807.06209 [astro-ph.CO] .
- Akrami et al. (2018) Y. Akrami et al. (Planck), (2018), arXiv:1807.06211 [astro-ph.CO] .
- Park and Yamaguchi (2008) S. C. Park and S. Yamaguchi, JCAP 0808, 009 (2008), arXiv:0801.1722 [hep-ph] .
- Burgess et al. (2009) C. P. Burgess, H. M. Lee, and M. Trott, JHEP 09, 103 (2009), arXiv:0902.4465 [hep-ph] .
- Barbon and Espinosa (2009) J. L. F. Barbon and J. R. Espinosa, Phys. Rev. D79, 081302 (2009), arXiv:0903.0355 [hep-ph] .
- Burgess et al. (2010) C. P. Burgess, H. M. Lee, and M. Trott, JHEP 07, 007 (2010), arXiv:1002.2730 [hep-ph] .
- Lerner and McDonald (2010) R. N. Lerner and J. McDonald, JCAP 1004, 015 (2010), arXiv:0912.5463 [hep-ph] .
- Park and Shin (2019) S. C. Park and C. S. Shin, Eur. Phys. J. C79, 529 (2019), arXiv:1807.09952 [hep-ph] .
- Bezrukov et al. (2011) F. Bezrukov, A. Magnin, M. Shaposhnikov, and S. Sibiryakov, JHEP 01, 016 (2011), arXiv:1008.5157 [hep-ph] .
- Hamada et al. (2014) Y. Hamada, H. Kawai, K.-y. Oda, and S. C. Park, Phys. Rev. Lett. 112, 241301 (2014), arXiv:1403.5043 [hep-ph] .
- Bezrukov and Shaposhnikov (2014) F. Bezrukov and M. Shaposhnikov, Phys. Lett. B734, 249 (2014), arXiv:1403.6078 [hep-ph] .
- Hamada et al. (2015) Y. Hamada, H. Kawai, K.-y. Oda, and S. C. Park, Phys. Rev. D91, 053008 (2015), arXiv:1408.4864 [hep-ph] .
- Giudice and Lee (2011) G. F. Giudice and H. M. Lee, Phys. Lett. B694, 294 (2011), arXiv:1010.1417 [hep-ph] .
- Barbon et al. (2015) J. L. F. Barbon, J. A. Casas, J. Elias-Miro, and J. R. Espinosa, JHEP 09, 027 (2015), arXiv:1501.02231 [hep-ph] .
- Giudice and Lee (2014) G. F. Giudice and H. M. Lee, Phys. Lett. B733, 58 (2014), arXiv:1402.2129 [hep-ph] .
- Ema (2017) Y. Ema, Phys. Lett. B770, 403 (2017), arXiv:1701.07665 [hep-ph] .
- Gorbunov and Tokareva (2019) D. Gorbunov and A. Tokareva, Phys. Lett. B788, 37 (2019), arXiv:1807.02392 [hep-ph] .
- Salvio and Mazumdar (2015) A. Salvio and A. Mazumdar, Phys. Lett. B750, 194 (2015), arXiv:1506.07520 [hep-ph] .
- Calmet and Kuntz (2016) X. Calmet and I. Kuntz, Eur. Phys. J. C76, 289 (2016), arXiv:1605.02236 [hep-th] .
- Wang and Wang (2017) Y.-C. Wang and T. Wang, Phys. Rev. D96, 123506 (2017), arXiv:1701.06636 [gr-qc] .
- Ghilencea (2018) D. M. Ghilencea, Phys. Rev. D98, 103524 (2018), arXiv:1807.06900 [hep-ph] .
- Ema (2019) Y. Ema, JCAP 1909, 027 (2019), arXiv:1907.00993 [hep-ph] .
- Canko et al. (2019) D. D. Canko, I. D. Gialamas, and G. P. Kodaxis, (2019), arXiv:1901.06296 [hep-th] .
- He et al. (2019) M. He, R. Jinno, K. Kamada, S. C. Park, A. A. Starobinsky, and J. Yokoyama, Phys. Lett. B791, 36 (2019), arXiv:1812.10099 [hep-ph] .
- He et al. (2018) M. He, A. A. Starobinsky, and J. Yokoyama, JCAP 1805, 064 (2018), arXiv:1804.00409 [astro-ph.CO] .
- Gundhi and Steinwachs (2018) A. Gundhi and C. F. Steinwachs, (2018), arXiv:1810.10546 [hep-th] .
- Ema et al. (2017) Y. Ema, R. Jinno, K. Mukaida, and K. Nakayama, JCAP 1702, 045 (2017), arXiv:1609.05209 [hep-ph] .
- Jinno et al. (2020) R. Jinno, M. Kubota, K.-y. Oda, and S. C. Park, JCAP 2003, 063 (2020), arXiv:1904.05699 [hep-ph] .
- Cheong et al. (2019a) D. Y. Cheong, S. M. Lee, and S. C. Park, Phys. Lett. B789, 336 (2019a), arXiv:1811.03622 [hep-ph] .
- Park (2019) S. C. Park, JCAP 1901, 053 (2019), arXiv:1810.11279 [hep-ph] .
- Degrassi et al. (2012) G. Degrassi, S. Di Vita, J. Elias-Miro, J. R. Espinosa, G. F. Giudice, G. Isidori, and A. Strumia, JHEP 08, 098 (2012), arXiv:1205.6497 [hep-ph] .
- Bezrukov et al. (2015) F. Bezrukov, J. Rubio, and M. Shaposhnikov, Phys. Rev. D 92, 083512 (2015), arXiv:1412.3811 [hep-ph] .
- Markkanen et al. (2018a) T. Markkanen, A. Rajantie, and S. Stopyra, Front. Astron. Space Sci. 5, 40 (2018a), arXiv:1809.06923 [astro-ph.CO] .
- Corcella (2019) G. Corcella, Front. in Phys. 7, 54 (2019), arXiv:1903.06574 [hep-ph] .
- Zyla et al. (2020) P. Zyla et al. (Particle Data Group), PTEP 2020, 083C01 (2020).
- Buttazzo et al. (2013) D. Buttazzo, G. Degrassi, P. P. Giardino, G. F. Giudice, F. Sala, A. Salvio, and A. Strumia, JHEP 12, 089 (2013), arXiv:1307.3536 [hep-ph] .
- Hamada et al. (2017) Y. Hamada, H. Kawai, Y. Nakanishi, and K.-y. Oda, Phys. Rev. D 95, 103524 (2017), arXiv:1610.05885 [hep-th] .
- Hamada et al. (2020) Y. Hamada, K. Kawana, and A. Scherlis, (2020), arXiv:2007.04701 [hep-ph] .
- Ema et al. (2020) Y. Ema, K. Mukaida, and J. van de Vis, (2020), arXiv:2008.01096 [hep-ph] .
- Bezrukov et al. (2019) F. Bezrukov, D. Gorbunov, C. Shepherd, and A. Tokareva, Phys. Lett. B 795, 657 (2019), arXiv:1904.04737 [hep-ph] .
- He et al. (2020) M. He, R. Jinno, K. Kamada, A. A. Starobinsky, and J. Yokoyama, (2020), arXiv:2007.10369 [hep-ph] .
- Bezrukov and Shepherd (2020) F. Bezrukov and C. Shepherd, (2020), arXiv:2007.10978 [hep-ph] .
- Katz et al. (2018) A. Katz, J. Kopp, S. Sibiryakov, and W. Xue, JCAP 1812, 005 (2018), arXiv:1807.11495 [astro-ph.CO] .
- Jung and Kim (2019) S. Jung and T. Kim, (2019), arXiv:1908.00078 [astro-ph.CO] .
- Dasgupta et al. (2019) B. Dasgupta, R. Laha, and A. Ray, (2019), arXiv:1912.01014 [hep-ph] .
- Ezquiaga et al. (2018) J. M. Ezquiaga, J. Garcia-Bellido, and E. Ruiz Morales, Phys. Lett. B776, 345 (2018), arXiv:1705.04861 [astro-ph.CO] .
- Kannike et al. (2017) K. Kannike, L. Marzola, M. Raidal, and H. Veermäe, JCAP 1709, 020 (2017), arXiv:1705.06225 [astro-ph.CO] .
- Germani and Prokopec (2017) C. Germani and T. Prokopec, Phys. Dark Univ. 18, 6 (2017), arXiv:1706.04226 [astro-ph.CO] .
- Bezrukov et al. (2018) F. Bezrukov, M. Pauly, and J. Rubio, JCAP 1802, 040 (2018), arXiv:1706.05007 [hep-ph] .
- Motohashi and Hu (2017) H. Motohashi and W. Hu, Phys. Rev. D96, 063503 (2017), arXiv:1706.06784 [astro-ph.CO] .
- Masina (2018) I. Masina, Phys. Rev. D98, 043536 (2018), arXiv:1805.02160 [hep-ph] .
- Drees and Xu (2019) M. Drees and Y. Xu, (2019), arXiv:1905.13581 [hep-ph] .
- Cheong et al. (2019b) D. Y. Cheong, S. M. Lee, and S. C. Park, (2019b), arXiv:1912.12032 [hep-ph] .
- Green et al. (2004) A. M. Green, A. R. Liddle, K. A. Malik, and M. Sasaki, Phys. Rev. D70, 041502 (2004), arXiv:astro-ph/0403181 [astro-ph] .
- Harada et al. (2013) T. Harada, C.-M. Yoo, and K. Kohri, Phys. Rev. D88, 084051 (2013), [Erratum: Phys. Rev.D89,no.2,029903(2014)], arXiv:1309.4201 [astro-ph.CO] .
- Musco (2019) I. Musco, Phys. Rev. D100, 123524 (2019), arXiv:1809.02127 [gr-qc] .
- Carr (1975) B. J. Carr, Astrophys. J. 201, 1 (1975).
- Carr et al. (2010) B. J. Carr, K. Kohri, Y. Sendouda, and J. Yokoyama, Phys. Rev. D81, 104019 (2010), arXiv:0912.5297 [astro-ph.CO] .
- Young et al. (2014) S. Young, C. T. Byrnes, and M. Sasaki, JCAP 1407, 045 (2014), arXiv:1405.7023 [gr-qc] .
- Codello and Jain (2016) A. Codello and R. K. Jain, Class. Quant. Grav. 33, 225006 (2016), arXiv:1507.06308 [gr-qc] .
- Markkanen et al. (2018b) T. Markkanen, S. Nurmi, A. Rajantie, and S. Stopyra, JHEP 06, 040 (2018b), arXiv:1804.02020 [hep-ph] .
- De Simone et al. (2009) A. De Simone, M. P. Hertzberg, and F. Wilczek, Phys. Lett. B678, 1 (2009), arXiv:0812.4946 [hep-ph] .
- Huang (2014) Q.-G. Huang, JCAP 1402, 035 (2014), arXiv:1309.3514 [hep-th] .
- Sebastiani et al. (2014) L. Sebastiani, G. Cognola, R. Myrzakulov, S. D. Odintsov, and S. Zerbini, Phys. Rev. D89, 023518 (2014), arXiv:1311.0744 [gr-qc] .
- Kamada and Yokoyama (2014) K. Kamada and J. Yokoyama, Phys. Rev. D90, 103520 (2014), arXiv:1405.6732 [hep-th] .
- Artymowski et al. (2015) M. Artymowski, Z. Lalak, and M. Lewicki, JCAP 1506, 031 (2015), arXiv:1412.8075 [hep-th] .
- Cheong et al. (2020) D. Y. Cheong, H. M. Lee, and S. C. Park, Phys. Lett. B 805, 135453 (2020), arXiv:2002.07981 [hep-ph] .