Production of hidden-heavy and double-heavy hadronic molecules at the $Z$ factory of CEPC

Since 2003, many of so-called $XYZ$ states have been observed in the hidden-charm sector, which exhibit different properties from the traditional hadrons in the quark model and thus are candidates of exotic hadrons. One of the most famous $XYZ$ states is the $X(3872)$ Choi et al. (2003), also called $\chi_{c1}(3872)$ Workman et al. (2022), observed in the $J/\psi\pi\pi$ invariant mass distribution by the Belle Collaboration and confirmed by many other experiments Acosta et al. (2004); Abazov et al. (2004); Aaij et al. (2013); Chatrchyan et al. (2013); Ablikim et al. (2014); Aaij et al. (2014, 2012); del Amo Sanchez et al. (2010); Aubert et al. (2009, 2008a, 2008b). Another important state is the isovector $Z_{c}(3900)$ discovered in the $J/\psi\pi$ invariant mass distribution by the BESIII and Belle Collaborations Ablikim et al. (2013); Liu et al. (2013); Ablikim et al. (2015), which must have nontrivial structures beyond the traditional charmonium. In the past few years, the LHCb Collaboration has reported the hidden-charm pentaquark candidates $P_{c}(4380)^{+}$, $P_{c}(4440)^{+}$, $P_{c}(4450)^{+}$, and $P_{c}(4312)^{+}$ in the $J/\psi p$ invariant mass distribution Aaij et al. (2015, 2019); the strange pentaquark candidates $P_{cs}(4459)$ and $P_{cs}(4338)$ states in the $J/\psi\Lambda$ spectrum Aaij et al. (2021, 2023); and the double-charm tetraquark candidate $T_{cc}(3875)^{+}$ in the $D^{0}D^{0}\pi^{+}$ distribution Aaij et al. (2022a). The masses of these states are close to the thresholds of at least a pair of heavy hadrons, making them candidates of hadronic molecules. There are also other interpretations. For instance, the compact multiquark picture has also been utilized to understand the structures of exotic states (for recent reviews, see Chen et al. (2016); Hosaka et al. (2016); Esposito et al. (2017); Lebed et al. (2017); Ali et al. (2017); Olsen et al. (2018); Guo et al. (2018); Albuquerque et al. (2019); Liu et al. (2019); Guo et al. (2020); Brambilla et al. (2020); Chen et al. (2023)). According to heavy quark flavor symmetry (HQFS), the bottom counterparts of these states like the $X_{b}$, $Z_{b}$, $P_{b}$, and $T_{bb}$ should also exist and have been predicted in various models Ebert et al. (2006); Hou (2006); Bondar et al. (2012); Yang et al. (2019); Sharma and Upadhyay (2024); Ren et al. (2022); Deng and Zhu (2022), but so far only two bottomonium-like $Z_{b}$ states, $Z_{b}^{\pm}(10610)$ and $Z_{b}^{\pm}(10650)$, have been observed by the Belle experiment in the $\Upsilon(5S)$ decay processes Bondar et al. (2012). One of the decisive reasons for the deficiency of the signals from exotic states in the bottom sector is the limitation of the collision energy and detection efficiency of the present high-energy colliders. The $Z$ factory of future Circular Electron Positron Collider (CEPC) Gao (2022) with high center-of-mass (c.m.) energy (close to the mass of the $Z$ boson), clean background, high resolution and detection ability can provide great opportunity to study the heavy exotic states.

The c.m. energy, luminosity and event yields of the $Z$ factory are listed in Table 1 Gao (2022); Sun et al. (2023). At parton level, the hidden-charm, hidden-bottom, double-charm, and double-bottom exotic states are produced in the processes $Z\to c\bar{c}$, $Z\to b\bar{b}$, $Z\to c\bar{c}c\bar{c}$, and $Z\to b\bar{b}b\bar{b}$, respectively. The branching radios measured at LEP are $\mathrm{Br}[Z\to c\bar{c}]=12.03\pm 0.21\%$, $\mathrm{Br}[Z\to b\bar{b}]=15.12\pm 0.05\%$, and $\mathrm{Br}[Z\to b\bar{b}b\bar{b}]=(3.6\pm 1.3)\times 10^{-4}$ Workman et al. (2022). The production of the doubly heavy baryons $\Xi_{cc}$, $\Xi_{bc}$, and $\Xi_{bb}$ at the $Z$ factory with the underlying processes $Z\to c\bar{c}c\bar{c}$, $Z\to b\bar{b}c\bar{c}$, and $Z\to b\bar{b}b\bar{b}$ has been studied in Ref. Niu et al. (2023) in the NRQCD framework, and the total production cross sections for $\Xi_{cc}$, $\Xi_{bc}$, and $\Xi_{bb}$ are 848.03 fb, 2260.51 fb, and 41.16 fb, respectively. The production of the $T_{bb}$ state in the compact tetraquark configuration at the $Z$ factory has also been studied in Refs. Ali et al. (2018, 2019) by employing the Monte Carlo (MC) event generators MadGraph5_aMC@NLO Alwall et al. (2014) and Pythia6 Sjostrand et al. (2006), and the estimated production cross section is about 36 fb, corresponding to $3.6\times 10^{6}$ events produced at the $Z$ factory during a two-year operation. The MC generator Pythia has also been widely used to simulate the production of the multiquark states in the $e^{+}e^{-}$ Artoisenet and Braaten (2011); Qin et al. (2021), $ep$ Yang and Guo (2021); Shi et al. (2022a), $pp$ Guo et al. (2014a, b, c); Albaladejo et al. (2017); Ling et al. (2021); Shi et al. (2022b); Jin et al. (2021); Hua et al. (2023), and $p\bar{p}$ Guo et al. (2014a); Bignamini et al. (2009, 2009); Guo et al. (2014c); Albaladejo et al. (2017) collisions.

In this work, we will employ the Pythia8 Bierlich et al. (2022) to estimate the production cross sections of the charmonium-like states $X(3872)$ and $Z_{c}(3900)$, the double-charm tetraquark state $T_{cc}(3875)^{+}$, the hidden-charm pentaquark states $P_{c}(4380)^{+}$, $P_{c}(4440)^{+}$, $P_{c}(4450)^{+}$, $P_{c}(4312)^{+}$, and $P_{cs}(4459)$, and the bottomonium-like states $Z_{b}(10610)$ and $Z_{b}(10650)$ in the $e^{+}e^{-}$ collisions at the $Z$ factory, assuming they are $S$-wave hadronic molecules. The production cross sections of some typical hidden-charm and double-charm hadronic molecules predicted in Refs. Dong et al. (2021a, b) as well as the $T_{bb}$ state as a $\bar{B}\bar{B}^{*}$ molecule will also be calculated.

The remaining parts of this paper is organized as follows. In Sec. II, we introduce the inclusive production mechanism of the hadronic molecules. The numerical results of the cross sections are presented in Sec. III. A brief summary is given in Sec. IV.

In this section, we introduce the inclusive production mechanism of the hadronic molecule $X$ in $e^{+}e^{-}$ collisions. As shown in Fig. 1, a heavy-hadron pair $HH^{\prime}$ is inclusively generated in the $e^{+}e^{-}$ collision, which is of short-distance nature, and then they are bound through the final state interaction (FSI) to form a hadronic molecule. At the $Z$ factory, the typical short-distance pair-production process is mediated by a virtual photon and $Z$ boson, while the contribution from the intermediate photon is negligible Niu et al. (2023). To give an order-of-magnitude estimation for the production cross sections of the hadronic molecules in $e^{+}e^{-}$ collision, we utilize the Pythia8 to simulate the short-distance inclusive production of the $HH^{\prime}$ pair and other particles, and the long-distance FSI is derived in the nonrelativistic effective field theory (NREFT) framework. In general, the amplitude for the production of the hadronic molecule state $X$ can be factorized as Braaten and Kusunoki (2005); Artoisenet and Braaten (2010); Guo et al. (2014c)

where $\mathcal{M}[HH^{\prime}+\text{all}]$ is the short-distance amplitude for the inclusive production process $e^{+}e^{-}\to HH^{\prime}+\text{all}$, $G$ is the Green function of the intermediate heavy hadron $HH^{\prime}$ pair, and $T_{X}$ is the long-distance amplitude for $HH^{\prime}\to X$. Here the Green’s function $G$ is UV divergent and is regularized by the Gaussian regulator Nieves and Valderrama (2012)

where $\gamma=\sqrt{2\mu(E-m_{H}-m_{H^{\prime}})}$ is the binding momentum of the $HH^{\prime}$ pair with $\mu$ the reduced mass of $H$ and $H^{\prime}$, $\text{erfi}(z)=2/\sqrt{\pi}\int_{0}^{z}e^{t^{2}}dt$ is the imaginary error function, and the cutoff $\Lambda$ is in the range of 0.5–1.0 GeV, following Refs. Guo et al. (2013, 2014c); Shi et al. (2022a).

For the $S$-wave shallow hadronic molecule, the amplitude $T_{X}$ can be approximated by the effective coupling constant $g_{X}$, which can be extracted from the residues of the low-energy $HH^{\prime}\to HH^{\prime}$ scattering amplitude $T(E)$ as

where $E_{0}$ is the pole position in the complex $E$-plane, satisfying $\text{det}[1-VG(E_{0},\Lambda)]=0$. One has $E_{0}=M_{X}$ for a bound state on the physical Riemann sheet (RS) or virtual state on the unphysical RS, and $E_{0}=M_{X}-i\Gamma/2$ for a resonance on the unphysical RS with mass $M_{X}$ and width $\Gamma$. For the near-threshold hadronic molecules, one can use a constant separateable potential $V$ for the $HH^{\prime}\to HH^{\prime}$ scattering, and the scattering amplitude $T(E)$ can be solved from the Lippmann-Schwinger equation as

The production cross section of the hadronic molecule $X$ can also be factorized into short-distance and long-distance parts. The short-distance part is given by the differential MC cross section of the inclusive $HH^{\prime}$ production,

where $k$ is the three-momentum in the c.m. frame of the $HH^{\prime}$ system. The overall factor $K_{HH^{\prime}}\sim\mathcal{O}(1)$ represents the difference between the MC simulation and the experimental data, and can be roughly taken as $K_{HH^{\prime}}\simeq 1$ for an order-of-magnitude estimate Guo et al. (2014c); Shi et al. (2022a). The short-distance production amplitude $\mathcal{M}[HH^{\prime}+\text{all}]$, which is insensitive to the final-state relative momentum $k$  Guo et al. (2014c); Shi et al. (2022a), can be approximated as a constant and taken outside from the integration of the final-state momentum $k$. Consequently, the differential cross section for $HH^{\prime}$ production in the MC event generator is proportional to $k^{2}$,

The total cross section for the hadronic molecule $X$ production is given by

where the phase-space integration is the same as that in Eq. (5) Guo et al. (2014c). With the use of Eqs. (1) and  (5), the production cross section of $X$ can be derived as

where $m_{H}$ and $m_{H^{\prime}}$ are the masses of the heavy hadrons $H$ and $H^{\prime}$, respectively.

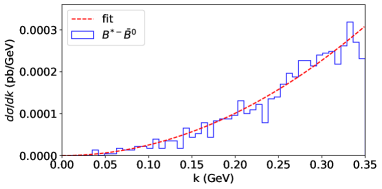
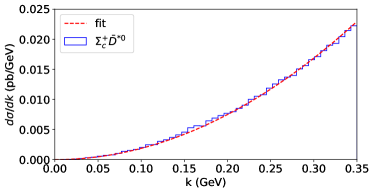
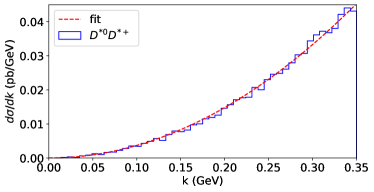
In this section, the production cross sections of the typical hidden-heavy and double-heavy hadronic molecules at the $Z$ factory are estimated at an order-of-magnitude level using Eq. (8). The differential cross sections $(d\sigma[HH^{\prime}+\text{all}]/dk)_{\text{MC}}$ of the $HH^{\prime}$ pair production in the $e^{+}e^{-}$ collisions are obtained using the MC event generator Pythia Sjostrand et al. (2006). Some typical differential cross sections for the production of the charm-anticharm, double-charm, bottom-antibottom, and double-bottom hadron pairs are shown in Fig. 2, and the differential cross sections for other heavy hadron pairs can be found in Appendix A. The formation of a hadronic molecule requires the constituent hadrons move collinearly with a small relative momentum. The choice of the cut of momentum $k$ has a small effect to the cross section and does not change our order-of-magnitude estimate. Therefore we follow the works in Refs. Yang and Guo (2021); Shi et al. (2022a) and choose a small relative momentum range $|k|<350\,\rm{MeV}$ where

and the coefficient $a$ is obtained by fitting the differential pair-production cross sections simulated by the MC event generator. The final expression of the production cross section of $X$ can be written as

The predicted cross sections for the hidden-charm, double-charm, and hidden-bottom hadronic molecules with $\Lambda=0.5$ GeV (out of the parentheses) and $\Lambda=1.0$ GeV (in the parentheses) are listed in Tables 2, 3, and 4, respectively, where the binding energy is defined as $E_{B}=m_{H}+m_{H^{\prime}}-m_{X}$¹¹1Here we use the isospin averaged mass for the heavy hadron $H^{(\prime)}$ in the isospin multiplet. with $m_{X}$ the mass of the produced hadronic molecule. The binding energies at the outside and inside of the square brackets in these tables correspond to $\Lambda=0.5$ and $1.0$ GeV, respectively.

The results in Tables 2, 3, and 4 reveal that:

• •

  The production cross sections of the hidden-charm hadronic molecules $X(3872)$ and $Z_{c}(3900)$ at the $Z$ factory are at pb level, and the production cross section of the $Z_{c}(3900)$ state is about $5$ – $10$ times larger than that of the $X(3872)$, which is comparable with the prediction in the semi-inclusive leptoproduction process Yang and Guo (2021). Considering the integrated luminosity $\int L=100~{}\mathrm{ab}^{-1}$ as listed in Table 1, there will be approximately $3\times 10^{7}$ – $1.6\times 10^{8}$ and $4\times 10^{8}$ – $8\times 10^{8}$ events of the $X(3872)$ and $Z_{c}(3900)$ produced in the two-year operation of the $Z$ factory, respectively.

• •

  The production cross sections of the hidden-charm pentaquark candidates $P_{c}$ and $P_{cs}$ states at the $Z$ factory are at the same level (about a few to tens of fb), two to three orders of magnitude smaller than those of the $X(3872)$ and $Z_{c}(3900)$. Such cross sections give $10^{5}$ – $10^{6}$ production events at the $Z$ factory during the two-year operation.

  	Constituents	$I(J^{PC})$	Binding energy (MeV)	$\sigma[X]~{}(\rm{pb})$
  $T_{cc}^{+}$	$DD^{*}$	$0(1^{+})$	$0.273$Aaij et al. (2022b, a)	$2.3\times 10^{-3}(9.7\times 10^{-3})$
  $T_{cc}^{*+}$	$D^{*}D^{*}$	$0(1^{+})$	$0.503$Du et al. (2022)	$1.3\times 10^{-3}(5.5\times 10^{-3})$
  	$\Lambda_{c}D$	$\frac{1}{2}(\frac{1}{2}^{-})$	$3.44[5.62]$Dong et al. (2021a)	$2.4\times 10^{-4}(1.8\times 10^{-3})$
  	$\Lambda_{c}D^{*}$	$\frac{1}{2}(\frac{1}{2}^{-})$	$2.53[6.73]$Dong et al. (2021a)	$5.6\times 10^{-5}(5.3\times 10^{-4})$
  	$\Lambda_{c}D^{*}$	$\frac{1}{2}(\frac{3}{2}^{-})$	$2.53[6.73]$Dong et al. (2021a)	$1.1\times 10^{-4}(1.1\times 10^{-3})$

• •

  The production cross sections of the double-charm tetraquark candidates $T_{cc}^{+}$ and its heavy-quark-spin symmetry (HQSS) partner $T_{cc}^{\ast+}$ Du et al. (2022) are comparable with the cross sections of the $P_{c}$ and $P_{cs}$ states, two to three orders of magnitude smaller than those of the hidden-charm tetraquarks. Such a large gap between the production cross sections of the $T_{cc}$ and the hidden-charm tetraquarks can be attributed to the parton level where the production of double-charm molecules requires two pairs of $c\bar{c}$ produced from the $Z$ boson decay. The branching ratio of $Z\to c\bar{c}c\bar{c}$ is much smaller than that of $Z\to c\bar{c}$, which is the underlying process for the production of the hidden-charm hadronic molecules. There will be about $2.3\times 10^{5}$ – $9.7\times 10^{5}$ and $1.3\times 10^{5}$ – $5.5\times 10^{5}$ events for the production of $T_{cc}$ and $T_{cc}^{*}$ at the $Z$ factory, respectively. The $T_{cc}$ events produced at the $Z$ factory is roughly three times larger than those in the proposed electron-ion colliders in US in the two-year operation Shi et al. (2022a). Furthermore, assuming Br$[T_{cc}^{+}\to D^{0}\bar{D}^{0}\pi^{+}]\simeq 59.6\%$ in terms of the leading-order estimation of the XEFT Dai et al. (2023) and Br$[D^{0}\to K^{-}\pi^{+}]=3.9\%$ Workman et al. (2022), the number of $T_{cc}$ events reconstructed in the $D^{0}D^{0}\pi^{+}$ invariant mass distribution can reach ${\cal O}(10^{3})$ at the $Z$ factory. The event number for $T_{cc}^{+}\to D^{0}(\to K^{-}\pi^{+})\bar{D}^{0}(\to K^{-}\pi^{+})\pi^{+}$ observed by the LHCb Collaboration is $117\pm 16$ with an integrated luminosity of $9~{}\rm{fb}^{-1}$ Aaij et al. (2022a). Therefore, the $Z$ factory could be a much better platform to study the $T_{cc}$ in detail and to search for its spin partner $T_{cc}^{*}$.

• •

  The production cross sections of the hidden-charm baryon-antibaryon hadronic molecules predicted in Ref. Dong et al. (2021b) and the double-charm meson-baryon hadronic molecules predicted in Ref. Dong et al. (2021a) are at the same order of magnitude, about $0.1$ – $1.0$ fb, one order of magnitude smaller than those of the $P_{c}$, $P_{cs}$, and $T_{cc}^{(*)}$. An exception is the $\Lambda_{c}\bar{\Lambda}_{c}$ molecule, whose production cross section is one magnitude larger than other hidden-charm baryon-antibaryon hadronic molecules, and the resulting events for the $\Lambda_{c}\bar{\Lambda}_{c}$ molecule production at the $Z$ factory is about $4.9\times 10^{5}$ – $6\times 10^{6}$. Therefore it is purposeful to search for the $\Lambda_{c}\bar{\Lambda}_{c}$ molecule at the $Z$ factory of CEPC.

  	Constituents	$I(J^{PC})$	Binding energy (MeV)	$\sigma[X]~{}(\rm{pb})$
  $Z_{b}(10610)^{\pm}$	$B\bar{B}^{*}$	$1(1^{+})$	$-2.99$ Workman et al. (2022)	$6.5\times 10^{-2}(8.7\times 10^{-2})$
  $Z_{b}(10610)^{0}$	$B\bar{B}^{*}$	$1(1^{+-})$	$-4.79$ Workman et al. (2022)	$7.2\times 10^{-2}(1.0\times 10^{-1})$
  $Z_{b}(10650)^{\pm}$	$B^{*}\bar{B}^{*}$	$1(1^{+})$	$-2.78$ Workman et al. (2022)	$6.6\times 10^{-2}(1.2\times 10^{-1})$
  $Z_{b}(10650)^{0}$	$B^{*}\bar{B}^{*}$	$1(1^{+-})$	$-2.78$ Workman et al. (2022)	$7.8\times 10^{-2}(1.4\times 10^{-1})$

• •

  In the bottom sector, the production cross sections of the hidden-bottom hadronic molecules $Z_{b}(10610)$ and $Z_{b}(10650)$ can reach tens to hundreds of fb, about one to two order(s) of magnitude smaller than those of the $X(3872)$ and $Z_{c}(3900)$, and one order of magnitude larger than the production cross section of the double-charm states $T_{cc}$ and $T_{cc}^{*}$. The expected number of $Z_{b}$ events at CEPC over a two-year period is around $10^{7}$, indicating promising prospects for its discovery and detailed study. Considering that the branching ratios of the $Z_{b}(10610)$ decays to the $\Upsilon(1S)\pi$, $\Upsilon(2S)\pi$, and $\Upsilon(3S)\pi$ final states are $5.4_{-1.5}^{+1.9}\times 10^{-3}$, $3.6_{-0.8}^{+1.1}\%$, and $2.1_{-0.6}^{+0.8}\%$ , respectively, and $Z_{b}(10650)$ decays to the $\Upsilon(1S)\pi$, $\Upsilon(2S)\pi$, and $\Upsilon(3S)\pi$ final states are $1.7_{-0.6}^{+0.8}\times 10^{-3}$, $1.4_{-0.4}^{+0.6}\%$, and $1.6_{-0.5}^{+0.7}\%$, respectively Workman et al. (2022), the event yields of $e^{+}e^{-}\to Z\to Z_{b}(10650)/Z_{b}(10610)+\mathrm{all}\to\Upsilon(nS)\pi+\mathrm{all},\;n=1,2,3$ are about $10^{4}$–$10^{5}$. Although the production cross sections of $e^{+}e^{-}\to Z\to Z_{b}(10650)/Z_{b}(10610)+\mathrm{all}\to\Upsilon(nS)\pi+\mathrm{all},\;n=1,2,3$ at the $Z$ factory is about two orders of magnitude smaller than the cross sections at Belle²²2The exclusive production of $Z_{b}$ can occur through the process $e^{+}e^{-}\to\Upsilon(5S)\to Z_{b}\pi$ via the intermediate states $B_{1}^{\prime}\bar{B}$ and $B_{0}^{*}\bar{B}^{*}$. The enhancement of this process, as discussed in Ref. Wu et al. (2019), can lead to a large exclusive cross section. Bondar et al. (2012); Garmash et al. (2015), the integrated luminosity at the $Z$ factory, roughly three orders of magnitude higher than Belle’s ($121.4~{}\mathrm{fb}^{-1}$), results in approximately one order of magnitude larger $Z_{b}$ event yields compared to Belle.

Despite the absence of the experimental signal from the double-bottom tetraquark ($bb\bar{u}\bar{d}$) $T_{bb}$ state at present, the existence of the $T_{bb}$ with quantum numbers $I(J^{P})=0(1^{+})$ has been approved by the lattice QCD (LQCD) calculation Aoki et al. (2023) in the HAL QCD method, where the $T_{bb}$ is predicted to be a deeply bound state with a binding energy $E_{T_{bb}}^{\mathrm{single}}=155\pm 17$ MeV only considering the $\bar{B}\bar{B}^{\ast}$ single channel and a binding energy $E_{T_{bb}}^{\mathrm{coupled}}=83\pm 10$ MeV considering the $\bar{B}\bar{B}^{\ast}-\bar{B}^{\ast}\bar{B}^{\ast}$ coupled channel treatment relative to the $\bar{B}\bar{B}^{\ast}$ threshold. In addition, the $\bar{b}\bar{b}ud$ and $\bar{b}\bar{b}us$ tetraquarks have also been predicted by the LQCD calculation in Ref. Alexandrou et al. (2024), with binding energies $100\pm 10^{+43}_{-36}$ MeV and $30\pm 3^{+31}_{-11}$ MeV relative to the $BB^{\ast}$ and $BB_{s}^{\ast}$ thresholds, respectively. The large binding energies for both the double bottom and anti-bottom tetraquarks indicate the $T_{bb}$ could not be simply regarded as a pure $\bar{B}\bar{B}^{\ast}$ hadronic molecule. To give an order-of-magnitude estimate, we assume that the $T_{bb}$ and $T_{bb}^{*}$ have the same binding energy (83 MeV), and still calculate their production cross sections in the hadronic molecule picture. The results are about $\sigma[T_{bb}^{(\ast)}]\approx 10^{-3}(10^{-1})$ fb for $\Lambda=0.5(1.0)$ GeV, 2 – 5 orders of magnitude smaller than those of the $Z_{b}$ states and the $T_{bb}$ state in the compact tetraquark configuration predicted in Refs. Ali et al. (2018, 2019).

In summary, we have investigated the inclusive differential production cross sections of the $e^{+}e^{-}\to HH^{\prime}+\text{all}$ processes using the Monte Carlo event generator Pythia8 and estimated the production cross sections of typical hidden/double-charm, and hidden/double-bottom hadronic molecules at the $Z$ factory by considering the FSI between the hadron pairs $HH^{\prime}$. The predicted production cross sections of the hidden-charm molecules $X(3872)$ and $Z_{c}(3900)$ are at the $\rm{pb}$ level, and the expected event yields of these molecules are about $10^{7}$–$10^{8}$. The production cross sections of the hidden-charm pentaquark candidates $P_{c}$ and $P_{cs}$, and the double-charm tetraquark candidates $T_{cc}$ and $T_{cc}^{\ast}$ as $S$-wave hadronic molecules are at the same order of magnitude, about two to three orders of magnitude smaller than the cross sections of $X(3872)$ and $Z_{c}(3900)$. The production cross sections of some possible hidden-charm baryon-antibaryon and double-charm meson-baryon hadronic molecules predicted in Refs. Dong et al. (2021a, b) are further smaller than those of the $P_{c}$, $P_{cs}$, and $T_{cc}^{(*)}$ by about one order of magnitude, except the $\Lambda_{c}\bar{\Lambda}_{c}$ molecule whose production cross section is one order of magnitude larger than those of other hidden-charm baryon-antibaryon molecules. As the $Z$ boson can decay to one and two pairs of $b\bar{b}$ in the parton level with sizeable branching ratios, the $Z$ factory is a ideal platform for the study of hidden/double bottom exotic states. The estimated production cross sections of the $Z_{b}$ states can reach tens to hundreds of pb, giving $10^{4}$–$10^{5}$ event yields of $e^{+}e^{-}\to Z\to Z_{b}(10650)/Z_{b}(10610)+\mathrm{all}\to\Upsilon(nS)\pi+\mathrm{all},\;n=1,2,3$ with the two-year integrated luminosity $\int L=100~{}\mathrm{ab}^{-1}$, which is about one order of magnitude larger than the event yields in the Belle experiment. The production cross sections of the double-bottom tetraquark candidate $T_{bb}$ as a deeply bound $S$-wave $\bar{B}\bar{B}^{\ast}$ molecule is also estimated using the binding energy from LQCD calculation as an input, and the result is about $\sigma[T_{bb}^{(\ast)}]\approx 10^{-3}(10^{-1})$ fb for $\Lambda=0.5(1.0)$ GeV, 2–5 orders of magnitude smaller than those of the $Z_{b}$ states and the $T_{bb}$ state in the compact tetraquark configuration predicted in Refs. Ali et al. (2018, 2019). Our order-of-magnitude estimates indicate appreciable production event yields of these hidden/double-charm and hidden/double-bottom hadronic molecules at the $Z$ factory.

We are grateful to Feng-Kun Guo for suggestions, Shu-Ming Wu for useful discussions, and Shi-Dong Liu for a careful reading of this manuscript. The numerical calculations were done at the HPC Cluster of ITP-CAS. This work is supported in part by the Chinese Academy of Sciences under Grant No. XDB34030000; by the National Natural Science Foundation of China (NSFC) under Grants No. 12125507, No. 11835015, No. 12047503, and No. 12075133; and by the NSFC and the Deutsche Forschungsgemeinschaft (DFG) through the funds provided to the TRR110 “Symmetries and the Emergence of Structure in QCD” (NSFC Grant No. 12070131001, DFG Project-ID No. 196253076). This work is also supported by the Natural Science Foundation of Shandong province under the Grant No. ZR2022ZD26, Taishan Scholar Project of Shandong Province under Grant No. tsqn202103062 and the Higher Educational Youth Innovation Science and Technology Program Shandong Province under Grant No. 2020KJJ004. P.-P.S. also acknowledges the Generalitat valenciana (GVA) for the project with ref. CIDEGENT/2019/015.