Production of $\bm{X(3872)}$ at High Multiplicity

Introduction. Since the unexpected discovery of the $X(3872)$ meson (also known as $\chi_{c1}(3872)$) in 2003 Choi:2003ue , dozens of other exotic heavy hadrons not predicted by the quark model have been discovered Ali:2017jda ; Olsen:2017bmm ; Karliner:2017qhf ; Brambilla:2019esw . They present a major challenge to our understanding of QCD. The nature of $X(3872)$ ($X$ for short) is a particularly important issue, because it remains the exotic heavy hadron for which the most detailed experimental information is available. The $X$ was discovered in the decay mode $J/\psi\,\pi^{+}\pi^{-}$, and it has since been observed in 6 other decay modes. Its quantum numbers were determined in 2013 to be $J^{PC}=1^{++}$ Aaij:2013zoa . The LHCb collaboration recently made the most precise measurements of its mass $M_{X}$ and the first measurements of its decay width Aaij:2020xjx ; Aaij:2020qga . The difference between $M_{X}$ and the $D^{*0}\bar{D}^{0}$ threshold is $\varepsilon_{X}=-0.07\pm 0.12$ MeV. This implies an upper bound on the binding energy of $X$: $|\varepsilon_{X}|<0.22$ MeV at 90% confidence level.

The information $J^{PC}=1^{++}$ and $|\varepsilon_{X}|<0.22$ MeV is sufficient to conclude that $X$ must be a loosely bound S-wave molecule with the particle content $(D^{*0}\bar{D}^{0}+D^{0}\bar{D}^{*0})/\sqrt{2}$ and with universal properties determined by $\varepsilon_{X}$ Braaten:2003he . The mean separation of its constituents is $r_{X}=(8\mu|\varepsilon_{X}|)^{-1/2}$, where $\mu$ is the reduced mass of $D^{*0}\bar{D}^{0}$. The upper bound $|\varepsilon_{X}|<0.22$ MeV implies $r_{X}>4.8$ fm. Thus this amazing hadron has a radius more than an order of magnitude larger than that of ordinary hadrons. More relevant to the other exotic heavy hadrons is what $X$ would have been if not for the fine-tuning of its mass to the $D^{*0}\bar{D}^{0}$ threshold. The possibilities that have been proposed include the P-wave charmonium state $\chi_{c1}(2P)$, an isospin-0 charm-meson molecule, and an isospin-1 compact tetraquark. In all these cases, the tuning of the mass to the $D^{*0}\bar{D^{0}}$ threshold produces resonant couplings to $D^{*0}\bar{D}^{0}$ and $D^{0}\bar{D}^{*0}$ that transforms $X$ into a loosely bound molecule of neutral charm mesons.

Shortly after the discovery of $X$ in $B$-meson decays Choi:2003ue , its existence was confirmed in $p\bar{p}$ collisions Acosta:2003zx . The production of $X$ at a hadron collider can be resolved into two contributions: prompt production by strong interactions at the primary collision vertex and the $b$-decay contribution from weak decays of hadrons containing a bottom quark or antiquark at a displaced secondary vertex. The behavior of these two contributions may provide evidence for the nature of $X$. One significant difference is the hadronic environment in which $X$ is embedded. In the decay of a $b$ hadron, at most a few additional hadrons emerge from the secondary vertex. In prompt production at the LHC, hundreds of additional hadrons may emerge from the primary vertex. Collisions with comoving hadrons could break $X$ up into its charm-meson constituents and thus decrease its prompt cross section.

The LHCb collaboration has studied the dependence on the hadron multiplicity of the production of $X$ in $pp$ collisions at the center-of-mass energy $\sqrt{s}=8$ TeV Aaij:2020hpf . The charmonium state $\psi(2S)$ ($\psi^{\prime}$ for short) provides a convenient benchmark, because it also decays into $J/\psi\,\pi^{+}\pi^{-}$ and its mass is close to $M_{X}$. The LHCb collaboration measured the ratio of the prompt production rates for $X$ and $\psi^{\prime}$ in the $J/\psi\,\pi^{+}\pi^{-}$ decay channel as functions of the number $N_{\mathrm{tracks}}$ of tracks in the vertex detector. The prompt $X$-to-$\psi^{\prime}$ ratio decreases significantly with increasing $N_{\mathrm{tracks}}$.

Esposito et al. have used the comover interaction (CI) model to calculate the dependence of the prompt $X$-to-$\psi^{\prime}$ ratio on the charged-particle multiplicity $N_{\mathrm{ch}}$ Esposito:2020ywk . Their result if $X$ is a compact tetraquark is consistent with the LHCb data, while their result if $X$ is a molecule with a geometric cross section decreases much too rapidly with $N_{\mathrm{ch}}$. They concluded that the LHCb data supports $X$ being a tetraquark and strongly disfavors it being a molecule. Their results if $X$ is a molecule were based in part on the incorrect assumption that its breakup reaction rate can be approximated by the geometric cross section $\pi r_{X}^{2}$, which is proportional to $1/|\varepsilon_{X}|$. It should instead be approximated by the cross section for scattering from the charm-meson constituents of $X$, which is insensitive to $\varepsilon_{X}$. We show below that a simple modification of the CI model provides excellent fits to the LHCb data on the multiplicity dependence of $X$ and $\psi^{\prime}$ production with parameters compatible with $X$ being a loosely bound charm-meson molecule.

Comover Interaction Model. The CI model was developed to describe the suppression of charmonium states in relativistic $p$-nucleus and nucleus-nucleus collisions by taking into account final-state interactions with comoving hadrons created by the collision Capella:1996va ; Gavin:1996yd ; Kharzeev:1996yx . Ferreiro used the CI model Ferreiro:2014bia to describe the suppression of $\psi^{\prime}$ relative to $J/\psi$ in $d$-Au and $p$-Pb collisions at RHIC Adare:2013ezl ; Abelev:2014zpa ; Arnaldi:2014kta . Ferreiro and Lansberg developed a more elaborate version of the CI model Ferreiro:2018wbd to describe the suppression of $\Upsilon(2S)$ and $\Upsilon(3S)$ relative to $\Upsilon$ in $p$-Pb collisions at LHC Chatrchyan:2013nza ; Aaboud:2017cif . A modified version of their model was applied by Esposito et al. to the production of $X$ in $pp$ collisions Esposito:2020ywk .

In the CI model, the survival probability of a $c\bar{c}$ or $b\bar{b}$ meson $\mathcal{Q}$ in $pp$ collisions is Armesto:1997sa

where $dN/dy$ is the light-hadron multiplicity per unit range of rapidity and $\langle v\sigma_{\mathcal{Q}}\rangle$ is the reaction rate for the breakup of $\mathcal{Q}$ averaged over comovers. The nondiffractive cross section $\sigma_{pp}(s)$ depends on the center-of-mass energy $\sqrt{s}$, while $N_{pp}(s,y)$ may also depend on the rapidity $y$. $N_{pp}$ is the multiplicity below which the effects of comovers are negligible: $S_{\mathcal{Q}}=1$ if $dN/dy<N_{pp}$. The estimates for $\sigma_{pp}$ in Ref. Esposito:2020ywk are 63 mb at $\sqrt{s}=7$ TeV and 70 mb at 13 TeV. A logarithmic interpolation in $s$ gives $\sigma_{pp}=65$ mb at $\sqrt{s}=8$ TeV. The range of pseudorapidity for the LHCb spectrometer is $2.0<\eta<4.8$. An estimate of $N_{pp}$ in that region can be obtained by multiplying the mean charged-particle multiplicity for the LHCb detector Aaij:2014pza by 3/2 to take into account neutral particles and then dividing by $\Delta y=2.8$, which gives $N_{pp}\approx 6$.

In the CI model, the comovers are usually assumed to be either pions with mass $m_{\pi}\approx 140$ MeV or massless gluons. In Ref. Ferreiro:2018wbd , the momentum distribution of the comovers in the $\mathcal{Q}$ rest frame was assumed to be a Bose-Einstein distribution in the 2-dimensional transverse plane with an effective temperature $T_{\mathrm{eff}}$. In Ref. Esposito:2020ywk , it was assumed to be a 3-dimensional Bose-Einstein distribution. Ref. Ferreiro:2018wbd introduced a simplistic model for the breakup cross section $\sigma_{\mathcal{Q}}$ as a function of the comover energy $E_{\pi}$: $\pi r_{\mathcal{Q}}^{2}(1-E^{\mathrm{thr}}_{\mathcal{Q}}/E_{\pi})^{n}$, where $E^{\mathrm{thr}}_{\mathcal{Q}}$ is the threshold energy for the breakup of $\mathcal{Q}$. In Ref. Esposito:2020ywk , that same model was used instead for the breakup reaction rate $v\sigma_{\mathcal{Q}}$. In Ref. Ferreiro:2018wbd , $T_{\mathrm{eff}}$ was determined by fitting data on the the suppression of $\Upsilon(2S)$ and $\Upsilon(3S)$ in $p$-Pb and Pb-Pb collisions. The fitted value of $T_{\mathrm{eff}}$ is approximately linear in $n$ between $\tfrac{1}{2}$ and 2, and its extrapolation to $n=0$ is roughly 100 MeV. For $n=1$, the effective temperature is $T_{\mathrm{eff}}=(250\pm 50)$ MeV. These same values of $n$ and $T_{\mathrm{eff}}$ were used in Ref. Esposito:2020ywk .

Analysis of Ref. Esposito:2020ywk . In Ref. Esposito:2020ywk , their results for the prompt $X$-to-$\psi^{\prime}$ ratio were compared with preliminary LHCb data LHCb:2019obz . The theoretical results were normalized to the first LHCb data point at $N_{\mathrm{tracks}}=20$. As shown in Fig. 1, their narrow error band for a molecule decreases precipitously to almost 0 near $N_{\mathrm{tracks}}=25$, while their error band for a tetraquark gives a good fit to the LHCb data in the next three bins of $N_{\mathrm{tracks}}$, which extend from 40 to 100.

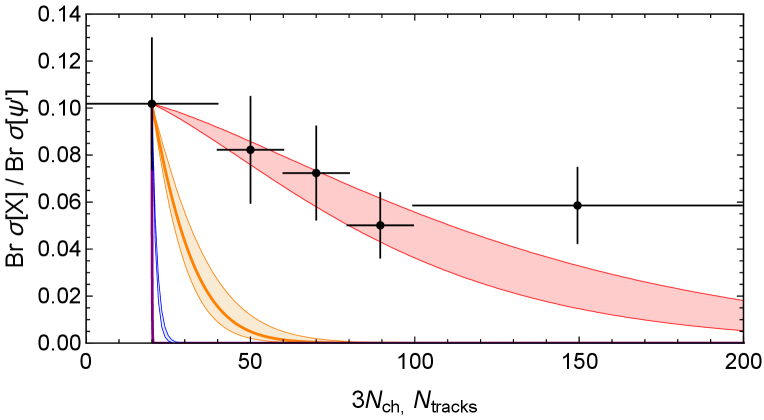
It is implied in Ref. Esposito:2020ywk that their error bands follow from inserting their breakup reaction rates $\langle v\sigma_{\mathcal{Q}}\rangle$ into the ratio $S_{X}/S_{\psi^{\prime}}$ of the survival probabilities given by Eq. (1). The values of $\langle v\sigma_{\mathcal{Q}}\rangle$ in Ref. Esposito:2020ywk are $5.15\pm 0.84$ mb for $\psi^{\prime}$, $11.61\pm 1.69$ mb for $X$ if it is a tetraquark, and $1197\pm 171$ mb for $X$ if it is a molecule with $|\varepsilon_{X}|=116$ keV. The prescription used to obtain these values was not specified. The resulting error bands are shown in Fig. 1. The error band using their value of $\langle v\sigma_{X}\rangle$ if $X$ is a tetraquark decreases almost exponentially to 0, and it lies well below the LHCb data even in the second bin of $N_{\mathrm{tracks}}$. Thus the error bands in Ref. Esposito:2020ywk must be determined by physics not captured by the survival probability in Eq. (1).

$\bm{\pi X}$ Breakup Reaction Rates. Cross sections for low-energy $\pi X$ scattering can be calculated using a nonrelativistic effective field theory for charm mesons and pions called XEFT Fleming:2007rp . It provides a systematically improvable description of the sector of QCD consisting of $D^{*}\bar{D}$, $D\bar{D}^{*}$, $D\bar{D}\pi$, or $X$ with total energy near the $D^{*}\bar{D}$ threshold Fleming:2007rp and also the sector consisting of $D^{*}\bar{D}^{*}$, $D^{*}\bar{D}\pi$, $D\bar{D}^{*}\pi$, $D\bar{D}\pi\pi$, or $X\pi$ near the $D^{*}\bar{D}^{*}$ threshold Braaten:2010mg . A Galilean-invariant formulation of XEFT that exploits the approximate conservation of mass in the transitions $D^{*}\leftrightarrow D\pi$ was introduced in Ref. Braaten:2015tga and further developed in Ref. Braaten:2020nmc . Galilean invariance guarantees that cross sections are the same in all Galilean frames, and it reduces the number of Feynman diagrams by requiring conservation of the total number of $\pi$, $D^{*}$, $\bar{D}^{*}$, and $X$ mesons.

The breakup cross section for $\pi^{+}X\to D^{*+}\bar{D}^{*0}$ was first calculated in Ref. Braaten:2010mg in the CM frame using original XEFT. The cross sections for $\pi^{+}X\to D^{*+}\bar{D}^{*0}$ and $\pi^{0}X\to D^{*0}\bar{D}^{*0}$ are calculated using Galilean-invariant XEFT in Ref. piXscattering . In Fig. 2, the cross sections are shown as functions of the collision energy $E_{c}$, which is the total kinetic energy in the CM frame. They have dramatic peaks near their thresholds, with peak values comparable to the geometric cross section $\pi r_{X}^{2}$, which is 1200 mb if $\varepsilon_{X}=116$ keV. In the limit $\varepsilon_{X}\to 0$, the cross section for $\pi^{+}X\to D^{*+}\bar{D}^{*0}$ approaches a delta function in $E_{c}$ at $(\mu_{\pi X}/\mu_{\pi})\delta_{0+}$, where $\delta_{0+}=5.9$ MeV is the $D^{*+}$-to-$D^{0}\pi^{+}$ energy difference and $\mu_{\pi X}$ and $\mu_{\pi}$ are the reduced masses for $\pi X$ and $\pi D$. The energy-weighted integral of the cross section reduces in the limit to

where $g/(2\sqrt{m_{\pi}}f_{\pi})$ is the $D^{*0}$-to-$D^{0}\pi^{0}$ coupling constant. This is the integral required to calculate the contribution to $\langle v\sigma_{X}\rangle$ from a 3-dimensional Bose-Einstein distribution of pions. The corresponding integral for $\pi^{0}X\to D^{*0}\bar{D}^{*0}$ is obtained by replacing $\delta_{0+}$ by the $D^{*0}$-to-$D^{0}\pi^{0}$ energy difference $\delta_{00}=7.0$ MeV. Their contribution to $\langle v\sigma_{X}\rangle$ decreases from 0.2 to 0.04 to 0.02 mb as $T_{\mathrm{eff}}$ increases from 100 to 200 to 300 MeV.

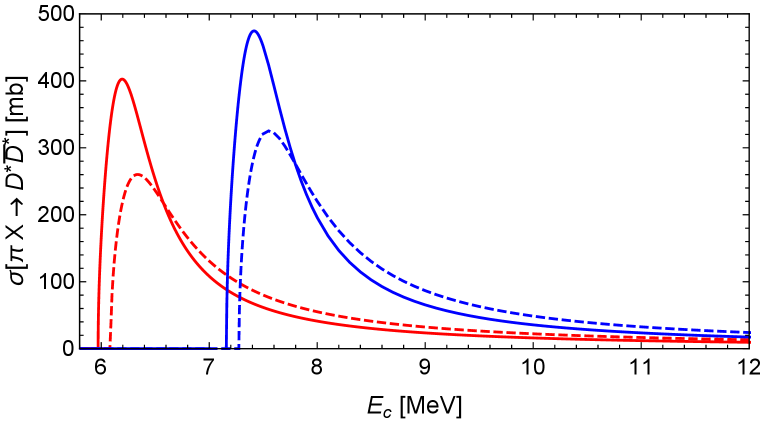
When the $\pi X$ collision energy is well above the resonance region in Fig. 2, the pion can scatter off an individual constituent of $X$ and this will necessarily break up the bound state. The constituents of $X$ are $D^{*0}$ and $\bar{D}^{0}$ with probability 1/2 and $D^{0}$ and $\bar{D}^{*0}$ with probability 1/2. The total $\pi X$ breakup cross section can be approximated by the weighted sum of $\pi D$ and $\pi D^{*}$ cross sections:

A sufficient condition for the validity of this approximation is that $E_{c}$ is well above the resonance region shown in Fig. 2.

For nonrelativistic collision energies, the largest cross sections are those allowed in Galilean-invariant XEFT. The specific final states from $\pi X$ scattering taken into account by Eq. (3) are $D^{*}\bar{D}\pi$ and $D\bar{D}^{*}\pi$ with at least one neutral charm meson. The cross sections for $\pi D^{0}\to\pi D$ and $\pi D^{*0}\to\pi D^{*}$ are calculated in Ref. piXscattering . In the region $\delta_{00}\ll E_{c}\ll m_{\pi}$, they are approximately constant. The total $\pi X$ breakup cross section using Eq. (3) is

where $\mu_{\pi*}$ is the $\pi D^{*}$ reduced mass. An over-estimate of the contribution of this region to $\langle v\sigma_{X}\rangle$ can be obtained by integrating over the range $\delta_{00}<E_{c}<m_{\pi}$. This estimate decreases from 0.05 to 0.02 to 0.01 mb as $T_{\mathrm{eff}}$ increases from 100 to 200 to 300 MeV.

For relativistic collision energies of order $m_{\pi}$ and larger, XEFT is not applicable. In Ref. Cho:2013rpa , a hadron scattering model was used to calculate the contribution to $\langle v\sigma_{X}\rangle$ from the reactions $\pi X\to D^{*}\bar{D}^{*}$ in a thermal gas of hadrons. Their result decreases from 0.5 to 0.2 mb as the temperature $T$ increases from 100 to 200 MeV. In Ref. Lin:2000jp , a hadron scattering model was used to calculate the $\pi D$ and $\pi D^{*}$ reaction rates in a thermal gas of hadrons. The structure of hadrons was taken into account by using a form factor with cutoff momentum $\Lambda$. For $\Lambda=\infty$, the estimate of $\langle v\sigma_{X}\rangle$ using Eq. (3) increases from 25 to 37 mb as $T$ increases from 100 to 200 MeV, while for $\Lambda=1$ GeV, $\langle v\sigma_{X}\rangle\approx 15$ mb almost independent of $T$.

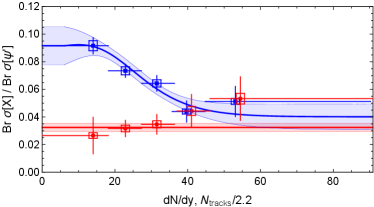
Analysis of LHCb Data. The LHCb data in Ref. Aaij:2020hpf consists of the prompt fractions for both $X$ and $\psi^{\prime}$ and the $X$-to-$\psi^{\prime}$ ratios for both prompt and $b$-decay production in Fig. 3. Since the pseudorapidity range of the LHCb vertex detector is $1.6<\eta<4.9$ Alves:2008zz , the multiplicity $dN/dy$ can be approximated by $\tfrac{3}{2}(N_{\mathrm{tracks}}/3.3)$. The prompt fraction $f_{\mathrm{prompt}}$ for $\psi^{\prime}$ is about 87% in the first bin of $N_{\mathrm{tracks}}$. It first decreases as $N_{\mathrm{tracks}}$ increases, but then it appears to level off at about 70%. This behavior is incompatible with the assumption that the prompt cross section is proportional to the survival probability $S_{\psi^{\prime}}$ given by Eq. (1). That assumption requires $f_{\mathrm{prompt}}$ to decrease almost exponentially to 0 as $N_{\mathrm{tracks}}$ increases.

A possible interpretation of the LHCb data on the prompt $\psi^{\prime}$ fraction in Fig. 3 is that the prompt cross section has two components: one independent of $dN/dy$ and the other proportional to $S_{\psi^{\prime}}$. The two components could arise from the phase-space structure of the $pp$ collisions. Prompt $\psi^{\prime}$’s created at a space-time point and with a momentum that puts them out of reach of most of the comoving pions give a contribution to the cross section that does not depend on $dN/dy$. The remaining prompt $\psi^{\prime}$’s are broken up with the probability $1-S_{\psi^{\prime}}$, so their contribution to the prompt cross section is proportional to $S_{\psi^{\prime}}$.

This interpretation motivates a simple modification of the CI model. We denote the fraction of the prompt $\mathcal{Q}$ mesons out of reach of comoving pions by $f_{\mathrm{out},\mathcal{Q}}$ and their contribution to the prompt cross section by $\sigma_{\mathrm{out},\mathcal{Q}}$. The prompt cross section can be expressed as

which depends on $dN/dy$ through $S_{\mathcal{Q}}$. We assume the $b$-decay cross section $\sigma_{b\,\mathrm{decay},\mathcal{Q}}$ does not depend on $dN/dy$. The prompt fraction for $\mathcal{Q}$ is

where $F_{\mathrm{out},\mathcal{Q}}=\sigma_{\mathrm{out},\mathcal{Q}}/\sigma_{b\,\mathrm{decay},\mathcal{Q}}$. The prompt $X$-to-$\psi^{\prime}$ ratio is

where $N_{X/\psi^{\prime}}$ is the product of $\sigma_{\mathrm{out},X}/\sigma_{\mathrm{out},\psi^{\prime}}$ and the ratio of the branching fractions into $J/\psi\,\pi^{+}\pi^{-}$. The $b$-decay $X$-to-$\psi^{\prime}$ ratio is

We have carried out a global fit to the LHCb data by minimizing the $\chi^{2}$ for the 26 data points in Fig. 3 with respect to the 5 adjustable parameters in Eqs. (6)-(8) and the two breakup reaction rates $\langle v\sigma_{X}\rangle$ and $\langle v\sigma_{\psi^{\prime}}\rangle$. The statistical and correlated errors were added in quadrature. The resulting fits are shown in Fig. 3. The error bands correspond to an increase of $\chi^{2}$ by less than 1. The quality of the fits is very good with $\chi^{2}/\mathrm{dof}=0.99$. The fit to the $b$-decay $X$-to-$\psi^{\prime}$ ratio could be improved by adding a parameter that allows $\sigma_{\mathrm{out},\psi^{\prime}}$ or $\sigma_{b\,\mathrm{decay},X}$ to increase linearly with $dN/dy$. The fractions of the prompt cross sections out of reach of comoving pions are $f_{\mathrm{out},\psi^{\prime}}=0.40\pm 0.03$ and $f_{\mathrm{out},X}=0.18\pm 0.04$. The ratios of the prompt and $b$-decay cross sections at large $dN/dy$ are $F_{\mathrm{out},\psi^{\prime}}=2.3\pm 0.1$ and $F_{\mathrm{out},X}=2.9\pm 0.7$. The breakup reaction rates are $\langle v\sigma_{\psi^{\prime}}\rangle=3.9\pm 0.8$ mb and $\langle v\sigma_{X}\rangle=2.6\pm 0.7$ mb. The prefactor in Eqs. (7) and (8) is $N_{X/\psi^{\prime}}=0.04\pm 0.01$.

The fitted value of $\langle v\sigma_{\psi^{\prime}}\rangle$ is about 1$\sigma$ smaller than the value in Ref. Esposito:2020ywk . It is about 5$\sigma$ smaller than the value in Ref. Esposito:2020ywk if $X$ is a tetraquark. The fitted value of $\langle v\sigma_{X}\rangle$ is about 4 times larger than the contribution from $\pi X\to D^{*}\bar{D}^{*}$ in a thermal gas of hadrons with $T=100$ MeV in Ref. Cho:2013rpa . The fitted value of $\langle v\sigma_{X}\rangle$ is less than 1/4 the total breakup reaction rate from Ref. Lin:2000jp . This could be attributed to a failure of the 3-dimensional Bose-Einstein distribution as a model for comoving pions. A momentum distribution that is isotropic in the two transverse dimensions and the longitudinal dimension seems implausible.

Outlook. The LHCb data on the multiplicity dependence of the production of $X$ and $\psi^{\prime}$ in $pp$ collisions is incompatible with the assumption that the prompt cross section is proportional to the survival probability in Eq. (1). However, as shown in Fig. 3, a good global fit can be obtained by adding the assumption that some fraction $f_{\mathrm{out},\mathcal{Q}}$ of the prompt $\mathcal{Q}$ cross section is out of reach of comoving pions. A microscopic description of $pp$ collisions in which these fractions could be calculated would be useful.

The quantum numbers $J^{PC}=1^{++}$ and the upper bound $|\varepsilon_{X}|<0.22$ MeV imply that $X$ must be a loosely bound S-wave molecule of neutral charm mesons with universal properties determined by $\varepsilon_{X}$. Universality is a double-edged sword. It allows definite statements about some properties of $X$, such as $r_{X}$ and the $\pi X$ breakup reaction rate, but it also makes them insensitive to what $X$ would have been if not for the fine-tuning of its mass to the $D^{*0}\bar{D}^{0}$ threshold. $X$ could have been a more compact charmonium or molecule or tetraquark, but it is transformed into a large neutral-charm-meson molecule by its resonant interactions with $D^{*0}\bar{D}^{0}$ and $D^{0}\bar{D}^{*0}$. Given the upper bound on $|\varepsilon_{X}|$, a model for $X$ as a compact hadron should be interpreted as a fictitious hadron that does not couple to the charm mesons at the nearby $D^{*0}\bar{D}^{0}$ threshold. It may be an interesting exercise to rule out such a possibility using experimental data, but it is already excluded by theoretical considerations.

The universal physics of a loosely bound S-wave molecule reveals a dramatic failure of the simplistic model in Refs. Esposito:2020ywk and Ferreiro:2018wbd for $\langle v\sigma_{\mathcal{Q}}\rangle$ based on the geometric cross section $\pi r^{2}_{\mathcal{Q}}$. That model overestimates $\langle v\sigma_{X}\rangle$ by orders of magnitude. The breakup cross section $\sigma_{X}$ is comparable to $\pi r^{2}_{X}$, which is proportional to $1/|\varepsilon_{X}|$, only at energies very close to the threshold as shown in Fig. 2. At higher energies, $\sigma_{X}$ is determined by the cross sections for scattering from the constituents of $X$ in Eq. (3), so $\langle v\sigma_{X}\rangle$ is insensitive to $\varepsilon_{X}$.

Our fit to the LHCb data in Fig. 3 may be a step towards a quantitative understanding of the production of $X$ in high-energy hadron collisions. In a hadron collision, once $X$ is broken up into charm mesons by the collision with a comoving pion, the probability that one of the charm mesons will encounter another charm meson and that they will coalesce into $X$ is extremely small. An attempt to calculate the coalescence contribution to the production in $pp$ collisions of $X$ if it is a molecule was made in Ref. Esposito:2020ywk . Coalescence can be much more important in $p$-nucleus and nucleus-nucleus collisions, because the number of charm meson that are created is much larger. The first observation of the production of $X$ in heavy-ion collisions by the CMS collaboration indicated that the prompt $X$-to-$\psi^{\prime}$ ratio may be much larger in Pb-Pb collisions than in $pp$ collisions CMS:2019vma . Understanding the production of $X$ in $p$-nucleus and nucleus-nucleus collisions even at the qualitative level remains a challenging open problem.