Production mechanism of the hidden charm pentaquark states
Abstract
We investigate hidden-charm pentaquark states using an off-shell coupled-channel formalism involving heavy meson and singly heavy baryon scattering. Our approach utilizes an effective Lagrangian to construct the kernel amplitudes, which respect both heavy quark symmetry and hidden local symmetry. After solving the coupled integral equations, we obtain the transition amplitudes for scattering and various heavy meson and singly heavy baryon scattering processes. We identify seven distinct peaks related to molecular states of heavy mesons () and singly heavy baryons (). Four of these peaks can be associated with the known states: , , , and . We predict two additional resonances with masses around 4.5 GeV, which we interpret as molecular states, and identify one cusp structure. Additionally, we predict two -wave pentaquark states with positive parity, which may be candidates for genuine pentaquark configurations. Notably, these pentaquark states undergo significant modifications in the elastic channel, with some even disappearing due to interference from the positive parity channel. The present investigation may provide insight into the absence of pentaquark states in photoproduction observed by the GlueX collaboration.
I Introduction
The discovery of the pentaquarks by the LHCb collaboration has invigorated research in heavy exotic baryon spectroscopy. Pentaquarks with the minimal quark content were first identified in the invariant mass spectrum from decays [1, 2]. To date, four states have been observed: three narrow states below the threshold and one broad state below the threshold. Recently, a new state designated as was identified in decays, while the previously observed was notably absent [3] 111The naming convention of heavy pentaquarks is not yet settled. While the LHCb Collaboration suggested a naming convention for exotic hadrons [4], the Particle Data Group (PDG) uses a different one [5]. In the current work, we will follow the PDG convention.. Intriguingly, the GlueX collaboration has found no evidence for these pentaquark states in recent photoproduction experiments on protons [6, 7]. Rather than invalidating previous findings, these seemingly conflicting results offer an opportunity to deepen our understanding of pentaquark nature. The LHCb Collaboration has also identified the strangeness partner of the pentaquark in the invariant mass spectrum from decays [8]. Recently, they discovered the strangeness partner of (4330) at a nearly identical mass, just 5 MeV higher [9]. Investigations into pentaquark spectra with strangeness and are ongoing, with the CMS collaboration recently observing the decay [10]. However, low yield and poor resolution precluded observation of a clear spectrum in the invariant mass.
Since the LHCb discovery of hidden charm pentaquarks , a plethora of theoretical works has been proposed to explain their nature. Two distinct approaches suggest that ’s are molecular states, lying below the thresholds of various heavy mesons and singly heavy baryons. The first model posits bound states arising from quark potential models in configuration space [11, 12]. The second interprets them as poles in the lower Riemann sheet, generated by non-perturbatively produced scattering matrices [13, 14, 15]. Furthermore, constituent quark interpretations offer another potential scheme for explaining the pentaquark spectrum [16, 17, 18]. Additionally, alternative hypotheses suggest that the peak structure is a consequence of kinematic singularities [19, 20, 21, 22, 23]. It is not possible to distinguish these schemes from the LHCb data alone. However, results from the GlueX collaboration allow some constituent pentaquark spectra to be ruled out due to their absence in photoproduction. In contrast, the triangle singularity scheme offers a partial explanation for the disappearance of states observed by the GlueX collaboration. This is attributed to the inability of photoproduction to generate the double triangle diagram, as pointed out in Ref. [22]. On the other hand, in the context of the molecular picture, no mechanism has yet been identified that can explain this disappearance.
In the current work, we investigate hidden-charm pentaquark states using heavy meson and singly heavy baryon scattering in an off-shell coupled channel formalism. To facilitate understanding of experimental findings, we also include charmonium-nucleon scattering. The transition amplitudes are generated by solving coupled integral equations, with kernel amplitudes constructed from meson-exchange diagrams. These processes are governed by an effective Lagrangian that respects both heavy quark symmetry and hidden local symmetry. Our analysis yields seven distinct peaks are related to molecular states of the heavy mesons () and singly heavy baryons (). Four of these peaks can be identified with the known states: , , , and . The other three resonances, with masses around 4.5 GeV, are predicted to be molecular states and are yet to be discovered. Notably, these peaks undergo significant modifications in the elastic channel, with some even disappearing due to interference from the positive parity channel. This phenomenon may provide insight into the absence of pentaquark states in photoproduction, where elastic scattering plays a crucial role. A more quantitative explanation requires comparison of our theoretical model with experimental data. This will be the subject of future studies, employing more rigorous fitting strategies to provide a more comprehensive and valid explanation of the observed phenomena.
The current work is organized as follows: In Section II, we present the off-shell coupled-channel formalism used to study the hidden-charm pentaquark states. This includes the effective Lagrangian, the partial-wave expansion of the scattering amplitude, and the method for solving the coupled integral equations. Section III is devoted to the results and discussions, where we analyze the scattering matrices for both negative and positive parity states, identify the pole positions, and compare our findings with experimental data. We also address the apparent conflict between LHCb and GlueX results, proposing a qualitative explanation based on our molecular scheme. Finally, we summarize our findings and conclude in Section IV, discussing the implications of our results and outlining future directions.
II Coupled-channel formalism
The scattering amplitude is defined as
| (1) |
where and stand for the total four momenta of the initial and final states, respectively. The transition amplitudes can be derived from the Bethe-Salpeter integral equation
| (2) |
where and denote the relative four-momenta of the initial and final states, respectively. is the off-mass-shell momentum for the intermediate states in the center of mass (CM) frame. represents the square of the total energy, which is just one of the Mandelstam variables, . The coupled integral equations given in Eq. (2) can be depicted as in Fig. 1.

To avoid the complexity due to the four-dimensional integral equations, we make a three-dimensional reduction. While there are several different methods for the three-dimensional reduction, we employ the Blankenbecler-Sugar scheme [24, 25], which takes the two-body propagator in the form of
| (3) |
where represents the total on-mass-shell energy of the intermediate state, , and denotes the three-momentum of the intermediate state. Note that the spinor factors from the meson-baryon propagator have been absorbed to the matrix elements of and . Utilizing Eq. (3), we obtain the following coupled integral equations
| (4) |
where and are the relative three-momenta of the initial and final states in the CM frame, respectively.

We construct two-body coupled channels by combining the charmed meson triplet and singly charmed baryon antitriplet and sextet with total strangeness number to study the pentaquark . In addition, we also introduce the channel, since ’s were experimentally known to decay into . Thus, we have the seven different channels as follows: , , , , , and . Thus, we first construct the kernel matrix expressed as
| (5) |
Each component of the kernel matrix is constructed by using one-meson exchange tree-level diagram which is shown in Fig. 2. We do not include pole diagrams in the channel. We consider the -channel diagrams, which are essential for generating the states dynamically. The contributions of -channel diagrams are very small, so we ignore them. The interactions at the vertex are governed by the effective Lagrangian that respects heavy-quark spin symmetry, hidden local gauge symmetry, and flavor SU(3) symmetry [26]. The mesonic vertices are then computed by the effective Lagrangian given as
| (6) | ||||
| (7) | ||||
| (8) | ||||
| (9) | ||||
| (10) | ||||
| (11) | ||||
| (12) | ||||
| (13) | ||||
| (14) |
with . The lowest isoscalar-scalar meson is denoted by . The heavy meson and anti heavy meson matrices and are given by
| (15) |
while the light pseudoscalar and vector meson matrices are
| (16) |
The coupling constants in the Lagrangian are obtained from Ref. [27], i.e., from experimental results of full width, by using the KSRF relation with MeV, by assuming vector meson dominance in the radiative decay of heavy mesons, and by using light-cone sum rules and lattice QCD. Notice that we use a different sign of from Ref. [27], since we use the same phase of heavy vector meson as in Ref. [26]. The coupling constant for the sigma meson is utilized to calculate the transition of in Ref. [28]. The lowest isoscalar-scalar meson coupling is with .
As for the effective Lagrangian for the heavy baryon, we take it from Ref. [29], where a more general form of the Lagrangian was considered [30]. The interaction vertices for the baryonic sector in the tree level diagram of the meson-exchange diagram are governed by the following effective Lagrangian
| (17) | ||||
| (18) | ||||
| (19) | ||||
| (20) | ||||
| (21) | ||||
| (22) | ||||
| (23) | ||||
| (24) | ||||
| (25) | ||||
| (26) | ||||
| (27) | ||||
| (28) | ||||
| (29) | ||||
| (30) |
where the heavy baryon fields are given by
| (31) |
denotes the spin 3/2 Rarita-Schwinger field, which satisfies the following constraint
| (32) |
The coupling constants in the effective Lagrangian are given as follows [29, 31]: , , , , and . The different signs used above are taken from Refs. [31, 32].
Since we include the hidden-charm channel, we need effective Lagrangian to describe the coupling between heavy mesons and quarkonium. Here we use the Lagrangian from Ref. [33], i.e.,
| (33) | ||||
| (34) | ||||
| (35) |
In this work, we only consider the vector quarkonia since it is directly related to experiments. However, the extension to the pseudoscalar state is straightforward since we assume the heavy quark spin symmetry to the quarkonia state as well [34]. Since there is no experimental data on the decay, Shimizu et al. [35] estimated the value of the coupling constant as follows: the coupling constant can be determined from the experimental decay width for the decay. Assuming that the decay of is similar to that of apart from their masses, Shimizu et al. estimated to be . The coupling constants of the heavy baryons and heavy mesons are expressed [35] as
| (36) | ||||
| (37) | ||||
| (38) | ||||
| (39) | ||||
| (40) |
We employ the coupling constants and taken from Ref. [35]. It is important to note that the coupling to the hidden charm channels have only a marginal effect to the production mechanism of the resonance. The current calculation implies that though these values of the coupling constants are taken from the rough estimation, the predicted masses of the hidden charm pentaquarks almost do not vary. This already indicates that the channel has a tiny effect on the production of the heavy pentaquarks.
The Feynman amplitude for one-meson exchange diagram can be written as
| (41) |
where and denote the helicity and momentum of the corresponding particle respectively, while is the momentum of the exchange particle. The IS factor is related to the SU(3) Clebsch-Gordan coefficient and isospin factor. The IS factor for each exchanged diagram is listed in Table 1.
| Reactions | Exchange particles | IS | |
|---|---|---|---|
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
The vertex is derived by using the effective Lagrangian previously described and the propagators for the spin-0 and spin-1 mesons are expressed as
| (42) |
We use the static propagator for pion exchange, for simplicity. As for the heavy-meson propagators, we employ the same form as the light mesons, since the heavy-quark mass is actually finite. The parity invariance further reduces a number of proceseses. The parity relation is given by
| (43) |
where is expressed as
| (44) |
and denote the intrinsic parity and spin of the particle, respectively, while designates the total angular momentum.
Since hadrons have finite sizes, we introduce a form factor at each vertex. To this end, we employ the following parametrization [36]
| (45) |
where is determined by the power of the momentum in the vertex. This parametrization has the advantage that we do not need to adjust the value of when we change . It is worth noting that when we take the limit , Eq. (45) becomes a Gaussian form. While the cut-off masses in Eq. (45) are not experimentally known for heavy hadron processes, we adopt a strategy to minimize the associated uncertainties. We determine by adding approximately MeV to the corresponding masses of the exchange meson. Recent studies have explicitly shown that heavy hadrons are more compact than light ones [37, 38]. This indicates that the cutoff masses for heavy hadrons must be larger than those of light ones. Consequently, we set the value of cutoff mass as , where is the mass of the exchange meson. Thus, we choose to be approximately MeV for each channel, as listed in Table. 1. This approach allows us to perform a minimal fitting procedure.
To further simplify the numerical calculation and the spin-parity assignments for the states, we carry out a partial-wave expansion of the and matrices. This yields a one-dimensional integral equation given by
| (46) |
where , and denote the helicities of the final (), initial () and intermediate () states, respectively. The partial-wave kernel amplitudes can be expressed as
| (47) |
where represents the scattering angle and denotes the matrix elements of the Wigner functions.
The integral equation in Eq. (46) contains the singularity originating from the two-body propagator . To manage this singularity, we isolate its singular part and treat it separately. The resulting regularized integral equation is expressed as
| (48) |
with
| (49) |
and is the momentum when . The regularization is applied only when the total energy exceeds the threshold energy of the -th channel . It is important to note that the form factors introduced in the amplitude provide sufficient suppression in the high-momentum region, which allows for the regularization of the integration.
To compute from Eq. (48) numerically, we expand the matrix in helicity states and momentum space, with momenta obtained by using the Gaussian quadrature method. We then derive the matrix using the Haftel-Tabakin method for matrix inversion [39]
| (50) |
The resulting matrix is in the helicity basis and lacks definite parity. To study parity assignments for , we decompose the transition amplitudes into the partial-wave amplitudes with definite parity given by
| (51) |
where denotes the partial-wave transition amplitude with total angular momentum and parity . The prefactor ensures that no additional factor is required when transforming back to the partial-wave component:
| (52) |
At this stage, we want to emphasize that we do not need to decompose the partial-wave component with definite parity in Eq. (46), as parity invariance is already imposed in the effective Lagrangian and in the calculation of the amplitudes shown in Eq. (43). To study the dynamical generation of the resonances, we express the matrix in the particle basis [40]. The relations between the matrix elements in the two bases are given by
| (53) |
In this work, we will only present the diagonal part as it is relevant to particle production.
III Results and discussions
The molecular nature of the hidden charm pentaquarks is not a novel concept. Prior to their discovery, numerous theoretical studies predicted their existence as molecular states of the heavy meson and heavy baryon system [41, 42, 43, 44]. The hidden charm pentaquark states, , discovered by the LHCb Collaboration [1, 2, 3] are positioned below various thresholds of the , , and channels. Consequently, many researchers considered the states to be molecular states. Recently, however, the GlueX Collaboration [7] did not observe any clear signal for the heavy pentaquarks in the invariant mass spectrum when measuring photoproduction off the proton. Regarding this discrepancy, there is only one theoretical work addressing it. Nakamura [22] proposed a reason for the absence of the pentaquarks in the GlueX experiment: the hidden charm pentaquarks, except for the (4440), are cusp structures arising from the kinematical effects of single and double triangle diagrams. This can partially explain the disappearance of the pentaquark peaks in photoproduction, although a pole diagram is still needed to describe (4440) [22]. In contrast, we aim to elucidate why it is very difficult to observe the signals of the pentaquarks from photoproduction. We will demonstrate that the origin of the discrepancy is dynamical, not kinematical in this Section.
Before presenting the numerical results, we first describe the fitting procedure. While the coupling constants for various vertices are theoretically fixed, the cutoff masses contain uncertainties due to the lack of experimental data and theoretical estimation. As explained in the previous Section, we fixed the cutoff masses using the relation MeV. We will adjust these values minimally. As shown in Table 1, we set MeV for reactions involving heavy hadrons with low-lying masses, while choosing MeV for those with higher-lying masses. This approach allows us to describe the four existing hidden charm pentaquarks and predict three additional with larger masses.
As discussed in Ref. [45], it is natural to expect that there may be seven hidden charm pentaquark states in the -wave with negative parity, since we have seven different attractive channels: , , , , , , and with possible total angular momenta considered. As will be shown below, we observe that there are indeed seven peaks, among which six are identified as hidden charm pentaquarks, while one peak exhibits a cusp structure rather than a resonance. More interestingly, we find two additional -wave pentaquark resonances with positive parity. We will first investigate the relevant transition amplitudes in the -wave and examine the nature of the hidden charm pentaquarks with negative parity. Then, we will analyze the two pentaquark states with positive parity. Finally, we will address the null results from the GlueX Collaboration.
III.1 Negative parity ( wave interaction)
We will first discuss the numerical results for the ’s with negative parity. Though the parity for the ’s are not yet experimentally given, the present results indicate that the existing ’s must have the negative parity. To examine it, we define the partial-wave cross section with a given spin-parity assignment as
| (54) |



In Fig.3, we present the partial-wave cross sections as functions of energy in the CM frame, focusing on transitions from several heavy meson and singly heavy baryon channels to the channel. The upper left panel of Fig.3 displays the partial-wave transition cross sections with total angular momentum . The pentaquark state is clearly visible in the transition. While the same resonance appears in the transition, its strength is weaker compared to the channel. No signal is observed in the channel, as only the -wave contributes to this channel, which is too weak to form . Only vague hints of are present in the and channels. The transition exhibits only a destructive interference pattern. Notably, there is almost no indication of in scattering. Note that we have multiplied by . Below the threshold, we clearly observe a peak in the transition, corresponding to . As shown by the dashed curve, a peak structure is also found in the transition, but it is multiplied by a factor of . In other transitions, we observe patterns of destructive interference. As with , we do not find any peak structure in scattering. This observation may explain the null results for hidden charm pentaquarks from the GlueX experiment, as will be discussed later in detail. Interestingly, there are no clear signals for pentaquark resonances below the threshold; instead, we only observe cusp structures.
The upper right panel of Fig. 3 presents the partial-wave total cross sections for seven different transitions with . We observe clear peaks for in the , , and channels. However, as in the previous case, we do not detect any peak in scattering. The and channels do not exhibit any resonances. Below the threshold, we observe the resonance in the channel. A tiny resonance structure is also visible in the channel. Again, there is no peak structure in scattering. Additionally, we identify a new resonance in the transition, which has not yet been observed experimentally. This new state could be designated as . In the lower panel of Fig. 3, we observe , another state that has not been experimentally confirmed. Although the strength of the corresponding peak appears weaker than the other resonances, it is clearly visible in all channels. A unique feature of this new resonance is its coupling to both and channels.
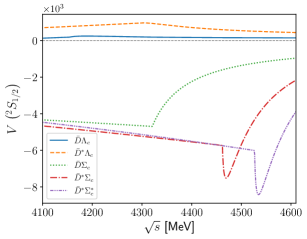


In the partial-wave expansion, the -wave provides the largest contribution. This indicates that -wave kernel amplitudes generally serve as the primary source for the dynamical generation of molecular states. Figure 4 presents the results for the -wave kernel amplitudes in elastic scattering. The upper left, upper right, and lower panels display the amplitudes for the , , and channels, respectively. We observe that the kernel amplitudes exhibit attractive interactions, which are essential in producing the resonance structures shown in Fig. 3. In contrast, the , which belongs to the baryon antitriplet, interacts repulsively with and . Consequently, resonances are not formed in the and channels.


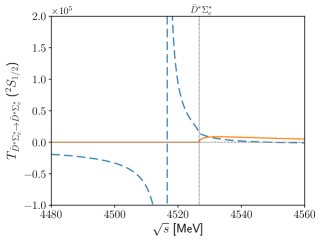
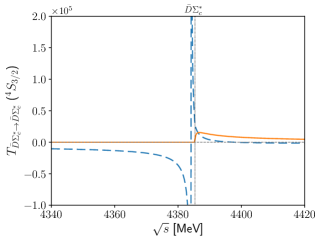



After examining the -wave kernel amplitudes, we investigate the corresponding transition amplitudes with the coupled-channel effects turned off. This allows us to explicitly observe how the poles corresponding to bound states appear. Figure 5 presents the results for the transition amplitudes across seven different scattering channels. From the upper right panel to the lowest panel, we identify six bound states in the following channels: , , , , , and . We do not observe a bound state in the channel, but we note an enhancement near the threshold. Although there is no bound state in this channel, a resonance emerges when we include all possible coupled channels. This observation emphasizes the significant role of coupled-channel effects in the dynamical generation of hidden charm pentaquark states. We observed a similar tendency in the dynamical generation of the meson [46].
| Molecular states | MeV | Known states | ||||
|---|---|---|---|---|---|---|
| Name | ||||||
| (4312) | ||||||
| (4440) | ||||||
| (4380) | ||||||
| (4457) | ||||||
The transition amplitudes obtained by solving the coupled integral equations contain poles corresponding to the hidden charm pentaquark states. By scanning these amplitudes in the complex energy plane, we can precisely locate the pole positions, which yield the masses and widths of the pentaquarks. Table 2 presents the masses and widths of six hidden charm pentaquark states. Among these, four resonances have been experimentally confirmed: and with , and and with . Thus, we predict the existence of and .
The cusp structure with total spin 1/2 below the threshold does not appear as a pole on the second Riemann sheet. Further investigation of other sheets revealed its presence on the upper sheet, formed by the branch point of the channel at MeV. This behavior stems from the coupled channel effect, which generates a repulsive interaction in the molecular state. Consequently, the pole is pushed above the channel threshold, becoming a virtual state. It is noteworthy that there exist more molecular states than those observed experimentally, particularly in the region around 4.5 GeV. Two new states have been identified, corresponding to molecular states of the system, while one is merely a cusp. In contrast, Ref.[45] predicted three new states. With the exception of the cusp structure we found, the present results align with those of Ref.[45].
Table 2 also compares the pole masses and widths from our work with experimental data. While there is considerable agreement overall, discrepancies emerge in some instances, such as for the and resonances. This is not unexpected, given that we did not fit the data. Furthermore, our analysis reveals that the peak position and the real part of the pole position are not identical. For instance, in the case of the molecular state with , the discrepancy is as large as 14 MeV. These findings underscore the importance of comprehensively examining the transition amplitudes to determine resonance characteristics, rather than focusing solely on the peak position, which can vary depending on the processes involved.
| [MeV] | ||||||
|---|---|---|---|---|---|---|
Table 3 lists the numerical results for the coupling strengths of the six states with negative parity, demonstrating the intensity of their couplings to all possible decay channels. The state, for instance, couples most strongly to the channel. This suggests that is likely a molecular state composed of and , given that its mass is below the threshold. Notably, it also exhibits strong coupling to the -wave and channels. The coupling to is particularly interesting, as it indicates that contains a mixture of and . Furthermore, the channel contributes to the decay of . While experimental observations have shown that decays into and , these results suggest that its decay into and should be even more pronounced.
The exhibits strong coupling to the -wave channel, suggesting it is a molecular state of and . It also couples to the -wave , , and channels, indicating a mixed state. Consequently, can kinematically decay into and , as well as and . The resonance couples most strongly to the channel, with significant contributions from and channels. This suggests is a molecular state mixed with and components. The resonance is predominantly governed by the -wave channel, with minor contributions from , , , and . This indicates that can be considered a molecular state. The last two columns of Table 3 list the numerical results for the coupling strengths of the new resonant states and . These results suggest that these two hidden charm pentaquarks are likely -wave molecular states.
III.2 Positive parity
A great virtue of the present coupled-channel formalism is that we can also predict -wave pentaquark states with positive parity. While the -wave contribution is the most dominant one, the -wave interaction is also strong enough to form a resonance. For example, the first baryonic resonance isobar is also a -wave resonance from scattering. The nature of these pentaquarks is distinguished from those with negative parity. The -wave hidden charm pentaquark states with positive parity emerge from the constructive interference of various channels, which will be discussed below.



The upper left panel of Fig.6 illustrates the partial-wave total cross sections for transitions from a heavy meson and a singly heavy baryon to with total spin . The complex energy plane reveals poles at MeV and MeV, corresponding to the resonances shown in this panel. These resonances exhibit markedly different characteristics compared to those with total spin and negative parity, depicted in the upper left panel of Fig.3. While Fig. 3 clearly shows and as molecular states, these two positive-parity resonances cannot be identified within a single molecular picture. The upper right panel of Fig. 6 displays the partial-wave total cross sections for . Two peak structures appear near the and thresholds. However, the absence of corresponding poles in the second Riemann sheet indicates no resonances for . The lower panel of Fig. 6 shows no peak structure for .
| [MeV] | ||
|---|---|---|
Table 4 lists the coupling strengths of the two pentaquark resonances with to all possible transition channels. The resonance at MeV primarily couples to , , and , while showing weak coupling to other channels. Notably, this resonance does not couple to transition channels with higher energy than its mass, distinguishing it from the negative-parity states. The resonance at MeV, detailed in the last column of Table 4, exhibits a more complex nature. Its formation involves eight different transition channels, indicating a intricate structure. These two resonances lack a clear molecular structure, suggesting they may be candidates for a genuine pentaquark configuration. A more comprehensive analysis of these states will be presented in future work.
III.3 Null results from the GlueX experiment


The GlueX Collaboration recently reported null results for states in photoproduction off the proton [7]. Our results may explain this absence. The key factor is the transition amplitude for scattering, which resembles photoproduction in the vector meson dominance picture. The rescattering equation for photoproduction can be expressed as:
| (55) |
where represents the seven channels associated with production. In Eq. (55), is likely the dominant kernel, as the photon is strongly coupled to the because of its vector nature (). Figure 7 illustrates the partial-wave total cross sections for scattering with spin , , and for negative (left panel) and positive (right panel) parities. The peaks corresponding to negative-parity states appear as dip structures. However, this alone does not explain the GlueX results, as peaks remain visible, particularly for . The positive-parity results show bump structures approximately ten times larger than those with negative parity. Figure 8 presents the combined partial-wave total cross sections. Consequently, state smears out along with all other ’s with negative parity, as illustrated in Fig. 8.



We can explain both the absence of states in the GlueX experiment and their observation in the LHCb experiment. In decay, six transition channels are unsuppressed, differing only in kinematic factors. The left panel of Fig.9 shows the total cross sections for these six transition channels, clearly displaying peak structures corresponding to hidden charm pentaquark states. As previously discussed, is clearly observed below the threshold in the and transitions. It is also evident in the transition, though the magnitude of the resonance is smaller than in the two aforementioned transitions. Below the threshold, we find the resonance in the and transitions. The resonance appears clearly below the threshold. The is located just below the threshold, overlapping with the state. Additionally, two new hidden charm pentaquark states, which are closely spaced, are shown below the threshold in the transition. Since the magnitudes of the predicted two pentaquark states with positive parity are notably smaller than those with negative parity, we do not see them in the total transition cross sections. The right panel of Fig.9 depicts the total cross sections for seven elastic scattering channels, revealing only negative-parity pentaquark states, as in the case of the transitions. While the total cross section for scattering is very small in comparison with other channels, we want to mention that the predicted two pentaquark states with positive parity can be also seen in it, as shown in Fig. 8.
IV Summary and conclusions
In this work, we investigated hidden-charm pentaquark states using an off-shell coupled-channel formalism involving heavy meson and singly heavy baryon scattering. Our analysis identified seven distinct peaks related to molecular states of heavy mesons () and singly heavy baryons (). Among these, six are identified as resonances, while one exhibits a cusp structure. Four of these peaks can be associated with known states: , , , and . Additionally, we predicted two new resonances with masses around 4.5 GeV, which we interpret as molecular states. Our study revealed that these pentaquark states undergo significant modifications in the elastic channel, with some even disappearing due to interference from the positive parity channel. The combined partial-wave total cross sections for scattering demonstrate how the state, along with other negative parity states, are smeared out due to interference with positive parity contributions. This contrasts with the clear visibility of pentaquark states in transitions from heavy meson and singly heavy baryon channels to . These findings provide potential insight into the absence of pentaquark states in photoproduction observed by the GlueX collaboration, while also explaining their observation in LHCb experiments.
We also identified two -wave pentaquark states with positive parity, which may be candidates for a genuine pentaquark configuration. However, several important points require further investigation. Further theoretical investigations are required to fully explain the disappearance of the states in photoproduction, which will be the subject of our next project. It may be possible to observe the LHCb states in the open charm final state of photoproduction, although this presents significant experimental challenges. Furthermore, the emergence of the state in the decay channel cannot be explained within our current molecular framework, suggesting the need for alternative or complementary approaches to fully account for all observations.
In conclusion, while our study provides valuable insights into the nature of hidden charm pentaquarks and offers a potential explanation for their absence in certain experimental settings, it also highlights the need for further theoretical and experimental work to comprehensively understand these exotic particles.
Acknowledgements.
S.C. and H.C.K. wish to express their gratitude to T. Mart at Universitas Indonesia for his hospitality during their visit to Depok, where part of the present work was conducted. The work was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Korean government (Ministry of Education, Science and Technology, MEST), Grant-No. 2021R1A2C2093368 and 2018R1A5A1025563 (SC and HChK), and by the PUTI Q1 Grant from University of Indonesia under contract No. NKB-441/UN2.RST/HKP.05.00/2024.References
- Aaij et al. [2015] R. Aaij et al. (LHCb), Phys. Rev. Lett. 115, 072001 (2015), arXiv:1507.03414 [hep-ex] .
- Aaij et al. [2019] R. Aaij et al. (LHCb), Phys. Rev. Lett. 122, 222001 (2019), arXiv:1904.03947 [hep-ex] .
- Aaij et al. [2022] R. Aaij et al. (LHCb), Phys. Rev. Lett. 128, 062001 (2022), arXiv:2108.04720 [hep-ex] .
- Gershon [2022] T. Gershon (LHCb), (2022), arXiv:2206.15233 [hep-ex] .
- Navas et al. [2024] S. Navas et al. (PDG), Phys. Rev. D 110, 030001 (2024).
- Ali et al. [2019] A. Ali et al. (GlueX), Phys. Rev. Lett. 123, 072001 (2019), arXiv:1905.10811 [nucl-ex] .
- Adhikari et al. [2023] S. Adhikari et al. (GlueX), Phys. Rev. C 108, 025201 (2023), arXiv:2304.03845 [nucl-ex] .
- Aaij et al. [2021] R. Aaij et al. (LHCb), Sci. Bull. 66, 1278 (2021), arXiv:2012.10380 [hep-ex] .
- Aaij et al. [2023] R. Aaij et al. (LHCb), Phys. Rev. Lett. 131, 031901 (2023), arXiv:2210.10346 [hep-ex] .
- Hayrapetyan et al. [2024] A. Hayrapetyan et al. (CMS), (2024), arXiv:2401.16303 [hep-ex] .
- Liu et al. [2021] M.-Z. Liu, T.-W. Wu, M. Sánchez Sánchez, M. P. Valderrama, L.-S. Geng, and J.-J. Xie, Phys. Rev. D 103, 054004 (2021), arXiv:1907.06093 [hep-ph] .
- Yalikun et al. [2021] N. Yalikun, Y.-H. Lin, F.-K. Guo, Y. Kamiya, and B.-S. Zou, Phys. Rev. D 104, 094039 (2021), arXiv:2109.03504 [hep-ph] .
- He [2019] J. He, Eur. Phys. J. C 79, 393 (2019), arXiv:1903.11872 [hep-ph] .
- Wang et al. [2022] Z.-L. Wang, C.-W. Shen, D. Rönchen, U.-G. Meißner, and B.-S. Zou, Eur. Phys. J. C 82, 497 (2022), arXiv:2204.12122 [hep-ph] .
- Shen et al. [2024] C.-W. Shen, D. Rönchen, U.-G. Meißner, B.-S. Zou, and Y.-F. Wang, (2024), arXiv:2405.02626 [hep-ph] .
- Maiani et al. [2015] L. Maiani, A. D. Polosa, and V. Riquer, Phys. Lett. B 749, 289 (2015), arXiv:1507.04980 [hep-ph] .
- Lebed [2015] R. F. Lebed, Phys. Lett. B 749, 454 (2015), arXiv:1507.05867 [hep-ph] .
- Wang [2016] Z.-G. Wang, Eur. Phys. J. C 76, 70 (2016), arXiv:1508.01468 [hep-ph] .
- Liu et al. [2016] X.-H. Liu, Q. Wang, and Q. Zhao, Phys. Lett. B 757, 231 (2016), arXiv:1507.05359 [hep-ph] .
- Guo et al. [2015] F.-K. Guo, U.-G. Meißner, W. Wang, and Z. Yang, Phys. Rev. D 92, 071502 (2015), arXiv:1507.04950 [hep-ph] .
- Bayar et al. [2016] M. Bayar, F. Aceti, F.-K. Guo, and E. Oset, Phys. Rev. D 94, 074039 (2016), arXiv:1609.04133 [hep-ph] .
- Nakamura [2021] S. X. Nakamura, Phys. Rev. D 103, 111503 (2021), arXiv:2103.06817 [hep-ph] .
- Nakamura et al. [2021] S. X. Nakamura, A. Hosaka, and Y. Yamaguchi, Phys. Rev. D 104, L091503 (2021), arXiv:2109.15235 [hep-ph] .
- Blankenbecler and Sugar [1966] R. Blankenbecler and R. Sugar, Phys. Rev. 142, 1051 (1966).
- Aaron et al. [1968] R. Aaron, R. D. Amado, and J. E. Young, Phys. Rev. 174, 2022 (1968).
- Casalbuoni et al. [1997] R. Casalbuoni, A. Deandrea, N. Di Bartolomeo, R. Gatto, F. Feruglio, and G. Nardulli, Phys. Rept. 281, 145 (1997), arXiv:hep-ph/9605342 .
- Isola et al. [2003] C. Isola, M. Ladisa, G. Nardulli, and P. Santorelli, Phys. Rev. D 68, 114001 (2003), arXiv:hep-ph/0307367 .
- Bardeen et al. [2003] W. A. Bardeen, E. J. Eichten, and C. T. Hill, Phys. Rev. D 68, 054024 (2003), arXiv:hep-ph/0305049 .
- Liu and Oka [2012] Y.-R. Liu and M. Oka, Phys. Rev. D 85, 014015 (2012), arXiv:1103.4624 [hep-ph] .
- Yan et al. [1992] T.-M. Yan, H.-Y. Cheng, C.-Y. Cheung, G.-L. Lin, Y. C. Lin, and H.-L. Yu, Phys. Rev. D 46, 1148 (1992), [Erratum: Phys.Rev.D 55, 5851 (1997)].
- Chen et al. [2019] R. Chen, Z.-F. Sun, X. Liu, and S.-L. Zhu, Phys. Rev. D 100, 011502 (2019), arXiv:1903.11013 [hep-ph] .
- Dong et al. [2021] X.-K. Dong, F.-K. Guo, and B.-S. Zou, Progr. Phys. 41, 65 (2021), arXiv:2101.01021 [hep-ph] .
- Colangelo et al. [2004] P. Colangelo, F. De Fazio, and T. N. Pham, Phys. Rev. D 69, 054023 (2004), arXiv:hep-ph/0310084 .
- Casalbuoni et al. [1993] R. Casalbuoni, A. Deandrea, N. Di Bartolomeo, R. Gatto, F. Feruglio, and G. Nardulli, Phys. Lett. B 309, 163 (1993), arXiv:hep-ph/9304280 .
- Shimizu and Harada [2017] Y. Shimizu and M. Harada, Phys. Rev. D 96, 094012 (2017), arXiv:1708.04743 [hep-ph] .
- Kim et al. [1994] H.-C. Kim, J. W. Durso, and K. Holinde, Phys. Rev. C 49, 2355 (1994).
- Kim and Kim [2018] J.-Y. Kim and H.-C. Kim, Phys. Rev. D 97, 114009 (2018), arXiv:1803.04069 [hep-ph] .
- Kim et al. [2021] J.-Y. Kim, H.-C. Kim, G.-S. Yang, and M. Oka, Phys. Rev. D 103, 074025 (2021), arXiv:2101.10653 [hep-ph] .
- Haftel and Tabakin [1970] M. I. Haftel and F. Tabakin, Nucl. Phys. A 158, 1 (1970).
- Machleidt et al. [1987] R. Machleidt, K. Holinde, and C. Elster, Phys. Rept. 149, 1 (1987).
- Wu et al. [2010] J.-J. Wu, R. Molina, E. Oset, and B. S. Zou, Phys. Rev. Lett. 105, 232001 (2010), arXiv:1007.0573 [nucl-th] .
- Wang et al. [2011] W. L. Wang, F. Huang, Z. Y. Zhang, and B. S. Zou, Phys. Rev. C 84, 015203 (2011), arXiv:1101.0453 [nucl-th] .
- Wu et al. [2012] J.-J. Wu, T. S. H. Lee, and B. S. Zou, Phys. Rev. C 85, 044002 (2012), arXiv:1202.1036 [nucl-th] .
- Xiao et al. [2013] C. W. Xiao, J. Nieves, and E. Oset, Phys. Rev. D 88, 056012 (2013), arXiv:1304.5368 [hep-ph] .
- Liu et al. [2019] M.-Z. Liu, Y.-W. Pan, F.-Z. Peng, M. Sánchez Sánchez, L.-S. Geng, A. Hosaka, and M. Pavon Valderrama, Phys. Rev. Lett. 122, 242001 (2019), arXiv:1903.11560 [hep-ph] .
- Clymton and Kim [2022] S. Clymton and H.-C. Kim, Phys. Rev. D 106, 114015 (2022), arXiv:2208.04124 [hep-ph] .