Probing the gauge boson at electron colliders
Abstract
We investigate the minimal model with extra heavy vector-like leptons or charged scalars. By studying the kinetic mixing between gauge boson and standard model photon, which is absent at tree level and will arise at one loop level due to , and new heavy charged leptons or scalars, the interesting behavior is shown. It can provide possibility for visible signatures of new heavy particles. We propose to search for at electron collider experiments, such as Belle II, BESIII and future Super Tau Charm Factory (STCF), using the monophoton final state. The parameter space of is probed, and scanned by its gauge coupling constant and mass . We find that electron colliders have sensitivity to the previously unexplored parameter space for with MeV-GeV mass. Future STCF experiments with GeV can exclude the anomalous muon magnetic moment favored area when GeV with the luminosity of 30 ab-1. For , can be down to at 2 GeV STCF.
I Introduction
The standard model (SM) of particle physics is a successful and highlypredictive theory of fundamental particles and interactions, but fails to explain many phenomena, including neutrino mass, baryon asymmetry of the universe, presence of dark matter (DM) and dark energy, among others. It implies that SM is only a low-energy approximation of the more fundamental theory; extensions of SM are strongly required.
Among various extended scenarios beyond SM, new U(1) gauge symmetries are of particular interest since this is one of the minimal extensions of the SM. In particular, the model Foot:1990mn ; He:1990pn ; He:1991qd , with a extension of SM, gauges the difference of the leptonic muon and tau number and induces a new vector boson . This model has gained a lot of attention, since it can be free from gauge anomaly without any extension of particel content. Moreover, it is potentially able to address important open issues in particle physics, such as the discrepancy in moun anomalous magnetic moment Bennett:2006fi ; Baek:2001kca ; Ma:2001md ; Altmannshofer:2016brv , decay anomalies Aaij:2013qta ; Aaij:2014ora ; Altmannshofer:2016jzy ; Crivellin:2015mga ; Baek:2017sew ; Ko:2017yrd and recent anomalous excess in Jho:2020jsa . Besides, the model has also been discussed in lepton-flavor-violating decay of the Higgs bosonCrivellin:2015mga ; Altmannshofer:2016oaq , the neutrino masses and mixing Ma:2001md ; Heeck:2011wj ; Baek:2015mna ; Biswas:2016yan , and dark matter Biswas:2016yan ; Altmannshofer:2016jzy ; Patra:2016shz ; Biswas:2016yjr ; Biswas:2017ait ; Arcadi:2018tly ; Kamada:2018zxi ; Foldenauer:2018zrz ; Cai:2018imb ; Han:2019diw .
Since can directly couple to muon, related searches for have been performed with the production of at collider experiments, including BaBar TheBABAR:2016rlg and Belle II Adachi:2019otg at electron colliders and CMS Sirunyan:2018nnz at hadron collider. Subsequently, decaying to muon-pair is considered at BaBar and CMS experiments, and invisible decay of is considered at Belle II. Phenomenally, Ref. Jho:2019cxq investegated the sensitivity on at Belle II with the planned target luminosity of 50 ab-1 in the channel of ; Refs. Kaneta:2016uyt ; Araki:2017wyg ; Chen:2017cic ; Banerjee:2018mnw proposed the search for at Belle II using the monophoton process , which depends on the kinetic mixing between the SM photon and .
In this work, we investigate the kinetic mixing in the minimal with extra heavy vector-like leptons or charged scalars. Then we propose to search for gauge boson at electron collider experiments, such as Belle II, BESIII and future Super Tau Charm Factory (STCF), using the monophoton final state. Belle II is an asymmetric detector and located at SuperKEKB which collides 7 GeV electrons with 4 GeV positrons. SuperKEKB has a largest instantaneous luminosity of cm-2 s-1 Kou:2018nap . The ambitious goal of SuperKEKB is to accumulate an integrated luminosity of 50 with 8-year data takings Kou:2018nap . The BESIII detector is symmetric and operated on the BEPCII with the beam energy ranging from 1.0 GeV to 2.3 GeV and a peak luminosity of cm-2 s-1 Asner:2008nq . STCF is a proposed symmetric detector experiment which collides electron with positron in the range of center-of-mass energies from 2.0 to 7.0 GeV with the peak luminosity cm-2 s-1 at 4 GeV Peng:2019 ; Luo:2018njj ; Bondar:2013cja .
The rest paper is organized as follows: First, we introduce the models and discuss their phenomenological features. Then, we calculate the cross sections of the signal and the backgrounds and analysis to improve the significance by appropriate event cuts at three different electron colliders operated at the GeV scale: BelleII, BESIII and STCF. The sensitivities for at these experiments are also investigated. Finally, a short summary and discussions are given.
II The models
II.1 The minimal model
We extend the SM with a new gauge symmetry, , where leptons of the second and third generation couple to the additional gauge boson with equal and opposite charge. The new leptonic gauge interactions can be given as
| (1) |
where is gauge coupling constant.
In the minimal model, the kinetic mixing between the and photon is absent at the tree level. Nevertheless, because and are both charged under the electromagnetic and , there exists an unavoidable kinetic mixing at one loop level, which can appear as Araki:2017wyg
| (2) |
Here is the electromagnetic charge, and are the masses of tau and muon leptons, is the transferred momentum.
For large momentum transfer , this mixing is power suppressed by , whereas for low momentum transfer , the mixing tends to be a constant
| (3) |
which seems like the dark photon model.
II.2 The model with extra heavy vector-like leptons
We add two extra singlet vectorlike leptons () in the extension of the SM, which are charged under opposite in sign similar as the and , and have electric charge of Chen:2017cic . Since we mainly focus on the gauge kinetic mixing, we would not provide much details of the model here. In this model, due to the leptons inside the loop, the kinetic mixing of and can be derived as
| (4) |
Here are the masses of and . When the momentum transfer , which is considered in this work, the mixing can be simplified as
| (5) |
where is the mass ratio of and .
II.3 The model with extra heavy charged scalars
In the extension of the SM, we add two extra scalars () with electric charge of and charged under opposite in sign Banerjee:2018mnw . Similarly, due to charged leptons and extra scalars contributions induced at one-loop level, the kinetic mixing can be given as
| (6) |
Here and are the masses of extra charged scalars ( and ). We mainly focus on the gauge kinetic mixing, thus much details of the model are not provided here.
In this work, we consider the momentum transfer always , thus the mixing can be also written as
| (7) |
where is the mass ratio of and .
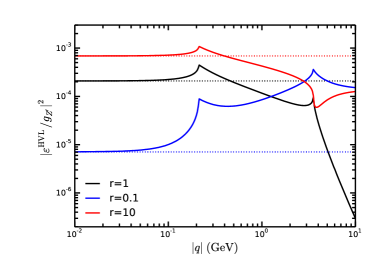
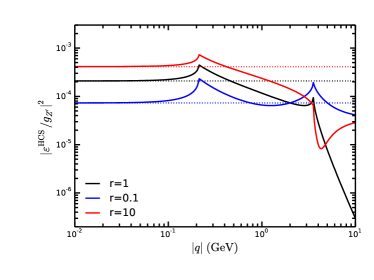
In Fig.1, we present the square of the kinetic mixing as a function of the momentum transfer with and 10. The horizontal dotted lines are the same situations but for the case of , which are shown as a comparison. When , the contribution for the kinetic mixing due to additinal leptons or scalars vanishes, and the results will become same as those in the minimal model, i.e., . In the minimal model, has two peaks at the position of and , and drops quickly with the increment of when . This feature distinguishes the phenomenology of the model from the dark photon models with a constant value of the kinetic mixing.
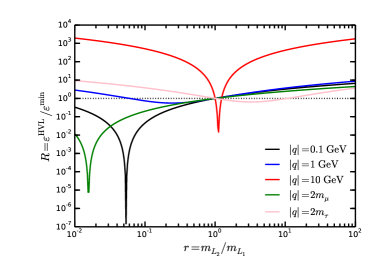
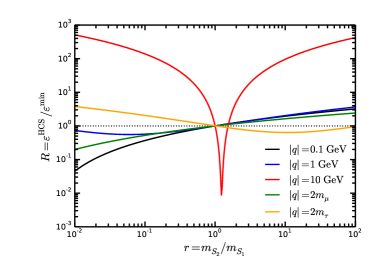
We also present the dependence of the kinetic mixing ratio between the model with two singlet vectorlike leptons or with two charged scalars and the minimal model on the mass ratio in Fig.2. There we consider five typical momentum transfers . It can be seen that, the additional lepton or scalar contributions could be significant, and the results are distinctly different from those of the minimal model. Though the additional leptons and scalars cannot be detected directly due to their heavy mass, they can provide significant contributions to the kinetic mixing.
II.4 Decay modes of
Since the direct couples with the leptons of second and third generation, it can decay into a pair of neutrinos, and also may decay into muon and tau leptons if kinematic allowed. In addition, since provides possible scenarios of dark matter, there can be the channel . The decay widths of are given by,
| (8) | ||||
| (9) | ||||
| (10) |
where , is the coupling constant of the with dark matter, and is assumed. We ignore the channel since it is suppressed by the kinetic mixing. Since neutrinos and dark matter are invisible at particle detectors, we take the invisible decay as , whose decay ratio can be expressed as
| (11) |
III Existing constraints
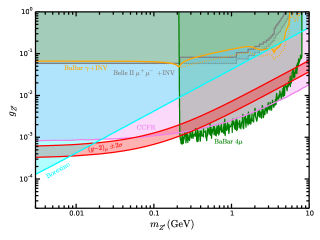
In this section, we summarize the existing constraints relevant to the parameter regions we are interested for the minimal model from various experiments as follows:
-
•
Muon anomalous magnetic moment. The significant discrepancy between the experimental measurement and the SM prediction in the magnetic moment of the muon remains one of the largest anomalies in particle physics Tanabashi:2018oca :
(12) where the errors are from experiment and theory prediction, respectively. We require the contribution in Eq.(12) to be within that leads to
(13) The minimal model, was first introduced to address the discrepancy, which can provide a new interaction with muons. An extra contribution to arises solely from a one-loop diagram involving , which can be giving by
(14) The parameter region on which the contribution in the minimal model resolves the discrepancy in the muon anomalous magnetic moment at is indicated with the red band in Fig. 3.
-
•
Neutrino trident production. The neutrino trident production is a muon neutrino scattering off the Coulomb field of a target nucleus (), producing two muons in the final state, . Besides the SM boson, in the model, the boson can also contribute to this process, which can offer a sensitive search for the light boson Altmannshofer:2014pba ; Magill:2016hgc . The measurements for the cross section have been reported by CCFR, which obtain the result . The bound is depicted in Fig. 3 and taken from Ref. Altmannshofer:2014pba .
-
•
Neutrino-electron scattering. The neutrino-electron elastic scattering processes can probe gauge boson, since gauge boson can contribute through the kinetic mixing. The most stringent constraints come from the Borexino solar neutrino experiment. Limits for gauge boson have been derived in Refs.Araki:2017wyg ; Bauer:2018onh by converting existing bounds on models Harnik:2012ni using earlier Borexino 7Be data Bellini:2011rx . The bounds are updated in Ref.Abdullah:2018ykz using the recently-released Borexino measurement of 7Be neutrinosAgostini:2017ixy . We show them in Fig. 3.
-
•
production associated with muon pair. Via the direct coupling to , can be produced at colliders in the process . Babar experiment has reported the bounds using 514 fb-1 data collected in the reaction for TheBABAR:2016rlg . Recently, Belle II experiment perform the first searches for the invisble decay of a in the process using 276 pb-1 collected Adachi:2019otg , which can touch the region of .
-
•
production associated with SM photon. At colliders, the boson can also be produced associated with SM photon via the kinetic mixing in the process Lees:2017lec . The search for invisible decays of dark photon has been preformed at BaBar experiment using the single-photon events with 53 fb-1 data. We translate the constraints for dark photon to gauge boson using
(15) where is the photon and dark photon kinetic mixing parameter in the dark photon model, and is the kinetic mixing in the model.
In Fig. 3, we asume does not decay into dark sector, i.e., . The cases are also shown as dotted line for a visual display. Taking the constraints above into account, a narrow window of the parameter region in the minimal model desired by the muon anomalous magnetic moment,
| (16) |
is still allowed.
IV Searching for gauge boson at electron colliders
At the electron colliders, the production of can be associated with a SM photon through the kinetic mixing in the process , whose diagrams are shown in Fig.4. Subsequently, the produced boson can decay into charged leptons, a pair of neutrinos or light dark matter. In this paper, we focus on the invisible decay channel , including and , to probe boson via the monophoton searches at electron colliders. We assume that the decay width of the is negligible compared to the experimental resolution, which justifies the use of the narrow width approximation.

In the monophoton signature at electron colliders, the major backgrounds (BGs) from SM contain two types: irreducible and reducible BG. The irreducible monophoton BG comes from the process , where is the three neutrinos. The reducible monophoton BG arises from the electromagnetic processes , where denotes other visible particles but undetected due to the limitations of the detector acceptance. We discuss the reducible BG in detail later for each experiment, since it strongly depends on the angular coverage of the detectors.
The differential cross section for an on-shell and a photon production process is Essig:2009nc
| (17) |
where is the fine structure constant, with being the relative angle between the electron beam axis and the photon momentum in the center-of-mass (CM) frame, is the square of the CM energy, is the mass of the gauge boson. The photon energy in the CM frame is related to the mass as
| (18) |
The cross section after integrating the polar angle is given as Essig:2009nc
| (19) | |||||
where
| (20) |
V Belle II
At Belle II, photons and electrons can be detected in the Electromagnetic Calorimeter (ECL), which is made up of three segments: forward endcap with , barrel with , and backward endcap in the lab frame Kou:2018nap . At Belle II, the reducible BG for monophoton singnature consists of two major parts: one is mainly due to the lack of polar angle coverage of the ECL near the beam directions, which is referred to as the “bBG”; the other one is mainly due to the gaps between the three segments in the ECL detector, which is referred to as the “gBG”.
The bBG comes from the electromagnetic processes , manily including and , where all the other final state particles except the detected photon are emitted along the beam directions with or in the lab frame. At Belle II, we adopt the detector cuts for the final detected photon (hereafter the “pre-selection cuts”): in the lab frame.
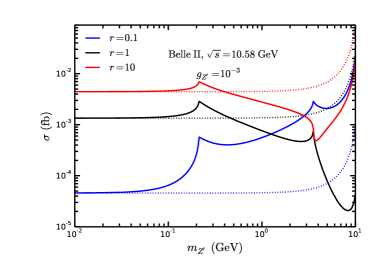
In Fig.5, we show the production rates of the process in models after the “pre-selection cuts” for the photon at Belle II with GeV. The dotted lines correspond to the case of constant , which are shown as a comparison. We can see that, with constant , the cross sections all increase with the increment of the mass of . In the minimal model, the production rates for the process at Belle II generally drop but exist two peaks at the positions of and when GeV, while raise at the tail of the plotted region.
For the Belle II detector, which is asymmetric, the maximum energy of the monophoton events in the bBG in the CM frame, , is given by Liang:2019zkb (if not exceeding )
| (21) |
where all angles are given in the CM frame, and , with and being the polar angles corresponding to the edges of the ECL detector. In order to remove the above bBG, we use the detector cut (hereafter the “bBG cuts”) for the final monophoton .
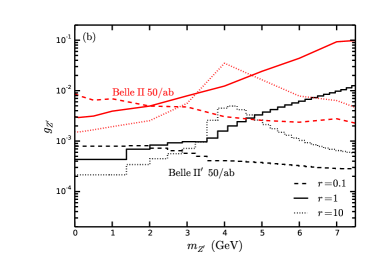
The gBG for the monophoton singnature have been simulated in the Ref. Kou:2018nap to search for dark photons decaying into light dark matter. The projetced upper limits on the kinetic mixing of dark photon and SM photon for a 20 fb-1 Belle II dataset are present there. The constranint for the kinetic mixing between gauge boson and SM photon can be translated from the dark photon using Eq. (15). We scale the expected sensitivity to the planned full of integrated luminosity of 50 ab-1 at Belle II using . Then the corresponding constraint based on the simulation in Ref. Kou:2018nap from 20 fb-1 to 50 ab-1 can be simply projected by a factor of , which is present in Fig.6 and the invisible decay ratio is assumed. It is shown that the sensitivity for at Belle-II experiment with 50 ab-1 via monophoton searches is expected to be worse in the minimal model with the increament of , while become better with extra heavy vector-like leptons (charged scalars) in the case of when 7 GeV. With in the model with extra heavy leptons (scalars), expected sensitivity gets improved when GeV and then gets worse.
We further carry out an analysis without gBG taking into account, to compare with other experiments in which detailed simulations with gBG are not available. We use the “bBG cuts” to remove the reducible BG events; this momentum the BG events survived the “bBG cuts” come from irreducible BG without gBG considered. Since the energy of the final photon in the signal process is related to , in addiction to the “bBG cuts”, we select final photon in the energy window of (hereafter the “optimized cut”) to enhance the discovery sensitivity, where is detector energy resolution for the photon. At Belle II, at 0.1 (8) GeV Kou:2018nap and we take MeV conservatively. In Fig. 6, we present the expected 95% confidence level (C.L.) exclusion limits on by considering the irreducible BG only after “optimized cut”, which is labeled as Belle-II′. We define Yin:2009mc , where () is the number of events in the signal (BG) processes. The 95% C.L. upper bound on is obtained by solving , and assuming photon detection efficiency as 95% Kou:2018nap . One can see that if we don’t consider the “gBG” and apply the “optimized cut”, the Belle II experiment with 50 ab-1 via monophoton searches is expected to be sensitive to the parameter region with GeV and in the minimal model, which can be improved by almost 1 order of magnitude comparing with considering the “gBG”.
VI BESIII and STCF
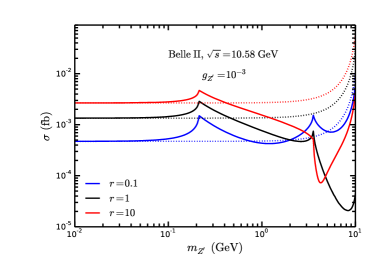
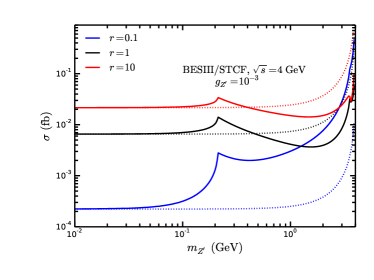
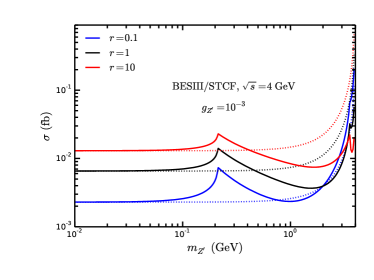
At BESIII and STCF, for the final state photons, we adopt the “preselection cuts” by BESIII Collaboration Ablikim:2017ixv : 25 MeV with or 50 MeV with . In Fig. 7, we present the cross section of the the process at BESIII and STCF with GeV in models after the “pre-selection cuts”. The dotted lines correspond to the case of constant , which are shown as a comparison. One can see that, the cross section always increases for larger in models with extra heavy leptons or scalars in the case of , while there is a twist near in the case of and .
At BESIII and STCF, which are symmetric, the maximum energy of the monophoton events in the bBG in the CM frame, , is given by Liu:2019ogn
| (22) |
where is the polar angle corresponding to the edge of the detector. Taking into account the coverage of MDC, EMC, and TOF, we have at the BESIII Liu:2018jdi . We further demand for the final monophoton to remove the reducible BG (hereafter the “bBG cuts”).
At BESIII, the photon energy resolution of the EMC Asner:2008nq , and we take MeV for all energy conservatively. At the BESIII, photon reconstruction efficiencies are all more than 99% Ablikim:2011kv , we assume them to be 100% in our paper. For the EMC at STCF, we assume the same energy resolution and reconstrunction efficiencies with BESIII to present a preliminary projection limit, because of the similarity of the two experiments. We take MeV for GeV. In addition to the “bBG cuts”, we select final photon in the energy window of (hereafter the “optimized cut”) to enhance the discovery sensitivity.
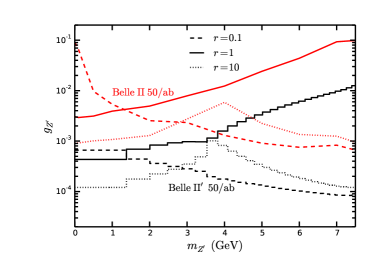
At BESIII, since 2012 monophoton trigger has been implemented and the corresponding data luminosity reach about 14 fb-1 with the CM energy from 2.125 GeV to 4.6 GeV Zhang:2019wnz . We define where for each BESIII colliding energy. The 95% C.L. upper bound on from BESIII is obtained by demanding . In Fig. 8, we present the corresponding results for the models with extra vector-like leptons and charged scalars in cases of via monophoton searches at BESIII with 14 fb-1 and at 4 GeV STCF with 30 ab-1, respectively. The invisible decay ratio of is assumed to be 1. The constraints on get looser with the increament of for both two considered models in cases of at BESIII and 4 GeV STCF, while tighter in cases of for the models with extra leptons (scalars) when GeV ( GeV) at 4 GeV STCF.
VII Results
Fig. 9 summarizes the sensitivity on gauge coupling in the minimal model from electron colliders, including Belle II, BESII, and STCF. The solid lines indicate the case of that cannot decay into dark matter, i.e., , and the dotted lines indicate case. The exisiting constraints are also presented in the shaded region, and the summary for these limits from different experiments can be found in Fig.3. The red band shows the region that could explain the muon anomalous magnetic moment . We present three expected limits with different experiments at Belle II,
-
1.
channel with bBG and gBG considered. We translate the constraints on the dark photon from the search of invisible decay at Belle II assuming a 20 fb-1 dataset Kou:2018nap , where the bBG and gBG are all considered, to gauge boson using the relation of Eq.(15). Then we scale the constraints to 50 ab-1 by a factor of . This case is labeled as “Belle II ” in Fig. (9).
-
2.
channel with only bBG considered. We compute the limits without gBG taking into account as mentioned above. The “bBG cuts” are applied to remove the reducible BG events and only the irreducible BG contribute to the BG events if gBG is not considered. After the “optimized cut”, we show the 95% C.L. upper bound on at Belle II with the integrated luminosity of 50 ab-1 in Fig.9, which is lablled as “Belle II”
-
3.
channel. In order to project the sensivity on the gauge boson with channel in 50 ab-1 Belle II experiment, we simply scale the recent 276 pb-1 results by a factor of for the kinetic mixing, which is lablled as “Belle II ”
One observes that on the searches for the invisible decay of , the sensitivity at 50 ab-1 Belle II with channel is slightly better with the channel. It can also be found that these two results are already excluded by current constraints. While without the gBG considered in the channel, the sensitivity can be improved almost 1 order and the gauge coupling constant down to about when , which still left a thin slice of mass region GeV to explain the moun () anomaly. The one order of magnitude difference in sensitivity between the two Belle II limits via the monophoton search, shows that the control on gGB is very important in probing the parameter space.
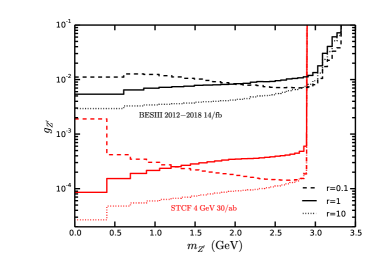
The STCF and BESIII limits are obtained when the BG due to the gaps in the detectors are neglected, since BESIII did not released any analysis about gBG. We emphasize that more rigorous BESIII and STCF sensitivities could be obtained with such gBG anlysis available in the future. With about 14 fb-1 integrated luminosity collected during 2012-2018 Zhang:2019wnz the upper limits from BESIII are exclued by CCFR experiment. The STCF limits are presented at GeV with the integrated luminosity of 30 ab-1. The future monophoton searches at the STCF experiment operated at GeV can eliminate the moun favored window when GeV. In the low mass region, 2 GeV STCF provide best sensitivity since the signal to BG ratio increases when the colliding energy decreases, and can be down to about when , which is improved about 1 order than the monophoton searches at 50 ab-1 Belle II with gBG omitted.
In Fig.10, we present the dependence for exclusion regions of corresponding to GeV on the mass ratio and via monophoton searches from BESIII with 14 fb-1, Belle II with 50 ab-1 and future 4 GeV STCF with 30 ab-1. The shaded grey region is already excluded by CCFR experiments, which is independent on the mass ratio. One can see that can down to when at 4 GeV STCF with 30 ab-1.
VIII Summary
In this paper, we probe the invisible decay of the gauge boson via monophoton signature at three different electron colliders operated at the GeV scale: Belle II, BESIII, and STCF. In the minimal model, we extend the SM with a gauge symmetry and assume that the kinetic mixing term between and photon is absent at tree level, but can arise at one loop level due to and leptons. We also further extend the minimal model with extra heavy vector-like leptons or charged scalars, where the additional contributions to the kinetic mixing arising from extra particles inside the loop. The exciting nondecoupling behavior of the contribution since the extra heavy vector-like leptons or charged scalars to the kinetic mixing is also demonstrated. The visible signatures of heavy leptons or charged scalars, too heavy to be directly detected at high energy colliders, maybe possible in processes modified by the mixing.
We translate the sensitivity for dark photon within monophoton signature projected by Belle II to gauge boson taking into account various SM BGs. We also recast the recent invisible search of in the production at Belle II. It is found that, By ignoring the BG due to the gaps in the detectors, we present the constraints at BESIII with 14 fb-1 luminosity and at future 30 ab-1 STCF. For comparison, we also compute the limits at 50 ab-1 Belle II without gBG taking into account. It is found that the future 2 GeV STCF can further improve the sensitivity to low mass than Belle II via monophoton signature since it is operated at lower energy. The future STCF can exclude the moun anomaly favored parameter region when GeV. And gauge coupling constant in the minimal model can be probed down to about when at future 30 ab-1 STCF with GeV.
IX Acknowledgement
This work was supported in part by the National Natural Science Foundation of China (Grants No. 11805001, No.11935001).
References
- (1) R. Foot, Mod. Phys. Lett. A 6 (1991), 527-530
- (2) X. He, G. C. Joshi, H. Lew and R. Volkas, Phys. Rev. D 43 (1991), 22-24
- (3) X. He, G. C. Joshi, H. Lew and R. Volkas, Phys. Rev. D 44 (1991), 2118-2132
- (4) G. W. Bennett et al. [Muon g-2 Collaboration], Phys. Rev. D 73 (2006) 072003 doi:10.1103/PhysRevD.73.072003 [hep-ex/0602035].
- (5) S. Baek, N. G. Deshpande, X. G. He and P. Ko, Phys. Rev. D 64 (2001) 055006 doi:10.1103/PhysRevD.64.055006 [hep-ph/0104141].
- (6) E. Ma, D. P. Roy and S. Roy, Phys. Lett. B 525 (2002) 101 doi:10.1016/S0370-2693(01)01428-9 [hep-ph/0110146].
- (7) W. Altmannshofer, C. Y. Chen, P. S. Bhupal Dev and A. Soni, Phys. Lett. B 762 (2016) 389 doi:10.1016/j.physletb.2016.09.046 [arXiv:1607.06832 [hep-ph]].
- (8) R. Aaij et al. [LHCb], Phys. Rev. Lett. 111 (2013), 191801 doi:10.1103/PhysRevLett.111.191801 [arXiv:1308.1707 [hep-ex]].
- (9) R. Aaij et al. [LHCb], Phys. Rev. Lett. 113 (2014), 151601 doi:10.1103/PhysRevLett.113.151601 [arXiv:1406.6482 [hep-ex]].
- (10) W. Altmannshofer, S. Gori, S. Profumo and F. S. Queiroz, JHEP 1612 (2016) 106 doi:10.1007/JHEP12(2016)106 [arXiv:1609.04026 [hep-ph]].
- (11) A. Crivellin, G. D’Ambrosio and J. Heeck, Phys. Rev. Lett. 114 (2015) 151801 doi:10.1103/PhysRevLett.114.151801 [arXiv:1501.00993 [hep-ph]].
- (12) P. Ko, T. Nomura and H. Okada, Phys. Rev. D 95 (2017) no.11, 111701 doi:10.1103/PhysRevD.95.111701 [arXiv:1702.02699 [hep-ph]].
- (13) S. Baek, Phys. Lett. B 781 (2018) 376 doi:10.1016/j.physletb.2018.04.012 [arXiv:1707.04573 [hep-ph]].
- (14) Y. Jho, S. M. Lee, S. C. Park, Y. Park and P. Y. Tseng, JHEP 2004 (2020) 086 doi:10.1007/JHEP04(2020)086 [arXiv:2001.06572 [hep-ph]].
- (15) W. Altmannshofer, M. Carena and A. Crivellin, Phys. Rev. D 94 (2016) no.9, 095026 doi:10.1103/PhysRevD.94.095026 [arXiv:1604.08221 [hep-ph]].
- (16) S. Baek, H. Okada and K. Yagyu, JHEP 1504 (2015) 049 doi:10.1007/JHEP04(2015)049 [arXiv:1501.01530 [hep-ph]].
- (17) J. Heeck and W. Rodejohann, Phys. Rev. D 84 (2011), 075007 [arXiv:1107.5238 [hep-ph]].
- (18) A. Biswas, S. Choubey and S. Khan, JHEP 09 (2016), 147 [arXiv:1608.04194 [hep-ph]].
- (19) S. Patra, S. Rao, N. Sahoo and N. Sahu, Nucl. Phys. B 917 (2017) 317 doi:10.1016/j.nuclphysb.2017.02.010 [arXiv:1607.04046 [hep-ph]].
- (20) A. Biswas, S. Choubey and S. Khan, JHEP 1702 (2017) 123 doi:10.1007/JHEP02(2017)123 [arXiv:1612.03067 [hep-ph]].
- (21) A. Biswas, S. Choubey, L. Covi and S. Khan, JCAP 1802 (2018) 002 doi:10.1088/1475-7516/2018/02/002 [arXiv:1711.00553 [hep-ph]].
- (22) G. Arcadi, T. Hugle and F. S. Queiroz, Phys. Lett. B 784 (2018) 151 doi:10.1016/j.physletb.2018.07.028 [arXiv:1803.05723 [hep-ph]].
- (23) A. Kamada, K. Kaneta, K. Yanagi and H. B. Yu, JHEP 1806 (2018) 117 doi:10.1007/JHEP06(2018)117 [arXiv:1805.00651 [hep-ph]].
- (24) P. Foldenauer, Phys. Rev. D 99 (2019) no.3, 035007 doi:10.1103/PhysRevD.99.035007 [arXiv:1808.03647 [hep-ph]].
- (25) Y. Cai and A. Spray, JHEP 1810 (2018) 075 doi:10.1007/JHEP10(2018)075 [arXiv:1807.00832 [hep-ph]].
- (26) Z. L. Han, R. Ding, S. J. Lin and B. Zhu, Eur. Phys. J. C 79 (2019) no.12, 1007 doi:10.1140/epjc/s10052-019-7526-5 [arXiv:1908.07192 [hep-ph]].
- (27) J. P. Lees et al. [BaBar Collaboration], Phys. Rev. D 94 (2016) no.1, 011102 doi:10.1103/PhysRevD.94.011102 [arXiv:1606.03501 [hep-ex]].
- (28) I. Adachi et al. [Belle-II Collaboration], Phys. Rev. Lett. 124 (2020) no.14, 141801 doi:10.1103/PhysRevLett.124.141801 [arXiv:1912.11276 [hep-ex]].
- (29) A. M. Sirunyan et al. [CMS Collaboration], Phys. Lett. B 792 (2019) 345 doi:10.1016/j.physletb.2019.01.072 [arXiv:1808.03684 [hep-ex]].
- (30) Y. Jho, Y. Kwon, S. C. Park and P. Y. Tseng, JHEP 10 (2019), 168 doi:10.1007/JHEP10(2019)168 [arXiv:1904.13053 [hep-ph]].
- (31) Y. Kaneta and T. Shimomura, PTEP 2017 (2017) no.5, 053B04 doi:10.1093/ptep/ptx050 [arXiv:1701.00156 [hep-ph]].
- (32) T. Araki, S. Hoshino, T. Ota, J. Sato and T. Shimomura, Phys. Rev. D 95 (2017) no.5, 055006 [arXiv:1702.01497 [hep-ph]].
- (33) C. H. Chen and T. Nomura, Phys. Rev. D 96 (2017) no.9, 095023 doi:10.1103/PhysRevD.96.095023 [arXiv:1704.04407 [hep-ph]].
- (34) H. Banerjee and S. Roy, Phys. Rev. D 99 (2019) no.3, 035035 doi:10.1103/PhysRevD.99.035035 [arXiv:1811.00407 [hep-ph]].
- (35) E. Kou et al. [Belle II Collaboration], arXiv:1808.10567 [hep-ex].
- (36) D. M. Asner et al., Int. J. Mod. Phys. A 24, S1 (2009) [arXiv:0809.1869 [hep-ex]].
- (37) A. E. Bondar et al. [Charm-Tau Factory], Yad. Fiz. 76 (2013) no.9, 1132-1145 doi:10.1134/S1063778813090032
- (38) Q. Luo and D. Xu, doi:10.18429/JACoW-IPAC2018-MOPML013
- (39) Haiping Peng, https://indico.inp.nsk.su/event/15/session/0/contribution/99/material/slides/0.pdf
- (40) M. Tanabashi et al. [Particle Data Group], Phys. Rev. D 98 (2018) no.3, 030001 doi:10.1103/PhysRevD.98.030001
- (41) W. Altmannshofer, S. Gori, M. Pospelov and I. Yavin, Phys. Rev. Lett. 113 (2014), 091801 doi:10.1103/PhysRevLett.113.091801 [arXiv:1406.2332 [hep-ph]].
- (42) G. Magill and R. Plestid, Phys. Rev. D 95 (2017) no.7, 073004 doi:10.1103/PhysRevD.95.073004 [arXiv:1612.05642 [hep-ph]].
- (43) M. Bauer, P. Foldenauer and J. Jaeckel, JHEP 18 (2020), 094 doi:10.1007/JHEP07(2018)094 [arXiv:1803.05466 [hep-ph]].
- (44) R. Harnik, J. Kopp and P. A. N. Machado, JCAP 07 (2012), 026 doi:10.1088/1475-7516/2012/07/026 [arXiv:1202.6073 [hep-ph]].
- (45) G. Bellini et al., Phys. Rev. Lett. 107 (2011) 141302 doi:10.1103/PhysRevLett.107.141302 [arXiv:1104.1816 [hep-ex]].
- (46) M. Abdullah, J. B. Dent, B. Dutta, G. L. Kane, S. Liao and L. E. Strigari, Phys. Rev. D 98 (2018) no.1, 015005 doi:10.1103/PhysRevD.98.015005 [arXiv:1803.01224 [hep-ph]].
- (47) M. Agostini et al. [Borexino Collaboration], Phys. Rev. D 100 (2019) no.8, 082004 doi:10.1103/PhysRevD.100.082004 [arXiv:1707.09279 [hep-ex]].
- (48) J. Lees et al. [BaBar], Phys. Rev. Lett. 119 (2017) no.13, 131804 [arXiv:1702.03327 [hep-ex]].
- (49) R. Essig, P. Schuster and N. Toro, Phys. Rev. D 80 (2009), 015003 doi:10.1103/PhysRevD.80.015003 [arXiv:0903.3941 [hep-ph]].
- (50) J. Liang, Z. Liu, Y. Ma and Y. Zhang, [arXiv:1909.06847 [hep-ph]].
- (51) P. f. Yin, J. Liu and S. h. Zhu, Phys. Lett. B 679, 362 (2009) [arXiv:0904.4644 [hep-ph]].
- (52) M. Ablikim et al. [BESIII Collaboration], Phys. Rev. D 96, no. 11, 112008 (2017) [arXiv:1707.05178 [hep-ex]].
- (53) Z. Liu, Y. H. Xu and Y. Zhang, JHEP 1906, 009 (2019) [arXiv:1903.12114 [hep-ph]].
- (54) Z. Liu and Y. Zhang, Phys. Rev. D 99, no. 1, 015004 (2019) [arXiv:1808.00983 [hep-ph]].
- (55) M. Ablikim et al. [BESIII Collaboration], Phys. Rev. D 83 (2011) 112005 doi:10.1103/PhysRevD.83.112005 [arXiv:1103.5564 [hep-ex]].
- (56) Y. Zhang, W. T. Zhang, M. Song, X. A. Pan, Z. M. Niu and G. Li, Phys. Rev. D 100 (2019) no.11, 115016 doi:10.1103/PhysRevD.100.115016 [arXiv:1907.07046 [hep-ph]].