Probing the electroweak $4b+\ell+{\hbox to0.0pt{\,/\hss}{E}_{T}}$ final state in type I 2HDM at the LHC

The Standard Model (SM) is currently the most extensively tested model for particle physics as all the collider experiments are in perfect agreement with it. The discovery of Higgs boson ATLAS:2012yve ; CMS:2012qbp ; ATLAS:2013dos ; CMS:2013btf gives SM the stature of the only acceptable theory in the energy scale of the present day colliders. However, despite its success, SM is believed neither a complete, nor a perfect theory because of several drawbacks. SM cannot explain the matter-antimatter asymmetry, neutrino oscillation, existence of dark matter, mass hierarchy within elementary particles and does not include gravity. Also there is no fundamental reason in support of one scalar particle, i.e. the Higgs sector in the SM is assumed to be minimal under the electroweak gauge symmetry. The observation of any other scalar particle, whether neutral or charged, will provide a strong indication of the non-minimal framework for the Electroweak Symmetry Breaking (EWSB).

The two Higgs doublet model (2HDM) Branco:2011iw ; Gunion:2002zf ; Gunion:1989we ; Davidson:2005cw is the simplest extension of SM which accomodates a second Higgs doublet with the same quantum numbers as the first one. The most general 2HDM where both the Higgs doublets couple to the fermions suffer from Flavor Changing Neutral Currents (FCNC) which contradicts with the experiments. To prevent the FCNC, a $\mathbb{Z}_{2}$ symmetry is imposed Glashow:1976nt ; Paschos:1976ay which restricts the Yukawa sector in to four possible types, viz type I, type II, type X and type Y. Each type of 2HDM has its own charecteristics, which makes 2HDM a phenomenologically very rich extension of SM. After the EWSB, the scalar sector in the $CP$ conserving framework of 2HDM consists of two $CP$ even scalars $h,~{}H$, a $CP$ odd scalar (pseudoscalar) $A$ and a pair of charged Higgs $H^{\pm}$. We follow the standard mass hierarchy where the observed 125 GeV Higgs boson, identified by $h$, is the lightest $CP$ even Higgs boson.

The conventional search strategies to look for neutral single Higgs or multi-Higgs states at the Large Hadron Collider (LHC) involves the QCD induced processes like gluon fusion process or the $b\bar{b}$-annihilation Arhrib:2008pw ; Hespel:2014sla ; Dicus:1998hs ; Balazs:1998sb ; Harlander:2003ai ; Duhr:2020kzd ; CMS:2018qmt ; ATLAS:2015rsn ; CMS:2019mij ; ATLAS:2019odt ; CMS:2018hir ; ATLAS:2020zms ; CMS:2019hvr , where the $b$-quarks are themselves produced from a (double) gluon splitting. Even for single production of the charged Higgs, the usual search for light charged Higgs is given by the top quark pair production cross section times the branching ratio of top into charged Higgs and the top-bottom asscociated production for heavy charged Higgs Flechl:2014wfa ; Degrande:2015vpa ; CMS:2019bfg ; ATLAS:2021upq . Thus all these channels are intrinsically $gg$-induced. However, the QCD induced processes can be subdominant in some beyond SM (BSM) frameworks where the fermionic couplings to the BSM particles are suppressed. The type I 2HDM fits this criteria as all the BSM Higgs bosons show fermiophobic behaviour Akeroyd:1995hg ; Akeroyd:1998ui ; Arhrib:2016wpw ; Enberg:2018pye ; Kling:2020hmi ; Wang:2021pxc ; Bahl:2021str ; Arhrib:2021xmc ; Mondal:2021bxa ; Kim:2022nmm ; Kim:2023lxc . In such situation the production of the BSM Higgses through EW processes get more importance than the QCD induced processes Enberg:2018pye ; Arhrib:2021xmc ; Mondal:2021bxa . Similarly, the bosonic decays of the BSM Higgses can overcome the fermionic decay modes if kinematically allowed Arhrib:2016wpw ; Kling:2020hmi ; Mondal:2021bxa . In type I 2HDM, the EW production of a light $A$ in association with $H^{\pm}$ and followed by $H^{\pm}$ decay to $AW$ can give the $AAW$ mode. Since the $AAW$ mode involves $q\bar{q}^{\prime}$-induced production where $q$ represents valence quark ($u,d$), the $AAW$ mode has no QCD production counterpart. For the situation of light $A$, the decays of $A$ are restricted only to the fermions and the branching ratio of $A\to b\bar{b}$ is dominant¹¹1We also have $A\to gg$ decay mode via top/bottom loop, but very suppressed. This gives rise to the $4b+W$ mode. Considering the leptonic decay of the $W$ boson, we can have $4b+\ell+{\hbox to0.0pt{\,/\hss}{E}_{T}}$ final state, which as mentioned before is the signature state characteristic of the EW processes and can dominate over the QCD induced $4b$ state for a large parameter space. The $4b+\ell+\hbox to0.0pt{\,/\hss}{E}_{T}$ final state also have subdominant contributions from other EW processes e.g. through the production channels $pp\to H^{\pm}H/H^{+}H^{-}$ and thereafter the decay chains $H^{\pm}\to AW$ and $H\to AA/AZ$. Contribution to $4b+W$ through $pp\to H^{\pm}h$ with $H^{\pm}\to hW$ and $h\to b\bar{b}$ are highly suppressed due to the alignment limit and hence not considered in our work. Since we are restricted to the standard mass hierarchy with light $A$, only $A\to b\bar{b}$ decay can give large cross section for the final state of our interest. Situation with inverted mass hierarchy with $125$ GeV Higgs as the heavier $CP$ even Higgs, identified by $H$, the light $CP$ even Higgs $h$ can decay dominantly to $b\bar{b}$ and we can obtain the $4b+W$ state via the $hhW$ production mode Arhrib:2021xmc ; Kang:2022mdy ; Li:2023btx . Interestingly, in the inverted scenario, fermiophobic limit of $h$ gives large $h\to\gamma\gamma/WW^{*}$ decay modes Arhrib:2017wmo ; Wang:2021pxc ; Kim:2023lxc compared to the $b\bar{b}$ mode. Whereas, slight deviation from the fermiophobic limit of $h$ makes the decay into $b\bar{b}$ and $\gamma\gamma$ modes comparable, leading to $2b2\gamma+W$ final state Bhatia:2022ugu which serves as a complementary channel to the $4b+W$ state.

At the LHC the dominant SM background for the proposed final state, the $t\bar{t}+$jets background, is significantly higher than the EW $4b+\ell+{\hbox to0.0pt{\,/\hss}{E}_{T}}$ final state. Hence we require strong selection cuts which can kill the background. In this work we construct a $\chi^{2}$ variable, which is based on the signal topology and the signal hypothesis (masses of $A$ and $H^{\pm}$). The $\chi^{2}$ can be used to discriminate the signal and the background and therefore highly effective in reducing the background significantly without affecting much the signal. The most appropriate use for $\chi^{2}$ would be for the mass reconstruction of the BSM Higgs bosons CMS:2017ixp ; Wang:2021pxc , however we can only reconstruct the masses of $A$ and $H^{\pm}$ via $4b+\ell+{\hbox to0.0pt{\,/\hss}{E}_{T}}$ final state. To probe the full Higgs spectrum, the EW induced inclusive $4b+X$ final state (where $X$ implies any additional jets even $b$-jets and /or leptons) is more suitable. In our recent study Mondal:2023wib , we showed that the EW initiated $4b+X$ can provide simultaneous reconstruction of all the BSM Higgs boson masses. Hence, instead of using $\chi^{2}$ for the reconstruction of the masses of $A$ and $H^{\pm}$, we use $\chi^{2}$ as a selection criteria to discriminate the signal from the background. Along with the $\chi^{2}$ we use other selection cuts like the asymmetry cut and di-jet $\eta$ separation cuts to obtain the discovery significance of the signal at the 13 TeV LHC with 3000 fb^-1 luminosity.

The article is organized as follows. In Sec.[2] we give an overview of type I 2HDM and discuss the fermionic and gauge couplings of the additional Higgs bosons to show the fermiophobic natures as well as the Higgs trilinear couplings. In Sec.[3], we discuss the signal topology of the $AAW$ mode, it’s production cross section at the LHC and the dominant $t\bar{t}+$jets background. We show the theoretical and experimental constraints on the model parameters, the formalism of $\chi^{2}$ method and the signal-background analysis. Finally we conclude in Sec.[4].

The most general scalar potential for the 2HDM is

	$\displaystyle\mathcal{V}(\Phi_{1},\Phi_{2})$	$\displaystyle=$	$\displaystyle m_{11}^{2}\Phi_{1}^{\dagger}\Phi_{1}+m_{22}^{2}\Phi_{2}^{\dagger}\Phi_{2}-[m_{12}^{2}\Phi_{1}^{\dagger}\Phi_{2}+h.c.]+\frac{1}{2}\lambda_{1}(\Phi_{1}^{\dagger}\Phi_{1})^{2}$		(1)
		$\displaystyle+$	$\displaystyle\frac{1}{2}\lambda_{2}(\Phi_{2}^{\dagger}\Phi_{2})^{2}+\lambda_{3}(\Phi_{1}^{\dagger}\Phi_{1})(\Phi_{2}^{\dagger}\Phi_{2})+\lambda_{4}(\Phi_{1}^{\dagger}\Phi_{2})(\Phi_{2}^{\dagger}\Phi_{1})$
		$\displaystyle+$	$\displaystyle\Big{\{}\frac{\lambda_{5}}{2}(\Phi_{1}^{\dagger}\Phi_{2})^{2}+[\lambda_{6}(\Phi_{1}^{\dagger}\Phi_{1})+\lambda_{7}(\Phi_{2}^{\dagger}\Phi_{2})](\Phi_{1}^{\dagger}\Phi_{2})+h.c.\Big{\}}$

where $\Phi_{1,2}$ are the two Higgs doublets with hypercharge $Y=1/2$ and the parameters $m_{11}^{2},~{}m^{2}_{22}$ and $\lambda_{1,2,3,4}$ are real for the scalar potential to be real. The other parameters $m_{12}^{2}$ and $\lambda_{5,6,7}$ in general can be complex. To avoid the tree level FCNC, a $\mathbb{Z}_{2}$ symmetry is imposed under which $\Phi_{1}\to\Phi_{1}$ and $\Phi_{2}\to-\Phi_{2}$ which implies $\lambda_{6,7}=0$. However, the $\mathbb{Z}_{2}$ symmetry is softly broken by the dimensionful parameter $m_{12}^{2}\neq 0$. Assuming $CP$ invariant framework, $m_{12}^{2}$ and $\lambda_{5}$ are considered real. The two Higgs doublets are parameterized as

$\displaystyle\Phi_{i}=\begin{pmatrix}H_{i}^{+}\\ \frac{v_{i}+h_{i}+iA_{i}}{\sqrt{2}}\end{pmatrix},\quad i=1,2.$

(2)

After EWSB, the scalar spectrum consists of two $CP$ even scalars $h$ and $H$, one $CP$ odd pseudoscalar $A$ and a pair of charged Higgs $H^{\pm}$. The physical mass eigenstates are related to the gauge eigenstates by the following equations

$\displaystyle\begin{pmatrix}H\\ h\end{pmatrix}=\begin{pmatrix}c_{\alpha}&&s_{\alpha}\\ -s_{\alpha}&&c_{\alpha}\end{pmatrix}\begin{pmatrix}h_{1}\\ h_{2}\end{pmatrix},\quad A=-s_{\beta}A_{1}+c_{\beta}A_{2},\quad H^{\pm}=-s_{\beta}H_{1}^{\pm}+c_{\beta}H_{2}^{\pm}$

(3)

where $v_{1,2}$ are the vacuum expectation values (VEVs) of the two Higgs doublets such that $v=\sqrt{v_{1}^{2}+v_{2}^{2}}=246$ GeV and we define the parameter $t_{\beta}=v_{2}/v_{1}$. We use the abbreviations, $s_{\alpha}(c_{\alpha})=\sin\alpha(\cos\alpha)$, $s_{\beta}(c_{\beta})=\sin\beta(\cos\beta)$, $t_{\beta}=\tan\beta$, etc. We identify the physical state $h$ as the SM-like observed Higgs boson of mass $125$ GeV as all the Higgs signal strength measurements CMS:2020xwi ; Buchbinder:2020ovf ; ATLAS:2020bhl ; CMS:2020zge ; ATLAS:2021nsx ; CMS:2021gxc ; ATLAS:2020syy ; ATLAS:2021upe ; CMS:2021ugl ; ATLAS:2020wny ; ATLAS:2020rej ; ATLAS:2020fzp ; ATLAS:2022ers are consistent with SM. Throughout the paper we collectively call $H,~{}A$ and $H^{\pm}$ as the beyond SM (BSM) Higgs bosons.

In type I 2HDM the fermion fields transform odd under the $\mathbb{Z}_{2}$ symmetry and therefore couple only to the second Higgs doublet $\Phi_{2}$. Hence the quarks and charged leptons get their masses from the VEV of $\Phi_{2}$. The Yukawa Lagrangian in type I 2HDM can be written as

$\displaystyle\mathcal{L}_{Y}^{I}=-\bar{Q}_{L}Y_{u}\tilde{\Phi}_{2}u_{R}-\bar{Q}_{L}Y_{u}\bar{\Phi}_{2}d_{R}-\bar{L}_{L}Y_{\ell}\Phi_{2}\ell_{R}+h.c.$

(4)

where $\tilde{\Phi}_{2}=i\tau_{2}\Phi_{2}^{*}$. After the EWSB, the Yukawa Lagrangian in terms of the mass eigenstates is

	$\displaystyle\mathcal{L}_{Y}^{I}$	$\displaystyle=$	$\displaystyle-\sum_{f=u,d,\ell}\frac{m_{f}}{v}\left(\xi_{h}^{f}\bar{f}fh+\xi_{H}^{f}\bar{f}fH-i\xi_{A}^{f}\bar{f}f\gamma_{5}A\right)$		(5)
		$\displaystyle-$	$\displaystyle\Big{\{}\frac{\sqrt{2}V_{ud}}{v}\bar{u}\Big{(}\xi^{u}_{A}m_{u}P_{L}+\xi^{d}_{A}m_{d}P_{R}\Big{)}dH^{+}+\frac{\sqrt{2}m_{\ell}}{v}\xi^{\ell}_{A}\bar{\nu}_{L}\ell_{R}H^{+}+h.c.\Big{\}}$

where $V$ is the CKM matrix and $P_{L,R}=\frac{1}{2}(1\mp\gamma_{5})$ are the chirality projection operators. The Yukawa coupling modifiers $\xi^{f}$ are given in Table. [1].

The gauge boson couplings to the scalar fields in 2HDM are independent of the Yukawa types. The couplings of the neutral scalars to a pair of gauge bosons are

$\displaystyle g_{h_{VV}}=s_{\beta-\alpha}g_{h{VV}}^{SM},\quad g_{H{VV}}=c_{\beta-\alpha}g_{h_{VV}}^{SM},\quad g_{A{VV}}=0$

(6)

where $V=W^{\pm},Z$. The $Z$ boson couplings to the neutral scalars are

$\displaystyle g_{hAZ_{\mu}}=\frac{g}{2c_{\theta_{W}}}c_{\beta-\alpha}(p_{h}-p_{A})_{\mu},\quad g_{HAZ_{\mu}}=-\frac{g}{2c_{\theta_{W}}}s_{\beta-\alpha}(p_{H}-p_{A})_{\mu}$

(7)

where $p_{\mu}$ represent the incoming four momenta of the Higgs bosons, $g$ denotes the $SU(2)_{L}$ gauge coupling and $\theta_{W}$ is the Weinberg angle. Similarly the $W$ boson couplings to the charged Higgs are

	$\displaystyle g_{H^{\mp}W^{\pm}h}$	$\displaystyle=$	$\displaystyle\mp\frac{ig}{2}c_{\beta-\alpha}(p_{h}-p_{H^{\mp}})_{\mu},$
	$\displaystyle g_{H^{\mp}W^{\pm}H}$	$\displaystyle=$	$\displaystyle\pm\frac{ig}{2}s_{\beta-\alpha}(p_{H}-p_{H^{\mp}})_{\mu},$
	$\displaystyle g_{H^{\mp}W^{\pm}A}$	$\displaystyle=$	$\displaystyle\frac{g}{2}(p_{A}-p_{H^{\mp}})_{\mu}$		(8)

with incoming four momenta of the neutral and charged Higgs. From the Table. [1], we can see that the fermionic couplings of $H^{\pm}$ and $A$ are suppressed at large $t_{\beta}$ and thus their behaviour is fermiophobic. Another important factor is the alignment limit $s_{\beta-\alpha}\to 1$ Basler:2017nzu ; Branchina:2018qlf which is mostly favored by the experimental contraints so that all the couplings of $h$ approach to that of the SM. The alignment limit together with large $t_{\beta}$ also make the $H$ fermiophobic. This can be seen from the Yukawa coupling modifier of $H$

$\displaystyle\xi^{f}_{H}=\frac{s_{\alpha}}{s_{\beta}}=c_{\beta-\alpha}-\frac{s_{\beta-\alpha}}{t_{\beta}}.$

(9)

In the limit of $s_{\beta-\alpha}\to 1$ and $t_{\beta}>>1$, $\xi^{f}_{H}$ approaches to zero. The fermiophobic behaviour of the BSM Higgs bosons is the most striking characteristics of type I 2HDM.

For $A$ lighter than half of the mass of the SM Higgs, strong constraint comes from the non-SM $h\to AA$ decay. The Higgs trilinear coupling which involves in this decay process is given by

$\displaystyle\lambda_{hAA}=\frac{1}{4v^{2}s_{\beta}c_{\beta}}\Big{\{}(4M^{2}-2m_{A}^{2}-3m_{h}^{2})c_{\alpha+\beta}+(2m_{A}^{2}-m_{h}^{2})c_{\alpha-3\beta}\Big{\}}$

(10)

and the decay width is given as

$\displaystyle\Gamma(h\to AA)=\frac{\lambda_{hAA}^{2}v^{2}}{32\pi m_{h}}\sqrt{1-\frac{4m_{A}^{2}}{m_{h}^{2}}}$

(11)

where $M^{2}=m^{2}_{12}/s_{\beta}c_{\beta}$. This trilinear coupling $\lambda_{hAA}$ is non vanishing even at the alignment limit $s_{\beta-\alpha}\to 1$.

$\displaystyle\lambda_{hAA}$

$\displaystyle=$

$\displaystyle\frac{1}{v^{2}}(2M^{2}-2m_{A}^{2}-m_{h}^{2}),\quad\forall s_{\beta-\alpha}\to 1.$

(12)

Other trilinear couplings related to the decays of $H$ are $\lambda_{Hhh}$ and $\lambda_{HAA}$, which are given as

$\displaystyle\lambda_{Hhh}=\frac{1}{2v^{2}s_{\beta}c_{\beta}}c_{\beta-\alpha}\Big{\{}(3M^{2}-2m_{h}^{2}-m_{H}^{2})s_{2\alpha}-M^{2}s_{2\beta}\Big{\}},$

(13)

$\displaystyle\lambda_{HAA}=\frac{1}{4v^{2}s_{\beta}c_{\beta}}\Big{\{}(4M^{2}-2m_{A}^{2}-3m_{H}^{2})s_{\alpha+\beta}-(m_{H}^{2}-2m_{A}^{2})s_{\alpha-3\beta}\Big{\}}$

(14)

and in the alignment limit, $\lambda_{Hhh}$ vanishes and $\lambda_{HAA}$ reduces to

$\displaystyle\lambda_{HAA}=\frac{2}{v^{2}t_{2\beta}}(m_{H}^{2}-M^{2}).$

(15)

For light $A$, the mass splitting between $H^{\pm}$ and $H$ is highly restricted by the electroweak precision observables, as we will see later, we do not discuss the $HH^{+}H^{-}$ coupling. Thus the fermiophobic nature restricts the decay of $H$ only to the $AA$ and $AZ$ modes in the alignment limit.

In type I 2HDM, the QCD production processes of BSM Higgs bosons are usually suppressed compared to the EW processes due to the fermiophobic behaviour. Not only that, the bosonic decays (both on-shell and off-shell) of $H^{\pm}\to AW^{(*)}$ and $H\to AA/AZ^{(*)}$ can be the dominant decay modes. Since in our paper we are restricted to light $A$, the branching ratio of $A\to b\overline{b}$ is dominant even though being fermiophobic. Hence, the most promising channel to search for light $A$ is

$\displaystyle AAW:pp\to H^{\pm}A\to(AW)A\to 4b+W$

(16)

where the signal topology suggests that the prompt $A$ should have higher $p_{T}$ compared to the $A$ from the decay of $H^{\pm}$ Mondal:2023wib . To reduce the QCD multijet background we consider the leptonic decay of $W$ boson. The $4b+\ell+\cancel{\it{E}}_{T}$ would be the final state we are looking for at the LHC. The cross section of the signal at the parton level is

$\displaystyle\sigma_{AAW}=\sigma(pp\to H^{\pm}A)BR(H^{\pm}\to AW)BR(A\to b\bar{b})^{2}BR(W\to l\nu)$

(17)

where in the lepton we also include $\tau$. We use a uniform Next-to-Next-to-Leading Order (NNLO) $k$-factor of 1.35 Bahl:2021str .

The dominant background will be the top quark pair production where top quarks decay dominantly to $bW$ mode and the semileptonic and leptonic (including $\tau$) decays of $W$ boson would give at least one lepton. The extra $b$-jets can come from the additional hard jets and from the hadronic decays of $W$ boson faking as $b$-jets. Also for our analysis we generate $t\bar{t}$ background matched up to one parton using the MLM scheme Alwall:2007fs ; Hoeche:2005vzu . The cross section for the $t\bar{t}+$jets background into fully leptonic and semileptonic states is 458 pb as calculated with Top++ Czakon:2011xx . Furthermore, in the case of other backgrounds such as $Wjj$ and $Zjj$, the probability of a QCD jet being misidentified as a $b$-jet is only around $1\%$ CMS:2012feb . Hence by mimicing four $b$-jets, the $Wjj$ and $Zjj$ backgrounds can be effectively suppressed and rendered subdominant. Thus for our analysis we consider $t\bar{t}+$jets as the only background. The cross section is given by

$\displaystyle\sigma_{BG}=\sigma(pp\to t\bar{t}+jets)BR(t\to bW)^{2}BR(W\to\ell\nu)[2-BR(W\to\ell\nu)].$

(18)

Before going to the phenomenological study of our signal, we scan the parameter space with two fixed masses of $A$ viz, 50 GeV and 70 GeV. We restrict our study in the scenario of standard mass hierarchy where we assign the lightest $CP$ even Higgs $h$ as the observed 125 GeV Higgs and $H$ as the heavier $CP$-even Higgs. The model parameters are scanned within the range

	$\displaystyle m_{H^{\pm}}$	$\displaystyle:$	$\displaystyle[80~{}-~{}350]~{}\text{GeV},\quad m_{H}:[140~{}-~{}350]~{}\text{GeV},\quad t_{\beta}:[1~{}-~{}60]$
	$\displaystyle s_{\beta-\alpha}$	$\displaystyle:$	$\displaystyle[0.9~{}-~{}1.0],\quad m_{12}^{2}:[0~{}-~{}350^{2}]~{}\text{GeV}^{2}.$		(19)

We randomly generate sample points within the scanning range and apply the theoretical and experimental constraints to obtain the allowed parameter space as listed below. It is worth noting that recent advances in machine learning driven sampling methods Hammad:2022wpq can greatly reduce the computational time of such scans.

1. 1.

   Theoretical Constraints: The quartic couplings of the scalar potential should be $|\lambda_{i}|<4\pi$ Chang:2015goa to satisfy the perturbativity condition. The vacuum stability requires the potential to be bounded from below and this gives us the constraints PhysRevD.18.2574

   $\displaystyle\lambda_{1,2}>0,\quad\lambda_{3}>-\sqrt{\lambda_{1}\lambda_{2}},\quad\lambda_{3}+\lambda_{4}-|\lambda_{5}|>-\sqrt{\lambda_{1}\lambda_{2}}.$

   (20)

   The tree-level unitarity of the Higgs boson and gauge boson scatterings at high energy as discussed in Kanemura:1993hm ; Akeroyd:2000wc are also considered. The theoretical constraints are computed using the public code 2HDMC-1.8.0 Eriksson:2009ws .

2. 2.

   Electroweak Precision Observables: The measurement of the oblique parameters, $S,~{}T$ and $U$ restricts the mass splitting between the BSM Higgs bosons in the 2HDM, particularly between the charged Higgs $H^{\pm}$ and the other BSM neutral Higgs bosons ($H,A$). The current best fit results 10.1093/ptep/ptac097 at $95\%$ C.L. are $S=-0.01\pm 0.07$ and $T=0.04\pm 0.06$ with the correlation $\rho_{ST}=0.92$ for $U=0$. For the scenario of light $A$, the mass splitting between $H^{\pm}$ and $H$ gets restricted. We use 2HDMC for the computation of the oblique parameters based on the Refs.Grimus:2007if ; Grimus:2008nb .

3. 3.

   Flavor Physics Constraints: The $B$-physics observables are calculated using the code SuperIso-v4.1 Mahmoudi:2008tp . The limits on $B\to X_{s}\gamma$ transition rate HFLAV:2016hnz ; Misiak:2017bgg excludes $t_{\beta}\lesssim 2$ at $95\%$ C.L. in the $m_{H^{\pm}}-t_{\beta}$ plane Misiak:2017bgg ; Sanyal:2019xcp for type I 2HDM, thus reflecting the fermiophobic behaviour of $H^{\pm}$ with respect to $t_{\beta}$.

4. 4.

   Collider Constraints: The exclusion limits for the direct Higgs boson searches at LEP, Tevatron and LHC at $95\%$ C.L. are imposed by using the public code HiggsBounds-v5.10.2 Bechtle:2020pkv . Along with the direct searches, we also check the consistency of the Higgs precision measurements using the code HiggsSignals-v2.6.2 Bechtle:2020uwn . We find the allowed parameter points at $95\%$ C.L. with respect to the best fit point in two dimensional parameter spaces, which corresponds to $\Delta\chi^{2}_{\text{HS}}=\chi^{2}_{\text{HS}}-\chi^{2}_{\text{HS,min}}\lesssim 6$. The $\chi^{2}_{\text{HS,min}}$ for the best fit points of $m_{A}$ = 50 GeV and 70 GeV cases are approximately 92 and 90 respectively.

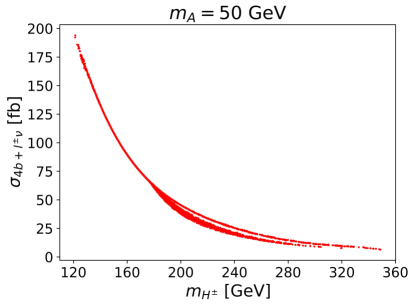
After imposing all the constraints we obtain the allowed parameter space, for which we compute the parton level cross sections for the signal [16], considering the leptonic decay of $W$ boson as shown in Fig.[1]. For $m_{A}=50$ GeV, $h\to AA$ decay is allowed. The constraints from the SM Higgs exotic decay includes $h\to AA\to bbbb$ ATLAS ATLAS:2018pvw , $h\to AA\to bb\tau\tau$ CMS CMS:2018zvv , $h\to AA\to bb\mu\mu$ ATLAS ATLAS:2018emt CMS CMS:2017dmg ; CMS:2018nsh , $h\to AA\to\tau\tau\tau\tau$ CMS CMS:2017dmg , $h\to AA\to\tau\tau\mu\mu$ CMS CMS:2017dmg ; CMS:2018qvj . Along with these, strong constraints also come from the precisely measured Higgs decay width CMS:2022dwd ; CMS:2019ekd ; CMS:2022ley ; ATLAS:2023dnm , thus restricting the Higgs trilinear coupling, $|\lambda_{hAA}|\lesssim 0.013$. To study the discovery prospects of the signal at the LHC, we proceed our analysis with some benchmark points (BPs) as given in Table. [2].