Probing Mixed Valence States by Nuclear Spin-Spin Relaxation Time Measurements

Y. Ihara [email protected] M. Shimohashi Department of Physics, Faculty of Science, Hokkaido University, Sapporo 060-0810, Japan M. Kriener [email protected] RIKEN Center for Emergent Matter Science (CEMS), Wako 351-0198, Japan

Abstract

Several elements in the periodic table exhibit an interesting and often overlooked feature: They skip certain valence states which is discussed in the field of superconductivity to be in favor of fostering higher transition temperatures $T_{c}$ . However, from the experimental point of view, it is often deemed difficult to probe changes in the valence state. Here we demonstrate that the latter are accessible by the spin-spin relaxation rate $1/T_{2}$ in nuclear magnetic resonance. As target material, we chose the solid solution Ge ${}_{1-x}$ In ${}_{x}$ Te, where valence-skipping In induces superconductivity and changes its valence state as a function of $x$ . We observe a strong enhancement in $1/T_{2}(x)$ and, most importantly, find that $1/T_{2}$ and $T_{c}$ exhibit a strikingly similar $x$ dependence. These results underline the importance of valence physics for the evolution of superconductivity in Ge ${}_{1-x}$ In ${}_{x}$ Te. A model based on a Ruderman-Kittel-Kasuya-Yosida type of interaction among the In nuclei is proposed which fully accounts for the experimental results.

I Introduction

The valence-skipping degree of freedom is observed in several elements, such as Bi, Sn, In, Tl among others. As an example, in prototypical BaBiO ${}_{3}$ a Bi ion should take its $4+$ state which means that a single electron occupies the $6s$ shell. This situation is known to be energetically unfavorable. Therefore Bi is considered to appear as a mixture of Bi ${}^{3+}$ and Bi ${}^{5+}$ in BaBiO ${}_{3}$ and, hence, Bi ${}^{4+}$ is the skipped valence state. It was Varma [varma88a] who firstly pointed out that this feature may be responsible for the high-temperature superconductivity (transition temperature $T_{\rm c}\sim 30$ K) observed in K-doped BaBiO ${}_{3}$ [cava88a]. However, to date there is no unambiguously clear experimental evidence that valence skipping indeed supports superconductivity although quite some experimental and theoretical work on various materials has been done over the years [taraphder91a, themlin92a, taraphder95a, kazakov97a, armstrong99a, tsendin99a, dzero05a, matsushita05a, hase08a, ren13a, strand14a, sleight15a, plumb16a, hase16a, hase17a, wakita17a, kataria23a]. Apparently, one obstacle is the difficulty to capture the changes in the valence state as a function of an external parameter such as doping. Among the methods employed are photoemission spectroscopy (PES), x-ray emission spectroscopy, Mößbauer spectroscopy, or the spin-lattice relaxation rate $1/T_{1}$ in nuclear magnetic resonance (NMR). [themlin92a, armstrong99a, mito14a, wakita17a, kriener20a, mkim21a, nakanishi24a] Since the energies of the different involved valence states are usually close to each other, the measured spectra are often broad and difficult to split quantitatively complicating their interpretation. Against this background, we propose to measure the NMR spin-spin relaxation rate $1/T_{2}$ rather than $1/T_{1}$ to study valence-state physics in solid solutions which is rather sensitive to the valence-mixing induced disorder, i.e., the degree of mixture of the different valence states. To demonstrate the strength of this technique, we chose chemically simple Ge ${}_{1-x}$ In ${}_{x}$ Te as target material which has been reported to superconduct and where In is the valence-skipping element [kriener20a, kriener22a]: When introduced into GeTe with the formal valence state Ge ${}^{2+}$ (cf. Refs. [hase16a, sleight09a] for this nomenclature), In replaces Ge ${}^{2+}$ and, hence, should also appear in the same valence state. However, In ${}^{2+}$ is energetically unstable which creates the anticipated competition of its monovalent and trivalent states.

In Ref. [kriener20a], it is argued that initially trivalent In enters GeTe. In starts to appear also in its monovalent state when traversing $x\sim 0.12$ and the majority of the dopants becomes monovalent at intermediate $x\sim 0.4$ . The authors also propose a phenomenological model based on this valence-state change which successfully accounts for all experimentally observed features. A brief summary of the impact of In doping into the polar semiconductor GeTe can be found in Section S1 of the accompanying Supplemental Materials (SM) [Suppl].

The motivation of the present work is to test and further elucidate the valence-skipping scenario proposed in the literature by a different and complementary approach. Here we present a comprehensive ${}^{115}$ In-NMR study on polycrystalline samples Ge ${}_{1-x}$ In ${}_{x}$ Te with $0<x\leq 1$ . We find a step-like change of the nuclear quadrupole resonance (NQR) frequency $\nu_{z}$ when traversing $x\sim 0.4$ which coincides with a shift of the peak position in PES data on this system reported in [kriener20a]. Concomitantly, the nuclear spin-spin relaxation rate $1/T_{2}$ is strongly enhanced which is explained as indicative of the anticipated change in the In valence state. Based on these data, we propose a Ruderman-Kittel-Kasuya-Yosida (RKKY)-type interaction model among the In nuclear spins through the conduction electrons at $E_{\rm F}$ which accounts for the observed changes in $1/T_{2}$ . The most important result of this work is that $1/T_{2}$ and $T_{\rm c}$ exhibit a strikingly similar $x$ dependence underlining the sensitivity and significance of $1/T_{2}$ measurements in valence-skipping materials. Moreover, this observation implies a close relationship between these two quantities and suggests that in Ge ${}_{1-x}$ In ${}_{x}$ Te the valence degree of freedom may be indeed one driving force for the observed enhancement of the superconducting $T_{\rm c}$ with $x$ .

II Methods

II.1 Sample growth and characterization

The Ge ${}_{1-x}$ In ${}_{x}$ Te batches were synthesized by conventional melt growth of stoichiometric mixtures of GeTe and InTe in evacuated quartz glass tubes. These were fired for 48 – 72 h at 950 ${}^{\circ}$ C and then quenched into water. For the batch with $x=0.08$ , x-ray diffraction (XRD) data confirmed the rhombohedral $\alpha$ -GeTe structure (space group $R3m$ ). For all other batches with $0.25\leq x\leq 1$ , XRD data of the obtained material indicates traces of the ambient-condition tetragonal InTe structure whose volume fraction quickly increases with $x$ . To obtain superconducting cubic material, approximately 400 mg of each prereacted batch were treated in a second growth step in which a high-pressure synthesis method was employed (5 GPa, 600 – 1300 ${}^{\circ}$ C), cf. Ref. [kriener20a] for the details. The unit-cell volume shown in Fig. 1(b) was extracted from the XRD data taken on each final batch. We note that the lifetime of the metastable cubic structure is more than one year for samples containing Ge and In [kriener20a] and several months for pristine InTe [banus63a]. To ensure the superconductivity, the $T_{c}$ value for $x=1$ was confirmed before and after the NMR experiment.

On selected batches the chemical composition was checked by energy-dispersive x-ray analysis. It was found that the actual In concentration fits to the nominal one with the difference between them slightly increasing for $x\rightarrow 1$ , cf. the discussion in Ref. [kriener20a]. In the present work, the nominal composition is used when referring to a sample.

II.2 Measurements

The superconductivity of the batches with $0.25\leq x\leq 1$ was confirmed by temperature $T$ dependent magnetization $M(T)$ measurements in a Quantum Design magnetic property measurement system (MPMS3) equipped with a ${}^{3}$ He refrigerator on samples cut into a well-defined geometry. Each sample was cooled down in zero magnetic field to the base temperature and $M(T)$ subsequently measured upon increasing temperature in an applied magnetic field $B=1$ mT. The linear part of the magnetization below the transition was extrapolated and its intercept with the temperature axis defined as the superconducting $T_{\rm c}$ . The obtained $T_{\rm c}$ values fit well to the published data in Ref. [kriener20a].

The field-sweep NMR spectra were obtained by recording the fast-Fourier-transformed NMR intensity during magnetic field ( $\mu_{0}H$ ) sweeps. The NMR frequency was fixed to 41.51 MHz which corresponds to the reference field $\mu_{0}H_{\rm ref}\approx 4.4$ T [commentRefField]. For the spin-echo pulse sequence, we utilized a shaped pulse to uniformly irradiate the radio-frequency field within the specified bandwidth of 400 kHz. [ihara21a] The measurement procedure of the spin-spin relaxation rate $1/T_{2}$ is described in detail in Section S4 in the accompanying SM [Suppl].

III Results

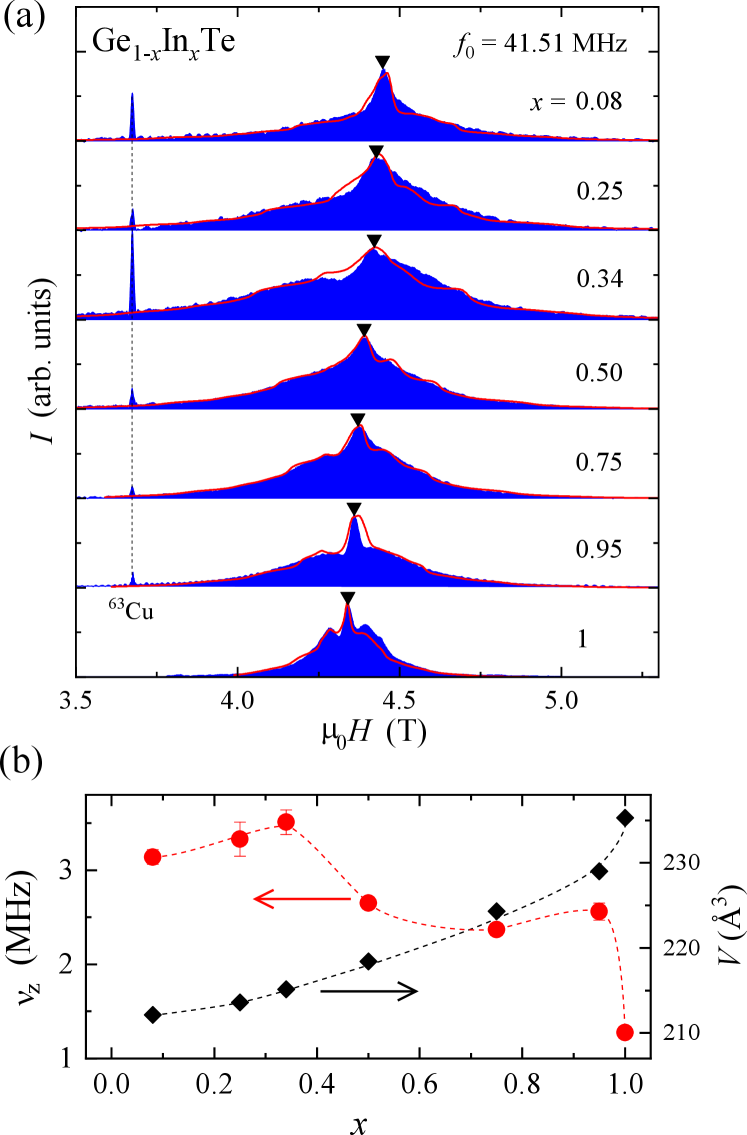
Refer to caption — Figure 1: (a) ${}^{115}$ In-NMR spectra of Ge ${}_{1-x}$ In ${}_{x}$ Te on different samples taken at $T=4.2$ K ( $0.08\leq x\leq 0.95$ ) and at $T=1.6$ K ( $x=1$ ). We note that the spectral shape does not exhibit any temperature dependence below 10 K. The spectra are vertically shifted for clarity. The black triangles highlight the central peak positions and red curves are fits of the spectral shapes, see text. The peaks at $\mu_{0}H\sim 3.7$ T in the data for $x<1$ are due to the Cu coil used in the NMR experiments. In the measurement of $x=1$ the narrower spectrum allowed to limit the field range to $3.8\leq\mu_{0}H\leq 5.0$ T explaining the absence of the Cu peak. (b) Extracted nuclear quadrupole resonance frequencies $\nu_{z}$ ( $x$ ) (red filled circles; left coordinate axis) and unit cell volume $V$ (black diamonds; right axis). The dashed lines are guides to the eyes.

Figure 1(a) summarizes ${}^{115}$ In-NMR spectra of Ge ${}_{1-x}$ In ${}_{x}$ TeȦll spectra consist of a central peak accompanied by broad tails on either side. The peak position evolves almost linearly with $x$ , shifting toward slightly smaller fields as indicated by triangle symbols in Fig. 1(a).

These NMR spectral shapes are understood as powder patterns for the ${}^{115}$ In nuclear spin $I=9/2$ with allowing some asymmetry as follows: The nuclear spin Hamiltonian is given by the sum of the Zeeman and the electric quadrupolar interactions [abragam83]:

\mathcal{H}=-\gamma\hbar(1+K)\mu_{0}\bm{H}_{0}\cdot\bm{I}+\frac{\nu_{z}}{6}\left[\left(3I_{z}^{2}-\bm{I}^{2}\right)+\frac{1}{2}\eta\left(I_{+}^{2}+I_{-}^{2}\right)\right].

Here, $\gamma$ is the gyromagnetic ratio [commentRefField], $K$ is the Knight shift along the given orientation of the external field $\mu_{0}\bm{H_{0}$},$ η $representstheasymmetryoftheelectricfieldgradient(EFG)tensoraroundeachInnuclearspin$ I $,and$ ℏ $thereducedPlanckconstant.Theoverallspectrumwidthisdeterminedbytheelectricquadrupolarinteraction,namelytheNQRfrequency$ ν_z $.ThisfrequencyisproportionaltothelargestEFGfoundalongoneofthethreeprincipalaxesoftheEFGtensor\cite[cite]{[\@@bibref{Number}{abragam83}{}{}]}.The$ ^115 $In-NMRspectra[Fig.~{}\ref{fig1}(a)]exhibitaslightbroadeningatintermediatedoping,suggestingasystematicvariationof$ ν_z $asafunctionof$ x $.Tofurtheranalyzethis,wefittedeachpowderpatternbyoptimizingtheparameters$ ν_z,η $,and$ K $.TheresultsareshownasredcurvesinFig.~{}\ref{fig1}(a)describingthedatareasonablywell;cf.\ alsoSection~{}S2in\cite[cite]{[\@@bibref{Number}{Suppl}{}{}]}.Wenotethatthefinite$ η= 0.3 ±0.1 $deducedfromourfittingsexhibitsonlyaweak$ x $dependence.\par Figure~{}\ref{fig1}(b)(leftaxis)shows\nu_{z}\ extractedforeach$ x $.Initially,\nu_{z}\ increaseswith$ x $.Thelargestvalueof\nu_{z}\ isfoundforthesamplewith$ x=0.34 $.Toward$ x = 0.5 $,\nu_{z}\ isstronglysuppressedandremainsroughlyconstantaboveexceptfor$ x=1 $,forwhichanotherabruptdecreaseof\nu_{z}\ isobserved.Tounderstandthe$ x $dependenceof\nu_{z},onehastokeepinmindthattheEFGattheInsitesismainlydeterminedbytwodifferentfactors:(i)thecrystal-latticecontributionsfromtheionssurroundinganInsiteand(ii)thecontributionsduetointeractionsbetweenchargecarriersandnuclearInspins.Theformer,whichshouldbezerowhenanInionexperiencesperfectcubicsymmetry,iscausedbylocaldistortionsbreakingthecubicsymmetryaroundanIndopantwhenreplacingaGeion.Hence,theInionsthemselvescreatetheEFGduetotheirdifferentpointchargesascomparedtoGe.Inthepresentcase,thiscontributionisexpectedtoleadtoamonotonicsuppressionof\nu_{z}\ with$ x $becausethecrystallatticeofGe$ _1-x $In$ _x $Te\ expandsmonotonicallyasafunctionof$ x $upto$ x = 1 $,asshowninFig.~{}\ref{fig1}(b)(rightaxis):TheincreasingdistancebetweenneighboringionsincreaseswhichinturnweakensthelatticeEFGs.ForpristineInTewithanidealcubicstructure,contributionsfromthelatticeEFGareexpectedtovanish.Hence,theobservednonmonotonic$ x $dependenceof$ ν_z $anditsfinitevaluefor$ x=1 $implythattheinteractionsbetweenthenuclearspinsandthechargecarriersproduceasizablecontributiontotheEFG,andthus,dominate$ ν_z(x) $.\par Interestingly,thestrongsuppressionof$ $\nu_{z}$ (x) $across$ x≥0.34 $coincideswithachangeofthepeakenergyinIn-3$ d_5/2 $core-levelPESdatareportedinRef.~{}\cite[cite]{[\@@bibref{Number}{kriener20a}{}{}]}.Therein,thischangewasattributedtoacrossoverinthemajorityvalencestateoftheInionsfromtrivalenttomonovalentsuggestingthatthesuppressionin$ $\nu_{z}$ (x) $h a s t h e s a m e o r i g i n . H o w e v e r, t h e s p e c t r o s c o p i c a p p r o a c h u s u a l l y y i e l d s i n t r i n s i c a l l y b r o a d s p e c t r a c o m p l i c a t i n g t h e d i s t i n c t i o n o f t h e i n v o l v e d m i x e d v a l e n c e s t a t e s . Figure 2Figure 22Figure 22(a)Sketchofs$