Probing Lorentz-Invariance-Violation Induced Nonthermal Unruh Effect in Quasi-Two-Dimensional Dipolar Condensates

Introduction.— One of the surprising fundamental consequences of relativistic quantum field theory is that the concept of particle number is observer dependent. A prominent paradigm is the so-called Unruh effect Unruh (1976): In the view of an uniformly accelerating observer, the Fock vacuum state of quantum field in the Minkowski spacetime appears as a thermal state rather than a zero-particle state. The corresponding characteristic temperature is proportional to the observer’s acceleration $a$, given by $k_{\text{B}}T_{\text{U}}=\frac{\hbar\,a}{2\pi\,c}$. To produce a measurable temperature for fundamental quantum fields, extremely huge accelerations are required (e.g., smaller than $1\,\mathrm{Kelvin}$ even for accelerations as high as $10^{20}\,\mathrm{m/s^{2}}$), and thus until now, the direct experimental confirmation of the Unruh effect still remains elusive.

Analogue gravity Unruh (1981); Barceló et al. (2011) opens up a new route to study various phenomenas predicted by relativistic quantum field theory, e.g., Hawking effect Garay et al. (2000); Nation et al. (2009); Lahav et al. (2010); Garay et al. (2000); Steinhauer (2014); Weinfurtner et al. (2011); Horstmann et al. (2010); Euvé et al. (2016); Steinhauer (2016); Roldán-Molina et al. (2017); Tian and Du (2019); Muñoz de Nova et al. (2019); Kolobov et al. (2021); Drori et al. (2019); Človečko et al. (2019); Kedem et al. (2020); Yang et al. (2020); Ribeiro et al. (2022); Tian et al. (2022), cosmological particle production Fedichev and Fischer (2004a); Hung et al. (2013); Prain et al. (2010); Fedichev and Fischer (2003); Alsing et al. (2005); Tian et al. (2017); Schützhold et al. (2007); Eckel et al. (2018); Lang and Schützhold (2019); Chä and Fischer (2017); Wittemer et al. (2019); Bhardwaj et al. (2021); Banik et al. (2022), and dynamical Casimir effect Johansson et al. (2009); Fujii et al. (2011); Wilson et al. (2011); Jaskula et al. (2012); Lähteenmäki et al. (2013); Macrì et al. (2018); Koghee and Wouters (2014); Dodonov (2020); Schneider et al. (2020), in a variety of electronic, acoustic, optical and even magnetic and superconducting settings. Recently, analogue gravity program for observing the Unruh effect has been successfully theoretically put forward Chen and Tajima (1999); Lochan et al. (2020); Schützhold et al. (2008); Retzker et al. (2008); Marino et al. (2020); Gooding et al. (2020); Sheng et al. (2021); Hegde et al. (2019); Zeng and Zubairy (2021); Cozzella et al. (2017); Barros et al. (2020); Guedes et al. (2019); Adjei et al. (2020), and through a BEC system Hu et al. experimentally realized the analogue Unruh effect relied on functional equivalence (i.e., simulating two-mode squeezed mechanics) Hu et al. (2019). Furthermore, in the quantum field theory, the contributions from the trans-Planckian modes as seen by an inertial observer are indispensable for deriving the Unruh effect with Bogoliubov transformation method. This particular feature makes the Unruh effect a potentially important arena for understanding and exploring implications of trans-Planckian physics Nicolini and Rinaldi (2011); Agulló et al. (2008); Hossain and Sardar (2015); Kajuri (2016); Hossain and Sardar (2016); Alkofer et al. (2016); Carballo-Rubio et al. (2019); Hammad et al. (2021); Louko and Upton (2018), and even the detecting means to probe some candidate theories of quantum gravity that may modify the trans-Planckian modes significantly. This modification usually accompanied by the breaking of Lorentz symmetry may even challenge the equivalence between Unruh effect and Hawking effect since the latter appears to be robust to high energy modifications of the dispersion relation Unruh (1995) while the former is not so immune and will lose its conventional thermal interpretation Nicolini and Rinaldi (2011); Agulló et al. (2008); Hossain and Sardar (2015, 2016); Carballo-Rubio et al. (2019) (see more details in the following). It is thus of great interest to experimentally investigate the consequences of trans-Planckian physics in a microscopically well-understood setup in a regime, that is inaccessible for quantum fields in real relativistic scenarios.

In this paper, we propose to study the interplay between the Unruh effect and trans-Planckian physics with an experimentally accessible platform consisting of a dipolar BEC Baranov (2008) and an immersed impurity Recati et al. (2005); Fedichev and Fischer (2003). From the perspective of analog, the density fluctuations in the condensate possessing trans-Planckian spectra leading to strong departures from Lorentz invariance Fischer (2006); Chä and Fischer (2017); Tian et al. (2018), resemble Lorentz-violating quantum field (LVQF), while the impurity, analogously dipole coupled to the density fluctuations, is modeled as an Unruh-DeWitt detector coupled to the LVQF. We will show that for the Lorentz-invariant (LI) spectrum the Unruh-DeWitt detector for an accelerated circular path indeed experiences a similar thermal response, while yields significant changes of this standard thermal feature when the spectra strongly deviate from Lorentz invariance. As far as we know, this represents the first example within analogue gravity where Unruh effect without thermality caused by the breaking of Lorentz symmetry can become experimentally manifest.

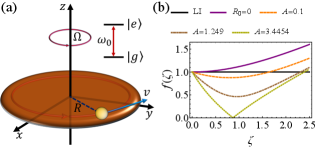
Lorentz-violating quantum field and analogue Unruh-DeWitt detector in dipolar BEC.— As schematically shown in Fig. 1, we establish the connection between an impurity immersed in a quasi-two-dimensional (quasi-2D) dipolar BEC with the Unruh-DeWitt detector model Unruh (1976); Birrell and Davies , inspired by the seminal atomic quantum dot idea introduced in Refs. Recati et al. (2005); Fedichev and Fischer (2003, 2004b).

We begin with the Lagrangian density of an interacting Bose gas comprising atoms or molecules of mass $m$,

where $\mathbf{R}=(\mathbf{r},z)$ are spatial 3D coordinates. The interaction reads $V_{\text{int}}(\mathbf{R}-\mathbf{R}^{\prime})=g_{c}\delta^{3}(\mathbf{R}-\mathbf{R}^{\prime})+3g_{d}\{[1-3(z-z^{\prime})^{2}/|\mathbf{R}-\mathbf{R}^{\prime}|^{2}]/|\mathbf{R}-\mathbf{R}^{\prime}|^{3}\}/4\pi$, where $g_{c}=4\pi\hbar^{2}a_{c}/m_{B}$ represents the contact interaction strength, with $a_{c}$ being the $s$-wave scattering length; the dipole-dipole interaction (DDI) strength $g_{d}=\mu_{0}\mu_{m}^{2}/3$, with $\mu_{0}$ and $\mu_{m}$ being the permeability of vacuum and the magnetic dipole moment that is polarized to the $z$ direction, respectively. Moreover, the gas is trapped by an external potential, $V_{\text{ext}}(\mathbf{R})=m_{B}\omega^{2}\mathbf{r}^{2}/2+m_{B}\omega^{2}_{z}z^{2}/2$, and is strongly confined along the $z$ axis, with aspect ratio $\kappa=\omega_{z}/\omega\gg 1$ over the whole time evolution. As a result of that, the motion of the Bose gas along the $z$ axis is frozen to the ground state with a Gaussian form, $\rho_{z}(z)=(\pi\,d^{2}_{z})^{-1/2}\exp[-z^{2}/d^{2}_{z}]$, with $d_{z}=\sqrt{\hbar/m_{B}\omega_{z}}$. Therefore, the whole system effectively reduces to a quasi-2D one which can ensure stability in the DDI-dominated regime Fischer (2006). Finally, we may assume that the Bose gas is condensed to the zero-momentum state with an area density $\rho_{0}$.

Within the Bogoliubov theory of small excitations on top of the condensate Pethick and Smith (2008); Pitaevskiĭ and Stringari (2016), density fluctuations in Heisenberg representation can be written as $\delta\hat{\rho}(t,\mathbf{r})=\sqrt{\rho_{0}}\int[d^{2}\mathbf{k}/(2\pi)^{2}](u_{\mathbf{k}}+v_{\mathbf{k}})[\hat{b}_{\mathbf{k}}(t)e^{i\mathbf{k}\cdot\mathbf{r}}+\hat{b}^{\dagger}_{\mathbf{k}}(t)e^{-i\mathbf{k}\cdot\mathbf{r}}]$ which closely resemble the quantum field in terms of bosonic operators $\hat{b}_{\mathbf{k}}(t)=\hat{b}_{\mathbf{k}}\,e^{-i\omega_{\mathbf{k}}\,t}$, satisfying the usual Bose commutation rules $[\hat{b}_{\mathbf{k}},\hat{b}_{\mathbf{k}^{\prime}}^{\dagger}]=(2\pi)^{2}\delta^{2}(\mathbf{k}-\mathbf{k}^{\prime})$. Note that $u_{\mathbf{k}}=(\sqrt{\mathcal{H}_{\mathbf{k}}}+\sqrt{\mathcal{H}_{\mathbf{k}}+2\mathcal{A}_{\mathbf{k}}})/2(\mathcal{H}^{2}_{\mathbf{k}}+2\mathcal{H}_{\mathbf{k}}\mathcal{A}_{\mathbf{k}})^{1/4}$ and $v_{\mathbf{k}}=(\sqrt{\mathcal{H}_{\mathbf{k}}}-\sqrt{\mathcal{H}_{\mathbf{k}}+2\mathcal{A}_{\mathbf{k}}})/2(\mathcal{H}^{2}_{\mathbf{k}}+2\mathcal{H}_{\mathbf{k}}\mathcal{A}_{\mathbf{k}})^{1/4}$ are Bogoliubov parameters, and the quasiparticle frequency $\omega_{\mathbf{k}}=\sqrt{\mathcal{H}^{2}_{\mathbf{k}}+2\mathcal{H}_{\mathbf{k}}\mathcal{A}_{\mathbf{k}}}$ with $\mathcal{H}_{\mathbf{k}}=k^{2}/2m$ and $\mathcal{A}_{\mathbf{k}}=\rho_{0}V^{\text{2D}}_{\text{int, 0}}(k)$ Tian et al. (2018). Here $k=|\mathbf{k}|$ and the Fourier transformation of DDI $V^{\text{2D}}_{\text{int, 0}}(k)=g^{\text{eff}}_{0}(1-\frac{3R_{0}}{2}kd_{z}w[\frac{kd_{z}}{\sqrt{2}}])$, with $w[x]=\exp[x^{2}](1-\operatorname{erf}[x])$, an effective contact coupling $g^{\text{eff}}_{0}=\frac{1}{\sqrt{2\pi}d_{z}}(g_{c}+2g_{d})$, and the dimensionless ratio $R_{0}=\sqrt{\pi/2}/(1+g_{c}/2g_{d})$. The parameter $R_{0}$ could be tunable via Feshbach resonance Courteille et al. (1998); Inouye et al. (1998); Chin et al. (2010); Timmermans et al. (1999) and rotating polarizing field Giovanazzi et al. (2002); Tang et al. (2018), ranging from $R_{0}=0$ (when $g_{d}/g_{c}\rightarrow 0$, i.e., contact dominance), to $R_{0}=\sqrt{\pi/2}$ (when $g_{d}/g_{c}\rightarrow\infty$, i.e., DDI dominance).

The density fluctuations described above closely resemble a LVQF with a explicit dispersion relation given by

where $\zeta=\hbar\,c_{0}k/M_{\ast}$, $c_{0}=\sqrt{g^{\text{eff}}_{0}\rho_{0}/m_{B}}$ is the speed of sound, $A=g^{\text{eff}}_{0}\rho_{0}/\hbar\omega_{z}$ represents the effective chemical potential as measured relative to the transverse trapping, and $M_{\ast}=m_{B}c^{2}_{0}$ is the analog energy scale of Lorentz violation. This dispersion relation (2) is approximately Lorentz invariant $(f(\zeta)\simeq 1)$ for $\zeta\ll 1$. By appropriately setting the relevant parameters $A$ and $R_{0}$, the dispersion could be analogously superluminal $(f(\zeta)>1)$ and subluminal $(f(\zeta)<1)$. In Fig. 1, we plot the function $f(\zeta)$ shown in (2) to see how the Lorentz invariance is violated in this dispersion. For the DDI dominance, $R_{0}=\sqrt{\pi/2}$, the analogous subluminal spectrum develops a roton minimum for sufficiently large $A$, and the Lorentz invariance is strongly broken near $\zeta\simeq 0.9$ Tian et al. (2018).

In order to probe the analogue LVQF in the dipolar BEC, we use an impurity as the analogue Unruh-DeWitt detector, which consists of a two-level atom ($1$ and $2$) and its motion is supposed to be externally imposed by a tightly confining and relatively moving trap potential, so that its only degrees of freedom are the internal ones. Furthermore, the impurity is assumed to be controlled by a driving of a monochromatic external electromagnetic field at the frequency $\omega_{L}$ close to resonance with $1\rightarrow 2$ transition $\omega\simeq\omega_{21}$, with a Rabi frequency $\omega_{0}$. Then the Hamiltonian of the whole system can be written as

where the last term denotes the collisional coupling between the impurity and Bose gas, and $\hat{\rho}(\mathbf{r}_{A})=\hat{\psi}^{\dagger}(\mathbf{r}_{A})\hat{\psi}(\mathbf{r}_{A})\simeq\rho_{0}+\delta\hat{\rho}(\mathbf{r}_{A})$ represents the field density operator of the Bose gas with $\mathbf{r}_{A}(t)$ being the time-dependent position of the impurity.

In the rotated $|g,e\rangle=(|1\rangle\pm 2\rangle)/\sqrt{2}$ basis, the Rabi frequency $\omega_{0}$ determines the splitting between the $|g,e\rangle$ states, while the detuning $\delta=\omega_{L}-\omega_{21}$ gives a coupling terms. In such case, the impurity immersed in the condensate is collisionally coupled to the Bose gas via two channels Marino et al. (2017, 2020); Tian and Du (2021): The first term resembles the interaction of a static charge to an external scalar potential and can be canceled through proper tuning of the interaction constants $g_{1,2}$ (e.g., via Feshbach resonance Courteille et al. (1998); Inouye et al. (1998); Chin et al. (2010); Timmermans et al. (1999)), while the second term resembles a standard electric-dipole coupling. Choosing proper detuning $\delta$ to exactly compensate the coupling to the average density, we can finally find the impurity-fluctuations interaction Hamiltonian

reproducing the usual Unruh-DeWitt detector-field interaction with $g_{-}=(g_{1}-g_{2})/2$ satisfying $\hbar\delta/2+g_{-}\rho_{0}=0$. However, here the LVQF is coupled to the detector.

Note that when $\zeta=\hbar\,c_{0}k/M_{\ast}\ll 1$ the density fluctuations resemble massless scalar field with spectrum, $\omega_{\mathbf{k}}\simeq\,c_{0}k$, the linearly moving impurity remains unexcited when its velocity satisfying $v<c_{0}$ , while behaves dramatically differently when moving at a supersonic speed $v\gtrsim\,c_{0}$. Specifically, although the “charge neutrality” of the impurity rules out Bogoliubov-Cherenkov emission Carusotto et al. (2006); Astrakharchik and Pitaevskii (2004), the anomalous Doppler effect may induce it to be excited from its ground state while emitting Bogoliubov phonon and still conserving energy. This is the analogue Ginzburg emission for superluminal moving particles Ginzburg and Frolov (1986); Ginzburg (1996), occurring in BEC. When the spectrum breaks the Lorentz symmetry satisfying $\omega_{\mathbf{k}}=c_{0}kf(\zeta)$: If $0<f(\zeta)<1$ for an interval of $\zeta$, the impurity would get excited when its velocity exceeds the critical $v_{c}=c_{0}f_{c}(\zeta)$ with $f_{c}(\zeta)=\inf\,f(\zeta)$ Tian and Du (2021). This particular property provides us a potential effective tool to constrain on the possible families of modified dispersion relations with the experimental results of the Relativistic Heavy Ion Collider Husain and Louko (2016). We will in the following consider a circularly moving impurity to observer the circular Unruh effect Bell and Leinaas (1983, 1987); Unruh (1998), and in particular examine whether the circular Unruh effect is robust to the breaking of Lorentz symmetry.

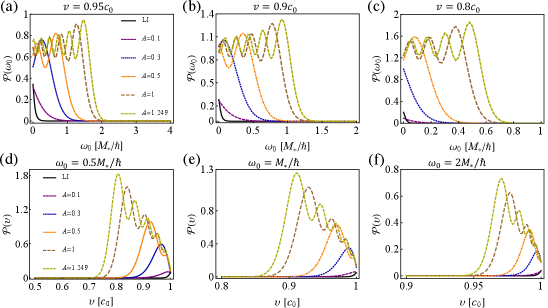
Spontaneous excitation of the circularly moving detector.— If the detector moves with a circular trajectory $(c_{0}t(\tau),{\bf x}(\tau))=(c_{0}\gamma\tau,R\cos(\Omega\gamma\tau),R\sin(\Omega\gamma\tau),0)$, with constant radius $R$, the angular velocity $\Omega$, the usual relativistic factor $\gamma=1/\sqrt{1-R^{2}\Omega^{2}/c^{2}_{0}}$, and the corresponding acceleration $a=\Omega^{2}\gamma^{2}R$, we find the transition rate of the detector from its ground state to excited state Sup

where $\tilde{M}=RM_{\ast}/\hbar\,c_{0}$, $\tilde{E}=R\omega_{0}/c_{0}$, and $v=R\Omega/c_{0}$ are dimensionless parameters. Note that we focus on the detector’s speed in the preferred Lorentz frame satisfying $0\leq\,v<1$.

For the LI scenario where $R_{0}=0$ and $\omega_{\mathbf{k}}=c_{0}k\sqrt{1+\zeta^{2}/4}\approx\,c_{0}k$ for $k\ll\,k_{c}=M_{\ast}/c_{0}\hbar$, we find in the ultrarelativistic limit, $\gamma\gg 1$, the equilibrium population of the upper level relative to the lower is Sup

when the energy splitting of the detector is not too small $\omega_{0}\gg\,a/c_{0}$ Bell and Leinaas (1983), which leads to an effective temperature

This temperature is higher by a factor $\sqrt{5/6}\pi$ than the Unruh temperature for the linear acceleration, and higher by a factor $\sqrt{5/2}$ than the Unruh temperature for the real massless scalar field case as a result of the Bogoliubov transformation for the quasiparticles.

If $(\zeta\,f(\zeta))^{\prime}>0$, we can find in the limit, $\tilde{M}\rightarrow\infty$, the transition rate (5) behaves quite differently for $0<v<f_{c}$ and $f_{c}<v<1$, where $f_{c}=f(\zeta_{c})$ is a global minimum at $\zeta=\zeta_{c}>0$. Specifically, for the former, the transition rate ${\cal P}(\omega_{0})\rightarrow{\cal P}_{0}(\omega_{0})$, given by

where $\Gamma_{0}=\frac{g^{2}_{-}\rho_{0}}{2\hbar\,M_{\ast}\,R^{2}}$. Note this is the response for the analogue massless scalar field, and thus no low-energy Lorentz violation can been seen when $v<f_{c}$. While for the latter there is a correction to the former case, ${\cal P}(\omega_{0})\rightarrow{\cal P}_{0}(\omega_{0})+\Delta{\cal P}$, with

where $\zeta_{-}\in(0,\zeta_{c})$ and $\zeta_{+}\in(\zeta_{c},\infty)$ are unique solutions to $f(\zeta)=v$ in the respective intervals. This correction means the detector sees a low-energy Lorentz violation when $v>f_{c}$, and alternatively the departure from the standard prediction of Unruh effect appears as a consequence of the Lorentz violation.

Experimental implementation.— Recent experimental advances have allowed for groundbreaking observations of strongly dipolar BEC, its excitation spectrum displaying roton minimum, and dynamics of impurity immersed in BEC Lu et al. (2011); Aikawa et al. (2012); Norcia et al. (2021); Chomaz et al. (2018); Petter et al. (2019); Schmidt et al. (2021); Natale et al. (2019); Hertkorn et al. (2021); Tomza et al. (2019); Weckesser et al. (2021); Skou et al. (2021); Dieterle et al. (2021). These experiments hold promise to realize our experimental scenario proposed above. Specifically, we can consider a single ${}^{87}\mathrm{Rb}$ atom immersed in a BEC of $\mathrm{Dy}$ atom Lu et al. (2011); Schmidt et al. (2021); Norcia et al. (2021) which possesses a magnetic dipole moment of $10\mu_{B}$ with $\mu_{B}$ being the Bohr magneton. The condensate density is assumed to be $\rho_{0}\sim 4.4\times 10^{3}\mathrm{\mu m}^{-2}$; The observer trajectory radius $R\sim 10\mathrm{\mu m}$; A typical trap frequency $\omega_{z}=2\pi\times 10^{3}\mathrm{Hz}$, the corresponding harmonic oscillator width is $d_{z}\simeq 0.25\times 10^{-6}\mathrm{m}$. Fig. 2 displays the transition rate in (5), and clearly shows the spontaneous excitation of the detector as a result of the circular acceleration in a Minkowski vacuum. This would be viewed as the circular Unruh effect: Thermal bath is predicted for an accelerated detector moving through the inertial vacuum. In addition, the transition rates clearly show the deviation from the LI field case, occurring for strongly dipolar interactions. Specifically, when the field slightly deviates from the LI case, e.g., $A=0.1$ case, their corresponding transition rates share similar behaviors. When this deviation becomes stronger, the excitation rates increase and behave sharply differently compared with the LI case, especially in the high velocity and low energy spacing regimes. However, for the low velocity case and large energy spacing of the detector, the excitation rates change slightly in the presence of Lorentz violation (i.e., they are not so sensitive to the breaking of Lorentz symmetry), since in such cases the detector is harder to excite.

To further check whether the Unruh effect is robust to the breaking of Lorentz symmetry, we naively define the Unruh temperature $T$ to estimate the fluctuations sampled by the impurity, using the Einstein’s detailed balanced condtion,

This temperature is independent of $\omega_{0}$ for uniformly linearly accelerated detectors, given by $T_{\text{U}}=\frac{\hbar\,a}{2\pi\,k_{\text{B}}\,c}$, since whose response function satisfies the Kubo-Martin-Schwinger condition Kubo (1957); Martin and Schwinger (1959); Haag et al. (1967). For the circular acceleration cases, such definition of $T$ may depend on $\omega_{0}$, however, keeps monotonous increase via the effective acceleration parameter for the LI case Biermann et al. (2020). We here plot this temperature registered by the impurity coupled to the analogue LVQF as shown in Fig. 3. For the LI case, the temperature increases monotonously with the increase of the detector’s speed $v$ as expected. If the spectrum of the field deviates from the LI case slightly, e.g., $A=0.1$ case, the present temperature behaves similarly as the LI case but with a larger magnitude. Remarkably, when the spectra of the analogue LVQF strongly deviate from the LI spectrum, the temperature first increases with the increase of the detector’s speed and then oscillates if the detector’s speed exceeds a critical value which depends on the degree of the deviation. The counterintuitive oscillation phenomenon means that Lorentz violation may break the thermal characteristic of Unruh effect, and even cause the analogue anti-Unruh effect Brenna et al. (2016): Unruh temperature decreases with the increase of acceleration. Besides, the effective negative temperature Purcell and Pound (1951); Ramsey (1956) occurs during the oscillation, which implies that as a result of Lorentz violation, the corresponding detector’s state is characterized by an inverted occupation distribution, where excited state is populated more than ground state.

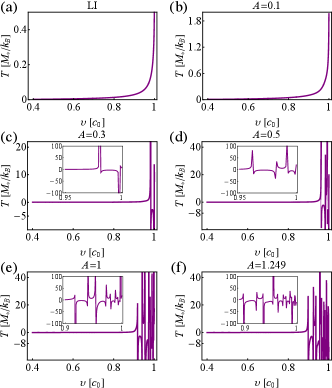
Conclusions.— We present a concrete experimental proposal to test how the Lorentz violation affects the circular Unruh effect using an impurity immersed in a dipolar BEC. We find that if the spectra of quantum field deviate from the LI case strongly, the transition rates and the predicted temperature of the analogue Unruh-DeWitt detector behave quite differently compared with the LI case, and the Lorentz violation even more may induce the counter-intuitive anti-Unruh effect on certain conditions. Our preliminary estimates indicate that the proposed experimental implementation of the analogue circular Unruh effect and its interaction with the Lorentz-breaking physics is within reach of current state-of-the-art ultracold-atom experiments.

Our proposed quantum fluid platform may also allow us in the experimentally accessible regime to explore open questions concerning Unruh effect Retzker et al. (2008), and why its robustness to high energy modifications of the dispersion relation Carballo-Rubio et al. (2019) behaves differently from that of its equivalence principle dual—Hawking effect Unruh (1995). In addition, two impurities could be used as detectors to explore correlations harvest from the quantum vacuum of analogue quantum fields Pozas-Kerstjens and Martín-Martínez (2015).

Supplementary Material