Probing Krylov Complexity in Scalar Field Theory with General Temperatures

In quantum mechanics, time evolution of an operator $\mathcal{O}$ is determined by the Heisenberg equation

$$\partial_{t}\mathcal{O}(t)=i[H,\mathcal{O}(t)],$$

(1)

where $H$ is the Hamiltonian of the system. The solution of the above equation is

$$\mathcal{O}(t)=e^{iHt}\mathcal{O}(0)e^{-iHt}.$$

(2)

where $\mathcal{O}(0)$ is the value of the operator at time $t=0$. From the well-known Baker-Campbell-Hausdorff formula wachter2011relativistic

$$e^{A}Be^{-A}=\sum_{n=0}^{\infty}\frac{1}{n!}[A^{(n)},B],$$

(3)

where $[A^{(n)},B]\equiv[\underbrace{A,\cdots,[A,[A}_{n},B]]$, the Eq.(2) can be rewritten as

$$\mathcal{O}(t)=\sum_{n=0}^{\infty}\frac{(it)^{n}}{n!}[H^{(n)},\mathcal{O}]\equiv\sum_{n=0}^{\infty}\frac{(it)^{n}}{n!}\tilde{\mathcal{O}}_{n},$$

(4)

where we have defined $\tilde{\mathcal{O}}_{n}\equiv[H^{(n)},\mathcal{O}]$ and set $\mathcal{O}\equiv\mathcal{O}(0)$. This equation describes how a “simple” operator may become increasingly “complex” as time evolves. Then one can introduce a super-operator called Liouvillian

$$\mathcal{L}:=[H,\cdot],$$

(5)

which is a linear map in the space of operators such that

$$\mathcal{L}\mathcal{O}=[H,\mathcal{O}].$$

(6)

Obviously we have

$$\mathcal{L}^{n}\mathcal{O}=\tilde{\mathcal{O}}_{n},$$

(7)

and the Eq.(2) can be reformulated as

$$\mathcal{O}(t)=\sum_{n=0}^{\infty}\frac{(it)^{n}}{n!}\mathcal{L}^{n}\mathcal{O}=e^{it\mathcal{L}}\mathcal{O}.$$

(8)

Compared to the Schrödinger’s picture of ordinary wave function, the above equation can be explained as the operator’s “wave function” expanded in some local basis of “states” $\tilde{\mathcal{O}}_{n}$ belonging to a local Hilbert space $\mathcal{H}_{\mathcal{O}}$, known as Krylov space. Formally, Eq.(8) resembles the wave function in the Schrödinger picture, with $\mathcal{L}$ playing a role as the Hamiltonian. In the following, we will use the symbol $\left|A\right)$ to represent a state in the Krylov space, i.e. $|A)\in\mathcal{H}_{\mathcal{O}}$.

Since we are interested in the effects of finite temperature, we can define the inner product in Krylov space as the Wightman inner product

$$\left(A|B\right):=\expectationvalue{e^{\beta H/2}A^{\dagger}e^{-\beta H/2}B}_{\beta}\equiv\frac{1}{\mathcal{Z}_{\beta}}\tr(e^{-\beta H/2}A^{\dagger}e^{-\beta H/2}B),$$

(9)

where $\beta$ is the inverse of the temperature $T=\beta^{-1}$ and $\mathcal{Z}_{\beta}=\tr(e^{-\beta H})$ is the thermal partition function. With the definition of the Wightman inner product, the Liouvillian $\mathcal{L}$ is Hermitian, i.e, $(A|\mathcal{L}B)=(\mathcal{L}A|B)$. Note that Eq.(8) can be considered as the expansion of $\left|\mathcal{O}(t)\right)$ in the basis $\{\mathcal{L}^{n}\left|\mathcal{O}\right)\}$, which are not necessarily orthonormal. However, we can use the Gram-Schmidt orthogonalization procedure gram1883ueber ; schmidt1907theorie to obtain a set of orthonormal basis $\{\left|\mathcal{O}_{n}\right)\}$ called the Krylov basis Parker:2018yvk . Suppose the initially given operator $\mathcal{O}$ itself is a normalized state in the Krylov space. We can define

$$\left|\mathcal{O}_{0}\right):=\left|\mathcal{O}\right).$$

(10)

Afterwards, we can continuously construct vectors that are orthonormal to the existing basis vectors to obtain the Krylov basis. ²²2Besides, we assume $\mathcal{O}$ is a Hermitian operator $\mathcal{O}^{\dagger}=\mathcal{O}$, so that it is an observable. Thus, $\left|\mathcal{O}_{1}\right)$ can be constructed as follows ³³3From the inner product Eq.(9) and Eq.(6), it is readily to get that $\left(\mathcal{O}_{0}\right|\mathcal{L}\left|\mathcal{O}_{0}\right)=0$.

$$b_{1}\left|\mathcal{O}_{1}\right)=\mathcal{L}\left|\mathcal{O}_{0}\right)-\left|\mathcal{O}_{0}\right)\left(\mathcal{O}_{0}\right|\mathcal{L}\left|\mathcal{O}_{0}\right)=\mathcal{L}\left|\mathcal{O}_{0}\right),$$

(11)

where $b_{1}:=(\mathcal{L}{\mathcal{O}_{0}}|\mathcal{L}{\mathcal{O}_{0}})^{1/2}$. For $n>1$, $\left|\mathcal{O}_{n}\right)$ can be constructed as

$$b_{n}\left|\mathcal{O}_{n}\right):=\left|A_{n}\right)=\mathcal{L}\left|\mathcal{O}_{n-1}\right)-b_{n-1}\left|\mathcal{O}_{n-2}\right),$$

(12)

where $b_{n}=(A_{n}|A_{n})^{1/2}$. The sequence $\{b_{n}\}$ is called the Lanczos coefficients. The above procedure is also known as Lanczos algorithm.

The information about the growth of the operator $\mathcal{O}(t)$ is contained in the sequence Eq.(12). We can expand $\left|\mathcal{O}(t)\right)$ in terms of Krylov basis $\{\left|\mathcal{O}_{n}\right)\}$ as

$$\left|\mathcal{O}(t)\right)=\sum_{n=0}^{\infty}\left|\mathcal{O}_{n}\right)\left(\mathcal{O}_{n}\right|\left.\mathcal{O}(t)\right)\equiv\sum_{n=0}^{\infty}i^{n}\varphi_{n}(t)\left|\mathcal{O}_{n}\right),$$

(13)

where $\varphi_{n}(t)$ are the probability amplitudes and satisfy

$$\sum_{n=0}^{\infty}\absolutevalue{\varphi_{n}(t)}^{2}=1.$$

(14)

Combined with Eq.(1), we can obtain a discrete “Schrödinger” equation

$$\partial_{t}\varphi_{n}(t)=b_{n}\varphi_{n-1}(t)-b_{n+1}\varphi_{n+1}(t).$$

(15)

According to Eq.(13), one can find that $\varphi_{n}(0)=\delta_{n,0}$ and from the recursion Eq.(15) we can define $\varphi_{-1}(t)\equiv 0$. The Krylov complexity of an operator $\mathcal{O}$ is defined as

$$K(t):=\left(\mathcal{O}(t)|n|\mathcal{O}(t)\right)=\sum_{n=0}^{\infty}n\absolutevalue{\varphi_{n}(t)}^{2}.$$

(16)

For convenience, the definition of Krylov complexity we are going to use will differ slightly from Eq.(16). In order to be consistent with the Krylov complexity in Dymarsky:2021bjq , we redefine it as

$$K(t):=1+\sum_{n=0}^{\infty}n\absolutevalue{\varphi_{n}(t)}^{2}.$$

(17)

It is worth noting that Eq.(15) links the growth of the operator with the hopping problem on a one-dimensional chain, where the Lanczos coefficients $b_{n}$ can be considered as the hopping amplitudes Parker:2018yvk . Therefore, the definition of the Krylov complexity indicates that $K(t)$ represents the average position of the wave function on the chain. Hence, the growth of the operator implies an increase in the number of $n$ that contributes to $K(t)$.

In the study of Krylov complexity, there exists a very important quantity, i.e., the autocorrelation function or thermal Wightman 2-point function,

	$\displaystyle C(t)$	$\displaystyle:=\varphi_{0}(t)\equiv(\mathcal{O}(t)\mid\mathcal{O}(0))$		(18)
		$\displaystyle\equiv\left\langle e^{i(t-i\beta/2)H}\mathcal{O}^{\dagger}(0)e^{-i(t-i\beta/2)H}\mathcal{O}(0)\right\rangle_{\beta}$
		$\displaystyle=\left\langle\mathcal{O}^{\dagger}(t-i\beta/2)\mathcal{O}(0)\right\rangle_{\beta}:=\Pi^{W}(t).$

It is not difficult to find that as long as the derivatives of the autocorrelation function at all orders are known, the Krylov complexity can also be determined. To this end, we can expand the autocorrelation function around $t=0$,

	$\displaystyle\Pi^{W}(t)$	$\displaystyle=\sum_{n=0}^{\infty}\left(\mathcal{O}\right|\frac{(-it)^{n}}{n!}\mathcal{L}^{n}\left|\mathcal{O}\right)$		(19)
		$\displaystyle=\sum_{n=0}^{\infty}\mu_{2n}\frac{(it)^{2n}}{(2n)!},$

in which we have used the facts that $(\mathcal{O}|\mathcal{L}^{p}|\mathcal{O})=0$ with $p$ an odd number. Therefore, only terms with even powers of $\mathcal{L}$ are left. In the above Eq.(19), $\{\mu_{2n}\}$ is called the moments with the expression

$$\mu_{2n}:=\left(\mathcal{O}\right|\mathcal{L}^{2n}\left|\mathcal{O}\right)=\left.\frac{1}{i^{2n}}\frac{d^{2n}}{dt^{2n}}\Pi^{W}(t)\right|_{t=0}.$$

(20)

These moments can also be obtained from the Wightman power spectrum $f^{W}(\omega)$, which is related to the Wightman 2-point function via a Fourier transformation

$$f^{W}(\omega)=\int_{-\infty}^{\infty}dte^{i\omega t}\Pi^{W}(t).$$

(21)

From Eqs.(20) and (21), the moments are related to $f^{W}(\omega)$ via

$$\mu_{2n}=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\omega^{2n}f^{W}(\omega).$$

(22)

In particular, there is a nonlinear recursive relationship between moments and Lanczos coefficients, $b_{1}^{2n}\cdots b_{n}^{2}=\det\left(\mu_{i+j}\right)_{0\leq i,j\leq n}$, where $\mu_{i+j}$ is a Hankel matrix built from the moments viswanath1994recursion . Alternatively, this expression can be reformulated in the following recursive relations,

$$\displaystyle b_{n}=\sqrt{M_{2n}^{(n)}},$$

(23)

where,

$$\displaystyle M^{(j)}_{2l}=\frac{M^{(j-1)}_{2l}}{b_{j-1}^{2}}-\frac{M^{(j-2)}_{2l-2}}{b^{2}_{j-2}},\qquad l=j,\dots,n,$$

(24)

with $M^{(0)}_{2l}=\mu_{2l},b_{-1}\equiv b_{0}:=1,M^{(-1)}_{2l}=0$.

In this subsection, we will give a brief review on the Krylov complexity in low-temperature scalar field theory based on Camargo:2022rnt . Consider a real massive scalar field $\phi$ in five-dimensional spacetime, we can write its Lagrangian in the following form

$$L_{\phi}=\frac{1}{2}(\partial_{\mu}\phi\partial^{\mu}\phi-m^{2}\phi^{2}),$$

(25)

where $\mu=0,1,2,3,4$ and $x^{0}=-i\tau$ with $\tau$ the Euclidean time. Then the Wightman power spectrum $f^{W}(\omega)$ can be obtained at the finite temperature $\beta^{-1}=T$ as,

$$f^{W}(\omega)=\tilde{N}(m,\beta)(\omega^{2}-m^{2})\Theta(\absolutevalue{\omega}-m)\bigg{/}\sinh\left(\frac{\beta|\omega|}{2}\right),$$

(26)

where the symbol $\Theta$ represents the Heaviside step function and $\tilde{N}(m,\beta)$ is the normalization factor satisfying

$$\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega{f^{W}(\omega)}=1.$$

(27)

In order to get the Krylov complexity, we need to calculate the Lanczos coefficients $b_{n}$ by solving the discrete Schrödinger equation (15). In general, this problem is not easy to do. However, it is relatively simple at low temperatures Camargo:2022rnt . It is worth noting that in finite temperature field theories, low temperature means $\beta m\gg 1$, i.e., temperature is much less than the mass of the field, rather than simply $\beta\gg 1$ Kapusta:2006pm . Therefore, even if $\beta$ is not very large, it may still be considered as low temperature if $m$ is sufficiently large. In the low temperature limit $\beta m\gg 1$, we can rewrite the Wightman power spectrum Eq.(26) as

$$f^{W}(\omega)\approx N(m,\beta)e^{-\beta\absolutevalue{\omega}/2}(\omega^{2}-m^{2})\Theta(\absolutevalue{\omega}-m),\qquad\beta m\gg 1,$$

(28)

in which we have absorbed the extra term $2$ into the normalization factor $N(m,\beta)$, i.e., $N(m,\beta)=2\tilde{N}(m,\beta)$. Using Eq.(27), $N(m,\beta)$ can be determined analytically,

$$N(m,\beta)=\frac{\pi\beta^{3}e^{\beta m/2}}{16+8\beta m},\qquad~{}\beta m\gg 1.$$

(29)

Therefore, the moments $\mu_{2n}$ in Eq.(22) can be directly computed as

$$\mu_{2n}=\frac{2^{-2}e^{\frac{\beta m}{2}}}{2+\beta m}\left(\frac{2}{\beta}\right)^{2n}\left[4\tilde{\Gamma}\left(3+2n,\frac{\beta m}{2}\right)-\beta^{2}m^{2}\tilde{\Gamma}\left(1+2n,\frac{\beta m}{2}\right)\right],$$

(30)

where $\tilde{\Gamma}(n,z)$ is the incomplete Gamma function.

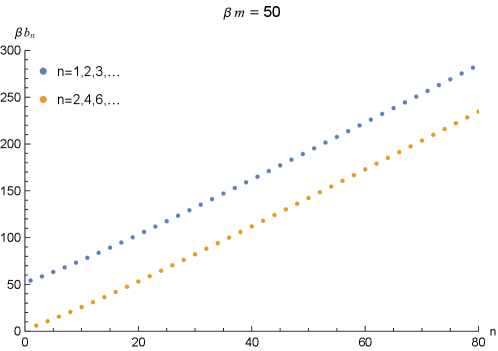
Following the non-linear recursive relation in Eqs.(23)-(24), the Lanczos coefficients $\{b_{n}\}$ can be obtained from the Eq.(30). For example, we show the behavior of the Lanczos coefficients in Figure 1 with $\beta m=50$. We see that $b_{n}$ exhibits staggering behavior, meaning that it is divided into two groups: one is with odd $n$ (blue dots) while the other is with even $n$ (brown dots). Each group is a monotonically increasing function with respect to $n$. In Camargo:2022rnt the authors also observed that the separation $\Delta b_{n}:=|b_{n}^{\rm odd}-b_{n}^{\rm even}|$ is of the order of the mass $m$.

The Krylov complexity can be computed from the auto-correlation function $\varphi_{0}(t)$ in Eq.(18) and the Lanczos coefficients by means of Eq.(15). Performing the Fourier transformation of $f^{W}(\omega)$ one can yield the auto-correlation function as

	$\displaystyle\varphi_{0}(t)$	$\displaystyle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{-i\omega t}f^{W}(\omega)$		(31)
		$\displaystyle=\frac{1}{\pi}\int_{0}^{\infty}d\omega\cos(\omega t)f^{W}(\omega)$
		$\displaystyle=\frac{\beta^{3}\left((\beta^{3}(2+\beta m)-24\beta t^{2}-16mt^{4})\cos(mt)-4t(\beta^{2}(3+\beta m)+4(\beta m-1)t^{2})\sin(mt)\right)}{(2+\beta m)(\beta^{2}+4t^{2})^{3}}.$

in which we have used the fact that $\varphi_{0}(t)$ is a real function and $f^{W}(\omega)$ is an even function of $\omega$. Afterwards, we can use the fourth Runge-Kutta method to numerically solve Eq.(15) and consequently obtain the Krylov complexity $K(t)$ and the Krylov entropy $S_{K}(t)$, which is defined by Barbon:2019wsy

$$S_{K}(t):=-\sum_{n=0}^{\infty}\absolutevalue{\varphi_{n}(t)}^{2}\log\absolutevalue{\varphi_{n}(t)}^{2}.$$

(32)

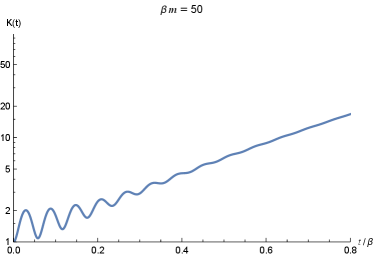
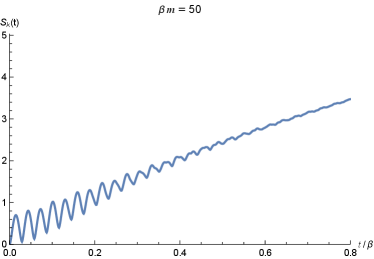
We show the time evolution of $K(t)$ and $S_{K}(t)$ in Figure 2 as an example with $\beta m=50$. In the left panel of Figure 2, it is found that the Krylov complexity oscillates when time is short. As was explained in Camargo:2022rnt , these oscillations are due to the trigonometric functions in the auto-correlation function (31). The oscillatory behavior of $\varphi_{0}(t)$ will subsequently pass on to $\varphi_{n}(t)$ according to the discrete Schrödinger equation (15). In the early time the period of the oscillations is roughly $\pi/m$, which is consistent with the plots in the left panel of Figure 2 where the period is roughly $0.06$. In the late time, the amplitudes of the oscillations becomes smaller, which is due to the cancellation of $\varphi_{n}(t)$ coming from various $n$. However, in the early time only small number of $n$ will contribute to $\varphi_{n}(t)$. Thus, the oscillation in the early time is more significant than in the late time. Intuitively, it might seem difficult to comprehend this oscillatory behavior, as a ‘simple’ operator will evolve towards a more ‘complex’ one Parker:2018yvk . However, in fact, the operator becoming more ‘complex’ is directly related to $K(t)$ which receives contributions from more number of $n$. Therefore, $K(t)$ as the position of the wave function on the one-dimensional chain, is not necessarily monotonically increasing. In the following subsection 3.3 we will explain in detail whether the position of the wave function increases monotonically or not is related to the behavior of the hopping amplitude $b_{n}$ as well as the wave function $\varphi_{0}(t)$.

The above calculations only applies to the low temperature case of $\beta m\gg 1$ since Eq.(28) merely works for $\beta m\gg 1$. Therefore, we cannot use it for more general temperatures. In the next section, we will provide detailed studies of Krylov complexity and Krylov entropy for more general situations of $\beta m$.

For general values of $\beta m$, the Wightman power spectrum (26) can be rewritten as an infinite series. For convenience, we consider only the part for $\omega>m$ and the other part for $-\omega>m$ can be obtained from the fact that Eq.(26) is an even function with respect to $\omega$. Therefore, for $\omega>m$ we have

	$\displaystyle f^{W}(\omega)$	$\displaystyle=\tilde{N}(\beta,m)(\omega^{2}-m^{2})/\sinh(\frac{\beta\omega}{2})$		(33)
		$\displaystyle=2\tilde{N}(\beta,m)(\omega^{2}-m^{2})\frac{e^{-\frac{\beta\omega}{2}}}{1-e^{-\beta\omega}}$
		$\displaystyle=2\tilde{N}(\beta,m)(\omega^{2}-m^{2})e^{-\frac{\beta\omega}{2}}\sum_{k=0}^{\infty}e^{-\beta\omega k}$
		$\displaystyle=2\sum_{k=0}^{\infty}\tilde{N}(\beta,m)(\omega^{2}-m^{2})e^{-\beta\omega(k+1/2)},$

in which we have used the series expansion $\frac{1}{1-x}=\sum_{k=0}^{\infty}x^{k}$. Let $\beta_{k}\equiv\beta(2k+1)$ and absorb the factor $2$ into $N(\beta,m)$ we obtain

$$f^{W}(\omega)=N(\beta,m)\sum_{k=0}^{\infty}(\omega^{2}-m^{2})e^{-\beta_{k}\omega/2},$$

(34)

where $N(\beta,m)$ can be calculated from the normalization conditions (27) and its exact form is

$$N(\beta,m)=\frac{\pi\beta^{3}e^{\frac{3\beta m}{2}}}{2\beta m\Phi(e^{-\beta m},2,3/2)+2e^{\beta m}(4\beta m+\Phi(e^{-\beta m},3,1/2))},$$

(35)

in which $\Phi(z,s,a)\equiv\sum_{k=0}^{\infty}z^{k}/(k+a)^{s}$ is the Lerch transcendent function lerch . Therefore, the series of the Wightman power spectrum in Eq.(34) can in principle work for general $\beta m$’s. It has much broader applications than that in Eq.(28) from Camargo:2022rnt , which can only apply in the low temperature limit.

In order to compute the moments $\mu_{2n}$ (22) we first define

$$I(n)\equiv\int_{m}^{\infty}\omega^{n}e^{-\frac{\beta_{k}\omega}{2}}d\omega$$

(36)

which can be integrated by parts as,

$$\displaystyle I(n)=\frac{2}{\beta_{k}}e^{-\frac{\beta_{k}m}{2}}m^{n}+\frac{2n}{\beta_{k}}I(n-1).$$

(37)

In particular, for $n=0$ we can get it directly from the integration Eq.(36),

$$\displaystyle I(0)=\int_{m}^{\infty}e^{-\frac{\beta_{k}\omega}{2}}d\omega=\frac{2}{\beta_{k}}e^{-\frac{\beta_{k}m}{2}}.$$

(38)

These equations imply that

$\displaystyle I(n)$

$\displaystyle=\left(\frac{2}{\beta_{k}}\right)^{n+1}\tilde{\Gamma}\left(n+1,\frac{\beta_{k}m}{2}\right).$

(39)

Therefore, from the definition of moments Eq.(22), we have

	$\displaystyle\mu_{2n}$	$\displaystyle=\int_{-\infty}^{\infty}\frac{\omega^{2n}}{2\pi}\left[N(\beta m)\sum_{k=0}^{\infty}(\omega^{2}-m^{2})e^{-\beta_{k}\omega/2}\right]$		(40)
		$\displaystyle=\frac{N(\beta,m)}{\pi}\sum_{k=0}^{\infty}\left[I(2(n+1))-m^{2}I(2n)\right]$
		$\displaystyle=N(\beta,m)\sum_{k=0}^{\infty}\frac{2^{2n+1}\beta_{k}^{-(2n+3)}}{\pi}\left[4\tilde{\Gamma}\left(2n+3,\frac{\beta_{k}m}{2}\right)-\beta_{k}^{2}m^{2}\tilde{\Gamma}\left(2n+1,\frac{\beta_{k}m}{2}\right)\right].$

Unfortunately, this formula is too complex to be computed analytically. Therefore, we resort to numerical computations. To this end, we can truncate the summation of $\mu_{2n}$ in Eq.(40) at a suitable $k$ to obtain approximate results. In order to ensure sufficient computational speed and accuracy, the truncation position of $k$ should not be too large or too small. We find that a suitable choice is to make the normalization factor of the truncated Wightman power spectrum close to the exact form in Eq.(35). In the remainder of this paper, we always take

$$f^{W}\approx N(\beta,m)\sum_{k=0}^{k_{\text{max}}}(\omega^{2}-m^{2})e^{-\beta_{k}\omega/2},$$

(41)

in which $k_{\rm max}$ is a large cut-off of $k$. We can see that the exact $f^{W}(\omega)$ in Eq.(34) satisfies $k_{\text{max}}=\infty$, while the approximated $f^{W}(\omega)$ in Eq.(28) in the low temperature limit satisfies $k_{\text{max}}=0$. In our case we choose $k_{\text{max}}=200$ in Eq.(41), because in most cases it is sufficient to obtain accurate numerical results. In Figure 3 we compare the exact Wightman power spectrum $f^{W}$ to the approximated functions with $\beta=1$ and $m=0.01$, i.e. $\beta m\ll 1$ in the limit of high temperature. In the left panel of Figure 3, we see that $f^{W}(\omega)$ for $k_{\rm max}=0$ (blue dash-dotted line) is only consistent with the exact form (black line with $k_{\rm max}=\infty$) in the regime of large frequency; However, they will deviate from each other as $\omega\lesssim 12$, which means the formula in Eq.(28) is not accurate in the low frequency regime with high temperatures. On the contrary, still in the left panel of Figure 3, we can see that there is no distinguishable differences for the Wightman power spectrum $f^{W}(\omega)$ between $k_{\text{max}}=\infty$ (black line) and $k_{\text{max}}=200$ (red dashed line) in the whole regime of the frequency, which verifies that our choice of $k_{\text{max}}=200$ is sufficient for the accuracy.

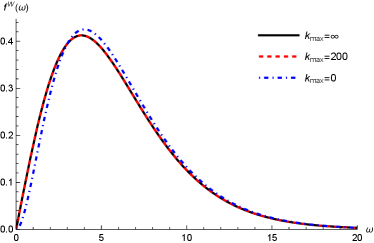
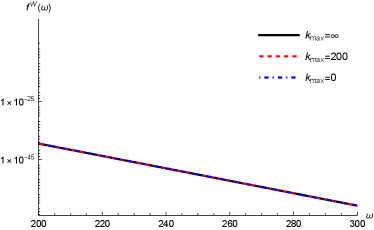
In the right panel of Figure 3 we show the logarithmic relations between $f^{W}(\omega)$ and $\omega$ in the large frequency limit. We can find that in the large frequency limit, the Wightman power spectrum with various $k_{\rm max}$’s will overlap together and decay exponentially with the frequency,

$\displaystyle f^{W}(\omega)\sim e^{-\omega/\omega_{0}},\qquad~{}~{}\omega\to\infty.$

(42)

The fitted line (green dashed line) in the right panel of Figure 3 shows that this decay rate is $1/\omega_{0}\approx 0.4919$ as $\omega\to\infty$. Therefore, we get $\omega_{0}\approx 2.0329$, which is consistent with discussions in Camargo:2022rnt that the leading exponential decay of the power spectrum is $\omega_{0}=2/\beta$ where we have set $\beta=1$.

Before studying the Krylov complexity, let’s first look at the behaviors of the Lanczos coefficients $b_{n}$ with the truncations $k_{\rm max}=200$.

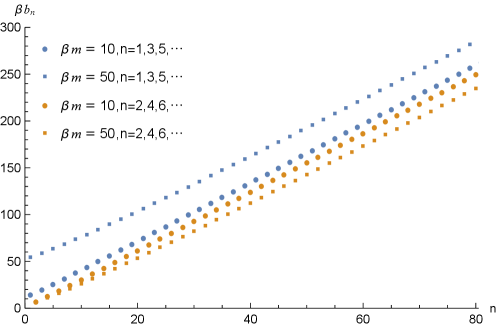
In Figure 4, we present the behaviors of $b_{n}$ for $\beta m=10$ (dots) and $\beta m=50$ (squares). These coefficients also exhibit clear behavior of “staggering”, which are grouped in two families with odd (in blue) and even $n$ (in brown). As $n$ is relatively large, $b_{n}$ becomes linearly proportional to $n$. Intuitively, we can find that the separation $\Delta b_{n}$ between $b_{n}$ for the odd $n$ and even $n$ with $\beta m=50$ are greater than those with $\beta m=10$. This phenomenon is consistent with the discussions in the preceding section that $\Delta b_{n}$ is of the order of the mass $m$ Camargo:2022rnt . In order to analyze them quantitatively, we fit $b_{n}$ linearly for odd $n$ and even $n$ separately similar to Camargo:2022rnt :

	$$\displaystyle b_{n}\sim\alpha_{\text{odd}}n+\gamma_{\text{odd}},\qquad\text{odd $n$},$$		(43)
	$$\displaystyle b_{n}\sim\alpha_{\text{even}}n+\gamma_{\text{even}},\qquad\text{even $n$},$$		(44)

where $\alpha_{\text{odd}},\alpha_{\text{even}},\gamma_{\text{odd}}$ and $\gamma_{\text{even}}$ are constants which are independent of $n$. Specifically, we perform the linear fitting for $b_{n}$ in the range of $n\in[100,450]$.

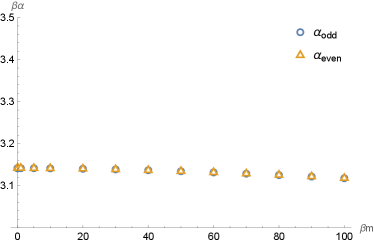
In the left panel of Figure 5, we show the relation between $\beta\alpha$ ($\alpha$ means $\alpha_{\rm odd}$ (blue) and $\alpha_{\rm even}$ (brown)) against $\beta m$. It is not difficult to observe that the two coefficients $\alpha_{\text{odd}}$ and $\alpha_{\text{even}}$ will overlap exactly, meaning that the slope in the fitting relations Eq.(43) and Eq.(44) are exactly identical. Moreover, we see that as $\beta m\to 0$ the value of $\alpha_{\text{odd}}$ and $\alpha_{\text{even}}$ are approaching $\pi/\beta$. However, as $\beta m$ increases, $\alpha_{\text{odd}}$ and $\alpha_{\text{even}}$ slightly decrease from $\pi/\beta$. This may come from the selected range of $n$ when fitting $b_{n}$ as argued in Camargo:2022rnt . It is expected that larger range of $n$ will improve the value of $\alpha$, and it will finally approach $\pi/\beta$ more closely Camargo:2022rnt . Therefore, in our case we can speculate that $\alpha_{\text{odd}}=\alpha_{\text{even}}\approx\pi/\beta$. This analysis is also consistent with the universal operator growth hypothesis in Parker:2018yvk that the Lanczos coefficients $b_{n}$ in a generic chaotic system will grow as fast as $b_{n}\sim\alpha n+\gamma$ with $\alpha=\pi\omega_{0}/2$ as $n\to\infty$. In the fitting of the Wightman power spectrum Eq.(42) we already get $\omega_{0}\approx 2/\beta$, therefore, we can get $\alpha\approx\pi/\beta$ which is consistent with the left panel of Figure 5.

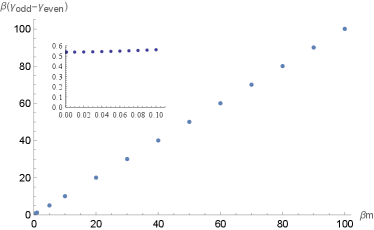
In the right panel of Figure 5, we show the relation between the difference $\beta(\gamma_{\text{odd}}-\gamma_{\text{even}})$ with respect to $\beta m$. For larger $m$, we can see that $\beta(\gamma_{\text{odd}}-\gamma_{\text{even}})$ is linearly proportional to $\beta m$ with the ratio $\beta(\gamma_{\text{odd}}-\gamma_{\text{even}})/(\beta m)\approx 1$, which is consistent with the separations of $b_{n}$ in Figure 4 that $\Delta b_{n}$ is of the order of the mass $m$. However, we find that this proportionality will break down for small $\beta m\in[0,0.1]$, as shown in the inset plot in the right panel of Figure 5. In the inset plot, the ratio in the range of small $\beta m$ is roughly $\beta(\gamma_{\text{odd}}-\gamma_{\text{even}})/(\beta m)\approx 0.2$ which is much smaller than the ratio $1$ in the large $\beta m$ regime. In the region of small $\beta m\ll 1$, the system is in the high temperature limit, therefore, we speculate that the linear proportionality between $\gamma_{\text{odd}}-\gamma_{\text{even}}$ and $m$ may not apply due to the high temperatures. As far as we know, this phenomenon is not explored previously.

Therefore, we see that high temperature limit will bring out different phenomena from the studies in Camargo:2022rnt with low temperatures. Next, we will first study the Krylov complexity and Krylov entropy in high-temperature limit, i.e., $\beta m\ll 1$ and then discuss the general cases with general $\beta m$. After that, we apply the results to the finite-temperature Higgs scalar field theory.

For convenience, in the numerics we always keep $\beta\equiv 1$ and study the variations of the Krylov complexity and Krylov entropy with respect to $\beta m$ by adjusting the values of $m$. The high temperature limit implies $\beta m\ll 1$ Kapusta:2006pm , therefore, the approximation of Wightman power spectrum in Eq.(28) from Camargo:2022rnt is in invalid in this case. We need to use Eq.(41) to numerically study the Wightman power spectrum and then to study other quantities such as Krylov complexity and Krylov entropy.

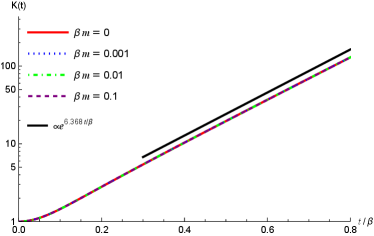
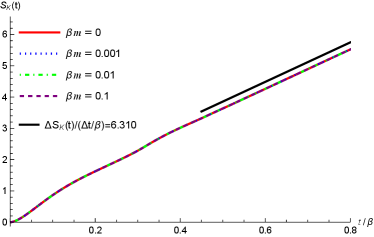
As examples, we will take the cases of $\beta m=0,0.001$, $0.01$ and $0.1$. We have plotted the time evolution of Krylov complexity $K(t)$ (in logarithmic scale) and Krylov entropy $S_{K}(t)$ in the Figure 6. In both panels, the red lines for $\beta m=0$ are taken from the conformal field theory in Dymarsky:2021bjq . From the figure, we can see that these curves (i.e., $\beta m=0.001$, $0.01$, $0.1$ and $0$) will overlap together and cannot be distinguished from each other. This is consistent in numerics itself since in this case $\beta m$ are very small and close to zero. Figure 6 indicates that at high temperatures $\beta m\ll 1$, the behaviors of the Krylov complexity and Krylov entropy for a free scalar field theory are quite similar to those of the conformal field theory.

From the discussions in Parker:2018yvk , Krylov complexity will grow exponentially at late time as

$\displaystyle K(t)\propto e^{\lambda_{K}t},$

(45)

in which $\lambda_{K}=\pi\omega_{0}=2\pi/\beta$. In the left panel of Figure 6, the black line is the reference line for the Krylov complexity at late time. Therefore, we see that in the high temperature limit, the exponential growth rate for Krylov complexity is roughly $\lambda_{K}\approx 6.368$ which is a little bit greater than $2\pi/\beta$. This is because we are fitting the line in a finite time region. For larger time, the slope of the exponential growth will tend to $2\pi/\beta$ which is consistent with the discussions in Camargo:2022rnt ; Dymarsky:2021bjq .

In the right panel of Figure 6 the black line is the reference line and scale as $\Delta S_{K}(t)/(\Delta t/\beta)=6.310$, indicating the linear growth of the Krylov entropy in late time. The linear slope is also close to $\lambda_{K}$, which is consistent with the results in Fan:2022xaa ; Camargo:2022rnt that $S_{K}(t)\sim\log K(t)$ at late time.

In the high-temperature limit, the behavior of the Krylov complexity and Krylov entropy is significantly different from that observed at low temperatures. Specifically, the oscillations that are present at low temperatures are absent at high temperatures. From the discrete Schrödinger equation, we can speculate that the behavior of $\varphi_{n}(t)$ will depend on the hopping amplitudes $b_{n}$ and the value of the wave function $\varphi_{0}(t)$. The hopping amplitudes $b_{n}$ describes how the wave function can ‘jump’ from one position to the next position. Therefore, if $b_{n}$ is staggering between even and odd positions, we can intuitively speculate that this staggering behavior will certainly affect the monotonic increase of $\varphi_{n}(t)$, and further affects the behavior the Krylov complexity. Moreover, the recursive relation of $\varphi_{n}(t)$ in the discrete Schrödinger equation indicates that the behavior of $\varphi_{n}(t)$ will also depend on $\varphi_{0}(t)$. Therefore, the behavior of $\varphi_{0}(t)$ will also affect the behavior of $\varphi_{n}(t)$ as well as the Krylov complexity. In the following we will compare the behaviors of $b_{n}$ and $\varphi_{0}(t)$ in the high-temperature and in the low-temperature regions, and we will see that the numerical results are consistent with our speculations.

• •

  Dependence on $\varphi_{0}(t)$: In the Figure 7, we have plotted the profiles of the $\varphi_{0}(t)$ for various values of $\beta m$, i.e., $\beta m=0.01$, $\beta m=10$ and $\beta m=50$. We can observe that in the low-temperature ($\beta m=50$) regime, $\varphi_{0}(t)$ (green line) has significant oscillations. However, on the contrary, in the high-temperature ($\beta m=0.01$) regime, $\varphi_{0}(t)$ (blue line) does not oscillate! Therefore, from the behavior of $\varphi_{0}(t)$, we can conclude that the lower the temperature is, the more oscillations of $\varphi_{0}(t)$ will become. Therefore, in the high-temperature regime, the absence of oscillations of Krylov complexity can be attributed to the lack of oscillations in $\varphi_{0}(t)$.

  

• •

  Dependence on $b_{n}$: It is known that if $b_{n}$ is linearly related to $n$, then the Krylov complexity grows exponentially Parker:2018yvk . However, in our case $b_{n}$ separates into two groups of linear dependence on $n$, i.e., there is staggering behavior of $b_{n}$. Therefore, we can speculate that the staggering behavior of $b_{n}$ may cause the Krylov complexity to oscillate as well. Let $\gamma_{1}\equiv\beta(\gamma_{\text{odd}}+\gamma_{\text{even}})$, $\gamma_{2}\equiv\beta(\gamma_{\text{odd}}-\gamma_{\text{even}})$, then we can reformulate $b_{n}$ in Eqs.(43)-(44) as,

  $$\beta b_{n}=\beta\alpha n+\dfrac{\gamma_{1}}{2}+(-1)^{n+1}\frac{\gamma_{2}}{2},~{}~{}~{}~{}n\in Z.$$

  (46)

  When $n$ is sufficiently large, the linear term becomes significant. Then, the third term on the right side of Eq.(46) can be neglected. Therefore, at this point, the Krylov complexity should grow exponentially. To clarify why there is no oscillation at high temperatures and why the oscillation disappears over time at low temperatures, we can make the function $\varphi_{n}(t)$ continuous such that

  $$\varphi(x,t):=\varphi_{n}(t),\qquad x=\epsilon n,$$

  (47)

  where $\epsilon$ is a small lattice cutoff. Assuming that when $n>\hat{n}$, the third term of $\beta b_{n}$ in Eq.(46) can be neglected, and let $\hat{x}=\epsilon\hat{n}$. Then, the Krylov complexity can also be rewritten in a continuous form

  	$\displaystyle K(t)$	$\displaystyle=$	$\displaystyle 1+\sum_{n=0}^{\infty}n\absolutevalue{\varphi_{n}(t)}^{2}$		(48)
  		$\displaystyle=$	$\displaystyle 1+\frac{1}{\epsilon^{2}}\int_{0}^{\infty}dx~{}x\absolutevalue{\varphi(x,t)}^{2}$
  		$\displaystyle=$	$\displaystyle 1+\frac{1}{\epsilon^{2}}\int_{0}^{\hat{x}}dx~{}x\absolutevalue{\varphi(x,t)}^{2}+\frac{1}{\epsilon^{2}}\int_{\hat{x}}^{\infty}dx~{}x\absolutevalue{\varphi(x,t)}^{2}.$

  The Krylov complexity represents the position of the wave function $\varphi(x,t)$ on the Krylov chain. When $t$ is small, its position is relatively close to the origin $(x,t)=(0,0)$, and the Krylov complexity is dominated by the second term in (48), which can disrupt the exponential growth and potentially lead to oscillations. When $t$ is sufficiently large, the position of the wave function is far from the origin, and the Krylov complexity is dominated by the third term in equation (48), thus exhibiting exponential growth behavior. This is why oscillations gradually fade away over time in low-temperature conditions. For a detailed discussion on this topic, please refer to reference Barbon:2019wsy .

  In the high-temperature limit, the Krylov complexity exhibits exponential growth from the very beginning. From our speculations, then the third term of $\beta b_{n}$ should be negligible when $n$ is very small. Therefore, in the high-temperature limit and when $n$ is very small, it should satisfy $\gamma_{2}/2\ll\beta\alpha n+\gamma_{1}/2$. This corresponds exactly to the high-temperature region as shown in the right panel of Figure 5 and in the Figure 8 below. In the high-temperature region, $\gamma_{1}$ is approximately around 6.3 (as $\beta m$ is small in the Figure 8), and $\gamma_{2}$ is less than 0.6 (see the inset plot in the right panel of Figure 5), i.e., $\gamma_{2}/2\ll\beta\alpha n+\gamma_{1}/2$ for $n$ is small.

  

  Therefore, in high-temperature regime, Krylov complexity does not have oscillations. However, in the low-temperature regime (as $\beta m$ is big enough) and when $n$ is small, $\gamma_{2}$ cannot be neglected. As we can see from the right panel of Figure 5 and the Figure 8, when $\beta m=100$, $\beta\gamma_{1}$ is roughly $35$ and $\beta\gamma_{2}$ is roughly $100$ which cannot be neglected. This means the staggering behavior of $b_{n}$ cannot be neglected in low-temperature regime. Therefore, the Krylov complexity will exhibit oscillations in the low-temperature as $n$ is small.

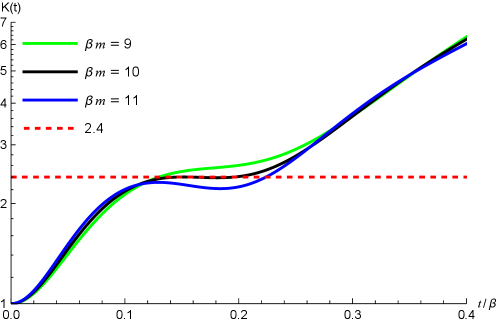
It will be interesting to see whether theres exists a transition temperature that Krylov complexity will change its behavior from the oscillations to monotonic increase. After careful seeking, we numerically found that at around $\beta m=10$ there indeed exists such kind of transition temperature. We plot the profile of $K(t)$ as $\beta m=9,10,11$ in the Figure 9. We observe that at this transition temperature there exists a plateau at $K(t)\approx 2.4$ (red dashed line). The existence of plateau indicates that $K(t)$ at $\beta m=10$ is a critical line, since as $\beta m<10$ the Krylov complexity will increase monotonically and while $\beta m>10$ the Krylov complexity will have oscillation behaviors. Therefore, $\beta m=10$ is such kind of transition temperature.

For the case of $\beta m\sim 1$, the Eq.(28) for the low temperature limit in Camargo:2022rnt is also not applicable. Only the approximation in Eq.(41) is feasible in this case.

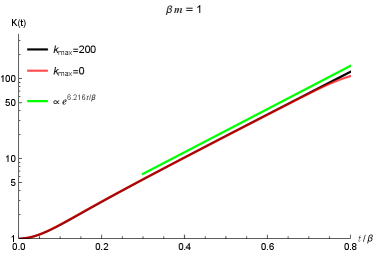
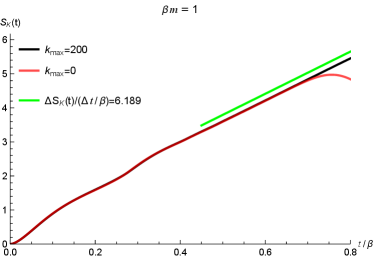
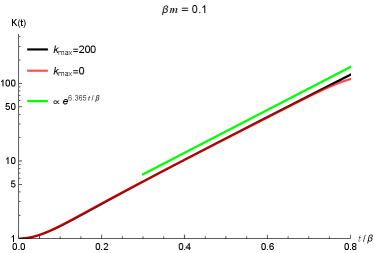
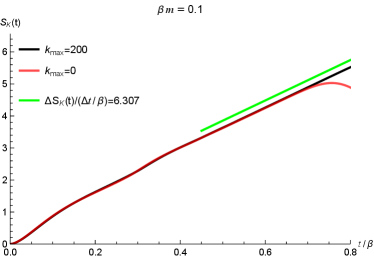
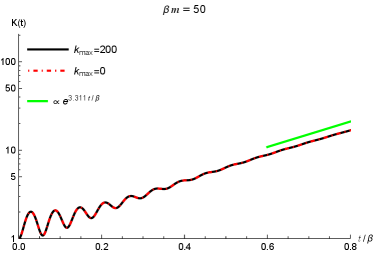
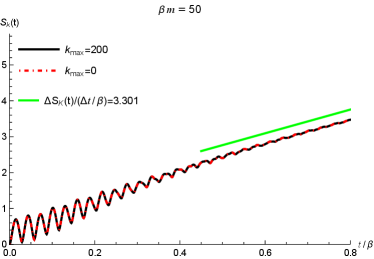
In Figure 10, we show the time evolution of the Krylov complexity $K(t)$ (in left column) and Krylov entropy $S_{K}(t)$ (in right column) for different values of $\beta m$. In these plots, the black curves are for $k_{\rm max}=200$ corresponding to Eq.(41) while the red (dashed) curves are for $k_{\rm max}=0$ corresponding to Eq.(28). From the panels in the first row, i.e. $\beta m=1$, we can see that the red lines will deviate from the black lines at late time. This reflects that the approximations in Eq.(28) is not accurate as the approximations in Eq.(41) at late time, which confirms our assertion that the approximation in Eq.(28) is only applicable in low temperature limit, i.e., $\beta m\gg 1$. The green lines in the first row are the reference lines for $K(t)$ and $S_{K}(t)$, respectively. In the panel (a) of Figure 10 we can see that the exponential growth rate of the Krylov complexity is roughly $\lambda_{K}\approx 6.216$ which is close to $2\pi/\beta$. This exponential scaling is consistent with our discussions in the preceding subsection. In the panel (b) of Figure 10, the linear scaling of the Krylov entropy is roughly $\Delta S_{K}(t)/(\Delta t/\beta)\approx 6.189$, which is consistent with the claims that $S_{K}(t)\sim\log K(t)$ at late time as we discussed in the preceding subsection. The small differences between the two scalings, i.e., $6.216$ and $6.189$ are due to the fittings of the two quantities at a finite time. It is expected that much longer time fitting will reduce this difference.

In the second row of Figure 10 we compare the Krylov complexity and Krylov entropy with distinct $k_{\rm max}$ (i.e., $k_{\rm max}=200$ and $k_{\rm max}=0$) in high temperature limit ($\beta m=0.1\ll 1$). Again, the deviations between the red lines ($k_{\rm max}=0$) and black lines ($k_{\rm max}=200$) tell us that in the high temperature limit, the approximation in Eq.(28) is not valid. The late time scalings in $K(t)$ and $S_{K}(t)$ (blue reference lines) are also close to $2\pi/\beta$ and consistent with the preceding discussions.

However, for $\beta m\gg 1$, both the approximations in Eqs.(28) and (41) are valid, see for instance the last row in Figure 10, where we have set $\beta m=50$ for the computation of Krylov complexity and Krylov entropy. In the time region we have considered, both of $k_{\rm max}=200$ and $k_{\rm max}=0$ collapse together and cannot be distinguished from each other. This is different from the cases with $\beta m=1$ and $\beta m=0.1$ in the first two rows of Figure 10. Interestingly, the late time scalings for both Krylov quantities are much smaller than $2\pi/\beta$, i.e., $\lambda_{K}<2\pi/\beta$ in the low temperature limit $\beta m\gg 1$. Compared to high temperature limit, we may conjecture that the exponential growth rate of the Krylov complexity has a bound $\lambda_{K}\leq 2\pi/\beta$, which is consistent with the discussions in Camargo:2022rnt .