Probing isovector scalar mesons in the charmless three-body decays
Abstract
We propose to study the multiparticle configurations of isovector scalar mesons, saying and , in the charmless three-body decays by considering the width effects. Two scenarios of configurations are assumed, in which the first one take as the lowest-lying state and as the first radial excited state, the second one take as the lowest-lying state and as the first radial excited state while is not a state. Within these two scenarios, we do the PQCD calculation for the quasi-two-body decays and extract the corresponding branching fractions of two-body decays under the narrow width approximation. Our predictions show that the first scenario of configuration can not be excluded by the available measurements in decays, the contributions from to the branching fractions in most channels are comparable in the first and second scenarios. Several channels are suggested for the forthcoming experimental measurements to reveal the multiparticle configurations of , such as the channel with the largest predicted branching fraction, the channels whose branching fractions obtained in the second scenario is about three times larger in magnitude than that obtained in the first scenario, and also the channels whose branching fractions are linear dependent on the partial width .
pacs:
13.20.He, 13.25.Hw, 13.30.EgI Introduction
It is known that the scalar mesons with the masses below and near , saying the isoscalar mesons and , the isovector and the isodoublet , form a flavor nonet, meanwhile, the mesons heavier than with including , and make up another nonet. The underlying assignment of the heavier nonet is almost accepted as the quark-antiquark configuration replenished with some possible gluon content JaffeIG ; CloseZU ; AchasovHM ; AchasovFH , while the inner nature of scalar mesons in the lighter nonet is still not clear WeinsteinGC ; WeinsteinGD ; Agaev:2017cfz , even though the compact tetraquark state Alford:2000mm ; Maiani:2004uc ; Maiani:2007iw and the bound state Weinstein:1990gu are the most favorite two candidates nowadays. This is easy to understand from the views of spectral analysis at low energy because the scalar meson in configuration has a unit of orbital angular momentum which increases their masses, in contrast, it is not necessary to introduce the orbital angular momentum when the scalar meson is being in configuration ChengNB . The case becomes different in the weak decays like with large recoiling, where the conventional assignment can be expected to be dominated in the energetic since the possibility to form a tetra-quark state is power suppressed with comparing to the state of quark pair Cheng:2019tgh , meanwhile, the final state interaction (FSI) is weak too. But this argument encounters challenge from the perturbative QCD (PQCD) calculation of decays Shen:2006ms , where the theoretical predictions of branching fractions are much larger than that of the measured upper limits. We would like to comment that their calculation is carried out in the static approximation while the experiment measurement is actually fulfilled by the invariant mass spectral. It is apparent that the salient property of scalar mesons, say, the large decay width which cause a strong overlap between resonances and background, and subsequently influence the PQCD prediction.
The width effect of intermediate resonant states have been studied in three-body decays with a large number of channels by variable theoretical approaches based on QCD, due to the significant physics to understand the hadron structures and also the matter-antimatter asymmetry. We here highlight some developments in this research filed in the order of different theoretical approaches.
- PQCD
-
A global analysis of three-body charmless decays in the type of 111Here denote the vector and pseudoscalar meson, respectively, and indicates the scalar meson in the following. In the fit, only the channels are considered due to the experiment precision. is performed Li:2021cnd to determine the lowest several gegenbauer moments of two-meson system, which are the nonperturbative inputs describing the non-asymptotic QCD correction effect in the light-cone distribution amplitudes (LCDAs). In Ref.Rui:2021kbn , the factorization formulas of PQCD is expanded in the four-body decay to two pairs with the invariant mass around the resonance, some further observations like the triple-product asymmetries and the -wave induced direct CP asymmetries are presented with the interference between different helicity amplitudes. Motivated by the measurement of significant derivations from the simple phase-space model in the channels and at B factories and LHC, the virtual contribution clarified by the experiment collaborations is understood theoretically by the Breit-Wigner-tail (BWT) effects from the corresponding intermediate resonant states, say and , respectively Wang:2020nel ; Chai:2021kie .
- QCDF
-
The QCD factorization (QCDF) formula of amplitudes in three-body decays Klein:2017xti is parameterised in a new way where the contributions from valence and quark are separated, and a new source of CP violation can be generated via the strong phase with the opening of threshold in the high invariant mass region Mannel:2020abt . Motived by the NNLO correction and the finite width effect, three-body decay is studied from the point of view of factorisation for the heavy-to-heavy decays in the kinematics with small invariant mass of dimeson system Huber:2020pqb . Very recently, a novel observation named the forward-backward asymmetry induced asymmetry (FBI-CPA) is introduced in the three-body heavy meson decays, the estimation based on the generalized factorization approach implies that the FBI-CPA in the channel is about a milli, which is at the same order of current experiment measurement capability Zhang:2021zhr . In Refs. Cheng:2020iwk ; Cheng:2022vbw , the finite-width effects of intermediate resonant states in three-body decays is expressed by a correlation parameter and the evaluation is carried out in QCDF.
- LCSRs
-
The width effect of intermediate resonant and its radial excited states is discussed in detail in the -wave transition form factors from the meson light-cone sum rules (LCSRs) approach Cheng:2017smj , revealing the sizeable effects from width and background () to the conventional treatment in the single narrow-width approximation for the LCSRs prediction of the transition form factors. This result is confirmed by the other independent LCSRs with dipion distribution amplitudes (DAs) where the hadronic dipion state has a small invariant mass and simultaneously a large recoil Hambrock:2015aor ; Cheng:2017sfk . The further studies are carried out for the -wave form factors with the isodouble intermediate resonances Descotes-Genon:2019bud and the form factors with the isoscalar scalar intermediate resonances and Cheng:2019tgh .
The above considerations mainly focus on the -wave and isoscalar -wave contributions from the intermediate resonant states, while the study of isovector scalar intermediate resonance is still missing. In this paper we will demonstrate this issue in the framework of PQCD approach. The motivations of this study is twofold. Firstly, we perform the PQCD prediction of decays go beyond the single pole approximation, trying to explain the measurement status. Secondly, we consider the roles of and in the decays inspired by the recent measurements of charm meson decays where and are observed in the invariant mass spectral CLEO:2008msk ; LHCb:2015lnk ; BaBar:2015kii , supplementing to the decays observed firstly at Crystal Barrel Collaboration long time ago CrystalBarrel:1994arw ; CrystalBarrel:1995dzq . The study would be executed in parallel by taking two different scenarios of states, where the first one says that is the lowest lying state and is the first excited state, and the second one states that and are the lowest lying state and the first excited state, respectively. Our calculations show that the configuration of is not be excluded by the available measurements in decays, which confirms the statements we made above. Predictions in this work would help us to probe the inner structure of energetic isovector scalar mesons. For examples, (a) the channel has the largest branching fraction under the configuration of , (b) the branching fractions of channels obtained in the second scenario is about three times larger in magnitude than that obtained in the first scenario, even though the result obtained from two scenarios are close to each other in the most channels with the intermediate state , (c) the branching fractions of channels are linear dependent on the partial width in the second scenario.
This article is organized as follows. In section II, the framework of PQCD approach to deal with the resonance contribution in three-body decays is briefly described in turns of kinematics and dynamics. Section III presents the PQCD predictions of the decays with some discussions. We summary in section IV. The PQCD predictions on decays are presented in appendix A, and the factorization formulas of the related quasi-two-body decay amplitudes are listed in appendix B.
II Kinematics and Dynamics
Concerning three-body decays, there are three typical kinematical configurations in the physical Dalitz plot of two independent invariant mass by considering the four-momentum conservation, in which only the kinematical region with collinear decay products can be calculated reliably from the perturbative theory based on the factorization hypothesis Chai:2021kie . The other two kinematical regions with the three energetic decay products and a soft decay product configurations are either in lack of the rigorous factorization proof or beyond the available perturbative picture of heavy meson decays. Collinear decay products means that two energetic hadrons move ahead with collinear momenta while the rest one recoiling back222 and in the massless approximation of final mesons., corresponding to the intermediate parts of three edges in the Dalitz plot.
The matrix element from vacuum to collinear two meson system sandwiched with certain two quark operators is defined by the dimeson DAs, the chirally even two quark dimeson DA is quoted for example as Polyakov:1998ze
| (1) |
where the indexes respect the (anti-)quark flavor; indicate the electric charge of each meson, is the isospin symmetry coefficient which in the case of dipion system reads and , is the total momentum of dimeson state, correspond to the isoscalar and isovector dimeson DAs, respectively. The generalized dimeson DA is characterised by three independent kinematical variables, saying the momentum fraction carried by the antiquark, the longitudinal momentum fraction carried by one of the mesons and the invariant mass squared . Besides the conventional Gegenbauer expansion stemmed from the eigenfunction of QCD evolution equation, the partial wave expansion considered in the dimeson system contributes the other Legendre polynomial . The double expansion of two quark dimeson DA is written as
| (2) |
here the even Gegenbauer index and the odd partial-wave index are guaranteed by the parity. For the expansion coefficients , they have the similar scale dependence as the Gegenbauer moments of single pion and rho mesons. In the narrow width approximation in the vicinity of the resonance, dimenson DAs reduce to the DAs of the relative resonance, indicating that the Gegenbuer moments of the intermediate resonance is actually proportional to the expansion coefficient at zero point with the lowest partial wave, says . In this way, the decay constant of intermediate resonance is proportional to the product of its decay width with the imaginary part of first expansion coefficient at the resonant pole, that is Cheng:2019hpq .
With this definition, the dimeson DAs are the most general objects to describe the dimeson mass spectrum in hard production processes whose asymptotic formula indicates the information of the deviation from the unstable intermediate resonant meson DAs. After integrating over the momentum fraction of antiquark, the isovector scalar dimeson DA in our interest is normalised to timelike meson form factor as
| (3) |
where the timelike form factor at zero energy point is normalised to unit as . When the invariant mass of dimeson system is small, the higher terms in the expansion of coefficient around the resonance pole can be safely neglected due to the large suppression in contrast to the energetic dimeson system in decay, so the relation can be obtained in the lowest partial wave approximation. This argument induces the basic assumption in PQCD that the energetic dimeson DAs can be deduced from the DAs of resonant meson by replacing the decay constant by the timelike form factor.
The isovector scalar form factor of and systems are defined by the local matrix elements sandwiched by two quark operator Donoghue:1990xh ; Albaladejo:2015aca
| (4) |
with the normalization conditions and . In the single resonance approximation, we insert a state in the matrix elements
| (5) | |||||
and ultimately arrive at
| (6) |
Several comments are supplemented in turns to demonstrate this expression.
-
•
The decay constants of scalar meson are defined with the scalar and vector currents,
(7) They are related by the equations of motion , indicating that the neutral scalar meson can not be produced via the vector current because of the charge conjugation invariance or the conservation of vector current, but the constant is still finite.
-
•
Under the narrow approximation, the matrix element of strong decay is defined by the coupling Wang:2020saq
(8) with the energy independent partial decay width333The partial widths of decays have the relations . . In the definition, is the magnitude of daughter meson ( or ) momentum
(9) at mass. We take the renormalized mass of rather than the pole mass obtained from -matrix analysis, since the mass and width parameter are strongly distorted with lying just below the opening of channel and hence generating an important cusp-like behaviour in the resonant amplitude Abele:1998qd . Actually, with being the nondimensional phase space factor of system, which reflects the information of momentum difference described by the variable mentioned in the dimeson DAs.
-
•
We take the conventional energy-dependent Breit-Wigner denominator for and mesons444Hereafter we use the abbreviations and to denote and , respectively.,
(10) where is the total decay widths of resonant state meson . For the meson , we consider the Flatt model Flatte:1976xu
(11) the coupling constants GeV and is fixed by the isobar model fits Abele:1998qd . Furthermore, we can get GeV and GeV with the relations and . We mark that, in the channel, the phase factor could also be pure imaginary number when the invariant mass of state is small than the threshold value of state, the contribution from this region interacts destructively with that from the rest region of invariant mass.
With rearranging the kinematical variable into the daughter meson momentum and considering the symmetry, the matrix element from vacuum to S-wave state can be decomposed as ChengNB
| (12) |
In the lowest partial-wave accuracy, the twist 2 LCDA is written as Cheng:2013fba
| (13) |
with . It is clear that the even Gegenbauer coefficients are suppressed and the odd Gegenabauer moments is dominated in the twist 2 LCDA of scalar meson, this is definitely different from the and mesons in which the odd moments vanish. The twist 3 LCDAs are
| (14) |
The definitions of meson and light meson wave functions and the models of their LCDAs, as well as the basic procedures of PQCD approach to deal with the so called quasi two-body decays as a marriage problem, can be found in detail in Ref. Chai:2021kie .

In figure 1, we depict the typical feynman diagrams of the decays with in the PQCD approach, in which the symbols and denotes the vertex of weak interaction and the possible attachments of hard gluons, respectively, the rectangle indicates the intermediate resonant states and the subsequent strong decays . In the meson rest frame, the explicit definitions of kinematics in the decays are considered as follow,
| (15) |
where and are the momenta carried by the antiquark in the meson states with the momentum fractions and , respectively. The new variable indicates the momentum transfer from meson to resonant state . The differential branching ratios for the quasi-two-body decays is written as PDG-2020
| (16) |
in which daughter meson momentum has been defined in Eq. (9), and is the magnitude of momentum for the bachelor meson
| (17) |
The decaying amplitudes is exactly written as a convolution of the hard kernel with the hadron distribution amplitudes (DAs) and
| (18) | |||||
in which indicates the dimeson system in our interesting, is the factorization scale, are the conjugate distances of transversal momenta. We present the expressions of amplitudes for the considered decaying processes in the appendix B. Under the narrow width approximation
| (19) |
we can extract the branching fractions of two-body decays from the quasi-two-body decays by
| (20) |
III Numerics and Discussions
| BaBar:2015kii |
In table 1, we present the PDG averaged value for the masses and total widths of single mesons, as well as the Wolfenstein parameters of CKM matrix. meson wave function relies on the three independent parameters, saying the mass , the decay constant and the first inverse moment . For the inverse moment , we take the interval and obtained by the QCD sum rules Braun:2003wx with considering smaller uncertainty. The mean lifes of mesons are also taken from PDG, they are , and .
The PDG value of light meson decay constant follows from the lattice QCD average Aoki:2016frl . We truncate to the second moments for the Gegenbauer expansion of leading twist LCDAs, and take and obtained recently from the LCSR fit Cheng:2020vwr of the pion electromagnetic form factor555This result agrees with the previous LCSRs extractions from spacelike pion electromagnetic form factor Agaev:2005gu , form factor Ball:2005tb ; Duplancic:2008ix ; Khodjamirian:2011ub , and also the QCD sum rule prediction Ball:2006wn , but much larger than the recent lattice QCD evaluation () with the new developed momentum smearing technique RQCD:2019osh .. For the kaon meson, we take the lattice result obtained by using sea quarks and the domain-wall fermions Arthur:2010xf , say, and , which is comparable with the QCD sum rules calculations Khodjamirian:2004ga ; Ball:2006wn and the result from Dyson-Schwinger equations with dynamical chiral spontaneously breaking (DCSB)-improved kernel Shi:2015esa . We takes the chiral masses at with considering the well-known chiral perturbative theory () relations Leutwyler:1996qg
| (21) |
in which , , the current quark masses are , and . For the twist 3 LCDA, we only take into account the asymptotic terms in the numerical analysis.
Concerning the intermediate resonant isovector scalar states s, the main inputs are the timelike form factor entered in each LCDA and the Gegenbauer moments in the leading twist LCDA. To reveal the timelike form factor described in Eq. (6), we use the QCD sum rules predictions on the decay constants ChengNB , they are and obtained in the first scenario where is treated as the lowest lying state and as the first excited state, and and obtained in the second scenario where is the lowest lying state and as the first excited state. As shown in Eq. (8), the strong coupling constants and are decided by the partial decay width, which are fixed by the following considerations
-
•
With the measurements and Amsler:1997up , one get . We do not use eq. (8) to determine the partial width since it is an approximation expression under the narrow width limit. Furthermore, one can get with the measurement PDG-2020 .
-
•
The partial decay widths of to and states are decided by the measured branching ratios and PDG-2020 .
-
•
For the decays, there is no direct measurement and the predictions from different models vary widely. For example, the Extended Linear Sigma Model (eLSM) states that and Parganlija:2016yxq , while the quark model gives the result and correspondently Wang:2017pxm . So in our evaluation, we take the largest interval of this variable to account its uncertainty.
-
•
To close the descriptions, we summary the intervals of partial decay widths as
(22)
Concerning the Gegenbauer expansion of scalar mesons, we take into account the first two odd moments and in the twist 2 LCDAs Cheng:2005nb and the asymptotic terms in the twist 3 LCDAs due to the large theoretical uncertainty of and Lu:2006fr ; Han:2013zg ; Wang:2014vra . They are
| (23) |
in the first scenario, and
| (24) |
in the second scenario, where the default scale at is indicated.
| Decay modes | Quasi-two-body | narrow approx. | two-body | data PDG-2020 | CPV |
| Zhang:2010fcy | |||||
| Cheng:2013fba | |||||
| Zhang:2010fcy | |||||
| Cheng:2013fba | |||||
| Shen:2006ms | |||||
| Cheng:2013fba | |||||
| Shen:2006ms | |||||
| Cheng:2013fba | |||||
| Zhang:2010fcy | |||||
| Cheng:2013fba | |||||
| Zhang:2010fcy | |||||
| Cheng:2013fba | |||||
| Zhang:2010fcy | |||||
| Cheng:2013fba | |||||
| Shen:2006ms | |||||
| Cheng:2013fba | |||||
| Shen:2006ms | |||||
| Cheng:2013fba |
Our numerical evaluations are carried out in two scenarios. In the first scenario, we treat as the lowest-lying state and as its first excited state, and study the contributions from and in the decays. The second scenario indicates that is the lowest-lying state and is the first excited state, with this ansatz we study their contributions in the decays.
| Decay modes | Quasi-two-body | narrow approx. | two-body Cheng:2013fba | CPV |
In table 2 and table 3, we present the PQCD predictions of of and decays in the first scenario of multiparticle configurations of , respectively. Besides the result of quasi-two-body decays, saying the branching fractions (in the 2nd column) and the violations (in the last column), we list the branching fractions of two-body decays666The narrow width approximation is not applicable to the modes involving due to the threshold effect, so in table 2 we do not list the result of two-body decay obtained in the narrow width approximation (in the 3rd column), for the sake of comparison, the direct two-body calculations based on PQCD Shen:2006ms and QCDF approach Cheng:2013fba , and also the available data are list too (in the 4th and 5th columns). The theoretical uncertainties come from the inputs of LCDAs, mainly from the inverse moment which we put as the first error source, the uncertainties from Gegenbauer moments of dimeson systems are add together as the second error, we do not consider the uncertainty from other parameters, like since their influences are small. We comment in orders,
-
(a)
The branching fractions of quasi-two-body channels with strong decays is about 5 times larger than that with the strong decay , which is understood by the suppressed phase space for state.
-
(b)
Under the narrow width approximation of the quasi-two-body decays, we extract the branching fractions of relevant two body decays . The result obtained from the and modes are consist with each other with in the uncertainties, more important is that this result have a large discrepancy with the direct two-body calculation from PQCD Shen:2006ms and QCDF Cheng:2013fba , revealing the important role of width effects of and .
-
(c)
In the and the following decays, only the partial width expression is used due to the lacking of direct measurements, that’s why the branching fractions of these decays extracted from and modes are very close to each other.
-
(d)
The PQCD predictions of branching fractions of the six quasi-two-body decays do not excess the experimental upper limit, the predictions of two channels excess the experimental upper limit PDG-2020 at the first glance, but the large uncertainties would be more larger if we considering the uncertainty of . So with in acceptable limits, the configuration of is still survival in decays. It is shown that the decaying channel has the largest branching fraction, and we suggest the measurement to examine the configuration.
| Decay modes | Quasi-two-body | narrow approx. | two-body Cheng:2013fba | CPV |
| Decay modes | Quasi-two-body | narrow approx. | CPV |
|---|---|---|---|
We list in table 4 and table 5 with the PQCD predictions of and decays in the second scenario of multiparticle configurations of , respectively. For the later one, we also present the uncertainty (as the third error) in the quasi-two-body decays from the partial decay width as demonstrated in Eq. (22), this parameter would not bring additional uncertainty to the two-body decays under narrow approximation. Similar result is obtained with showing that the decaying channels have the largest branching fractions both for the quasi-two-body and the extracted two-body decays. We would like to mark that our predictions of the contributions are comparable in the most of decays no matter what’s the scenarios of configurations are taken, while for the channels and , the predictions of branching fractions in the second scenario are about three time larger in magnitude than that predicted in the first scenario777The PQCD predictions in the second scenario for these channels consist with the result from factorisation approach under symmetry Li:2014oca , and the predictions in both two scenarios are under the experiment upper limit., which provide another opportunity to check which one is the right with the future measurement. In these tables we also list violations which provide another observables to study the interactions between different operators and/or topological amplitudes, especially the different sources of strong phases.






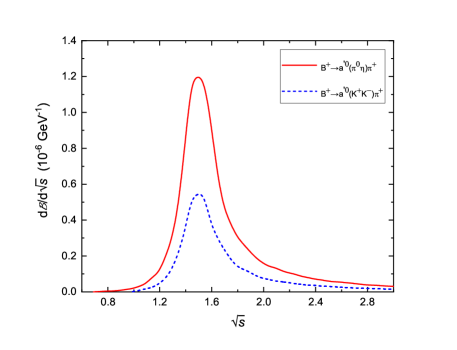





The width effect of intermediate isovector scalar mesons is exhibited explicitly by the invariant mass spectral. In the first scenario of multiparticle configurations of , we plot in figure 2 for the differential branching fractions of the typical decaying channels on the invariant masses, in which the top panel shows the result of channels (left) and (right) with varying the invariant mass from thresholds to , the medium panel is the result of (left) and (right) decays with varying the invariant mass from thresholds to , the comparison of and contributions in (left) and (right) decays is depicted in the bottom panel. We take these typical charged channels because they carry almost all the characteristics of the relevant quasi-two-body decays: (a) the contribution from mode is much smaller than it from modes as expected by the highly phase space suppression888We multiply the result of mode by a factor of ten to show apparently for the curves., (b) the contributions from these two modes are comparable, we comment that the lower curves in the left plot can be compensated by the channel which is not depicted here, (c) in contrast to the contributions, the contribution is negligible in the channel and small in the channel, while its contributions in the and channels are (much) larger than the contributions from , this is mainly decided by the different phase spaces. We can also see the difference between the three plots in the left panel for the channels with and the other three plots on the right panel for the channels with , this is determined by the weak decay of relevant two-body decays and whose invariant amplitudes are collected in the appendix B. These points support the corresponding result in tables 2 and 3 for the partial decay branching fractions obtained by integrating the differential branching fractions over the invariant masses.

We similarly plot the and contributions in the typical decay in the second scenario of multiparticle configurations of , as depicted in figure 3, where the top panel shows the result of channels (left) and (right) with the invariant mass starting from the thresholds and closing up at , the plots in medium panel is depicted for the channels (left) and (right) with varying the invariant mass from thresholds to , and the Bottom panel presents the result of channels (left) and (right). We can easily get that (a) the contributions from in the channels and in the second scenario of multiparticle configurations of are very close to that obtained in the first scenario, we would like to mark again that the neutral meson decaying channels , even though have the similar shapes, have apparent different predictions in magnitude in these two scenarios, (b) the contributions from are larger than that from , in the channels even larger by about a order, this is an impressive result but not surprise if we look at the twist 2 LCDAs in Eq. (13) and the relevant parameters, and we looking forward for the experiment check, (c) the contributions in the channels and are almost overlap because the is far away from the and thresholds, as we can also find in the channels and if we consider both the and contributions, (d) the partial widths of effect significantly for the result of the quasi-two-body, we plot the varying band in the bottom panel by taking the result and obtained from the eLSM model Parganlija:2016yxq . We depict in figure 4 the dependence of the branching fractions of on the partial widths with considering the largest uncertainties in Eq. (22). It is shown that the width effect of in the relevant quasi-two-body decays is linear, so we suggest these channels in decays to determine the partial widths .
IV Conclusion
Motivated by the discrepancy between the experimental measurements of three-body decays and the theoretical predictions of two-body decays, we study the contributions from in the three-body decays in the framework of PQCD approach, where the width effects of the intermediated isovector scalar mesons are demonstrated in detail, this is also the first systematical study of the width effect in decays. In the face of controversy for the multipaticle configurations of , particularly in the decays, we consider two scenarios where the first one states that is the lowest-lying state, and the second one says that the lowest-lying state is while is a compact tetraquark state or bound state.
We find that the width effect from intermediate states is significant in the relevant quasi-two-body decaying channels, with which we extract the branching fractions of corresponding two-body decays under narrow width approximation, showing a large difference to the previous direct two-body calculation under the static assumption. Our calculations show that the as the lowest-lying state can not be ruled out in decays within acceptable limits with the current measurements. To examine the nature of state in decays, we suggest several channels for the future experiments. The first candidate is the mode with the largest branching fraction from the calculation under the first scenario, the second ones are the modes, whose branching fractions obtained in the first scenario is about three times smaller in magnitude than that obtained in the second scenario, the last, but not the least, is the partial widths () dependence of the partial branching fractions of modes, this dependence is shown in the linear behaviour and could be examined by the future data. As a byproduct, we present mesons contributions in the suppressed decays, which seems more harder for the near future experiments.
V Acknowledgments
We would like to thank Wen-fei Wang for proposing this project to us, and to Hai-yang Cheng for the fruitful discussion. This work is supported by the National Science Foundation of China (NSFC) under the Nos. 11805060, 11975112,11947011 and the Joint Large Scale Scientific Facility Funds of the NSFC and CAS under Contract No. U1932110. SC is also supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ4160), AJM is also supported by the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20191010) and the Scientific Research Foundation of Nanjing Institute of Technology (Grant No. YKJ201854).
Appendix A Probing mesons in the quasi-two-body decays
We also predict the contributions from isovector scalar mesons in the suppressed decays under, as presented in table 6 and table 7 under scenario I and II, respectively, the channel with the predicted branching fraction is the most possible available at the near future experiments.
| Decay modes | Quasi-two-body | narrow approx. | CPV |
|---|---|---|---|
| Decay modes | Quasi-two-body | narrow approx. | CPV |
|---|---|---|---|
Appendix B Decay amplitudes
In this section, we list the Lorentz invariant decay amplitude for the considered quasi-two-body decay in the PQCD approach.
| (25) | |||||
| (26) | |||||
| (27) | |||||
| (28) | |||||
| (29) | |||||
| (30) | |||||
| (31) | |||||
| (32) | |||||
| (33) | |||||
| (34) | |||||
| (35) | |||||
| (36) | |||||
| (37) | |||||
| (38) | |||||
In these expressions, is the fermi coupling constant, ’s are the CKM matrix elements, the combined Wilson coefficients are defined as
| (39) |
The factorizable and nonfactorizable amplitudes, saying and respectively, can be found in Refs. Wang:2020saq .
References
- (1) R. L. Jaffe, Phys. Rev. D 15, 267 (1977). Phys. Rev. D 15, 281 (1977).
- (2) F. E. Close and N. A. Tornqvist, J. Phys. G 28, R249 (2002).
- (3) N. N. Achasov and A. V. Kiselev, Phys. Rev. D 73, 054029 (2006), Erratum: [Phys. Rev. D 74, 059902 (2006)].
- (4) N. N. Achasov and A. V. Kiselev, Phys. Rev. D 83, 054008 (2011).
- (5) J. D. Weinstein and N. Isgur, Phys. Rev. Lett. 48, 659 (1982).
- (6) J. D. Weinstein and N. Isgur, Phys. Rev. D 27, 588 (1983).
- (7) S. Agaev, K. Azizi and H. Sundu, Phys. Lett. B 781, 279-282 (2018).
- (8) M. G. Alford and R. L. Jaffe, Nucl. Phys. B 578, 367-382 (2000).
- (9) L. Maiani, F. Piccinini, A. D. Polosa and V. Riquer, Phys. Rev. Lett. 93, 212002 (2004).
- (10) L. Maiani, A. D. Polosa and V. Riquer, Phys. Lett. B 651, 129-134 (2007).
- (11) J. D. Weinstein and N. Isgur, Phys. Rev. D 41, 2236 (1990).
- (12) H. Y. Cheng, C. K. Chua and K. C. Yang, Phys. Rev. D 73, 014017 (2006).
- (13) S. Cheng and J. M. Shen, Eur. Phys. J. C 80, 554 (2020).
- (14) Y. L. Shen, W. Wang, J. Zhu and C. D. Lu, Eur. Phys. J. C 50, 877-887 (2007).
- (15) Y. Li, D. C. Yan, J. Hua, Z. Rui and H. n. Li, [arXiv:2105.03899 [hep-ph]].
- (16) Z. Rui, Y. Li and H. n. Li, JHEP 05, 082 (2021).
- (17) W. F. Wang, Phys. Rev. D 103, 056021 (2021).
- (18) J. Chai, S. Cheng and W. F. Wang, Phys. Rev. D 103, 096016 (2021).
- (19) R. Klein, T. Mannel, J. Virto and K. K. Vos, JHEP 10, 117 (2017)
- (20) T. Mannel, K. Olschewsky and K. K. Vos, JHEP 06, 073 (2020).
- (21) T. Huber, J. Virto and K. K. Vos, JHEP 11, 103 (2020).
- (22) Z. H. Zhang, Phys. Lett. B 820, 136537 (2021).
- (23) H. Y. Cheng, C. W. Chiang and C. K. Chua, Phys. Rev. D 103, no.3, 036017 (2021).
- (24) H. Y. Cheng, C. W. Chiang and Z. Q. Zhang, [arXiv:2201.00460 [hep-ph]].
- (25) S. Cheng, A. Khodjamirian and J. Virto, JHEP 05, 157 (2017).
- (26) C. Hambrock and A. Khodjamirian, Nucl. Phys. B 905, 373-390 (2016).
- (27) S. Cheng, A. Khodjamirian and J. Virto, Phys. Rev. D 96, 051901 (2017).
- (28) S. Descotes-Genon, A. Khodjamirian and J. Virto, JHEP 12, 083 (2019).
- (29) J. P. Lees et al. [BaBar], Phys. Rev. D 93, 012005 (2016).
- (30) P. Rubin et al. [CLEO], Phys. Rev. D 78, 072003 (2008).
- (31) R. Aaij et al. [LHCb], Phys. Rev. D 93, 052018 (2016).
- (32) C. Amsler et al. [Crystal Barrel], Phys. Lett. B 333, 277-282 (1994).
- (33) C. Amsler et al. [Crystal Barrel], Phys. Lett. B 355, 425-432 (1995).
- (34) M. V. Polyakov, Nucl. Phys. B 555, 231 (1999).
- (35) S. Cheng, Phys. Rev. D 99, no.5, 053005 (2019).
- (36) J. F. Donoghue, J. Gasser and H. Leutwyler, Nucl. Phys. B 343, 341-368 (1990).
- (37) M. Albaladejo and B. Moussallam, Eur. Phys. J. C 75, no.10, 488 (2015).
- (38) W. F. Wang, J. Chai and A. J. Ma, JHEP 03, 162 (2020).
- (39) A. Abele, S. Bischoff, P. Blum, N. Djaoshvili, D. Engelhardt, A. Herbstrith, C. Holtzhaussen, M. Tischhauser, J. Adomeit and B. Kammle, et al. Phys. Rev. D 57, 3860-3872 (1998).
- (40) S. M. Flatte, Phys. Lett. B 63 (1976), 224-227.
- (41) H. Y. Cheng, C. K. Chua, K. C. Yang and Z. Q. Zhang, Phys. Rev. D 87, no.11, 114001 (2013).
- (42) Particle Data Group, P. A. Zyla et al., PTEP 2020, 083C01(2020).
- (43) V. M. Braun, D. Y. Ivanov and G. P. Korchemsky, Phys. Rev. D 69, 034014 (2004).
- (44) S. Aoki, Y. Aoki, D. Becirevic, C. Bernard, T. Blum, G. Colangelo, M. Della Morte, P. Dimopoulos, S. Dürr and H. Fukaya, et al. Eur. Phys. J. C 77, no.2, 112 (2017).
- (45) S. Cheng, A. Khodjamirian and A. V. Rusov, Phys. Rev. D 102, no.7, 074022 (2020).
- (46) S. S. Agaev, Phys. Rev. D 72, 074020 (2005).
- (47) P. Ball and R. Zwicky, Phys. Lett. B 625, 225-233 (2005).
- (48) G. Duplancic, A. Khodjamirian, T. Mannel, B. Melic and N. Offen, JHEP 04, 014 (2008).
- (49) A. Khodjamirian, T. Mannel, N. Offen and Y. M. Wang, Phys. Rev. D 83, 094031 (2011).
- (50) P. Ball, V. M. Braun and A. Lenz, JHEP 05, 004 (2006).
- (51) G. S. Bali et al. [RQCD], JHEP 08, 065 (2019).
- (52) R. Arthur, P. A. Boyle, D. Brommel, M. A. Donnellan, J. M. Flynn, A. Juttner, T. D. Rae and C. T. C. Sachrajda, Phys. Rev. D 83, 074505 (2011).
- (53) A. Khodjamirian, T. Mannel and M. Melcher, Phys. Rev. D 70, 094002 (2004).
- (54) C. Shi, C. Chen, L. Chang, C. D. Roberts, S. M. Schmidt and H. S. Zong, Phys. Rev. D 92, 014035 (2015).
- (55) H. Leutwyler, Phys. Lett. B 378, 313-318 (1996).
- (56) C. Amsler, Rev. Mod. Phys. 70, 1293-1340 (1998).
- (57) D. Parganlija and F. Giacosa, Eur. Phys. J. C 77, no.7, 450 (2017).
- (58) G. Y. Wang, S. C. Xue, G. N. Li, E. Wang and D. M. Li, Phys. Rev. D 97, no.3, 034030 (2018).
- (59) H. Y. Cheng, C. K. Chua and K. C. Yang, Phys. Rev. D 73, 014017 (2006).
- (60) C. D. Lu, Y. M. Wang and H. Zou, Phys. Rev. D 75, 056001 (2007).
- (61) H. Y. Han, X. G. Wu, H. B. Fu, Q. L. Zhang and T. Zhong, Eur. Phys. J. A 49, 78 (2013).
- (62) Z. G. Wang, Eur. Phys. J. C 75, no.2, 50 (2015).
- (63) Z. Q. Zhang and Z. J. Xiao, Chin. Phys. C 34, 528-534 (2010).
- (64) Y. Li, Phys. Rev. D 89, no.9, 094007 (2014).