\volnopage

2012 Vol. X No. XX, 000–000

¹¹institutetext: Changchun Observatory, National Astronomical Observatories, Chinese Academy of Sciences, Changchun 130117, China; Corresponding Author. Y.Xu, [email protected]; Z.Yu, ziyu_-[email protected]
²²institutetext: School of Astronomy and Space Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
³³institutetext: College of Science, Nanjing Forestry University, Nanjing 210037, China
\vs\noReceived xxxx June xx; accepted xxxx July xx

Probing into the Possible Range of the U Bosonic Coupling Constants in Neutron Stars Containing Hyperons

Yan Xu 1122 Bin Diao 1122 Yi-Bo Wang 11 Xiu-Lin Huang 11 Xing-Xing Hu 11 Zi Yu 33

Abstract

The range of the U bosonic coupling constants in neutron star matter is a very interesting but still unsolved problem which has multifaceted influences in nuclear physics, particle physics, astrophysics and cosmology. The combination of the theoretical numerical simulation and the recent observations provides a very good opportunity to solve this problem. In the present work, the range of the U bosonic coupling constants is inferred based on the three relations of the mass-radius, mass-frequency and mass-tidal deformability in neutron star containing hyperons using the GM1, TM1 and NL3 parameter sets under the two flavor symmetries of the SU(6) and SU(3) in the framework of the relativistic mean field theory. Combined with observations from PSRs J1614-2230, J0348+0432, J2215-5135, J0952-0607, J0740+6620, J0030-0451, J1748-2446ad, XTE J1739-285, GW170817 and GW190814 events, our numerical results show that the U bosonic coupling constants may tend to be within the range from 0 to 20 GeV^-2 in neutron star containing hyperons. Moreover, the numerical results of the three relations obtained by the SU(3) symmetry are better in accordance with observation data than those obtained by the SU(6) symmetry. The results will help us to improve the strict constraints of the equation of state for neutron stars containing hyperons.

keywords:

dense matter;stars: neutron;equation of state

1 Introduction

In May 1932, Chadwick discovered that there is a new uncharged particle in the nucleus, named neutron(Landau 1932). It made people realize that the nucleus is composed of neutrons and protons. In the same year, Landau predicted that the possible existence of stars which is composed of neutrons, who called them ”gigantic nuclei”. In 1934, Baade and Zwicky separately proposed that neutron stars are born in supernova explosions, who coined the term ”neutron stars”(Baade & Zwicky 1934). In 1939, Oppenheimer and Volkoff first performed the theoretical calculations on the structure of neutron stars by using the work of Tolman on the spherical symmetry metric, who regarded as neutrons as an ideal degenerate Fermi gas and established the Tolman-Oppenheimer-Volkoff equations. This is the first quantitative neutron star model for deriving the mass limit of neutron star. They found such stars would have a maximum mass of 0.7 $M_{\odot}$ which is significantly lower than the maximum mass limit 1.4 $M_{\odot}$ of white dwarf(Oppenheimer & Volkoff 1939; Tolman 1939; Dar 2014). Up to now, the researches in the structures of neutron stars are more and more deeply with the continuous development in pulsar observations and the theoretical studies of neutron stars(Han & Yuen 2021; Pant et al. 2021; Zhou et al. 2022). Although many assumptions have been considered to calculate the mass limit and explored the internal composition of neutron stars, the above problems still remains mysteries due to the likely more complex structures of neutron stars.

In 2015, the gravitational waves(GWs) from the merger of a binary black hole were first directly detected, namely GW150914(Abbott et al. 2016). After two years, the gravitational waves from the merger of a binary neutron star was discovered by the LIGO and Virgo, namely GW170817(Abbott et al. 2017). It is the first time in human history that the gravitational wave observatory and the electromagnetic wave telescope are used to observe the same astrophysical event, marking the beginning of a multi-messenger era of neutron star research. In 2019, the gravitational waves from the merger of a binary compact star was discovered by the LIGO and Virgo, namely GW190814(Abbott et al. 2020). In particular, the recent astrophysical constraints on tidal deformability $\Lambda_{1.4}$ of a canonical 1.4 $M_{\odot}$ neutron star from the GW170817 and GW190814 are $\Lambda_{1.4}=190^{+390}_{-120}$ and $\Lambda_{1.4}=616^{+273}_{-158}$ , respectively(Abbott et al. 2018, 2020). The observed massive neutron stars mainly include PSRs J1614-2230 ( $1.908\pm 0.016$ $M_{\odot}$ ) (Arzoumanian et al. 2018), J0348+0432 ( $2.01\pm 0.04$ $M_{\odot}$ ) (Antoniadis et al. 2013), J0740+6620 ( $2.072^{+0.067}_{-0.066}$ $M_{\odot}$ with radius $12.39^{+1.30}_{-0.98}$ km) (Cromartie et al. 2020; Fonseca et al. 2021; Riley et al. 2021; Ferreira & Providência 2021) and J2215+5135 ( $2.27^{+0.17}_{-0.15}$ $M_{\odot}$ )(Linares et al. 2018), etc. Especially PSR J0952-0607 with $2.35\pm 0.17$ $M_{\odot}$ which is already far more than the masses of the previous massive neutron stars(Kuzuhara et al. 2022; Ecker & Rezzolla 2023). In addition, the mass and radius of PSR J0030-0451 have estimated by NICER mission, respectively( $1.34^{+0.15}_{-0.16}$ $M_{\odot}$ , $12.71^{+1.14}_{-1.19}$ km and $1.44^{+0.15}_{-0.14}$ $M_{\odot}$ , $13.02^{+1.24}_{-1.06}$ km)(Riley et al. 2019; Li et al. 2021). In all, the breakthrough detections of the GW170817 and GW190814 by the LIGO and Virgo, and the precise measurements such as the mass, radius and rotation frequency of neutron star by multi-messenger advanced telescopes such as FAST, NICER, and SKA have jointly provided a large amount of reliable observational data for the research of neutron star structure and internal composition(Abbott et al. 2018; Riley et al. 2019; Miller et al. 2019; Chatziioannou 2020; Li et al. 2021; Gao et al. 2022). However, many of us face the questions: whether there are new degrees of freedom such as hyperons besides nucleons in neutron stars? What the kind of interactions would be allowed the appearance of the new degrees of freedom in the massive neutron stars(Xia et al. 2014; Vidaña 2019; Zhao 2020; Khadkikar et al. 2022; Zhao & Liu 2022; Sun et al. 2023)?

In 1980, Fayet firstly proposed that the possible existence of a neutral weakly coupling light spin-1 vector U boson which has been considered to provide a new kind of repulsive interaction in neutron stars(Fayet 1980). The researches shows that the interaction between U bosons and baryons can modify the equation of states, gravities and increase the maximum masses of neutron stars obviously (Krivoruchenko et al. 2009; Yu et al. 2011; Zhang et al. 2011, 2016; Ding et al. 2016; Yu et al. 2018). However, there is little work about whether and how U bosons affect the tidal deformation properties of neutron stars. In addition, though the range of the U bosonic coupling constants in neutron star matter has aroused a wide attention, it remains unsolved. The comparison between the theoretical results of neutron stars and the observed data provides a possible solution to solve these problems.

In the work, the equation of states, the three relations of the mass-radius, mass-frequency and mass-tidal deformability of neutron stars containing hyperons are obtained using the GM1, TM1 and NL3 parameter sets in the relativistic mean field theory including the U bosons(Glendenning 1985; Bednarek & Manka 2005; Yang & Shen 2008; Miyatsu et al. 2013). A combination of the observed data from PSRs J1614-2230, J0348+0432, J2215-5135, J0952-0607, J0740+6620, J0030-0451, J1748-2446ad, XTE J1739-285, GW170817 and GW190814 events, we will mainly explore the possible range of the U bosonic coupling constants based on the macroscopic properties of neutron stars containing hyperons such as mass, radius, frequency and tidal deformability.

2 Theoretical framework

2.1 Relativistic Mean Field Theory

Here we apply the relativistic mean field approximation including $\sigma$ , $\omega$ , $\rho$ , $\sigma^{*}$ and $\phi$ mesons to describe the properties of the cores of neutron stars(Miyatsu et al. 2013; Xu et al. 2015, 2021; Miyatsu et al. 2022). The total Lagrangian density can be expressed as

\displaystyle\mathcal{L}=\sum_{B}\mathcal{L}_{B}+\sum_{l}\mathcal{L}_{l}+\mathcal{L}_{m}+\mathcal{L}_{u},

(1)

where B, l and m represents the baryons, leptons and mesons, respectively. The sum on B runs over the octet baryons(n, p, $\Lambda$ , $\Sigma^{+}$ , $\Sigma^{0}$ , $\Sigma^{-}$ , $\Xi^{-}$ and $\Xi^{0}$ ), and the sum on l is over electrons and muons(e and $\mu$ ). Explicitly, the Lagrangian is

	$\displaystyle\mathcal{L}_{B}=\overline{\psi}_{B}[i\gamma_{\mu}\partial^{\mu}-(m_{B}-g_{\sigma B}\sigma-g_{\sigma^{}B}\sigma^{})-g_{\rho B}\gamma_{\mu}{\vec{\mathbf{\rho}}^{\mu}}\cdot\vec{I}_{B}-g_{\omega B}\gamma_{\mu}\omega^{\mu}-g_{\phi B}\gamma_{\mu}\phi^{\mu}]\psi_{B},$		(2)
	$\displaystyle\mathcal{L}_{l}=\overline{\psi}_{l}[i\gamma_{\mu}\partial^{\mu}-m_{l}]\psi_{l},$		(3)
	$\displaystyle\mathcal{L}_{m}=-\frac{1}{4}W^{\mu v}W_{\mu v}-\frac{1}{4}\vec{R}^{\mu v}\cdot\vec{R}_{\mu v}-\frac{1}{4}P^{\mu v}P_{\mu v}+\frac{1}{2}m_{\omega}^{2}\omega_{\mu}\omega^{\mu}+\frac{1}{2}m_{\rho}^{2}{\vec{\mathbf{\rho}}}_{\mu}\cdot{\vec{\mathbf{\rho}}}^{\mu}+\frac{1}{2}m^{2}_{\phi}\phi_{\mu}\phi^{\mu}$
	$\displaystyle+\frac{1}{2}(\partial_{\mu}\sigma\partial^{\mu}\sigma-m_{\sigma}^{2}\sigma^{2})+\frac{1}{2}(\partial_{v}\sigma^{}\partial^{v}\sigma^{}-m^{2}_{\sigma^{}}\sigma^{2})-\frac{1}{3}a\sigma^{3}-\frac{1}{4}b\sigma^{4}+\frac{1}{4}c_{3}(\omega_{\mu}\omega^{\mu})^{2},$		(4)

Moreover, we consider the contribution of the U bosons to the total Lagrangian density. On the basis of the conventional view, the Yukawa term correction to Newtonian gravity is only applied at the matter part without the geometric part in general relativity(Fujii 1971, 1988). $\mathcal{L}_{u}$ is given by

\displaystyle\mathcal{L}_{u}=-\overline{\psi}_{B}g_{uB}\gamma_{\mu}u^{\mu}\psi_{B}-\frac{1}{4}U^{\mu v}U_{\mu v}+\frac{1}{2}m_{u}^{2}u_{\mu}u^{\mu}.

(5)

Here $\psi_{B}$ and $\psi_{l}$ are the baryonic and leptonic Dirac fields, respectively. $\gamma_{u}$ represents the Dirac matrice. $\vec{I}_{B}$ is the baryonic isospin matrix. $g_{mB}$ ( $g_{uB}$ ) denotes the mesonic (U bosonic) and baryonic coupling constants. The field strength tensors of $\omega$ , $\rho$ , $\phi$ and U can be defined as $W_{\mu v}=\partial_{\mu}\omega_{v}-\partial_{v}\omega_{\mu}$ , $R_{\mu v}=\partial_{\mu}{\mathbf{\rho}}_{v}-\partial_{v}{\mathbf{\rho}}_{\mu}$ , $P_{\mu v}=\partial_{\mu}\phi_{v}-\partial_{v}\phi_{\mu}$ and $U_{\mu v}=\partial_{\mu}u_{v}-\partial_{v}u_{\mu}$ , respectively. $m_{B}$ , $m_{l}$ and $m_{u}$ are the masses of baryons, leptons and U bosons, respectively.

According to the standard Euler-Lagrange equation, the equations of motion of baryons, mesons and U bosons can be derived from the total Lagrangian density in Eq.(1). The fields of the five mesons and U bosons are replaced by their classical expectation values in the relativistic mean field approximation, thus the equations of motion are given as follows

$\displaystyle(i\gamma_{\mu}\partial^{\mu}-m_{B}+g_{\sigma B}\sigma$	$\displaystyle+$	$\displaystyle g_{\sigma^{}B}\sigma^{}-g_{\omega B}\gamma_{0}\omega^{0}-g_{\rho B}\gamma_{0}I_{3B}\rho^{0}_{3}-g_{\phi B}\gamma_{0}\phi^{0}-g_{uB}\gamma_{0}u^{0})\psi_{B}=0,$	(12)
		$\displaystyle\sum_{B}g_{\sigma B}n_{SB}=m_{\sigma}^{2}\sigma+a\sigma^{2}+b\sigma^{3},$
		$\displaystyle\sum_{B}g_{\omega B}n_{B}=m_{\omega}^{2}\omega_{0}+c_{3}\omega^{3}_{0},$
		$\displaystyle\sum_{B}g_{\rho B}n_{B}I_{3B}=m_{\rho}^{2}\rho_{03},$
		$\displaystyle\sum_{B}g_{\sigma^{}B}n_{SB}=m_{\sigma^{}}^{2}\sigma^{*},$
		$\displaystyle\sum_{B}g_{\phi B}n_{B}=m_{\phi}^{2}\phi_{0},$
		$\displaystyle\sum_{B}g_{uB}n_{B}=m_{u}^{2}u_{0}.$

Here, $m_{B}^{*}=m_{B}-g_{\sigma B}\sigma-g_{\sigma^{*}B}\sigma^{*}$ is the baryonic effective mass. $n_{SB}$ and $n_{B}$ represent the scalar and baryonic number densities, respectively. The equations of state within the framework of the relativistic mean field theory can be written as

\displaystyle\varepsilon=\varepsilon_{0}+\varepsilon_{uB},\ \ \ P=P_{0}+P_{uB}.

(13)

Here $\varepsilon_{0}$ and $P_{0}$ are the the conventional energy density and pressure in the neutron star matter, respectively. Their formulas as follows:

$\displaystyle\varepsilon_{0}$	$\displaystyle=$	$\displaystyle\sum_{B}\frac{1}{\pi^{2}}\int_{0}^{p_{FB}}\sqrt{p_{B}^{2}+m_{B}^{*2}}p_{B}^{2}dp_{B}+\frac{1}{2}m_{\sigma}^{2}\sigma^{2}+\frac{1}{3}a\sigma^{3}$	(14)
	$\displaystyle+$	$\displaystyle\frac{1}{4}b\sigma^{4}+\frac{1}{2}m_{\sigma^{}}^{2}\sigma^{2}+\frac{1}{2}m_{\omega}^{2}\omega^{2}+\frac{3}{4}c_{3}\omega^{4}+\frac{1}{2}m_{\phi}^{2}\phi^{2}$
	$\displaystyle+$	$\displaystyle\frac{1}{2}m_{\rho}^{2}\rho^{2}+\sum_{l}\frac{1}{\pi^{2}}\int_{0}^{p_{Fl}}\sqrt{p_{l}^{2}+m_{l}^{*2}}p_{l}^{2}dp_{l},$
$\displaystyle P_{0}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\sum_{B}\frac{1}{\pi^{2}}\int_{0}^{p_{FB}}\frac{p_{B}^{4}dp_{B}}{\sqrt{p_{B}^{2}+m_{B}^{*2}}}-\frac{1}{2}m_{\sigma}^{2}\sigma^{2}-\frac{1}{3}a\sigma^{3}$	(15)
	$\displaystyle-$	$\displaystyle\frac{1}{4}b\sigma^{4}-\frac{1}{2}m_{\sigma^{}}^{2}\sigma^{2}+\frac{1}{2}m_{\omega}^{2}\omega^{2}+\frac{1}{4}c_{3}\omega^{4}+\frac{1}{2}m_{\phi}^{2}\phi^{2}$
	$\displaystyle+$	$\displaystyle\frac{1}{2}m_{\rho}^{2}\rho^{2}+\frac{1}{3}\sum_{l}\frac{1}{\pi^{2}}\int_{0}^{p_{Fl}}\frac{p_{l}^{4}dk}{\sqrt{p_{l}^{2}+m_{l}^{*2}}p_{l}^{2}}dp_{l},$

where $p_{FB}$ expresses the baryonic Fermi momentum. Moreover, the bosonic additional contribution for the equations of state can be expressed as

\displaystyle\varepsilon_{uB}=P_{uB}=\frac{g_{uB}^{2}n_{B}^{2}}{2m_{u}^{2}}.

(16)

For the convenience of discussion, the baryonic and U bosonic coupling constant is defined as $g_{u}=(g_{uB}/m_{u})^{2}$ . We can calculate the equations of state of neutron star matter under the $\beta$ -equilibrium and charge neutrality conditions,

\displaystyle\mu_{B}=\mu_{n}-q_{B}\mu_{e},\ \ \ \sum_{B}q_{B}\rho_{B}=0.

(17)

Here $q_{B}$ expresses the baryonic electric charge in unit of e.

2.2 Tolman-Oppenheimer-Volkoff equations

The mass-radius relations of neutron stars can be obtained by inputing the numerical results of the equations of state in the Tolman-Oppenheimer-Volkoff equations(Oppenheimer & Volkoff 1939; Tolman 1939)

	$\displaystyle\frac{dP(r)}{dr}$	$\displaystyle=$	$\displaystyle-\frac{[P(r)+\varepsilon(r)][M(r)+4\pi r^{3}P(r)]}{r(r-2M(r))},$		(18)
	$\displaystyle\frac{dM(r)}{dr}$	$\displaystyle=$	$\displaystyle 4\pi r^{2}\varepsilon(r).$		(19)

Here Eqs. (18) and (19) satisfy the boundary conditions $P(r=0)=0$ , $P(r=R)=0$ and $M(r=0)=0$ . $R$ is the radius of a neutron star.

2.3 Tidal Deformability

The dimensionless tidal deformability $\Lambda$ is defined as

\displaystyle\Lambda=\frac{2}{3}k_{2}(M/R)^{-5}.

(20)

Here $k_{2}$ is the tidal Love number and describes the reaction of a neutron star to the appearance of the external tidal field. It is given by

$\displaystyle k_{2}$	$\displaystyle=$	$\displaystyle\frac{1}{20}\biggl{(}\frac{2M}{R}\biggr{)}^{5}\biggl{(}1-\frac{2M}{R}\biggr{)}^{2}\biggl{[}2-y_{R}+(y_{R}-1)\frac{2M}{R}\biggr{]}$	(21)
		$\displaystyle\times\biggl{\{}\frac{2M}{R}\biggl{(}6-3y_{R}+\frac{3M}{R}(5y_{R}-8)+\frac{1}{4}\biggl{(}\frac{2M}{R}\biggr{)}^{2}$
		$\displaystyle\times\biggl{[}26-22y_{R}+\biggl{(}\frac{2M}{R}\biggr{)}(3y_{R}-2)+\biggl{(}\frac{2M}{R}\biggr{)}^{2}(1+y_{R})\biggr{]}\biggr{)}$
		$\displaystyle+3\biggl{(}1-\frac{2M}{R}\biggr{)}^{2}\bigg{[}2-y_{R}+(y_{R}-1)\frac{2M}{R}\bigg{]}$
		$\displaystyle\times\ln\biggl{(}1-\frac{2M}{R}\biggr{)}\biggr{\}}^{-1}.$

The quantity $y_{R}$ can be obtained by solving the following differential equation

\displaystyle r\frac{dy(r)}{dr}+y(r)^{2}+y(r)F(r)+r^{2}Q(r)=0.

(22)

Here Eq. (22) satisfies the initial condition $y(0)=2$ . $F(r)$ and $Q(r)$ are

	$\displaystyle F(r)$	$\displaystyle=$	$\displaystyle\frac{r-4\pi r^{3}[\mathcal{E}(r)-P(r)]}{r-2M(r)},$		(23)
	$\displaystyle Q(r)$	$\displaystyle=$	$\displaystyle\frac{4\pi r\biggl{(}5\mathcal{E}(r)+9P(r)+\frac{\mathcal{E}(r)+P(r)}{\partial P/\partial\mathcal{E}}-\frac{6}{4\pi r^{2}}\biggr{)}}{r-2M(r)}-4\biggl{[}\frac{M(r)+4\pi r^{3}P(r)}{r^{2}(1-2M(r)/r)}\biggr{]}^{2}.$		(24)

It can be seen from these Eqs. (21-24) that the dimensionless tidal deformability $\Lambda$ is depending on the equations of state, the compactness $M/R$ and the quantity $y_{R}$ of a neutron star.

Table 1: The three parameter sets(Miyatsu et al. 2013).

m_{\sigma}

= 550, 508.194, 511.198 MeV,

m_{\omega}

= 783, 783 and 782.501 MeV,

m_{\rho}

= 770, 770 and 763 MeV and

m_{N}

= 939, 938 and 939 MeV in GM1,TM1 and NL3, respectively(Sugahara & Toki 1994; Lalazissis et al. 1997; Banik & Bandyopadhyay 2001; Lopes & Menezes 2012). The coupling relations are set to

g_{\sigma^{*}N}=g_{\rho_{\Lambda}}=0

and

g_{\sigma^{*}\Lambda}=g_{\sigma^{*}\Sigma}=0

Properties of the symmetric nuclear matter
Parameter sets	GM1		TM1		NL3
Symmetries	SU(6)	SU(3)	SU(6)	SU(3)	SU(6)	SU(3)
$g_{\sigma N}$	9.57	9.57	10.029	10.029	10.217	10.217
$g_{2}$ (fm^-1)	12.28	12.28	7.233	7.233	10.431	10.431
$g_{3}$	-8.98	-8.98	0.618	0.618	-28.885	-28.885
$c_{3}$	—	—	71.308	81.601	—	—
$g_{\omega N}$	10.61	10.26	12.614	12.199	12.868	12.450
$g_{\rho N}$	4.10	4.10	4.632	4.640	4.474	4.474
$g_{\phi N}$	—	-3.50	—	-4.164	—	-4.250
$g_{\sigma\Lambda}$	5.84	7.25	6.170	7.733	6.269	7.853
$g_{\sigma\Sigma}$	3.87	5.28	4.472	6.035	4.709	6.293
$g_{\sigma\Xi}$	3.06	5.87	3.202	6.328	3.242	6.408
$g_{\sigma^{\ast}\Lambda}$	3.73	2.60	5.015	3.691	5.374	4.174
$g_{\sigma^{\ast}\Xi}$	9.67	6.82	11.516	8.100	11.765	8.378
$n_{B}^{0}$ (fm^-3)	0.153	0.153	0.145	0.145	0.148	0.148
$\omega_{0}$ (MeV)	-16.3	-16.3	-16.3	-16.3	-16.299	-16.299
$m_{B}^{*}$ $/m_{B}$	0.70	0.70	0.634	0.634	0.60	0.60
$K_{\nu}$ (MeV)	300	300	281	284	271.76	271.76
$a_{4}$ (MeV)	32.5	32.5	36.9	36.9	37.4	37.4
$L$ (MeV)	93.9	93.9	110.9	110.8	118.0	118.0

2.4 Coupling constants

To gain the numerical results of the equations of state and the properties of neutron star matter, we need three kinds of coupling constants in order to solving the above equations. The first one is the nucleonic and mesonic coupling constants which could reflect the saturation properties of the symmetric nuclear matter. The second one is the hyperonic and mesonic coupling constants. They are impossible to be determined by the saturation properties of the symmetric nuclear matter because the hyperonic critical densities are much higher than the saturation density of nuclear matter. The hyperonic and mesonic coupling constants can be determined so as to reproduce the observed properties of nuclear matter and the experimental data of hypernuclei. Thus the baryonic and mesonic coupling constants under SU(6) spin-flavor and SU(3) flavor symmetries are widely used in the study of neutron stars. In two symmetries, the $\omega$ and $\phi$ mesons are described by the pure singlet ${\left|1\right\rangle}$ and octet ${\left|8\right\rangle}$ , then read

\displaystyle\omega=\cos\theta_{v}+\sin\theta_{v},\ \ \ \phi=-\sin\theta_{v}+\cos\theta_{v}.

(25)

In the SU(6) spin-flavor symmetry, the mixing angle and the coupling ratio are given by

\displaystyle\theta_{v}^{ideal}=\simeq 35.26^{\circ},\ \ \ z=\frac{1}{\sqrt{6}}\simeq 0.4082.

(26)

The usual SU(6) relations are as follows:

\displaystyle g_{\omega N}=\frac{3}{2}g_{\omega\Lambda}=\frac{3}{2}g_{\omega\Sigma}=3g_{\omega\Xi},\ \ \ g_{\phi N}=0,\ \ \ g_{\phi\Lambda}=g_{\phi\Sigma}=\frac{1}{2}g_{\phi\Xi}=\frac{\sqrt{2}}{3}g_{\omega N}.

(27)

The SU(3) symmetry can be seen as the symmetry group with three flavors of up, down and strange quarks denoting the strong interactions. In the SU(3) flavor symmetry, the mixing angle and the coupling ratio are given by

\displaystyle\theta_{v}^{ideal}=\simeq 37.50^{\circ},\ \ \ z=0.1949.

(28)

The SU(3) relations are as follows:

	$\displaystyle g_{\omega\Lambda}=g_{\omega\Sigma}=\frac{1}{1+\sqrt{3}z\tan\theta_{v}}g_{\omega N},\ \ \ g_{\omega\Xi}=\frac{1-\sqrt{3}z\tan\theta_{v}}{1+\sqrt{3}z\tan\theta_{v}}g_{\omega N},$
	$\displaystyle g_{\phi\Lambda}=g_{\phi\Sigma}=\frac{-\tan\theta_{v}}{1+\sqrt{3}z\tan\theta_{v}}g_{\omega N},\ \ \ g_{\phi\Xi}=-\frac{\sqrt{3}z+\tan\theta_{v}}{1+\sqrt{3}z\tan\theta_{v}}g_{\omega N},$
	$\displaystyle g_{\phi N}=\frac{\sqrt{3}z-\tan\theta_{v}}{1+\sqrt{3}z\tan\theta_{v}}g_{\omega N}.$		(29)

The third one is the baryonic and U bosonic coupling constants. In order to ensure the stability of neutron stars using the equations of state constrained by the FOPI/GSI data, Wen et al. point out that $g_{u}$ should be located in 0-100 GeV^-2(Xiao et al. 2009; Wen et al. 2009; Zhang et al. 2011). In this work, the U bosonic influence is researched within the region of $g_{u}=$ 0-40 GeV^-2. Three typical parameter sets GM1, TM1 and NL3 are selected to describe the interactions and the corresponding the saturation properties are listed in Table 1.

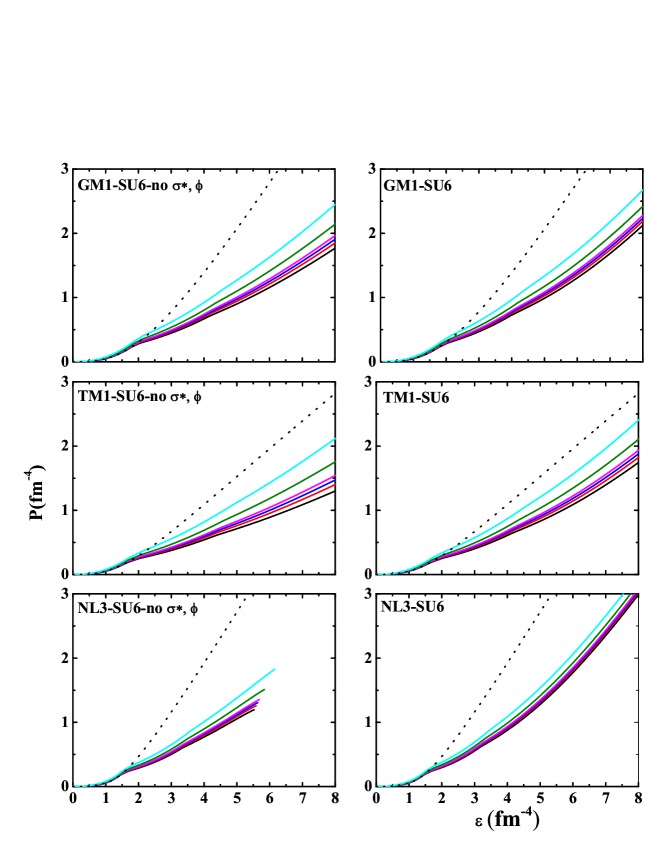
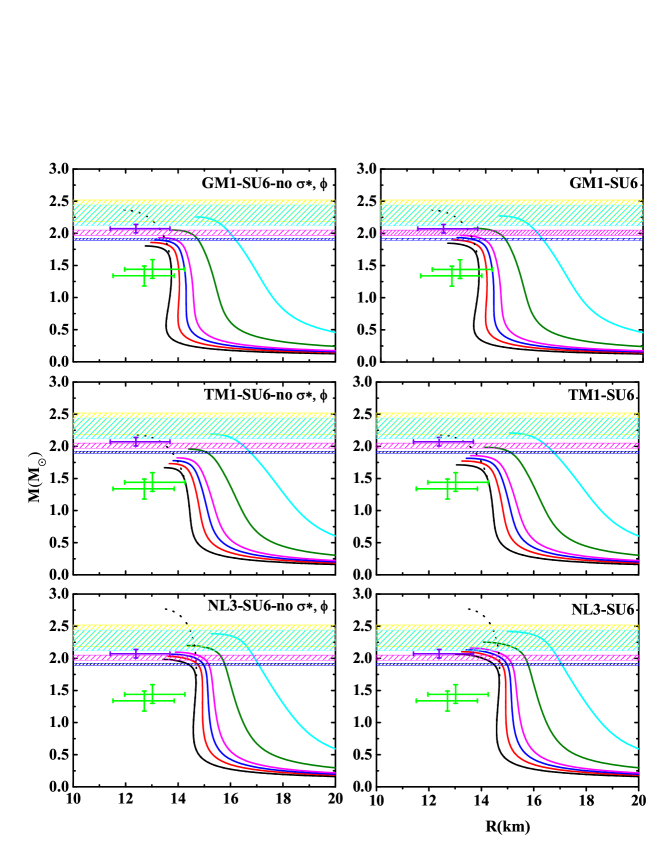
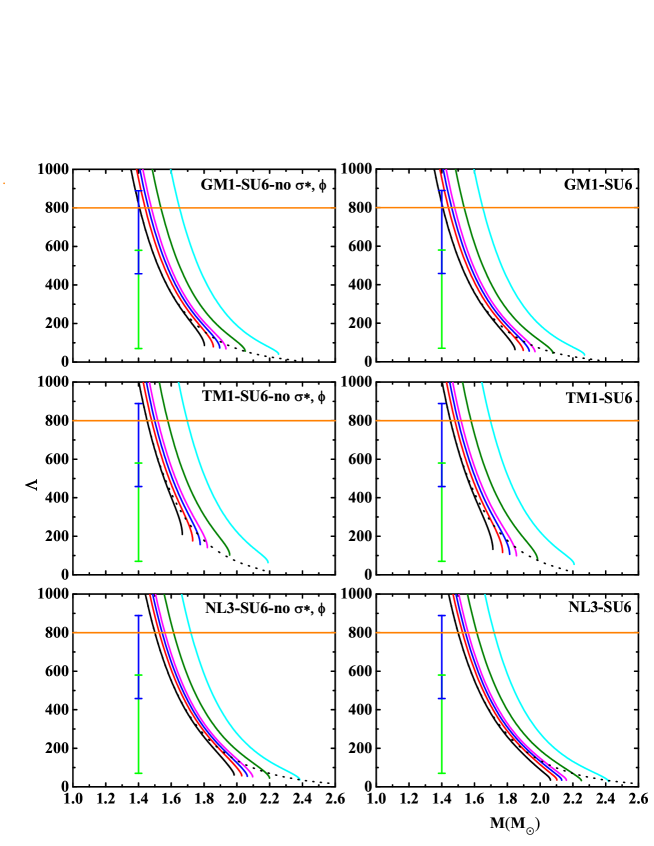
Refer to caption — Figure 1: Pressures $P$ vs energy densities $\varepsilon$ of neutron stars for the three cases, SU6-no $\sigma^{*}$ , $\phi$ , SU6 and SU3 under each parameter set. In the paper, the the black, red, blue, magenta, olive and oyan colored lines express the six cases of $g_{u}$ = = 0, 4, 7, 10, 20 and 40 GeV^-2 in npH matter, respectively. The dot line stands for the case of $g_{u}$ = 0 GeV^-2 in np matter.

3 Result and Discussion

In the work, we consider two categories of neutron star matter: one contains just neutrons, protons, electrons and muons, which is denoted as np. And the other contains neutrons, protons, electrons, muons and hyperons, which is denoted as npH. We start our calculation with three parameter sets GM1, TM1 and NL3 using the relativistic mean field model involved U boson to describe neutron star matter. The equations of state are derived under satisfying constraints of the recent nuclear and astrophysics (see Fig. 1). In Fig. 1, the black, red, blue, magenta, olive and oyan colored lines correspond to the six cases of the U bosonic coupling constants $g_{u}$ = 0, 4, 7, 10, 20 and 40 GeV^-2 in npH matter, while the dot one corresponds to the case of $g_{u}$ = 0 GeV^-2 in np matter. We give three cases in Eq. (13) for the relativistic mean field theory: (i) the $\sigma$ , $\omega$ and $\rho$ mesons are involved in the SU(6) spin-flavor symmetry based upon the naive quark model, which is denoted as SU6-no $\sigma^{*}$ , $\phi$ , (ii) the $\sigma$ , $\omega$ , $\rho$ including strange mesons $\sigma^{*}$ and $\phi$ are involved in the SU(6) spin-flavor symmetry, which is denoted as SU6, (iii) the $\sigma$ , $\omega$ , $\rho$ , $\sigma^{*}$ and $\phi$ mesons are involved in the general SU(3) flavor symmetry, which is denoted as SU3. Between the same kind of line type in npH matter, the results of $g_{u}$ = 40 GeV^-2 and 0 GeV^-2 correspond to stiffer and softer equations of state, repectively. After the appearance of hyperons in Fig. 1, the equations of state in npH matter become obviously softer compared with these in np matter, and the gaps between the equations of state of np matter and npH matter are smaller and smaller with the values of $g_{u}$ rising, especially in the case of SU3.

Table 2: Maximum masses

m_{max}=M_{max}/M_{\odot}

and the corresponding radii R and Kepler frequencies

\nu_{k}

of neutron stars for the U bosonic coupling constant

g_{u}

= 0, 4, 7, 10, 20 and 40 GeV^-2, respectively.

		npH matter							np matter
		$g_{u}$ (GeV^-2)	0	4	7	10	20	40	0
GM1	SU6-no $\sigma^{*}$ , $\phi$	$m_{max}$	1.802	1.857	1.896	1.933	2.051	2.255	2.361
	SU6	$m_{max}$	1.847	1.897	1.933	1.968	2.078	2.271	2.361
	SU3	$m_{max}$	1.964	1.996	2.020	2.043	2.120	2.266	2.312
	SU6-no $\sigma^{*}$ , $\phi$	$R$ (km)	12.763	12.965	13.111	13.262	13.758	14.647	11.931
	SU6	$R$ (km)	12.558	12.758	12.910	13.065	13.552	14.512	11.931
	SU3	$R$ (km)	11.127	11.344	11.501	11.672	12.208	13.243	11.530
	SU6-no $\sigma^{*}$ , $\phi$	$\nu_{k}$ (Hz)	931.079	922.991	917.104	910.400	887.373	847.069	1178.955
	SU6	$\nu_{k}$ (Hz)	965.623	955.788	947.901	939.502	913.746	862.060	1178.955
	SU3	$\nu_{k}$ (Hz)	1193.912	1169.249	1152.194	1133.520	1079.445	987.844	1228.212
TM1	SU6-no $\sigma^{*}$ , $\phi$	$m_{max}$	1.667	1.731	1.776	1.820	1.957	2.190	2.179
	SU6	$m_{max}$	1.712	1.771	1.814	1.856	1.984	2.207	2.179
	SU3	$m_{max}$	1.732	1.779	1.812	1.845	1.949	2.137	2.094
	SU6-no $\sigma^{*}$ , $\phi$	$R$ (km)	13.482	13.666	13.812	13.959	14.412	15.256	12.375
	SU6	$R$ (km)	13.055	13.263	13.430	13.602	14.141	15.079	12.375
	SU3	$R$ (km)	11.019	11.275	11.461	11.642	12.237	13.384	11.721
	SU6-no $\sigma^{*}$ , $\phi$	$\nu_{k}$ (Hz)	824.845	823.475	821.058	818.070	808.466	785.386	1072.340
	SU6	$\nu_{k}$ (Hz)	877.143	871.360	865.427	858.686	837.671	802.355	1072.340
	SU3	$\nu_{k}$ (Hz)	1137.765	1113.920	1097.188	1081.381	1031.356	944.047	1140.338
NL3	SU6-no $\sigma^{*}$ , $\phi$	$m_{max}$	1.983	2.030	2.064	2.096	2.200	2.383	2.774
	SU6	$m_{max}$	2.063	2.102	2.132	2.160	2.251	2.418	2.774
	SU3	$m_{max}$	2.291	2.312	2.327	2.342	2.392	2.492	2.732
	SU6-no $\sigma^{*}$ , $\phi$	$R$ (km)	13.425	13.618	13.752	13.902	14.355	15.268	13.295
	SU6	$R$ (km)	13.010	13.255	13.424	13.580	14.089	14.997	13.295
	SU3	$R$ (km)	11.920	12.070	12.184	12.301	12.701	13.482	12.900
	SU6-no $\sigma^{*}$ , $\phi$	$\nu_{k}$ (Hz)	905.328	896.214	890.761	883.326	862.322	818.337	1086.499
	SU6	$\nu_{k}$ (Hz)	967.838	950.138	938.688	928.723	897.237	846.646	1086.499
	SU3	$\nu_{k}$ (Hz)	1163.119	1146.556	1134.214	1121.710	1080.568	1008.414	1128.045

After the numerical solution of the Tolman-Oppenheimer-Volkoff equations of hydrostatic equilibrium for the isolated cold neutron stars, combined with the recent constraints on the mass and radius inferred from PSRs J1614-2230, J0348+0432, J2215-5135, J0952-0607, J0740+6620 and J0030-0451, we obtained the mass-radius relation diagram (see Fig. 2). The maximum masses and the corresponding radii and Kepler frequencies for the three cases of each parameter set are listed in Table 2. As shown in Fig. 2 and Table 2, the maximum masses of neutron stars increase with the values of $g_{u}$ increasing in npH matter. It is clear that the maximum masses of npH matter for the GM1, TM1 and NL3 parameter sets using the different U bosonic coupling constants vary by big margins and lie in the scope of 1.667-2.492 $M_{\odot}$ . The corresponding radii lie in the range 11.019 to 15.268 km. For the np matter, the maximum mass and the corresponding radius ranges at $g_{u}$ = 0 GeV^-2 are 2.094-2.774 $M_{\odot}$ and 11.530-13.295 km, respectively. In addition, the masses can simultaneously satisfy the constraints of the four massive pulsars other than PSR J0740+6620 in the three cases for the GM1 and TM1 parameter sets with $g_{u}$ = 40 GeV^-2 as well as for the NL3 parameter set with $g_{u}$ = 20 and 40 GeV^-2. The mass-radius relations can simultaneously satisfy the mass and radius constraints of the six pulsars only in the cases of SU3 for the NL3 parameter set with $g_{u}$ = 0, 4, 7 and 10 GeV^-2. In paticular, the radius at the canonical mass of a neutron star with 1.4 $M_{\odot}$ has a far greater influence than the radius at the maximum mass and lies in the scope of 12.957-17.825 km.

Fig. 3 displays the mass-frequency relation for the GM1, TM1 and NL3 parameter sets with the different U bosonic coupling constants, combined with the observational limits on the frequency inferred from the rapidly rotating pulsars PSR J1748-2446ad ( $\nu$ = 716 Hz) and XTE J1739-285 ( $\nu$ = 1122 Hz) (Hessels et al. 2006; Kaaret et al. 2007). However, Bult et al. observed XTE J1739-285 in 2020, they did not find the rotation frequency near 1122 Hz and concluded that it is unlikely to have the sub-millisecond rotation period 0.89 ms (Bult et al. 2021). We take $\nu$ = 1000 Hz as the threshold of the upper limit to limit our numerical results in Fig. 3. As shown in Fig. 2 and Table 2, the Kepler frequencies at the maximum masses in npH matter decrease with the values of $g_{u}$ increasing and lie in the scope of 785.386 - 1193.912 Hz, which happen with a relatively large variation since the variations of the maximum masses obtained for all equation of states are greater. The Kepler frequencies at the maximum masses lie in the scope of 1072.340 - 1228.212 Hz with $g_{u}$ = 0 GeV^-2 in np matter. At the same value of the Kepler frequency, the growth of $g_{u}$ value makes the mass of neutron star increase. At the same value of the mass, the growth of $g_{u}$ value makes the Kepler frequency of neutron star decrease. In particular, the Kepler frequencies at the canonical mass are also much larger and lie in the scope of 496.962 - 802.806 Hz in npH matter. The corresponding values at the canonical mass lie in the scope of 666.514 - 770.347 Hz with $g_{u}$ = 0 GeV^-2 in np matter. In the absence of U bosons, for np matter, the Kepler frequencies can reach above 1000 Hz in the massive neutron stars in the three cases for the GM1, TM1 and NL3 parameter sets; for npH matter, the Kepler frequencies can also reach above 1000 Hz in the massive neutron stars only in the cases of SU3 for the GM1, TM1 and NL3 parameter sets. In the presence of U bosons, for npH matter, the Kepler frequencies can reach above 1000 Hz in the massive neutron stars only in the cases of SU3 for the GM1 and TM1 parameter sets with $g_{u}$ = 4, 7, 10 and 20 GeV^-2. They can also reach above 1000 Hz at $g_{u}$ = 40 GeV^-2 in the case of SU3 for the NL3 parameter set. The above results show that if the rapidly rotating pulsars with the frequencies above 716 Hz are detected in the future, which will help us to effectively constrain the specific range of the U bosonic coupling constants in npH matter.

Fig. 4 depicts the variation of the dimensionless tidal deformabilities with the masses of neutron stars for the GM1, TM1 and NL3 parameter sets with the different U bosonic coupling constants. The constraints on $\Lambda$ from the recent gravitational wave data are also depicted. The green and blue overlaid arrows represent the recent constraints on the $\Lambda_{1.4}$ from the GW170817 ( $\Lambda_{1.4}=190^{+390}_{-120}$ ) and GW190814 ( $\Lambda_{1.4}=616^{+273}_{-158}$ ) data (Abbott et al. 2018, 2020; Miyatsu et al. 2022). The orange line is the upper limit on the dimensionless tidal deformability at the canonical mass from the initial GW170817 data, $\Lambda_{1.4}$ = 800 (Abbott et al. 2017). In Fig. 4, the dimensionless tidal deformabilities are monotonically decreasing with the masses of neutron stars. At the same value of the tidal deformability, the growth of $g_{u}$ value makes the mass of neutron star increase. At the same value of the mass, the growth of $g_{u}$ value makes the tidal deformability of neutron star increase. In particular, the tidal deformabilities at the canonical mass are also much larger and lie in the scope of 461.273 - 3088.382 in npH matter, $\Lambda_{1.4}$ are consistent with the observed results from the GW170817, GW190814 and $\Lambda_{1.4}\leq$ 800 data only in the cases of SU3 for the GM1 and TM1 parameter sets with $g_{u}$ = 0 and 4 GeV^-2, $\Lambda_{1.4}$ in the cases of SU3 for the NL3 parameter set with $g_{u}$ = 0 and 4 GeV^-2 can only satisfy the constraints of the GW190814 and $\Lambda_{1.4}\leq$ 800 data. The corresponding values at the canonical mass lie in the scope of 469.244 - 1189.347 with $g_{u}$ = 0 GeV^-2 in np matter, $\Lambda_{1.4}$ can satisfy the constraints of the GW170817, GW190814 and $\Lambda_{1.4}\leq$ 800 data at the same time only in the cases of SU3 for the GM1 and TM1 parameter sets with $g_{u}$ = 0 GeV^-2, $\Lambda_{1.4}$ in the case of SU3 for the NL3 parameter set with $g_{u}$ = 0 GeV^-2 can only satisfy the constraint of the GW190814 and $\Lambda_{1.4}\leq$ 800 data. In the future, more and more the gravitational wave data related to neutron stars will be detected, which will be very meaningful for us to analyze the species of particles and the range of the U bosonic coupling constants in neutron stars.

4 Conclusion

In the work, we analysed the possible constraints on the range of the U bosonic coupling constants in neutron star containing hyperons which are combined with measurements and estimations of the mass and radius inferred from PSRs J1614-2230, J0348+0432, J2215-5135, J0952-0607, J0740+6620 and J0030-0451, the frequency inferred from the rapidly rotating pulsars PSR J1748-2446ad and XTE J1739-285 as well as gravitational wave data inferred from the events GW170817 and GW190814. The equations of state for neutron stars are obtained by the relativistic mean field model with the parameter sets of GM1, TM1 and NL3 under the SU(6) spin-flavor and SU(3) flavor symmetries. The results show that the growth of the U bosonic coupling constants $g_{u}$ makes the gaps between the equations of state of npH and np matter smaller. Especially when in the case of SU(3) flavor symmetry for the TM1 parameter set with $g_{u}$ = 40 GeV^-2, the two the equations of state for npH and np matter almost coincide. For npH matter, the masses and radii of neutron stars can simultaneously satisfy the constraint of the above six pulsars only in the cases of the SU(3) flavor symmetry for the NL3 parameter set with $g_{u}$ = 0, 4, 7 and 10 GeV^-2. The Kepler frequencies can reach above 1000 Hz only in the case of the SU(3) flavor symmetry for the GM1 and TM1 parameter sets without $g_{u}$ = 40 GeV^-2 and for the NL3 parameter set with $g_{u}$ = 0, 4, 7, 10, 20 and 40 GeV^-2. The tidal deformabilities can meet the constraints of the GW170817 and GW190814 data at the same time only in the case of the SU(3) flavor symmetry for the GM1 and TM1 parameter sets with $g_{u}$ = 0 and 4 GeV^-2.

Although our results depend on the adopted model and parameters, it is clear from the results that the U bosonic coupling constants based on the current observational data is very likely to be located in the range of 0 - 20 GeV^-2 from the three relations of the mass-radius, mass-frequency and mass-tidal deformability in neutron star containing hyperons. It might help us further constrain the equations of state of neutron stars containing hyperons. In addition, the numerical results of the baryonic and mesonic coupling constants under SU(3) flavor symmetry are more reasonable than those under SU(6) spin-flavor symmetry combined with the astronomical observations. We will continue to carry out in-depth research in the future. It is believed that the internal structure of neutron stars will finally be revealed with the continuous improvement of astronomical observations and nuclear physics data related to neutron stars.

Acknowledgements.

The authors sincerely thank Dr. J. L. Han from National Astronomical Observatory, Chinese Academy of Sciences for his constructive comments on the theoretical research of neutron stars.

Data Availability

The data are not publicly available due to the restrictions, e.g.,their containing information that could compromise the third-party rights and the privacy of research participants.

References

Abbott et al. (2016) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Physical Review Letters, 116, 061102
Abbott et al. (2017) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Physical Review Letters, 119, 161101
Abbott et al. (2018) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2018, Physical Review Letters, 121, 161101
Abbott et al. (2020) Abbott, R., Abbott, T. D., Abraham, S., LIGO Scientific Collaboration, & Virgo Collaboration 2020, ApJ, 896, L44
Antoniadis et al. (2013) Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448
Arzoumanian et al. (2018) Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2018, ApJS, 235, 37
Baade & Zwicky (1934) Baade, W., & Zwicky, F. 1934, Physical review, 45, 138
Banik & Bandyopadhyay (2001) Banik, S., & Bandyopadhyay, D. 2001, Phys. Rev. C, 64, 055805
Bednarek & Manka (2005) Bednarek, I., & Manka, R. 2005, J Phys G: Nucl Part Phys, 31, 1009
Bult et al. (2021) Bult, P., Altamirano, D., Arzoumanian, Z., et al. 2021, ApJ, 907, 79
Chatziioannou (2020) Chatziioannou, K. 2020, General Relativity and Gravitation, 52, 109
Cromartie et al. (2020) Cromartie, H. T., Fonseca, E., Ransom, S. M., et al. 2020, Nature Astronomy, 4, 72
Dar (2014) Dar, J. A. 2014, International Journal of Astronomy and Astrophysics, 4, 414
Ding et al. (2016) Ding, W.-B., Hou, J.-W., Qi, Z.-Q., et al. 2016, Communications in Theoretical Physics, 65, 772
Ecker & Rezzolla (2023) Ecker, C., & Rezzolla, L. 2023, MNRAS, 519, 2615
Fayet (1980) Fayet, P. 1980, Physics Letters B, 95, 285
Ferreira & Providência (2021) Ferreira, M., & Providência, C. 2021, Phys. Rev. D, 104, 063006
Fonseca et al. (2021) Fonseca, E., Cromartie, H. T., Pennucci, T. T., et al. 2021, ApJ, 915, L12
Fujii (1971) Fujii, Y. 1971, Nature Physical Science, 234, 5
Fujii (1988) Fujii, Y. 1988, International Astronomical Union, 471–477
Gao et al. (2022) Gao, Y., Lai, X.-Y., Shao, L., & Xu, R.-X. 2022, MNRAS, 509, 2758
Glendenning (1985) Glendenning, N. K. 1985, ApJ, 293, 470
Han & Yuen (2021) Han, X.-H., & Yuen, R. 2021, Research in Astronomy and Astrophysics, 21, 228
Hessels et al. (2006) Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901
Kaaret et al. (2007) Kaaret, P., Prieskorn, Z., in ’t Zand, J. J. M., et al. 2007, ApJ, 657, L97
Khadkikar et al. (2022) Khadkikar, S., Mangat, C. S., & Banik, S. 2022, Journal of Astrophysics and Astronomy, 43, 57
Krivoruchenko et al. (2009) Krivoruchenko, M. I., Šimkovic, F., & Faessler, A. 2009, Phys. Rev. D, 79, 125023
Kuzuhara et al. (2022) Kuzuhara, M., Currie, T., Takarada, T., et al. 2022, ApJ, 934, L18
Lalazissis et al. (1997) Lalazissis, G. A., König, J., & Ring, P. 1997, Phys. Rev. C, 55, 540
Landau (1932) Landau, L. 1932, Physikalische Zeitschrift der Sowjetunion, 1, 285
Li et al. (2021) Li, A., Miao, Z., Han, S., & Zhang, B. 2021, ApJ, 913, 27
Linares et al. (2018) Linares, M., Shahbaz, T., & Casares, J. 2018, ApJ, 859, 54
Lopes & Menezes (2012) Lopes, L. L., & Menezes, D. P. 2012, Brazilian Journal of Physics, 42, 428
Miller et al. (2019) Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24
Miyatsu et al. (2022) Miyatsu, T., Cheoun, M.-K., Kim, K., & Saito, K. 2022, arXiv e-prints, arXiv:2209.02861
Miyatsu et al. (2013) Miyatsu, T., Cheoun, M.-K., & Saito, K. 2013, Phys. Rev. C, 88, 015802
Oppenheimer & Volkoff (1939) Oppenheimer, J. R., & Volkoff, G. M. 1939, Physical Review, 55, 374
Pant et al. (2021) Pant, N., Govender, M., & Gedela, S. 2021, Research in Astronomy and Astrophysics, 21, 109
Riley et al. (2019) Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21
Riley et al. (2021) Riley, T. E., Watts, A. L., Ray, P. S., et al. 2021, ApJ, 918, L27
Sugahara & Toki (1994) Sugahara, Y., & Toki, H. 1994, Nucl. Phys. A, 579, 557
Sun et al. (2023) Sun, X., Miao, Z., Sun, B., & Li, A. 2023, ApJ, 942, 55
Tolman (1939) Tolman, R. C. 1939, Physical Review, 55, 364
Vidaña (2019) Vidaña, I. 2019, in The 13th International Conference on HyperNuclear and Strange Particle Physics: HYP2018, American Institute of Physics Conference Series, vol. 2130, 040011
Wen et al. (2009) Wen, D.-H., Li, B.-A., & Chen, L.-W. 2009, Phys. Rev. Lett., 103, 211102
Xia et al. (2014) Xia, C. J., Peng, G. X., Chen, S. W., Lu, Z. Y., & Xu, J. F. 2014, Phys. Rev. D, 89, 105027
Xiao et al. (2009) Xiao, Z.-G., Li, B.-A., Chen, L.-W., Yong, G.-C., & Zhang, M. 2009, Phys. Rev. Lett., 102, 062502
Xu et al. (2021) Xu, Y., Huang, X. L., Wang, Y. B., Liu, C. Z., & Han, J. L. 2021, International Journal of Modern Physics D, 30, 2150054
Xu et al. (2015) Xu, Y., Liu, C.-Z., Fan, C.-B., et al. 2015, Research in Astronomy and Astrophysics, 15, 725
Yang & Shen (2008) Yang, F., & Shen, H. 2008, Phys. Rev. C, 77, 025801
Yu et al. (2011) Yu, Z., Ding, W.-B., Bao, T., & Liu, N.-N. 2011, Chinese Physics Letters, 28, 089701
Yu et al. (2018) Yu, Z., Xu, Y., Zhang, G.-Q., & Hu, T.-P. 2018, Communications in Theoretical Physics, 69, 417
Zhang et al. (2016) Zhang, D.-R., Jiang, W.-Z., Wei, S.-N., Yang, R.-Y., & Xiang, Q.-F. 2016, European Physical Journal A, 52, 142
Zhang et al. (2011) Zhang, D.-R., Yin, P.-L., Wang, W., Wang, Q.-C., & Jiang, W.-Z. 2011, Phys. Rev. C, 83, 035801
Zhao (2020) Zhao, X.-F. 2020, Chinese Journal of Physics, 63, 240
Zhao & Liu (2022) Zhao, X.-F., & Liu, T.-P. 2022, European Physical Journal C, 82, 682
Zhou et al. (2022) Zhou, D. J., Han, J. L., Zhang, B., et al. 2022, Research in Astronomy and Astrophysics, 22, 124001