Probing dark matter interactions with 21cm observations
Abstract
Similarly to warm dark matter which features a cut-off in the matter power spectrum due to free-streaming, many interacting dark matter models predict a suppression of the matter power spectrum on small length scales through collisional damping. Forecasts for 21cm line intensity mapping have shown that an instrument like the SKA will be able to probe a suppression of power in warm dark matter scenarios in a statistically significant way. Here we investigate the implications of these findings on interacting dark matter scenarios, particularly dark matter-neutrino interactions, which we use as an example. Using a suite of cosmological -body simulations, we demonstrate that interacting scenarios show a suppression of the non-linear power spectrum similar to warm dark matter models. This implies that 21cm line intensity mapping will be able to set the strongest limits yet on dark matter-neutrino scattering, improving the constraints by two orders of magnitude over current Lyman- bounds, and by four orders of magnitude over cosmic microwave background and baryon acoustic oscillations limits. However, to distinguish between warm dark matter and interacting scenarios, our simulations show that percent-level precision measurements of the matter power spectrum at redshifts are necessary, as the key features of interacting scenarios are washed out by non-linear evolution at later times.
CPPC-2022-06
1 Introduction
The universe on large scales seems to be well described by the simple cosmological CDM model. The model reproduces to a high accuracy the statistical properties of both the cosmic microwave background (CMB) anisotropies and the large-scale matter distribution—including the baryon acoustic oscillations (BAO)—using only six parameters [1, 2, 3]. However, this simplicity comes at a price: in order to achieve concordance with observations, the model must invoke two mysterious components, namely, dark matter and dark energy. The standard assumptions for these are, respectively, a collisionless massive particle—the so-called Cold Dark Matter (CDM)—and a cosmological constant (). Many particle physics models have been designed to include a viable particle candidate for the dark matter; similarly, there is no shortage of gravity theories capable of mimicking the phenomenology of a cosmological constant. However, there is no consensus yet on the nature of either component [4, 5, 6].
Focusing on the dark matter question, we note that generic CDM particle candidates predict structures on all length scales. However, we cannot preclude the possibility that structures may not be present on small length scales not yet accessible to observations. Indeed, several classes of dark matter scenarios predict exactly that. The warm dark matter (WDM) scenarios, for example, are typically characterised by a relatively low particle mass (in the low keV range). Such light masses enable the free-streaming of these particles to erase the primordial seeds for cosmological structure formation, thus leading to a heavily suppressed number of small-scale structures relative to the CDM case [7, 8, 9, 10, 11, 12, 13, 14, 15, 16].
Another interesting possibility are the interacting dark matter (IDM) scenarios, wherein the interaction of the dark matter—with other constituents of the universe or with itself—persists until the primordial nucleosynthesis epoch or later. This class of dark matter also predicts a loss of small-scale structures on cosmologically testable scales, but through collisional damping rather than free-streaming. In addition, IDM scenarios predict the appearance of dark acoustic oscillations, as has been demonstrated in the linear regime of evolution, a strong distinguishing feature of this class of dark matter scenarios from the classic WDM. A variety of IDM scenarios has been investigated in the literature. These include interactions of dark matter with itself [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28], with baryons [27, 29, 28, 30, 31, 32, 33, 34, 35, 36, 37], with photons [27, 38, 28, 39, 40, 32, 31, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50], as well as with neutrinos [27, 28, 51, 52, 53, 45, 54, 55, 56, 57] and more recently with a dark sector radiation species [58, 59, 60, 61, 62, 63, 64, 65, 66].
While both WDM and IDM are often invoked as a possible solution to the observational challenges confronting CDM on small scales [67], we emphasise that, ultimately, the way to acquire a complete picture of the fundamental nature of dark matter is to reconstruct the matter power spectrum down to the smallest scales and at the highest redshifts possible. Indeed, although both WDM and IDM predict a damped power spectrum in the linear regime and IDM scenarios have additional tell-tale features, the evolution of structure formation in the non-linear regime tends to erase these differences, bringing the observable effects of these scenarios closer to the CDM predictions with time [68]. Hence, the closer the observations are to probing the linear regime of evolution, the better they would be for distinguishing between these scenarios and possibly confirming the particle nature of dark matter.
As technology advances and ever better experiments are built, we gain access to more powerful probes to constrain deviations from CDM (or perhaps even rule out CDM itself). In this work, we confirm that measurements of the matter power spectrum at high redshifts will be a key observable to probe the existence of dark matter interactions and show that 21cm intensity mapping, which traces neutral hydrogen—commonly denoted HI—through its emission from a hyperfine transition to its ground state, will provide a critical tool to do so. Although the all-sky average signal, including redshift information, has already been measured by EDGES [69], which can also be used to constrain dark matter interactions [50], its lack of angular resolution does not allow for intensity mapping. Future observatories such as SKA, however, will have a much better resolution than EDGES and its measurements of the 21cm emission intensity as a function of the angular position will yield density maps similar to maps of the CMB anisotropies [70, 71, 72, 73, 74, 75]. Together with redshift information out to , these angular maps will enable the 3D reconstruction of the distribution of emitters in the sky [76]. Thus, high resolution radio surveys to be performed with such instruments as SKA will be ideal to help distinguish between different types of dark matter scenarios.
To make our predictions, we perform a suite of numerical simulations using the public code gadget-4 [77], for several WDM and IDM scenarios as well as CDM which we use as reference. In the case of IDM, we use as a generic example a dark matter-neutrino scattering scenario, as this can help probe very weak dark matter interactions with the Standard Model and might also be related to the neutrino mass generation mechanism [78]. The linear evolution of this IDM scenario is computed using a modified version of class [79, 80] described in Ref. [56], which includes the full Boltzmann hierarchy for massive neutrinos interacting with a heavy dark matter species. Our simulations show that, while the small-scale suppression of the IDM matter power spectrum remains—thereby making the scenario distinguishable from CDM—the dark acoustic oscillations that characterise IDM are washed out by non-linear growth at late times, particularly at redshifts . The predictions of IDM at late times should therefore resemble those of WDM. Thus, like for the WDM scenarios studied in Ref. [81, 82, 83], one expects future 21cm data to set a limit on the IDM damping scale. Here, we show that using these data would improve the constraints on the elastic dark matter-neutrino scattering cross section by two orders of magnitude with respect to the Lyman- constraints [57] and four orders of magnitude with respect to CMB+BAO bounds [56].
To quantify just how well future matter power spectrum measurements will be able to distinguish between IDM and WDM scenarios, we investigate also the predictions of these scenarios at higher redshifts. For IDM interaction strengths tuned to mimic as closely as possible the linear predictions of specific WDM masses, we find that the non-linear matter power spectra of these two classes of dark matter scenarios match to a few percent or better at . Therefore, to distinguish them, one would need percent-level precise measurements at redshifts , i.e., just before the dark acoustic oscillations in the matter power spectrum become completely washed out.
The structure of this work is as follows. In Section 2 we present the interacting and warm dark matter scenarios we wish to investigate, while in Section 3 we provide a short overview of the 21cm emission and how the signal is predicted. Section 4 presents a comparison of our interacting and warm dark matter initial conditions and a description of our -body simulations. We present the results of our -body simulations in Section 5. Section 6 contains our conclusions.
2 Dark matter scenarios
We present in this section the interacting dark matter and warm dark matter scenarios investigated in this work. We describe in particular their linear evolution, which is in turn used to set the initial conditions for our numerical simulations in Section 4.
2.1 Interacting dark matter
Our IDM analysis is based on the dark matter-neutrino interaction scenario presented in Ref. [56]. In this scenario, the dark matter scatters elastically with three Standard Model neutrinos with nonzero masses and the scattering cross-section is taken to be independent of temperature. This phenomenological description is similar to the Thomson scattering process of electrons and photons, and the effective parameter that controls the phenomenology is normally given in the form [38]
| (2.1) |
where is the Thomson scattering cross-section, and is the dark matter particle mass.
Introducing an elastic scattering interaction between dark matter particles and neutrinos leads to a suppression of the power spectrum through collisional damping, i.e., the collisions between dark matter particles and neutrinos prevent the gravitational collapse of structures below the diffusion scale set by the interaction strength . This process is similar to the scattering between baryons and photons, which prevents baryons from collapsing to form structures until they are released from the photon drag at . Just as photon-baryon interactions set up acoustic oscillations in both the photon and the baryonic fluctuations, the competition between the force of gravity and the pressure exerted by the coupled dark matter-neutrino fluid will imprint oscillations in both the dark matter and neutrino power spectra. This is the so-called “dark acoustic oscillations” [84].
For relatively weak interaction strengths compatible with current cosmological observations, the dark matter-neutrino interaction decouples well before recombination, i.e., . After dark matter-neutrino decoupling, we take both the neutrino and dark matter populations to be completely collisionless species. We have previously described in Ref. [56] the linear evolution of cosmological perturbations in this scenario and implemented it in a modified version of class. Here, we shall use the output of this linear evolution at as initial conditions for collisionless dark matter simulations.
Note that neutrinos may or may not be already kinetically decoupled when the dark matter stops being influenced by its interactions with neutrinos, depending on the value of the mass and interaction cross sections. In particular, for MeV dark matter particles and when the neutrino kinetic decoupling is with electrons, neutrinos can transfer their free-streaming to the dark matter fluctuations through their collisions with the dark matter particles due to the shear ratio of the dark matter-to-neutrino number densities. This damping mode can be particularly efficient and was considered in [55] in great detail. However, this so-called“mixed damping” is a special case of collisional damping and, as such, will not be explicitly considered in the present work.
Lastly, we expect our findings to be generalisable to other types of dark matter interactions that suppress the matter power spectrum at small scales. We have explicitly checked this for dark matter interacting with photons, following the prescriptions of Ref. [48] and the implementation in CLASS described in Ref. [85]. Any scattering between the 21cm photons and dark matter is suppressed and can thus be safely neglected, making the numerical modelling of the 21cm signal essentially the same as for dark matter-neutrino interactions. In the case of dark matter-baryon interactions, however, the impact of the interaction on the baryon temperature and its influence on the global 21cm signal would need to be taken into account. Such a study was recently performed in Ref. [86], putting strong constraints on millicharged dark matter.
2.2 Warm dark matter
Warm dark matter also suppresses structure formation on small scales, but the physics behind this suppression is fundamentally different from collisional damping caused by dark matter scattering. In WDM scenarios, dark matter particles with large initial velocities and negligible interaction free-stream away from initial overdensities of small spatial extents over a time scale much shorter than the gravitational collapse time scale. This free-streaming prevents gravitational collapse and hence the formation of structures on scales below a so-called free-streaming scale [7, 8]. For a thermally produced WDM, the free-streaming scale is determined by the temperature-mass ratio of the particle species.
The free-streaming suppression in the linear matter power spectrum should in principle be computed in the same way as we track massive Standard-Model neutrinos. However, it has been known for some time that the WDM power spectrum can be captured quite neatly by a fitting function of the form [8]
| (2.2) |
where is the equivalent CDM power spectrum in the same cosmology modulo the dark matter content, and
| (2.3) |
is the suppression transfer function, with index determined from a fit to numerical simulations. For a given present-day reduced dark matter density and assuming a thermally-produced WDM, the damping scale is given by
| (2.4) |
where is the WDM particle mass, and is the dimensionless Hubble parameter. The numerical values of the indices have again been determined from fits [8].
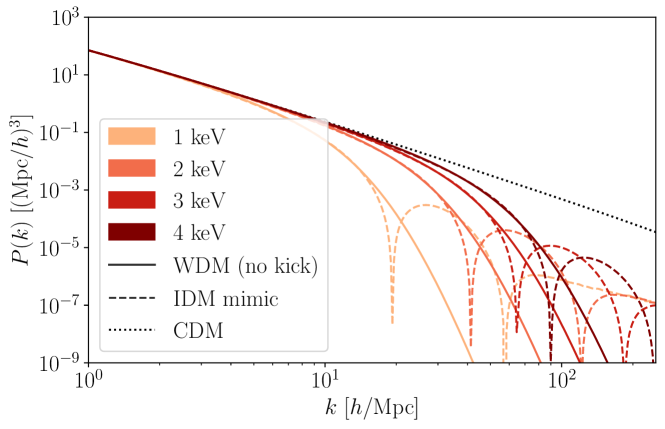
| Mimic | Mimic | |
|---|---|---|
| 1 keV | ||
| 2 keV | ||
| 3 keV | ||
| 4 keV |
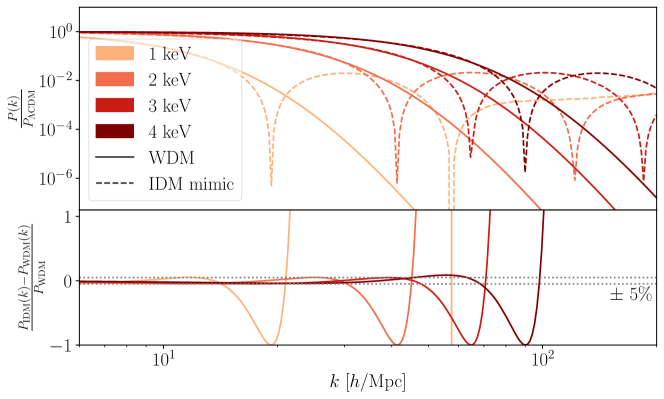
Figure 1 shows the WDM linear power spectrum for a range of values. In addition, we display on the same figure predictions of IDM scenarios with the interaction strengths tuned to mimic the WDM linear power spectrum at to %-accuracy at , where is the scale of the first oscillation (see Table 1). Beyond the matching region the IDM scenarios all begin to show their characteristic dark acoustic oscillations, making their linear predictions drastically different from those of WDM scenarios. This is illustrated in detail in Fig. 2.
3 The 21cm emission line
The 21cm line is an electromagnetic spectral line emitted from a spin-flip transition in neutral hydrogen (HI) between the two levels of a hyperfine splitting in the state. The transition is usually deemed forbidden under laboratory conditions, but is nonetheless possible to observe in astronomical settings if there is a sufficient abundance of neutral hydrogen.
In the context of standard cosmology after recombination, some 75% of the universe’s baryon content comes in the form of HI. After they have been released by the CMB from the baryon drag at and cooled sufficiently, the higher-energy triplet state can be excited from the singlet ground state by background photons, collisions between hydrogen atoms, or via an intermediate state after excitation from Lyman- photons [71]. The ratio of atoms in the two energy levels is usually parameterised in terms of a “spin temperature” ,
| (3.1) |
where eV corresponds to the transition energy between the two states, and the factor of 3 accounts for the degeneracy of the triplet state.
Because of the multitude of processes, such as those listed above, that can alter the spin distribution, the evolution of the ratio and hence the spin temperature is generally highly non-trivial. Crucially, however, if the spin temperature is higher than the CMB background temperature, i.e., , then the 21cm line is observable against the CMB background as a net emission, while the opposite case of results in net absorption. This variation of relative to leads to variations in the intensity of the global 21cm signal against the CMB back light as a function of redshift, normally expressed in terms of the differential brightness temperature [71],
| (3.2) |
where is the optical depth at the 21cm frequency . Measurements of the gloabl can therefore serve as a powerful probe of processes that affect the evolution of the HI content of the universe, from standard effects such as the onset of star formation, to non-standard interactions between hydrogen and the dark sector. See, for example, Ref. [87] for investigations of the latter in relation to the EDGES result.
Furthermore, because the spatial distribution of the underlying dark matter density field is inhomogeneous, the HI density and hence the 21cm signal intensity must also trace this inhomogeneity to a large extent. The 21cm signal can therefore be used to map structures through line intensity mapping. In this endeavour, the intensity of the 21cm line is measured for locations across the sky, similarly to the construction of a CMB map. The mapping does not require individual sources to be resolved, but provides a tracer for the density of atomic hydrogen, which is itself a (biased) tracer of structures. Because the emission is a well-defined line, the redshift can be measured precisely, thereby allowing the distance to be inferred. Together with the angular information, this distance measurement will allow us to reconstruct in 3D the spatial distribution of the HI in the early universe, from which to infer the underlying dark matter density field.
3.1 Predicting the 21cm signal
In order to predict the 21cm power spectrum for a given cosmological model, it is usually necessary to perform some kind of numerical simulations. The authors of Refs. [81, 88], for example, modelled the non-linear evolution of dark matter and baryons using hydrodynamic -body simulations and then populated the simulation box with HI following two different schemes, namely, a halo-based method and a particle-based method. The former assumes all neutral hydrogen to be located in halos, with an amount pro-rata the halo mass, and the total of neutral hydrogen at – is normalised to a reference value of , though this is subject to uncertainty [89]. The latter assigns neutral hydrogen to every gas particle in the simulation, based on the gas particle’s density and internal energy, as well as whether it is star-forming. These two methods should generally bracket the possible distributions of HI, with the halo-based method overestimating the clustering and the particle-based method underestimating it.
Then, assuming further that the 21cm emission intensity traces the HI density exactly, the differential brightness temperature everywhere in the box can be estimated from the simulation outcome via
| (3.3) |
with mean HI density is the mean HI, and a mean brightness temperature given by
| (3.4) |
where is the reduced baryon density, the reduced matter density, and is the mean neutral hydrogen fraction in the simulation box.
Reference [81] found that, at redshifts – when the 21cm emitting HI atoms are mainly found in halos, the brightness temperature power spectrum for WDM scenarios show an enhanced amplitude on scales , relative to the reference CDM scenario. This effect is stronger for smaller WDM masses and can be explained by the fact that WDM cosmologies contain fewer halos for HI to cluster in, so that for a fixed total amount of HI, halos that do manage to form must contain more hydrogen. The SKA1-LOW should be able to measure this effect with hours of observation, which would make it possible to rule out thermal warm dark matter masses up to 4 keV, or conversely, confirm a deviation from standard CDM cosmology [81, 76, 75]. Since our IDM scenario also predicts a suppression of low-mass halo formation in much the same fashion as WDM, a quick inspection of Table 1 would suggest that the same measurement could also be used to rule out dark matter-neutrino interaction strengths up to . We shall investigate in more detail, via a suite of collisionless -body simulations, how well these WDM bounds translate to IDM cosmologies. Both CDM and models beyond have also been investigated with simulations using more advanced hydrodynamics in, e.g., the THESAN project [89].
Note that there are also fast alternatives to hydrodynamic simulations capable of predicting the 21cm power spectrum to a reasonable accuracy. For example, the 21cmFAST code [90, 91, 92, 93, 94, 95], itself built upon the DexM [96], uses a combination of first-order Lagrangian perturbation theory and excursion sets to generate 3D realisations of HI field. The method is fast enough that a Markov Chain Monte Carlo analysis is feasible using the 21CMMC tool [91]. Following this approach, Ref. [82] argues that warm dark matter masses up to 8 keV can be constrained by the global 21cm signal with an EDGES-like experiment, and up to 14 keV by the small-scale 21cm power spectrum using HERA [97].
4 Comparing interacting and warm dark matter scenarios
Provided that the particle velocity is not too large, the late-time (i.e., ) evolution of a WDM cosmology should be very similar to that of a previously interacting but now decoupled IDM cosmology tuned to give matching linear predictions in the manner described in Section 2. As a direct consequence of the suppressed linear power on small scales—whether due to free-streaming or collisional damping—the onset of gravitational collapse into structures would be similarly delayed relative to the standard CDM case. Thus, for an IDM scenario with no late-time interaction with baryons and photons, WDM forecasts should be directly translatable to the case of IDM—as we have proposed to do at the end of Section 3.1—without the need to recompute the hydrodynamic evolution of the baryons and/or the HI distribution. This is convenient, as forecasts for how well SKA can distinguish between CDM and WDM cosmolgies via the 21cm brightness temperature power spectrum at –5 already exist [81], as discussed above in Section 3.1.
What remains to be done is therefore two-fold. First, we need to confirm that non-linear evolution does tend to bring closer together the gross predictions of a WDM scenario to that of an IDM scenario tuned to match as closely as possible the former’s linear predictions. Second, what observable differences between the two cosmologies remain, and hence whether the 21cm observations can help distinguish WDM from IDM. To this end, we perform a suite of collisionless -body simulations for several WDM and IDM cosmologies, paying particular attention to the high-redshift () predictions, where the differences between them are most likely to remain. We describe briefly the simulation settings below. The simulation results are presented in Section 5.
4.1 Simulation settings
We perform collisionless -body simulations using the public code gadget-4 [77], modified to include massive neutrino density perturbations as a linear response as per Ref. [98]. We adopt almost the same simulation settings and cosmological parameters as those used in Ref. [81]. That is, we use dark matter particles, a comoving box of side length Mpc, and the cosmological parameters given in Table 2.
| Parameter | Value | |
|---|---|---|
| Matter density | 0.3175 | |
| Baryon density | 0.049 | |
| Neutrino density | 0.00157 | |
| Spectral index | 1 | |
| Dimensionless Hubble parameter | 0.6711 | |
| Amplitude of primordial power spectrum |
We initialise our simulations at redshift , using the linear spectrum output evolved with a modified version of class [56] in the case of IDM. In the case of WDM, we use a standard CDM linear power spectrum output from class, modulated with the transfer function (2.3) as per Eq. (2.2). As discussed in Section 2, the IDM initial power spectrum can be chosen to mimic the suppression scales of a chosen WDM scenario to % accuracy before the onset of dark acoustic oscillations at larger wave numbers . The inclusion of massive neutrinos with eV spread equally amongst three species only has a small effect on structure formation, and should therefore not appreciably affect the 21cm predictions in the presence of the more dominant effects of interactions or WDM; we have included it in our simulations only as a matter of internal consistency for the IDM scenarios.
The information contained in the linear power spectrum of a chosen cosmology is translated into an initial displacement and kick for each -body particle in the simulation box using the usual Zel’dovich approximation. In the case of WDM, we note that the authors of Ref. [81] also folded the thermal velocity dispersion of the WDM particles into the initial conditions, by adding to each -body particle an extra thermal velocity kick drawn randomly from a relativistic Fermi-Dirac distribution, , where, assuming the WDM to constitute the entire dark matter content, the mean velocity is given by [81, 8]
| (4.1) |
This thermal velocity has sometimes been neglected in the literature because of the large amount of Poisson noise it generates in the simulation volume at early times, which may render the subsequent simulation outcome on unreliable on small scales [99]. On the other hand, omitting the thermal kick could mean that we are missing important physics related to the thermal velocity [8, 100, 101, 102, 103]. We therefore perform two sets of WDM simulations in this work, one set including the thermal kick, and one set omitting it.
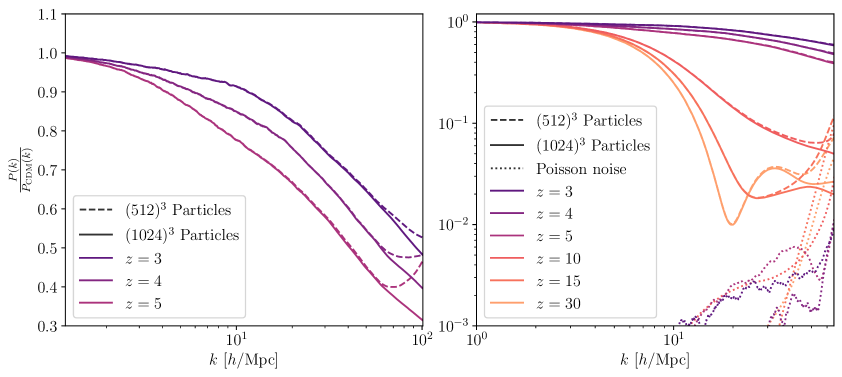
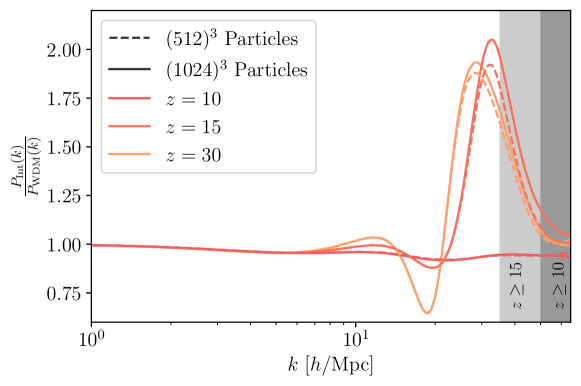
Lastly, to quantify the degree of convergence of our -particle simulations, we perform a set of high-resolution comparison simulations using particles. We find that there is evidence of unphysical Poisson noise effects at large wave numbers . However, up to the scales of interest these effects are relatively small effect compared with the overall suppression trend expected of WDM and IDM scenario, as shown in Fig. 3.
5 Simulation results
Figures 4, 5, and 6 summarise our simulation results in a set of matter power spectra at various redshifts.
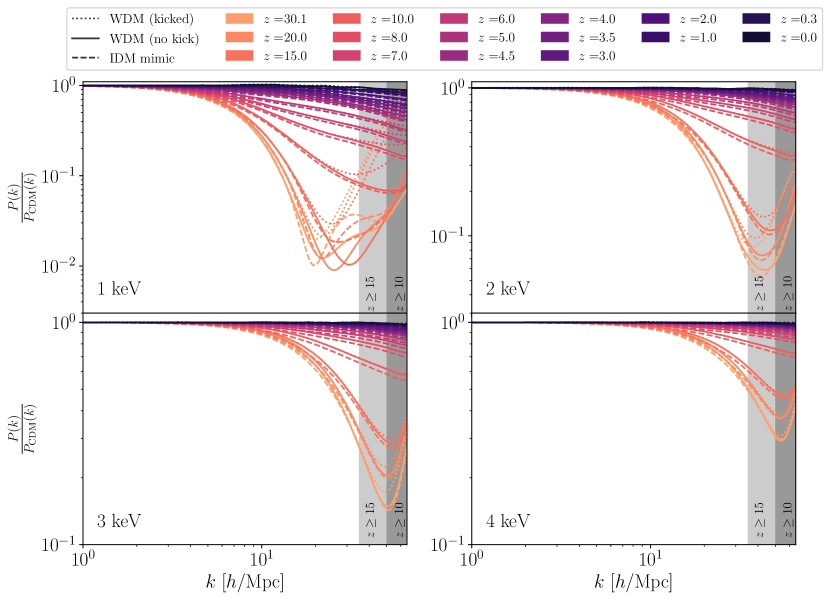
The first key takeaway is that non-linear evolution causes the difference between CDM, WDM, and IDM cosmologies to diminish with time. This is well illustrated in Fig. 4, where it is evident that despite significant differences at early times (), the late-time () matter power spectra of these different cosmologies differ only by a few percent. Endowing WDM particles with a thermal velocity kick does not significantly alter the outcome, apart from adding Poisson noise at large wave numbers , as was also noted in Ref. [99]. It is therefore clear that high-precision measurements at high redshifts are a key part of constraining departures from CDM.
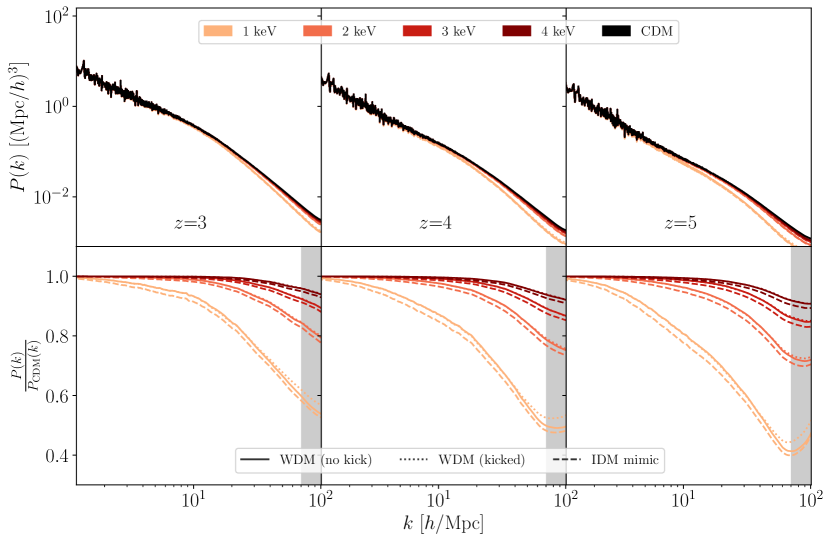
Focusing on the –5 matter power spectra shown in Fig. 5, we see that a maximum 10%–60% suppression remains for the WDM and IDM cosmologies relative to the reference CDM case in the reference wave number range . However, non-linear evolution has completely washed out the characteristic oscillatory features of IDM cosmologies, leading to power spectrum predictions that differ from those of WDM scenarios only by a few percent. Importantly though, the difference between WDM and IDM at these redshifts appears to be smaller than the free-streaming or collision damping suppression of the small-scale power spectrum itself relative to CDM. This means we should also expect the 21cm brightness temperature power spectrum of IDM cosmologies to be characterised by an enhancement in the amplitude relative to the CDM case, where the enhancement increases with interaction strength in a manner directly relatable to WDM masses via Table 1.111Note that our CDM and WDM power spectra are not an exact match to those found in Ref. [81]. Specifically, we see a slightly greater small-scale suppression of power in the WDM cosmologies relative to the reference CDM model. For example the right panel of Fig. 5 shows a 60% suppression in the 1 keV WDM scenario at /Mpc and ; the equivalent result of Ref. [81], displayed in their Fig. 1, finds a 40% suppression. The slightly different values adopted in the simulations may have contributed to the discrepancy. However, the most likely explanation is that, unlike Ref. [81], we have not accorded baryons a hydrodynamical treatment, but merely lumped them together with the dark matter as one single collisionless species. This is undoubtedly a drastic simplification. However, for the purpose of demonstrating that the collisionless dark matter in both WDM and IDM cosmologies evolve similarly, it is a sufficient treatment. Furthermore, because neither the WDM nor the IDM has direct, non-gravitational interactions with baryons, full hydrodynamical simulations of these cosmologies should not change the qualitative conclusion that WDM and IDM are phenomenologically very similar at –5. Thus we arrive at our second key takeaway: constraints on WDM masses from non-linear structure measurements at –5 can be immediately translated to constraints on the equivalent . As demonstrated in Ref. [81], observations by SKA1-LOW will be able to constrain WDM masses to keV, which translates into a limit of for IDM. The strongest constraint on at the time of writing is [57] obtained from the Lyman- forest. Thus, 21cm intensity mapping could improve upon current cosmological constraints on IDM scenarios by at least two orders of magnitude.
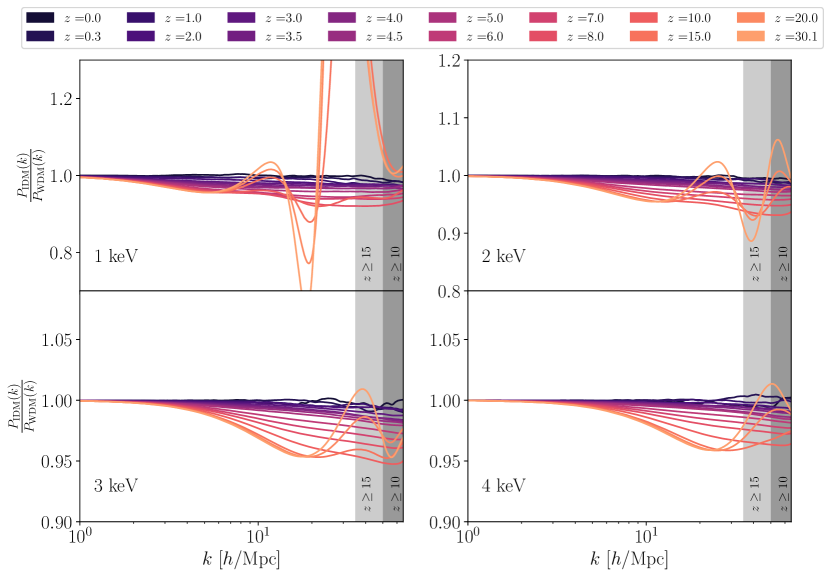
Our findings also imply that, in order to distinguish between IDM and WDM, higher-redshift observations are necessary. Indeed, as shown in Fig. 6 (and verified at a higher simulation resolution in Fig. 7 for the 1 keV and cases), the characteristic dark acoustic oscillations of IDM become discernible at , and are, for a fixed redshift, more evident for larger interaction strengths , i.e., smaller equivalent WDM masses. The latter effect is due largely to the dark acoustic acoustic oscillations appearing on smaller length scales as we decrease , where non-linear dynamics kicks in at an earlier time. If we were to decrease even further to values outside of the range investigated in this work, we would expect the dark acoustic oscillations to be pushed into a region below the resolution of these simulations; to numerically probe these cases would necessitate dedicated high-resolution simulations.
However, even with the simulations performed for this work, we are able to give conservative estimates of the precision needed in measurements to distinguish between WDM and IDM scenarios. For the strongest interactions investigated, , only and % precision is needed at and , respectively, to distinguish it from a WDM cosmology with keV. For the weaker and its keV equivalent, the precision requirements for distinction tighten to and %. Even greater precision would be required for weaker interactions/larger , or we would need to observe at even higher redshifts and/or larger wave numbers.
6 Conclusions
Using a suite of collisionless -body simulations, we have shown in this work that the observable consequences of interacting dark matter cosmologies closely mimic those of warm dark matter scenarios at redshifts . This means that cosmological observations at these redshifts sensitive to WDM properties must also be able to probe IDM in a similar manner, and forecasts for future WDM constraints should be easily adaptable to constraints on IDM.
Specifically, we have considered the constraining power of future 21cm line intensity mapping in the context of a dark matter-neutrino interaction scenario. Previous works in the literature showed that the 21cm brightness temperature power spectrum as will be measured by SKA1-LOW will be able to constrain the WDM mass to keV [81] with hours of observation. The analysis of Ref. [82] forecasted constraints that are even stronger by up to a factor of 3.5. Through mapping IDM to WDM simulation outcomes, we find that the more conservative eV can be translated to an upper limit on the dark matter-neutrino interaction strength of . This represents a forecasted improvement of more than two orders of magnitude with respect to the current constraint from the Lyman- forest [57], and will likewise tighten by four orders of magnitude current bounds from CMB+BAO [56].
While the observable similarity between WDM and IDM at makes it a plus in terms of computational convenience, at the same time it also detracts from our ability to distinguish between these two classes of models observationally. Indeed, we find that in order to obtain a “smoking gun” signal for an IDM scenario, it is necessary to observe the matter power spectrum at redshifts to a precision of 2–10%, depending on the interaction strength, before the characteristic dark acoustic oscillations of this type of scenarios become completely washed out by non-linear evolution. The weaker the interaction, the more stringent the redshift and precision requirements, as the characteristic dark acoustic oscillations get pushed out to smaller and more non-linear scales with decreasing interaction strength.
The SKA should be able to probe the 21cm signal out to [104, 76] and therefore has the potential to make the distinction between WDM and IDM. Observing at such high redshifts also offers another advantage over lower redshifts: it allows us to reduce the uncertainties introduced by astrophysics in the form of feedback from star formation, supernovae, and galaxy formation, which are important effects at . At earlier times, the hydrogen found in filaments also has a higher relative importance [88] compared to halos, changing the dependence of the 21cm power spectrum on the halo number, and the HI-to-DM bias at these redshifts would need to be well-modelled. Such predictions would require a dedicated study beyond the scope of this paper, and is therefore left for future work.
Note added:
While we were finalising this manuscript, Ref. [105] appeared on the arXiv which explores a very similar scenario. Their conclusions are that SKA1-LOW observations of the 21cm signal at will be able to constrain the dark matter-neutrino interaction strength to . This forecasted bound is weaker than our prediction of , and is likely due to a different set of detection criteria used to derive the constraint.
Acknowledgments
We thank Joe Chen for useful discussions on the implementation of thermal velocities. Y3W is supported in part by the Australian Government through the Australian Research Council’s Future Fellowship (project FT180100031). This research includes computations using the computational cluster Katana supported by Research Technology Services at UNSW Sydney. Part of this work was performed on the OzSTAR national facility at Swinburne University of Technology. The OzSTAR program receives funding in part from the Astronomy National Collaborative Research Infrastructure Strategy (NCRIS) allocation provided by the Australian Government.
References
- [1] Planck Collaboration, N. Aghanim et al., Planck 2018 results. I. Overview and the cosmological legacy of Planck, Astron. Astrophys. 641 (2020) A1, [arXiv:1807.06205].
- [2] DES Collaboration, A. Amon et al., Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to data calibration, Phys. Rev. D 105 (2022), no. 2 023514, [arXiv:2105.13543].
- [3] DES Collaboration, T. M. C. Abbott et al., Dark Energy Survey Year 3 results: A 2.7% measurement of baryon acoustic oscillation distance scale at redshift 0.835, Phys. Rev. D 105 (2022), no. 4 043512, [arXiv:2107.04646].
- [4] P. J. E. Peebles and Bharat Ratra, The Cosmological Constant and Dark Energy, Rev. Mod. Phys. 75 (2003) 559–606, [astro-ph/0207347].
- [5] Edmund J. Copeland, M. Sami, and Shinji Tsujikawa, Dynamics of dark energy, Int. J. Mod. Phys. D 15 (2006) 1753–1936, [hep-th/0603057].
- [6] Joshua Frieman, Michael Turner, and Dragan Huterer, Dark Energy and the Accelerating Universe, Ann. Rev. Astron. Astrophys. 46 (2008) 385–432, [arXiv:0803.0982].
- [7] Scott Dodelson and Lawrence M. Widrow, Sterile-neutrinos as dark matter, Phys. Rev. Lett. 72 (1994) 17–20, [hep-ph/9303287].
- [8] Paul Bode, Jeremiah P. Ostriker, and Neil Turok, Halo formation in warm dark matter models, Astrophys. J. 556 (2001) 93–107, [astro-ph/0010389].
- [9] Steen H. Hansen, Julien Lesgourgues, Sergio Pastor, and Joseph Silk, Constraining the window on sterile neutrinos as warm dark matter, Mon. Not. Roy. Astron. Soc. 333 (2002) 544–546, [astro-ph/0106108].
- [10] Takehiko Asaka, Steve Blanchet, and Mikhail Shaposhnikov, The nuMSM, dark matter and neutrino masses, Phys. Lett. B 631 (2005) 151–156, [hep-ph/0503065].
- [11] Matteo Viel, Julien Lesgourgues, Martin G. Haehnelt, Sabino Matarrese, and Antonio Riotto, Constraining warm dark matter candidates including sterile neutrinos and light gravitinos with WMAP and the Lyman-alpha forest, Phys. Rev. D 71 (2005) 063534, [astro-ph/0501562].
- [12] Alexey Boyarsky, Oleg Ruchayskiy, and Mikhail Shaposhnikov, The Role of sterile neutrinos in cosmology and astrophysics, Ann. Rev. Nucl. Part. Sci. 59 (2009) 191–214, [arXiv:0901.0011].
- [13] Matteo Viel, George D. Becker, James S. Bolton, and Martin G. Haehnelt, Warm dark matter as a solution to the small scale crisis: New constraints from high redshift Lyman- forest data, Phys. Rev. D 88 (2013) 043502, [arXiv:1306.2314].
- [14] Kevork Abazajian, George M. Fuller, and Mitesh Patel, Sterile neutrino hot, warm, and cold dark matter, Phys. Rev. D 64 (2001) 023501, [astro-ph/0101524].
- [15] Alexey Boyarsky, Julien Lesgourgues, Oleg Ruchayskiy, and Matteo Viel, Lyman-alpha constraints on warm and on warm-plus-cold dark matter models, JCAP 05 (2009) 012, [arXiv:0812.0010].
- [16] A.D. Dolgov and S.H. Hansen, Massive sterile neutrinos as warm dark matter, Astropart. Phys. 16 (2002) 339–344, [hep-ph/0009083].
- [17] Eric D. Carlson, Marie E. Machacek, and Lawrence J. Hall, Self-interacting dark matter, Astrophys. J. 398 (1992) 43–52.
- [18] Andrew A. de Laix, Robert J. Scherrer, and Robert K. Schaefer, Constraints of selfinteracting dark matter, Astrophys. J. 452 (1995) 495, [astro-ph/9502087].
- [19] David N. Spergel and Paul J. Steinhardt, Observational evidence for selfinteracting cold dark matter, Phys. Rev. Lett. 84 (2000) 3760–3763, [astro-ph/9909386].
- [20] Romeel Dave, David N. Spergel, Paul J. Steinhardt, and Benjamin D. Wandelt, Halo properties in cosmological simulations of selfinteracting cold dark matter, Astrophys. J. 547 (2001) 574–589, [astro-ph/0006218].
- [21] Peter Creasey, Omid Sameie, Laura V. Sales, et al., Spreading out and staying sharp – creating diverse rotation curves via baryonic and self-interaction effects, Mon. Not. Roy. Astron. Soc. 468 (2017), no. 2 2283–2295, [arXiv:1612.03903].
- [22] Miguel Rocha, Annika H. G. Peter, James S. Bullock, et al., Cosmological Simulations with Self-Interacting Dark Matter I: Constant Density Cores and Substructure, Mon. Not. Roy. Astron. Soc. 430 (2013) 81–104, [arXiv:1208.3025].
- [23] Stacy Y. Kim, Annika H. G. Peter, and David Wittman, In the Wake of Dark Giants: New Signatures of Dark Matter Self Interactions in Equal Mass Mergers of Galaxy Clusters, Mon. Not. Roy. Astron. Soc. 469 (2017), no. 2 1414–1444, [arXiv:1608.08630].
- [24] Ran Huo, Manoj Kaplinghat, Zhen Pan, and Hai-Bo Yu, Signatures of Self-Interacting Dark Matter in the Matter Power Spectrum and the CMB, Phys. Lett. B 783 (2018) 76–81, [arXiv:1709.09717].
- [25] Maxim Markevitch, A. H. Gonzalez, D. Clowe, et al., Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56, Astrophys. J. 606 (2004) 819–824, [astro-ph/0309303].
- [26] Scott W. Randall, Maxim Markevitch, Douglas Clowe, Anthony H. Gonzalez, and Marusa Bradac, Constraints on the Self-Interaction Cross-Section of Dark Matter from Numerical Simulations of the Merging Galaxy Cluster 1E 0657-56, Astrophys. J. 679 (2008) 1173–1180, [arXiv:0704.0261].
- [27] C. Boehm, Pierre Fayet, and R. Schaeffer, Constraining dark matter candidates from structure formation, Phys. Lett. B518 (2001) 8–14, [astro-ph/0012504].
- [28] Celine Boehm and Richard Schaeffer, Constraints on dark matter interactions from structure formation: Damping lengths, Astron. Astrophys. 438 (2005) 419–442, [astro-ph/0410591].
- [29] Xue-lei Chen, Steen Hannestad, and Robert J. Scherrer, Cosmic microwave background and large scale structure limits on the interaction between dark matter and baryons, Phys. Rev. D65 (2002) 123515, [astro-ph/0202496].
- [30] Cora Dvorkin, Kfir Blum, and Marc Kamionkowski, Constraining Dark Matter-Baryon Scattering with Linear Cosmology, Phys. Rev. D89 (2014), no. 2 023519, [arXiv:1311.2937].
- [31] A. D. Dolgov, S. L. Dubovsky, G. I. Rubtsov, and I. I. Tkachev, Constraints on millicharged particles from Planck data, Phys. Rev. D88 (2013), no. 11 117701, [arXiv:1310.2376].
- [32] Francis-Yan Cyr-Racine and Kris Sigurdson, Cosmology of atomic dark matter, Phys. Rev. D87 (2013), no. 10 103515, [arXiv:1209.5752].
- [33] A. A. Prinz et al., Search for millicharged particles at SLAC, Phys. Rev. Lett. 81 (1998) 1175–1178, [hep-ex/9804008].
- [34] Kimberly K. Boddy and Vera Gluscevic, First Cosmological Constraint on the Effective Theory of Dark Matter-Proton Interactions, Phys. Rev. D 98 (2018), no. 8 083510, [arXiv:1801.08609].
- [35] Tracy R. Slatyer and Chih-Liang Wu, Early-Universe constraints on dark matter-baryon scattering and their implications for a global 21 cm signal, Phys. Rev. D 98 (2018), no. 2 023013, [arXiv:1803.09734].
- [36] Weishuang Linda Xu, Cora Dvorkin, and Andrew Chael, Probing sub-GeV Dark Matter-Baryon Scattering with Cosmological Observables, Phys. Rev. D 97 (2018), no. 10 103530, [arXiv:1802.06788].
- [37] Kimberly K. Boddy, Vera Gluscevic, Vivian Poulin, et al., Critical assessment of CMB limits on dark matter-baryon scattering: New treatment of the relative bulk velocity, Phys. Rev. D 98 (2018), no. 12 123506, [arXiv:1808.00001].
- [38] Celine Boehm, Alain Riazuelo, Steen H. Hansen, and Richard Schaeffer, Interacting dark matter disguised as warm dark matter, Phys. Rev. D 66 (2002) 083505, [astro-ph/0112522].
- [39] Kris Sigurdson, Michael Doran, Andriy Kurylov, Robert R. Caldwell, and Marc Kamionkowski, Dark-matter electric and magnetic dipole moments, Phys. Rev. D70 (2004) 083501, [astro-ph/0406355]. [Erratum: Phys. Rev.D73,089903(2006)].
- [40] Samuel D. McDermott, Hai-Bo Yu, and Kathryn M. Zurek, Turning off the Lights: How Dark is Dark Matter?, Phys. Rev. D83 (2011) 063509, [arXiv:1011.2907].
- [41] Ryan J. Wilkinson, Julien Lesgourgues, and Céline Boehm, Using the CMB angular power spectrum to study Dark Matter-photon interactions, JCAP 1404 (2014) 026, [arXiv:1309.7588].
- [42] C. Boehm, J. A. Schewtschenko, R. J. Wilkinson, C. M. Baugh, and S. Pascoli, Using the Milky Way satellites to study interactions between cold dark matter and radiation, Mon. Not. Roy. Astron. Soc. 445 (2014) L31–L35, [arXiv:1404.7012].
- [43] J. A. Schewtschenko, R. J. Wilkinson, C. M. Baugh, C. Bœhm, and S. Pascoli, Dark matter–radiation interactions: the impact on dark matter haloes, Mon. Not. Roy. Astron. Soc. 449 (2015), no. 4 3587–3596, [arXiv:1412.4905].
- [44] J. A. Schewtschenko, C. M. Baugh, R. J. Wilkinson, et al., Dark matter–radiation interactions: the structure of Milky Way satellite galaxies, Mon. Not. Roy. Astron. Soc. 461 (2016), no. 3 2282–2287, [arXiv:1512.06774].
- [45] Yacine Ali-Haïmoud, Jens Chluba, and Marc Kamionkowski, Constraints on Dark Matter Interactions with Standard Model Particles from Cosmic Microwave Background Spectral Distortions, Phys. Rev. Lett. 115 (2015), no. 7 071304, [arXiv:1506.04745].
- [46] Miguel Escudero, Olga Mena, Aaron C. Vincent, Ryan J. Wilkinson, and Céline Bœhm, Exploring dark matter microphysics with galaxy surveys, JCAP 1509 (2015), no. 09 034, [arXiv:1505.06735].
- [47] James A. D. Diacoumis and Yvonne Y. Y. Wong, Using CMB spectral distortions to distinguish between dark matter solutions to the small-scale crisis, JCAP 1709 (2017), no. 09 011, [arXiv:1707.07050].
- [48] Julia Stadler and Céline Bœhm, Constraints on -CDM interactions matching the Planck data precision, JCAP 1810 (2018), no. 10 009, [arXiv:1802.06589].
- [49] Julia Stadler, Celine Bœhm, and Olga Mena, Is it Mixed dark matter or neutrino masses?, JCAP 01 (2020) 039, [arXiv:1807.10034].
- [50] Laura Lopez-Honorez, Olga Mena, and Pablo Villanueva-Domingo, Dark matter microphysics and 21 cm observations, Phys. Rev. D 99 (2019), no. 2 023522, [arXiv:1811.02716].
- [51] Gianpiero Mangano, Alessandro Melchiorri, Paolo Serra, Asantha Cooray, and Marc Kamionkowski, Cosmological bounds on dark matter-neutrino interactions, Phys. Rev. D74 (2006) 043517, [astro-ph/0606190].
- [52] P. Serra, F. Zalamea, A. Cooray, G. Mangano, and A. Melchiorri, Constraints on neutrino-dark matter interactions from cosmic microwave background and large scale structure data, Phys. Rev. D 81 (Feb., 2010) 043507, [arXiv:0911.4411].
- [53] Ryan J. Wilkinson, Celine Boehm, and Julien Lesgourgues, Constraining Dark Matter-Neutrino Interactions using the CMB and Large-Scale Structure, JCAP 1405 (2014) 011, [arXiv:1401.7597].
- [54] Eleonora Di Valentino, Céline Bøehm, Eric Hivon, and François R. Bouchet, Reducing the and tensions with Dark Matter-neutrino interactions, Phys. Rev. D 97 (2018), no. 4 043513, [arXiv:1710.02559].
- [55] Julia Stadler, Céline Bœhm, and Olga Mena, Comprehensive Study of Neutrino-Dark Matter Mixed Damping, JCAP 08 (2019) 014, [arXiv:1903.00540].
- [56] Markus R. Mosbech, Celine Boehm, Steen Hannestad, et al., The full Boltzmann hierarchy for dark matter-massive neutrino interactions, JCAP 03 (2021) 066, [arXiv:2011.04206]. Code available at https://github.com/MarkMos/CLASS_nu-DM.
- [57] Deanna C. Hooper and Matteo Lucca, Hints of dark matter-neutrino interactions in Lyman- data, Phys. Rev. D 105 (2022), no. 10 103504, [arXiv:2110.04024].
- [58] David E. Kaplan, Gordan Z. Krnjaic, Keith R. Rehermann, and Christopher M. Wells, Atomic Dark Matter, JCAP 1005 (2010) 021, [arXiv:0909.0753].
- [59] Subinoy Das and Kris Sigurdson, Cosmological Limits on Hidden Sector Dark Matter, Phys. Rev. D85 (2012) 063510, [arXiv:1012.4458].
- [60] Roberta Diamanti, Elena Giusarma, Olga Mena, Maria Archidiacono, and Alessandro Melchiorri, Dark Radiation and interacting scenarios, Phys. Rev. D87 (2013), no. 6 063509, [arXiv:1212.6007].
- [61] Manuel A. Buen-Abad, Gustavo Marques-Tavares, and Martin Schmaltz, Non-Abelian dark matter and dark radiation, Phys. Rev. D92 (2015), no. 2 023531, [arXiv:1505.03542].
- [62] Julien Lesgourgues, Gustavo Marques-Tavares, and Martin Schmaltz, Evidence for dark matter interactions in cosmological precision data?, JCAP 1602 (2016), no. 02 037, [arXiv:1507.04351].
- [63] Subinoy Das, Rajesh Mondal, Vikram Rentala, and Srikanth Suresh, On dark matter - dark radiation interaction and cosmic reionization, JCAP 08 (2018) 045, [arXiv:1712.03976].
- [64] P. Ko, Natsumi Nagata, and Yong Tang, Hidden Charged Dark Matter and Chiral Dark Radiation, Phys. Lett. B773 (2017) 513–520, [arXiv:1706.05605].
- [65] Miguel Escudero, Laura Lopez-Honorez, Olga Mena, Sergio Palomares-Ruiz, and Pablo Villanueva Domingo, A fresh look into the interacting dark matter scenario, JCAP 1806 (2018), no. 06 007, [arXiv:1803.08427].
- [66] Maria Archidiacono, Deanna C. Hooper, Riccardo Murgia, et al., Constraining Dark Matter – Dark Radiation interactions with CMB, BAO, and Lyman-, JCAP 1910 (2019), no. 10 055, [arXiv:1907.01496].
- [67] Leandros Perivolaropoulos and Foteini Skara, Challenges for CDM: An update, arXiv:2105.05208.
- [68] C. Boehm, H. Mathis, J. Devriendt, and J. Silk, Non-linear evolution of suppressed dark matter primordial power spectra, Mon. Not. Roy. Astron. Soc. 360 (2005) 282–287, [astro-ph/0309652].
- [69] Raul A. Monsalve, Alan E. E. Rogers, Judd D. Bowman, and Thomas J. Mozdzen, Results from EDGES High-Band: I. Constraints on Phenomenological Models for the Global cm Signal, Astrophys. J. 847 (2017), no. 1 64, [arXiv:1708.05817].
- [70] Matias Zaldarriaga, Steven R. Furlanetto, and Lars Hernquist, 21 Centimeter fluctuations from cosmic gas at high redshifts, Astrophys. J. 608 (2004) 622–635, [astro-ph/0311514].
- [71] Jonathan R. Pritchard and Abraham Loeb, 21-cm cosmology, Rept. Prog. Phys. 75 (2012) 086901, [arXiv:1109.6012].
- [72] Stefano Camera, Mario G. Santos, Pedro G. Ferreira, and Luis Ferramacho, Cosmology on Ultra-Large Scales with HI Intensity Mapping: Limits on Primordial non-Gaussianity, Phys. Rev. Lett. 111 (2013) 171302, [arXiv:1305.6928].
- [73] Philip Bull, Pedro G. Ferreira, Prina Patel, and Mario G. Santos, Late-time cosmology with 21cm intensity mapping experiments, Astrophys. J. 803 (2015), no. 1 21, [arXiv:1405.1452].
- [74] Aviad Cohen, Anastasia Fialkov, Rennan Barkana, and Matan Lotem, Charting the Parameter Space of the Global 21-cm Signal, Mon. Not. Roy. Astron. Soc. 472 (2017), no. 2 1915–1931, [arXiv:1609.02312].
- [75] SKA Collaboration, David J. Bacon et al., Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts, Publ. Astron. Soc. Austral. 37 (2020) e007, [arXiv:1811.02743].
- [76] A. Weltman et al., Fundamental physics with the Square Kilometre Array, Publ. Astron. Soc. Austral. 37 (2020) e002, [arXiv:1810.02680].
- [77] Volker Springel, Rüdiger Pakmor, Oliver Zier, and Martin Reinecke, Simulating cosmic structure formation with the gadget-4 code, Mon. Not. Roy. Astron. Soc. 506 (2021), no. 2 2871–2949, [arXiv:2010.03567].
- [78] Celine Boehm, Yasaman Farzan, Thomas Hambye, Sergio Palomares-Ruiz, and Silvia Pascoli, Is it possible to explain neutrino masses with scalar dark matter?, Phys. Rev. D 77 (2008) 043516, [hep-ph/0612228].
- [79] Diego Blas, Julien Lesgourgues, and Thomas Tram, The Cosmic Linear Anisotropy Solving System (CLASS) II: Approximation schemes, JCAP 07 (2011) 034, [arXiv:1104.2933].
- [80] Julien Lesgourgues and Thomas Tram, The Cosmic Linear Anisotropy Solving System (CLASS) IV: efficient implementation of non-cold relics, JCAP 09 (2011) 032, [arXiv:1104.2935].
- [81] Isabella P. Carucci, Francisco Villaescusa-Navarro, Matteo Viel, and Andrea Lapi, Warm dark matter signatures on the 21cm power spectrum: Intensity mapping forecasts for SKA, JCAP 07 (2015) 047, [arXiv:1502.06961].
- [82] Julian B. Muñoz, Cora Dvorkin, and Francis-Yan Cyr-Racine, Probing the Small-Scale Matter Power Spectrum with Large-Scale 21-cm Data, Phys. Rev. D 101 (2020), no. 6 063526, [arXiv:1911.11144].
- [83] Sambit K. Giri and Aurel Schneider, Imprints of fermionic and bosonic mixed dark matter on the 21-cm signal at cosmic dawn, Phys. Rev. D 105 (2022), no. 8 083011, [arXiv:2201.02210].
- [84] Francis-Yan Cyr-Racine, Roland de Putter, Alvise Raccanelli, and Kris Sigurdson, Constraints on Large-Scale Dark Acoustic Oscillations from Cosmology, Phys. Rev. D 89 (2014), no. 6 063517, [arXiv:1310.3278].
- [85] Niklas Becker, Deanna C. Hooper, Felix Kahlhoefer, Julien Lesgourgues, and Nils Schöneberg, Cosmological constraints on multi-interacting dark matter, JCAP 02 (2021) 019, [arXiv:2010.04074].
- [86] Trey Driskell, Ethan O. Nadler, Jordan Mirocha, et al., Structure Formation and the Global 21-cm Signal in the Presence of Coulomb-like Dark Matter-Baryon Interactions, arXiv:2209.04499.
- [87] Sean Fraser et al., The EDGES 21 cm Anomaly and Properties of Dark Matter, Phys. Lett. B 785 (2018) 159–164, [arXiv:1803.03245].
- [88] Francisco Villaescusa-Navarro, Matteo Viel, Kanan K. Datta, and T. Roy Choudhury, Modeling the neutral hydrogen distribution in the post-reionization Universe: intensity mapping, JCAP 09 (2014) 050, [arXiv:1405.6713].
- [89] R. Kannan, E. Garaldi, A. Smith, et al., Introducing the thesan project: radiation-magnetohydrodynamic simulations of the epoch of reionization, Mon. Not. Roy. Astron. Soc. 511 (2022), no. 3 4005–4030, [arXiv:2110.00584].
- [90] Andrei Mesinger, Steven Furlanetto, and Renyue Cen, 21cmFAST: A Fast, Semi-Numerical Simulation of the High-Redshift 21-cm Signal, Mon. Not. Roy. Astron. Soc. 411 (2011) 955, [arXiv:1003.3878].
- [91] Bradley Greig and Andrei Mesinger, 21CMMC: an MCMC analysis tool enabling astrophysical parameter studies of the cosmic 21 cm signal, Mon. Not. Roy. Astron. Soc. 449 (2015), no. 4 4246–4263, [arXiv:1501.06576].
- [92] Bradley Greig and Andrei Mesinger, Simultaneously constraining the astrophysics of reionization and the epoch of heating with 21CMMC, Mon. Not. Roy. Astron. Soc. 472 (2017), no. 3 2651–2669, [arXiv:1705.03471].
- [93] Bradley Greig and Andrei Mesinger, 21CMMC with a 3D light-cone: the impact of the co-evolution approximation on the astrophysics of reionization and cosmic dawn, Mon. Not. Roy. Astron. Soc. 477 (2018), no. 3 3217–3229, [arXiv:1801.01592].
- [94] Julian B. Muñoz, Standard Ruler at Cosmic Dawn, Phys. Rev. Lett. 123 (2019), no. 13 131301, [arXiv:1904.07868].
- [95] Julian B. Muñoz, Robust Velocity-induced Acoustic Oscillations at Cosmic Dawn, Phys. Rev. D 100 (2019), no. 6 063538, [arXiv:1904.07881].
- [96] Andrei Mesinger and Steven Furlanetto, Efficient Simulations of Early Structure Formation and Reionization, Astrophys. J. 669 (2007) 663, [arXiv:0704.0946].
- [97] David R. DeBoer et al., Hydrogen Epoch of Reionization Array (HERA), Publ. Astron. Soc. Pac. 129 (2017), no. 974 045001, [arXiv:1606.07473].
- [98] Joe Zhiyu Chen, Amol Upadhye, and Yvonne Y. Y. Wong, One line to run them all: SuperEasy massive neutrino linear response in -body simulations, JCAP 04 (2021) [arXiv:2011.12504]. Code available at https://github.com/joechenUNSW/gadget4-supereasy.
- [99] Matteo Leo, Carlton M. Baugh, Baojiu Li, and Silvia Pascoli, The Effect of Thermal Velocities on Structure Formation in N-body Simulations of Warm Dark Matter, JCAP 11 (2017) 017, [arXiv:1706.07837].
- [100] Vladimir Avila-Reese, Pefro Colin, Octavio Valenzuela, Elena D’Onghia, and Claudio Firmani, Formation and structure of halos in a warm dark matter cosmology, Astrophys. J. 559 (2001) 516–530, [astro-ph/0010525].
- [101] Jie Wang and Simon D. M. White, Discreteness effects in simulations of Hot/Warm dark matter, Mon. Not. Roy. Astron. Soc. 380 (2007) 93–103, [astro-ph/0702575].
- [102] Francisco Villaescusa-Navarro and Neal Dalal, Cores and Cusps in Warm Dark Matter Halos, JCAP 03 (2011) 024, [arXiv:1010.3008].
- [103] Arka Banerjee and Neal Dalal, Simulating nonlinear cosmological structure formation with massive neutrinos, JCAP 11 (2016) 015, [arXiv:1606.06167].
- [104] Michael Sitwell, Andrei Mesinger, Yin-Zhe Ma, and Kris Sigurdson, The Imprint of Warm Dark Matter on the Cosmological 21-cm Signal, Mon. Not. Roy. Astron. Soc. 438 (2014), no. 3 2664–2671, [arXiv:1310.0029].
- [105] Antara Dey, Arnab Paul, and Supratik Pal, Constraints on Dark Matter-Neutrino Interaction from 21-cm Cosmology and Forecasts on SKA1-Low, arXiv:2207.02451.