Primordial Black Hole Merger Rate in Ellipsoidal-Collapse Dark Matter Halo Models
Abstract
We have studied the merger rate of primordial black holes (PBHs) in the ellipsoidal-collapse model of halo to explain the dark matter abundance by the PBH merger estimated from the gravitational waves detections via the Advanced LIGO (aLIGO) detectors. We have indicated that the PBH merger rate within each halo for the ellipsoidal models is more significant than for the spherical models. We have specified that the PBH merger rate per unit time and per unit volume for the ellipsoidal-collapse halo models is about one order of magnitude higher than the corresponding spherical models. Moreover, we have calculated the evolution of the PBH total merger rate as a function of redshift. The results indicate that the evolution for the ellipsoidal halo models is more sensitive than spherical halo models, as expected from the models. Finally, we have presented a constraint on the PBH abundance within the context of ellipsoidal and spherical models. By comparing the results with the aLIGO mergers during the third observing run (O3), we have shown that the merger rate in the ellipsoidal-collapse halo models falls within the aLIGO window, while the same result is not valid for the spherical-collapse ones. Furthermore, we have compared the total merger rate of PBHs in terms of their fraction in the ellipsoidal-collapse halo models for several masses of PBHs. The results suggest that the total merger rate of PBHs changes inversely with their masses. We have also estimated the relation between the fraction of PBHs and their masses in the ellipsoidal-collapse halo model and have shown it for a narrow mass distribution of PBHs. The outcome shows that the constraint inferred from the PBH merger rate for the ellipsoidal-collapse halo models can be potentially stronger than the corresponding result obtained for the spherical-collapse ones.
pacs:
97.60.Lf; 04.25.dg; 95.35.+d; 98.62.Gq.I Introduction
The detection of binary black holes with the LIGO Abbott:2016blz ; Abbott:2016nmj ; TheLIGOScientific:2017qsa ; Abbott:2020khf ; Abbott:2020tfl has opened a new epoch in probing the nature and behavior of compact objects in the cosmos. In the past years, the gravitational wave detectors have directly confirmed the existence of black holes Abbott:2016nmj , and have provided powerful tests of general relativity TheLIGOScientific:2016src . These detectors are also guided in the era of multi-messenger astronomy GBM:2017lvd . While the gravitational wave observatories are continued to probe the population of black holes, another significant discovery arises as to whether mergers may provide direct evidence for the existence of PBHs.
It is widely accepted that the astrophysical objects are originated from the early universe quantum fluctuations which became classical as were stretched to super-horizon scales in an exponentially expanding period. If the density perturbations of these fluctuations exceed some threshold value, the PBHs might form. Since passing by the threshold value is the critical point of formation, many numerical investigations have been done to study the threshold value for the density perturbations, see e.g., Refs. Carr:1975qj ; Niemeyer:1999ak ; Musco:2004ak ; Young:2 ; Shibata:1999zs ; new-thre ; musco ; bloom ; allah . Besides PBHs, there might be other formation channels for black holes with the non-stellar beginning such as the gravitational collapse in dark matter candidates Khlopov:2008qy ; Belotsky:2014kca ; Shandera:2018xkn , or the collapse of other compact objects due to new physics deLavallaz:2010wp . During the last two decades, many works have been done in the subject of PBHs and related area, see e.g., Ref. Carr:2020xqk and references therein.
Since the massive PBHs interact only via gravitation, and since a large set of black holes behaves as perfect fluids on sufficiently large scales, the PBHs are a natural nominee for dark matter. Nowadays, though the existence of PBHs is yet neither proven nor refuted, the very observational limits on its abundance represent themselves a powerful and unique probe of the early universe at small scales, which is difficult to probe with any other method Lehmann:2018ejc ; Carr:2017jsz ; Carr:2020gox . Besides other observational constraints such as Icarus Carr:2020gox , one of the (serious) bounds on the abundance of PBHs in the mass range around can be obtained from the LIGO observations that are assumed in involving the merging of PBHs pairs. Shortly after the first observation of a binary black hole merger, in Refs. bird ; Sasaki:2016jop , it has been stated that the merger rate by the LIGO discovery is potentially consistent with a mass fraction of PBHs accounting for the total of dark matter, assuming that those two black holes involved had a primordial origin and LIGO had detected dark matter.
Since the PBHs merge in the halo and consist of a fraction of dark matter, the halo mass function can affect the merger rate of PBHs. In addition, the concentration parameter changes the relative velocity distribution of PBHs within each halo, which determines their merger rate within each halo.
On the other hand, there are different types of halo collapse models. The analytically simple model is the spherical-collapse which has been found to over-predict the abundance of small halos and under-predict for the massive ones. This issue is because the halo collapses are generally triaxial rather than spherical. The Sheth-Mo-Tormen model Sheth:1999mn ; st uses the ellipsoidal-collapse model and the obtained fitting functions provide a closer match to the unconditional halo mass function in N-body simulations. Furthermore, the ellipsoidal-collapse model has its mass-concentration relation which gives deep insight into the formation and structure of halos afshordi .
In this work, we propose to use the ellipsoidal-collapse model to calculate the merger rate of PBHs, which are in the dark matter halo. In this respect, the outline of the work is as follows. In Sec. II, we introduce the dark matter halo model and its concentration. Moreover, we discuss the halo mass function for both the spherical- and ellipsoidal-collapse models. Then, in Sec. III, we calculate the PBH merger rate in the ellipsoidal-collapse model and compare it with the corresponding results of the spherical-collapse model. Furthermore, we discuss the constraints arising from the merger rate of PBHs in the ellipsoidal-collapse model. Finally, we scrutinize the results and summarize the findings in Sec. IV.
II Halo Models
II.1 Halo Density Profile
Dark matter halos are considered as nonlinear cosmological structures whose masses can be modeled as a function of radius called density profile. In recent years, the analytical models and numerical simulations have provided a clearer picture of the properties and behavior of these structures. In addition, many studies have been performed to extract a convenient density profile that can provide an acceptable description for the observational data dehnen ; Hernquist:1990be ; Jaffe:1983iv ; deZeeuw:1985sk ; Plummer:1911zza ; Navarro:1995iw ; ein .
Let us mention two of the most commonly used density profiles as follows. The first one is the Navarro-Frenk-White (NFW) profile, which is extracted from the -body simulations and is well compatible with most of the rotation curve data Navarro:1995iw . The relation of this density profile is
| (1) |
The other one, which is derived from analytical models, is the Einasto profile that is also well consistent with the observational data ein , and has the form
| (2) |
In these relations, and are the scaled parameters that vary from halo to halo, and is the shape parameter for the Einasto profile. It should be noted that for both of the above forms, one has
| (3) |
i.e. the logarithmic slope of the density distribution is .
On the other hand, the halo density profile can be described in terms of two parameters, namely the mass and concentration. The halo concentration describes the central density of halos and is defined as
| (4) |
where is a viral radius considered as a radius within which the average halo density reaches to times the critical density of the universe. Also, the -body simulations show that the concentration parameter is a decreasing function of the halo mass and is a redshift dependent function at fixed mass afshordi ; prada ; Dutton:2014xda ; ludlow . We will discuss about the mass distribution of dark matter halos in the next subsection.
II.2 Halo Mass Function
The existence of dark matter halos provides a convenient and fundamental framework to study nonlinear gravitational collapse in the universe. Hence, having a proper statistical view of the mass distribution of these halos can improve our understanding of the physics governing those. With this argument, a function called the halo mass function has been proposed, which describes the mass distribution of these halos within a given volume. In other words, the halo mass function describes the mass of those structures whose overdensities exceed the threshold overdensity, separate from the expansion of the universe, and collapse. Furthermore, in the standard cosmology, one may define a linear quantity called density contrast as , where is the local density at any point and is the mean background energy density. As noted earlier, this quantity may grow to the critical point while the universe expands, exceeds linear regimes, and enters into nonlinear regimes. This situation occurs when the overdensities separate from the expansion of the universe, enter the turnaround phase and collapse. That is, the structures are formed at this stage. For an Einstein-de Sitter universe and a spherical-collapse halo model, the threshold overdensity has been calculated to be . This threshold depends only on the redshift value and is independent of all local quantities such as mass and radius Lukic:2007fc . Hence, it can be considered as a fixed threshold in a narrow redshift range. However, this threshold varies for ellipsoidal-collapse halo models, which we will discuss later.
In Ref. Jenkins:2000bv , in order to specify various fits for dark matter halos, an appropriate definition of the differential mass function has been presented as
| (5) |
where is the number density of halos with mass , is the cosmological matter density, and depends on the geometry of overdensities at the collapse time. The function is the linear root mean square fluctuation of overdensities on mass and redshift , which is defined as
| (6) |
In this relation, is the Fourier spectrum of the top-hat filter which depends on mass and wavenumber , and is the power spectrum of the fluctuations.
There is a wide range of studies that have been conducted to extrapolate the halo mass function based on analytical approaches and numerical simulations. The purpose of these studies is to provide the best fit for the cosmic observations. The first model for the dark matter halo mass function, assuming a homogeneous and isotropic collapse, was presented by Press and Schechter (P-S) ps as
| (7) |
which is called the P-S mass function. This formalism is based on the assumption that every astrophysical or cosmological object is formed via a gravitational collapse of overdensities. Moreover, although the final collapse is a nonlinear process, it is assumed that, in the early universe, the density fluctuations had been very small and resulted in a linear approximation. As is clear from relation (7), at a fixed redshift, the mass function depends only on the mass of halos via , and it is expected that no significant change can be observed. This mass function has been proposed as the simplest model for the formation of dark matter halos, i.e. a spherical-collapse model, and, in many cases, is consistent with the observational data. Nevertheless, it quantitatively deviates from the numerical results at some mass limits Jenkins:2000bv . Therefore, some improvements have been made to address this issue. One of the most successful improvements was provided by Sheth and Tormen (S-T), which is based on a more realistic model and fits simulation results better Sheth:1999mn ; st . Their formalism was based on an ellipsoidal-collapse model with dynamical threshold density fluctuations, in contrast to an almost global threshold in the P-S model.
As mentioned earlier, the threshold overdensity for spherical-collapses, , has been introduced as a global value. It means that, in about certain redshifts, all structures with overdensities higher than such a threshold can collapse. S-T have proposed the idea that dynamically considering the threshold overdensity for the ellipsoidal-collapses, , can provide a more realistic picture of the halo mass function. With this assumption and considering prolateness to be zero st , they have extracted this quantity as
| (8) |
with , and . It is clear that this quantity not only implicitly depends on the redshift, but also on the mass of the structure, and is called the moving barrier. With this assumption, one can find the halo mass function for the ellipsoidal-collapse, which is also called the S-T mass function, to be
| (9) |
with , and . This mass function is expected to be more sensitive than the P-S mass function with redshift changes. Thus, we now have all the tools that one needs to study PBHs in dark matter halos. In this regard, in the next section, we will talk about the probability of encountering PBHs, their binary formation, and their merger rate within a certain volume and time interval.
III Primordial Black Hole Merger Rate
III.1 Merger Rate Within Each Halo
The PBHs are a special type of black holes that are formed in the early universe due to the direct collapse of density fluctuations or equivalently curvature perturbations. The PBHs were not only able to form binaries when the universe had been dominated by radiation but also could encounter each other in the late time universe due to their random distribution.
More important is that these types of black holes have been considered as candidates for dark matter for over years. In this regard, it is believed that the gravitational wave events recorded by the LIGO detectors can be described by the PBH scenario at typical mass , if these black holes could be considered as a component of dark matter. Hence, we have focused on the stellar-mass PBHs that may reside in the galactic halos and have potentially been proposed as a dark matter candidate. Indeed, the recent detections of stellar-mass black hole mergers have drawn much attention to study their origins, and the PBH scenario is one of the plausible theories.
The presence of PBHs with random distributions in dark matter halos gives those a chance to form binaries via the close encounter and emitting gravitational waves. In particular, the numerical simulations Moore:1999nt and analytical approaches Kamionkowski:2008vw to investigate the subhalos resided in the larger halos show that the dark matter in the subhalos has lower velocity dispersion and higher density than the host halos bird . Hence, the subhalos are likely to have the largest contribution to the formation of PBH binaries. Thus, the probability of PBH merger in the subhalos is more significant than in the host halos bird .
Suppose two PBHs with masses and and relative velocity at the large separation accidentally encounter each other in a dark matter halo. At the closest physical separation (i.e., at periastron), due to the maximum scattering amplitude, a significant gravitational radiation occurs. Regarding the emission of the gravitational radiation , the Keplerian mechanics implies that the time-averaged radiated energy to be peter:1964
| (10) |
where is the gravitational constant, is the velocity of light, is the semi-major axis of the orbit, is the eccentricity of the orbit and is the periastron. As the head-on collision rarely happens, it can be assumed that near the periastron, due to the emission of the maximum gravitational radiation, the trajectory is an ellipse with a maximum eccentricity (i.e. ). Under these assumptions, after one orbital period , the radiated gravitational energy is
| (11) |
If , where is the kinetic energy and is the reduced mass, then the PBHs will form binary systems. This condition provides a maximum for the periastron as
| (12) |
which means that leads to the binary formation. In addition, in the Newtonian limit, the impact parameter is calculated as a function of Sasaki:2018dmp , namely
| (13) |
In other words, if the value of the impact parameter for the encounter is less than , one can expect to form a PBH binary. Therefore, the cross-section for the binary formation is obtained to be quinlan ; Mouri:2002mc
| (14) |
where the strong limit of the gravitational focusing, i.e. , has been applied.
Our focus is on the merger rate of the PBHs that are compatible with the LIGO sensitivity, i.e. events in the galactic halos. Accordingly, we have normalized those masses to with their relative velocities as the average velocities of dark matter halos, i.e. .
By inserting Eq. (12) into Eq. (14) and assuming and , one can reach an explicit form of the cross-section related to the normalized mass and velocity of the PBHs as
| (15) |
With these considerations, the merger rate of PBHs within each halo can be calculated via the formula bird ; Nishikawa:2017chy
| (16) |
where is the halo density profile that can be considered to be the NFW or the Einasto density profile, and represents an average over the relative velocity distribution of PBHs in the galactic halos.
Moreover, the mass located within the virial radius of the halo, the virialized mass, can be found by
| (17) |
By inserting relation (1) into relation (17) and integrating, one can find the virialized mass for the NFW density profile as
| (18) |
Similarly, by considering relation (2), the virialized mass for the Einasto density profile dan ; retana can be obtained as
| (19) |
In this relation, is a function of concentration and shape parameter and has the following form
where is the incomplete Gamma function.


To calculate the halo velocity dispersion, one can use its relation to the maximum velocity in an radius, which has been introduced in Ref. prada as
| (20) |
In this work, we assume that the relative velocity distributions of PBHs in a halo are random and follow the Maxwell-Boltzmann statistics. Hence, one can write the velocity probability distribution function as
| (21) |
where is determined when the condition is satisfied and a cutoff is considered at the halo virial velocity.
It is clear from Eqs. (16), (18) and (19) that, in order to calculate the merger rate in each halo, the mass-concentration relation, , has to be determined. For this purpose, according to the initial conditions governing the dark matter halos during the collapse, various results can be found. In Ref. bird , the merger rate has been performed by using two famous spherical concentration-mass relations of Prada, et al. prada and Ludlow, et al. ludlow .
In this research, we have employed the ellipsoidal-collapse concentration-mass relation introduced in Ref. afshordi that we refer to it as Okoli-Afshordi (O-A) concentration-mass relation. Furthermore, for the Einasto density profile, we have chosen the value of the shape parameter presented in Ref. Klypin:2014kpa . Also, we have set the mass of PBHs to be . In Fig. 1, we have indicated the merger rate of PBHs per halo as a function of halo mass by considering the O-A concentration-mass relation as an ellipsoidal model, and the Ludlow concentration-mass relation for a spherical model obtained in Ref. bird . The results show that the merger rate of PBHs grows with increasing halo mass for both models. A noteworthy point is that in smaller mass halos for the case of the O-A model the merger rate is almost one order of magnitude larger than the corresponding result for the Ludlow model.
In the following, we propose to determine the effect of these changes on the total merger rate of PBHs in a given volume and time interval.
| Halo Density Profile | Halo Mass Function | Lower Limit Halo Mass | Total Merger Rate | |
| P-S | Ludlow | |||
| S-T | O-A | |||
| P-S | Ludlow | |||
| NFW | S-T | O-A | ||
| P-S | Ludlow | |||
| S-T | O-A | |||
| P-S | Ludlow | |||
| S-T | O-A | |||
| P-S | Ludlow | |||
| Einasto | S-T | O-A | ||
| P-S | Ludlow | |||
| S-T | O-A |
III.2 Total Merger Rate
III.2.1 Present-Time Universe
Up to here, the merger rate has been considered within each dark matter halo. However, as the gravitational wave detectors statistically receive the cumulative events, it is necessary to calculate the total merger event rate per unit volume and per unit time. For this purpose, convolving the merger rate per halo, , with the halo mass function, , leads to the total merger event rate per unit volume and per unit time as
| (22) |
where is the halo mass, which can be estimated as the virialized mass, . As is clear from Eqs. (5), (7) and (9), the exponential decay of the mass function means that the upper limit of the integral does not affect the final result. Instead, the lower limit plays a crucial role.


It should be noted that the merger time of BH binaries is a function of the velocity dispersion of halos (from hours to kiloyears) OLeary:2008myb . Thus, BH binaries, that are formed due to dissipative two-body encounters, have merger time much shorter than the age of the universe. Moreover, non-dissipative three-body encounters can also lead to the formation of BH binaries. These types of binaries have no strong enough binding energy to decay instantaneously via the emission of gravitational radiation. Therefore, these binaries frequently lead to the formation of wide binaries in a way that their merger times are longer than a Hubble time quinlan . Consequently, these binaries should not affect the aLIGO merger rate.
It is known that the smallest halos are the most concentrated halos, and those have already become virialized. Moreover, the dynamical relaxation processes lead to the evaporation of the smallest halos through the ejection of objects. The timescale of such an evaporation has been stated to be , where is the number of BHs in a halo, is the ejection rate of objects, and is the half-mass relaxation time binney2011galactic . The calculated evaporation time for halos with a typical mass (while containing PBHs each with mass of ) is about bird . However, it would be plausible that halos with masses less than (while maintaining the same PBH mass) have the evaporation timescale less than .
On the other hand, during the matter-dominated era, the halo evaporation is a process that is compensated by the accretion of outer objects onto the halo and/or the formation of new halos due to the merging of smaller objects. While the relative separation of structures increases during the dark energy dominated era (i.e. recent ), due to the increasing expansion rate of the universe, the compensatory factors (i.e. merging and accretion) against the halo evaporation become very slow. Hence, it can be inferred that the signal from halos with masses would be negligible.
To quantify the total merger rate introduced in Eq. (22), two crucial quantities, namely the halo mass function and the concentration-mass relation, must be specified in proportion to the dark matter halo formation conditions. The idea is to look at the merger rate of PBHs for the ellipsoidal-collapse halo models. For this purpose, we use the S-T mass function and the O-A concentration-mass relation which have been introduced for the ellipsoidal-collapse halo models.
Fig. 2 shows the merger rate of PBHs for the ellipsoidal halo models per unit time and per unit volume, and compares it with the results of the spherical model, which has been evaluated in Ref. bird , while taking into account the NFW density profile (top) and the Einasto density profile (bottom). In the ellipsoidal model, the S-T mass function and the ellipsoidal O-A concentration-mass relation have been considered, while in the spherical model, the P-S mass function and the Ludlow concentration-mass relation are used. As expected, the total merger rate of PBHs for ellipsoidal models, like the spherical models, increases with decreasing halo mass due to the significance of merger events in the smallest halos. For the halo masses larger than , the merger rate is approximately the same in both models. However, for masses smaller than with the ellipsoidal model, it is prominently increased by about one order of magnitude compared with the spherical model. The total merger rate has been obtained by integrating over the surface below the curves, and the results for different lower limits of halo masses have been presented in Table 1 for the present-time universe. This table, and also Fig. 2, indicates that the PBH total merger rate decreases as the lower limit of the halo mass increases.
III.2.2 Redshift Evolution of PBH Merger Rate
The time evolution of the BH merger rate has always been one of the most interesting topics to study. Because it can potentially provide a clearer picture to distinguish among the BH formation scenarios Sasaki:2018dmp . On the other side, the sensitivity of the aLIGO detectors can observe the binaries up to which includes a comoving volume around Aasi:2013wya ; TheLIGOScientific:2016zmo ; LIGOScientific:2018jsj .
Here, we intend to represent the redshift evolution of the PBH merger rate for the ellipsoidal and spherical halo models, and compare their results with each other. In this respect, by definition of the concentration parameter (Eq. (4)), it is obvious that is redshift dependent through the halo virial radius Mandic:2016lcn . On the other hand, the halo mass function also depends on the redshift through . Thus, via Eq. (22), one can obtain the redshift evolution of the PBH total merger rate .
In Fig. 3, we have demonstrated the total merger event rate for both the ellipsoidal and spherical models as a function of redshift, wherein two halo profile models of the NFW and the Einasto have been compared. The results indicate that the merger rate in higher redshifts has been more significant than the present-day universe, which is consistent with the results obtained in Refs. Sasaki:2018dmp ; Gow:2019pok . Furthermore, this figure indicates that the evolution of the PBH merger rate in the ellipsoidal model is much more pronounced than in the spherical model. Hence, the results completely confirm what we have expected, since the ellipsoidal model uses the S-T mass function, which is sensitive to redshift changes, while the spherical model is not significantly sensitive to redshift changes due to using the P-S mass function.


III.2.3 Constraint on PBH Fraction
As the last part, let us concentrate on the expected PBH fraction, , extracted from the ellipsoidal-collapse halo model. The problem of PBH abundance has been an important issue since the beginning of the emergence of the PBH scenario. Moreover, one of the most important constraints imposed on PBHs is their abundance in the late-time universe. The fraction of PBHs determines their contribution to dark matter. Many studies have been performed in this area, and today it is believed that this fraction is lower than one for most of the PBH mass ranges Sasaki:2016jop ; Raidal:2017mfl ; Ali-Haimoud:2017rtz ; Kocsis:2017yty ; Wang:2016ana ; Kohri:2018qtx ; Wang:2019kaf ; Carr:2020gox ; DeLuca:2020fpg ; DeLuca:2020qqa ; Wong:2020yig . It means that dark matter consists of several components, one of which is the PBHs. However, it should be noted that a small mass range of PBHs, known as asteroid-mass PBHs Carr:2020gox ; Carr:2020xqk ; Katz:2018zrn ; Smyth:2019whb ; Montero-Camacho:2019jte ; coogan ; Picker:2021jxl ; Ray:2021mxu , has not yet been strongly constrained, and this window (i.e. ) may make up a significant fraction of dark matter.
| PBH Mass | Density Profile | Total Merger Rate |
|---|---|---|
| 10 | NFW | |
| 10 | Einasto | |
| 20 | NFW | |
| 20 | Einasto | |
| 50 | NFW | |
| 50 | Einasto | |
| 100 | NFW | |
| 100 | Einasto |
On the other hand, one of the best references to investigate suitable models of dark matter halos is to compare the obtained merger rate from each model with the determined one via the aLIGO detectors. However, since the aLIGO mergers could contain the astrophysical BH mergers, the inferred PBH fraction from theoretical models is an upper limit that is allowed by the aLIGO observations.

In Fig. 4, we have depicted the PBH total merger rate as a function of for the ellipsoidal halo model while considering those two density profiles of the NFW and the Einasto, and have compared the results with the corresponding ones for the spherical model Sasaki:2018dmp . In this figure, the shaded band is the estimated merger event rate by the third observing run (O3) of the aLIGO detectors Abbott:2020niy . Although there are some theoretical uncertainties, the results indicate that the calculated merger rate, for the PBHs while considering the ellipsoidal halo model, falls within the aLIGO window when . However, the corresponding result of the spherical halo model does not enter in this window for any value of . This means that ellipsoidal halo models are capable to generate enough PBH mergers consistent with the estimated ones by the aLIGO detectors. Whereas, if the spherical models are trusted, the population of PBHs should be reduced by some mechanism and most of the aLIGO mergers must be of astrophysical origins. Moreover, as mentioned earlier, the aLIGO detectors can probe events up to that corresponds to the comoving volume around . Thus, within the context of ellipsoidal halo models, over one year, one expects that aLIGO can detect approximately events with , while the number of events during this time should be at least if , and at least one if .
Up to here, we have have considered the PBHs only with masses, and one may ponder whether the results change with smaller or larger masses. In these cases, recall the argument regarding limits on the lower bound of halo masses that have not yet evaporated by the present-time. Then, for PBHs with masses less than resided in dark matter halos, it can be inferred that the smallest host halos, which have an evaporation time around , should have masses less than . Similarly, the smallest host halos containing PBHs with masses larger than must have masses greater than . In addition, the PBH total merger rate depends sensitively on the lower limit of the halo mass in a way that the smaller the halo mass, the higher the total merger rate. Nevertheless, to achieve the merger rate of PBHs with different masses, one should consider this criterion for the lower limit of halo masses, and repeat the calculations.
In this regard, in Fig. 5, we have depicted the total merger rate of PBHs for ellipsoidal models in terms of the PBH fraction and mass. The results have been presented for several masses of PBHs (i.e. and ). As it is clear, the total merger rate changes inversely with the PBH mass. Also, the merger rate of smaller masses, compared to larger ones, falls within a wider range of the aLIGO band. It should be noted that we have only shown the results for the Einasto density profile. The total merger rate of PBHs with different masses in ellipsoidal halo models has been presented in Table 2 for the NFW and the Einasto density profiles.
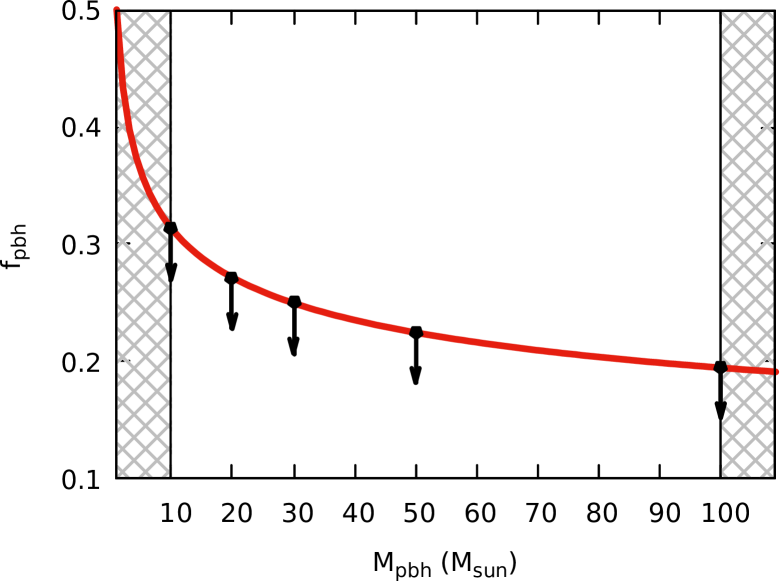
Furthermore, it is constructive to discuss about the relation between the fraction of PBHs and their masses. According to the relations obtained for the total merger rate in Refs. bird ; Ali-Haimoud:2017rtz , one can estimate the dependence of the fraction of PBHs on their masses to be . This relation is consistent with our findings on the merger rate and the constraints of PBHs with different masses. In Fig. 6, we have depicted the expected upper bounds on the fraction of PBHs in terms of their masses for ellipsoidal halo models while considering a narrow mass distribution for PBHs, i.e. . It is clear that the fraction of PBHs decreases as their masses increase. We have also marked upper limits on the fraction of PBHs with smaller and larger masses than . The top plot shows this relation for the situation in which one should expect to detect at least one event over one year in the comoving volume , whereas the bottom plot indicates the corresponding result for the same event but in the comoving volume .


IV Conclusions
In this work, we have focused on the modeling of the stellar-mass PBH merger rate assuming the ellipsoidal-collapse of dark matter halos. Specifically, to perform this task, we have considered two crucial components that have been calculated for the case of ellipsoidal-collapse dark matter halos, namely the S-T mass function, and the ellipsoidal concentration-mass relation obtained in Ref. afshordi . The main idea behind the extraction of these two important components in the ellipsoidal-collapse halos has been to propose a dynamical threshold overdensity, , instead of a constant threshold one, , which has already been introduced for the spherical-collapse dark matter halos. This generalization of threshold overdensity has led to a more realistic model that fits the observational data.
Subsequently, we have mentioned the scattering amplitude of the PBHs by considering the encounter conditions in the medium of dark matter halos. We have also used the NFW and the Einasto density profiles. Under these assumptions, we have calculated the merger rate of PBHs per halo for the ellipsoidal-collapse halos and have compared it with the corresponding result of the spherical-collapse ones. It has been observed that, in the smallest halo masses, the merger rate per halo for the ellipsoidal model is about one order of magnitude larger than that in the corresponding one for the spherical model. The results amplify the fact that the probability of binary black hole formation within halos with the lowest mass is more prominent because these halos are more compact and have less the virial velocity compared with the larger mass halos.
Furthermore, we have focused on the PBH merger rate per unit volume and per unit time in an ellipsoidal halo model. In these calculations, the significance of the merger rate in the ellipsoidal model has been evident compared with the results of the spherical model for the halos with the lowest mass. As a result, cumulatively, the significance of the merger rate in the ellipsoidal halos is confirmed.
Given the possibility of the PBH binary formation during the age of the universe, as an interesting case study, we have calculated their total merger rate evolution as a function of redshift. It has been observed that the evolution of the total merger rate of PBHs in the case of ellipsoidal halo models with redshift is more sensitive than its evolution in the spherical model. This sensitivity is due to the consideration of the dynamical threshold overdensity in the ellipsoidal model.
We have plotted the total merger rate of PBHs in the ellipsoidal halo models in terms of their fraction, and have compared it with the corresponding results of the spherical halo models obtained in Ref. bird . The criterion used for this comparison is the merger rate estimated by the aLIGO detectors during the third observing run (O3), i.e. . Such an evaluation is important because it can estimate the contribution of PBHs in dark matter. We have shown that the total merger rate of PBHs in the ellipsoidal halo models, despite some theoretical uncertainties, falls within the aLIGO window, while the corresponding results for the spherical halo models are not consistent with the aLIGO merger rate. This result suggests that the merger of PBHs within the framework of the ellipsoidal halo models is still a potential candidate for dark matter, but the spherical halo models are no longer able to justify the PBH mergers compared to the aLIGO window. Otherwise, it reinforces the argument that the aLIGO detectors are more likely to detect the BHs of astrophysical origin if the spherical halo models would be reliable. Besides, based on the result of the ellipsoidal halo models for PBHs, it can also be inferred that over one year aLIGO can detect approximately events with , while the number of events during this time should be at least if , and at least one if . Relying on the evaporation time of the smallest halos and repeating the calculations, we have indicated that the total merger rate for the ellipsoidal halo models in terms of the PBH fraction for several different masses of PBHs. The results suggest that the total merger rate changes inversely with the PBH mass. Also, we have estimated the relation between the fraction of PBHs and their masses, and have shown it for a mass distribution between . The results indicate that the fraction of PBHs for the ellipsoidal halo models should be around , if one could expect to detect at least one PBH event in the comoving volume over one year. Whereas the corresponding fraction should be around for the same event but in the comoving volume . Interestingly, the constraint obtained in this work can be potentially stronger than the one obtained bird from the merger rate of PBHs in the spherical halo models.
However, within the mentioned mass range of PBHs, there are other strong observational constraints that come from the accretion limits from the observed number of X-ray binaries Inoue:2017csr , the Planck data on the CMB anisotropies Ali-Haimoud:2016mbv ; Serpico:2020ehh , dynamical processes from star clusters in nearby dwarf galaxies Brandt:2016aco ; Koushiappas:2017chw and the gravitational lensing of type Ia supernovae Zumalacarregui:2017qqd .
It is noteworthy to mention that the constraint of PBHs is subject to many uncertainties including various models of halo, e.g. spherical and non-spherical collapses, various physical processes that may lead to the growth (e.g. merging and accretion) or the evaporation (e.g. the substantial spin) of PBHs, the mass distribution of PBHs in the dark matter halos, the uncertainties in the estimated merger rate by the aLIGO detectors, the considered PBH mass (or the mass range) and contribution of (astrophysical and primordial) BH binary mergers to the merger rate recorded by the aLIGO detectors. These uncertainties lead to the advent of unknown factors in calculations. However, we may better understand the physics governing those to reach stronger constraints on PBHs in the future.
Acknowledgments
Fakhry and Farhoudi thank the Research Council of Shahid Beheshti University. The authors gratefully acknowledge the anonymous referee for the constructive comments.
References
- (1) B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], “Observation of gravitational waves from a binary black hole merger”, Phys. Rev. Lett. 116, 061102 (2016).
- (2) B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], “GW151226: Observation of gravitational waves from a 22-solar-mass binary black hole coalescence”, Phys. Rev. Lett. 116, 241103 (2016).
- (3) B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], “GW170817: Observation of gravitational waves from a binary neutron star inspiral”, Phys. Rev. Lett. 119, 161101 (2017).
- (4) R. Abbott et al. [LIGO Scientific and Virgo Collaborations], “GW190814: Gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object”, Astrophys. J. Lett. 896, L44 (2020).
- (5) R. Abbott et al. [LIGO Scientific and Virgo Collaborations], “GW190521: A binary black hole merger with a total mass of ”, Phys. Rev. Lett. 125, 101102 (2020).
- (6) B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], “Tests of general relativity with GW150914”, Phys. Rev. Lett. 116, 221101 (2016); Erratum: Phys. Rev. Lett. 121, 129902(E) (2018).
- (7) B.P. Abbott et al. [LIGO Scientific, Virgo and other Collaborations], “Multi-messenger observations of a binary neutron star merger”, Astrophys. J. Lett. 848, L12 (2017).
- (8) B.J. Carr, “The primordial black hole mass spectrum”, Astrophys. J. 201, 1 (1975).
- (9) J.C. Niemeyer and K. Jedamzik, “Dynamics of primordial black hole formation”, Phys. Rev. D 59, 124013 (1999).
- (10) M. Shibata and M. Sasaki, “Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity”, Phys. Rev. D 60, 084002 (1999).
- (11) I. Musco, J.C. Miller and L. Rezzolla, “Computations of primordial black hole formation”, Class. Quant. Grav. 22, 1405 (2005).
- (12) A.G. Polnarev and I. Musco, “Curvature profiles as initial conditions for primordial black hole formation”, Class. Quant. Grav. 24, 1405 (2007).
- (13) I. Musco and J.C. Miller, “Primordial black hole formation in the early universe: Critical behaviour and self-similarity”, Class. Quant. Grav. 30, 145009 (2013).
- (14) S. Young, C.T. Byrnes and M. Sasaki, “Calculating the mass fraction of primordial black holes”, J. Cosmol. Astropart. Phys. 1407, 045 (2014).
- (15) J. Bloomfield, D. Bulhosa and S. Face, “Formalism for primordial black hole formation in spherical symmetry”, arXiv:1504.02071.
- (16) A. Allahyari, J.T. Firouzjaee and A.A. Abolhasani, “Primordial black holes in linear and non-linear regimes”, J. Cosmol. Astropart. Phys. 1706, 041 (2017).
- (17) M.Y. Khlopov, “Primordial black holes”, Res. Astron. Astrophys. 10, 495 (2010).
- (18) K.M. Belotsky et al., “Signatures of primordial black hole dark matter”, Mod. Phys. Lett. A 29, 1440005 (2014).
- (19) S. Shandera, D. Jeong and H.S.G. Gebhardt, “Gravitational waves from binary mergers of subsolar mass dark black holes”, Phys. Rev. Lett. 120, 241102 (2018).
- (20) A. de Lavallaz and M. Fairbairn, “Neutron stars as dark matter probes”, Phys. Rev. D 81, 123521 (2010).
- (21) B. Carr and F. Kühnel, “Primordial black holes as dark matter: Recent developments”, Annu. Rev. Nucl. Part. Sci. 70, 355 (2020).
- (22) B. Carr, M. Raidal, T. Tenkanen, V. Vaskonen and H. Veermäe, “Primordial black hole constraints for extended mass functions”, Phys. Rev. D 96, 023514 (2017).
- (23) B.V. Lehmann, S. Profumo and J. Yant, “The maximal-density mass function for primordial black hole dark matter”, J. Cosmol. Astropart. Phys. 1804, 007 (2018).
- (24) B. Carr, K. Kohri, Y. Sendouda and J. Yokoyama, “Constraints on primordial black holes”, arXiv:2002.12778.
- (25) S. Bird et al., “Did LIGO detect dark matter?”, Phys. Rev. Lett. 116, 201301 (2016).
- (26) M. Sasaki, T. Suyama, T. Tanaka and S. Yokoyama, “Primordial black hole scenario for the gravitational-wave event GW150914”, Phys. Rev. Lett. 117, 061101 (2016); Erratum: Phys. Rev. Lett. 121, 059901(E) (2018)
- (27) R.K. Sheth and G. Tormen, “Large scale bias and the peak background split”, Mon. Not. Roy. Astron. Soc. 308, 119 (1999).
- (28) R.K. Sheth, H.J. Mo and G. Tormen, “Ellipsoidal collapse and an improved model for the number and spatial distribution of dark matter haloes”, Mon. Not. Roy. Astron. Soc. 323, 1 (2001).
- (29) C. Okoli and N. Afshordi, “Concentration, ellipsoidal collapse, and the densest dark matter haloes”, Mon. Not. Roy. Astron. Soc. 456, 3068 (2016).
- (30) H.C. Plummer, “On the problem of distribution in globular star clusters”, Mon. Not. Roy. Astron. Soc. 71, 460 (1911).
- (31) J. Einasto, “On the construction of a composite model for the galaxy and on the determination of the system of galactic parameters”, Trudy Astrofizicheskogo Instituta Alma-Ata 5, 87 (1965).
- (32) W. Jaffe, “A Simple model for the distribution of light in spherical galaxies”, Mon. Not. Roy. Astron. Soc. 202, 995 (1983).
- (33) T. de Zeeuw, “Elliptical galaxies with separable potentials”, Mon. Not. Roy. Astron. Soc. 216, 273 (1985).
- (34) L. Hernquist, “An analytical model for spherical galaxies and bulges”, Astrophys. J. 356, 359 (1990).
- (35) W. Dehnen, “A family of potential-density pairs for spherical galaxies and bulges”, Mon. Not. Roy. Astron. Soc. 265, 250 (1993).
- (36) J.F. Navarro, C.S. Frenk and S.D.M. White, “The structure of cold dark matter halos”, Astrophys. J. 462, 563 (1996).
- (37) F. Prada et al., “Halo concentrations in the standard cold dark matter cosmology”, Mon. Not. Roy. Astron. Soc. 423, 3018 (2012).
- (38) A.A. Dutton and A.V. Macciò, “Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles”, Mon. Not. Roy. Astron. Soc. 441, 3359 (2014).
- (39) A.D. Ludlow et al., “The mass-concentration-redshift relation of cold and warm dark matter haloes”, Mon. Not. Roy. Astron. Soc. 460, 1214 (2016).
- (40) Z. Lukic, K. Heitmann, S. Habib, S. Bashinsky and P.M. Ricker, “The halo mass function: High redshift evolution and universality”, Astrophys. J. 671, 1160 (2007).
- (41) A. Jenkins et al., “The mass function of dark matter halos”, Mon. Not. Roy. Astron. Soc. 321, 372 (2001).
- (42) W.H. Press and P. Schechter, “Formation of galaxies and clusters of galaxies by self-similar gravitational condensation”, Astrophys. J. 187, 425 (1974).
- (43) B. Moore et al., “Dark matter substructure within galactic halos”, Astrophys. J. Lett. 524, L19 (1999).
- (44) M. Kamionkowski and S.M. Koushiappas, “Galactic substructure and direct detection of dark matter”, Phys. Rev. D 77, 103509 (2008).
- (45) P.C. Peters, “Gravitational radiation and the motion of two point masses”, Phys. Rev. 136, B1224 (1964).
- (46) M. Sasaki, T. Suyama, T. Tanaka and S. Yokoyama, “Primordial black holes—perspectives in gravitational wave astronomy”, Class. Quant. Grav. 35, 063001 (2018).
- (47) G.D. Quinlan and S.L. Shapiro, “Dynamical evolution of dense clusters of compact stars”, Astrophys. J. 343, 725 (1989).
- (48) H. Mouri and Y. Taniguchi, “Runaway merging of black holes: Analytical constraint on the timescale”, Astrophys. J. Lett. 566, L17 (2002).
- (49) H. Nishikawa, E.D. Kovetz, M. Kamionkowski and J. Silk, “Primordial-black-hole mergers in dark-matter spikes”, Phys. Rev. D 99, 043533 (2019).
- (50) D. Coe, “Dark matter halo mass profiles”, arXiv:1005.0411.
- (51) E. Retana-Montenegro, E. Van Hese, G. Gentile, M. Baes and F. Frutos-Alfaro “Analytical properties of Einasto dark matter haloes”, Astron. Astrophys. 540, A70 (2012).
- (52) A. Klypin, G. Yepes, S. Gottlober, F. Prada and S. Hess, “MultiDark simulations: The story of dark matter halo concentrations and density profiles”, Mon. Not. Roy. Astron. Soc. 457, 4340 (2016).
- (53) R.M. O’Leary, B. Kocsis and A. Loeb, “Gravitational waves from scattering of stellar-mass black holes in galactic nuclei”, Mon. Not. Roy. Astron. Soc. 395, 2127 (2009).
- (54) J. Binney, and S. Tremaine, “Galactic Dynamics” (Princeton University Press, Princeton, 2011).
- (55) B.P. Abbott et al. [LIGO Scientific and Virgo], “Characterization of transient noise in advanced LIGO relevant to gravitational wave signal GW150914”, Class. Quant. Grav. 33, 134001 (2016).
- (56) B.P. Abbott et al. [KAGRA, LIGO Scientific and Virgo], “Prospects for observing and localizing gravitational-wave transients with advanced LIGO, advanced Virgo and KAGRA”, Living Rev. Rel. 21, 3 (2018).
- (57) B.P. Abbott et al. [LIGO Scientific and Virgo], “Binary black hole population properties inferred from the first and second observing runs of advanced LIGO and advanced Virgo”, Astrophys. J. Lett. 882, L24 (2019).
- (58) V. Mandic, S. Bird and I. Cholis, “Stochastic gravitational-wave background due to primordial binary black hole mergers”, Phys. Rev. Lett. 117, 201102 (2016).
- (59) A.D. Gow, C.T. Byrnes, A. Hall and J.A. Peacock, “Primordial black hole merger rates: Distributions for multiple LIGO observables”, J. Cosmol. Astropart. Phys. 01, 031 (2020).
- (60) M. Raidal, V. Vaskonen and H. Veermäe, “Gravitational waves from primordial black hole mergers”, J. Cosmol. Astropart. Phys. 09, 037 (2017).
- (61) Y. Ali-Haïmoud, E.D. Kovetz and M. Kamionkowski, “Merger rate of primordial black-hole binaries”, Phys. Rev. D 96, 123523 (2017).
- (62) B. Kocsis, T. Suyama, T. Tanaka and S. Yokoyama, “Hidden universality in the merger rate distribution in the primordial black hole scenario”, Astrophys. J. 854, 41 (2018).
- (63) S. Wang, Y.F. Wang, Q.G. Huang and T.G.F. Li, “Constraints on the primordial black hole abundance from the first advanced LIGO observation run using the stochastic gravitational-wave background”, Phys. Rev. Lett. 120, 191102 (2018).
- (64) K. Kohri and T. Terada, “Primordial black hole dark matter and LIGO/Virgo merger rate from inflation with running spectral indices: Formation in the matter- and/or radiation-dominated universe”, Class. Quant. Grav. 35, 235017 (2018).
- (65) S. Wang, T. Terada and K. Kohri, “Prospective constraints on the primordial black hole abundance from the stochastic gravitational-wave backgrounds produced by coalescing events and curvature perturbations”, Phys. Rev. D 99, 103531 (2019); Erratum: Phys. Rev. D 101, 069901(E) (2020).
- (66) V. De Luca, G. Franciolini, P. Pani and A. Riotto, “Constraints on primordial black holes: The importance of accretion”, Phys. Rev. D 102, 043505 (2020).
- (67) V. De Luca, G. Franciolini, P. Pani and A. Riotto, “Primordial black holes confront LIGO/Virgo data: Current situation”, J. Cosmol. Astropart. Phys. 06, 044 (2020).
- (68) K.W.K. Wong et al., “Constraining the primordial black hole scenario with Bayesian inference and machine learning: The GWTC-2 gravitational wave catalog”, arXiv:2011.01865.
- (69) A. Katz, J. Kopp, S. Sibiryakov and W. Xue, “Femtolensing by dark matter revisited”, J. Cosmol. Astropart. Phys. 12, 005 (2018).
- (70) P. Montero-Camacho, X. Fang, G. Vasquez, M. Silva and C.M. Hirata, “Revisiting constraints on asteroid-mass primordial black holes as dark matter candidates”, J. Cosmol. Astropart. Phys. 08, 031 (2019).
- (71) N. Smyth, et al., “Updated constraints on asteroid-mass primordial black holes as dark matter”, Phys. Rev. D 101, 063005 (2020).
- (72) A. Coogan, L. Morrison and S. Profumo, “Direct detection of Hawking radiation from asteroid-mass primordial black holes”, arXiv:2010.04797.
- (73) A. Ray, R. Laha, J.B. Muñoz and R. Caputo, “Closing the gap: Near future MeV telescopes can discover asteroid-mass primordial black hole dark matter”, arXiv:2102.06714.
- (74) Z.S.C. Picker, “Navigating the asteroid field: New evaporation constraints for primordial black holes as dark matter”, arXiv:2103.02815.
- (75) R. Abbott et al. [LIGO Scientific and Virgo], “GWTC-2: Compact binary coalescences observed by LIGO and Virgo during the first half of the third observing run”, arXiv:2010.14527.
- (76) Y. Inoue and A. Kusenko, “New x-ray bound on density of primordial black holes”, J. Cosmol. Astropart. Phys. 10, 034 (2017).
- (77) Y. Ali-Haïmoud and M. Kamionkowski, “Cosmic microwave background limits on accreting primordial black holes”, Phys. Rev. D 95, 043534 (2017).
- (78) P.D. Serpico, V. Poulin, D. Inman and K. Kohri, “Cosmic microwave background bounds on primordial black holes including dark matter halo accretion”, Phys. Rev. Res. 2, 023204 (2020).
- (79) T.D. Brandt, “Constraints on MACHO dark matter from compact stellar systems in ultra-faint dwarf galaxies”, Astrophys. J. Lett. 824, L31 (2016).
- (80) S.M. Koushiappas and A. Loeb, “Dynamics of dwarf galaxies disfavor stellar-mass black holes as dark matter”, Phys. Rev. Lett. 119, 041102 (2017).
- (81) M. Zumalacarregui and U. Seljak, “Limits on stellar-mass compact objects as dark matter from gravitational lensing of type Ia supernovae”, Phys. Rev. Lett. 121, 141101 (2018).