Primitive, proper power, and Seifert curves in the boundary of a genus two handlebody
Abstract.
A simple closed curve in the boundary of a genus two handlebody is primitive if adding a 2-handle to along yields a solid torus. If adding a 2-handle to along yields a Seifert-fibered space and not a solid torus, the curve is called Seifert. If is disjoint from an essential separating disk in , does not bound a disk in , and is not primitive in , then it is said to be proper power.
As one of the background papers of the classification project of hyperbolic primitive/Seifert knots in whose complete list is given in [BK20], this paper classifies in terms of R-R diagrams primitive, proper power, and Seifert curves. In other words, we provide up to equivalence all possible R-R diagrams of such curves. Furthermore, we further classify all possible R-R diagrams of proper power curves with respect to an arbitrary complete set of cutting disks of a genus two handlebody.
1. Introduction and main results
In this paper, we provide the classifications of three types of simple closed curves lying in the boundary of a genus two handlebody: primitive, proper power, and Seifert curves. These classifications will be used in the classification project of hyperbolic primitive/Seifert knots in whose complete list is given in [BK20].
Primitive/Seifert(or simply P/SF) knots, which were introduced in [D03], are a natural generalization of primtive/primitive(or simply P/P) knots defined by Berge in [B90] or an available version [B18]. Both P/P knots and P/SF knots are represented by simple closed curves lying in a genus two Heegaard surface of bounding two handlebodies such that 2-handle additions to the handlebodies along the curves are solid tori for P/P knots and one 2-handle addition is a solid torus and the other is a Seifert-fibered space and not a solid torus for P/SF knots. One component of the intersection of a regular neighborhood of a knot and the Heegaard surface defines a so-called surface-slope.
Berge constructed twelve families of P/P knots which are referred to as the Berge knots. The Berge knots admit lens space Dehn surgeries at surface-slopes. The Berge conjecture, which is still unsolved, says that if a knot in admits a lens space Dehn surgery, then it is a Berge knot and the surgery is the corresponding surface-slope surgery. Therefore the conjecture implies the complete classification of knots admitting lens space Dehn surgeries. Toward the Berge conjecture, it is proved in [B08] or independently in [G13] that all P/P knots are the Berge knots. This implies that the Berge knots are the complete list of P/P knots.
Meanwhile, P/SF knot are also of interest, because P/SF knots admit Seifert-fibered Dehn surgeries at surface-surface slopes and knots with Dehn surgeries yielding Seifert-fibered spaces are not well understood. The classification project of hyperbolic primitive/Seifert knots in has been carried out for years and has recently been completed. The complete list of hyperbolic primitive/Seifert knots in is given in [BK20] where the surface-slope of the exceptional surgery on each P/SF knot that yields a Seifert-fibered space and the indexes of each exceptional fiber in the resulting Seifert-fibered space are also provided.
Now we describe the results of this paper, which is the classifications of primitive, proper power, and Seifert curves in the boundary of a genus two handlebody. The definitions of such curves are as follows.
Definition 1.1.
Let be a genus two handlebody, an essential simple closed curve in , and the 3-manifold obtained by adding a 2-handle to along .
-
(1)
is said to be primitive if is a solid torus.
-
(2)
is said to be proper power if is disjoint from an essential separating disk in , does not bound a disk in , and is not primitive in .
-
(3)
is said to be Seifert if is a Seifert-fibered space and not a solid torus.
There are subtypes of Seifert curves in . Since is a genus two handlebody, that is Seifert in implies that is an orientable Seifert-fibered space over with two exceptional fibers, or an orientable Seifert-fibered space over the Möbius band with at most one exceptional fiber. Therefore, we further divide Seifert curves into two subtypes. If is Seifert-fibered over , we say that is Seifert-d. If is Seifert-fibered over the Möbius band, we say that is Seifert-m.
The following theorems present the classifications of primitive, proper power, and Seifert curves. They are described in terms of R-R diagrams. For the definition and properties of R-R diagrams, see [K20].
Theorem 1.2.
Suppose is a simple closed curve in the boundary of a genus two handlebody .
-
(1)
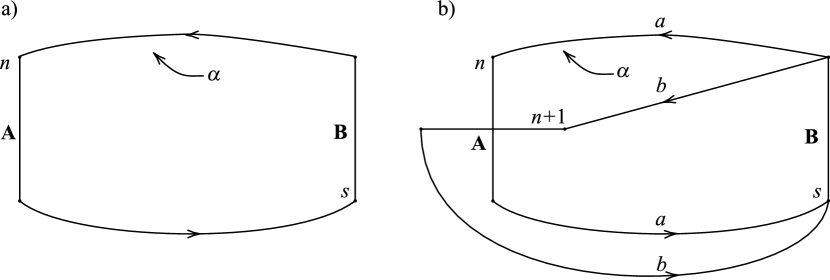
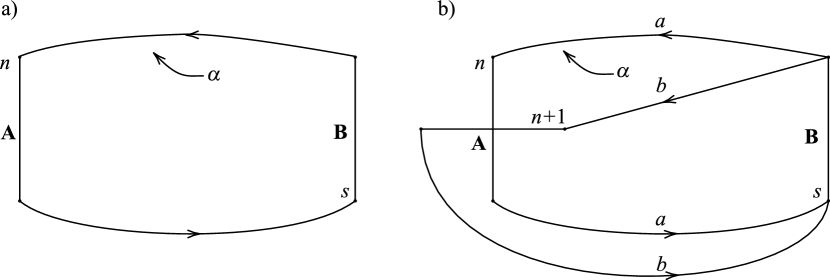
If is a primitive curve, then has an R-R diagram of the form shown in Figure 1.
-
(2)
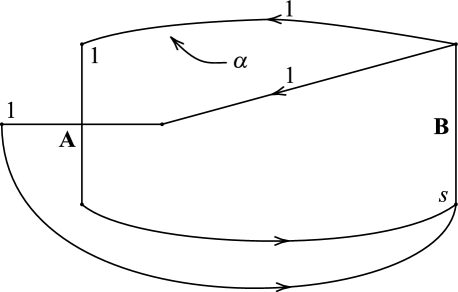
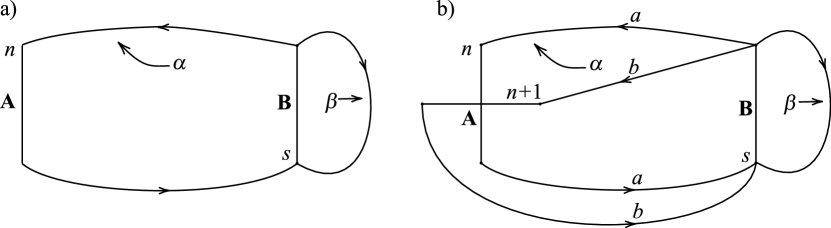
If is a Seifert-d curve, then has an R-R diagram of the form shown in Figure 2 with , , and .
-
(3)
If is a Seifert-m curve, then has an R-R diagram of the form shown in Figure 3 with .
-
(4)
If is a proper power curve, then has an R-R diagram of the form shown in Figure 4 with .
Regarding Seifert curves, if has an R-R diagram of the form shown in Figure 2a (b, respectively), then is a Seifert-fibered space over with two exceptional fibers of indexes and ( and , respectively). If has an R-R diagram of the form shown in Figure 3, then is a Seifert-fibered space over the Möbius band with one exceptional fiber of index .

We can further classify proper power curves in the following theorem. From now on, to distinguish proper power curves from primitive or Seifert curves, we use the letter instead of to represent proper power curves. We will see such a situation in Sections 4 and 5.
Theorem 1.3 (Further classification of proper power curves).
Suppose is a genus two handlebody with a complete set of cutting disks with , where the generators and are dual to and respectively. If is a proper power curve in , then has one of the following R-R diagrams with respect to the complete set of cutting disks up to the homeomorphisms of inducing the automorphisms exchanging and , and replacing by or by :
-
(1)
Type I: has an R-R diagram with a -connection in at least one of the handles.
-
(2)
Type II: has an R-R diagram of the form shown in Figure 4 with .
-
(3)
Type III: has an R-R diagram of the form shown in Figure 5 with and .
-
(4)
Type IV: has an R-R diagram of the form shown in Figure 6 with .
-
(5)
Type V: has an R-R diagram of the form shown in Figure 7 with .




The classifications of such curves play very important role in the classification of all hyperbolic primitive/Seifert(or simply P/SF) knots in whose complete list is given in [BK20]. The classifications of primitive and Seifert curves are the first step in the classification of hyperbolic P/SF knots in . Additionally if is Seifert in such that embeds in , then is homeomorphic to the exterior of a torus knot. Therefore the classification of Seifert curves in naturally carries that of all simple closed curves such that is homeomorphic to the exterior of a torus knot.
The classification of proper power curves has various applications. First it is used to determine if P/P(primitive/primitive) or P/SF knots are hyperbolic or not. It turns out that if P/P or P/SF knots are not hyperbolic, then there exists a proper power curve in some circumstances. Another application is that when a curve is Seifert in ,
i.e., is an orientable Seifert-fibered space, a proper power curve disjoint from becomes a regular fiber of the Seifert-fibered space and can be used to compute the indexes of exceptional fibers. Also in order to classify some type of primitive/Seifert knots, called knots in Once-Punctured Tori(or simply OPT), properties of proper power curves are used.
Acknowledgement. In 2008, in a week-long series of talks to a seminar in the department of mathematics of the University of Texas as Austin, John Berge outlined a project to completely classify and describe the primitive/Seifert knots in . The present paper, which provides some of the background materials necessary to carry out the project, is originated from the joint work with John Berge for the project. I should like to express my gratitude to John Berge for his support and collaboration. I would also like to thank Cameron Gordon and John Luecke for their support while I stayed in the University of Texas at Austin.
2. R-R diagrams of primitive curves
In this section, we classify R-R diagrams of primitive curves in the boundary of a genus two handlebody. Let be a primitive curve in a genus two handlebody . In other words, is a solid torus. In order to obtain R-R diagrams of we use the following lemma which shows equivalent conditions of primitivity. The proof may be found in [W36], [Z70], or [G87].
Lemma 2.1.
The following are equivalent:
-
(1)
is primitive in , i.e., is a solid torus;
-
(2)
belongs to a basis for the free group ;
-
(3)
is transverse to a properly embedded disk in .
Theorem 2.2.
If is a nonseparating simple closed curve in the boundary of a genus two handlebody such that is primitive on , then has an R-R diagram with the form of Figure 1.
Proof.
By Lemma 2.1, there exists a cutting disk in such that meets transversely in a single point. Consider the regular neighborhood of in . Then is a once-punctured torus which contains , and whose boundary bounds a separating disk of . Let . Then it follows by cutting open along that there exists a unique cutting disk of up to isotopy whose boundary lies on .
This partition of with and gives rise to an R-R diagram of in which and correspond to the -handle and -handle respectively. Since lies in and intersects in a single point, has an R-R diagram of the form shown in Figure 1. This completes the proof. ∎
3. R-R diagrams of a proper power curve and more classifications
In this section, we classify proper power curves. Let be a proper power curve in the boundary of a genus two handlebody . The following lemma is an easy consequence of Lemma 2.1.
Lemma 3.1.
The following are equivalent:
-
(1)
is a proper power curve in , i.e., is disjoint from an essential separating disk, does not bound a disk, and is not primitive in ;
-
(2)
is conjugate to of , where is a free generator of ;
-
(3)
There exists a complete set of cutting disks of such that is disjoint to, say, and is transverse to times.
The main results of this section are the following.
Theorem 3.2.
Suppose is a simple closed curve in the boundary of a genus two handlebody . If is a proper power curve in , then has an R-R diagram of the form shown in Figure 4.
Theorem 3.3.
Suppose is a genus two handlebody with a complete set of cutting disks with , where the generators and are dual to and respectively. If is a proper power curve in , then has one of the following R-R diagrams with respect to the complete set of cutting disks up to the homeomorphisms of inducing the automorphisms exchanging and , and replacing by or by :
-
(1)
Type I: has an R-R diagram with a -connection in at least one of the handles.
-
(2)
Type II: has an R-R diagram of the form shown in Figure 4 with ..
-
(3)
Type III: has an R-R diagram of the form shown in Figure 5 with and .
-
(4)
Type IV: has an R-R diagram of the form shown in Figure 6 with .
-
(5)
Type V: has an R-R diagram of the form shown in Figure 7 with .
The proof of Theorem 3.2 follows immediately from the definition of a proper power curve. In order to prove Theorem 3.3, we need the following minor generalization of a result of Cohen, Metzler, and Zimmerman [CMZ81] which allows one to determine easily if a given cyclically reduced word in a free group of rank two is a primitive or a proper power of a primitive.
Theorem 3.4.
[CMZ81] Suppose a cyclic conjugate of
is a member of a basis of or a proper power of a member of a basis of , where and each indicated exponent is nonzero. Then, after perhaps replacing by or by , there exists such that:
or
The proof of Theorem 3.3.
In order to find all possible R-R diagrams of a proper power curve , we consider the following cases separately.
-
(1)
has a 0-connection in at least one of the handles in its R-R diagram.
-
(2)
has no 0-connections in either handle in its R-R diagram.
The case where has a -connection in one handle gives restriction to other curves in disjoint from . In other words, if is a simple closed curve in disjoint from , then must have only bands of connections labeled by or in that handle. Therefore we put this case into one type of possible proper power curves, which gives Type I in Theorem 1.2.
Now we assume that has no 0-connections in either handle.
Suppose has only one generator in . Then up to replacement of with , with , or exchange of and , we may assume that for some . Since has no 0-connections, this implies that has no connections in the -handle and only one connection in the -handle. Thus this case gives rise to Type II of a proper power curve in Theorem 3.2 with an R-R diagram of the form shown in Figure 4.
Now suppose that has the two generators and in . By Theorem 3.4, we may assume that , where with and min. This implies that every connection in the -handle is labeled by 1. There are two cases to consider:
-
(1)
has only one band of 1-connections in the -handle,
-
(2)
has two bands of 1-connections in the -handle.
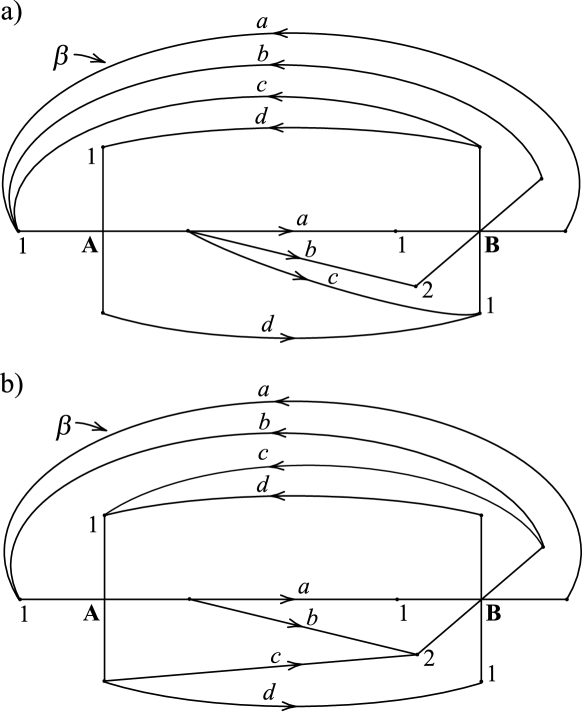
Case (1): Assume that has only one band of 1-connections in the -handle.
Suppose . Without loss of generality, we may assume that . If , then there must be only one band of -connections in the -handle, in which case is a primitive curve with . Therefore and there must be two bands of 1-connections in the -handle. Then with and exchanged, this case belongs to Type III of a proper power curve in Theorem 3.2 with an R-R diagram of the form shown in Figure 5.
Suppose . Then has at least two bands of connections in the -handle. If has two bands of connections in the -handle, must have an R-R diagram of the form shown in Figure 9 and by Lemma 3.5, is not a proper power curve. If has three bands of connections in the -handle, then these three bands of connections should be labeled by 1, 2 and 1 respectively, and has the R-R diagram of the form shown in Figure 11. By Lemma 3.6, is not a proper power curve.
Case (2): has two bands of 1-connections in the -handle.
Suppose . Without loss of generality, we may assume that . Then if has only one band of connections in the -handle, then the band must be labeled by , in which case Type III of a proper power curve in Theorem 3.2 arises with an R-R diagram of the form shown in Figure 5. If has two bands of connections in the -handle, then must be 1 and this case yields Type IV of a proper power curve in Theorem 3.2 with an R-R diagram of the form shown in Figure 6.
Suppose . If there are only two bands of connections in the -handle, then must have R-R diagram of the form shown in Figure 12 and by Lemma 3.7, is not a proper power curve.
If there are three bands of connections in the -handle, then has two types of R-R diagrams as shown in Figure 8. By Lemma 3.8, the R-R diagram of in Figure 8a cannot be a proper power curve. Therefore we have the R-R diagram of in Figure 8b, which gives Type V of a proper power curve in Theorem 3.2.
Thus we complete the proof of Theorem 3.2 ∎
Lemma 3.5.
Suppose a simple closed curve has an R-R diagram with the form shown in Figure 9 where with min, and . Then is a primitive curve.

Proof.
Note that since is a simple closed curve, gcd. Let , where and (if , then and ). Now we record the curve algebraically by starting the parallel arcs, i.e., the band of width , entering into the -connection in the -handle. It follows that is the product of two subwords and with and . Here, for example, denotes the total number of appearances of in the word of in .
There is a change of cutting disks of the handlebody , which induces an automorphism of that takes and leaves fixed. Then by this change of cutting disks, and are sent to and respectively. Therefore the resulting Heegaard diagram of realizes a new R-R diagram of the form in Figure 10, where the positions of the and -handles are switched. The new R-R diagram has the same form as that in Figure 9 with less number of arcs. One can continue inductively until one of the labels of parallel arcs is 0, in which case for some up to replacement of with , with , or exchange of and . Such a curve is a primitive curve. ∎

Lemma 3.6.
Suppose a simple closed curve has an R-R diagram with the form shown in Figure 11 where . Then is not a proper power curve.

Proof.
First, note that gcd in order for to be a simple closed curve. Since and appear in , by considering as a generating set of and by Theorem 3.4 one of the two must appear with exponent . However, from the R-R diagram one can see that if one reads from the right-hand edge of the band of width entering the 1-connection in the -handle, then appears twice consecutively. Therefore must have only exponent .
If , then appears only once and thus is a primitive curve. Suppose . Consider following the band of width around the R-R diagram. Since is a simple closed curve, this band must split into two subbands at the endpoint of the -connection in the -handle. If the band splits into two subbands belonging to the bands of width and respectively, then by tracing arcs of this band we see that has two subwords and for some positive integers and with . It follows from Theorem 3.4 that cannot be a proper power curve. Similarly for the case where the band splits into two subbands belonging to the bands of width and respectively. ∎
Lemma 3.7.
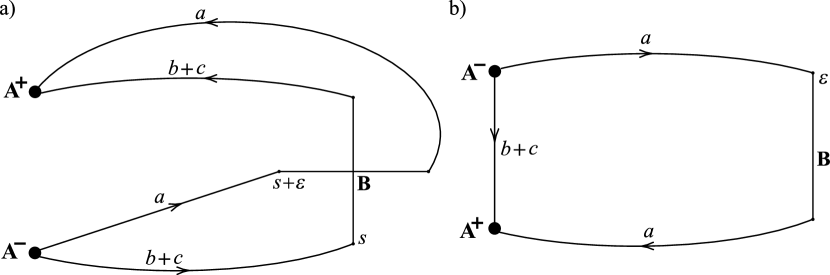
Suppose a simple closed curve has an R-R diagram with the form shown in Figure 12 where with min, and . Then is not a proper power curve.

Proof.
We use the argument of hybrid diagrams which are introduced in [K20]. Consider the corresponding hybrid diagram as shown in Figure 13a. Then we drag the vertex A- together with the edges meeting the vertex A- over the -connection in the -handle. This corresponds to the change of the cutting disks of inducing an automorphism of which takes and leaves fixed. The resulting hybrid diagram is shown in Figure 13b.
Transforming the hybrid diagram in Figure 13b back into an R-R diagram, there are three possible cases to consider as follows:
-
(1)
There is only one band of connections in the -handle;
-
(2)
There are only two bands of connections in the -handle;
-
(3)
There are three bands of connections in the -handle.
Note from Figure 13b that since , all of the labels of bands of connections in the -handle are greater than and at least one of the bands of connections has label greater than .
(1) Suppose that there is only one band of connections in the -handle. Then must be 1 and , which is primitive.
(2) Suppose that there are only two bands of connections in the -handle. Let and be the labels of the two bands of connections. Since and thus at least one of the bands of connections has label greater than , . Theorem 3.4 forces to be . However, by Lemma 3.5 such a curve is a primitive curve.
(3) Suppose that there are three bands of connections in the -handle. Let and be the labels of the three bands of connections with . In order for to be a proper power, . However, by Lemma 3.6, is not a proper power curve. ∎
Lemma 3.8.
Suppose a simple closed curve has an R-R diagram with the form shown in Figure 14 where . Then is not a proper power curve.

Proof.
Consider the corresponding hybrid diagram as shown in Figure 15a.
Then we drag the vertex A- together with the edges meeting the vertex A- over the -connection in the -handle. This corresponds to the change of the cutting disks of inducing an automorphism of which takes and leaves fixed. The resulting hybrid diagram is shown in Figure 15b.
Transforming the hybrid diagram in Figure 15b back into an R-R diagram, there are three possible cases to consider as follows:
-
(1)
There is only one band of connections in the -handle;
-
(2)
There are only two bands of connections in the -handle;
-
(3)
There are three bands of connections in the -handle.
Note from Figure 15b that since , all of the labels of bands of connections in the -handle are greater than and at least one of the bands of connections has label greater than .
(1) Suppose that there is only one band of connections in the -handle. Let be the label of the band of connections. Since there are the edges connecting A+ and A-, . On the other hand, in Figure 14, consider chasing back and forth the outermost arc in the band of width entering the 1-connection in the -handle. This represents , which is carried into by the automorphism . This implies that has a 1-connection in the -handle, a contradiction.
(2) Suppose that there are only two bands of connections in the -handle. Let and be the labels of the two bands of connections. By the similar argument in the proof of Lemma 3.7, . However, by Lemma 3.7 such a curve cannot be a proper power.
(3) Suppose that there are three bands of connections in the -handle. Let and be the labels of the three bands of connections with . In order for to be a proper power, . Then by switching the - and -handles, and the signs of the labels, the R-R diagram of has the same form as in Figure 14 with less number of the arcs connecting the - and -handles. So if we can continue to perform the change of cutting disks of , then since the number of the edges is strictly decreasing under the change of cutting disks, this case must eventually belong to the cases (1) and (2). ∎
4. R-R diagrams of Seifert-d curves
In this section, we classify the R-R diagrams of a simple closed curve which is Seifert-d in a genus two handlebody. If is a Seifert-d curve in a genus two handlebody , then by its definition is a Seifert-fibered space over with two exceptional fibers. In order to compute the type of exceptional fibers in , we need the following notation and lemma.
Notation. If is an element of , let denote the element of , and let ‘’ denote the usual inner product or dot product of vectors.
Lemma 4.1.
Let , and be three elements of such that . If is expressed as a linear combination of and , say , then .
Proof.
We take an inner product by on both sides of . Then since and , the result follows. ∎
The main result of this section is the following theorem.
Theorem 4.2.
If is a nonseparating simple closed curve in the boundary of a genus two handlebody such that is Seifert-fibered over with two exceptional fibers, then has an R-R diagram with the form of Figure 16a with , or 16b with , , and .
Proof.
We start by showing that if is Seifert-fibered over with two exceptional fibers, then has an R-R diagram of the claimed form.
The key idea is that , which is defined to be the manifold obtained by adding a 2-handle to along , induces a genus two Heegaard decomposition of a Seifert-fibered space over with two exceptional fibers. However Heegaard decompositions of a Seifert-fibered space over are well understood. For instance, Theorem 4.4, of Boileau, Rost and Zieschang, completely describes the genus two Heegaard diagrams of a Seifert-fibered space over with two exceptional fibers. Using this result, Theorem 4.5 shows how the Heegaard diagrams described in Theorem 4.4 translate into R-R diagrams. And then Lemma 4.6 adds a finishing detail to the proof of this direction by showing that it is always possible to assume that in Figure 16b.
With the proof of one direction of Theorem 4.2 finished, it remains to show that if has an R-R diagram with the form of Figure 16a with , or Figure 16b with , , and , then is Seifert-fibered over with two exceptional fibers.
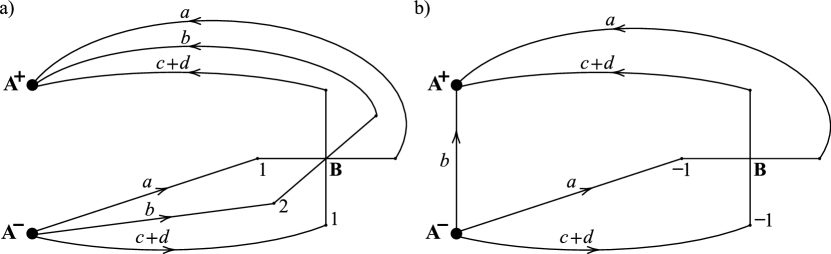
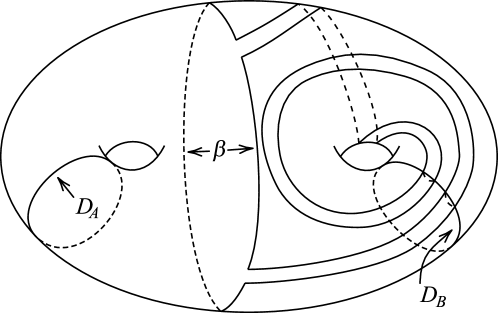
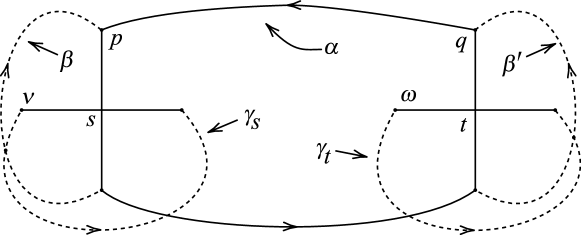
To see that this is the case, consider Figure 17 in which each of the R-R diagrams of Figure 16 has been augmented with a simple closed curve disjoint from . Then, in each diagram of Figure 17, two parallel copies of bound an essential separating annulus in . (Figure 18 illustrates the situation when , and and are cutting disks of underlying the A-handle and B-handle of the R-R diagram of .)
Cutting apart along yields a genus two handlebody and a solid torus . Note that lies in as a primitive curve in implying that is a solid torus, because any component of is a cutting disk of such that an R-R diagram of with respect to of has the form in Figure 16 with replaced by , in which case in Figure 16a intersects only once and thus is primitive, and in Figure16b is primitive by Lemma 3.5. It follows that is obtained by gluing the two solid tori and together along . So is Seifert-fibered over with as a regular fiber and the cores of and as exceptional fibers.
The last step is to compute the indexes of the two exceptional fibers of . It is clear that the annulus wraps around the solid torus times longitudinally, so the core of is an exceptional fiber of index . For the other index, it follows by computing that if has an R-R diagram with the form of Figure 16a, then the core of is an exceptional fiber of index .
Finally, suppose the R-R diagram of has the form of Figure 16b. In this case, Lemma 4.1 can be used to compute the index of the second exceptional fiber formed by the core of .
Abelianizing , we have: = and = . By Lemma 4.1:
in . Thus the regular fiber wraps around the solid torus longitudinally times, so the core of is an exceptional fiber of index . ∎
Remark 4.3.
(1) If has an R-R diagram of the form shown in Figure 16a(Figure 16b, resp.), is said to be a Seifert-d curve of rectangular(non-rectangular, resp.) form.
(2) The regular fiber is a proper power curve representing in , where and are dual to the cutting disks and underlying the -handle and -handle respectively of the R-R diagram. In addition, since the R-R diagram of Figure 16a is symmetric, the argument of the fifth paragraph in the proof above shows that that the proper power curve representing in the R-R diagram of Figure 16a is also a regular fiber of .
Turning to the description of Heegaard decompositions of orientable Seifert-fibered spaces over with two exceptional fibers, let denote an orientable Seifert-fibered space over the disk which has two exceptional fibers of types and with and .
Also let be the unique primitive word up to conjugacy in the free group which has as its abelianization. Then, if and are words in and , is the word obtained from by substituting for and for in .
Then the following theorem of Boileau, Rost and Zieschang(Theorem 5.4 in [BRZ88]) completely describes the genus two Heegaard diagrams of . For the notations in Theorem 4.4, see Sections 2, 4, and 5 in [BRZ88].
Theorem 4.4.
[BRZ88] The manifold admits three genus two Heegaard decompositions , , and , represented by the following Heegaard diagrams:
Here and . Any Heegaard decomposition of genus two of is homeomorphic to one of these. Moreover:
-
(1)
is homeomorphic to (or ) if and only if ( or , respectively).
-
(2)
If and , then , , and are all homeomorphic.
-
(3)
and are homeomorphic if and only if either case (2) occurs or (that is, and ).
Theorem 4.5.
Proof.
Next, consider the diagram of Figure 19, and let and be cores of the A-handle and B-handle of . Then and are the exceptional fibers of the Seifert-fibration of . Let and be closed regular neighborhoods of and respectively in , and let and be meridional disks of and respectively.
Observe that the pair of dotted curves , on the A-handle of Figure 19 can be considered to lie on , while the pair of dotted curves , on the B-handle of Figure 19 can be considered to lie on . Also observe that as indicated in Remark 4.3, the curves and represent regular fibers of the Seifert-fibration of . Then = in , while = in . So and are exceptional fibers of types and in the Seifert-fibration of .
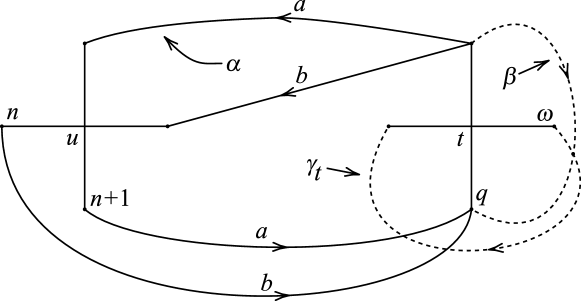
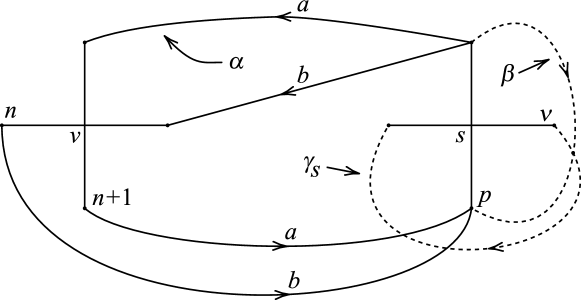
This leaves the diagrams of Figures 20 and 21. Since these diagrams are similar, we will only consider Figure 20 in detail. To start, note that the configuration of the curves and on the B-handle of Figure 20 is identical to that of and on the B-handle of Figure 19. Since is again a regular fiber in the Seifert-fibration of when has an R-R diagram on with the form of Figure 20, the core of the B-handle of is again an exceptional fiber of type . The other exceptional fiber that exists in when has an R-R diagram on with the form of Figure 20, arises in a slightly different way.
As in Figure 18, two parallel copies of the regular fiber in Figure 20 bound an essential separating annulus in . Cutting open along cuts into a genus two handlebody and a solid torus which has as its core. The curve lies on , and the R-R diagram of on appears in Figure 22. Since is primitive in , is a solid torus . Let be the core of . Then is the second exceptional fiber of the Seifert-fibration of .
Let be the meridional disk of , and note that the curves and of Figure 22 lie on and and form a basis for . The next step is to obtain an expression for in in terms of the basis , of .
We can do this by using Lemma 4.1. Abelianizing , we have: = = , = , and = . By Lemma 4.1:
in , where . It follows that = in . So is an exceptional fiber of type in the Seifert-fibration of when has an R-R diagram with the form of Figure 20.
Similarly, one sees that if has an R-R diagram with the form of Figure 21, then is also Seifert-fibered over with two exceptional fibers of types and . ∎
It will be convenient to be able to assume that in Figure 16b. The following lemma shows this can always be done.
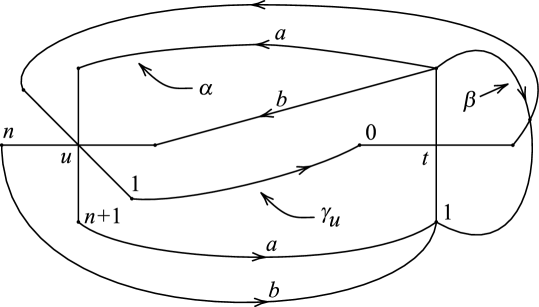
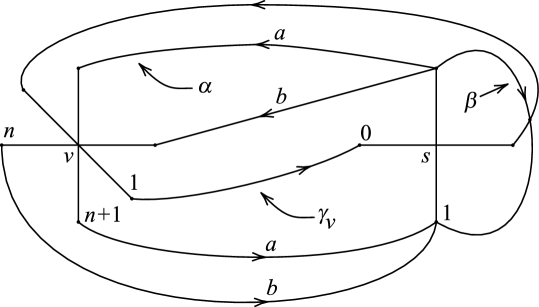
Lemma 4.6.
Proof.
Suppose a simple closed curve in the boundary of a genus two handlebody has an R-R diagram with the form of Figure 20 with . For the form of Figure 21, the similar argument can apply. Note that since , and . It is easy to see that the underlying Heegaard diagram of on does not have minimal complexity. Thus in order to have minimal complexity, we can perform a change of cutting disks of , i.e., replace the cutting disk of which underlies the -handle with a new cutting disk by bandsumming with the cutting disk in the -handle along the arc of .
Specifically, for the weights and in the R-R diagram, since gcd, we can let , where and . However we may assume , otherwise and thus and , which implies that and it follows from Theorem 4.4 that this Heegaard decomposition is homeomorphic to .
Now we record by starting the parallel arcs entering into the -connection in the -handle. It follows from the R-R diagram that is the product of two subwords and with and . We perform a change of cutting disks of the handlebody which induces an automorphism of that takes . Then by this change of cutting disks, and are sent to and . Therefore the resulting Heegaard diagram of has minimal complexity and realizes a new R-R diagram of the form in Figure 24, which is the same form as in Figure 20 with . ∎
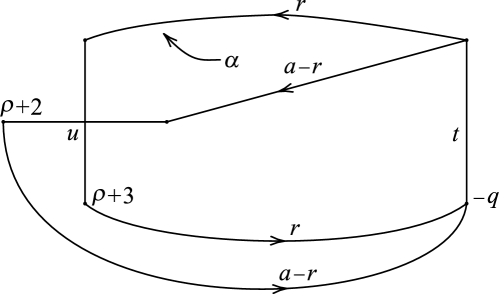
Remark 4.7.
The following observations are relevant for Lemma 4.6.
-
(1)
The change of cutting disks of inducing the automorphism in corresponds to the change of the cutting disk to a new cutting disk which is obtained by bandsumming with the cutting disk along the arcs of times.
-
(2)
The diagram of Figure 24 corresponds to the Heegaard decomposition of , which is homeomorphic to as desired.
5. R-R diagrams of Seifert-m curves
If is a Seifert-m curve on a genus two handlebody , then by its definition is a Sefiert-fibered space over the Möbius band with at most one exceptional fiber. The main result of this section is the following theorem.
Theorem 5.1.
If is a nonseparating simple closed curve in the boundary of a genus two handlebody such that is a Seifert-fibered space over the Möbius band, then has an R-R diagram of the form shown in Figure 25, and represents in . There is no loss in taking , and then has an exceptional fiber if and only if , in which case, equals the index of the exceptional fiber of .
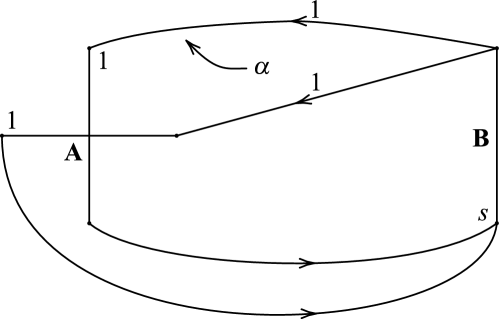
Proof.
Suppose is homeomorphic to a Seifert-fibered space over the Möbius band. Then contains an essential nonseparating annulus which is vertical in the Seifert fibration of . (Such an annulus can be easily obtained by starting with a nonseparating arc in the Möbius band—taking care to choose an arc which misses any exceptional fiber of —and then saturating that arc in the Seifert-fibration of .)
Since is Seifert-fibered, and not a solid torus, is -irreducible. This implies intersects every cutting disk of . Now a theorem of Eudave-Muñoz applies. It is shown in [EM94] that if contains an essential nonseparating annulus, then there exists an essential nonseparating annulus in , with and disjoint, such that is essential in . (Note that in [EM94] the definition of an essential annulus which is properly embedded in a 3-manifold is that it is incompressible and not -parallel.) Furthermore, it follows from Lemmas 1.10, 1.11 and the argument following them in [H07] that is vertical in the Seifert-fibration of .
This suggests looking for all possible R-R diagrams of by starting with an R-R diagram of the boundary components of a nonseparating annulus in . Then any R-R diagram of must be obtained by adding to so that is disjoint from the curves and of , and intersects every cutting disk of .
Lemma 5.3 carries out the first step of this scheme by showing that if is a nonseparating essential annulus in a genus two handlebody , and and are the components of in , then and have an R-R diagram of the form shown in Figure 28.
Next, Lemma 5.5 shows that if is an R-R diagram with the form of Figure 28, and a simple closed curve is added to so that is disjoint from and in , and intersects every cutting disk of , then the resulting R-R diagram must have the form shown in Figure 31.
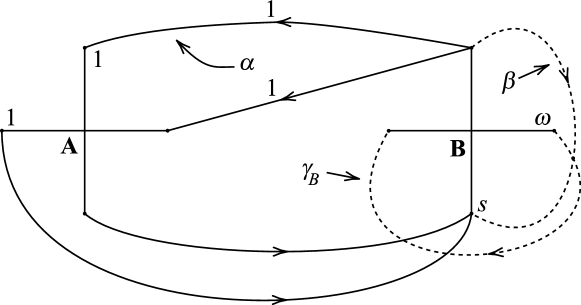
Lemmas 5.6 and 5.7 finish the argument by showing that if is Seifert-fibered over the Möbius band, then in Figure 31, so Figure 31 reduces to Figure 25. In addition, these lemmas show that has an exceptional fiber if and only if , and when , equals the index of the exceptional fiber of .
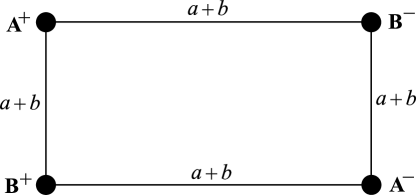
Now we prove the second statement of the theorem. First, suppose and have an R-R diagram of the form shown in Figure 26 with replaced by , which is an augmentation of the R-R diagram of in Figure 25. We will show that is a Seifert-fibered space over the Möbius band with no exceptional fibers whose regular fiber is represented by the curve . Consider a properly embedded nonseparating annulus in whose boundary consists of the curves and , where is a curve illustrated in Figure 28. Figure 27a shows the genus two handlebody , the simple closed curve on , and the annulus with oriented, which realize the R-R diagram of and in Figure 26 with and the R-R diagram of in Figure 28. Let be the manifold obtained by cutting along . Let and , and , and and be the copies of , , and in . Then it is easy to see that is a genus two handlebody such that and together with and lie in as shown in Figure 27b.
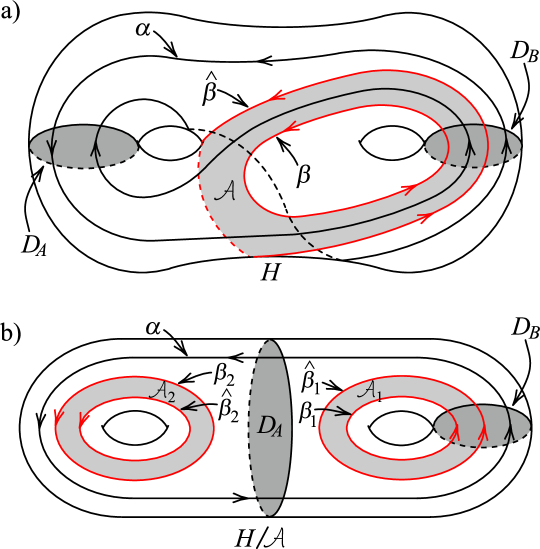
Since is disjoint from , is obtained from by gluing the two copies and such that the orientations of their boundaries and match. However, we can observe from Figure 27b that is primitive in the genus two handlebody and thus is a solid torus. Thus gluing and in the boundary of the solid torus yields Seifert-fibered over the Möbius band with no exceptional fibers such that is a regular fiber. Therefore is a Seifert-fibered space over the Möbius band with no exceptional fibers whose regular fiber is represented by the curve .
Now we suppose that and have an R-R diagram of the form shown in Figure 26 with . Similarly as in the proof of Theorem 4.2, the two parallel copies of bound an essential separating annulus in as shown in Figure 18, which cuts apart into a genus two handlebody and a solid torus . Note that lies in the boundary of . To complete the proof, it suffices to show that is a Seifert-fibered space over the Möbius band with no exceptional fibers and the curve is a regular fiber of .
A component of is a cutting disk of such that and intersect transversely once. This implies that the R-R diagram of and with respect to has the form in Figure 26 with replaced by . Therefore by the argument above in the case that , we see that is a Seifert-fibered space over the Möbius band with no exceptional fibers and the curve is a regular fiber of , as desired. ∎
Remark 5.2.
In Theorem 5.1, if , then is a Seifert-fibered space over the Möbius band with no exceptional fibers. Then admits another Seifert-fibered structure, i.e., is a Seifert-fibered space over with two exceptional fibers of both indexes 2. Therefore we can regard a Seifert-m curve in this case as a Seifert-d curve, and thus we may assume in the R-R diagram of a Seifert-m curve .
(2) Figure 26 shows an R-R diagram of such that is a Seifert-fibered space over the Möbius band with one exceptional fiber of type , whose regular fiber is the curve .
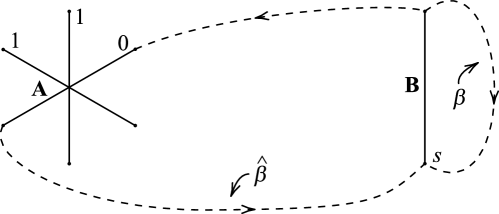
Lemma 5.3.
Suppose is an essential nonseparating annulus properly embedded in a genus two handlebody . Let and be the two curves in that form . Then the pair , have an R-R diagram that appears in Figure 28.
Proof.
Given and its boundary components and , we claim the following.
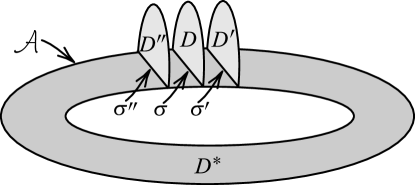
Claim 5.4.
There exists a complete set of cutting disks of such that one of the cutting disks, say , is disjoint from and consists of a set of essential spanning arcs in .
Proof.
First, we show that there exists a cutting disk of disjoint from . Let be a cutting disk of which intersects minimally.
Suppose . Then we may assume that intersects essentially and consists of properly embedded disjoint arcs and disjoint circles. However by the incompressibility of , irreducibility of , and the minimality condition rule out circle intersections. Suppose is an outermost arc of which cuts a disk of . Then also cuts into two subdisks and of . Consider two disks and , which are obtained by gluing and , and and respectively along . Then since is a cutting disk which means that it is nonseparating, at least one of and is nonseparting and thus is a cutting disk. But this cutting disk intersects less than . This is a contradiction to the minimality.
Suppose is a spanning arc of in which is outermost in . Let and be two copies of , and let and as shown in Figure 29. Also let be a disk such that and are included in . Gluing the two copies and to the disk along and yields a disk . Since is nonseparating, from the construction is nonseparating (and thus is a cutting disk) and also does not intersect , a contradiction. Therefore there exists a cutting disk of disjoint from .
Now let be a cutting disk of chosen so that is a complete set of cutting disks of and intersects minimally. By applying the same argument above, we can show that consists of spanning arcs of . Note that , otherwise would embed properly in a 3-ball and thus not be essential. This completes the proof of the claim. ∎
By the claim, there exists a complete set of cutting disks of such that is disjoint from and consists of a set of essential spanning arcs in . Now consider the solid torus obtained by cutting open along . Then contains two disks and , which are copies of . The simple closed curves and also lie in and cut into two annuli, say and . Since and are not isotopic in , lies in the interior of one of these annuli, and lies in the interior of the other. It is easy to see that there exists an arc in connecting and which . Furthermore since a regular neighborhood of is a disk in , we can isotope keeping so that is disjoint from the meridional disk of . Since , now we may assume that .
Next, let be a once-punctured torus in which is a regular neighborhood in of , with chosen so that is disjoint from , and so that intersects minimally. Then, if is the R-R diagram of and , whose A-handle corresponds to , then crosses the A-handle of in a single connection without intersecting , while lies completely in the B-handle of . So has the form of the diagram in Figure 28. ∎
Lemma 5.5.
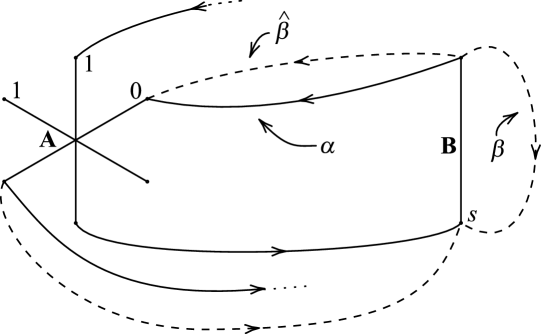
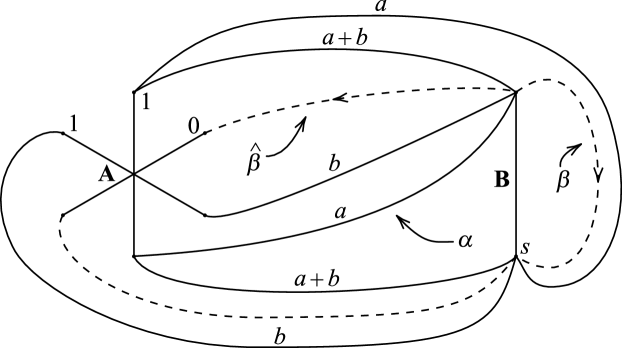
Proof.
Since must intersect every cutting disk of , it must traverse both the A-handle and the B-handle of . In particular, must have 1-connections on the A-handle of and s-connections on the B-handle of . Now Figure 30 shows that can’t have both 1-connections and 0-connections on the A-handle of , otherwise is forced to spiral endlessly. So has only 1-connections on the A-handle of . Now it is not hard to see that there must exist nonnegative integers and such that the diagram of , , and has the form of Figure 31. ∎
Lemma 5.6.
Proof.
Since the annulus is vertical in the Seifert-fibration of , its boundary components and are regular fibers. Then as in Figure 18 two parallel copies of bound an essential separating annulus in such that is saturated and vertical in the Seifert-fibration of , and cuts into a solid torus and a genus two handlebody , with lying on .
Let be the core of . (Note that is also a core of the B-handle of .) Then, since , is an exceptional fiber of index in the Seifert-fibration of . And, since the Seifert-fibration of can have at most one exceptional fiber, is the only exceptional fiber in . It follows that the manifold is Seifert-fibered over the Möbius band with no exceptional fibers. Then, using well-known formulas for presentations of Seifert-fibered spaces, one gets = .
By a result of Zieschang in [Z77], has only one Nielsen equivalence class of generators. It follows that if is a one-relator presentation of , then there is an automorphism of the free group which carries onto a cyclic conjugate of or its inverse.
Now it is not hard to see that one obtains a one-relator presentation of from the one-relator presentation of by setting in Figure 31. But if in Figure 31, then the Heegaard diagram underlying the R-R diagram in Figure 31 has a graph with the form of Figure 32. This graph shows has minimal length under automorphisms of . It follows that if is a cyclic conjugate of or its inverse in , then . So or . If , then , which is a commutator, separates , and is not an automorph of in . The only remaining possibility is . In this case, Figure 31 reduces to Figure 25, and in , as desired. ∎
Lemma 5.7.
Proof.
As in Lemma 5.6, the annulus is vertical in the Seifert-fibration of , and its boundary components and are regular fibers. Then two parallel copies of bound a separating annulus in such that is saturated and vertical in the Seifert-fibration of , and cuts into a solid torus and a genus two handlebody , with lying on . Let be the core of . (Note that like the case of Lemma 5.6, is also a core of the B-handle of , but unlike the case, here is parallel into .) Then, since , is a regular fiber in the Seifert-fibration of . By performing Dehn surgery on , one can change into another genus two handlebody such that is Seifert-fibered over the Möbius band with as an exceptional fiber of index . And then, since is Seifert-fibered over the Möbius band, must be its only exceptional fiber. This implies that the Seifert-fibration of had no exceptional fibers.
References
- [B90] Berge, J., Some Knots with Surgeries Yielding Lens Spaces, Unpublished manuscript. Univ. of Texas at Austin, 1990.
- [B18] Berge, J., Some Knots with Surgeries Yielding Lens Spaces, arXiv preprint arXiv:1802.09722, 2018. original unpublished work from 1990.
- [B08] Berge, J., The simple closed curves in genus two Heegaard surface of which are double-primitives, Unpublished manuscript.
- [BK20] Berge, J. and Kang, S. The hyperbolic primitive/Seifert knots in , preprint.
- [BRZ88] Boileau, M., Rost, M., and Zieschang, H., On Heegaard decompositions of torus knot exteriors and related Seifert fibre spaces. Math. Ann. 279 (1988), 553–581.
- [CMZ81] Cohen, M., Metzler, W. and Zimmerman, A., What Does a Basis of F(a,b) Look Like?, Math. Ann. 257 (1981), 435–445.
- [D03] Dean, J., Small Seifert-fibered Dehn surgery on hyperbolic knots, Algebraic and Geometric Topology 3 (2003), 435–472.
- [EM94] Eudave-Muñoz, M., On non-simple 3-manifolds and 2-handle addition, Topology Appl. 55 no. 2, (1994), 131–152.
- [G87] Gordon, C. McA., On non-simple 3-manifolds and 2-handle addition, Topology Appl. 27 (1987), 285–299.
- [G13] Green, J. E., The lens space realization problem, Ann. of Math. (2) 177 (2013), 449–511.
- [H07] Hatcher, A., Notes on Basic 3-Manifold Topology, Unpublished, available on author’s webpage, http://www.math.cornell.edu/ hatcher.
- [K20] Kang, S. Tunnel-number-one knot exteriors in disjoint from proper power curves, preprint.
- [W36] Whitehead, J. H. C., On equivalent sets of elements in a free group, Ann. of Math. 37 no. 2 (1936), 782–800.
- [Z77] Zieschang, H., Generators of the Free Product with Amalgamation of two Infinite Cyclic Groups, Math. Ann. 227 no. 3 (1977), 195–221.
- [Z70] Zieschang, H., On simple systems of paths on complete pretzels, Aemr. Math. Soc. Transl. 92 no. 2 (1970), 127–137.