Pressure effects on the electronic structure, phonons, and superconductivity of noncentrosymmetric ThCoC₂

ThCoC₂ crystallizes in the base-centered orthorhombic structure Amm2, spacegroup no. 38, shown in Fig. 1. In the structure we may distinguish the layers of Th separated by the layers of Co-C rings, stacked along $a$ axis. Evolution of the unit cell parameters is presented in Table 1 and Fig. 2. The strongest compression of the unit cell under pressure is seen in the $a$ direction, i.e. perpendicular to the aforementioned Th and Co-C layers, whereas the most resistant to pressure is $b$ direction, along the covalent Co-C and C-C bonds. As a consequence, $b/a$ and $c/a$ ratios increase with pressure. Atomic positions change only slightly, and to illustrate how the crystal structure evolved, the distances between neighboring atoms are shown in Table 2. The carbon-carbon bond is the stiffest as its bond length shortens an order of magnitude less than in the other pairs. Distances between cobalt and carbon decrease roughly two times less than for the carbon - thorium and thorium - cobalt pairs.

The change in the unit cell volume with pressure is shown in Fig. 2(a) where it is fitted using the Birch-Murnaghan equation of state Birch (1947). The computed bulk modulus is equal to $B=188$ GPa.

Evolution of the electronic dispersion relations in ThCoC₂ with pressure is presented in Fig. 3. Panels (a-c) show dispersion relations for 0, 10 and 20 GPa, while panel (d) gathers all results in one graph to visualize their relative differences. In a similar way we will present changes in electronic densities of states, phonon dispersions, phonon densities of states and Eliashberg functions. As discussed in Kuderowicz et al. (2021), at ambient pressure in the scalar-relativistic case, two bands cross the Fermi level forming two sheets of the Fermi surface (FS), with one large, dominating FS sheet and the other consisting of two small electron pockets. When the spin-orbit coupling is taken into account, due to the lack of the inversion center, the band structure is split, forming four FS sheets, shown for p = 0, 10, and 20 GPa in Fig. 4. The largest change in $E({\bf k})$ relation due to pressure is observed near $\mathrm{\Gamma}$ and T points. The electron band at $\mathrm{\Gamma}$, which is just above $E_{F}$ for p = 0 GPa, is pushed down and eventually crosses the Fermi level, contributing to FS by forming an additional tube along $k_{z}$ direction, seen in Fig. 4 for p = 10 GPa.

Orbital characters of the main Fermi surface sheet for pressures of 0, 10 and 20 GPa are shown in Supplemental Material sup . Contribution to Fermi surface is mostly from Th-6d, Co-3d and C-2p orbitals, with some contribution from Th-f states, in agreement with contributions to total DOS at $E_{F}$ discussed below (see Fig. 5). The anisotropy of orbital character of FS is moderate and is enhanced under pressure – the tube which is formed in the central part of FS above 10 GPa has mostly C-p and Th-f character, which were more uniformly distributed at ambient pressure. That may enhance the anisotropic properties of the superconducting phase under pressure in ThCoC₂.

The average value of $E({\bf k})$ splitting due to SOC for the states located around the Fermi level as a function of pressure is shown in Fig. 6(b). The $\overline{\Delta E}_{SOC}$ starts to increase above 5 GPa when the additional, $\Gamma$-centered tube starts to contribute to FS. The growth is approximately linear with the a rate of 1.5 meV/GPa, reaching 185 meV at 20 GPa¹¹1The average splitting at p = 0 GPa reported here is 162 meV is slightly larger than the (rounded down) value of 150 meV reported in Ref.Kuderowicz et al. (2021) due to a denser $k$-mesh used to calculate the average.. That suggests that the unconventional features of superconductivity in ThCoC₂, likely driven by the strong antisymmetric spin-orbit coupling, should be even more pronounced under elevated pressure.

The electronic density of states (DOS) near the Fermi level is presented in Fig. 5 and the change of DOS($E_{F}$) with pressure in Fig. 6(a) and Table 3. Under the pressure, the DOS curve around $E_{F}$ is flattened, due to pressure-enhanced hybridization we can observe lowering of maxima and rising of minima of DOS($E$). The DOS($E_{F}$) gradually decreases with pressure with a ratio of $-1.1\times 10^{-2}$ eV${}^{-1}/$GPa which compares to $-2.7\times 10^{-3}$ eV${}^{-1}/$GPa in LaNiC₂ Wiendlocha et al. (2016), thus, the effect is much stronger in ThCoC₂. The largest contributions to the total DOS at the Fermi level are from the 6d Th, 3d Co, and 2p C states, with a noticeable contribution from 5f states of Th. The major contributors to DOS$(E_{F})$ do not change with pressure, however the relative importance of Th-5f states is growing with increasing pressure, due to the above-mentioned increase in the Fermi surface area with the Th-5f orbital character.

As we found for the zero pressure case Kuderowicz et al. (2021), spin-orbit coupling makes no significant changes for the phonon spectrum of ThCoC₂, as well as for the electron-phonon interactions. The computed scalar-relativistic value of the EPC constant for p = 0, $\lambda=0.583$, is only slightly smaller than the relativistic $\lambda=0.590$. Because of this, we restricted our calculations of the pressure evolution of the dynamic properties and EPC in ThCoC₂ to the scalar-relativistic case. To make sure that SOC may be also neglected for phonons under pressure, giving the correct evolution of $\lambda(p)$, calculations including SOC were done for a single case of p = 10 GPa and also here no important differences were found (see Supplemental Material sup for further details). Similarly to the p = 0 case, at 10 GPa the scalar-relativistic $\lambda=0.609$ is slightly smaller than the relativistic $\lambda=0.618$. The relative effect of pressure on the EPC parameter between 10 GPa and 0 GPa, $\lambda(10)/\lambda(0)$, is 4.7% increase, when computed with SOC, and 4.5% increase, when SOC is neglected, thus the scalar-relativistic approximation is sufficient to drive conclusions for the evolution of $\lambda$ with pressure.

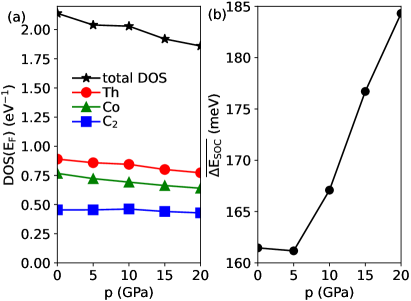
Figure 7 presents the phonon dispersion curves $\omega(\mathbf{q})$ and the phonon density of states $F(\omega)$ for selected pressures. The characteristic structure of the phonon spectrum, driven by the large difference in atomic masses between Th, Co, and C, is the separation into three regions, seen in the partial $F(\omega)$ plots. The lowest-frequency part has the majority of Th vibrations, next Co phonon branches dominate and the high frequency part is contributed by carbon atoms. The highest single mode near $35$ THz (p = 0 GPa) is contributed by the C-C bond-stretching mode.

Under elevated pressure, most of the phonon branches move towards higher frequencies, which is especially visible for carbon modes. The average phonon frequency increases with an approximate rate of 0.057 THz/GPa, reaching 11.76 THz at 20 GPa, as shown in Fig. 8(a). On the other hand, near R, T, and Z points, the lowest acoustic mode is softened. Similar softening was found in LaNiC₂ Wiendlocha et al. (2016). The real-space atomic displacements for these phonon modes are visualized in the Supplemental Material sup . In T point, where the effect is the strongest, Th vibrates along the $c$ axis, whereas Co and C move out of phase, along $a$.

Before moving to the discussion of the electron-phonon coupling, it is worth to recall how the quantities important for the interaction strength depend on the phonon frequencies. The electron-phonon coupling matrix elements $g_{{\bf q}\nu}({\bf k},i,j)$ are defined as Wierzbowska et al. (2005); Heid et al. (2010); Giustino (2017)

$$\begin{split}g_{{\bf q}\nu}({\bf k},i,j)&=\\ =\sum_{s}&\sqrt{{\hbar\over 2M_{s}\omega_{{\bf q}\nu}}}\langle\psi_{i,{\bf k+q}}|{dV_{\rm SCF}\over d{\hat{u}}_{\nu s}}\cdot\hat{\epsilon}_{\nu s}|\psi_{j,{\bf k}}\rangle,\end{split}$$

(1)

where $s$ enumerates atoms in the unit cell, $i,j$ are band indexes, $M_{s}$ is the atomic mass, ${dV_{\rm SCF}\over d{\hat{u}}_{\nu s}}$ is a change of electronic potential calculated in self-consistent cycle due to the displacement ${\hat{u}}_{\nu s}$ of an atom $s$, $\hat{\epsilon}_{\nu s}$ is the $\nu$-th phonon polarization vector and $\psi_{i,{\bf k}}$ is the electronic wave function. In eq.(1) phonon frequency appears under the square root in the denominator. The square of matrix elements are integrated over the Fermi surface and multiplied by frequency to contribute to the phonon linewidths $\gamma_{{\bf q}\nu}$: Wierzbowska et al. (2005); Grimvall (1981); Giustino (2017):

$$\begin{split}\gamma_{{\bf q}\nu}=&2\pi\omega_{{\bf q}\nu}\sum_{ij}\int{d^{3}k\over\Omega_{\rm BZ}}|g_{{\bf q}\nu}({\bf k},i,j)|^{2}\\ &\times\delta(E_{{\bf k},i}-E_{F})\delta(E_{{\bf k+q},j}-E_{F}).\end{split}$$

(2)

This multiplication cancels the direct frequency dependence, thus the linewidths do not directly depend on $\omega_{{\bf q}\nu}$, rather than on the wavefunction matrix elements, which enter eq.(1).

The summation of the phonon linewidths divided by frequency gives the Eliashberg function $\alpha^{2}F(\omega)$:

$$\alpha^{2}F(\omega)={1\over 2\pi N(E_{F})}\sum_{{\bf q}\nu}\delta(\omega-\omega_{{\bf q}\nu}){\gamma_{{\bf q}\nu}\over\hbar\omega_{{\bf q}\nu}},$$

(3)

which is then inversely proportional to $\omega_{{\bf q}\nu}$. Finally, the EPC constant $\lambda$ is calculated as the integral of the Eliashberg function, again divided by frequency Grimvall (1981),

$$\lambda=2\int_{0}^{\omega_{\rm max}}\frac{\alpha^{2}F(\omega)}{\omega}\text{d}\omega,$$

(4)

which results in the proportionality of $\lambda\propto\frac{\gamma_{{\bf q}\nu}}{\omega_{{\bf q}\nu}^{2}}$, thus for majority of the electron-phonon superconductors pressure-induced lattice stiffening (increase in $\omega_{{\bf q}\nu}$) dominates, reducing $\lambda$.

To have a convenient single-number parameter which shows how the electronic contribution to the electron-phonon coupling changes with pressure, cutting off the direct dependence on the phonon frequency, one might calculate the sum of all phonon linewidths. The more straightforward way to do it is to calculate the integral of the Eliashberg function multiplied by frequency:

$$I=\int_{0}^{\omega_{\rm max}}\omega\cdot\alpha^{2}F(\omega){\rm d}\omega,$$

(5)

as it carries similar physical information. Substituting eq.(1-3) to the above formula, one can see that $I$ does not explicitly depend on phonon frequency Gutowska et al. (2021):

$$\begin{split}I=&\frac{1}{2\pi\hbar N(E_{F})}\int_{0}^{\omega_{max}}d\omega\sum_{{\bf q}\nu}\delta(\omega-\omega_{{\bf q}\nu})\gamma_{\textbf{q}\nu}\\ =&\frac{1}{N(E_{F})}\int_{0}^{\omega_{max}}d\omega\sum_{{\bf q}\nu}\delta(\omega-\omega_{{\bf q}\nu})\\ &\times\sum_{ij}\int\frac{d^{3}k}{\Omega_{BZ}}\left|\sum_{s}\frac{1}{\sqrt{2M_{s}}}\langle\psi_{i,{\bf k+q}}|{dV_{\rm SCF}\over d{\hat{u}}_{\nu s}}\cdot\hat{\epsilon}_{\nu s}|\psi_{j,{\bf k}}\rangle\right|^{2}\\ &\times\delta(E_{{\bf k},i}-E_{F})\delta(E_{{\bf k+q},j}-E_{F}).\\ \end{split}$$

(6)

In Fig. 7 we see that some of the phonon linewidths are increasing with pressure, especially for the softened acoustic part of the spectrum between T, Z, and A points, which shows that the softening is associated with the enhanced electron-phonon coupling. On the other hand, for the optic Co and C modes, e.g., in the X-$\Gamma$ direction, $\gamma_{\boldsymbol{q}\nu}$ are decreasing. Eliashberg functions for selected pressures are presented in Fig. 9 and an increase in the lower-frequency part can be seen. The overall effect on the electron-phonon coupling is the resultant of competing factors: the increase of the ”electronic” $I$ integral, plotted in Fig. 8(c), and increase in the average phonon frequency, shown in Fig. 8(a). The tendency towards stronger coupling takes over and the EPC constant $\lambda$ is increasing with pressure with a rate of about $3.5\times 10^{-3}$/GPa, as shown in Fig. 8(d). This is 20% slower than found for LaNiC₂, where it was equal to $4.4\times 10^{-3}$/GPa Wiendlocha et al. (2016).

Analyzing the increase in $\lambda$ in more details, Fig.  10 additionally compares the p = 0 and 20 GPa Eliashberg functions decoupled over all the phonon modes [panels (a,b)], as well as $\alpha^{2}F(\omega)/\omega$ in panel (c). The substantial increase of the Eliashberg function for the first acoustic mode is well visible. For other modes generally the increase in phonon frequencies is accompanied by the increase in $\alpha^{2}F(\omega)$ values due to the larger phonon linewidths. This gives a larger $\alpha^{2}F(\omega)/\omega$ function, whose integral determines the value of $\lambda$ via eq.(4). Electron-phonon coupling constants for each of the 12 phonon modes $\lambda_{i}$, computed based on the data presented in Fig. 10(a,b) are collected in Table 4. The pressure changes in the cumulative electron-phonon coupling constant $\lambda(\omega)$ are shown in Fig. 11. What we can conclude is that the increase in $\lambda$ is mainly driven by the increase in $\lambda_{1}$ which is contributed by the lowest acoustic phonon mode, the one which softens under pressure in some regions of the Brillouin zone. As a consequence, the average frequency of this mode (see $\langle\omega\rangle_{1}$ in Table 4) increases only a little, allowing for the increase in $\lambda_{1}$. Changes in $\lambda_{\nu}$ of the other modes generally compensate each other when summed over, thus the change in $\lambda_{1}$ is a key factor for the $\lambda$ enhancement. The increase in $\lambda$ will tend to increase the critical temperature $T_{c}$.

The second important parameter in terms of $T_{c}$ is the characteristic phonon frequency, which sets the energy window for the electron-phonon interaction, and to which $T_{c}$ is proportional to. That is the Debye frequency in the BCS theory and in the McMillan $T_{c}$ formula McMillan (1968). The pressure-induced increase in the average phonon frequency suggests that this parameter should increase as well. However, in the more accurate Allen-Dynes formula:

$$k_{B}T_{c}=\frac{\hbar\omega_{\rm ln}}{1.2}\exp\left(-\frac{1.04(1+\lambda)}{\lambda-\mu^{*}(1+0.62\lambda)}\right),$$

(7)

which is an analytic approximated solution of the isotropic Eliashberg gap equations Allen and Dynes (1975), the characteristic frequency is the ”logarithmic average”, defined on the basis of the Eliashberg function:

$$\omega_{\rm ln}=\exp\left(\frac{2}{\lambda}\int_{0}^{\omega_{max}}\alpha^{2}F(\omega)\ln\omega\frac{d\omega}{\omega}\right).$$

(8)

Increases in both the average phonon frequency and the EPC constant $\lambda$ results in a non-monotonic evolution of $\omega_{\rm ln}$, shown in Fig. 8(b). Logarithmic average increases at low pressures, reaches maximum at 5 GPa and then decreases.

The results obtained in the preceding sections allow to simulate the pressure effects on superconductivity in ThCoC₂ for the electron-phonon coupling scenario. As we have discussed in Ref. Kuderowicz et al. (2021), the experimental value of the critical temperature $T_{c}$ at zero pressure can be obtained from the calculated Eliashberg function and the standard Allen-Dynes eq.(7), if the Coulomb pseudopotential parameter is set to $\mu^{*}\simeq 0.16$. The need of using this higher than typical (0.10 - 0.13) value is most likely related to the more complex nature of the superconducting phase than covered by the Allen-Dynes formula, derived based on the isotropic Eliashberg formalism. Similarly, by direct numerical solving the isotropic Eliashberg equations, we have reproduced Kuderowicz et al. (2021) the experimental value of $T_{c}$ for $\mu^{*}=0.268$ when $\alpha^{2}F(\omega)$ computed with SOC was used.²²2The value of $\mu^{*}$ used for solving the Eliashberg gap equations, if is to be compared to the parameter used with the Allen-Dynes formula, has to be re-scaled due to the dependence of $\mu^{*}$ on the numerical cutoff frequency: $\frac{1}{\widetilde{\mu^{*}}}=\frac{1}{\mu^{*}}+\ln\left(\frac{\omega_{c}}{\omega_{\rm max}}\right)$. That gives $\widetilde{\mu^{*}}=0.195$, see Refs. Allen and Dynes (1975); Kuderowicz et al. (2021) for further details. This and the deviation of the calculated thermodynamic properties of the superconducting phase (temperature dependence of the electronic specific heat, magnetic field penetration depth, and critical field) pointed to the conclusion that the superconductivity in ThCoC₂ goes beyond the isotropic Eliashberg picture, nevertheless with a high probability of the electron-phonon coupling mechanism Kuderowicz et al. (2021). As we are, however, able to reproduce the magnitude of $T_{c}$ at p = 0 accepting the enhanced $\mu^{*}$ values, we may simulate the pressure effect on $T_{c}$ by keeping the zero-pressure $\mu^{*}$ that reproduces the initial $T_{c}$.

Starting with $T_{c}$ computed using the Allen-Dynes formula, $T_{c}$ increases almost linearly with pressure, as shown in Fig. 12 (blue squares). $\mu^{*}=0.161$ is used here, as it reproduces the experimental $T_{c}=2.55$ K at 0 GPa when SOC is neglected. In spite of the decline of the density of state $N(E_{F})$, in general detrimental to superconductivity, we observe increase of the critical temperature with a pressure, caused by the enhancement of EPC. The increase in $\lambda$ takes over the decrease in $\omega_{\rm ln}$ observed above 5 GPa, thus the critical temperature increases monotonically with an approximately constant ratio of 0.073 K/GPa, reaching 3.11 K at 10 GPa and 4.01 K at 20 GPa. That is quite a strong pressure effect, experimentally accessible for verification even under moderate pressures of several GPa. Following the trend in $\lambda(p)$, the magnitude of the pressure-induced change in $T_{c}$ in ThCoC₂ is lower comparing to that computed for LaNiC₂ Wiendlocha et al. (2016), where the ratio was 0.129 K/GPa.

Further on, we simulate how the $T_{c}$ and other thermodynamic properties would change with pressure when computed using the Eliashberg isotropic gap equations. That will allow to conclude on the deviations of superconductivity in ThCoC₂ under pressure from the isotropic state once the experimental works are reported. A full description of the applied theoretical model with mathematical formulas can be found in Ref. Kuderowicz et al. (2021). Here we keep the same numerical parameters used in solving the Eliashberg equations, i.e., the cut-off frequency $\omega_{c}=4\omega_{max}$ Carbotte (1990) and the number of Matsubara frequencies $M=6500$. As mentioned, the Coulomb pseudopotential has been chosen in a way to reproduce the critical temperature $T_{c}=2.55$ K for p = 0. In the model without the spin-orbit coupling, this is $\mu^{*}=0.257$, which corresponds to re-scaled Allen-Dynes formula value  Allen and Dynes (1975); Kuderowicz et al. (2021) $\widetilde{\mu^{*}}=0.189$, still above the commonly used approximations of $0.10-0.13$ Morel and Anderson (1962). The changes of the critical temperature under pressure are presented in Fig. 12 (red dots), and are slightly smaller, comparing to predictions from the Allen-Dynes formula (rate of 0.64 K/GPa), nevertheless the substantial increase in $T_{c}$ is predicted as well.

The temperature dependence of $\Delta_{n=1}(T)$ for different pressures are presented in the inset of Fig. 12 and undergo the following formula

$$\Delta(T)=\Delta(0)\sqrt{1-\left(\frac{T}{T_{c}}\right)^{\Gamma}},$$

(9)

with $\Gamma$ which only slightly depends on p, $\Gamma=3.28\pm 0.01$, remaining close to that predicted from the BCS theory, $\Gamma_{BCS}\approx 3.0$. When increasing the pressure, the dimensionless ratio $R_{\Delta}=2\Delta(0)/k_{B}T_{c}$ changes in the range $3.55-3.58$, being close to the BCS value of $3.53$.

The self-consistent solution of the Eliashberg equations can then be used to calculate the electronic specific heat in the superconducting state $C_{e}^{S}$ Kuderowicz et al. (2021). Above $T_{c}$, the specific heat of the normal state is given by $C_{e}^{N}(T)=\frac{\pi^{2}}{3}k_{B}^{2}N(E_{F})(1+\lambda)T$. The temperature dependences of the specific heat for different pressure values are presented in Fig. 13.

For comparison, by dashed lines, we have also marked the BCS curves, which predict the exponential behavior of the specific heat at low temperatures. In this regime, as shown in Fig. 13, the Eliashberg solutions slightly deviate from the BCS curves and do not exhibit the $C_{e}\propto\exp[-\Delta(0)/k_{B}T]$ dependence. At high temperatures, $C_{e}^{S}(T)$ is close to BCS relation, reaching the jump of reduced specific heat at $T_{c}$, $\Delta C_{e}/\gamma T_{c}$ from $1.37$ for p = 0 to $1.47$ for $p=20$ GPa, almost equal to the weak-coupling BCS limit of $1.43$.

Although electronic specific heat exhibits a temperature dependence close to ordinary BCS theory, the London penetration depth $\lambda_{L}$ behaves differently. In Fig. 14 we present $\lambda_{L}/\lambda_{L}(T=0,p=0)$ calculated from the Eliashberg formalism Kuderowicz et al. (2021); Carbotte (1990). Regardless of pressure, $\lambda_{L}$ significantly deviates from the BCS prediction, which is an effect of the retardation processes included in the Eliashberg theory.

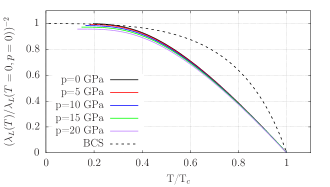
With increasing pressure, the London penetration depth decreases slightly in the low temperature regime.

Finally, we have also analyzed how the upper critical field, $H_{c2}$, changes within the pressure, if evaluated within the Eliashberg model Kuderowicz et al. (2021); Carbotte (1990). Our calculations for zero pressure Kuderowicz et al. (2021) showed that ThCoC₂ was close to the clean limit, thus in present calculations we use the clean limit, assuming zero scattering rate.

The obtained temperature dependence of the upper critical field normalized to $H_{c2}$ at $T=0$ and p = 0 is shown in Fig. 15. In opposite to the penetration depth which does not change significantly with the pressure, the upper critical field increases more than twice when the pressure changes from $0$ to $20$ GPa. Similarly as in the case of the critical temperature, it results from the increase of the EPC induced by pressure.