Predictions in the eye of the beholder: an active inference account of
Watt governors
Abstract
Active inference introduces a theory describing action-perception loops via the minimisation of variational (and expected) free energy or, under simplifying assumptions, (weighted) prediction error. Recently, active inference has been proposed as part of a new and unifying framework in the cognitive sciences: predictive processing. Predictive processing is often associated with traditional computational theories of the mind, strongly relying on internal representations presented in the form of generative models thought to explain different functions of living and cognitive systems. In this work, we introduce an active inference formulation of the Watt centrifugal governor, a system often portrayed as the canonical “anti-representational” metaphor for cognition. We identify a generative model of a steam engine for the governor, and derive a set of equations describing “perception” and “action” processes as a form of prediction error minimisation. In doing so, we firstly challenge the idea of generative models as explicit internal representations for cognitive systems, suggesting that such models serve only as implicit descriptions for an observer. Secondly, we consider current proposals of predictive processing as a theory of cognition, focusing on some of its potential shortcomings and in particular on the idea that virtually any system admits a description in terms of prediction error minimisation, suggesting that this theory may offer limited explanatory power for cognitive systems. Finally, as a silver lining we emphasise the instrumental role this framework can nonetheless play as a mathematical tool for modelling cognitive architectures interpreted in terms of Bayesian (active) inference.
Introduction
The free energy principle (FEP) has been proposed as a framework to study perception, action and higher order cognitive functions using probabilistic generative models (Friston et al.,, 2010; Hohwy,, 2013; Clark,, 2015; Buckley et al.,, 2017). Under the FEP and related approaches, including the Bayesian brain hypothesis, perception is usually characterised as a process of (approximate Bayesian) inference on the hidden states and causes that generate sensory input. Predictive coding models describe how this process may be implemented in a biologically plausible fashion by minimising a mismatch error between incoming sensations and predictions, or rather estimates, of these sensations produced by a probabilistic generative model (Rao and Ballard,, 1999; Spratling,, 2016). Active inference extends this account of perceptual processes by 1) noting that they can be treated as a special case of a more general framework based on the minimisation of variational free energy under Gaussian assumptions and by 2) proposing a description of action and behaviour consistent with the minimisation of prediction error and variational (and expected) free energy (Friston et al.,, 2010, 2017). Active inference thus proposes that agents minimise prediction errors by both generating better estimates of current and future sensory input and, at the same time, acting in the environment to directly update this input to better fit current predictions. These actions are biased towards normative constraints (in the form of prior Bayesian beliefs) that ensure their very existence, closing the sensorimotor loop and sidestepping “dark room” paradoxes (Friston et al.,, 2010, 2012; Buckley et al.,, 2017; Friston et al.,, 2017; Baltieri and Buckley, 2019a, ).
In (philosophy of) cognitive science, active inference is usually identified within the framework of predictive processing (Clark,, 2013). Predictive processing and active inference are often thought to align with more representationalist views of cognition (Froese and Ikegami,, 2013; Gładziejewski,, 2018). One part of the cognitive science community sees this as a possible advantage (Hohwy,, 2013; Wiese and Metzinger,, 2017; Gładziejewski,, 2018) while others see it as one of its main drawbacks (Froese and Ikegami,, 2013; Anderson,, 2017; Zahavi,, 2017). Others have argued it may be consistent with embodied and enactive perspectives of cognition, claiming that the strengths of the FEP reside in generative models with no explicit representational role (Bruineberg et al.,, 2018; Kirchhoff and Froese,, 2017). A different perspective highlights the potential of the FEP for the formalisation of “action-oriented” views of cognition (Engel et al.,, 2016; Clark,, 2015), attempting to reconcile computational views and embodied/enactive positions.
As a thinking tool on the role of predictive processing as a theory of cognition, we introduce an active inference re-interpretation of a now classical example in the literature of “anti-representational” accounts of cognitive systems, the Watt governor. The Watt (flyball or centrifugal) steam governor was used by Van Gelder, (1995, 1998) as a paradigmatic system to challenge the dominant cognitivist understanding of cognition. Van Gelder, (1995, 1998) claimed that dynamical systems theory provided a better language to explain the inner workings of cognitive agents, similarly to what engineers have done with the Watt governor in terms of attractors, stability analysis, etc.. At the same time, he then questioned whether computational descriptions of the governor offered any explanatory power – over – the use of dynamical systems theory. While many proponents of the dynamicist view see the computational metaphor as superfluous in many cases (Chemero,, 2009), or intimately tied to a deeply flawed philosophy of mind (Dreyfus,, 1972), others see computational and information-theoretic descriptions of a system as useful epistemic tools offering interpretations that are complementary to a dynamical systems analysis (Bechtel,, 1998; Beer and Williams,, 2015). In both cases, the nature of the tight coupling between a flyball governor and its steam engine is accepted, and the resulting mode of cognition departs from the cognitivist one, i.e., a governor does not “read” the speed of the engine to “compute”, offline, the next best action. In this light, a more appropriate explanation of such coupled systems mandates circular, rather than linear causality, in line with embodied/enactive approaches to cognitive science highlighting the importance of studying the dynamical interaction of an agent and its environment.
The Watt governor
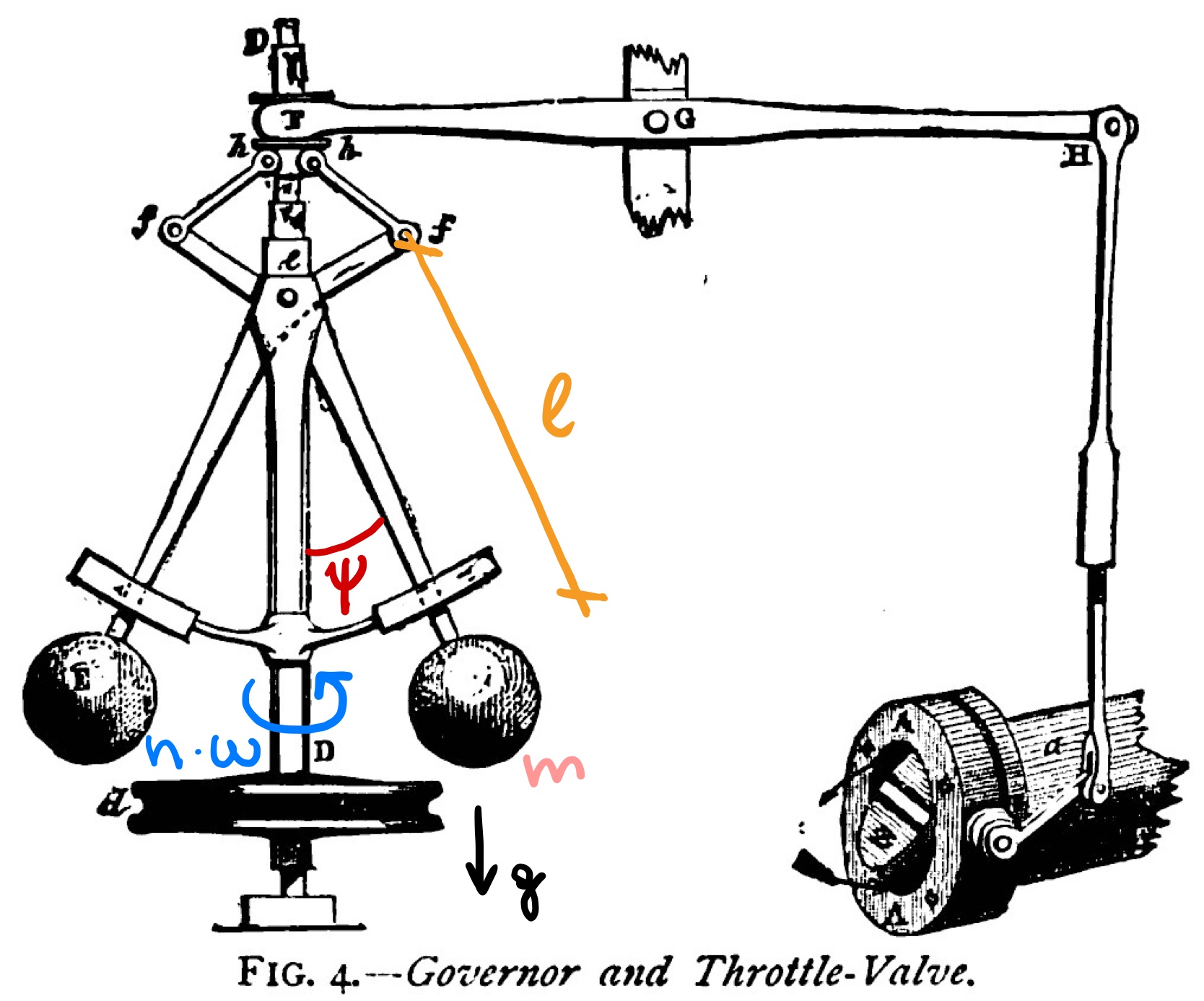
The centrifugal (or flyball) governor was introduced as a mechanism to harvest steam power for industrial applications, controlling the speed of steam engines using properties of negative feedback loops (Åström and Murray,, 2010). The centrifugal governor regulates the amount of steam admitted into a cylinder via a mechanism that opens and closes a valve controlling the amount of steam released by an engine. This regulation requires balancing the forces applied to a pair of flyballs secured via two arms to a rotating spindle, geared to a flywheel driven by a steam engine (Fig. 1).
At rest, the flyballs are subject to gravitational force and the two arms are in a vertical position while the engine’s valve is fully open. As the engine is powered and steam flows into the cylinders via the fully open valve, the engine’s flywheel velocity is increased, alongside the vertical spindle’s angular velocity. The attached flyballs’ kinetic energy thus also increases, counteracting the effects of the gravitational force, slowly bringing the arms away from a vertical position. Once the spindle’s velocity reaches a certain bound set by the physical properties of the system (and thus indirectly by the engineer who built it), the steam valve of the engine is slowly closed via a beam linkage connected to a thrust bearing attached to the flyballs’ arms. When the steam flow decreases, the vertical spindle slows down, reopening the valve that will move the flyballs to increase once more the speed of the shaft, closing the valve, etc. until a stable equilibrium is reached for a certain steam flow associated to a specific angle between the flyballs’ arms and the vertical shaft.
Using a standard formulation by Pontryagin, (1962), based on previous work by Vyshnegradsky, (1877) and Maxwell, (1868), we define a Watt governor as a conical pendulum with two flyballs (the “bobs”) travelling at constant angular speed
| (1) |
based on a simple derivation of Newtonian’s laws from Fig. 1, and with all variables explained in more detail in table 1.
| Description | |
|---|---|
| Flyball arm angle and velocity () | |
| Steam engine flywheel angular speed | |
| Steam engine flywheel moment of inertia | |
| Torque induced by engine load | |
| Gear or transmission ratio | |
| Gravitational acceleration | |
| Length of flyball arms | |
| Friction constant | |
| Flyball mass | |
| Constant relating flyball height and engine torque |
A steam engine is then attached via a flywheel with angular speed , moment of inertia and a load torque
| (2) |
The flywheel is geared to the vertical spindle so that the angular velocities of the engine’s flywheel and the vertical spindle are proportional, , up to a constant , the gear ratio. With these assumptions, we can reduce the system to a set of first order coupled differential equations,
| (3) |
We then find the equilibrium of this system by equating to zero the left-hand side of equation (3) and by defining a constant shaft velocity and fixed arm angle where the arm angular velocity is zero, ,
| (4) |
The system is henceforth linearised near its equilibrium to simplify the analysis, see Maxwell, (1868); Pontryagin, (1962), defining small disturbances as
After neglecting terms quadratic in disturbances , we finally obtain
| (5) |
These equations are typically used for the analysis of this engine-governor coupled system, and represent a simplified version of the governor’s behaviour near equilibrium. The spindle angular velocity is initially assumed to be constant (by construction) to simplify the treatment from a spherical to a conical pendulum where the flyball arms’ velocity is zero (). Details about the steam engine are usually not provided, only explaining its effects through a torque which depends on the arm angle given a certain geometry of the governor, as here expressed in equation (2).
The governor’s generative model
Using active inference, we can re-derive similar equations, in particular for the engine’s flywheel angular velocity in equation (5), building on a previous formulation of PID control under this framework (Baltieri and Buckley, 2019c, ). Our formulation includes a generative model in state-space form that describes observations/measurements, hidden states, inputs and parameters of the engine “from the perspective of a governor”.
This description shouldn’t however be taken too literally, as we will discuss later. In the spirit of Van Gelder, (1995, 1998), we will rather highlight the somewhat bizarre nature of concepts such as measurements performed by a physical system. In light of this, we thus stress an as-if interpretation of generative models (McGregor, 2017a, ; Robert,, 2007). According to this idea, physical systems can be interpreted as if they were cognitive agents, with generative models specifying their Bayesian beliefs, governing preferences and dynamics that produce equations describing perception-action loops (see also Discussion). In our formulation, this corresponds to a rather unusual reading of the engine-governor coupled system: an agent trying to stabilise its observations, i.e., the perceived angle of the flyball arms, by adapting its own actions, i.e., the valve opening111Usually one looks at this system in terms of stabilising the velocity of the steam engine via the regulation of the arms angle, however the opposite perspective adopted here 1) currently better fits with the model presented in Baltieri and Buckley, 2019c and 2) is perfectly equivalent to the more traditional way of looking at this problem, since the angle is a single-valued monotonic function of the angular velocity (Pontryagin,, 1962) due to the mechanics of the vertical shaft and the flyball arms, a “stand-in” in the sense of Bechtel, (1998). Interestingly, this view suggests that we might just as well consider the engine as an “agent” acting to control its observations of the “environment”, the governor. One way to treat this issue in a more principled manner is to look at views of agency that are defined in terms of “interactional asymmetry” of the coupling between agent and environment (Barandiaran et al.,, 2009). An in depth discussion of this idea is however left for future work. (cf. “behaviour as the control of perception” (Powers,, 1973)).
We thus start by defining the following generative model:
| (6) |
where , , , and are, in state-space models terms, observations, parameters, hidden states and their derivatives222Here we denote derivatives in the generative model with a dash rather than a dot. The dynamics described by the generative model are not integrated directly, and are only used to derive a set of equations describing the recognition dynamics as a gradient on variational free energy (Friston,, 2008; Buckley et al.,, 2017) (see equation (10)). The dot notation is used for the generative process in equation (5), and for the recognition dynamics equation (10) (simplified, under a few assumptions, in equation (16)), which would be forward-integrated in a simulation., and exogenous inputs of the engine from the (as-if) perspective of the controller. Here the observations represent measurements performed by our agent, i.e., its incoming sensory input about the arm angle. Variables , define states (and their derivatives) of the engine hidden to the governor and assumed to generate these measurements (similar to the way one normally hides most details about the functioning of a real steam engine in equation (2)). Inputs stand for the presence of external factors affecting the system in the form of torque loads , see equation (4). The first equation describes how hidden states are mapped to observations using an identity function, with a random variable introduced to express measurement noise, or rather uncertainty, from the perspective of our agent. In the second equation, the parameter specifies the convergence rate of the intrinsic dynamics modelled by hidden states given inputs . The fluctuations are introduced as an uncertainty term on the dynamics of the engine-governor coupled system, representing for instance errors due to the use of a linear approximation of the real dynamics near equilibrium.
Using this generative model, the recognition dynamics of the system can be obtained by, 1) finding an expression for the variational free energy, and 2) under the assumption that the quantity of free energy is minimized over time, deriving a set of differential equations that minimize the free energy (i.e., following its negative gradient). Under a couple of assumptions described later, these differential equations (i.e., the recognition dynamics) reduce to the equation describing the dynamics of the linearised engine in equation (5).
An expression for the variational free energy can be derived after defining the distributions of , in the simplest case assuming they are both Gaussian, and by considering the following expression for the (Laplace-encoded) free energy (Friston,, 2008)333For a full derivation of this particular form see for instance Friston et al., (2008); Buckley et al., (2017); Baltieri, (2019).
| (7) |
where is evaluated near the most likely estimate of hidden states , i.e., for a Gaussian distribution, its mean or median, . After rewriting the generative model in equation (6) in probabilistic form using the definitions of , one obtains the following expression
| (8) |
where we introduced precisions as the inverse variances of random variables , i.e., . Actions are then defined under the very general assumption that they have an effect on observations (Friston et al.,, 2010; Baltieri,, 2019), i.e.,
| (9) |
By minimising free energy on both the means of hidden states and actions , we then obtain the recognition dynamics (Buckley et al.,, 2017), i.e., a set of differential equations describing the dynamics of our agent. The recognition dynamics implement perception (estimation of states ) and action (control via actions ) of an agent described as a closed sensorimotor loop. The minimisation of free energy is then achieved via the following gradient descent
| (10) |
with learning rates and . Notice that these equations use the same dot notation adopted to describe the generative process of the governor-engine coupled system in equation (5) and represent an agent’s dynamics actually integrated to implement (as-if) inference and control processes. Here we also introduced the use the tilde previously adopted by Friston, (2008); Buckley et al., (2017); Baltieri, (2019) to represent higher embedding orders, in this case, . More generally, when higher embedding orders are introduced as a possible way to represent non-Markovian processes (Friston,, 2008; Baltieri,, 2019), this requires an extra term, , to ensure the convergence to a trajectory (rather than a point attractor) in a moving frame of reference (Friston,, 2008). For a Watt governor at equilibrium, we will however assume that the flyball arm angular velocity is zero, thus defining a point attractor where . In this case, equation (10) thus reduces to
| (11) |
Under a few standard assumptions, this system can then be further simplified to show actions consistent with the regulation of the speed of a steam engine.
Assumption 1: The dynamics of the generative model are overdamped
The recognition dynamics in equation (11) specify a gradient descent on the variational free energy in equation (8) given the generative model in equation (6). Importantly, this generative model is parameterized by , a parameter that describes the rate of convergence of its internal dynamics. As previously shown, for instance in Baltieri, (2019) (Chapter 7.), different choices of allow for the implementation of qualitatively different behaviours: from the regulation of a process to a certain goal (large ), to a purely passive (e.g., no actions) process of inference of the hidden properties of observed stimuli in the spirit of predictive coding models of perception (Rao and Ballard,, 1999; Baltieri and Buckley, 2019a, ) (small ). Here we will assume a very large parameter (i.e., and ), leading to overdamped dynamics of the generative model in equation (6) dominated by the first (drift) term. This translates into recognition dynamics now describing updates of the average hidden state dominated by terms quadratic in (Baltieri and Buckley, 2019c, ) (cf. equation (11)). The expected hidden state thus quickly converges to its steady state (i.e., average velocity ), defined by the input (or bias term) ,
| (12) |
which readily ensures that the goal of the system is now to stabilise the flyball arms angle towards (NB: in general need not be a fixed point attractor), which in turn reflects regulation of the velocity of the engine444Under suitable parameters meeting typical stability criteria (Pontryagin,, 1962). (seen also Note 1). Moreover, since we have assumed , converges much more quickly than and thus the minimisation of free energy in equation (11) can be further simplified to include only the equation for action
| (13) |
Assumption 2: Action updates are proportional to arm angle updates
To show a direct correspondence between the active inference derivation and the original equations, here we assume that the measurement precision is inversely proportional to the moment of inertia of the steam engine flywheel ,
| (14) |
or more precisely that , using the constant relating flyball height and engine torque defined in table 1 (Pontryagin,, 1962). We then consider the case where the learning rate, a hyperparameter of the minimisation scheme (not of the generative model) is set to 1, , and essentially replaced by another hyperparameter playing a similar role, the precision . We also assume a linear relationship between actions and observations in equation (9), such that
| (15) |
using the fact that need only be positive to ensure convergence via a negative feedback loop (Denny,, 2002). For convenience we impose , and finally obtain
| (16) |
which is equivalent to the simplified engine in equation (5), under the assumption that reflects changes due to different loads as in the original formulation of the governor-engine system (Pontryagin,, 1962). In active inference terms, equation (16) describes the behaviour of an agent observing its arms angle (thus indirectly inferring the speed of the engine, see Note 2). At the same time, this agent acts to produce a rotational energy of its flyballs based on deviations from the engine load torque , and minimising a prediction error between its observations and the load arm angle specifying an engine speed via a relation known as “nonuniformity of performance” (Pontryagin,, 1962; Denny,, 2002). Ultimately, this leads to a change in the engine’s speed, here simplified as the angular velocity of the engine shaft (geared into the engine flywheel), . Expected hidden states are only implicitly defined and effectively removed in the limit of deterministic dynamics using Assumption 1.
Discussion
In this work, we introduced a rather unconventional treatment of a Watt governor based on active inference. The Watt (centrifugal) governor has played a central role in the debate between dynamicist and cognitivist ways of thinking about cognitive systems. Proposed as a dynamicist alternative analogy to the cognitivist digital computer (Van Gelder,, 1995) and the sense-model-plan-act strategy implemented by several cognitivist frameworks (Brooks,, 1991; Hurley,, 2001), since its introduction, a number of different works have argued for the merits and limitations of this analogy in addressing relevant questions in (philosophy of) cognitive science, including for instance Eliasmith, (1997); Bechtel, (1998); Beer, (2000); Chemero, (2009); Seth, (2014). The discussion often focuses on the importance of representations to study and explain cognitive agents, echoing a long standing debate over the role of these constructs for theories of cognition (Fodor,, 1983; Harvey,, 1992; Varela et al.,, 1991; Beer,, 2000; Gallagher,, 2006; Chemero,, 2009; Di Paolo et al.,, 2017). Echoing Harvey, (1992) and following in particular Chemero, (2009), we distinguish between metaphysical and epistemological claims when it comes to representationalism. The first pertain to the nature of cognitive systems, the second to our (the scientists’) best explanation of cognitive systems. In the case of the Watt governor, one is hard pressed to defend the metaphysical claim. Rather, the debate usually focuses on the epistemological status of the system: is it useful to explain a Watt governor in representational terms or, in other words, does taking the governor flyball arm angle to represent the speed of the engine help us understand the workings of the governor?
Active inference is a recent framework developed in theoretical neuroscience that describes several aspects of living and cognitive systems in terms of the minimisation of variational (or expected) free energy, which under simplifying (Gaussian) assumptions reduces to a weighted sum of prediction errors. According to active inference, action-perception loops can be seen as a gradient descent on a free energy functional describing normative behaviour for a system. Perception is characterised as a process of Bayesian inference on hidden world variables and action is portrayed as the update of environmental properties to better reflect current perceptual inferences, mediated by the goals of an organism, e.g., its survival, in the form of prior Bayesian beliefs. It has been argued that this framework, often addressed in terms of predictive processing, constitutes a new paradigm for the study of cognitive agents (Clark,, 2013; Hohwy,, 2013; Seth,, 2014; Clark,, 2015; Wiese and Metzinger,, 2017; Hohwy,, 2020). At the moment however, its role in cognitive science remains highly controversial (Kirchhoff and Froese,, 2017; Colombo et al.,, 2018). In particular, some authors suggest that internal representations are central to predictive processing and are used to define computational processes in a more classical sense (Hohwy,, 2013, 2020), some others claim that representations are detrimental for a proper understanding of predictive processing (Bruineberg et al.,, 2018), while others attempt to reconcile these different interpretations (Seth,, 2014; Clark,, 2015). Much of this literature, however, seems to remain (almost deliberately) unclear as to the metaphysical status of the central constructs involved, with a few relevant works explicitly favouring an instrumentalist interpretation (Anderson,, 2017; Colombo and Wright,, 2017; Colombo et al.,, 2018; van Es,, 2020).
Here we take a rather sobering perspective on the role of active inference theories for cognitive and living systems, especially arguing against claims regarding internal representations in predictive processing and the metaphysical status often implicitly granted to processes of variational free energy/prediction error minimisation (Friston,, 2013; Clark,, 2013; Hohwy,, 2013; Gładziejewski,, 2018; Friston,, 2019). Our perspective aligns with epistemological stances (Robert,, 2007; Beer and Williams,, 2015) supporting an instrumental role for frameworks such as Bayesian decision theory, information theory, dynamical systems, and in this case active inference and predictive processing (Colombo and Wright,, 2017), as possible interpretations of physical and cognitive systems. In this light, a generative model may simply provide a possible way to describe a system’s behaviour, rather than an ontological characterisation of its very nature and inner workings (Baltieri and Buckley, 2019b, ). Generative models can act as representations for an observer, as a valuable tool for the study of physical, living and cognitive systems, to describe them from an experimenter’s perspective (Bechtel,, 1998; Harvey,, 2008; Chemero,, 2009; Beer and Williams,, 2015; McGregor, 2017b, ), e.g., to understand the relationship between the spindle arm angle in a Watt governor, and the speed of a steam engine. Their interpretation as intrinsic properties of a system, i.e., generative models as “internal models” used by the system itself (Fodor,, 1983), is on the other hand misleading.
Should one try to find a generative model of the kind expressed in equation (6) – inside – a Watt governor? No, as this is simply a category mistake: observer-dependent uncertainties (e.g., ) and arbitrary assumptions (e.g., parameter ) are relational terms that cannot be found within this physical system (Harvey,, 2008). A generative model provides details for a scientist to specify a cost functional, variational free energy, that can be used to describe the (recognition) dynamics of a system (Buckley et al.,, 2017; Ramstead et al.,, 2019) as seen in equation (11). The presence of a “generative model for a Watt governor” in equation (6), and the ensuing claims of an agent “minimising variational free energy” while regulating the opening of a steam valve, should thus be handled with care555In the same way one should be careful when explaining, for example, Coulomb’s law: saying that an electron calculates its distance from another electron, computes the force applied to that electron and actuates said force in the real world would make for a rather unusual and possibly confusing explanation (Latash,, 2010)..
This suggests that we should exercise caution in making metaphysical claims using predictive processing, the free energy principle and active inference. Statements regarding their mechanistic (Clark,, 2013; Hohwy,, 2013, 2020) or representational (Rescorla,, 2016; Hohwy,, 2016) contents for cognitive systems are in fact often ambiguous and mostly based only on “evidence consistent with” generative models in the brain (Colombo and Wright,, 2017; Colombo et al.,, 2018), as even the most recent reviews show (Walsh et al.,, 2020).
At this point one might wonder what the relevance of active inference and predictive processing might be in the cognitive sciences. Here we suggest that probabilistic generative models ought to be recognised for their effectiveness as a mathematical formalism connecting and extending ideas such as the good regulator theorem in cybernetics (Conant and Ashby,, 1970) (see Seth, (2014)), the internal model principle in control theory (Francis and Wonham,, 1976) (see Baltieri, (2019)), perceptual control theory (Powers,, 1973) in psychology, or the notion of entailment in theoretical biology (Rosen,, 1991) (see Friston, (2012); Ramstead et al., (2019)). In this light, active inference can play an important instrumental role for the overarching attempt of unifying previous results in the study of adaptive agents in cybernetics, control theory, psychology, neuroscience, dynamical systems, information theory and physics. Under a more general framework, notions such as feedback, stability, inference, attractors, uncertainty and dynamics can be seen from different, but complementary, perspectives that allow for more complete descriptions of agents and agency, similarly to the approach adopted, for instance, by Beer and Williams, (2015).
For example, while the notion of “inference” in cognitive science often hinges on the intuition of (passive) inference to the best explanation (Chemero,, 2009) and its limited explanatory power for behaviour and agency (Seth,, 2015; Baltieri,, 2019), a more general treatment of Bayesian inference schemes and their connections to different fields can extend this narrow notion to include more useful interpretations of inference. These include connections to stochastic processes in non-equilibrium thermodynamics (Seifert,, 2012), where biological agents can be better characterised as systems away from (thermodynamic) equilibrium (Schrödinger,, 1944). In this case, inference becomes simply a way to (mathematically) describe the statistical properties of agents represented in terms of non-equilibrium steady states of a random process (Friston,, 2019). A control theoretic reading of inference (Kappen et al.,, 2012) then introduces the idea of inference to the most useful (normative) behaviour (Baltieri,, 2019; Seth,, 2015), rather than to the best explanation. Here, actions and policies of an agent are described as an inferential process biased towards ensuring that its normative constraints are met (i.e., a Bayesian inference process conditioned on a system’s norms, such as its survival and very existence (Barto et al.,, 2013; Baltieri,, 2019)). Furthermore, one can then also recognise inference as a relevant description of theories in evolutionary biology, where following adaptive paths on the fitness landscape is for example likened to a problem of Bayesian model selection (Czégel et al.,, 2019).
Conclusion
Using the Watt governor as a toy model, in this work we discussed the importance of generative models in the context of predictive processing and active inference, extending our previous critiques on their role as internal representations (Bruineberg et al.,, 2018; Baltieri and Buckley,, 2017; Baltieri and Buckley, 2019b, ). By defining a linear probabilistic generative model describing “observations” and “hidden states” from the perspective of a Watt governor, we built a cost functional (i.e., variational free energy) to describe the behaviour of this system as if (McGregor, 2017a, ) it was an agent trying to minimise its prediction error to control its observations and regulate the speed of a steam engine. Via the minimisation of this cost functional under a couple of relatively straightforward and common assumptions, i.e., overdamped dynamics and an appropriate use of constants that ensure regulation via a negative feedback loop, we then re-derived equations equivalent to the mathematical treatment of an engine for the Watt governor linearised near equilibrium. Using this as an example, we then discussed epistemological and metaphysical stances (Chemero,, 2009) for generative models in predictive processing and active inference, focusing on the former and exerting caution on the latter. Our formulation shows that generative models can easily be used to describe canonical cases of the dynamical systems approach in cognitive science.
This paper suggests that generative models are best understood as an epistemic tools for an observer to specify the properties of a system they wish to study and their own assumptions and sources of uncertainty during a process of epistemological analysis (Colombo et al.,, 2018; van Es,, 2020). As such, they are not internal representations for a system, but rather constitute just a descriptive framework (a representation, not internal (Harvey,, 2008)) for an observer. Seeing generative models as internal representations may simply reflect a “mind projection fallacy” (Jaynes,, 1990), where epistemic constructs used by a scientist are assumed to be real objects in the physical world.
Within the existing literature on the free energy principle, active inference and predictive processing, we find an almost deliberate conflation of realist and instrumentalist perspectives, addressing how aspects of one’s model come to explain or constitute aspects of the mind. One example is the discussion on boundaries of the mind (presumably aspects of the world), which is premised on where Markov Blankets (i.e., statistical properties of a model specifying conditional independence between random variables) are located (Clark,, 2017; Hohwy,, 2017; Kirchhoff and Kiverstein,, 2019). This case will however be addressed in more detail in the near future.
The present work supports active inference as a potentially useful descriptive language for cognition, highlighting its instrumental role in studying action-perception within a general mathematical framework including complementary interpretations of an agent’s behaviour (Tishby and Polani,, 2011; Beer and Williams,, 2015), but remains cautious on the metaphysical implications of generative models as internal representations often found in the literature (Hohwy,, 2013; Clark,, 2015; Rescorla,, 2016).
Acknowledgments
MB is a JSPS International Research Fellow supported by a JSPS Grant-in-Aid for Scientific Research (No. 19F19809). CLB was supported in part by a BBSRC Grant BB/P022197/1. JB was supported by a Macquarie University Research Fellowship. MB wishes to thank Inman Harvey and Filippo Torresan for insightful discussions that helped improving different aspects of this work.
References
- Anderson, (2017) Anderson, M. L. (2017). Of bayes and bullets: An embodied, situated, targeting-based account of predictive processing. In Wiese, W. and Metzinger, T. K., editors, In Philosophy and predictive processing: 3, pages 60–73. Frankfurt am Main, Germany: MIND Group.
- Åström and Murray, (2010) Åström, K. J. and Murray, R. M. (2010). Feedback systems: an introduction for scientists and engineers. Princeton university press.
- Baltieri, (2019) Baltieri, M. (2019). Active inference: building a new bridge between control theory and embodied cognitive science. PhD thesis, University of Sussex.
- Baltieri and Buckley, (2017) Baltieri, M. and Buckley, C. L. (2017). An active inference implementation of phototaxis. In Artificial Life Conference Proceedings, pages 36–43. MIT Press.
- (5) Baltieri, M. and Buckley, C. L. (2019a). The dark room problem in predictive processing and active inference, a legacy of cognitivism? In Artificial Life Conference Proceedings, pages 40–47. MIT Press.
- (6) Baltieri, M. and Buckley, C. L. (2019b). Generative models as parsimonious descriptions of sensorimotor loops. Behavioral and Brain Sciences, 42:e218.
- (7) Baltieri, M. and Buckley, C. L. (2019c). PID control as a process of active inference with linear generative models. Entropy, 21(3):257.
- Barandiaran et al., (2009) Barandiaran, X. E., Di Paolo, E. A., and Rohde, M. (2009). Defining agency: Individuality, normativity, asymmetry, and spatio-temporality in action. Adaptive Behavior, 17(5):367–386.
- Barto et al., (2013) Barto, A., Mirolli, M., and Baldassarre, G. (2013). Novelty or surprise? Frontiers in psychology, 4:907.
- Bechtel, (1998) Bechtel, W. (1998). Representations and cognitive explanations: Assessing the dynamicist’s challenge in cognitive science. Cognitive Science, 22(3):295–317.
- Beer, (2000) Beer, R. D. (2000). Dynamical approaches to cognitive science. Trends in cognitive sciences, 4(3):91–99.
- Beer and Williams, (2015) Beer, R. D. and Williams, P. L. (2015). Information processing and dynamics in minimally cognitive agents. Cognitive science, 39(1):1–38.
- Brooks, (1991) Brooks, R. A. (1991). New approaches to robotics. Science, 253(5025):1227–1232.
- Bruineberg et al., (2018) Bruineberg, J., Kiverstein, J., and Rietveld, E. (2018). The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective. Synthese, 195(6):2417–2444.
- Buckley et al., (2017) Buckley, C. L., Kim, C. S., McGregor, S., and Seth, A. K. (2017). The free energy principle for action and perception: A mathematical review. Journal of Mathematical Psychology, 14:55–79.
- Chemero, (2009) Chemero, A. (2009). Radical embodied cognitive science. MIT press.
- Clark, (2013) Clark, A. (2013). Whatever next? predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences, 36(03):181–204.
- Clark, (2015) Clark, A. (2015). Surfing Uncertainty: Prediction, Action, and the Embodied Mind. Oxford University Press.
- Clark, (2017) Clark, A. (2017). How to knit your own markov blanket. In Metzinger, T. K. and Wiese, W., editors, In Philosophy and predictive processing: 3. Open MIND. Frankfurt am Main: MIND Group.
- Colombo et al., (2018) Colombo, M., Elkin, L., and Hartmann, S. (2018). Being Realist about Bayes, and the Predictive Processing Theory of Mind. The British Journal for the Philosophy of Science.
- Colombo and Wright, (2017) Colombo, M. and Wright, C. (2017). Explanatory pluralism: An unrewarding prediction error for free energy theorists. Brain and Cognition, 112:3–12.
- Conant and Ashby, (1970) Conant, R. C. and Ashby, W. R. (1970). Every good regulator of a system must be a model of that system. International journal of systems science, 1(2):89–97.
- Czégel et al., (2019) Czégel, D., Zachar, I., and Szathmáry, E. (2019). Multilevel selection as bayesian inference, major transitions in individuality as structure learning. Royal Society Open Science, 6(8):190202.
- Denny, (2002) Denny, M. (2002). Watt steam governor stability. European journal of physics, 23(3):339.
- Di Paolo et al., (2017) Di Paolo, E. A., Buhrmann, T., and Barandiaran, X. (2017). Sensorimotor Life: An Enactive Proposal. Oxford University Press.
- Dreyfus, (1972) Dreyfus, H. (1972). What Computers Can’t Do. New York: MIT Press.
- Eliasmith, (1997) Eliasmith, C. (1997). Computation and dynamical models of mind. Minds and Machines, 7(4):531–541.
- Engel et al., (2016) Engel, A. K., Friston, K. J., and Kragic, D. (2016). The pragmatic turn: Toward action-oriented views in cognitive science, volume 18. MIT Press.
- Fodor, (1983) Fodor, J. A. (1983). The Modularity of Mind. MIT Press.
- Francis and Wonham, (1976) Francis, B. A. and Wonham, W. M. (1976). The internal model principle of control theory. Automatica, 12(5):457–465.
- Friston, (2008) Friston, K. J. (2008). Hierarchical models in the brain. PLoS Computational Biology, 4(11).
- Friston, (2012) Friston, K. J. (2012). A free energy principle for biological systems. Entropy, 14(11):2100–2121.
- Friston, (2013) Friston, K. J. (2013). Life as we know it. Journal of the Royal Society Interface, 10(86):20130475.
- Friston, (2019) Friston, K. J. (2019). A free energy principle for a particular physics. arXiv preprint arXiv:1906.10184.
- Friston et al., (2010) Friston, K. J., Daunizeau, J., Kilner, J., and Kiebel, S. J. (2010). Action and behavior: A free-energy formulation. Biological Cybernetics, 102(3):227–260.
- Friston et al., (2017) Friston, K. J., FitzGerald, T., Rigoli, F., Schwartenbeck, P., and Pezzulo, G. (2017). Active inference: a process theory. Neural Computation, 29(1):1–49.
- Friston et al., (2012) Friston, K. J., Thornton, C., and Clark, A. (2012). Free-energy minimization and the dark-room problem. Frontiers in psychology, 3:130.
- Friston et al., (2008) Friston, K. J., Trujillo-Barreto, N., and Daunizeau, J. (2008). DEM: A variational treatment of dynamic systems. NeuroImage, 41(3):849–885.
- Froese and Ikegami, (2013) Froese, T. and Ikegami, T. (2013). The brain is not an isolated “black box,” nor is its goal to become one. Behavioral and Brain Sciences, 36(3):213–214.
- Gallagher, (2006) Gallagher, S. (2006). How the body shapes the mind. Clarendon Press.
- Gładziejewski, (2018) Gładziejewski, P. (2018). Predictive coding and representationalism. Synthese, 193(2):559–582.
- Harvey, (1992) Harvey, I. (1992). Untimed and misrepresented: Connectionism and the computer metaphor. Technical report, University of Sussex, School of Cognitive and Computing Sciences.
- Harvey, (2008) Harvey, I. (2008). Misrepresentations. In Proceedings of the Eleventh International Conference on the Simulation and Synthesis of Living Systems. MIT Press.
- Hohwy, (2013) Hohwy, J. (2013). The predictive mind. OUP Oxford.
- Hohwy, (2016) Hohwy, J. (2016). The self-evidencing brain. Noûs, 50(2):259–285.
- Hohwy, (2017) Hohwy, J. (2017). How to entrain your evil demon. In Metzinger, T. K. and Wiese, W., editors, In Philosophy and predictive processing: 2. Open MIND. Frankfurt am Main: MIND Group.
- Hohwy, (2020) Hohwy, J. (2020). New directions in predictive processing. Mind & Language.
- Hurley, (2001) Hurley, S. (2001). Perception and action: Alternative views. Synthese, 129(1):3–40.
- Jaynes, (1990) Jaynes, E. T. (1990). Probability theory as logic. In Maximum entropy and Bayesian methods, pages 1–16. Springer.
- Kappen et al., (2012) Kappen, H. J., Gómez, V., and Opper, M. (2012). Optimal control as a graphical model inference problem. Machine learning, 87(2):159–182.
- Kirchhoff and Froese, (2017) Kirchhoff, M. D. and Froese, T. (2017). Where there is life there is mind: In support of a strong life-mind continuity thesis. Entropy, 19(4):169.
- Kirchhoff and Kiverstein, (2019) Kirchhoff, M. D. and Kiverstein, J. (2019). How to determine the boundaries of the mind: a markov blanket proposal. Synthese, pages 1–20.
- Latash, (2010) Latash, M. L. (2010). Two archetypes of motor control research. Motor control, 14(3):e41.
- Maxwell, (1868) Maxwell, J. C. (1868). On governors. Proceedings of the Royal Society of London, 16:270–283.
- (55) McGregor, S. (2017a). The bayesian stance: Equations for ‘as-if’sensorimotor agency. Adaptive Behavior, 25(2):72–82.
- (56) McGregor, S. (2017b). Let the explanation fit the theorist-enactive explanatory pluralism and the representation debate. In Artificial Life Conference Proceedings, pages 283–289. MIT Press.
- Pontryagin, (1962) Pontryagin, L. (1962). Ordinary Differential Equations (L. Kacinska and WB Counts trans.). Addison-Wesley Publishing Company INC., Reading.
- Powers, (1973) Powers, W. T. (1973). Behavior: The control of perception. Aldine Chicago.
- Ramstead et al., (2019) Ramstead, M. J., Kirchhoff, M. D., and Friston, K. J. (2019). A tale of two densities: Active inference is enactive inference. Adaptive Behavior, page 1059712319862774.
- Rao and Ballard, (1999) Rao, R. P. and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature neuroscience, 2(1):79–87.
- Rescorla, (2016) Rescorla, M. (2016). Bayesian sensorimotor psychology. Mind & Language, 31(1):3–36.
- Robert, (2007) Robert, C. (2007). The Bayesian choice: from decision-theoretic foundations to computational implementation. Springer Science & Business Media.
- Rosen, (1991) Rosen, R. (1991). Life itself: a comprehensive inquiry into the nature, origin, and fabrication of life. Columbia University Press.
- Schrödinger, (1944) Schrödinger, E. (1944). What Is Life? the physical aspect of the living cell and mind. Cambridge University Press, Cambridge.
- Seifert, (2012) Seifert, U. (2012). Stochastic thermodynamics, fluctuation theorems and molecular machines. Reports on progress in physics, 75(12):126001.
- Seth, (2014) Seth, A. K. (2014). The Cybernetic Bayesian Brain. In Wiese, W. and Metzinger, T. K., editors, Open MIND, pages 9–24. Frankfurt am Main, Germany: MIND Group.
- Seth, (2015) Seth, A. K. (2015). Inference to the best prediction. In Metzinger, T. K. and Windt, J. M., editors, Open MIND. Frankfurt am Main, Germany: MIND Group.
- Spratling, (2016) Spratling, M. (2016). Predictive coding as a model of cognition. Cognitive processing, pages 1–27.
- Tishby and Polani, (2011) Tishby, N. and Polani, D. (2011). Information theory of decisions and actions. In Perception-action cycle, pages 601–636. Springer.
- van Es, (2020) van Es, T. (2020). Living models or life modelled? on the use of models in the free energy principle. Adaptive Behavior.
- Van Gelder, (1995) Van Gelder, T. (1995). What might cognition be, if not computation? The Journal of Philosophy, 92(7):345–381.
- Van Gelder, (1998) Van Gelder, T. (1998). The dynamical hypothesis in cognitive science. Behavioral and brain sciences, 21(5):615–628.
- Varela et al., (1991) Varela, F. J., Thompson, E., and Rosch, E. (1991). The Embodied Mind: Cognitive Science and Human Experience. MIT Press.
- Vyshnegradsky, (1877) Vyshnegradsky, I. (1877). On direct-action controllers. Izvestiya St. Petersburg Practical technological Institute, 1:21–62.
- Walsh et al., (2020) Walsh, K., McGovern, D., Clark, A., and O’Connell, R. (2020). Evaluating the neurophysiological evidence for predictive processing as a model of perception. Annals of the New York Academy of Sciences.
- Wiese and Metzinger, (2017) Wiese, W. and Metzinger, T. K. (2017). Vanilla PP for philosophers: A primer on predictive processing. In Metzinger, T. K. and Wiese, W., editors, In Philosophy and predictive processing: 1. Open MIND. Frankfurt am Main: MIND Group.
- Zahavi, (2017) Zahavi, D. (2017). Brain, mind, world: Predictive coding, neo-kantianism, and transcendental idealism. Husserl Studies, pages 1–15.