Practical Quasi-Newton Methods for Training Deep Neural Networks
Abstract
We consider the development of practical stochastic quasi-Newton, and in particular Kronecker-factored block-diagonal BFGS and L-BFGS methods, for training deep neural networks (DNNs). In DNN training, the number of variables and components of the gradient is often of the order of tens of millions and the Hessian has elements. Consequently, computing and storing a full BFGS approximation or storing a modest number of (step, change in gradient) vector pairs for use in an L-BFGS implementation is out of the question. In our proposed methods, we approximate the Hessian by a block-diagonal matrix and use the structure of the gradient and Hessian to further approximate these blocks, each of which corresponds to a layer, as the Kronecker product of two much smaller matrices. This is analogous to the approach in KFAC [30], which computes a Kronecker-factored block-diagonal approximation to the Fisher matrix in a stochastic natural gradient method. Because of the indefinite and highly variable nature of the Hessian in a DNN, we also propose a new damping approach to keep the upper as well as the lower bounds of the BFGS and L-BFGS approximations bounded. In tests on autoencoder feed-forward neural network models with either nine or thirteen layers applied to three datasets, our methods outperformed or performed comparably to KFAC and state-of-the-art first-order stochastic methods.
1 Introduction
We consider in this paper the development of practical stochastic quasi-Newton (QN), and in particular Kronecker-factored block-diagonal BFGS [6, 13, 16, 39] and L-BFGS [27], methods for training deep neural networks (DNNs). Recall that the BFGS method starts each iteration with a symmetric positive definite matrix (or ) that approximates the current Hessian matrix (or its inverse), computes the gradient of at the current iterate and then takes a step , where is a step length (usually) determined by some inexact line-search procedure, such that , where and is the gradient of at the new point . The method then computes an updated approximation to (or to ) that remains symmetric and positive-definite and satisfies the so-called quasi-Newton (QN) condition (or equivalently, ). A consequence of this is that the matrix operates on the vector in exactly the same way as the average of the Hessian matrix along the line segment between and operates on .
In DNN training, the number of variables and components of the gradient is often of the order of tens of millions and the Hessian has elements. Hence, computing and storing a full BFGS approximation or storing pairs, where is approximately or larger for use in an L-BFGS implementation, is out of the question. Consequently, in our methods, we approximate the Hessian by a block-diagonal matrix, where each diagonal block corresponds to a layer, further approximating them as the Kronecker product of two much smaller matrices, as in [30, 5, 19, 10].
Literature Review on Using Second-order Information for DNN Training. For solving the stochastic optimization problems with high-dimensional data that arise in machine learning (ML), stochastic gradient descent (SGD) [36] and its variants are the methods that are most often used, especially for training DNNs. These variants include such methods as AdaGrad [12], RMSprop [21], and Adam [24], all of which scale the stochastic gradient by a diagonal matrix based on estimates of the first and second moments of the individual gradient components. Nonetheless, there has been a lot of effort to find ways to take advantage of second-order information in solving ML optimization problems. Approaches have run the gamut from the use of a diagonal re-scaling of the stochastic gradient, based on the secant condition associated with quasi-Newton (QN) methods [4], to sub-sampled Newton methods (e.g. see [43], and references therein), including those that solve the Newton system using the linear conjugate gradient method (see [8]).
In between these two extremes are stochastic methods that are based either on QN methods or generalized Gauss-Newton (GGN) and natural gradient [1] methods. For example, a stochastic L-BFGS method for solving strongly convex problems was proposed in [9] that uses sampled Hessian-vector products rather than gradient differences, which was proved in [33] to be linearly convergent by incorporating the variance reduction technique (SVRG [23]) to alleviate the effect of noisy gradients. A closely related variance reduced block L-BFGS method was proposed in [17]. A regularized stochastic BFGS method was proposed in [31], and an online L-BFGS method was proposed in [32] for strongly convex problems and extended in [28] to incorporate SVRG variance reduction. Stochastic BFGS and L-BFGS methods were also developed for online convex optimization in [38]. For nonconvex problems, a damped L-BFGS method which incorporated SVRG variance reduction was developed and its convergence properties was studied in [41].
GGN methods that approximate the Hessian have been proposed, including the Hessian-free method [29] and the Krylov subspace method [40]. Variants of the closely related natural gradient method that use block-diagonal approximations to the Fisher information matrix, where blocks correspond to layers, have been proposed in e.g. [20, 11, 30, 14]. Using further approximation of each of these (empirical) Fisher matrix and GGN blocks by the Kronecker product of two much smaller matrices, the efficient KFAC [30], KFRA [5], EKFAC [15], and Shampoo [19] methods were developed. See also [2] and [10], [37], which combine both Hessian and covariance (Fisher-like) matrix information in stochastic Newton type methods, Also, methods are given in [26, 42] that replace the Kullback-Leibler divergence by the Wasserstein distance to define the natural gradient, but with a greater computational cost.
Our Contributions. The main contributions of this paper can be summarized as follows:
-
1.
New BFGS and limited-memory variants (i.e. L-BFGS) that take advantage of the structure of feed-forward DNN training problems;
-
2.
Efficient non-diagonal second-order algorithms for deep learning that require a comparable amount of memory and computational cost per iteration as first-order methods;
-
3.
A new damping scheme for BFGS and L-BFGS updating of an inverse Hessian approximation, that not only preserves its positive definiteness, but also limits the decrease (and increase) in its smallest (and largest) eigenvalues for non-convex problems;
-
4.
A novel application of Hessian-action BFGS;
-
5.
The first proof of convergence (to the best of our knowledge) of a stochastic Kronecker-factored quasi-Newton method.
2 Kronecker-factored Quasi-Newton Method for DNN
After reviewing the computations used in DNN training, we describe the Kronecker structures of the gradient and Hessian for a single data point, followed by their extension to approximate expectations of these quantities for multiple data-points and give a generic algorithm that employs BFGS (or L-BFGS) approximations for the Hessians.
Deep Neural Networks. We consider a feed-forward DNN with layers, defined by weight matrices (whose last columns are bias vectors ), activation functions for and loss function . For a data-point , the loss between the output of the DNN and is a non-convex function of . The network’s forward and backward pass for a single input data point is described in Algorithm 1.
For a training dataset that contains multiple data-points indexed by , let denote the loss for the th data-point. Then, viewing the dataset as an empirical distribution, the total loss function that we wish to minimize is
Single Data-point: Layer-wise Structure of the Gradient and Hessian. Let and denote, respectively, the restriction of and to the weights in layer . For a single data-point and have a tensor (Kronecker) structure, as shown in [30] and [5]. Specifically,
| (1) | |||
| (2) |
where the pre-activation gradient , and the pre-activation Hessian . Our algorithm uses an approximation to , which is updated via the BFGS updating formulas based upon a secant condition that relates the change in with the change in .
Although we focus on fully-connected layers in this paper, the idea of Kronecker-factored approximations to the diagonal blocks , of the Hessian can be extended to other layers used in deep learning, such as convolutional and recurrent layers.
Multiple Data-points: Kronecker-factored QN Approach. Now consider the case where we have a dataset of data-points indexed by . By (2), we have
| (3) |
Note that the approximation in (3) that the expectation of the Kronecker product of two matrices equals the Kronecker product of their expectations is the same as the one used by KFAC [30]. Now, based on this structural approximation, we use as our QN approximation to , where and are positive definite approximations to and , respectively. Hence, using our layer-wise block-diagonal approximation to the Hessian, a step in our algorithm for each layer is computed as
| (4) |
where denotes the estimate to and is the learning rate. After computing and performing another forward/backward pass, our method computes or updates and as follows:
-
1.
For , we use a damped version of BFGS (or L-BFGS) (See Section 3) based on the pairs corresponding to the average change in and in the gradient with respect to ; i.e.,
(5) -
2.
For we use the "Hessian-action" BFGS method described in Section 4. The issue of possible singularity of the positive semi-definite matrix approximated by is also addressed there by incorporating a Levenberg-Marquardt (LM) damping term.
Algorithm 2 gives a high-level summary of our K-BFGS or K-BFGS(L) algorithms (which use BFGS or L-BFGS to update , respectively). See Algoirthm 4 in the appendix for a detailed pseudocode. The use of mini-batches is described in Section 6. Note that, an additional forward-backward pass is used in Algorithm 2 because the quantities in (5) need to be estimated using the same mini-batch.
3 BFGS and L-BFGS for
Damped BFGS Updating. It is well-known that training a DNN is a non-convex optimization problem. As (2) and (3) show, this non-convexity manifests in the fact that often does not hold. Thus, for the BFGS update of , the approximation to , to remain positive definite, we have to ensure that . Due to the stochastic setting, ensuring this condition by line-search, as is done in deterministic settings, is impractical. In addition, due to the large changes in curvature in DNN models that occur as the parameters are varied, we also need to suppress large changes to as it is updated. To deal with both of these issues, we propose a double damping (DD) procedure (Algorithm 3), which is based upon Powell’s damped-BFGS approach [35], for modifying the pair. To motivate Algorithm 3, consider the formulas used for BFGS updating of and :
| (6) |
where . If we can ensure that and , then we can obtain the following bounds:
| (7) | ||||
| (8) |
and
| (9) | ||||
| (10) |
Thus, the change in (and ) is controlled if and . Our DD approach is a two-step procedure, where the first step (i.e. Powell’s damping of ) guarantees that and the second step (i.e., Powell’s damping with ) guarantees that . Note that there is no guarantee of after the second step. However, we can skip updating in this case so that the bounds on these matrices hold. In our implementation, we always do the update, since in empirical testing, we observed that at least 90% of the pairs satisfy . See Section C in the appendix for more details on damping.
L-BFGS Implementation. L-BFGS can also be used to update . However, implementing L-BFGS using the standard "two-loop recursion" (see Algorithm 7.4 in [34]) is not efficient. This is because the main work in computing in line 4 of Algorithm 2 would require matrix-vector multiplications, each requiring operations, where denotes the number of pairs stored by L-BFGS. (Recall that .) Instead, we use a "non-loop" implementation [7] of L-BFGS, whose main work involves 2 matrix-matrix multiplications, each requiring operations. When is not small (we used in our tests), and and are large, this is much more efficient, especially on GPUs.
4 "Hessian action" BFGS for
In addition to approximating by using BFGS, we also propose approximating by using BFGS. Note that does not correspond to some Hessian of the objective function. However, we can generate pairs for it by "Hessian action" (see e.g. [9, 17, 18]).
Connection between Hessian-action BFGS and Matrix Inversion. In our methods, we choose and , which as we now show, is closely connected to using the Sherman-Morrison modification formula to invert . In particular, suppose that ; i.e., only a rank-one update is made to . This corresponds to the case where the information of is accumulated from iteration to iteration, and the size of the mini-batch is 1 or represents the average of the vectors from multiple data-points.
Theorem 1.
Suppose that and are symmetric and positive definite, and that . If we choose and , where (). Then, the generated by any QN update in the Broyden family
| (11) |
where , , and is a scalar parameter in , equals . Note that yields the BFGS update (6) and yields the DFP update.
Proof.
If and , then , so all choices of yield the same matrix . Since and for any vector that is orthogonal to , , since and , it follows that , using the fact that together with any linearly independent set of vectors orthogonal to spans . (Note that , since that is not orthogonal to .) ∎
In fact, all updates in the Broyden family are equivalent to applying the Sherman-Morrison modification formula to , given , since after substituting for and in (11) and simplifying, one obtains
When using momentum, (). Hence, if we still want Theorem 1 to hold, we have to scale by before updating it. This, however, turns out to be unstable. Hence, in practice, we use the non-scaled version of "Hessian action" BFGS.
Levenberg-Marquardt Damping for . Since may not be positive definite, or may have very small positive eigenvalues, we add an Levenberg-Marquardt (LM) damping term to make our "Hessian-action" BFGS stable; i.e., we use instead of , when we update . Specifically, "Hessian action" BFGS for is performed as
-
1.
; .
-
2.
, ; use BFGS with to update .
5 Convergence Analysis
Following the framework for stochastic quasi-Newton methods (SQN) established in [41] for solving nonconvex stochastic optimization problems (see Section B in the appendix for this framework), we prove that, under fairly standard assumptions, for our K-BFGS(L) algorithm with skipping DD and exact inversion on (see Algorithm 5 in Section B), the number of iterations needed to obtain is , for step size chosen proportional to , where is a constant. Our proofs, which are delayed until Section B, make use of the following assumptions, the first two of which, were made in [41].
AS. 1.
is continuously differentiable. , for any . is globally -Lipschitz continuous; namely for any ,
AS. 2.
For any iteration , the stochastic gradient
satisfies:
a)
,
b)
,
where ,
and are independent samples
that are independent of
.
AS. 3.
The activation functions have bounded values: s.t. .
To use the convergence analysis in [41], we need to show that the block-diagonal approximation of the inverse Hessian used in Algorithm 5 satisfies the assumption that it is bounded above and below by positive-definite matrices. Given the Kronecker structure of our Hessian inverse approximation, it suffices to prove boundness of both and for all iterations . Making the additional assumption AS.3, we are able to prove Lemma 1, and hence Lemma 3, below. Note that many popular activation functions satisfy AS.3, such as sigmoid and tanh.
Lemma 1.
Suppose that AS.3 holds. There exist two positive constants , such that
Lemma 2.
There exist two positive constants and , such that
Lemma 3.
Theorem 2.
Suppose that assumptions AS.1-3 hold for generated by Algorithm 5 with mini-batch size m for all , and is chosen as , with . Then
where denotes the iteration number and depends only on . Moreover, for a given to guarantee that , the number of iterations needed is at most .
Note: other theorems in [41], namely Theorems 2.5 and 2.6, also apply here under our assumptions.
6 Experiments
Before we present some experimental results, we address the use of moving averages, and the computational and storage requirements of the algorithms that we tested.
Mini-batch and Moving Average. Clearly, using the whole dataset at each iteration is inefficient; hence, we use a mini-batch to estimate desired quantities. We use to denote the averaged value of across the mini-batch for any quantity . To incorporate information from the past as well as reducing the variability, we use an exponentially decaying moving average to estimate desired quantities with decay parameter :
-
1.
To estimate the gradient , at each iteration, we update .
-
2.
: To estimate , at each iteration we update Note that although we compute as , we update with (i.e. the average over the minibatch, not ).
-
3.
: BFGS "uses" momentum implicitly incorporated in the matrices . To further stabilize the BFGS update, we also use a moving-averaged (before damping); i.e., We update , and .
Finally, when computing and , we use the same mini-batch as was used to compute and . This doubles the number of forward-backward passes at each iteration.
Storage and Computational Complexity. Tables 1 and 2 compare the storage and computational requirements, respectively, for a layer with inputs and outputs for K-BFGS, K-BFGS(L), KFAC, and Adam/RMSprop. We denote the size of mini-batch by , the number of pairs stored for L-BFGS by , and the frequency of matrix inversion in KFAC by . Besides the requirements listed in Table 1, all algorithms need storage for the parameters and the estimate of the gradient, , (i.e. ). Besides the work listed in Table 2, all algorithms also need to do a forward-backward pass to compute as well as updating , (i.e. ). Also note that, even though we use big- notation in these tables, the constants for all of the terms in each of the rows are roughly at the same level and relatively small.
In Table 2, for K-BFGS and K-BFGS(L), "Additional pass" refers to Line 5 of Algorithm 2; under "Curvature", arises from "Hessian action" BFGS to update (see the algorithm at the end of Section 4), arises from (5), arises from updating (only for K-BFGS); and "Step " refers to (4). For KFAC, referring to Algorithm 7 (in the appendix), "Additional pass" refers to Line 7; under "Curvature", refers to Line 8, and refers to Line 10; and "Step " refers to Line 5.
From Table 1, we see that the Kronecker property enables K-BFGS and K-BFGS(L) (as well as KFAC) to have storage requirements comparable to those of first-order methods. Moreover, from Table 2, we see that K-BFGS and K-BFGS(L) require less computation per iteration than KFAC, since they only involve matrix multiplications, whereas KFAC requires matrix inversions which depend cubically on both and . The cost of matrix inversion in KFAC (and singular value decomposition in [19]) is amortized by performing these operations only once every iterations; nonetheless, these amortized operations usually become much slower than matrix multiplication as models scale up.
| Algorithm | Total | |||
| K-BFGS | — | |||
| K-BFGS(L) | — | |||
| KFAC | — | |||
| Adam/RMSprop | — | — |
| Algorithm | Additional pass | Curvature | Step |
|---|---|---|---|
| K-BFGS | |||
| K-BFGS(L) | |||
| KFAC | |||
| Adam/RMSprop | — |
Experimental Results. We tested K-BFGS and K-BFGS(L), as well as KFAC, Adam/RMSprop and SGD-m (SGD with momentum) on three autoencoder problems, namely, MNIST [25], FACES, and CURVES, which are used in e.g. [22, 29, 30], except that we replaced the sigmoid activation with ReLU. See Section D in the appendix for a complete description of these problems and the competing algorithms.
Since one can view Powell’s damping with as LM damping, we write , where denotes the LM damping parameter for . We then define as the overall damping term of our QN approximation. To simplify matters, we chose , so that we needed to tune only one hyper-parameter (HP) .



To obtain the results in Figure 1, we first did a grid-search on (learning rate, damping) pairs for all algorithms (except for SGD-m, whose grid-search was only on learning rate), where damping refers to for K-BFGS/K-BFGS(L)/KFAC, and for RMSprop/Adam. We then selected the best (learning rate, damping) pairs with the lowest training loss encountered. The range for the grid-search and the best HP values (as well as other fixed HP values) are listed in Section D in the appendix. Using the best HP values that we found, we then made 20 runs employing different random seeds, and plotted the mean value of the 20 runs as the solid line and the standard deviation as the shaded area.111 Results were obtained on a machine with 8 x Intel(R) Xeon(R) CPU @ 2.30GHz and 1 x NVIDIA Tesla P100. Code is available at https://github.com/renyiryry/kbfgs_neurips2020_public.
From the training loss plots in Figure 1, our algorithms clearly outperformed the first-order methods, except for RMSprop/Adam on CURVES, with respect to CPU time, and performed comparably to KFAC in terms of both CPU time and number of epochs taken. The testing error plots in Figure 1 show that our K-BFGS(L) method and KFAC behave very similarly and substantially outperform all of the first-order methods in terms of both of these measures. This suggests that our algorithms not only optimize well, but also generalize well.
To further demonstrate the robustness of our algorithms, we examined the loss under various HP settings, which showed that our algorithms are stable under a fairly wide range for the HPs (see Section D.4 in the appendix).
We also repeated our experiments using mini-batches of size 100 for all algorithms (see Figures 4, 5, and 6 in the appendix, where HPs are optimally tuned for batch sizes of 100) and our proposed methods continue to demonstrate advantageous performance, both in training and testing. For these experiments, we did not experiment with 20 random seeds. These results show that our approach works as well for relatively small mini-batch sizes of 100, as those of size 1000, which are less noisy, and hence is robust in the stochastic setting employed to train DNNs.
Compared with other methods mentioned in this paper, our K-BFGS and K-BFGS(L) have the extra advantage of being able to double the size of minibatch for computing the stochastic gradient with almost no extra cost, which might be of particular interest in a highly stochastic setting. See Section D.6 in the appendix for more discussion on this and some preliminary experimental results.
7 Conclusion
We proposed Kronecker-factored QN methods, namely, K-BFGS and K-BFGS(L), for training multi-layer feed-forward neural network models, that use layer-wise second-order information and require modest memory and computational resources. Experimental results indicate that our methods outperform or perform comparably to the state-of-the-art first-order and second-order methods. Our methods can also be extended to convolutional and recurrent NNs.
Broader Impact
The research presented in this paper provides a new method for training DNNs that our experimental testing has shown to be more efficient in several cases than current state-of-the-art optimization methods for this task. Consequently, because of the wide use of DNNs in machine learning, this should help save a substantial amount of energy. Our new algorithms simply attempt to minimize the loss function that are given to it and the computations that it performs are all transparent. In machine learning, DNNs can be trained to address many types of problems, some of which should lead to positive societal outcomes, such as ones in medicine (e.g., diagnostics and drug effectiveness), autonomous vehicle development, voice recognition and climate change. Of course, optimization algorithms for training DNNs can be used to train models that may have negative consequences, such as those intended to develop psychological profiles, invade privacy and justify biases. The misuse of any efficient optimization algorithm for machine learning, and in particular our algorithms, is beyond the control of the work presented here.
Acknowledgments and Disclosure of Funding
DG and YR were supported in part by NSF Grant IIS-1838061. DG acknowledges the computational support provided by Google Cloud Platform Education Grant, Q81G-U4X3-5AG5-F5CG.
References
- Amari et al. [2000] S.-I. Amari, H. Park, and K. Fukumizu. Adaptive method of realizing natural gradient learning for multilayer perceptrons. Neural computation, 12(6):1399–1409, 2000.
- Ba et al. [2017] J. Ba, R. B. Grosse, and J. Martens. Distributed second-order optimization using kronecker-factored approximations. In ICLR, 2017.
- Badreddine et al. [2014] H. Badreddine, S. Vandewalle, and J. Meyers. Sequential quadratic programming (sqp) for optimal control in direct numerical simulation of turbulent flow. Journal of Computational Physics, 256:1–16, 2014.
- Bordes et al. [2009] A. Bordes, L. Bottou, and P. Gallinari. Sgd-qn: Careful quasi-newton stochastic gradient descent. Journal of Machine Learning Research, 10(Jul):1737–1754, 2009.
- Botev et al. [2017] A. Botev, H. Ritter, and D. Barber. Practical gauss-newton optimisation for deep learning. In Proceedings of the 34th International Conference on Machine Learning-Volume 70, pages 557–565. JMLR. org, 2017.
- Broyden [1970] C. G. Broyden. The convergence of a class of double-rank minimization algorithms 1. general considerations. IMA Journal of Applied Mathematics, 6(1):76–90, 1970.
- Byrd et al. [1994] R. H. Byrd, J. Nocedal, and R. B. Schnabel. Representations of quasi-newton matrices and their use in limited memory methods. Mathematical Programming, 63(1-3):129–156, 1994.
- Byrd et al. [2011] R. H. Byrd, G. M. Chin, W. Neveitt, and J. Nocedal. On the use of stochastic hessian information in optimization methods for machine learning. SIAM Journal on Optimization, 21(3):977–995, 2011.
- Byrd et al. [2016] R. H. Byrd, S. L. Hansen, J. Nocedal, and Y. Singer. A stochastic quasi-newton method for large-scale optimization. SIAM Journal on Optimization, 26(2):1008–1031, 2016.
- Dangel et al. [2019] F. Dangel, P. Hennig, and S. Harmeling. Modular block-diagonal curvature approximations for feedforward architectures. arXiv preprint arXiv:1902.01813, 2019.
- Desjardins et al. [2015] G. Desjardins, K. Simonyan, R. Pascanu, et al. Natural neural networks. In Advances in Neural Information Processing Systems, pages 2071–2079, 2015.
- Duchi et al. [2011] J. Duchi, E. Hazan, and Y. Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul):2121–2159, 2011.
- Fletcher [1970] R. Fletcher. A new approach to variable metric algorithms. The computer journal, 13(3):317–322, 1970.
- Fujimoto and Ohira [2018] Y. Fujimoto and T. Ohira. A neural network model with bidirectional whitening. In International Conference on Artificial Intelligence and Soft Computing, pages 47–57. Springer, 2018.
- George et al. [2018] T. George, C. Laurent, X. Bouthillier, N. Ballas, and P. Vincent. Fast approximate natural gradient descent in a kronecker factored eigenbasis. In Advances in Neural Information Processing Systems, pages 9550–9560, 2018.
- Goldfarb [1970] D. Goldfarb. A family of variable-metric methods derived by variational means. Mathematics of computation, 24(109):23–26, 1970.
- Gower et al. [2016] R. Gower, D. Goldfarb, and P. Richtárik. Stochastic block bfgs: Squeezing more curvature out of data. In International Conference on Machine Learning, pages 1869–1878, 2016.
- Gower and Richtárik [2017] R. M. Gower and P. Richtárik. Randomized quasi-newton updates are linearly convergent matrix inversion algorithms. SIAM Journal on Matrix Analysis and Applications, 38(4):1380–1409, 2017.
- Gupta et al. [2018] V. Gupta, T. Koren, and Y. Singer. Shampoo: Preconditioned stochastic tensor optimization. In J. Dy and A. Krause, editors, Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pages 1842–1850. PMLR, 2018.
- Heskes [2000] T. Heskes. On "natural" learning and pruning in multilayered perceptrons. Neural Computation, 12, 01 2000. doi: 10.1162/089976600300015637.
- Hinton et al. [2012] G. Hinton, N. Srivastava, and K. Swersky. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited on, 14(8), 2012.
- Hinton and Salakhutdinov [2006] G. E. Hinton and R. R. Salakhutdinov. Reducing the dimensionality of data with neural networks. science, 313(5786):504–507, 2006.
- Johnson and Zhang [2013] R. Johnson and T. Zhang. Accelerating stochastic gradient descent using predictive variance reduction. In Advances in neural information processing systems, pages 315–323, 2013.
- Kingma and Ba [2014] D. Kingma and J. Ba. Adam: A method for stochastic optimization. International Conference on Learning Representations, 2014.
- LeCun et al. [1998] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- Li and Montúfar [2018] W. Li and G. Montúfar. Natural gradient via optimal transport. Information Geometry, 1(2):181–214, 2018.
- Liu and Nocedal [1989] D. C. Liu and J. Nocedal. On the limited memory bfgs method for large scale optimization. Mathematical programming, 45(1-3):503–528, 1989.
- Lucchi et al. [2015] A. Lucchi, B. McWilliams, and T. Hofmann. A variance reduced stochastic newton method. arXiv preprint arXiv:1503.08316, 2015.
- Martens [2010] J. Martens. Deep learning via hessian-free optimization. In ICML, volume 27, pages 735–742, 2010.
- Martens and Grosse [2015] J. Martens and R. Grosse. Optimizing neural networks with kronecker-factored approximate curvature. In International conference on machine learning, pages 2408–2417, 2015.
- Mokhtari and Ribeiro [2014] A. Mokhtari and A. Ribeiro. Res: Regularized stochastic bfgs algorithm. IEEE Transactions on Signal Processing, 62(23):6089–6104, 2014.
- Mokhtari and Ribeiro [2015] A. Mokhtari and A. Ribeiro. Global convergence of online limited memory bfgs. The Journal of Machine Learning Research, 16(1):3151–3181, 2015.
- Moritz et al. [2016] P. Moritz, R. Nishihara, and M. Jordan. A linearly-convergent stochastic l-bfgs algorithm. In Artificial Intelligence and Statistics, pages 249–258, 2016.
- Nocedal and Wright [2006] J. Nocedal and S. Wright. Numerical optimization. Springer Science & Business Media, 2006.
- Powell [1978] M. J. Powell. Algorithms for nonlinear constraints that use lagrangian functions. Mathematical programming, 14(1):224–248, 1978.
- Robbins and Monro [1951] H. Robbins and S. Monro. A stochastic approximation method. The annals of mathematical statistics, pages 400–407, 1951.
- Roux and Fitzgibbon [2010] N. L. Roux and A. W. Fitzgibbon. A fast natural newton method. In ICML, 2010.
- Schraudolph et al. [2007] N. N. Schraudolph, J. Yu, and S. Günter. A stochastic quasi-newton method for online convex optimization. In Artificial intelligence and statistics, pages 436–443, 2007.
- Shanno [1970] D. F. Shanno. Conditioning of quasi-newton methods for function minimization. Mathematics of computation, 24(111):647–656, 1970.
- Vinyals and Povey [2012] O. Vinyals and D. Povey. Krylov subspace descent for deep learning. In Artificial Intelligence and Statistics, pages 1261–1268, 2012.
- Wang et al. [2017] X. Wang, S. Ma, D. Goldfarb, and W. Liu. Stochastic quasi-newton methods for nonconvex stochastic optimization. SIAM Journal on Optimization, 27(2):927–956, 2017.
- Wang and Li [2020] Y. Wang and W. Li. Information newton’s flow: second-order optimization method in probability space. arXiv preprint arXiv:2001.04341, 2020.
- Xu et al. [2019] P. Xu, F. Roosta, and M. W. Mahoney. Newton-type methods for non-convex optimization under inexact hessian information. Mathematical Programming, pages 1–36, 2019.
Appendix A Pseudocode for K-BFGS/K-BFGS(L)
Algorithm 4 gives pseudocode for K-BFGS/K-BFGS(L), which is implemented in the experiments. For details see Sections 3, 4, and Section C in the Appendix.
Appendix B Convergence: Proofs of Lemmas 1-3 and Theorem 2
In this section, we prove the convergence of Algorithm 5, a variant of K-BFGS(L). Algorithm 5 is very similar to our actual implementation of K-BFGS(L) (i.e. Algorithm 4), except that
To accomplish this, we prove Lemmas 1-3, which in addition to Assumptions AS.1-2, ensure that all of the assumptions in Theorem 2.8 in [41] are satisfied, and hence that the generic stochastic quasi-Newton (SQN) method, i.e. Algorithm 6, below converges. Specifically, Theorem 2.8 in [41] requires, in addition to Assumptions AS.1-2, the assumption
AS. 4.
There exist two positive constants , such that ; for any the random variable depends only on .
In the following proofs, denotes the 2-norm for vectors, and the spectral norm for matrices.
Proof of Lemma 1:
Proof.
Because , we have that , where .
On the other hand, for any , by Cauchy-Schwarz, . Hence, ; similarly, . Because , by induction, for any and . Thus, . Hence, , where .
∎
Proof of Lemma 2:
Proof.
To simplify notation, we omit the subscript , superscript and the iteration index in the proof. Hence, our goal is to prove , for any and . Let () denote the pairs used in an L-BFGS computation of . Since was not skipped, , where denotes the matrix used at the iteration in which and were computed. Note that this is not the matrix used in the recursive computation of at the current iterate .
Given an initial estimate of , the L-BFGS method updates recursively as
| (12) |
where , and equivalently,
where . Since we use DD with skipping, we have that and . Note that we don’t have , so we cannot direct apply (10). Hence, by (8), we have that . Hence, . Thus, , .
On the other hand, since is a uniform lower bound for for any and , . Thus,
Hence, using the fact that for any vectors ,
From the fact that , and induction, we have that .
∎
Proof of Lemma 3:
Proof of Theorem 2:
Proof.
To show that Algorithm 5 lies in the framework of Algorithm 6, it suffices to show that generated by Algorithm 5 is positive definite, which is true since and and are positive definite for all and . Then by Lemma 3, and the fact that depends on and , and and does not depend on random samplings in the th iteration, AS.4 holds. Hence, Theorem 2.8 of [41] applies to Algorithm 5, proving Theorem 2. ∎
Appendix C Powell’s Damped BFGS Updating
For BFGS and L-BFGS, one needs . However, when used to update , there is no guarantee that for any layer . In deterministic optimization, positive definiteness of the QN Hessian approximation (or its inverse) is maintained by performing an inexact line search that ensures that , which is always possible as long as the function being minimized is bounded below. However, this would be expensive to do for DNN. Thus, we propose the following heuristic based on Powell’s damped-BFGS approach [35].
Powell’s Damping on . Powell’s damping on , proposed in [35], replaces in the BFGS update, by , where
It is easy to verify that .
Powell’s Damping on . In Powell’s damping on (see e.g. [3]), replaces , where
This is used in lines 2 and 3 of the DD (Algorithm 3). It is also easy to verify that .
Powell’s Damping with . Powell’s damping on is not suitable for our algorithms because we do not keep track of . Moreover, it does not provide a simple bound on that is independent of . Therefore, we use Powell’s damping with , in lines 4 and 5 of the DD (Algorithm 3). It is easy to verify that it ensures that .
Powell’s damping with can be interpreted as adding an Levenberg-Marquardt (LM) damping term to . Note that an LM damping term would lead to . Then, the secant condition implies
which is the same inequality as we get using Powell’s damping with . Note that although the parameter in Powell’s damping with can be interpreted as an LM damping, we recommend setting the value of within so that is a convex combination of and . In all of our experimental tests, we found that the best value for the hyperparameter for both K-BFGS and K-BFGS(L) was less than or equal to , and hence that was in the interval .
C.1 Double Damping (DD)
Our double damping (Algorithm 3) is a two-step damping procedure, where the first step (i.e. Powell’s damping on ) can be viewed as an interpolation between the current curvature and the previous ones, and the second step (i.e. Powell’s damping with ) can be viewed as an LM damping.



Recall that there is no guarantee that holds after DD. While we skip using pairs that do not satisfy this inequality, when updating in proving the convergence of the K-BFGS(L) variant Algorithm 5 , we use all pairs to update in our implementations of both K-BFGS and K-BFGS(L) . However, whether one skips or not makes only slight difference in the performance of these algorithms, because as our empirical testing has shown, at least 90% of the iterations satisfy , even if we don’t skip. See Figure 2 which reports results on this for K-BFGS(L) when tested on the MNIST, FACES and CURVES datasets.
Appendix D Implementation Details and More Experiments
D.1 Description of Competing Algorithms
D.1.1 KFAC
We first describe KFAC in Algorithm 7. Note that in KFAC refers to the matrices in [30], which is different from the in K-BFGS.
D.1.2 Adam/RMSprop
D.1.3 Initialization of Algorithms
We now describe how each algorithm is initialized. For all algorithms, is always initialized as zero.
For second-order information, we use a "warm start" to estimate the curvature when applicable. In particular, we estimate the following curvature information using the entire training set before we start updating parameters. The information gathered is
-
•
for K-BFGS and K-BFGS(L);
-
•
and for KFAC;
-
•
for RMSprop;
-
•
Not applicable to Adam because of the bias correction.
Lastly, for K-BFGS and K-BFGS(L), is always initially set to an identity matrix. is also initially set to an identity matrix in K-BFGS; for K-BFGS(L), when updating using L-BFGS, the incorporation of the information from the pairs is applied to an initial matrix that is set to an identity matrix. Hence, the above initialization/warm start costs are roughly twice as large for KFAC as they are for K-BFGS and K-BFGS(L).
D.2 Autoencoder Problems
Table 3 lists information about the three datasets, namely, MNIST222 Downloadable at http://yann.lecun.com/exdb/mnist/ , FACES333 Downloadable at www.cs.toronto.edu/~jmartens/newfaces_rot_single.mat , and CURVES444 Downloadable at www.cs.toronto.edu/~jmartens/digs3pts_1.mat . Table 4 specifies the architecture of the 3 problems, where binary entropy , MSE . Besides the loss function in Table 4, we further add a regularization term to the loss function, where .
| Dataset | # data points | # training examples | # testing examples |
|---|---|---|---|
| MNIST | 70,000 | 60,000 | 10,000 |
| FACES | 165,600 | 103,500 | 62,100 |
| CURVES | 30,000 | 20,000 | 10,000 |
| Dataset | Layer width & activation | Loss function |
|---|---|---|
| MNIST | [784, 1000, 500, 250, 30, 250, 500, 1000, 784] | binary entropy |
| [ReLU, ReLU, ReLU, linear, ReLU, ReLU, ReLU, sigmoid] | ||
| FACES | [625, 2000, 1000, 500, 30, 500, 1000, 2000, 625] | MSE |
| [ReLU, ReLU, ReLU, linear, ReLU, ReLU, ReLU, linear] | ||
| CURVES | [784, 400, 200, 100, 50, 25, 6, 25, 50, 100, 200, 400, 784] | binary entropy |
| [ReLU, ReLU, ReLU, ReLU, ReLU, linear, | ||
| ReLU, ReLU, ReLU, ReLU, ReLU, sigmoid] |
D.3 Specification of Hyper-parameters
In our experiments, we focus our tuning effort onto learning rate and damping. The range of the tuning values is listed below:
-
•
learning rate 1e-5, 3e-5, 1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2, 1e-1, 3e-1, 1, 3, 10 .
-
•
damping:
-
–
for K-BFGS, K-BFGS(L) and KFAC: 3e-3, 1e-2, 3e-2, 1e-1, 3e-1, 1, 3 .
-
–
for RMSprop and Adam: 1e-10, 1e-8, 1e-6, 1e-4, 1e-3, 1e-2, 1e-1 .
-
–
Not applicable for SGD with momentum.
-
–
| K-BFGS | K-BFGS(L) | KFAC | Adam | RMSprop | SGD-m | |
|---|---|---|---|---|---|---|
| MNIST | (0.3, 0.3) | (0.3, 0.3) | (1, 3) | (1e-4, 1e-4) | (1e-4, 1e-4) | (0.03, -) |
| FACES | (0.1, 0.1) | (0.1, 0.1) | (0.1, 0.1) | (1e-4, 1e-4) | (1e-4, 1e-4) | (0.01, -) |
| CURVES | (0.1, 0.01) | (0.3, 0.3) | (0.3, 0.3) | (1e-3, 1e-3) | (1e-3, 1e-3) | (0.1, -) |
The best hyper-parameters were those that produced the lowest value of the deterministic loss function encountered at the end of every epoch until the algorithm was terminated. These values were used in Figure 1 and are listed in Table 5. Besides the tuning hyper-parameters, we also list other fixed hyper-parameters with their values:
-
•
Size of minibatch = 1000, which is also suggested in [5].
-
•
Decay parameter:
-
–
K-BFGS, K-BFGS(L): ;
-
–
KFAC: ;
- –
-
–
SGD with momentum: .
-
–
-
•
Other:
-
–
in double damping (DD):
We recommend to leave the value as default because represents the "ratio" between current and past, which is scaling invariant;
-
–
Number of pairs stored for K-BFGS(L) :
It might be more efficient to use a smaller for the narrow layers. We didn’t investigate this for simplicity and consistency;
-
–
Inverse frequency in KFAC.
-
–
D.4 Sensitivity to Hyper-parameters






Figure 3 shows the sensitivity of K-BFGS and K-BFGS(L) to hyper-parameter values (i.e. learning rate and damping). The -axis corresponds to the learning rate , while the -axis correspond to the damping value . Color corresponds to the loss after a certain amount of CPU time. We can see that both K-BFGS and K-BFGS(L) are robust within a fairly wide range of hyper-parameters.
To get the plot, we first obtained training loss with 1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2, 1e-1, 3e-1, 1 and 1e-2, 3e-2, 1e-1, 3e-1, 1, and then drew contour lines of the loss within the above ranges.
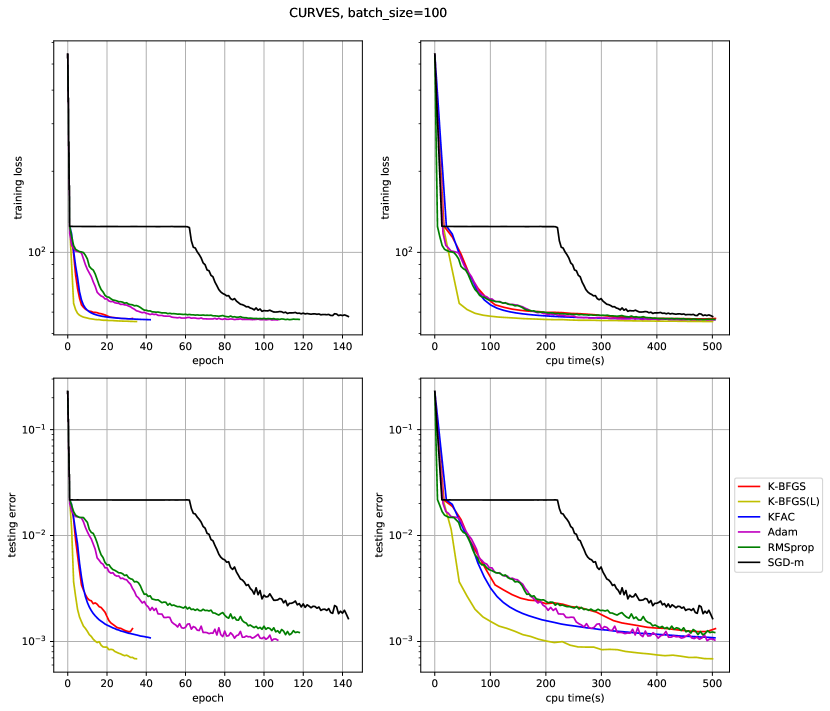
D.5 Experimental Results Using Mini-batches of Size 100
We repeated our experiments using mini-batches of size 100 for all algorithms (see Figures 4, 5, and 6). For each figure, the upper (lower) rower depict training loss (testing (mean square) error), whereas the left (right) column depicts training/test progress versus epoch (CPU time), respectively.
The best hyper-parameters were those that produce the lowest value of the deterministic loss function encountered at the end of every epoch until the algorithm was terminated. These values were used in Figures 4, 5, 6 and are listed in Table 6.
Our proposed methods continue to demonstrate advantageous performance, both in training and testing. It is interesting to note that, whereas for a minibatch size of 1000, KFAC slightly outperformed K-BFGS(L), for a minibatch size of 100, K-BFGS(L) clearly outperformed KFAC in training on CURVES.
| K-BFGS | K-BFGS(L) | KFAC | Adam | RMSprop | SGD-m | |
|---|---|---|---|---|---|---|
| MNIST | (0.1, 0.3) | (0.1, 0.3) | (0.1, 0.3) | (1e-4, 1e-4) | (1e-4, 1e-4) | (0.03, -) |
| FACES | (0.03, 0.03) | (0.03, 0.3) | (0.03, 0.3) | (3e-5, 1e-4) | (3e-5, 1e-4) | (0.01, -) |
| CURVES | (0.3, 1) | (0.3, 0.3) | (0.03, 0.1) | (3e-4, 1e-4) | (3e-3, 1e-4) | (0.03, -) |


D.6 Doubling the Mini-batch for the Gradient at Almost No Cost



Compared with other methods mentioned in this paper, our K-BFGS and K-BFGS(L) methods have the extra advantage of being able to double the size of the minibatch used to compute the stochastic gradient with almost no extra cost, which might be of particular interest in a highly stochastic setting. To accomplish this, we can make use of the stochastic gradient computed in the second pass of the previous iteration that is needed for computing the pair for applying the BFGS or L-BFGS updates, and average it with the stochastic gradient of the current iteration. For example if the size of minibatch is , the above "double-grad-minibatch" method computes a stochastic gradient from 2000 data points at each iteration, except at the very first iteration.
The results of some preliminary experiments are depicted in Figure 7, where we compare an earlier version of the K-BFGS algorithm (Algorithm 4), which uses a slightly different variant of Hessian-action to update , using a size of for mini-batches, with its "double-grad-minibatch" variants for and . Even though "double-grad" does not help much in these experiments, our K-BFGS algorithm performs stably across these different variants. These results indicate that there is a potential for further improvements; e.g., a finer grid search might identify hyper-parameter values that result in better performing algorithms.