Practical Quantum Sensing with Thermal Light

Introduction – Quantum sensing uses quantum phenomena to improve the measurements of physical parameters and can be implemented in photonic, atomic or solid-state systems [1]. Photonic quantum sensing techniques include ghost imaging and super-resolution imaging [2]. Many photonic quantum sensing schemes rely on photon pairs generated in spontaneous parametric down-conversion (SPDC) [3] that can be entangled in several degrees of freedom, but most often make use of the temporal correlation between the photons [4]. Examples are range finding [5, 6] and clock synchronization [7, 8] schemes, where quantum light sources have an advantage of being stationary, and therefore carrying no obvious timing structure that may be subject to manipulation or eavesdropping. The luminosity of SPDC-based photon pair sources is typically limited to sub-nanowatts.

In this work, we consider thermal light an alternative resource of time-correlated photons by utilizing its photon bunching property. We demonstrate quantum sensing using a relatively simple thermal light source based on a sub-threshold diode laser. The resulting spectral density of this source exceeds that of SPDC sources by approximately 10 orders of magnitude.

Time-correlated photon pairs – Photonic sensing applications often make use of modulated light sources and seek for correlations of a returned signal with the modulation. In an attempt of moving to low light levels, one can make use of inherent temporal correlations found in photon pairs emerging from SPDC in three- or four-wave mixing processes. These processes generate pairs of photons that exhibit a strongly peaked second order correlation function $g^{(2)}(\tau)=f(\tau/\tau_{c})$, which characterizes a probability to observe a pair at a time separation $\tau$. The function $f$ is strongly peaked around $\tau=0$ (with a spread on the order of a coherence time $\tau_{c}$), and can be observed in specialized quantum light sources. Sensing applications based on this effect are carried out by measuring detection time differences between one photon acting as a reference, and the other one acting as a probe.

A more natural type of light is thermal light. Thermal light, such as blackbody radiation, exhibits a characteristic temporal photon bunching behavior [9, 10], also known as the Hanbury-Brown–Twiss effect [11]. This can also be described by a peaked second-order timing correlation,

where $\tau$ is again the timing separation of the two photodetection events, and $\tau_{c}$ is the coherence timescale of the temporal photon bunching where thermal photons have a tendency to be detected closer together than described by Poissonian statistical timing distribution. Similar to light generated by SPDC, the coherence timescale $\tau_{c}$ is inversely proportional to the spectral width $\Delta f\approx c\Delta\lambda/\lambda^{2}$ of the thermal light, which is given by the Fourier transform of the source power spectrum [12], such that $\Delta f=1/\tau_{c}$ for single-line Gaussian spectrum. Here, $\lambda$ is the central wavelength of the light, $\Delta\lambda$ the wavelength spread, and $c$ the speed of light.

An important practical consideration for sensing applications is the brightness of the correlated light source. As shown in Fig. 1, SPDC light sources generate an output power below a nanowatt, or in the range of 10⁴ to 10⁹ photoevents per second. This limits the practicality of SPDC light-based sensing in environments with high attenuation or return loss. Another important property in a temporal correlation measurement is the accuracy that can be practically used to infer e.g. a time-of-flight for one of the photons. Timing uncertainties of semiconductor-based single-photon detectors are somewhere below a nanosecond, but more recent nanowire-based detectors may reach a few picoseconds. When identifying the temporal correlation feature in thermal light, however, it is necessary that the correlation peak is still detectable. If the coherence time of the thermal light is significantly smaller than the detector timing uncertainty, the visibility of the temporal correlation washes out and may make it impossible to identify it on top of the Poissonian background. It is therefore desirable to use thermal light sources with a spectral width below $\approx 1$ GHz.

Thermal light with such a narrow optical bandwidth has been generated in many different ways. Early examples include single emission lines of gas discharge lamps [11]. Other methods involve transmitting laser light through random dispersion media such as suspension of microspheres [13], or a rotating ground glass plate [22]. These sources, however, have either relatively low output power due to the spatial incoherence of the randomization mechanism, or (e.g. in the case of rotating ground glass modulators) a relatively long coherence time.

Here, we use a laser diode operating below the lasing threshold [23, 24] to generate thermal light [25, 26]. This amplified spontaneous emission process generates significantly higher output power in the range of 10 $\mu$W to 100 mW. Light sources of a similar category include superluminescent diodes, and Erbium-doped fiber amplifiers. These examples tend to have spectral densities above milliwatts per nanometer.

The diode laser we use (nominal lasing wavelength $\lambda=518$ nm, single spatial mode output) shows a lasing threshold current around 33 mA (see Fig. 2), where the output power exhibits a sharp increase of 3 orders of magnitude, and the spectrum narrows to a single emission line, limited by the grating spectrometer to about 0.3 nm. We operate the diode laser at a subthreshold current of 32.9 mA, where it exhibits the photon bunching behavior that is characteristic of thermal light. The light is then coupled into a single spatial mode optical fiber. We observe an optical power of $12.5\,\mu$W, corresponding to a photon rate $R\approx 3.3\times 10^{13}\,$s^-1, within a spectral window of $\Delta f=43$ MHz. This results in a thermal light source of extremely high spectral brightness of about $8\times 10^{17}$ photoevents per second and nanometer.

Quantum sensing setup – The stationary thermal light generated from a subthreshold laser diode is implemented into an optical ranging setup based on time-of-flight measurements, commonly known as light distance and ranging (lidar) (see Fig. 3). While conventional lidar introduces timing modulation [27, 28] into the intensity, amplitude, or phase of the light source, to provide timing correlations, this work relies on photon bunching of thermal light to provide the timing correlations. We do record the photodetection events with a high timing resolution to obtain the temporal photon bunching signature $g^{(2)}(\tau)$ similar to [29].

To ensure that we select only a single chip mode of thermal light from the sub-threshold laser diode, a combination of a polarization filter, a bandpass filter (BP1 in Fig. 3) and a temperature-tuned etalon is used. The etalon is based on a fused silica (Suprasil311) substrate and has a tuning parameter of 4 GHz/K for its resonances. Optical coatings with a reflectivity of $97\,\%$ on both sides result in a finesse of 103. The plano-parallel substrate has a thickness of 0.5 mm, resulting in a free spectral range of about 205 GHz, and spectral transmission windows of 2 GHz full width at half maximum (FWHM) [30]. This allows to effectively to suppress adjacent laser diode chip modes which are separated by about 50 GHz from the mode used. The bandpass interference filter BP1 has a 2 nm wide passband centered at $\lambda=518$ nm to suppress source light beyond the free spectral range of the etalon.

An asymmetric beamsplitter directs 92 % of the filtered thermal light into the probe beam and retains 4 % as a local reference beam sent to a first single photon detector.

The spectrally filtered thermal light beam passes through a 50:50 beamsplitter and a telescope formed by a lens pair (f=50 mm, f=300 mm) around a spatial filter, and is expanded to a diameter of about 50 mm. The probe beam returns from the target reflector through the same telescope and beamsplitter onto the probe photodetector. The spatial filter cleans up the returning probe beam and reduces ambient light contribution from reaching the detectors, and the use of a second beamsplitter ensures that no breakdown flash light from the target detector can reach the reference photodetector. A second band pass filter BP2 is used to suppress ambient light reaching the probe detector.

The $g^{(2)}(\tau)$ photon bunching peak is shifted by a time $\tau_{0}=2d/c$ in its timing position, corresponding to the optical path length difference between probe and reference beam, thus allowing to infer the distance $d$ of a target retroreflector from the peak position of $g^{(2)}(\tau)$.

Both single photon detectors are actively quenched Silicon avalanche photodiodes with a quantum efficiency about $50\,\%$ at 550 nm, and a timing jitter around 40 ps. The detected photoevents are timestamped by an oscilloscope with (sampling rate 40 GSPS), and time differences were histogrammed into 40 ps wide time bins for short distances $d$, or recorded with an FPGA-based timestamp device with a resolution of 2 ns and sorted into 2 ns wide time bins numerically for long distances $d$.

Range sensing demonstrations – Figure 4 shows two representative time difference histograms together with a fitted second-order timing correlation function $g^{(2)}(\tau)$ according to Eqn. 1. These allow to determine the positions $\tau_{0}$ of their respective bunching peaks and the corresponding ranging distances $d$ from the round trip time of the probe beam for a set of target placement positions (Fig. 4, bottom trace). The resulting ranges are in good agreement with their corresponding target placement positions, and compatible with a constraint in the detector timing jitter (about 40 ps FWHM).

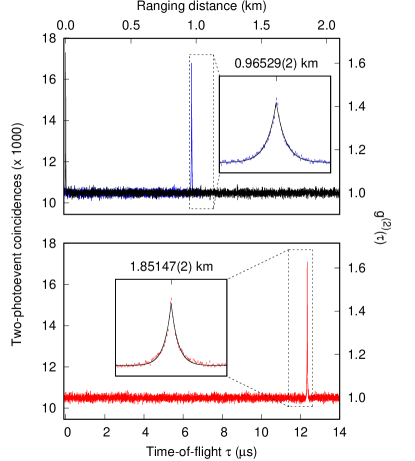
To demonstrate the robustness of the ranging setup, we conducted two outdoor field measurements. Figure 5 shows two long-range time-of-flight measurements together with a reference zero position (black trace), resulting in the ranging distances of $965.29\pm 0.02$ m (blue) and $1,851.48\pm 0.02$ m (red) fitted to Eqn. 1 with reduced $\chi^{2}$ of 1.09 and 1.05, respectively, under the assumption of a unit refractive index of air. The increased uncertainty compared to the short range measurements shown in Fig. 4 are due to the more coarse histogramming for this experiment.

For the long distance measurements, the etalon temperature tuning and stability was improved relative to the measurements in Fig. 4, increasing the coherence timescale $\tau_{c}=23.2\pm 0.4$ ns (red), corresponding to a spectral linewidth $\Delta f=43$ MHz.

The temporal photon bunching peak (red) is slightly reduced to $g^{(2)}(\tau=0)=1.591\pm 0.009$ (red) due to an increase of the bin width from 40 ps to 2 ns for the time differences, and by noise contribution from ambient light to the probe detector.

Signal-to-noise considerations – The very high spectral density of our light source helps to increase the signal-to-noise ratio [31, 32] of a bunching peak detection significantly. When photodetectors are fast enough to resolve the temporal coherence $\tau_{c}$ of the photon bunching signature, the signal-to-noise ratio (SNR) of the second order correlation function $g^{(2)}(\tau)$ will be dominated by shot noise of the photodetection events, and can be described by

with the photoevent rate $r$, the interferometric visibility $V=\sqrt{g^{(2)}(0)-1}$, the coherence time $\tau_{c}$, and the integration time $\Delta T$.

With a photon bunching peak value $V^{2}=0.6$ and a coherence timescale $\tau_{c}=23\,$ns, which corresponds to the measured values in Fig. 5, an upper bound for the signal-to-noise ratio of around 30 can already be achieved after an integration time $\Delta T=1$ ms at a photodetection rate of $r=10^{7}$ s^-1 given by typical avalanche photodetector saturation. This high tolerance to attenuation provides the thermal light source an advantage over SPDC light sources in practical sensing use-cases where significant losses can be expected.

Summary – This work explored the use of thermal light for applications where measurements (like range finding) are based on detecting correlations in time. Sub-threshold lasers with their intrinsic temporal correlations thus provide a powerful alternative to light sources based on spontaneous parametric down-conversion in quantum sensing applications, and may offer superior signal-to-noise ratios at a much reduced system complexity.

With such light sources, a technique originally used for estimating the size of stars half a century ago can boost a wide range of practical quantum sensing applications that mostly rely on temporal correlations.