Possible molecular states from interactions of charmed baryons

Dan Song, Lin-Qing Song, Shu-Yi Kong, Jun He¹¹1Corresponding author: [email protected] School of Physics and Technology, Nanjing Normal University, Nanjing 210097, China

Abstract

In this work, we perform a systematic study of possible molecular states composed of two charmed baryons including hidden-charm systems $\Lambda_{c}\bar{\Lambda}_{c}$ , $\Sigma_{c}^{(*)}\bar{\Sigma}_{c}^{(*)}$ , and $\Lambda_{c}\bar{\Sigma}_{c}^{(*)}$ , and corresponding double-charm systems $\Lambda_{c}\Lambda_{c}$ , $\Sigma_{c}^{(*)}\Sigma_{c}^{(*)}$ , and $\Lambda_{c}\Sigma_{c}^{(*)}$ . With the help of the heavy quark chiral effective Lagrangians, the interactions are described with $\pi$ , $\rho$ , $\eta$ , $\omega$ , $\phi$ , and $\sigma$ exchanges. The potential kernels are constructed, and inserted into the quasipotential Bethe-Salpeter equation. The bound states from the interactions considered is studied by searching for the poles of the scattering amplitude. The results suggest that strong attractions exist in both hidden-charm and double-charm systems considered in the current work, and bound states can be produced in most of the systems. More experimental studies about these molecular states are suggested though the nucleon-nucleon collision at LHC and nucleon-antinucleon collision at $\rm\bar{P}ANDA$ .

I Introduction

With the development of the experimental technology, a large amount of data accumulated in experiment provide opportunity to the study of the hadron spectrum. In the recent years, more and more hadrons have been observed in experiment PDG . Many of these new observed hadrons cannot be put into the conventional quark model, which is the basic frame to understand the hadron spectrum Godfrey:1985xj ; Capstick:1986ter . A growing number of efforts have been paid to explain their origin and internal structure. An obvious observation is that many newly observed particles are close to the threshold of two hadrons, so a popular picture to understand these exotic hadrons is the molecular state, which is a loosely bound state of hadrons. The $XYZ$ particles, such as $X(3872)$ , $Z_{c}(3900)$ and $Z_{b}(10610)$ and $Z_{c}(10650)$ , were widely assigned as molecular states in the literature Chen:2016qju ; Guo:2017jvc ; Tornqvist:1993ng ; He:2014nya ; Sun:2011uh . Particularly, the observed hidden-charm pentaquarks provide a wonderful spectrum of molecular states composed of an anticharmed meson and a charmed baryon Wu:2010jy ; Yang:2011wz ; Xiao:2013yca ; Chen:2015loa ; He:2015cea ; Liu:2019tjn ; He:2019ify . Such picture is enhanced by the recent observed strange hidden-charm pentaquarks Peng:2020hql ; Wang:2020eep ; Chen:2016ryt ; Zhu:2021lhd . However, though the well-known deuteron and the dibaryon with nucleon, $\Delta$ , and $\Lambda$ baryon were predicted and studied in both theory and experiment very far before the XYZ particle and pentaquarks, few predicted molecular states of two baryons are observed in experiment Clement:2016vnl ; PDG . Some theoretical studies have been performed to discuss the possibility of existence of molecular states composed of two baryons beyond nucleon, $\Delta$ , and $\Lambda$ baryon vanBeveren:2008rt ; Zhu:2019ibc ; Lee:2011rka ; Dong:2021juy ; Song:2022yfr ; Liu:2011xc .

Most of the molecular state candidates observed in the past two decades are in the hidden-charm sector. Hence, it is natural to expect the molecular state composed of a charmed baryon and an anticharmed baryon. In recent years, the structures near the $\Lambda_{c}\bar{\Lambda}_{c}$ threshold has attracted much attentions. A charmoniumlike $Y(4630)$ with quantum numbers $J^{PC}=1^{--}$ was observed at Belle Belle:2008xmh . After the experimental discovery of $Y(4630)$ , many theoretical works have performed to understand its origin, such as conventional charmonium state Badalian:2008dv ; Segovia:2008ta and compact multiquark state Maiani:2014aja ; Cotugno:2009ys ; Brodsky:2014xia ; Wang:2021qmn . Due to the closeness of the mass of $Y(4630)$ and the $\Lambda_{c}\bar{\Lambda}_{c}$ threshold, the relation between $Y(4630)$ and the threshold effect was studies in Ref. vanBeveren:2008rt . In Ref. Simonov:2011jc , the mechanism of $Y(4630)$ enhancement in $\Lambda_{c}\bar{\Lambda}_{c}$ electroproduction was also studied. The $\Lambda_{c}\bar{\Lambda}_{c}$ molecular state also attracts much attention Chen:2011cta ; Wang:2021qmn ; Lee:2011rka ; Simonov:2011jc . Theoretical calculations suggest strong attraction between a $\Lambda_{c}$ baryon and an $\bar{\Lambda}_{c}$ baryon by $\sigma$ and $\omega$ exchanges, which favors the existence of a $\Lambda_{c}\bar{\Lambda}_{c}$ molecular state Lee:2011rka ; Simonov:2011jc . In our previous work, the $\Lambda_{c}\bar{\Lambda}_{c}$ molecular state can be produced from the interaction, but it is difficult to be used to interpret the $Y(4630)$ Song:2022yfr . The studies of more molecular states with a charmed baryon and an anticharmed baryon are also helpful to understand this exotic structure. In the current work, the interactions $\Lambda_{c}\bar{\Lambda}_{c}$ , $\Sigma_{c}^{(*)}\bar{\Sigma}_{c}^{(*)}$ , and $\Lambda_{c}\bar{\Sigma}_{c}^{(*)}$ will be studied in a quasipotential Bethe-Salpeter equation (qBSE) approach.

In our model, the double-charm molecular states can be obtained by replacing the anticharmed hadron by a charmed hadron Ding:2020dio ; Ding:2021igr ; Kong:2021ohg . The recent experimental observation exhibits the ability to observe double-charm hadrons in experiment. The LHC Collaboration reported a state $\Xi_{cc}^{++}$ LHCb:2017iph , which indicts the possibility of experimental observation of double-heavy molecular state. Very recently, the LHCb Collaboration observed an open charm tetraquark state $T_{cc}^{+}$ below the $D^{0}D^{*+}$ mass threshold LHCb:2021vvq , which has already been predicted by a lot of theoretical works in the diquark and antidiquark picture Ader:1981db ; Zouzou:1986qh ; Lipkin:1986dw ; Heller:1986bt ; Carlson:1987hh ; Silvestre-Brac:1993zem ; Semay:1994ht ; Gelman:2002wf , also in the molecular picture Manohar:1992nd ; Pepin:1996id ; Molina:2010tx ; Li:2012ss ; Wang:2017uld ; Maiani:2019lpu ; Liu:2019stu . The doubly charm dibaryon attracts some attentions from the hadron physics community Li:2012bt ; Garcilazo:2020acl ; Carames:2015sya ; Chen:2021cfl ; Ling:2021asz ; Dong:2021bvy . Hence, in the current work, the double-charm systems $\Lambda_{c}\Lambda_{c}$ , $\Sigma_{c}^{(*)}\Sigma_{c}^{(*)}$ , and $\Lambda_{c}\Sigma_{c}^{(*)}$ will be also calculated.

This article is organized as follows. After the Introduction, Section II shows the details of dynamics of the charmed baryons interactions, reduction of potential kernel and a brief introduction of the qBSE. In Section III, the numerical results are given. Finally, summary and discussion are given in Section IV.

II Theoretical frame

To study the interactions of charmed baryons, we need to construct the potential kernel, which is performed by introducing the exchanges of peseudoscalar $\mathbb{P}$ , vector $\mathbb{V}$ and scalar $\sigma$ mesons. The Lagrangians depicting the couplings of light mesons and baryons are required and will be presented below.

II.1 Relevant Lagrangians

The Lagrangians for the couplings between charmed baryon and light mesons are constructed under the heavy quark limit and chiral symmetry as Liu:2011xc ; Isola:2003fh ; Falk:1992cx ,

$\displaystyle{\cal L}_{S}$	$\displaystyle=-\frac{3}{2}g_{1}(v_{\kappa})\epsilon^{\mu\nu\lambda\kappa}{\rm tr}[\bar{S}_{\mu}{\cal A}_{\nu}S_{\lambda}]+i\beta_{S}{\rm tr}[\bar{S}_{\mu}v_{\alpha}(\mathcal{V}^{\alpha}-\rho^{\alpha})S^{\mu}]$
	$\displaystyle+\lambda_{S}{\rm tr}[\bar{S}_{\mu}F^{\mu\nu}S_{\nu}]+\ell_{S}{\rm tr}[\bar{S}_{\mu}\sigma S^{\mu}],$
$\displaystyle{\cal L}_{B_{\bar{3}}}$	$\displaystyle=i\beta_{B}{\rm tr}[\bar{B}_{\bar{3}}v_{\mu}(\mathcal{V}^{\mu}-\rho^{\mu})B_{\bar{3}}]+\ell_{B}{\rm tr}[\bar{B}_{\bar{3}}{\sigma}B_{\bar{3}}],$
$\displaystyle{\cal L}_{int}$	$\displaystyle=ig_{4}{\rm tr}[\bar{S}^{\mu}{\cal A}_{\mu}B_{\bar{3}}]+i\lambda_{I}\epsilon^{\mu\nu\lambda\kappa}v_{\mu}{\rm tr}[\bar{S}_{\nu}F_{\lambda\kappa}B_{\bar{3}}]+H.c.,$	(1)

where $S^{\mu}_{ab}$ is composed of the Dirac spinor operators,

	$\displaystyle S^{ab}_{\mu}$	$\displaystyle=-\sqrt{\frac{1}{3}}(\gamma_{\mu}+v_{\mu})\gamma^{5}B^{ab}+B^{*ab}_{\mu}\equiv{B}^{ab}_{0\mu}+B^{ab}_{1\mu},$
	$\displaystyle\bar{S}^{ab}_{\mu}$	$\displaystyle=\sqrt{\frac{1}{3}}\bar{B}^{ab}\gamma^{5}(\gamma_{\mu}+v_{\mu})+\bar{B}^{*ab}_{\mu}\equiv{\bar{B}}^{ab}_{0\mu}+\bar{B}^{ab}_{1\mu},$		(2)

and the bottomed baryon matrices are defined as

	$\displaystyle B_{\bar{3}}$	$\displaystyle=\left(\begin{array}[]{ccc}0&\Lambda^{+}_{c}&\Xi_{c}^{+}\\ -\Lambda_{c}^{+}&0&\Xi_{c}^{0}\\ -\Xi^{+}_{c}&-\Xi_{c}^{0}&0\end{array}\right),\quad B=\left(\begin{array}[]{ccc}\Sigma_{c}^{++}&\frac{1}{\sqrt{2}}\Sigma^{+}_{c}&\frac{1}{\sqrt{2}}\Xi^{\prime+}_{c}\\ \frac{1}{\sqrt{2}}\Sigma^{+}_{c}&\Sigma_{c}^{0}&\frac{1}{\sqrt{2}}\Xi^{\prime 0}_{c}\\ \frac{1}{\sqrt{2}}\Xi^{\prime+}_{c}&\frac{1}{\sqrt{2}}\Xi^{\prime 0}_{c}&\Omega^{0}_{c}\end{array}\right).$		(9)
	$\displaystyle B^{*}$	$\displaystyle=\left(\begin{array}[]{ccc}\Sigma_{c}^{++}&\frac{1}{\sqrt{2}}\Sigma^{+}_{c}&\frac{1}{\sqrt{2}}\Xi^{+}_{c}\\ \frac{1}{\sqrt{2}}\Sigma^{+}_{c}&\Sigma_{c}^{0}&\frac{1}{\sqrt{2}}\Xi^{0}_{c}\\ \frac{1}{\sqrt{2}}\Xi^{+}_{c}&\frac{1}{\sqrt{2}}\Xi^{0}_{c}&\Omega^{*0}_{c}\end{array}\right).$		(13)

The explicit forms of the Lagrangians can be written as,

$\displaystyle{\cal L}_{BB\mathbb{P}}$	$\displaystyle=-i\frac{3g_{1}}{4f_{\pi}\sqrt{m_{\bar{B}}m_{B}}}~{}\epsilon^{\mu\nu\lambda\kappa}\partial^{\nu}\mathbb{P}~{}\sum_{i=0,1}\bar{B}_{i\mu}\overleftrightarrow{\partial}_{\kappa}B_{j\lambda},$
$\displaystyle{\cal L}_{BB\mathbb{V}}$	$\displaystyle=-\frac{\beta_{S}g_{V}}{2\sqrt{2m_{\bar{B}}m_{B}}}\mathbb{V}^{\nu}\sum_{i=0,1}\bar{B}_{i}^{\mu}\overleftrightarrow{\partial}_{\nu}B_{j\mu}$
	$\displaystyle-\frac{\lambda_{S}g_{V}}{\sqrt{2}}(\partial_{\mu}\mathbb{V}_{\nu}-\partial_{\nu}\mathbb{V}_{\mu})\sum_{i=0,1}\bar{B}_{i}^{\mu}B_{j}^{\nu},$
$\displaystyle{\cal L}_{BB\sigma}$	$\displaystyle=\ell_{S}\sigma\sum_{i=0,1}\bar{B}_{i}^{\mu}B_{j\mu},$
$\displaystyle{\cal L}_{B_{\bar{3}}B_{\bar{3}}\mathbb{V}}$	$\displaystyle=-\frac{g_{V}\beta_{B}}{2\sqrt{2m_{\bar{B}_{\bar{3}}}m_{B_{\bar{3}}}}}\mathbb{V}^{\mu}\bar{B}_{\bar{3}}\overleftrightarrow{\partial}_{\mu}B_{\bar{3}},$
$\displaystyle{\cal L}_{B_{\bar{3}}B_{\bar{3}}\sigma}$	$\displaystyle=i\ell_{B}\sigma\bar{B}_{\bar{3}}B_{\bar{3}},$
$\displaystyle{\cal L}_{BB_{\bar{3}}\mathbb{P}}$	$\displaystyle=-i\frac{g_{4}}{f_{\pi}}\sum_{i}\bar{B}_{i}^{\mu}\partial_{\mu}\mathbb{P}B_{\bar{3}}+{\rm H.c.},$
$\displaystyle{\cal L}_{BB_{\bar{3}}\mathbb{V}}$	$\displaystyle=\frac{g_{\mathbb{V}}\lambda_{I}}{\sqrt{2m_{\bar{B}}m_{B_{\bar{3}}}}}\epsilon^{\mu\nu\lambda\kappa}\partial_{\lambda}\mathbb{V}_{\kappa}\sum_{i}\bar{B}_{i\nu}\overleftrightarrow{\partial}_{\mu}B_{\bar{3}}+{\rm H.c.}.$	(14)

The $\mathbb{V}$ and $\mathbb{P}$ are the vector and pseudoscalar matrices as

\displaystyle{\mathbb{P}}=\left(\begin{array}[]{ccc}\frac{\sqrt{3}\pi^{0}+\eta}{\sqrt{6}}&\pi^{+}&K^{+}\\ \pi^{-}&\frac{-\sqrt{3}\pi^{0}+\eta}{\sqrt{6}}&K^{0}\\ K^{-}&\bar{K}^{0}&\frac{-2\eta}{\sqrt{6}}\end{array}\right),\mathbb{V}=\left(\begin{array}[]{ccc}\frac{\rho^{0}+\omega}{\sqrt{2}}&\rho^{+}&K^{*+}\\ \rho^{-}&\frac{-\rho^{0}+\omega}{\sqrt{2}}&K^{*0}\\ K^{*-}&\bar{K}^{*0}&\phi\end{array}\right).

(21)

The masses of particles involved in the calculation are chosen as suggested central values in the Review of Particle Physics (PDG) PDG . The mass of broad $\sigma$ meson is chosen as 500 MeV. The coupling constants involved are listed in Table 1.

Table 1: The coupling constants adopted in the calculation, which are cited from the literature Chen:2019asm ; Liu:2011xc ; Isola:2003fh ; Falk:1992cx ; Zhu:2022fyb ; Zhu:2021lhd . The

\lambda

and

\lambda_{S,I}

are in the units of GeV^-1. Others are in the units of

1

$\beta_{S}$	$\ell_{S}$	$g_{1}$	$\lambda_{S}$	$\beta_{B}$	$\ell_{B}$	$g_{4}$	$\lambda_{I}$
$\beta$	$g$	$g_{V}$	$\lambda$	$g_{s}$
0.9	0.59	5.9	0.56	0.76
-1.74	6.2	-0.94	-3.31	$-\beta_{S}/2$	$-\ell_{S}/2$	$3g_{1}/{(2\sqrt{2})}$	$-\lambda_{S}/\sqrt{8}$

First, we should construct flavor wave functions with definite isospin under $SU(3)$ symmetry. In this paper, we take the following charge conjugation conventions for two-baryon system as Dong:2021juy ,

|B_{1}B_{2}\rangle_{c}=\frac{1}{\sqrt{2}}|B_{1}\bar{B}_{2}-(-1)^{J-J_{1}-J_{2}}cc_{1}c_{2}|B_{2}\bar{B}_{1}\rangle,

(22)

where $J$ and $J_{i}$ are the spins of system $|B_{1}\bar{B}_{2}\rangle$ and $|B_{i}\rangle$ , respectively, and $c_{i}$ is defined by $\mathcal{C}|B_{i}\rangle=c_{i}\bar{B}_{i}\rangle$ . For the isovector state, the $C$ parity cannot be defined, so we will use the $G$ parity instead as $G=(-1)^{I}C$ with $C=c$ .

Following the method in Ref. He:2019rva , we input vertices $\Gamma$ and propagators $P$ into the code directly. The potential can be written as

{\cal V}_{\mathbb{P},\sigma}=I_{\mathbb{P},\sigma}\Gamma_{1}\Gamma_{2}P_{\mathbb{P},\sigma}f(q^{2}),\ \ {\cal V}_{\mathbb{V}}=I_{\mathbb{V}}\Gamma_{1\mu}\Gamma_{2\nu}P^{\mu\nu}_{\mathbb{V}}f(q^{2}).

(23)

In this work, both hidden-charm and double-charm systems will be considered in the calculation. The well-known $G$ -parity rule will be adopted to write the interaction of a charmed and an anticharmed baryon from the interaction of two charmed baryons. By inserting the $G^{-1}G$ operator into the potential, the $G$ -parity rule can be obtained easily as Phillips:1967zza ; Klempt:2002ap ; Lee:2011rka ; Zhu:2019ibc ,

\displaystyle V

\displaystyle=

\displaystyle\sum_{i}{\zeta_{i}V_{ihh}}.

(24)

The $G$ parity of the exchanged meson is left as a $\zeta_{i}$ factor for $i$ meson.

The propagators are defined as usual as

P_{\mathbb{P},\sigma}=\frac{i}{q^{2}-m_{\mathbb{P},\sigma}^{2}},\ \ P^{\mu\nu}_{\mathbb{V}}=i\frac{-g^{\mu\nu}+q^{\mu}q^{\nu}/m^{2}_{\mathbb{V}}}{q^{2}-m_{\mathbb{V}}^{2}},

(25)

where the form factor $f(q^{2})$ is adopted to compensate the off-shell effect of exchanged meson as $f(q^{2})=e^{-(m_{e}^{2}-q^{2})^{2}/\Lambda_{e}^{2}}$ with $m_{e}$ and $q$ being the $m_{\mathbb{P},\mathbb{V},\sigma}$ and the momentum of the exchanged meson. The $I_{i}$ is the flavor factor for certain meson exchange $i$ of certain interaction, and the explicit values are listed in Table 2.

Table 2: The flavor factors

I_{i}^{d}

and

(-1)^{(J+1)}I_{i}^{c}

of exchange

i

for direct diagram and cross diagram, respectively. The values in bracket are for the heavy-heavy baryons if the values are different from these of heavy-antiheavy baryons.

$I_{i}^{d}$	$I$	$\pi$	$\eta$	$\rho$	$\omega$	$\sigma$
$\Lambda_{c}\bar{\Lambda}_{c}[\Lambda_{c}\Lambda_{c}]$	$0$				$-2[2]$	$4[4]$
$\Sigma_{c}^{()}\bar{\Sigma}_{c}^{()}[\Sigma_{c}^{()}\Sigma_{c}^{()}]$	$0$	$1[-1]$	$\frac{1}{6}[\frac{1}{6}]$	$-1[-1]$	$-\frac{1}{2}[\frac{1}{2}]$	$1[1]$
	$1$	$\frac{1}{2}[-\frac{1}{2}]$	$\frac{1}{6}[\frac{1}{6}]$	$-\frac{1}{2}[-\frac{1}{2}]$	$-\frac{1}{2}[\frac{1}{2}]$	$1[1]$
	$2$	$-\frac{1}{2}[\frac{1}{2}]$	$\frac{1}{6}[\frac{1}{6}]$	$\frac{1}{2}[\frac{1}{2}]$	$-\frac{1}{2}[\frac{1}{2}]$	$1[1]$
$\Lambda_{c}\bar{\Sigma}_{c}^{()}[\Lambda_{c}\Sigma_{c}^{()}]$	$1$				$-1[1]$	$2[2]$
$(-1)^{(J+1)}I_{i}^{c}$	$I$	$\pi$	$\eta$	$\rho$	$\omega$
$\Lambda_{c}\bar{\Sigma}_{c}[\Lambda_{c}\Sigma_{c}]$	$1$	$c[1]$		$-c[1]$
$\Lambda_{c}\bar{\Sigma}_{c}^{}[\Lambda_{c}\Sigma_{c}^{}]$	$1$	$-c[1]$		$c[1]$
$\Sigma_{c}\bar{\Sigma}_{c}^{}[\Sigma_{c}\Sigma_{c}^{}]$	$0$	$c[-1]$	$\frac{c}{6}[\frac{1}{6}]$	$-c[-1]$	$-\frac{c}{2}[\frac{1}{2}]$
	$1$	$\frac{c}{2}[-\frac{1}{2}]$	$\frac{c}{6}[\frac{1}{6}]$	$-\frac{c}{2}[-\frac{1}{2}]$	$-\frac{c}{2}[\frac{1}{2}]$
	$2$	$-\frac{c}{2}[\frac{1}{2}]$	$\frac{c}{6}[\frac{1}{6}]$	$\frac{c}{2}[\frac{1}{2}]$	$-\frac{c}{2}[\frac{1}{2}]$

With the potential kernel obtained, the qBSE is adopted to solve the scattering amplitude He:2014nya ; He:2015mja ; He:2012zd ; He:2015yva ; He:2017aps ; Zhu:2021lhd ; Kong:2021ohg ; Ding:2020dio . The 4-dimensional Bethe-Saltpeter equation in the Minkowski space can be reduced to a 1-dimensional equation with fixed spin-parity $J^{P}$ as He:2015mja , after partial-wave decomposition and spectator quasipotential approximation.

	$\displaystyle i{\cal M}^{J^{P}}_{\lambda^{\prime}\lambda}({\rm p}^{\prime},{\rm p})$	$\displaystyle=i{\cal V}^{J^{P}}_{\lambda^{\prime},\lambda}({\rm p}^{\prime},{\rm p})+\sum_{\lambda^{\prime\prime}}\int\frac{{\rm p}^{\prime\prime 2}d{\rm p}^{\prime\prime}}{(2\pi)^{3}}$
		$\displaystyle\cdot i{\cal V}^{J^{P}}_{\lambda^{\prime}\lambda^{\prime\prime}}({\rm p}^{\prime},{\rm p}^{\prime\prime})G_{0}({\rm p}^{\prime\prime})i{\cal M}^{J^{P}}_{\lambda^{\prime\prime}\lambda}({\rm p}^{\prime\prime},{\rm p}),\quad\quad$		(26)

where the sum extends only over non-negative helicity $\lambda^{\prime\prime}$ . The $G_{0}({\rm p}^{\prime\prime})$ is reduced from the 4-dimensional propagator $G(p^{\prime\prime})$ under quasipotential approximation with one of two baryons on-shell as

	$\displaystyle G(p^{\prime\prime})$	$\displaystyle=\frac{\delta^{+}(p^{\prime\prime~{}2}_{h}-m_{h}^{2})}{p^{\prime\prime~{}2}_{l}-m_{l}^{2}}$
	$\displaystyle\to G_{0}({\rm p}^{\prime\prime})$	$\displaystyle=\frac{1}{2E_{h}({\rm p^{\prime\prime}})[(W-E_{h}({\rm p}^{\prime\prime}))^{2}-E_{l}^{2}({\rm p}^{\prime\prime})]}.$		(27)

where $p^{\prime\prime}_{l}$ and $m_{l}$ are the momentum and mass of light hadron, respectively. As required by the spectator approximation, the heavier particle is on shell, which satisfies $p^{\prime\prime 0}_{h}=E_{h}({\rm p}^{\prime\prime})=\sqrt{m_{h}^{~{}2}+\rm p^{\prime\prime 2}}$ . The $p^{\prime\prime 0}_{l}$ for the lighter particle is then $W-E_{h}({\rm p}^{\prime\prime})$ . Here and hereafter, a definition ${\rm p}=|{\bm{p}}|$ will be adopted.

The partial wave potential is defined with the potential of interaction obtained in the above in Eq. (23) as

	$\displaystyle{\cal V}_{\lambda^{\prime}\lambda}^{J^{P}}({\rm p}^{\prime},{\rm p})$	$\displaystyle=2\pi\int d\cos\theta~{}[d^{J}_{\lambda\lambda^{\prime}}(\theta){\cal V}_{\lambda^{\prime}\lambda}({\bm{p}}^{\prime},{\bm{p}})$
		$\displaystyle+\eta d^{J}_{-\lambda\lambda^{\prime}}(\theta){\cal V}_{\lambda^{\prime}-\lambda}({\bm{p}}^{\prime},{\bm{p}})],$		(28)

where $\eta=PP_{1}P_{2}(-1)^{J-J_{1}-J_{2}}$ with $P$ and $J$ being parity and spin for system. The initial and final relative momenta are chosen as ${\bm{p}}=(0,0,{\rm p})$ and ${\bm{p}}^{\prime}=({\rm p}^{\prime}\sin\theta,0,{\rm p}^{\prime}\cos\theta)$ . The $d^{J}_{\lambda\lambda^{\prime}}(\theta)$ is the Wigner d-matrix. We also adopt an exponential regularization by introducing a form factor into the propagator as $G_{0}({\rm p}^{\prime\prime})\to G_{0}({\rm p}^{\prime\prime})\left[e^{-(p^{\prime\prime 2}_{l}-m_{l}^{2})^{2}/\Lambda_{r}^{4}}\right]^{2}$ with $\Lambda_{r}$ being a cutoff He:2015mja .

III Numerical Results

With the preparation above, numerical calculation can be performed to study the molecular states from the interactions $\Lambda_{c}\bar{\Lambda}_{c}/\Lambda_{c}\Lambda_{c}$ , $\Sigma_{c}^{(*)}\bar{\Sigma}_{c}^{(*)}/\Sigma_{c}^{(*)}\Sigma_{c}^{(*)}$ , and $\Lambda_{c}\bar{\Sigma}_{c}^{(*)}/\Lambda_{c}\Sigma_{c}^{(*)}$ . After transformation of the one dimensional integral qBSE into a matrix equation, the scattering amplitude can be obtained, and the molecular states can be searched for as the poles of the amplitude. The parameters of the Lagrangians in the current work are chosen as the same as those in our previous study of the hidden-charm pentaquarks He:2019ify ; He:2019rva . The only free parameters are cutoffs $\Lambda_{e}$ and $\Lambda_{r}$ , which are rewritten as a form of $\Lambda_{r}=\Lambda_{e}=m+\alpha~{}0.22$ GeV with $m$ being the mass of the exchanged meson, which is also introduced into the regularization form factor to suppress large momentum, i. e., the short-range contribution of the exchange as warned in Ref Liu:2019zvb . Hence, in the current work, only one parameter $\alpha$ is involved.

III.1 Interactions $\Lambda_{c}\bar{\Lambda}_{c}$ and $\Lambda_{c}\Lambda_{c}$

In the current work, only S-wave states will be considered. For the two interactions considered, the results with spins $S$ =1 and 0 are shown in Fig. 1. The results suggest bound states are produced from all four channels. The states with spins 1 and 0 have almost the same binding energy, which is consistent with the results in Ref. Lee:2011rka . The two bound states from the $\Lambda_{c}\bar{\Lambda}_{c}$ interaction appear even with an $\alpha$ value below 0, which are smaller than two states for the double-charm $\Lambda_{c}\Lambda_{c}$ interaction, which indicts that the $\Lambda_{c}\bar{\Lambda}_{c}$ interaction is more attractive than the $\Lambda_{c}\Lambda_{c}$ interaction due to different contributions from the meson exchanges. Since the $\Lambda$ baryon is isoscalar, the interactions $\Lambda_{c}\bar{\Lambda}_{c}$ and $\Lambda_{c}\Lambda_{c}$ arises from the $\sigma$ and $\omega$ exchanges. In the $\Lambda_{c}\bar{\Lambda}_{c}$ interaction, both $\sigma$ and $\omega$ exchanges provide attraction. However, in the $\Lambda_{c}\Lambda_{c}$ interaction, the $\omega$ exchange is repulsive, which reduces the attraction.

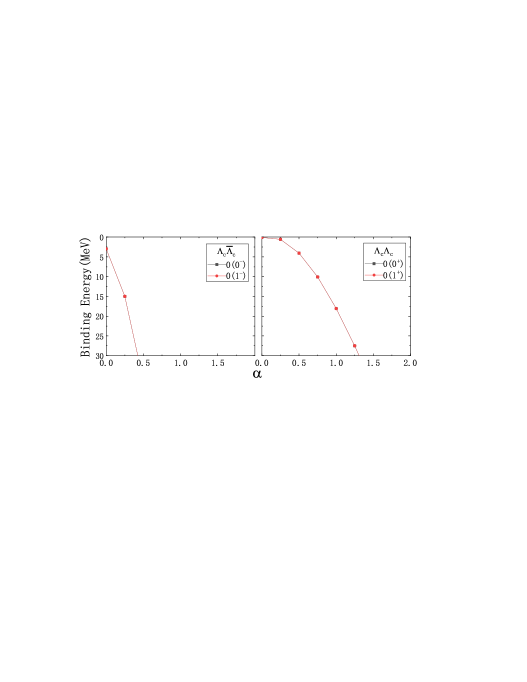
Refer to caption — Figure 1: The binding energies of the bound states from $\Lambda_{c}\bar{\Lambda}_{c}$ (left) and $\Lambda_{c}\Lambda_{c}$ (right) interactions with the variation of parameter $\alpha$ .

III.2 Interactions $\Sigma_{c}^{()}\bar{\Sigma}_{c}^{()}$ and $\Sigma_{c}^{()}\Sigma_{c}^{()}$

Different from the isoscalar $\Lambda_{c}$ baryon, the $\Sigma_{c}^{(*)}$ baryon is an isovector particle. Hence, more channels will be involved in certain interaction. In Fig. 2, the bound states from the $\Sigma_{c}\bar{\Sigma}_{c}$ interaction and their double-charm partners are presented. Here, the siospin $I$ can be 0, $1$ , or $2$ , and the spin $S$ =0 or $1$ , which leads to six channels for each interaction.

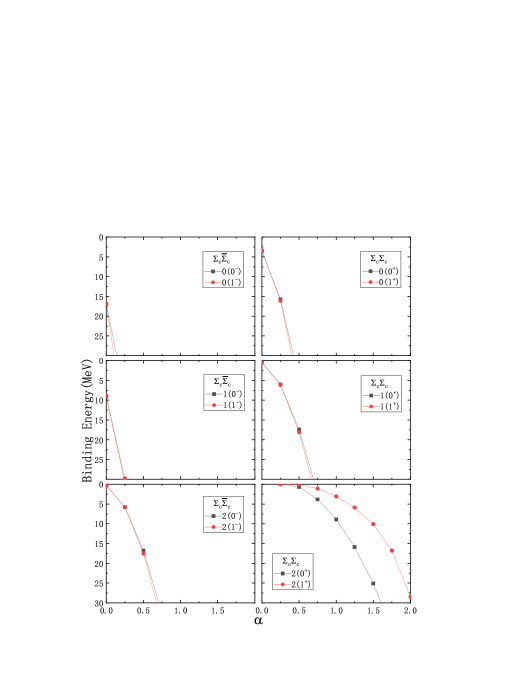
As shown in Fig. 2, bound states are produced in all channels, but with different behaviors with the variation of parameter $\alpha$ . For the isoscalar hidden-charm $\Sigma_{c}\bar{\Sigma}_{c}$ system, the bound states are produced at an $\alpha$ value below 0, and the binding energies increase rapidly with the increase of $\alpha$ value. As shown in Table 2, the strong attraction is from the $\rho$ exchange with a large flavor factor $-1$ . The corresponding double-charm partners appear at larger $\alpha$ value, which means that it is less attractive than the hidden-charm case due to the different signs for $\pi$ and $\omega$ exchanges. The binding energies for states with different spins are almost the same. For the states with $I=1$ , the binding energies at an $\alpha$ value of 0 are smaller than those with $I=0$ . As shown in Table 2, the flavor factors for $\rho$ and $\pi$ exchanges are half of those for $I=0$ , which leads to less attraction. For the states with $I=2$ , the attraction becomes weaker due to reversing the signs of the $\rho$ and $\pi$ exchanges. The hidden-charm states are produced at a small $\alpha$ value, and binding energies increase to a value larger than 30 GeV very quickly at an $\alpha$ value of about 0.7. However, the binding energies of their double-charm partners appear at $\alpha$ value of about 0.2, and increase relatively slowly.

The binding energies of the states produced from the $\Sigma_{c}^{*}\bar{\Sigma}_{c}^{*}$ interaction are shown in Fig. 3.

Except that there are four spins $S$ =0, 1, 2, and 3, due to the flavor factors are the same as those for the $\Sigma_{c}\bar{\Sigma}_{c}$ system, the results are similar to the results in Fig. 2. For the hidden-charm system with $I=0$ , there are three states with spins $J=1$ , 2, and 3 producing at an $\alpha$ values of about 0. As in the case of $\Sigma_{c}\bar{\Sigma}_{c}$ , the attractions for the corresponding double-charm systems are weaker than the hidden-charm systems. The hidden-charm bound states with $I=1$ appear at an $\alpha$ value of about 0, and the binding energies increase to 30 MeV at $\alpha$ value about 0.7. The hidden-charm states with $I=2$ appear at an $\alpha$ value little larger than 0 while their double-charm partners appear at $\alpha$ value of 0.5 or larger. Generally speaking, the attractions of $\Sigma_{c}^{*}\bar{\Sigma}_{c}^{*}/\Sigma_{c}^{*}{\Sigma}_{c}^{*}$ interaction are a little weaker than the case of $\Sigma_{c}\bar{\Sigma}_{c}/\Sigma_{c}\Sigma_{c}$ interaction.

The results for the $\Sigma_{c}\bar{\Sigma}_{c}^{*}$ and $\Sigma_{c}\Sigma_{c}^{*}$ interactions are presented in Fig 4. For the hidden-charm states, there are two $G$ parities, $G=\pm 1$ , which do not involve in the double-charm sector. For the hidden-charm systems with $I$ =0, the bound states appear at $\alpha$ value a little below 0, and increase with the increase of the parameter $\alpha$ to 30 MeV at $\alpha$ value of about 1. For their double-charm partners, the bound states appear at an $\alpha$ value about 0, and the binding energies increase more slowly than the hidden-charm states. In the case with $I$ =1, the states appear at an $\alpha$ value of about 0, and increase to 30 MeV at an $\alpha$ value about 1.2. The hidden-charm states with $I=2$ appear at $\alpha$ value of about 0, which is smaller than these for the double-charm states, about 0.5.

III.3 Interactions $\Lambda_{c}\bar{\Sigma}_{c}^{()}$ and $\Lambda_{c}\Sigma_{c}^{()}$

Now, we turn to the systems with a $\Lambda_{c}/\bar{\Lambda}_{c}$ and a $\Sigma^{(*)}$ baryon. The results of the $\Lambda_{c}\bar{\Sigma}_{c}^{(*)}$ states and their double-charm partners are shown in Fig. 5. Here, the S-wave states with spin $J=0$ and 1 are considered. Since the $\Lambda_{c}/\bar{\Lambda}_{c}$ baryon is isoscalar, the isospin only can be 1, and the $G$ parity will involve in the hidden charm sector. Due to the same flavor factors, the results of systems with $\Sigma_{c}$ and $\Sigma_{c}^{*}$ are similar. The hidden-charm states are first produced at an $\alpha$ value a little below 0, and the binding energies increase to 30 GeV at an $\alpha$ value about 1. The double-charm states appear at an $\alpha$ value a litter larger and the binding energies increase slowly, reach 30 MeV at an $\alpha$ value of about 2.

IV Summary

In the current work, the study of the molecular states from interactions of charmed baryons is performed. The hidden-charm systems $\Lambda_{c}\bar{\Lambda}_{c}$ , $\Sigma_{c}^{(*)}\bar{\Sigma}_{c}^{(*)}$ , and $\Lambda_{c}\Sigma_{c}^{(*)}$ , as well as their double-charm partners, are considered in the calculation. With the help of the Lagrangians in heavy quark limit and with chiral symmetry. The potential kernels are constructed in a one-boson-exchange model, and inserted into the qBSE to search the bound states.

The calculation suggests that the attractions widely exist in the systems of two charmed baryons. For the $\Lambda_{c}\bar{\Lambda}_{c}$ interaction, the bound states are produced with spin parities $J^{P}$ = $0^{-}$ and $1^{-}$ , and their double-charm partner can be produced with a binding energies smaller than 30 MeV in a larger range of the parameter $\alpha$ . Due to the same favor factors for the $\Sigma_{c}\bar{\Sigma}_{c}$ , $\Sigma_{c}^{*}\bar{\Sigma}_{c}^{*}$ , and $\Sigma_{c}\bar{\Sigma}_{c}^{*}$ interactions, the binding energies for these three interactions behave in a similar manner. The most strong attraction can be found in the case with $I=0$ for both hidden-charm and doubly-charm cases due to the large $\rho$ exchange as suggested by its flavor factor, which is consistent with the results in Ref. Dong:2021juy ; Dong:2021bvy . For the interactions $\Lambda_{c}\bar{\Sigma}_{c}^{(*)}$ and $\Lambda_{c}\Sigma_{c}^{(*)}$ , all bound states produced are relatively stable, has a binding energy below 30 MeV in a large range of $\alpha$ value. Generally speak, the interactions of two charmed baryons are attractive, and many bound states are produced. However, only a few candidates, such as $Y(4630)$ , were reported in experiment. More experiment studies about these states are suggested though the processes including the nucleon- nucleon collision at LHC and nucleon-antinucleon collision at $\rm\bar{P}ANDA$ .

Acknowledgement We would like to thank Prof. Feng-Kun Guo for helpful discussions. This project is supported by the National Natural Science Foundation of China (Grants No. 11675228).

References

(1) R.L. Workman et al. [Particle Data Group], “Review of Particle Physics,” Prog. Theor. Exp. Phys. 2022, 083C01 (2022)
(2) S. Godfrey and N. Isgur, “Mesons in a Relativized Quark Model with Chromodynamics,” Phys. Rev. D 32, 189-231 (1985)
(3) S. Capstick and N. Isgur, “Baryons in a relativized quark model with chromodynamics,” Phys. Rev. D 34, no.9, 2809-2835 (1986)
(4) H. X. Chen, W. Chen, X. Liu and S. L. Zhu, “The hidden-charm pentaquark and tetraquark states,” Phys. Rept. 639, 1-121 (2016)
(5) F. K. Guo, C. Hanhart, U. G. Meißner, Q. Wang, Q. Zhao and B. S. Zou, “Hadronic molecules,” Rev. Mod. Phys. 90, no.1, 015004 (2018) [erratum: Rev. Mod. Phys. 94, no.2, 029901 (2022)]
(6) N. A. Tornqvist, “From the deuteron to deusons, an analysis of deuteron - like meson meson bound states,” Z. Phys. C 61, 525-537 (1994)
(7) J. He, “Study of the $B\bar{B}^{*}/D\bar{D}^{*}$ bound states in a Bethe-Salpeter approach,” Phys. Rev. D 90, no. 7, 076008 (2014)
(8) Z. F. Sun, J. He, X. Liu, Z. G. Luo and S. L. Zhu, “ $Z_{b}(10610)^{\pm}$ and $Z_{b}(10650)^{\pm}$ as the $B^{*}\bar{B}$ and $B^{*}\bar{B}^{*}$ molecular states,” Phys. Rev. D 84, 054002 (2011)
(9) J. J. Wu, R. Molina, E. Oset and B. S. Zou, “Prediction of narrow $N^{*}$ and $\Lambda^{*}$ resonances with hidden charm above 4 GeV,” Phys. Rev. Lett. 105, 232001 (2010)
(10) Z. C. Yang, Z. F. Sun, J. He, X. Liu and S. L. Zhu, “The possible hidden-charm molecular baryons composed of anti-charmed meson and charmed baryon,” Chin. Phys. C 36, 6-13 (2012)
(11) C. W. Xiao, J. Nieves and E. Oset, “Combining heavy quark spin and local hidden gauge symmetries in the dynamical generation of hidden charm baryons,” Phys. Rev. D 88, 056012 (2013)
(12) R. Chen, X. Liu, X. Q. Li and S. L. Zhu, “Identifying exotic hidden-charm pentaquarks,” Phys. Rev. Lett. 115, no. 13, 132002 (2015)
(13) J. He, “ $\bar{D}\Sigma^{*}_{c}$ and $\bar{D}^{*}\Sigma_{c}$ interactions and the LHCb hidden-charmed pentaquarks,” Phys. Lett. B 753, 547 (2016)
(14) M. Z. Liu, Y. W. Pan, F. Z. Peng, M. Sánchez Sánchez, L. S. Geng, A. Hosaka and M. Pavon Valderrama, “Emergence of a complete heavy-quark spin symmetry multiplet: seven molecular pentaquarks in light of the latest LHCb analysis,” Phys. Rev. Lett. 122, no.24, 242001 (2019)
(15) J. He, “Study of $P_{c}(4457)$ , $P_{c}(4440)$ , and $P_{c}(4312)$ in a quasipotential Bethe-Salpeter equation approach,” Eur. Phys. J. C 79, no.5, 393 (2019)
(16) F. Z. Peng, M. J. Yan, M. Sánchez Sánchez and M. P. Valderrama, “The $P_{cs}(4459)$ pentaquark from a combined effective field theory and phenomenological perspective,” Eur. Phys. J. C 81, no.7, 666 (2021)
(17) Z. G. Wang, “Analysis of the $P_{cs}(4459)$ as the hidden-charm pentaquark state with QCD sum rules,” Int. J. Mod. Phys. A 36, no.10, 2150071 (2021)
(18) R. Chen, J. He and X. Liu, “Possible strange hidden-charm pentaquarks from $\Sigma_{c}^{(*)}\bar{D}_{s}^{*}$ and $\Xi^{(^{\prime},*)}_{c}\bar{D}^{*}$ interactions,” Chin. Phys. C 41, no.10, 103105 (2017)
(19) J. T. Zhu, L. Q. Song and J. He, “ $P_{cs}(4459)$ and other possible molecular states from $\Xi_{c}^{(*)}\bar{D}^{(*)}$ and $\Xi^{\prime}_{c}\bar{D}^{(*)}$ interactions,” Phys. Rev. D 103, no.7, 074007 (2021)
(20) H. Clement, “On the History of Dibaryons and their Final Observation,” Prog. Part. Nucl. Phys. 93, 195 (2017)
(21) N. Lee, Z. G. Luo, X. L. Chen and S. L. Zhu, “Possible Deuteron-like Molecular States Composed of Heavy Baryons,” Phys. Rev. D 84 (2011), 014031
(22) J. T. Zhu, Y. Liu, D. Y. Chen, L. Jiang and J. He, “ $X$ (2239) and $\eta(2225)$ as hidden-strange molecular states from $\Lambda\bar{\Lambda}$ interaction,” Chin. Phys. C 44 (2020) no.12, 123103
(23) X. K. Dong, F. K. Guo and B. S. Zou, “A survey of heavy-antiheavy hadronic molecules,” Progr. Phys. 41 (2021), 65-93
(24) E. van Beveren, X. Liu, R. Coimbra and G. Rupp, “Possible psi(5S), psi(4D), psi(6S) and psi(5D) signals in Lambda(c) anti-Lambda(c),” EPL 85 (2009) no.6, 61002
(25) L. Q. Song, D. Song, J. T. Zhu and J. He, “Possible $\Lambda_{c}\bar{\Lambda}_{c}$ molecular states and their productions in nulceon-antinulceon collision,” [arXiv:2207.13957 [hep-ph]].
(26) Y. R. Liu and M. Oka, “ $\Lambda_{c}N$ bound states revisited,” Phys. Rev. D 85, 014015 (2012)
(27) G. Pakhlova et al. [Belle], “Observation of a near-threshold enhancement in the $e^{+}e^{-}\to\Lambda^{+}_{c}\Lambda^{-}_{c}$ cross section using initial-state radiation,” Phys. Rev. Lett. 101, 172001 (2008)
(28) A. M. Badalian, B. L. G. Bakker and I. V. Danilkin, “The S - D mixing and di-electron widths of higher charmonium 1– states,” Phys. Atom. Nucl. 72 (2009), 638-646
(29) J. Segovia, D. R. Entem and F. Fernandez, “Charm spectroscopy beyond the constituent quark model,” [arXiv:0810.2875 [hep-ph]].
(30) L. Maiani, F. Piccinini, A. D. Polosa and V. Riquer, “The Z(4430) and a New Paradigm for Spin Interactions in Tetraquarks,” Phys. Rev. D 89 (2014), 114010
(31) S. J. Brodsky, D. S. Hwang and R. F. Lebed, “Dynamical Picture for the Formation and Decay of the Exotic XYZ Mesons,” Phys. Rev. Lett. 113 (2014) no.11, 112001
(32) G. Cotugno, R. Faccini, A. D. Polosa and C. Sabelli, “Charmed Baryonium,” Phys. Rev. Lett. 104 (2010), 132005
(33) X. W. Wang, Z. G. Wang and G. l. Yu, “Study of $\Lambda_{c}\Lambda_{c}$ dibaryon and $\Lambda_{c}{\bar{\Lambda}}_{c}$ baryonium states via QCD sum rules,” Eur. Phys. J. A 57, no.9, 275 (2021)
(34) Y. D. Chen and C. F. Qiao, “Baryonium Study in Heavy Baryon Chiral Perturbation Theory,” Phys. Rev. D 85 (2012), 034034
(35) Y. A. Simonov, “Theory of hadron decay into baryon-antibaryon final state,” Phys. Rev. D 85 (2012), 105025
(36) Z. M. Ding, H. Y. Jiang and J. He, “Molecular states from $D^{(*)}\bar{D}^{(*)}/B^{(*)}\bar{B}^{(*)}$ and $D^{(*)}D^{(*)}/\bar{B}^{(*)}\bar{B}^{(*)}$ interactions,” Eur. Phys. J. C 80 (2020) no.12, 1179
(37) Z. M. Ding, H. Y. Jiang, D. Song and J. He, “Hidden and doubly heavy molecular states from interactions $D^{(*)}_{(s)}{{\bar{D}}}^{(*)}_{s}$ / $B^{(*)}_{(s)}{{\bar{B}}}^{(*)}_{s}$ and ${D}^{(*)}_{(s)}D_{s}^{(*)}$ / ${B}^{(*)}_{(s)}B_{s}^{(*)}$ ,” Eur. Phys. J. C 81, no.8, 732 (2021)
(38) S. Y. Kong, J. T. Zhu, D. Song and J. He, “Heavy-strange meson molecules and possible candidates Ds0*(2317), Ds1(2460), and X0(2900),” Phys. Rev. D 104 (2021) no.9, 094012
(39) R. Aaij et al. [LHCb], “Observation of the doubly charmed baryon $\Xi_{cc}^{++}$ ,” Phys. Rev. Lett. 119 (2017) no.11, 112001
(40) R. Aaij et al. [LHCb], “Observation of an exotic narrow doubly charmed tetraquark,” [arXiv:2109.01038 [hep-ex]].
(41) J. P. Ader, J. M. Richard and P. Taxil, “Do Narrow Heavy Multi-quark States exist?,” Phys. Rev. D 25 (1982), 2370
(42) S. Zouzou, B. Silvestre-Brac, C. Gignoux and J. M. Richard, “Four Quark Bound States,” Z. Phys. C 30 (1986), 457
(43) H. J. Lipkin, “A Model Independent Appraoch to Multi-quark Bound States,” Phys. Lett. B 172 (1986), 242-247
(44) L. Heller and J. A. Tjon, “On the Existence of Stable Dimesons,” Phys. Rev. D 35 (1987), 969
(45) J. Carlson, L. Heller and J. A. Tjon, “Stability of Dimesons,” Phys. Rev. D 37 (1988), 744
(46) B. Silvestre-Brac and C. Semay, “Systematics of L = 0 q-2 anti-q-2 systems,” Z. Phys. C 57 (1993), 273-282
(47) C. Semay and B. Silvestre-Brac, “Diquonia and potential models,” Z. Phys. C 61 (1994), 271-275
(48) B. A. Gelman and S. Nussinov, “Does a narrow tetraquark cc anti-u anti-d state exist?,” Phys. Lett. B 551 (2003), 296-304
(49) A. V. Manohar and M. B. Wise, “Exotic Q Q anti-q anti-q states in QCD,” Nucl. Phys. B 399 (1993), 17-33
(50) S. Pepin, F. Stancu, M. Genovese and J. M. Richard, “Tetraquarks with color blind forces in chiral quark models,” Phys. Lett. B 393 (1997), 119-123
(51) R. Molina, T. Branz and E. Oset, “A new interpretation for the $D^{*}_{s2}(2573)$ and the prediction of novel exotic charmed mesons,” Phys. Rev. D 82 (2010), 014010
(52) N. Li, Z. F. Sun, X. Liu and S. L. Zhu, “Coupled-channel analysis of the possible $D^{(*)}D^{(*)},\overline{B}^{(*)}\overline{B}^{(*)}$ and $D^{(*)}\overline{B}^{(*)}$ molecular states,” Phys. Rev. D 88 (2013) no.11, 114008
(53) Z. G. Wang, “Analysis of the axialvector doubly heavy tetraquark states with QCD sum rules,” Acta Phys. Polon. B 49 (2018), 1781
(54) L. Maiani, A. D. Polosa and V. Riquer, “Hydrogen bond of QCD in doubly heavy baryons and tetraquarks,” Phys. Rev. D 100 (2019) no.7, 074002
(55) M. Z. Liu, T. W. Wu, M. Pavon Valderrama, J. J. Xie and L. S. Geng, “Heavy-quark spin and flavor symmetry partners of the X(3872) revisited: What can we learn from the one boson exchange model?,” Phys. Rev. D 99 (2019) no.9, 094018
(56) N. Li and S. L. Zhu, “Hadronic Molecular States Composed of Heavy Flavor Baryons,” Phys. Rev. D 86, 014020 (2012)
(57) H. Garcilazo and A. Valcarce, “Doubly charmed multibaryon systems,” Eur. Phys. J. C 80, no.8, 720 (2020)
(58) T. F. Carames and A. Valcarce, “Heavy flavor dibaryons,” Phys. Rev. D 92, no.3, 034015 (2015)
(59) K. Chen, R. Chen, L. Meng, B. Wang and S. L. Zhu, “Systematics of the heavy flavor hadronic molecules,” Eur. Phys. J. C 82, no.7, 581 (2022)
(60) X. Z. Ling, M. Z. Liu and L. S. Geng, “Masses and strong decays of open charm hexaquark states $\Sigma_{c}^{(*)}{\Sigma}_{c}^{(*)}$ ,” Eur. Phys. J. C 81 (2021) no.12, 1090
(61) X. K. Dong, F. K. Guo and B. S. Zou, “A survey of heavy–heavy hadronic molecules,” Commun. Theor. Phys. 73, no.12, 125201 (2021)
(62) C. Isola, M. Ladisa, G. Nardulli and P. Santorelli, “Charming penguins in $B\to K^{*}\pi,K(\rho,\omega,\phi)$ decays,” Phys. Rev. D 68, 114001 (2003)
(63) A. F. Falk and M. E. Luke, “Strong decays of excited heavy mesons in chiral perturbation theory,” Phys. Lett. B 292, 119 (1992)
(64) R. Chen, Z. F. Sun, X. Liu and S. L. Zhu, “Strong LHCb evidence supporting the existence of the hidden-charm molecular pentaquarks,” Phys. Rev. D 100, no.1, 011502 (2019)
(65) J. T. Zhu, S. Y. Kong, L. Q. Song and J. He, Phys. Rev. D 105 (2022) no.9, 094036 doi:10.1103/PhysRevD.105.094036 [arXiv:2205.07586 [hep-ph]].
(66) J. He and D. Y. Chen, “Molecular states from $\Sigma^{(*)}_{c}\bar{D}^{(*)}-\Lambda_{c}\bar{D}^{(*)}$ interaction,” Eur. Phys. J. C 79 no.11, 887 (2019)
(67) R. J. N. Phillips, “Antinuclear Forces,” Rev. Mod. Phys. 39, 681 (1967).
(68) E. Klempt, F. Bradamante, A. Martin and J. M. Richard, “Antinucleon nucleon interaction at low energy: Scattering and protonium,” Phys. Rept. 368, 119 (2002).
(69) J. He, “Internal structures of the nucleon resonances N(1875) and N(2120),” Phys. Rev. C 91, no.1, 018201 (2015)
(70) J. He, “Nucleon resonances $N(1875)$ and $N(2100)$ as strange partners of LHCb pentaquarks,” Phys. Rev. D 95, no.7, 074031 (2017)
(71) J. He, “The $Z_{c}(3900)$ as a resonance from the $D\bar{D}^{*}$ interaction,” Phys. Rev. D 92, no.3, 034004 (2015)
(72) J. He, D. Y. Chen and X. Liu, “New Structure Around 3250 MeV in the Baryonic B Decay and the $D^{*}_{0}(2400)N$ Molecular Hadron,” Eur. Phys. J. C 72, 2121 (2012)
(73) M. Z. Liu, T. W. Wu, M. Sánchez Sánchez, M. P. Valderrama, L. S. Geng and J. J. Xie, “Spin-parities of the $P_{c}(4440)$ and $P_{c}(4457)$ in the one-boson-exchange model,” Phys. Rev. D 103, no.5, 054004 (2021)