Position Heaps for Cartesian-tree Matching
on Strings and Tries

If the Cartesian trees $\mathsf{CT}(X)$ and $\mathsf{CT}(Y)$ of two strings $X$ and $Y$ are equal, then we say that $X$ and $Y$ Cartesian-tree match (ct-match). The Cartesian-tree pattern matching problem (ct-matching problem)  [18] is, given a text string $S$ and a pattern $P$, to find all substrings $S^{\prime}$ of $S$ that ct-match with $P$.

String equivalence with ct-matching belongs to the class of substring-consistent equivalence relation (SCER) [17], namely, the following holds: If two strings $X$ and $Y$ ct-match, then $X[i..j]$ and $Y[i..j]$ also ct-match for any $1\leq i\leq j\leq|X|$. Among other types of SCERs ([3, 4, 5, 14, 15]), ct-matching is the most related to order-peserving matching (op-matching) [16, 7, 9]. Two strings $X$ and $Y$ are said to op-match if the relative order of the characters in $X$ and the relative order of the characters in $Y$ are the same. It is known that with ct-matching one can detect some interesting occurrences of a pattern that cannot be captured with op-matching. More precisely, if two strings $X$ and $Y$ op-match, then $X$ and $Y$ also ct-match. However, the reverse is not true. With this property in hand, ct-matching is motivated for analysis of time series such as stock charts [18, 11].

This paper deals with the indexing version of the ct-matching problem. Park et al. [18] proposed the Cartesian suffix tree (CST) for a text string $S$ that can be built in $O(n\log n)$ worst-case time or $O(n)$ expected time, where $n$ is the length of the text string $S$. The $\log n$ factor in the worst-case complexity is due to the fact that the parent-encoding, a key concept for ct-matching introduced in [18], is a sequence of integers in range $[0..n-1]$. While it is not explicitly stated in Park et al.’s paper [18], our simple analysis (c.f. Lemma 9 in Section 5) reveals that the CST supports pattern matching queries in $O(m\log m+\mathit{occ})$ time, where $m$ is the pattern length and $\mathit{occ}$ is the number of pattern occurrences.

In this paper, we present a new indexing structure for this problem, called the Cartesian-tree Position Heap (CPH). We show that the CPH of $S$, which occupies $O(n)$ space, can be built in $O(n\log\sigma)$ time with $O(n)$ working space and supports pattern matching queries in $O(m(\sigma+\log(\min\{h,m\}))+\mathit{occ})$ time, where $h$ is the height of the CPH. Compared to the afore-mentioned CST, our CPH is the first index for ct-matching that can be built in worst-case linear time for constant-size alphabets, while pattern matching queries with our CPH can be slower than with the CST when $\sigma$ is large.

We then consider the case where the text is a labeled tree (i.e. a trie). Given a trie $\boldsymbol{T}$ with $N$ nodes, we show that the CPH of $\boldsymbol{T}$, which occupies $O(N\sigma)$ space, can be built in $O(N\sigma)$ time and $O(N\sigma)$ working space. We also show how to support pattern matching queries in $O(m(\sigma^{2}+\log(\min\{h,m\}))+\mathit{occ})$ time in the trie case. To our knowledge, our CPH is the first indexing structure for ct-matching on tries that uses linear space for constant-size alphabets.

Conceptually, our CPH is most related to the parameterized position heap (PPH) for a string [12] and for a trie [13], in that our CPHs and the PPHs are both constructed in an incremental manner where the suffixes of an input string and the suffixes of an input trie are processed in increasing order of their lengths. However, some new techniques are required in the construction of our CPH due to different nature of the parent encoding [18] of strings for ct-matching, from the previous encoding [3] of strings for parameterized matching.

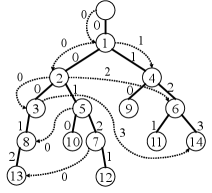
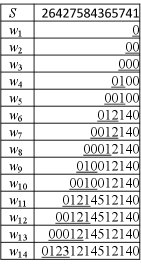
In this section, we introduce our new indexing structure for Problem 1. For a given text string $S$ of length $n$, let $\mathcal{W}_{S}$ denote the sequence of the parent distance encodings of the non-empty suffixes of $S$ which are sorted in increasing order of their lengths. Namely, $\mathcal{W}_{S}=\langle w_{1}$, …, $w_{n}\rangle=\langle\mathsf{PD}(S[n..])$, …, $\mathsf{PD}(S[1..])\rangle$, where $w_{n-i+1}=\mathsf{PD}(S[i..])$. The Cartesian-tree Position Heap (CPH) of string $S$, denoted $\mathsf{CPH}(S)$, is the sequence hash tree of $\mathcal{W}_{S}$, that is, $\mathsf{CPH}(S)=\mathsf{SHT}(\mathcal{W}_{S})$. Note that for each $1\leq i\leq n+1$, $\mathsf{CPH}(S[i..])=\mathsf{SHT}(\mathcal{W}_{S})^{n-i+1}$ holds.

Our algorithm builds $\mathsf{CPH}(S[i..])$ for decreasing $i=n,\ldots,1$, which means that we process the given text string $S$ in a right-to-left online manner, by prepending the new character $S[i]$ to the current suffix $S[i+1..]$.

For a sequence $v$ of integers, let $\mathcal{Z}_{v}$ denote the sorted list of positions $z$ in $v$ such that $v[z]=0$ iff $z\in\mathcal{Z}_{v}$. Clearly $|\mathcal{Z}_{v}|$ is equal to the number of $0$’s in $v$.

A position $i$ in a sequence $u$ of non-negative integers is said to be a front pointer in $u$ if $i-u[i]=1$ and $i\geq 2$. Let $\mathcal{F}_{u}$ denote the sorted list of front pointers in $u$. For example, if $u=01214501$, then $\mathcal{F}_{u}=\{2,3,5,6\}$. The positions of the suffix $S[i+1..]$ which are removed from $\mathcal{Z}_{\mathsf{PD}(S[i+1..])}$ correspond to the front pointers in $\mathcal{F}_{\mathsf{PD}(S[i..])}$ for the next suffix $S[i..]$.

Our construction algorithm updates $\mathsf{CPH}(S[i+1..])$ to $\mathsf{CPH}(S[i..])$ by inserting a new node for the next suffix $S[i..]$, processing the given string $S$ in a right-to-left online manner. Here the task is to efficiently locate the parent of the new node in the current CPH at each iteration.

As in the previous work on right-to-left online construction of indexing structures for other types of pattern matching [20, 10, 12, 13], we use the reversed suffix links in our construction algorithm for $\mathsf{CPH}(S)$. For ease of explanation, we first introduce the notion of the suffix links. Let $u$ be any non-root node of $\mathsf{CPH}(S)$. We identify $u$ with the path label from the root of $\mathsf{CPH}(S)$ to $u$, so that $u$ is a PD encoding of some substring of $S$. We define the suffix link of $u$, denoted $\mathsf{sl}(u)$, such that $\mathsf{sl}(u)=v$ iff $v$ is obtained by (1) removing the first $0$ ($=u[1]$), and (2) substituting $0$ for the character $u[f]$ at every front pointer $f\in\mathcal{F}_{u}\subseteq[2..|u|]$ of $u$. The reversed suffix link of $v$ with non-negative integer label $a$, denoted $\mathsf{rsl}(v,a)$, is defined such that $\mathsf{rsl}(v,a)=u$ iff $\mathsf{sl}(u)=v$ and $a=|\mathcal{F}_{u}|$. See also Figure 2.

The next lemma shows that the number of out-going reversed suffix links of each node $v$ is bounded by the alphabet size.

Our CPH construction algorithm makes use of the following monotonicity of the labels of reversed suffix links:

We are ready to design our right-to-left online construction algorithm for the CPH of a given string $S$. Since $\mathsf{PD}(S[i..])$ is the $(n-i+1)$-th string $w_{n-i+1}$ of the input sequence $\mathcal{W}_{S}$, for ease of explanation, we will use the convention that $u(i)=u_{n-i+1}$ and $p(i)=p_{n-i-1}$, where the new node $u(i)$ for $w_{n-i+1}=\mathsf{PD}(S[i..])$ is inserted as a child of $p(i)$. See Figure 3.

For computing the label $a=|\mathcal{F}_{\mathsf{PD}(S[i..i+|v(i)|])}|$ efficiently, we introduce a new encoding $\mathsf{FP}$ that is defined as follows: For any string $S$ of length $n$, let $\mathsf{FP}(S)[i]=|\mathcal{F}_{\mathsf{PD}(S[i..n])}|$. The $\mathsf{FP}$ encoding preserves the ct-matching equivalence:

For computing the label $a=|\mathcal{F}_{\mathsf{PD}(S[i..i+|v(i)|])}|=\mathsf{FP}(S[i..i+|v(i)|])[1]$ of the reversed suffix link in Algorithm 1, it is sufficient to maintain the induced graph $\mathsf{G}_{[i..j]}$ of DAG $\mathsf{G}$ for a variable-length sliding window $S[i..j]$ with the nodes $\{i,\ldots,j\}$. This can easily be maintained in $O(n)$ total time.

Due to Lemma 7, if we maintain a sorted list of out-going edges for each node during our online construction of $\mathsf{CPH}(S[i..])$, it would require $O(n\log n)$ time even for a constant-size alphabet. Still, after $\mathsf{CPH}(S)$ has been constructed, we can sort all the edges offline, as follows:

See Figure 5 in Appendix for an example of $\mathsf{CPH}(S)$ with maximal reach pointers.

Let $\boldsymbol{T}$ be the input text trie with $N$ nodes. A naïve extension of our CPH to a trie would be to build the CPH for the sequence $\langle\mathsf{PD}(\boldsymbol{T}[N..]),\ldots,\mathsf{PD}(\boldsymbol{T}[1..])\rangle$ of the parent encodings of all the path strings of $\boldsymbol{T}$ towards the root $\mathbf{r}$. However, this does not seem to work because the parent encodings are not consistent for suffixes. For instance, consider two strings $\mathtt{1432}$ and $\mathtt{4432}$. Their longest common suffix $\mathtt{432}$ is represented by a single path in a trie $\boldsymbol{T}$. However, the longest common suffix of $\mathsf{PD}(\mathtt{1432})=0123$ and $\mathsf{PD}(\mathtt{4432})=0100$ is $\varepsilon$. Thus, in the worst case, we would have to consider all the path strings $\boldsymbol{T}[N..]$, …, $\boldsymbol{T}[1..]$ in $\boldsymbol{T}$ separately, but the total length of these path strings in $\boldsymbol{T}$ is $\Omega(N^{2})$.

To overcome this difficulty, we reuse the $\mathsf{FP}$ encoding from Section 3. Since $\mathsf{FP}(S)[i]$ is determined merely by the suffix $S[i..]$, the $\mathsf{FP}$ encoding is suffix-consistent. For an input trie $\boldsymbol{T}$, let the FP-trie $\boldsymbol{T}_{\mathsf{FP}}$ be the reversed trie storing $\mathsf{FP}(\boldsymbol{T}[i..])$ for all the original path strings $\boldsymbol{T}[i..]$ towards the root. Let $N^{\prime}$ be the number of nodes in $\boldsymbol{T}_{\mathsf{FP}}$. Since $\mathsf{FP}$ is suffix-consistent, $N^{\prime}\leq N$ always holds. Namely, $\mathsf{FP}$ is a linear-size representation of the equivalence relation of the nodes of $\boldsymbol{T}$ w.r.t. $\approx$. Each node $v$ of $\boldsymbol{T}_{\mathsf{FP}}$ stores the equivalence class $\mathcal{C}_{v}=\{i\mid\boldsymbol{T}_{\mathsf{FP}}[v..]=\mathsf{FP}(\boldsymbol{T}[i..])\}$ of the nodes $i$ in $\boldsymbol{T}$ that correspond to $v$. We set $\min\{\mathcal{C}_{v}\}$ to be the representative of $\mathcal{C}_{v}$, as well as the id of node $v$. See Figure 8 in Appendix.

Let $\Sigma_{\boldsymbol{T}}$ be the set of distinct characters (i.e. edge labels) in $\boldsymbol{T}$ and let $\sigma_{\boldsymbol{T}}=|\Sigma_{\boldsymbol{T}}|$. The FP-trie $\boldsymbol{T}_{\mathsf{FP}}$ can be computed in $O(N\sigma_{\boldsymbol{T}})$ time and working space by a standard traversal on $\boldsymbol{T}$, where we store at most $\sigma_{\boldsymbol{T}}$ front pointers in each node of the current path in $\boldsymbol{T}$ due to Lemma 3.

Let $i_{N^{\prime}},\ldots,i_{1}$ be the node id’s of $\boldsymbol{T}_{\mathsf{FP}}$ which are sorted in decreasing order. The Cartesian-tree position heap for the input trie $\boldsymbol{T}$ is $\mathsf{CPH}(\boldsymbol{T})=\mathsf{SHT}(\mathcal{W}_{\boldsymbol{T}})$, where $\mathcal{W}_{\boldsymbol{T}}=\langle\mathsf{PD}(\boldsymbol{T}[i_{N^{\prime}}..],\ldots,\mathsf{PD}(\boldsymbol{T}[i_{1}..])\rangle$.

As in the case of string inputs in Section 3, we insert the shortest prefix of $\mathsf{PD}(\boldsymbol{T}[i_{k}..])$ that does not exist in $\mathsf{CPH}(\boldsymbol{T}[i_{k+1}..])$. To perform this insert operation, we use the following data structure for a random-access query on the PD encoding of any path string in $\boldsymbol{T}$: