Polymer Network Diffusion in Charged Gels

Charged gels, characterized by ionic species immobilized in the polymer network, exhibit enhanced swelling compared to electrically neutral gels because of the excess osmotic pressure caused by the Donnan effect donnan1911theory ; adair1923donnan . Their remarkable ability to swell up to $1000$ times their dry weight has facilitated their use as superabsorbent polymers for diapers, horticultural water retention agents, and self-healing concrete. This has led to extensive investigation of their swelling behaviors schneider2004discontinuous ; cheng2017preparation ; ricka1984swelling ; jeon1998swelling ; tang2020swelling .

Swelling kinetics are crucial for practical applications of these gels. Tanaka and co-workers tanaka1973spectrum ; tanaka1979kinetics modeled the swelling kinetics of electrically neutral polymer gels, introducing the collective diffusion coefficient $D$ of a polymer network as

where $K$ is the osmotic bulk modulus, $G$ is the shear modulus, and $f$ is the friction coefficient (per unit volume) between polymer networks and solvents. However, quantifying $D$ based on Eq. (1) remains challenging munch1977inelastic due to difficulties in estimating $K$ and $f$. Moreover, $G\ll K$ is often assumed, leading to $D=K/f$ tanaka1979kinetics , even though this is an oversimplification.

Equation (1) extends to charged gels by including ionic contribution to $K$ from Donnan equilibrium donnan1911theory ; ricka1984swelling ; adair1923donnan . However, validation of this approach is complicated due to the complex competition among polymer-solvent mixing, elastic, and ionic contributions. To date, only a few scaling laws between $D$ and the polymer volume fraction $\phi$ have been experimentally examined, including $D\sim\phi^{1/2}$ at low salt concentrations skouri1995swelling ; joosten1991dynamic ; raasmark2005fast and $D\sim\phi^{2/3}$ at high salt concentrations morozova2017elasticity . The main obstacle in experimental validation arises from the difficulty in controlling polymer networks. Consequently, studies often use natural polymers like xanthan, chitosan, and hyaluronic acid, which lack precise control over network structure, have been typically used, limiting accurate gel dynamics research.

Recently, we have developed a strategy to synthesize tunable model polymer networks sakai2008design and identified the equations governing gel elasticity, including negative energy elasticity yoshikawa2021negative ; sakumichi2021linear , as well as the equation of state of osmotic pressure yasuda2020universal ; sakumichi2022semidilute . We have also quantitatively validated Eq. (1) for neutral gels fujiyabu2018three ; fujiyabu2019shear ; kim2020mixing ; fujiyabu2021temperature , by decomposing $D$ into mixing ($D_{\mathrm{mix}}$) and elastic ($D_{\mathrm{el}}$) contributions as $D=D_{\mathrm{mix}}+D_{\mathrm{el}}$, where $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$ are expressed by measurable macroscopic properties.

This Letter extends the relationship $D=D_{\mathrm{mix}}+D_{\mathrm{el}}$ to charged gels, introducing an ionic contribution $D_{\mathrm{ion}}$:

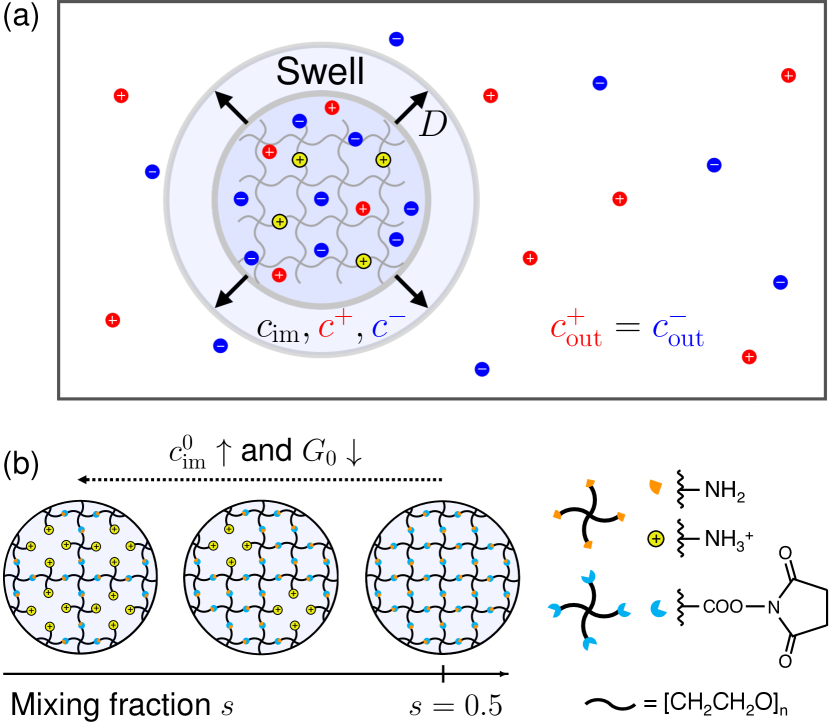
To validate Eq. (2), we experimentally investigated $D$ in charged gels with comparable $D_{\mathrm{mix}}$, $D_{\mathrm{el}}$, and $D_{\mathrm{ion}}$ via dynamic light scattering (DLS). We controlled the molar concentrations of immobilized charge in the gel at the as-prepared state $c_{\mathrm{im}}^{0}$ and equilibrated the gels in various outer salt solutions with diverse molar concentrations of mobile ions $c_{\mathrm{out}}$ [Fig. 1(a)]. Our results indicate that the significant contribution of $D_{\mathrm{ion}}$ to $D$ is explained by the excess osmotic pressure from the Donnan equilibrium donnan1911theory ; adair1923donnan . These findings demonstrate the successful prediction of dynamic property from the static properties of charged gels, suggesting broader applicability of this relationship to charged gels in good solvents.

Theoretical derivation of collective diffusion coefficient in charged gels.—We derive the contribution of $D_{\mathrm{ion}}$ to $D$, using a similar procedure as that for $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$ in neutral gels fujiyabu2018three ; fujiyabu2019shear ; kim2020mixing ; fujiyabu2021temperature . The osmotic bulk modulus $K\equiv c(\partial\Pi/\partial c)$ in Eq. (1) is quantified by total osmotic pressure $\Pi$, where $c$ is the polymer mass concentrations. For charged gels, $\Pi$ is considered as the sum of polymer-solvent mixing $\Pi_{\mathrm{mix}}$, elastic $\Pi_{\mathrm{el}}$, and ionic $\Pi_{\mathrm{ion}}$ contributions flory1953principles ; flory1943statistical1 ; flory1943statistical2 ; katchalsky1955polyelectrolyte ; katchalsky1951equation ; treloar1973elasticity ; duvsek1993responsive as $\Pi=\Pi_{\mathrm{mix}}+\Pi_{\mathrm{el}}+\Pi_{\mathrm{ion}}$, where $\Pi_{\mathrm{mix}}\sim c^{3\nu/(3\nu-1)}$ yasuda2020universal ; sakumichi2022semidilute and $\Pi_{\mathrm{el}}=-G_{0}(c/c_{0})^{1/3}$ james1949simple ; horkay2000osmotic . Here, $\nu\approx 0.588$ is the excluded volume parameter flory1953principles , and $G_{0}$ and $c_{0}$ is the shear modulus and polymer mass concentration, respectively, at the as-prepared state. Further, the friction coefficient per unit volume $f$ in Eq. (1) follows $f\sim c^{3/2}$ fujiyabu2017permeation ; fujiyabu2019shear ; kim2020mixing . Notably, $\Pi_{\mathrm{mix}}$ and $f$ depend only on $c$ at a constant $T$ within the same polymer-solvent system, regardless of the polymer network structures yasuda2020universal ; fujiyabu2017permeation ; fujiyabu2019shear ; kim2020mixing . Assuming same dependences of $\Pi_{\mathrm{mix}}$, $\Pi_{\mathrm{el}}$, and $f$ in charged gels, we can express each contribution to $D$ using Eq. (1) as

and

The $D_{\mathrm{ion}}$ originates from $\Pi_{\mathrm{ion}}$ produced by immobilized charge in polymer networks. Notably, Eqs. (3) have been validated for neutral gels at as-prepared states fujiyabu2018three ; fujiyabu2019shear ; fujiyabu2021temperature and swollen states kim2020mixing .

We quantified $\Pi_{\mathrm{ion}}$ using the Donnan equilibrium donnan1911theory ; ricka1984swelling ; adair1923donnan . For a polymer network with immobilized charge molar concentration $c_{\mathrm{im}}$ in a solution containing monovalent ions, the molar concentrations of mobile cations and anions inside the gel ($c^{\mathrm{+}}$ and $c^{\mathrm{-}}$) and in the outer salt solution ($c_{\mathrm{out}}^{+}$ and $c_{\mathrm{out}}^{-}$) satisfy the following electric neutrality conditions: (i) $c_{\mathrm{im}}+c^{\mathrm{+}}=c^{\mathrm{-}}$ for the inner gel, (ii) $c_{\mathrm{out}}\equiv c_{\mathrm{out}}^{+}=c_{\mathrm{out}}^{-}$ for the outer salt solution, and (iii) $c^{\mathrm{+}}c^{\mathrm{-}}=(c_{\mathrm{out}})^{2}$ between inner gel and outer salt solution. Combining the conditions (i) and (iii) yields $c^{\mathrm{\pm}}=\frac{1}{2}c_{\mathrm{im}}\left(\sqrt{1+4\alpha^{2}}\mp 1\right)$, where $\alpha\equiv c_{\mathrm{out}}/c_{\mathrm{im}}$ ($\geq 0$) is the molar concentration ratio between the mobile ion in the outer salt solution and the immobilized charge in the polymer network. Hence, the osmotic pressure due to the immobilized charge is

Substituting Eq. (5) into Eq. (4) gives

According to Eq. (6), $\alpha$ regulates the efficiency of $D_{\mathrm{ion}}$, with $D_{\mathrm{ion}}=c_{\mathrm{im}}RT/f$ in the charged gel limit ($\alpha\ll 1$) and $D_{\mathrm{ion}}=0$ in the neutral gel limit ($\alpha\gg 1$).

Materials and methods.—As a model system to investigate charged gels, we used a tetra-arm poly(ethylene glycol) (PEG) hydrogel, synthesized via the AB-type cross-end coupling of two prepolymers (tetra-arm PEG) of equal size. Each end of the tetra-arm PEG was modified with a mutually reactive amine (tetra-PEG-NH₂) and succinimidyl ester (tetra-PEG-OSu) (NOF Co., Tokyo, Japan). All other reagents were purchased from WAKO Pure Chemicals (Osaka, Japan). All materials were used without further purification. We dissolved tetra-PEG-NH₂ and tetra-PEG-OSu (molar mass $11$ kg$/$mol) in phosphate buffer ($p\mathrm{H}=7.0$, $60$ mM) to achieve a concentration of $c=60$ g$/$L.

To fabricate charged gels, we mixed two solutions at stoichiometrically imbalanced ratios of $s=0.325$, $0.350$, $0.375$, and $0.400$ (Table 1), where $s$ is the molar fraction of minor tetra-PEG polymers ([tetra-PEG-OSu]) to total tetra-PEG polymers ([tetra-PEG-NH₂] $+$ [tetra-PEG-OSu]). An excess tetra-PEG-NH₂ ($s>0.5$) allowed some amine groups to remain partly unreacted yoshikawa2019connectivity , serving as the immobilized cations in the polymer networks [see Fig. 1(b)]. We kept each sample in an enclosed space to maintain humid conditions at room temperature ($T\approx 298K$) for reaction completion.

We immersed each charged gel into the outer salt (HCl $+$ NaCl) solutions of $p\mathrm{H}=4.0$ and $c_{\mathrm{out}}=0.1$–$30$ mM (Table 1) to completely protonate immobilized cations and to tune the parameter $\alpha\equiv c_{\mathrm{out}}/c_{\mathrm{im}}$ in Eq. (6). We replaced the outer salt solution twice every $20$ hours to achieve equilibrium swollen state. The Henderson-Hasselbalch equation henderson1908concerning ; hasselbalch1917calculation determined the dissociation constant of immobilized residues as $K_{a}\approx 1.0\times 10^{-10}$ M (see Supplemental Material, Sec. S1 supplement ), confirming complete protonation of amines in all experimental conditions because $K_{a}$ was smaller than [H⁺] $=10^{-4}$ M.

We measured the diameter $d$ of each gel at equilibrium in the outer salt solutions, using an optical microscope (M165 C; Leica, Wetzlar, Germany) to calculate the volume swelling ratio $Q=(d/d_{0})^{3}$ (initial diameter $d_{0}=1.04$ mm), determining $c=c_{0}/Q$ and $c_{\mathrm{im}}=c_{\mathrm{im}}^{0}(c/c_{0})$. To ensure accurate $c_{0}$ and $c_{\mathrm{im}}^{0}$ values at each $s$, we assessed the sol fraction eluted out from the polymer network during the swelling process using the Bethe approximation supplement ; macosko1976new ; miller1976new (Further details are described in Supplemental Material, Sec. S2 supplement ).

We measured $D$ of charged gels via DLS (ALV/CGS-3 compact goniometer, Langen, Germany) in the same way as Refs. fujiyabu2018three ; fujiyabu2019shear ; kim2020mixing ; fujiyabu2021temperature . Each gel sample was fabricated in a scattering glass tube (disposable culture tube 9830-1007 with an inner diameter of $8.4$ mm; IWAKI, Japan) and was swollen in the outer salt solution. We carefully selected $d_{0}$ of each gel to prevent contact between a swollen gel and an inner wall of the glass tube. Once equilibrium was reached, we measured the scattering light intensity $I(t)$ at time $t$ over $600$ s at a scattering wavelength $\lambda=632.8$ nm and a scattering angle $\theta=\pi/2$, to evaluate the autocorrelation function johnson1994laser ; berne2000dynamic $g^{(2)}(\tau)\equiv\langle I(0)I(\tau)\rangle/\langle I(0)\rangle^{2}$ for delay time $\tau\approx 0.01$–$0.1$ ms, corresponding to the thermal fluctuation of a polymer network li2017probe ; fujiyabu2018three ; fujiyabu2019shear ; kim2020mixing ; fujiyabu2021temperature ; ohira2018dynamics (results are provided in Supplemental Material, Sec. S3 supplement ). Here, $\langle\rangle$ denotes the time-average. We fitted the autocorrelation functions using a stretched exponential function $g^{2}(\tau)-1=A\exp[-2(\tau/\tau_{g})^{B}]+\epsilon$, where $A$ is the initial amplitude, $B$ is the stretched exponent, and $\epsilon$ is the time-independent background. Using the partial heterodyne model joosten1991dynamic ; shibayama2002gel , we evaluate $D=(1+\sqrt{1+A})/(q^{2}\tau_{g})$, where $q=(4\pi n/\lambda)\sin(\theta/2)\approx 0.0187$ nm^-1 is the scattering vector with the refractive index $n\approx 1.333$ of the aqueous solvents.

We measured the (equilibrium) shear modulus of gels at the equilibrium swollen state $G$ for each $c_{\mathrm{out}}$ using a rheometer (MCR302; Anton Paar, Graz, Austria) with a $25$-mm parallel plate geometry. The gels, shaped into discs with a height $1$ mm and a diameter $35$ mm, were equilibrated in outer salt solutions with varying $c_{\mathrm{out}}$ (Table 1). We measured the storage modulus $G^{\prime}$ and loss modulus $G^{\prime\prime}$ at $T=298$ K with angular frequency $\omega=0.63$–$63$ rad$/$s and shear strain $\gamma=1.0$%, as well as $\omega=6.3$ rad$/$s and $\gamma=0.1$% –$10$%. For all samples, $G^{\prime}$ was independent of $\gamma$ and $\omega$, and was much larger than $G^{\prime\prime}$ (Supplemental Material, Sec. S4 supplement ). Hence, we selected $G^{\prime}$ measured at $\omega=6.3$ rad$/$s and $\gamma=1.0$% as the (equilibrium) shear modulus $G$. Using $G=G_{0}(c/c_{0})^{1/3}$ for swollen gels james1949simple ; horkay2000osmotic (see Supplemental Material, Sec. S5 supplement ), we evaluated $G_{0}$ at the as-prepared state as $G_{0}=G(c_{0}/c)^{1/3}$ for each $s$ (Table 1).

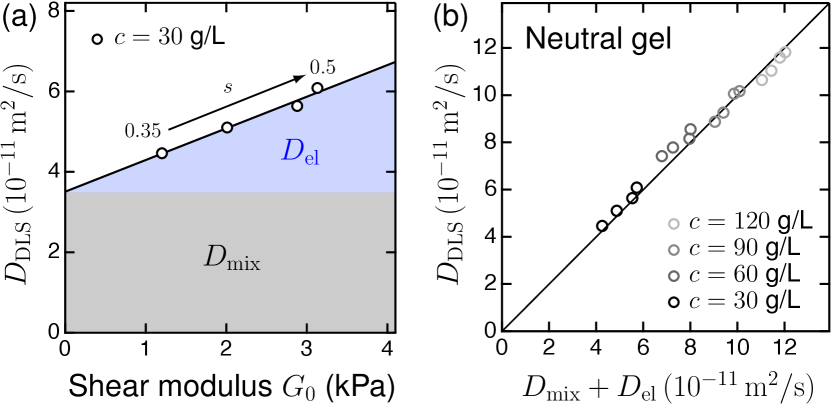
Estimating $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$ in neutral gels.—Before considering charged gels, we briefly revisit the decomposition of mixing ($D_{\mathrm{mix}}$) and elastic ($D_{\mathrm{el}}$) contributions to $D$ in a model neutral gels, based on our previous studies fujiyabu2018three ; fujiyabu2019shear ; kim2020mixing ; fujiyabu2021temperature . Figure 2(a) shows the collective diffusion coefficient measured via DLS $D_{\mathrm{DLS}}$ in neutral gels at the as-prepared state, plotted against $G_{0}$ for various $s$. The observed linear relationship between $D_{\mathrm{DLS}}$ and $G_{0}$ is consistent with Eqs. (3). Notably, $D_{\mathrm{mix}}$ is independent of $s$, because $\Pi_{\mathrm{mix}}$ and $f$ is independent of $s$ yasuda2020universal ; fujiyabu2017permeation ; fujiyabu2019shear ; kim2020mixing . Thus, we can decompose $D_{\mathrm{DLS}}$ into the mixing contribution $D_{\mathrm{mix}}=\lim_{G\to 0}D_{\mathrm{DLS}}$ and the elastic contribution $D_{\mathrm{el}}=D_{\mathrm{DLS}}-D_{\mathrm{mix}}$ [see Fig. 2(a)].

Through the decomposition of $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$, we obtain the empirical formulas $D_{\mathrm{mix}}=2.2\times 10^{-12}c^{0.8}$ and $f=8.0\times 10^{11}c^{1.5}$ for neutral gels (the detailed results are provided in Supplemental Material, Sec. S7), corroborating the scaling predictions $f\sim c^{1.5}$ tokita1991friction and $\Pi_{\mathrm{mix}}\sim c^{2.3}$ des1975lagrangian ; de1979scaling (for gels in a good solvent). These formulas are applicable to neutral gels at the as-prepared and swollen states, as confirmed in our previous study kim2020mixing . Using values of $c$ and $G$, we can accurately calculate $D$ for a neutral gel. Figure 2(b) demonstrates that the collective diffusion coefficient of neutral gels measured via DLS ($D_{\mathrm{DLS}}$) shows excellent agreement with Eqs. (3), using empirical formulas of $D_{\mathrm{mix}}$ and $f$.

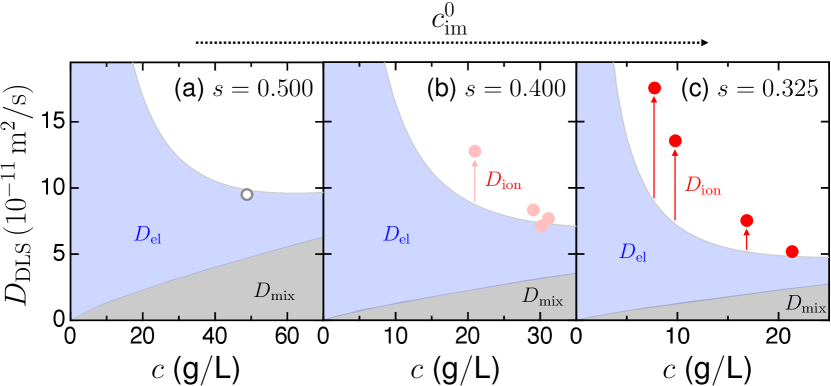
Estimating $D_{\mathrm{ion}}$ in charged gels.— We expand our analysis to electrically charged gels and examine Eq. (2), by hypothesizing that the formulas of $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$, as established for neutral gels, remain applicable. Figure 3 shows $D_{\mathrm{DLS}}$ for swollen neutral and charged gels (equilibrated in outer salt solutions with varying $c_{\mathrm{out}}$), as measured via DLS. For varying $s$ samples, a decrease in $s$ corresponded with an increase in $c_{\mathrm{im}}^{0}$ and a decrease in $G_{0}$. This resulted in an increase in $Q$ to be a decrease in $c$ ($=c_{0}/Q$) in outer salt solutions (Table 1). The decrease in $G_{0}$ is attributed to a decrease in elastically effective subchains in polymer networks sakai2008design . Moreover, for a fixed $s$, a decrease in $c_{\mathrm{out}}$ in outer salt solutions led to a lower $\alpha$ ($\equiv c_{\mathrm{out}}/c_{\mathrm{im}}$), resulting in increased $Q$ to be decreased $c$ ($=c_{0}/Q$) (Table 1).

For neutral gels [Fig. 3(a)], $D_{\mathrm{DLS}}$ agrees with $D_{\mathrm{mix}}+D_{\mathrm{el}}$, which is independent of $c_{\mathrm{out}}$ (see Supplemental Material, Sec. S8 supplement for further details). For charged gels with each $s$ [Fig. 3(b) and (c)], we calculate $D_{\mathrm{mix}}$ (gray region) and $D_{\mathrm{el}}$ (blue region), using the same empirical formulas for neutral gels with all measurable $G_{0}$ and $Q$. Here, we experimentally confirmed that $G=G_{0}(c/c_{0})^{1/3}$ holds for charged gels (see Supplemental Material, Sec. S5 supplement ), indicating that the immobilized charge does not significantly affect the elastic modulus. At high $c_{\mathrm{out}}$ ($\alpha\gg 1$), $D_{\mathrm{DLS}}$ approaches the neutral gel limit ($D_{\mathrm{mix}}+D_{\mathrm{el}}$), because $D_{\mathrm{ion}}\to 0$ in Eq. (6). In contrast, at low $c_{\mathrm{out}}$ ($\alpha\ll 1$), $D_{\mathrm{DLS}}$ deviates from the neutral gel limit ($D=D_{\mathrm{mix}}+D_{\mathrm{el}}$), indicating a significant $D_{\mathrm{ion}}$ to $D$ (indicated by red arrows), which contributed up to approximately half of $D$ at its maximum.

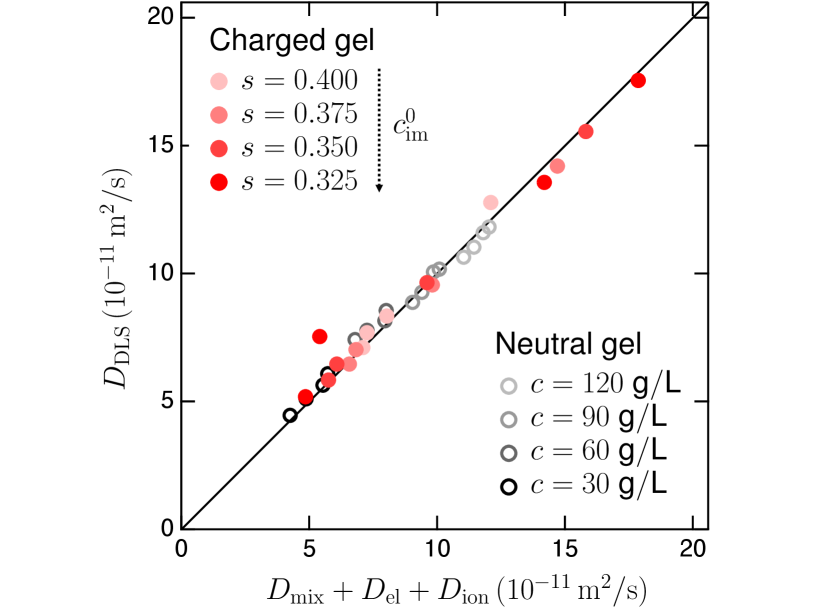
We show that $D$ of charged gels can be accurately described by simply adding $D_{\mathrm{ion}}$ in Eq. (6). Figure 4 demonstrates that the collective diffusion coefficient of charged gels measured via DLS ($D_{\mathrm{DLS}}$) shows excellent agreement with the predictions of Eqs. (3) and (4), using the same empirical formulas of $D_{\mathrm{mix}}$ and $f$ as in neutral, and applying Eq. (6) with each $c_{\mathrm{im}}$ and $\alpha$. These findings suggest that Eq. (1) can be extended to include charged gels by simply adding $D_{\mathrm{ion}}$ without evident cross-correlations. Notably, Eq. (6) is applicable in weakly charged gels and is less effective in polyelectrolyte gels with high $c_{\mathrm{im}}$, due to counterion condensation tang2020swelling ; manning1969limiting .

Concluding remarks.— We developed model charged gels [Fig. 1 and Table 1] with comparable $D_{\mathrm{mix}},D_{\mathrm{el}},$ and $D_{\mathrm{ion}}$ and measured their collective diffusion coefficient $D$ via DLS. Based on the same decomposition of $D_{\mathrm{mix}}$ and $D_{\mathrm{el}}$ to $D$ in neutral gels [Figs. 2 and 3], our results indicate that $D$ in the charged gel is governed by Eq. (1), where $D_{\mathrm{ion}}$ emerges as an additive component [Fig. 4]. The significant ionic contribution $D_{\mathrm{ion}}$ to $D$ is quantitatively described through the ionic osmotic pressure $\Pi_{\mathrm{ion}}$ [Eqs. (5) and (6)], which originates from the Donnan equilibrium.

Our findings demonstrate the successful prediction of the dynamic behaviors from the static properties of charged gels equilibrated in a good solvent. This aspect is particularly relevant considering the dynamics in gel-like biological systems such as extracellular matrices, which are predominantly negatively charged theocharis2016extracellular and influenced by the Donnan effect. Therefore, an in-depth understanding of the dynamics in charged gels will enhance our comprehension of the behaviors of biological systems.