Polarization dependent photoemission as a probe of the magnetic ground state in the layered ferromagnet VI₃

Layered ferromagnets, van der Waals materials that exhibit a magnetic order at the level of single layer, bring a new functionality to the family of 2-dimensional crystals, opening the door to ultrathin spintronic applications. Vanadium(III) iodide ($VI_{3}$) is a van der Waals (vdW) Mott insulator made of honeycomb vanadium layers separated by an iodine-iodine vdW gap with the remarkable property of intrinsic ferromagnetism. Despite the fact that VI₃ has proved to be extremely sensitive to air, its recently reported unusual thickness-dependent magnetism with an increase of the Curie temperature as the layer number decreases Lin et al. (2021), makes it a compelling platform for the engineering of magnetism in electronic devices. Angle Resolved Photoemission Spectroscopy (ARPES) is an excellent tool to study the electronic properties of layered materials. Its ultrahigh vacuum environment and in-situ cleaving capability reduces the limitations and challenges associated to probing air-sensitive materials.

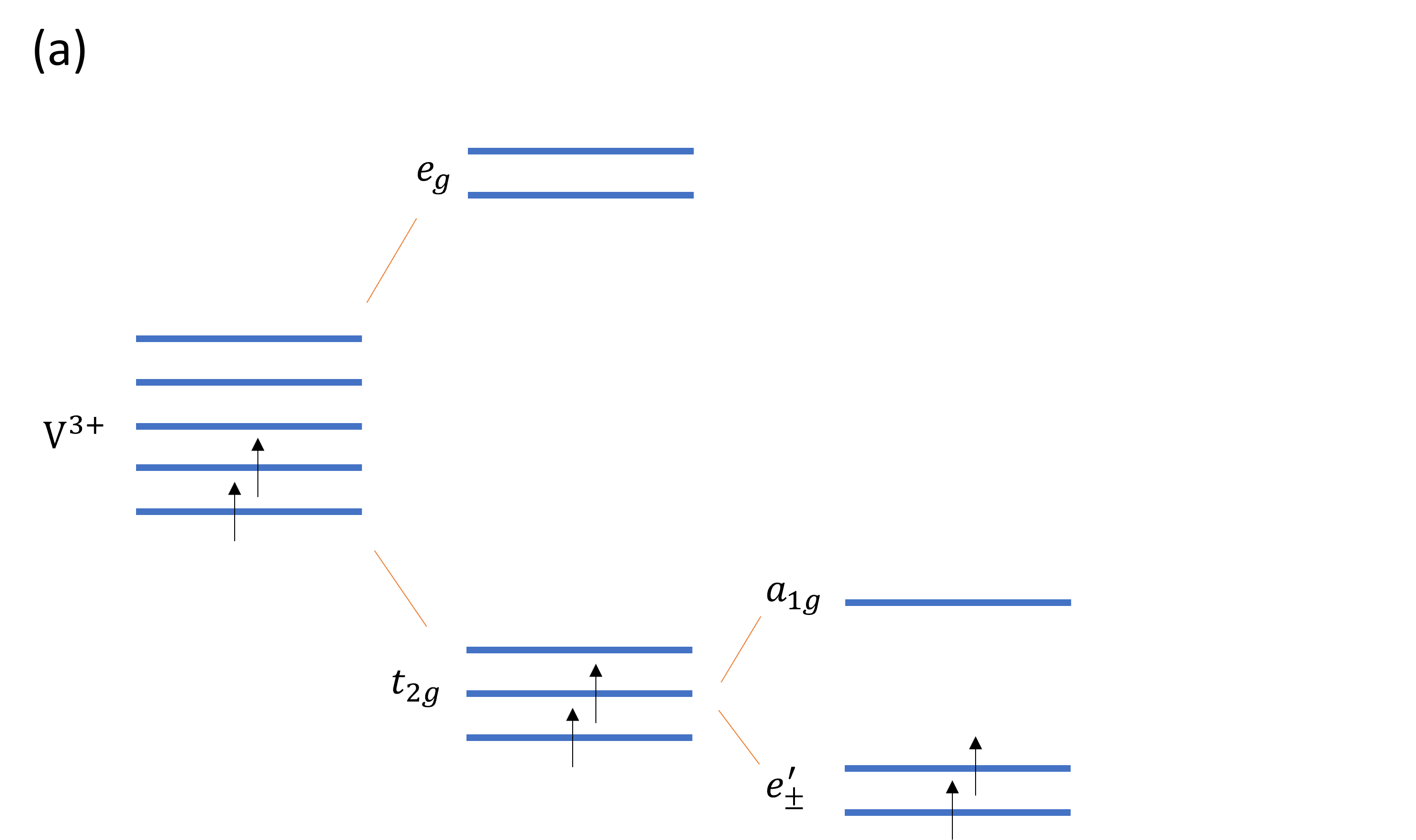
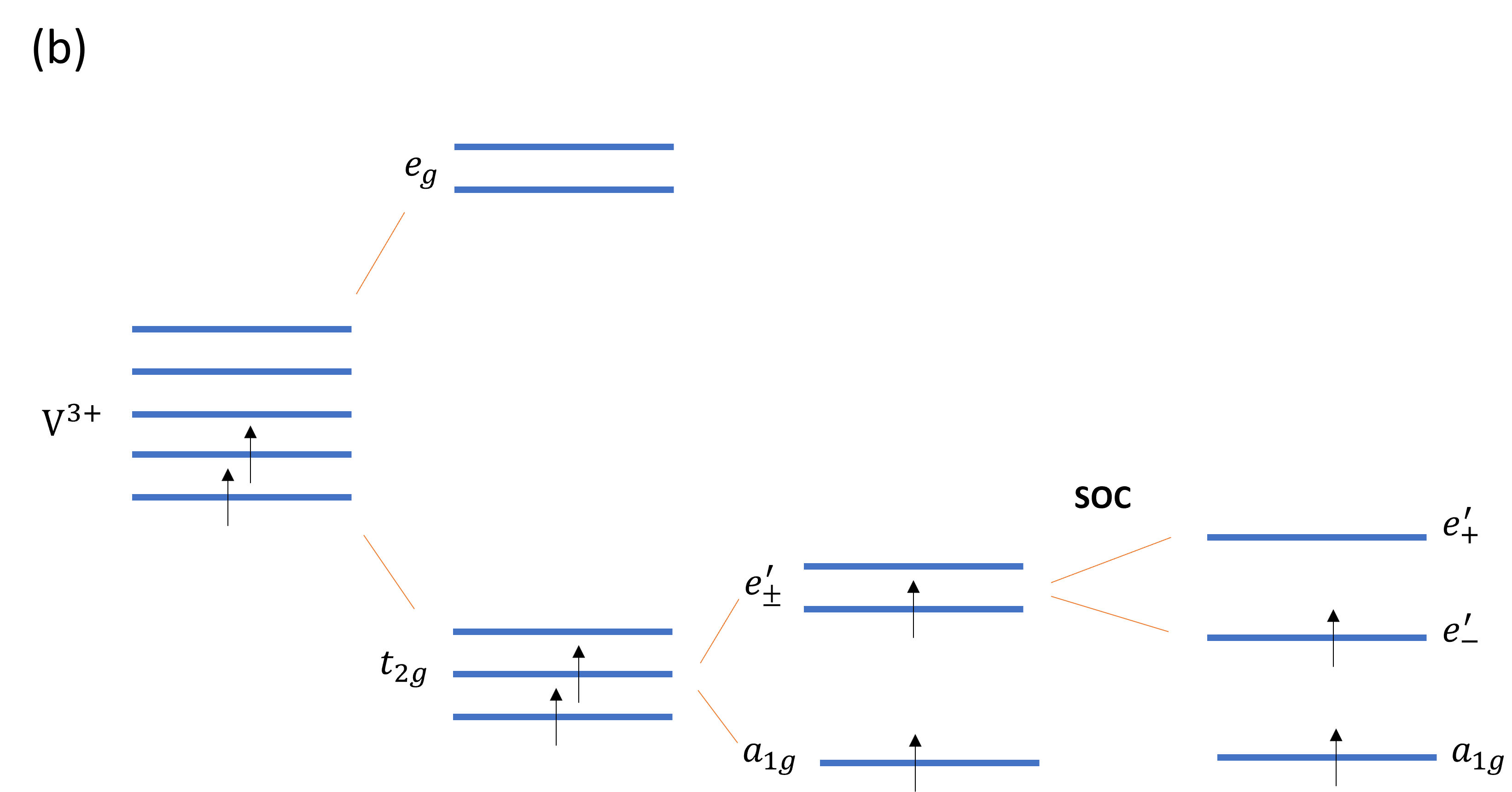
VI₃’s electronic properties derive from a combination of crystal field effects, electronic correlations and spin-orbit coupling. In VI₃, vanadium ions (V) are surrounded by I₆ octahedra which provides a crystal field that splits the five-fold degenerate V-d orbitals into a lower triplet t_2g and an upper doublet e_g. Additional trigonal distorsions caused by the elongation of of VI₆ octahedra along one of the [111] axes Khomskii (2014), causes an additional split of the t_2g levels into a singlet a_1g and a doublet e${}_{\pm}^{\prime}$ (see Figure 1). $|a_{1g}\rangle$ has a simple form in coordinates where the z axis aligns with the trigonal distorsion, and x and y axes are in the perpendicular plane, pointing along the z-direction. The other two t_2g orbitals $|e_{\pm}^{\prime}\rangle$ are complex and have the shape of a torus Khomskii (2014); Nguyen et al. (2021).

There is not yet consensus on what is the exact mechanism responsible of the observed bandgap in VI₃. The two V d² electrons in VI₃ may occupy the $|a_{1g}\rangle$ and $|e_{\pm}^{\prime}\rangle$ orbitals into the state $e_{\pm}^{2}a_{1g}^{0}$, that together with electronic correlations leads to a Mott insuator Nguyen et al. (2021); Wang and Long (2020); Huang et al. (2020), or electrons may partially fill the $|e_{\pm}^{\prime}\rangle$ orbitals, which leads in principle to a metallic ground state $a_{1g}^{1}e_{\pm}^{1}$; however spin-orbit coupling is capable of spliting the half filled $|e_{\pm}^{\prime}\rangle$, that in conjunction with electronic correlations leads also to a Mott insulator Yang et al. (2020); Huang et al. (2020). Both scenarios have been proved possible through first principle calculations, and are consistent with the known S=1 state for VI₃ Yang et al. (2020); Huang et al. (2020).

Understanding the t_2g orbitals in VI₃ is fundamental, as they not only set the insulating character of this vdW material but also determine its magnetic properties. Perpendicular magnetic anisotropy, that refers to the preferred orientation of magnetic vectors perpendicular to the layer plane, is a fundamental characteristic in magnetic materials for applications, and most importantly, it is essential for the existence of magnetic order at low dimensions Mermin and Wagner (1966). Perpendicular magnetic anisotropy comes from a microscopic effect, called single ion anisotropy or magnetocrystalline anisotropy, caused by the orbital momentum along the normal of the bonding plane quenching due to crystalline fields. The first layered ferromagnets reported in the literature were Cr based Huang et al. (2017); Gong et al. (2017), such as CrI₃, where crystal field effects also split the 5-fold degenerate Cr-d orbitals into t_2g and e_g states however, the degeneracy of the t_2g orbital for Cr d³ is unlifted and yields no magnetocrystalline anisotropy. Perpendicular magnetic anisotropy in CrI₃ comes rather from the weak exchange anisotropy brought by the heavy I 5p orbitals and their hybridization with Cr 3d orbitals Yang et al. (2020); Lado and Fernández-Rossier (2017); Kim et al. (2019). VI₃ has a large magnetocrystalline anisotropy (one order of magnitude larger than for CrI₃) that together with spin-orbit coupling, is responsible for the observed perpendicular magnetic anisotropy. In VI₃, it is spin-orbit coupling that aligns the magnetic moment of the V ions along the z-axis via the strong magnetocrystalline anisotropy and produces the observed perpendicular magnetic anisotropyYang et al. (2020). Angle-dependent magnetization measurements have demonstrated that the magnetic moment in VI₃ is in fact canted by $\approx$40^∘ from the normal to the ab plane in a wide temperature range (10 K - 60 K), within the range of the two ferromagnetic phases reported for VI₃ as well as its structural phase transition. The observed magnetization canted easy-axis differentiates VI₃ from the Ising-type magnetism reported for CrI₃ Koriki et al. (2021).

The orientation of the V 3d orbitals that host the magnetic Mott ground state, discernible through the use of different light polarizations in ARPES, can give insight on the ground state that brings magnetism to this vdW material. Previous photoemission experiments have characterized the valence band structure of bulk VI₃ Kundu et al. (2020) however, further understanding of the character of the observed band manifolds remains elusive. Here we report a deep study on the linear and circular dichroism of VI₃ photoemission, that together with the effects of light energy and alkaline doping brings insight on the orbitals’ properties that play an important role in 2-dimensional magnetism.

VI₃ millimeter-sized single crystals were synthesized by a chemical vapor transport method as reported in Kong et al., 2019. A stoichiometric mixture of vanadium powder and iodine pieces was loaded in a silica tube and sealed under vacuum. Growth was performed over 3-4 days in a horizontal tube furnace, with the hot end held at 400 °C and the cold end at ambient temperature. High-resolution ARPES experiments were performed at Beamline 4.0.3 (MERLIN) of the Advanced Light Source using 30 - 128 eV linearly or circularly polarized photons in a vacuum better than 5 × 10^-11 Torr. The total-energy resolution was 20 meV with an angular resolution $\Delta\theta$ of $\leq$0.2°.

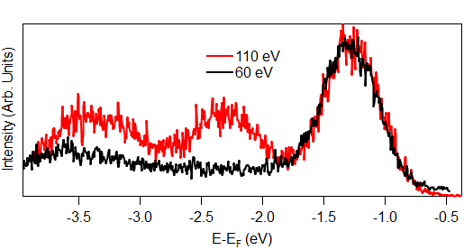
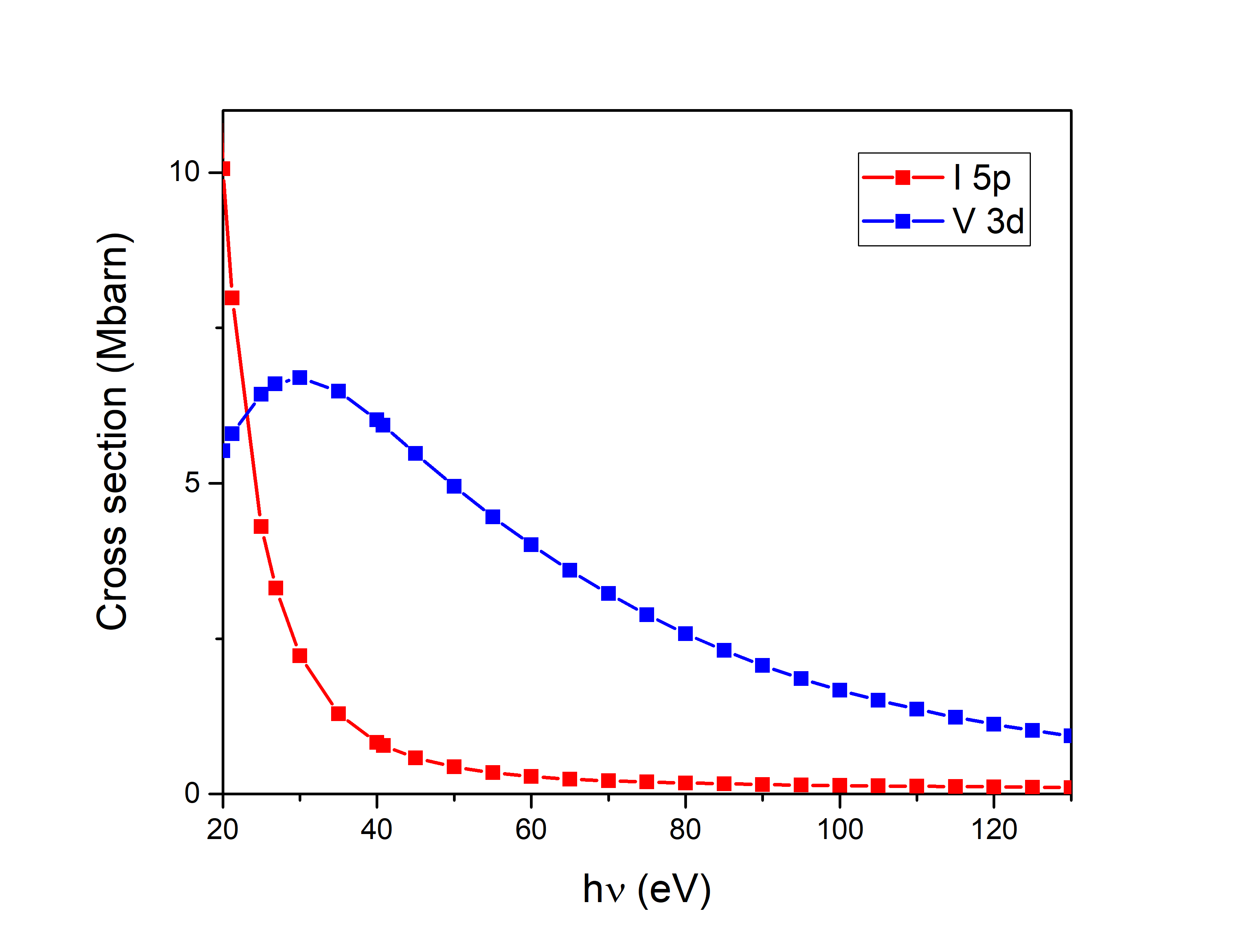
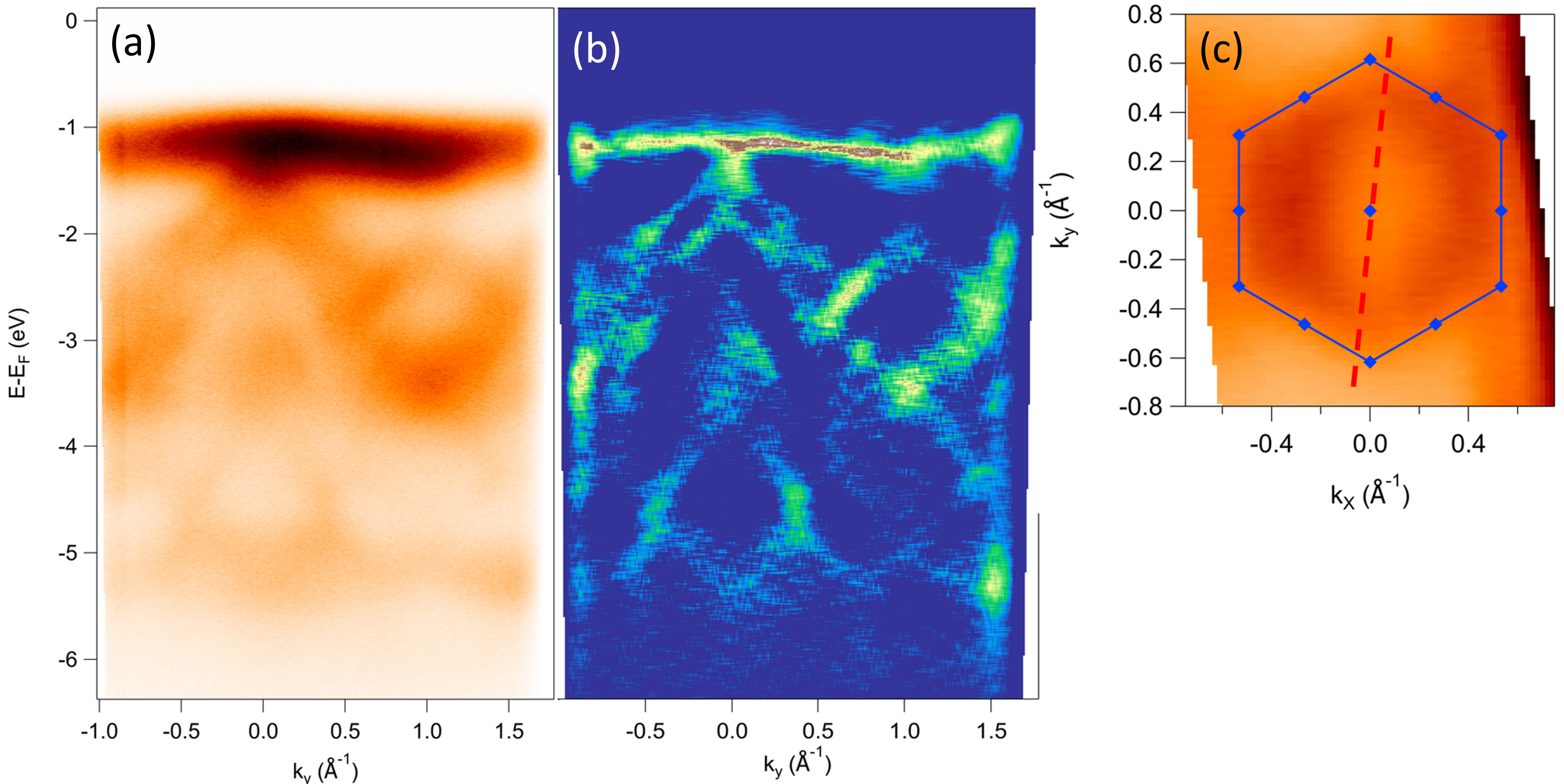
Figure 2 shows the measured electronic band structure at T$=264$ K using photon energy h$\nu=76$ eV and out-of-plane linearly polarized light, within the setup in Figure 4e (detailed later). Measurements were done at 265 K to avoid charging of the sample. Despite the fact that this is well above the magnetic transition temperature reported for VI₃ ($\approx$50 KKong et al. (2019)), previous ARPES measurements report no major differences in the band structure at 35 K and 300 K Kundu et al. (2020). We calculate the curvature of the data in the energy direction (Figure 2 (a)), using the method elaborated in Zhang et al., 2011 . At the high symmetry direction K-$\Gamma$-K, we observe a non-dispersive band at the top of the conduction band ($\approx$ 1eV below the Fermi level) and dispersive bands at higher binding energies. A constant energy map at 4.5 eV below the Fermi energy (2(c)), reveals a six-fold symmetry, consistent with the known trigonal structure for VI₃ at room temperature. The superimposed blue hexagon corresponds to the first Brillouin zone, calculated using the parameters a=b=6.89 Å^‐1 and c=19.81 Å^‐1 reported in the literature from single crystal x-ray diffraction experiments Kong et al. (2019); Doležal et al. (2019). As in reference Kundu et al., 2020, we identify the flat band near the top of the valence band of V 3d character. As stated by Kundu et al, other V based vdW materials such as VSe₂Feng et al. (2018) and VTe₂Wang et al. (2019), show equally weakly dispersing V 3d-electron-derived bands. The attributed V 3d character of this band at $\approx$1 eV below the Fermi energy is also consistent with our photon energy dependent photoemission data. Following the work by Kundu et al., we compare the calculated photoemission crosssections Parry (1994); Yeh and Lindau (1985) to energy distribution curves (EDC) for different photon energies (See Supplementary Materials), where we verify that V 3d-electron derived bands show a stronger intensity for certain photon energies (vs I 5p bands) as listed in Parry, 1994 and Yeh and Lindau, 1985.

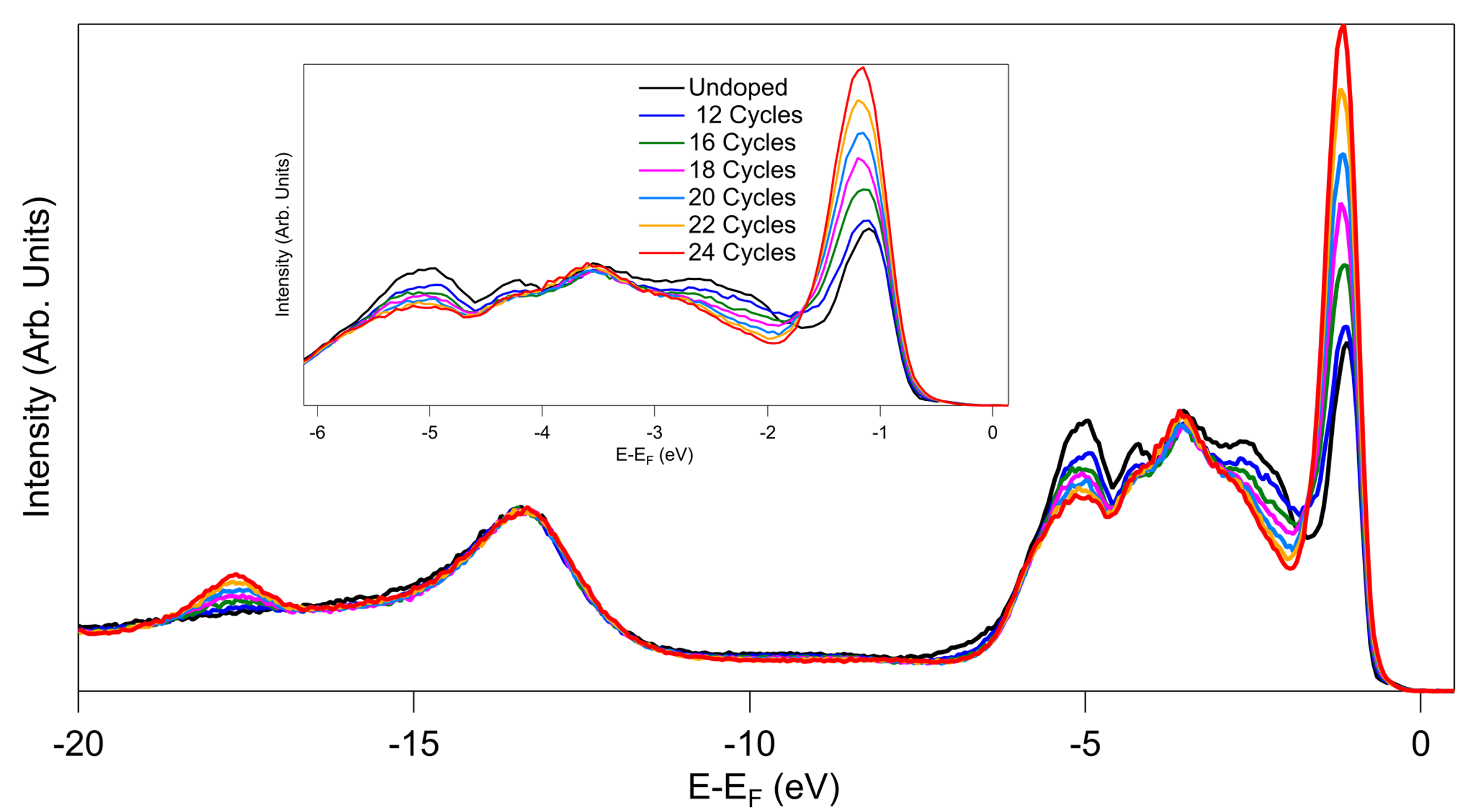
We explored the effect of electron doping by performing a gradual in-situ potassium (K) deposition. Doping created an interesting spectral weight redistribution, as shown in Figure 3. As we doped with electrons, weight grew significantly at the V 3d identified band, while increasing at lower amounts or staying the same at higher binding energies. The amount of K dosed on the surface of VI₃ had a very weak impact on the spectral weight at deep binding energies (below 7 eV). In contrast, the top of the valence band showed in addition to an important grow in weight, a noticeable broadening and a modest shift to higher binding energies as more K was deposited. This behavior is in sharp contrast with the effect of in-situ doping on semiconductors or even Mott insulators, where the K-donated electrons usually trigger a rigid shift of the valence bands toward higher binding energies with no spectral weight redistribution. In those cases, an energy band gap can be estimated from the consequential shift of the chemical potential into the conduction band Comin et al. (2012). Here, the observed change of the band structure with doping suggests a non-conventional evolution of the VI₃ Mott state with doping.

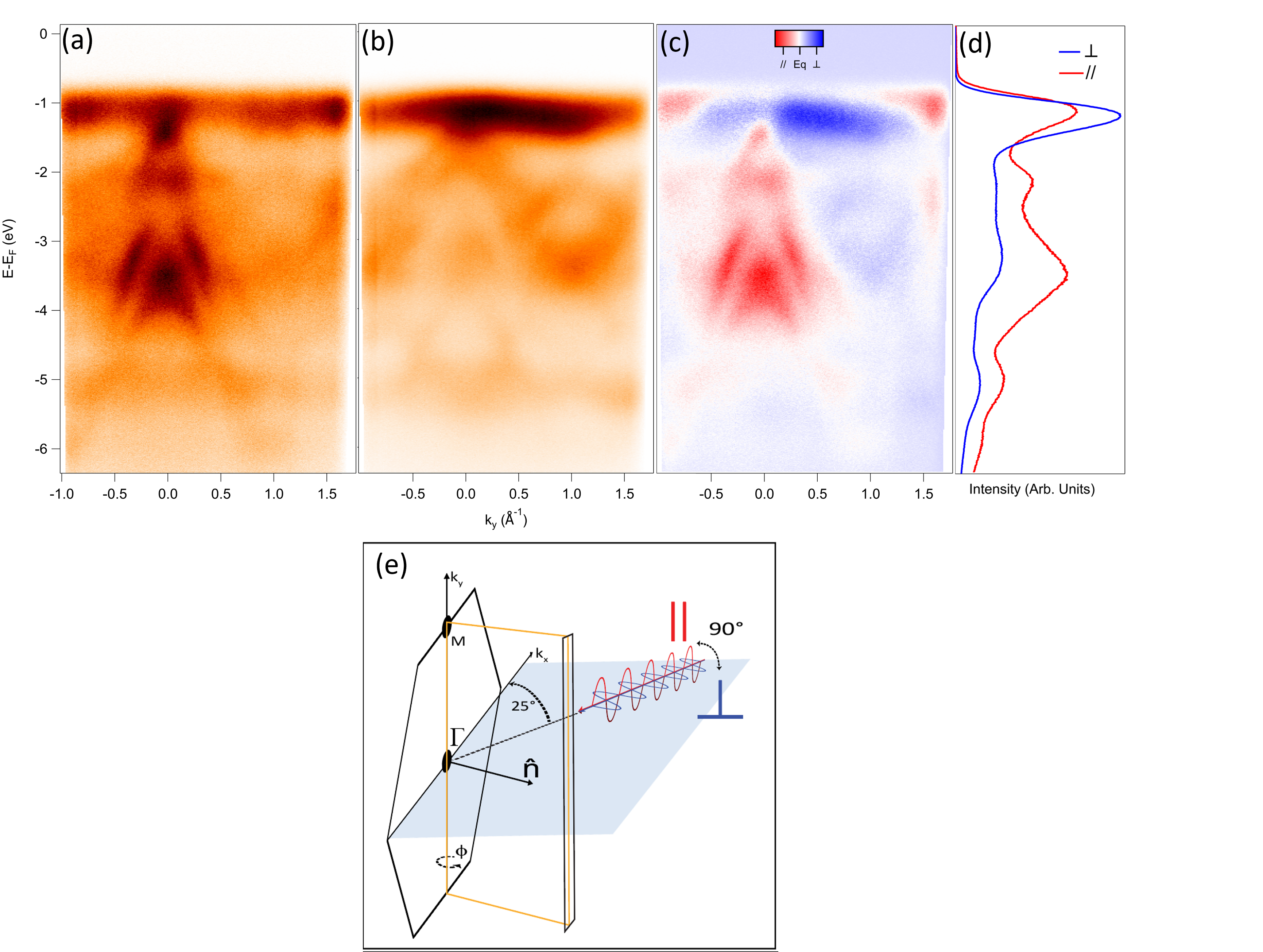
Using different polarizations of the synchrotron light in ARPES is known to reveal hidden traits in the electronic band structure, or to help identifying the orbital character of materials’ band manifolds Latzke et al. (2019); Wang et al. (2012); Volckaert et al. (2019); Cao et al. (2013). As observed in Figure 4, in our setup (Beamline 4.0.3 at the ALS) the high energetic light is incident in the $k_{y}$=0 plane (65^∘ relative to the analyzer lens), which breaks any geometrical symmetry about the crystal $k_{x}$=0 plane. As a consequence, there is no symmetry in the photoemission measured between $\pm k_{x}$ points for different light polarizations, and in contrast there is a generic geometrical dichroism (difference in the photoemission for two opposite light polarizations) above and below the $k_{y}=0$ incident plane (at $\pm k_{y}$ for any $k_{x}$), provided that the crystal has also a symmetry above and below the $k_{y}=0$ plane. In this study, we make use of linearly and circularly polarized light. In a first instance, we use out-of-plane $\perp$ (or LH) and in-plane $\parallel$ (or LV) light polarizations. In the case of $\perp$ light, the electric field vector of the incident photons has a perpendicular component with respect to the sample surface, while for of $\parallel$ light, the electric field is always parallel to the sample surface (see Figure 4e). Figures 4a and b show VI₃ ARPES measured for both in-plane $\parallel$ and out-of-plane $\perp$ light polarizations in the K-$\Gamma$-K direction, as indicated in Figure 2c. We observe that different bands are enhanced with the two light polarizations. In particular, $\perp$ light polarization reveals a stronger contribution from the band near $1$ eV below the Fermi energy with respect to other bands at higher binding energies. This is summarized in Figure 4c, where the difference in ARPES intensity using the two polarizations (blue $\perp$, red $\parallel$) known as linear dichroism, is calculated. We have represented in Figure 4d the momentum-integrated energy distribution curves (EDCs) for the $\perp$ (blue) and $\parallel$ (red) polarizations, normalized by the incident photon flux. We observe that the intensity of the band near $1$ eV below the Fermi energy is appreciably reduced for the $\parallel$ with respect to the $\perp$ light polarization (by 21$\%$). Our linear dichroism data shows therefore that the V-3d-electron-derived bands are particularly sensitive to $\perp$ light polarization, indicating that their orbitals are ordered mainly orthogonal to the sample surface, while bands at higher binding energies (associated to I 5p orbitals Kundu et al. (2020)) seem to be ordered mainly parallel to the sample surface (ab plane). The former bands host the t_2g orbitals that set the Mott insulating behavior in VI₃ as well as its magnetic properties. As mentioned in the introduction, two possible scenarios explain the electronic properties of VI₃. One in which V d² electrons occupy the $|e_{\pm}^{\prime}\rangle$ orbitals and another where the V d² electrons occupy the $|a_{1g}\rangle$ and $|e_{-}^{\prime}\rangle$ orbitals. The real part of the $|e_{\pm}^{\prime}\rangle$ orbitals can be represented in coordinates with the z axis along the [111] axes of the crystal ($|e_{g1}^{\prime}\rangle$ and $|e_{g2}^{\prime}\rangle$), where they lie in the x-y plane (with some tilting of $|e_{g2}^{\prime}\rangle$ with respect to $|e_{g1}^{\prime}\rangle$) Khomskii (2014)

On the other hand, the $|a_{1g}\rangle$ orbitals are real and oriented parallel to the z direction Khomskii (2014); Nguyen et al. (2021),

The measured linear dichroism for the V 3d bands points towards orbitals oriented mostly out-of-plane and therefore to a preferred $a_{1g}^{1}e_{\pm}^{1}$ ground state for VI₃, instead of a $e_{\pm}^{2}a_{1g}^{0}$ ground state where orbitals are expected to be fully on-plane.

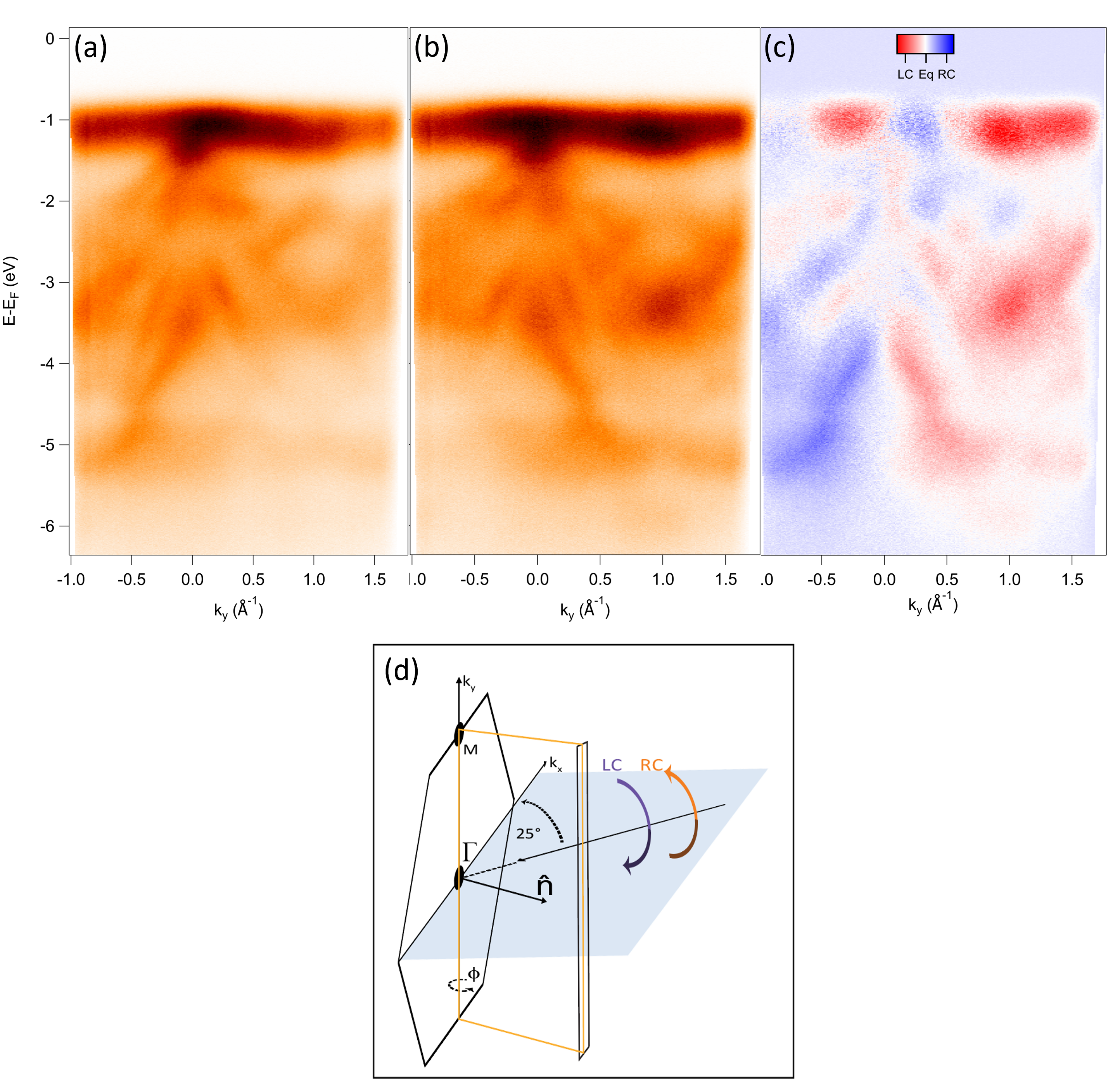
In order to explore further the orbital character details of the VI₃ valence bands, we studied the ARPES circular dichroism in the photoelectron angular distribution (CDAD), by using left- (LC) and right- hand (RC) circularly polarized light. In general, CDAD can be observed in an experimental geometry with a handedness. CDAD is absent when the geometry is such that a symmetry operation that transforms right- into left-circularly polarized light leaves the momentum vector of the photoelectrons k unaffected Scholz et al. (2013). This is the case of the $k_{y}=0$ plane (in blue in Figure 5d), that transforms right into left circularly polarized light without affecting k, parallel to $\hat{n}$, the normal to the sample. There is therefore zero CDAD for $k_{y}$=0. On the other hand on the detector plane (yellow plane in Figure 5d), a reversal of the light polarization changes the sign of the y component of k, leading to a non-zero CDAD. In our data, the CDAD is zero at $\Gamma$, as observed in Figure 5c. The handedness of the experimental setup combined with the symmetry of the orbitals making up the band structure of VI₃, result in an CDAD intensity with opposite sign when crossing $\Gamma$ along $k_{y}$. Despite the fact that CDAD has been argued to be a final state effect Scholz et al. (2013); Bigi et al. (2021), it is worth it to point out that here, the V 3d identified bands exhibit the same CDAD polarization, while bands at higher binding energies (below 1 eV) show a switching of the CDAD. This is in contrast with the linear dichroism, that shows the same important LV light polarization effect at binding energies below 1 eV.

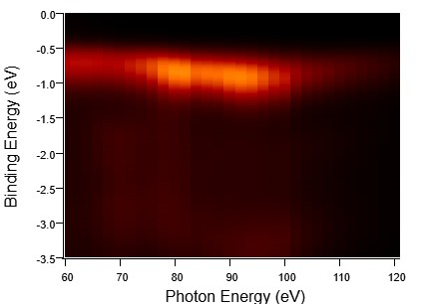
Finally, we study the photon energy dependence of VI₃ ARPES. Figure 6 shows data taken along the K-$\Gamma$-K direction with $\perp$ photons in a photon energy range of 60-120 eV. The top of the VI₃ valence band stays at about the same energy position for different photon energies, indicating a very weak band dispersion along the k_z direction, characteristic of layered materials with no interacting layers.

In summary, using different light polarizations, our ARPES study on the vdW Mott ferromagnet VI₃ points towards a ground state where V d² electrons occupy the $|a_{1g}\rangle$ and half fill the $|e_{\pm}^{\prime}\rangle$ state. Circularly polarized light shows the same dichroism (CDAD) for the identified V 3d states while alternating CDAD at higher binding energies, indicating the same orbital character of the V 3d bands near the top of the conduction band. Our photon energy dependent measurements confirm the layer character of VI₃, with weakly interacting layers. Most importantly, our measurements put in evidence in an indirect way the importance of spin-orbit coupling in this vdW ferromagnet, that leads to the $a_{1g}^{1}e_{\pm}^{1}$ state, expected to be metallic unless spin-orbit coupling and electronic correlations are active and open a Mott band gap. As detailed in the introduction, spin orbit coupling in VI₃ plays indeed an essential role in the observed perpendicular magnetic anisotropy, essential for electronic applications.