Pointer-Machine Algorithms for Fully-Online Construction of
Suffix Trees and DAWGs on Multiple Strings

Suffix trees are a fundamental string data structure with a myriad of applications [9]. The first efficient construction algorithm for suffix trees, proposed by Weiner [19], builds the suffix tree for a string in a right-to-left online manner, by updating the suffix tree each time a new character is prepended to the string. It runs in $O(n\log\sigma)$ time and $O(n)$ space, where $n$ is the length of the string and $\sigma$ is the alphabet size.

One of the most interesting features of Weiner’s algorithm is a very close relationship to Blumer et al.’s algorithm [2] that builds the directed acyclic word graph (DAWG) in a left-to-right online manner, by updating the DAWG each time a new character is prepended to the string. It is well known that the DAG of the Weiner links of the suffix tree of $T$ is equivalent to the DAWG of the reversal $rev{T}$ of $T$, or symmetrically, the suffix link tree of the DAWG of $\overline{T}$ is equivalent to the suffix tree of $T$. Thus, right-to-left online construction of suffix trees is essentially equivalent to left-to-right construction of DAWGs. This means that Blumer et al.’s DAWG construction algorithm also runs in $O(n\log\sigma)$ time and $O(n)$ space [2].

DAWGs also support efficient pattern matching queries, and have been applied to other important string problems such as local alignment [5], pattern matching with variable-length don’t cares [13], dynamic dictionary matching [10], compact online Lempel-Ziv factorization [21], finding minimal absent words [7], and finding gapped repeats [17], on the input string.

Takagi et al. [16] initiated the generalized problem of maintaining the suffix tree for a collection of strings in a fully-online manner, where a new character can be prepended to any string in the collection at any time. This fully-online scenario arises in real-time database systems e.g. for sensor networks or trajectories. Takagi et al. showed that a direct application of Weiner’s algorithm [19] to this fully-online setting requires to visit $\Theta(N\min(K,\sqrt{N}))$ nodes, where $N$ is the total length of the strings and $K$ is the number of strings in the collection. Note that this leads to a worst-case $\Theta(N^{1.5}\log\sigma)$-time construction when $K=\Omega(\sqrt{N})$.

In their analysis, it was shown that Weiner’s original algorithm applied to a fully-online string collection visits a total of $\Theta(N\min(K,\sqrt{N}))$ nodes. This means that the amortization argument of Weiner’s algorithm for the number of nodes visited in the climbing process for inserting a new leaf, does not work for multiple strings in the fully-online setting. To overcome difficulty, Takagi et al. proved the three following arguments: (1) By using $\sigma$ nearest marked ancestor (NMA) structures [20], one can skip the last part of the climbing process; (2) All the $\sigma$ NMA data structures can be stored in $O(n)$ space; (3) The number of nodes explicitly visited in the remaining part of each climbing process can be amortized $O(1)$ per new added character. This led to their $O(N\log\sigma)$-time and $O(N)$-space fully-online right-to-left construction of the suffix tree for multiple strings.

Takagi et al. [16] also showed that Blumer et al.’s algorithm applied to a fully-online left-to-right DAWG construction requires at least $\Theta(N\min(K,\sqrt{N}))$ work as well. They also showed how to maintain an implicit representation of the DAWG of $O(N)$ space which supports fully-online updates and simulates a DAWG edge traversal in $O(\log\sigma)$ time each. The key here was again the non-trivial use of the aforementioned $\sigma$ NMA data structures over the suffix tree of the reversed strings.

As was stated above, Takagi et al.’s construction heavily relies on the use of the NMA data structures [20]. Albeit NMA data structures are useful and powerful, all known NMA data structures for (static and dynamic) trees that support $O(1)$ (amortized) time queries and updates [8, 11, 20] are quite involved, and they are valid only on the word RAM model as they use look-up tables that explicitly store the answers for small sub-problems. Hence, in general, it would be preferable if one can achieve similar efficiency without NMA data structures.

In this paper, we show how to maintain the suffix tree for a right-to-left fully-online string collection in $O(N(\log\sigma+\log d))$ time and $O(N)$ space, where $d$ is the maximum number of in-coming Weiner links to a node of the suffix tree. Our construction does not use NMA data structures and works in the pointer-machine model [18], which is a simple computational model without address arithmetics. We note that $d$ is bounded by the height of the suffix tree. Clearly, the height of the suffix tree is at most the maximum length of the strings. Hence, the $d$ term can be dominated by the $\sigma$ term when the strings are over integer alphabets of polynomial size in $N$, or when a large number of strings of similar lengths are treated. To achieve the aforementioned bounds on the pointer-machine model, we reduce the problem of maintaining in-coming Weiner links of nodes to the ordered split-insert-find problem, which maintains dynamic sets of sorted elements allowing for split and insert operations, and find queries, which can be solved in a total of $O(N\log d)$ time and $O(N)$ space.

As a byproduct of the above result, we also obtain the first non-trivial algorithm that maintains an explicit representation of the DAWG for fully-online left-to-right multiple strings, which runs in $O(N(\log\sigma+\log d))$ time and $O(N)$ space. By an explicit representation, we mean that every edge of the DAWG is implemented as a pointer. This DAWG construction does not require complicated table look-ups and thus also works on the pointer machine model.

Let $\Sigma$ be a general ordered alphabet. Any element of $\Sigma^{*}$ is called a string. For any string $T$, let $|T|$ denote its length. Let $\varepsilon$ be the empty string, namely, $|\varepsilon|=0$. Let $\Sigma^{+}=\Sigma\setminus\{\varepsilon\}$. If $T=XYZ$, then $X$, $Y$, and $Z$ are called a prefix, a substring, and a suffix of $T$, respectively. For any $1\leq i\leq j\leq|T|$, let $T[i..j]$ denote the substring of $T$ that begins at position $i$ and ends at position $j$ in $T$. For any $1\leq i\leq|T|$, let $T[i]$ denote the $i$th character of $T$. For any string $T$, let $\mathsf{Suffix}(T)$ denote the set of suffixes of $T$, and for any set $\mathcal{T}$ of strings, let $\mathsf{Suffix}(\mathcal{T})$ denote the set of suffixes of all strings in $\mathcal{T}$. Namely, $\mathsf{Suffix}(\mathcal{T})=\bigcup_{T\in\mathcal{T}}\mathsf{Suffix}(T)$. For any string $T$, let $\overline{T}$ denote the reversed string of $T$, i.e., $\overline{T}=T[|T|]\cdots T[1]$. For any set $\mathcal{T}$ of strings, let $\overline{\mathcal{T}}=\{\overline{T}\mid T\in\mathcal{T}\}$.

For ease of description, we assume that each string $T_{i}$ in the collection $\mathcal{T}$ terminates with a unique character $\$_{i}$ that does not appear elsewhere in $\mathcal{T}$. However, our algorithms work without $\$_{i}$ symbols at the right end of strings as well.

A compacted trie is a rooted tree such that (1) each edge is labeled by a non-empty string, (2) each internal node is branching, and (3) the string labels of the out-going edges of each node begin with mutually distinct characters. The suffix tree [19] for a text collection $\mathcal{T}$, denoted $\mathsf{STree}(\mathcal{T})$, is a compacted trie which represents $\mathsf{Suffix}(\mathcal{T})$. The string depth of a node $v$ of $\mathsf{Suffix}(\mathcal{T})$ is the length of the substring that is represented by $v$. We sometimes identify node $v$ with the substring it represents. The suffix tree for a single string $T$ is denoted $\mathsf{STree}(T)$.

$\mathsf{STree}(\mathcal{T})$ has at most $2N-1$ nodes and thus $2N-2$ nodes, since every internal node of $\mathsf{STree}(\mathcal{T})$ is branching and there are $N$ leaves in $\mathsf{STree}(\mathcal{T})$. By representing each edge label $x$ with a triple $\langle k,i,j\rangle$ of integers such that $x=T_{k}[i..j]$, $\mathsf{STree}(\mathcal{T})$ can be stored with $O(N)$ space.

We define the suffix link of each non-root node $av$ of $\mathsf{STree}(\mathcal{T})$ with $a\in\Sigma$ and $v\in\Sigma^{*}$, by $\mathsf{slink}(av)=v$. For each explicit node $v$ and $a\in\Sigma$, we also define the reversed suffix link (a.k.a. Weiner link) by ${\mathsf{W\_link}}_{a}({v})=avx$, where $x\in\Sigma^{*}$ is the shortest string such that $avx$ is a node of $\mathsf{STree}(\mathcal{T})$. ${\mathsf{W\_link}}_{a}({v})$ is undefined if $av$ is not a substring of strings in $\mathcal{T}$. A Weiner link ${\mathsf{W\_link}}_{a}({v})=avx$ is said to be hard if $x=\varepsilon$, and soft if $x\in\Sigma^{+}$.

See the left diagram of Figure 1 for an example of $\mathsf{STree}(\mathcal{T})$ and Weiner links.

The directed acyclic word graph (DAWG in short) [2, 3] of a text collection $\mathcal{S}$, denoted $\mathsf{DAWG}(\mathcal{S})$, is a (partial) DFA which represents $\mathsf{Suffix}(\mathcal{S})$. It is proven in [3] that $\mathsf{DAWG}(\mathcal{S})$ has at most $2N-1$ nodes and $3N-4$ edges for $N\geq 3$. Since each DAWG edge is labeled by a single character, $\mathsf{DAWG}(\mathcal{S})$ can be stored with $O(N)$ space. The DAWG for a single string $S$ is denoted $\mathsf{DAWG}(S)$.

A node of $\mathsf{DAWG}(\mathcal{S})$ corresponds to the substrings in $\mathcal{S}$ which share the same set of ending positions in $\mathcal{S}$. Thus, for each node, there is a unique longest string represented by that node. For any node $v$ of $\mathsf{DAWG}(\mathcal{S})$, let $\mathit{long}(v)$ denote the longest string represented by $v$. An edge $(u,a,v)$ in the DAWG is called primary if $|\mathit{long}(u)|+1=|\mathit{long}(v)|$, and is called secondary otherwise. For each node $v$ of $\mathsf{DAWG}(\mathcal{S})$ with $|\mathit{long}(v)|\geq 1$, let $\mathsf{slink}(v)=y$, where $y$ is the longest suffix of $\mathit{long}(v)$ which is not represented by $v$.

Suppose $S=\overline{\mathcal{T}}$. It is known (c.f. [2, 3, 4]) that there is a node $v$ in $\mathsf{STree}(\mathcal{T})$ iff there is a node $x$ in $\mathsf{DAWG}(\mathcal{S})$ such that $\mathit{long}(x)=\overline{v}$. Also, the hard Weiner links and the soft Weiner links of $\mathsf{STree}(\mathcal{T})$ coincide with the primary edges and the secondary edges of $\mathsf{DAWG}(\mathcal{S})$, respectively. In a symmetric view, the reversed suffix links of $\mathsf{DAWG}(\mathcal{S})$ coincide with the suffix tree $\mathsf{STree}(\mathcal{T})$ for $\mathcal{T}$.

See Figure 1 for some concrete examples of the aforementioned symmetry. For instance, the nodes $\mathtt{abaa}$ and $\mathtt{baa}$ of $\mathsf{STree}(\mathcal{T})$ correspond to the nodes of $\mathsf{DAWG}(\mathcal{S})$ whose longest strings are $\overline{\mathtt{abaa}}=\mathtt{aaba}$ and $\overline{\mathtt{baa}}=\mathtt{aab}$, respectively. Observe that both $\mathsf{STree}(\mathcal{T})$ and $\mathsf{DAWG}(\mathcal{S})$ have 19 nodes each. The Weiner links of $\mathsf{STree}(\mathcal{T})$ labeled by character $\mathtt{c}$ correspond to the out-going edges of $\mathsf{DAWG}(\mathcal{S})$ labeled by $\mathtt{c}$. To see another example, the three Weiner links from node $\mathtt{a}$ in $\mathsf{STree}(\mathcal{T})$ labeled $\mathtt{a}$, $\mathtt{b}$, and $\mathtt{c}$ correspond to the three out-going edges of node $\{\mathtt{a}\}$ of $\mathsf{DAWG}(\mathcal{S})$ labeled $\mathtt{a}$, $\mathtt{b}$, and $\mathtt{c}$, respectively. For the symmetric view, focus on the suffix link of the node $\{\mathtt{\$_{2}baab},\mathtt{baab}\}$ of $\mathsf{DAWG}(\mathcal{S})$ to the node $\{\mathtt{aab},\mathtt{ab}\}$. This suffix link reversed corresponds to the edge labeled $\mathtt{b\$_{2}}$ from the node $\mathtt{baa}$ to the node $\mathtt{baab\$_{2}}$ in $\mathsf{STree}(\mathcal{T})$.

We now see that the two following tasks are essentially equivalent:

• (A)

  Building $\mathsf{STree}(\mathcal{T})$ for a fully-online right-to-left text collection $\mathcal{T}$, using hard and soft Weiner links.

• (B)

  Building $\mathsf{DAWG}(\mathcal{S})$ for a fully-online left-to-right text collection $\mathcal{S}$, using suffix links.

A pointer machine [18] is an abstract model of computation such that the state of computation is stored as a directed graph, where each node can contain a constant number of data (e.g. integers, symbols) and a constant number of pointers (i.e. out-going edges to other nodes). The instructions supported by the pointer machine model are basically creating new nodes and pointers, manipulating data, and performing comparisons. The crucial restriction in the pointer machine model, which distinguishes it from the word RAM model, is that pointer machines cannot perform address arithmetics, namely, memory access must be performed only by an explicit reference to a pointer. While the pointer machine model is apparently weaker than the word RAM model that supports address arithmetics and unit-cost bit-wise operations, the pointer machine model serves as a good basis for modeling linked structures such as trees and graphs, which are exactly our targets in this paper. In addition, pointer-machines are powerful enough to simulate list-processing based languages such as LISP and Prolog (and their variants), which have recurrently gained attention.

First, we briefly review how Weiner’s algorithm for a single string $T$ adds a new leaf to the suffix tree when a new character $a$ is prepended to $T$. Our description of Weiner’s algorithm slightly differs from the original one, in that we use both hard and soft Weiner links while Weiner’s original algorithm uses hard Weiner links only and it instead maintains Boolean vectors indicating the existence of soft Weiner links.

Suppose we have already constructed $\mathsf{STree}(T)$ with hard and soft Weiner links. Let $\ell$ be the leaf that represents $T$. Given a new character $a$, Weiner’s algorithm climbs up the path from the leaf $\ell$ until encountering the deepest ancestor $v$ of $\ell$ that has a Weiner link ${\mathsf{W\_link}}_{a}({v})$ defined. If there is no such ancestor of $\ell$ above, then a new leaf representing $aT$ is inserted from the root $r$ of the suffix tree. Otherwise, the algorithm follows the Weiner link ${\mathsf{W\_link}}_{a}({v})$ and arrives at its target node $u={\mathsf{W\_link}}_{a}({v})$. There are two sub-cases:

• (1)

  If ${\mathsf{W\_link}}_{a}({v})$ is a hard Weiner link, then a new leaf $\hat{\ell}$ representing $aT$ is inserted from $u$.

• (2)

  If ${\mathsf{W\_link}}_{a}({v})$ is a soft Weiner link, then the algorithm splits the incoming edge of $u$ into two edges by inserting a new node $y$ as a new parent of $u$ such that $|y|=|v|+1$ (See also Figure 2). A new leaf representing $aT$ is inserted from this new internal node $y$. We also copy each out-going Weiner link ${\mathsf{W\_link}}_{c}({u})$ from $u$ with a character $c$ as an out-going Weiner link ${\mathsf{W\_link}}_{c}({y})$ from $y$ so that their target nodes are the same (i.e. ${\mathsf{W\_link}}_{c}({u})$ = ${\mathsf{W\_link}}_{c}({y})$). See also Figure 3. Then, a new hard Weiner link is created from $v$ to $y$ with label $a$, in other words, an old soft Weiner link ${\mathsf{W\_link}}_{a}({v})=u$ is redirected to a new hard Weiner link ${\mathsf{W\_link}}_{a}({v})=y$. In addition, all the old soft Weiner links of ancestors $z$ of $v$ such that ${\mathsf{W\_link}}_{a}({z})=u$ in $\mathsf{STree}(T)$ have to be redirected to new soft Weiner links ${\mathsf{W\_link}}_{a}({z})=y$ in $\mathsf{STree}(aT)$. These redirections can be done by keeping climbing up the path from $v$ until finding the deepest node $x$ that has a hard Weiner link with character $a$ pointing to the parent of $u$ in $\mathsf{STree}(T)$.

In both Cases (1) and (2) above, new soft Weiner links ${\mathsf{W\_link}}_{a}({x})=\hat{\ell}$ are created from every node $x$ in the path from $\ell$ to the child of $v$.

The running time analysis of the above algorithm has three phases.

• (a)

  In both Cases (1) and (2), the number of nodes from leaf $\ell$ for $T$ to $v$ is bounded by the number of newly created soft Weiner links. This is amortized $O(1)$ per new character since the resulting suffix tree has a total of $O(n)$ soft Weiner links [2], where $n=|T|$.

• (b)

  In Case (2), the number of out-going Weiner links copied from $u$ to $y$ is bounded by the number of newly created Weiner link, which is also amortized $O(1)$ per new character by the same argument as (a).

• (c)

  In Case (2), the number redirected soft Weiner links is bounded by the number of nodes from $v$ to $x$. The analysis by Weiner [19] shows that this number of nodes from $v$ to $x$ can be amortized $O(1)$.

Wrapping up (a), (b), and (c), the total numbers of visited nodes, created Weiner links, and redirected Weiner links through constructing $\mathsf{STree}(T)$ by prepending $n$ characters are $O(n)$. Thus Weiner’s algorithm constructs $\mathsf{STree}(T)$ in right-to-left online manner in $O(n\log\sigma)$ time with $O(n)$ space, where the $\log\sigma$ term comes from the cost for maintaining Weiner links of each node in the lexicographically sorted order by e.g. a standard balanced binary search tree.

Since this algorithm correctly maintains all (hard and soft) Weiner links, it builds $\mathsf{DAWG}(S)$ for the reversed string $S=\overline{T}$ in a left-to-right manner, in $O(n\log\sigma)$ time with $O(n)$ space. In other words, this version of Weiner’s algorithm is equivalent to Blumer et al.’s DAWG online construction algorithm.

We remark that the aforementioned version of Weiner’s algorithm, and equivalently Blumer et al.’s algorithm, work on the pointer machine model as they do not use address arithmetics nor table look-ups.

When Weiner’s algorithm is applied to fully-online right-to-left construction of $\mathsf{STree}(\mathcal{T})$, the amortization in Analysis (c) does not work. Namely, it was shown by Takagi et al. [16] that the number of redirected soft Weiner links is $\Theta(N\min(K,\sqrt{N}))$ in the fully-online setting for multiple $K$ strings. A simpler upper bound $O(NK)$ immediately follows from an observation that the insertion of a new leaf for a string $T_{i}$ in $\mathcal{T}$ may also increase the depths of the leaves for all the other $K-1$ strings $T_{1},\ldots,T_{i-1},T_{i+1},\ldots,T_{K}$ in $\mathcal{T}$. Takagi et al. then obtained the aforementioned improved $O(N\min(K,\sqrt{N}))$ upper bound, and presented a lower bound instance that indeed requires $\Omega(N\min(K,\sqrt{N}))$ work. It should also be noted that the original version of Weiner’s algorithm that only maintains Boolean indicators for the existence of soft Weiner links, must also visit $\Theta(N\min(K,\sqrt{N}))$ nodes [16].

Takagi et al. gave a neat way to overcome this difficulty by using the nearest marked ancestor (NMA) data structure [20] for a rooted tree. This NMA data structure allows for making unmarked nodes, splitting edges, inserting new leaves, and answering NMA queries in $O(1)$ amortized time each, in the word RAM model of machine word size $\Omega(\log N)$. Takagi et al. showed how to skip the nodes between $v$ to $x$ in $O(1)$ amortized time using a single NMA query on the NMA data structure associated to a given character $a$ that is prepended to $T$. They also showed how to store $\sigma$ NMA data structures for all $\sigma$ distinct characters in $O(N)$ total space. Since the amortization argument (c) is no more needed by the use of the NMA data structures, and since the analyses (a) and (b) still hold for fully-online multiple strings, the total number of visited nodes was reduced to $O(N)$ in their algorithm. This led their construction in $O(N\log\sigma)$ time and $O(N)$ space, in the word RAM model.

Takagi et al.’s $\Theta(N\min(K,\sqrt{N}))$ bound also applies to the number of visited nodes and that of redirected secondary edges of $\mathsf{DAWG}(\mathcal{S})$ for multiple strings in the fully-online setting. Instead, they showed how to simulate secondary edge traversals of $\mathsf{DAWG}(\mathcal{S})$ in $O(\log\sigma)$ amortized time each, using the aforementioned NMA structures. We remark that their data structure is only an implicit representation of $\mathsf{DAWG}(\mathcal{S})$ in the sense that the secondary edges are not explicitly stored.

In this section, we present our new algorithm that constructs the suffix tree for a fully-online right-to-left string collection.

Consider a collection $\mathcal{T}^{\prime}=\{T_{1},\ldots,T_{K}\}$ of $K$ strings. Suppose that we have built $\mathsf{STree}(\mathcal{T}^{\prime})$ and that for each string $T_{i}\in\mathcal{T}^{\prime}$ we know the leaf $\ell_{i}$ that represents $T_{i}$.

In our fully-online setting, any new character from $\Sigma$ can be prepended to any string in the current string collection $\mathcal{T}$. Suppose that a new character $a\in\Sigma$ is prepended to a string $T$ in the collection $\mathcal{T}^{\prime}$, and let $\mathcal{T}=(\mathcal{T}^{\prime}\setminus\{T\})\cup\{aT\}$ be the collection after the update. Our task is to update $\mathsf{STree}(\mathcal{T}^{\prime})$ to $\mathsf{STree}(\mathcal{T})$.

Our approach is to reduce the sub-problem of redirecting Weiner links to the ordered split-insert-find problem that operates on ordered sets over dynamic universe of elements, and supports the following operations and queries efficiently:

• $\bullet$

  Make-set, which creates a new list that consists only of a single element;

• $\bullet$

  Split, which splits a given set into two disjoint sets, so that one set contains only smaller elements than the other set;

• $\bullet$

  Insert, which inserts a new single element to a given set;

• $\bullet$

  Find, which answers the name of the set that a given element belongs to.

Recall our description of Weiner’s algorithm in Section 3.1 and see Figure 2. Consider the set of in-coming Weiner links of node $u$ before updates (the left diagram of Figure 2), and assume that these Weiner links are sorted by the length of the origin nodes. After arriving the node $v$ in the climbing up process from the leaf for $T$, we take the Weiner link with character $a$ and arrive at node $u$. Then we access the set of in-coming Weiner-links of $u$ by a find query. When we create a new internal node $y$ as the parent of the new leaf for $aT$, we split this set into two sets, one as the set of in-coming Weiner links of $y$, and the other as the set of in-coming Weiner links of $u$ (see the right diagram of Figure 2). This can be maintained by a single call of a split operation.

Now we pay our attention to the copying process of Weiner links described in Figure 3. Observe that each newly copied Weiner links can be inserted by a single find operation and a single insert operation to the set of in-coming Weiner links of ${\mathsf{W\_link}}_{u}({c})$ for each character $c$ where ${\mathsf{W\_link}}_{u}({c})$ is defined.

Now we prove the next lemma:

Our ordered split-insert-find problem is a special case of the union-split-find problem on ordered sets, since each insert operation can be trivially simulated by make-set and union operations. Link-cut trees of Sleator and Tarjan [14] for a dynamic forest support make-tree, link, cut operations and find-root queries in $O(\log d)$ time each. Since link-cut trees can be used to path-trees, make-set, insert, split, and find in the ordered split-insert-find problem can be supported in $O(\log d)$ time each. Since link-cut trees work on the pointer machine model, this leads to a pointer-machine algorithm for our fully-online right-to-left construction of the suffix tree for multiple strings with $f=O(\log d)$. Here, in our context, $d$ denotes the maximum number of in-coming Weiner links to a node of the suffix tree.

A potential drawback of using link-cut trees is that in order to achieve $O(\log d)$-time operations and queries, link-cut trees use some auxiliary data structures such as splay trees [15] as its building block. Yet, in what follows, we describe that our ordered split-insert-find problem can be solved by a simpler balanced tree, AVL-trees [1], retaining $O(N(\log\sigma+\log d))$-time and $O(N)$-space complexities.

The next theorem immediately follows from Theorem 1.

We emphasize that Theorem 2 gives the first non-trivial algorithm that builds an explicit representation of the DAWG for fully-online multiple strings. Recall that a direct application of Blumer et al.’s algorithm to the case of fully-online $K$ multiple strings requires to visit $\Theta(N\min(K,\sqrt{N}))$ nodes in the DAWG, which leads to $O(N\min(K,\sqrt{N})\log\sigma)=O(N^{1.5}\log\sigma)$-time construction for $K=\Theta(\sqrt{N})$.

It should be noted that after all the $N$ characters have been processed, it is easy to modify, in $O(N)$ time in an offline manner, this representation of the DAWG so that each edge traversal takes $O(\log\sigma)$ time.

It is known that sorting a length-$N$ sequence of $\sigma$ distinct characters is an obvious lower bound for building the suffix tree [6] or alternatively the DAWG. This is because, when we build the suffix tree or the DAWG where the out-going edges of each node are sorted in the lexicographical order, then we can obtain a sorted list of characters at their root. Thus, $\Omega(N\log\sigma)$ is a comparison-based model lower bound for building the suffix tree or the DAWG. Since Takagi et al.’s $O(N\log\sigma)$-time algorithm [16] works only on the word RAM model, in which faster integer sorting algorithms exist, it would be interesting to explore some cases where our $O(N(\log\sigma+\log d))$-time algorithms for a weaker model of computation can perform in optimal $O(N\log\sigma)$ time.

It is clear that the maximum number $d$ of in-coming Weiner links to a node is bounded by the total length $N$ of the strings. Hence, in case of integer alphabets of size $\sigma=N^{O(1)}$, our algorithms run in optimal $O(N\log\sigma)=O(N\log N)$ time.

For the case of smaller alphabet size $\sigma=\mathrm{polylog}(N)$, the next lemma can be useful:

We note that the height of the suffix tree for multiple strings is bounded by the length of the longest string in the collection. In many applications such as time series from sensor data, it would be natural to assume that all the $K$ strings in the collection have similar lengths. Hence, when the collection consists of $K=N/\mathrm{polylog}(N)$ strings of length $\mathrm{polylog}(N)$ each, we have $d=\mathrm{polylog}(N)$. In such cases, our algorithms run in optimal $O(N\log\sigma)=O(N\log\log N)$ time.

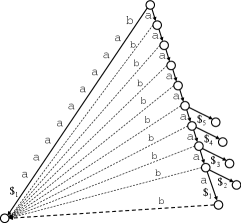
The next lemma shows some instance over a binary alphabet of size $\sigma=2$, which requires a certain amount of work for the splitting process.

Since $\sqrt{N}\log N=o(N)$, the $\sqrt{N}\log N$ term is always dominated by the $N\log\sigma$ term. It is left open whether there exists a set of strings with $\Theta(N)$ character additions, each of which requires splitting a set that involves $N^{O(1)}$ in-coming Weiner links. If such an instance exists, then our algorithm must take $\Theta(N\log N)$ time in the worst case.