Plasmonic tweezers based on connected nanoring apertures

The three-dimensional (3D) nano-aperture platform is illustrated in Fig. 1(a). Nanoring air apertures are engraved on a 50 nm thick gold (Au) metal layer deposited on a quartz substrate. Narrow nanoslot regions are formed by inserting connecting nanogaps between the ring apertures. The plasmonic substrate consists of a 12 (x-direction) $\times$ 13 (y-direction) array of individual nanoring apertures that are milled using the focussed ion beam (FIB) technique in a 50 nm thick Au film. Scanning electron microscope (SEM) images are used to obtain the dimensions of the nano-apertures, as shown in Fig. 1(b). The outer diameter of the nanoring is $d_{out}$= $285.14~{}\pm~{}3.73$ nm, the period of the array, $\Lambda$ = $361.71~{}\pm~{}1.29$ nm, the width of the connecting nanoslots (gap size between the two tips) $w_{slot}=~{}28.08~{}\pm~{}6.04$ nm, and the inner diameter of the coaxial inner disks, $d_{in}$, are 0 nm, $149.59~{}\pm~{}2.08$ nm, $173.51~{}\pm~{}2.18$ nm, and $195.28~{}\pm~{}1.71$ nm.

The incident light is polarised along the y-axis to highly confine the electric field (E-field) at the nanoslot area. We use the finite element method (FEM) with the COMSOL Multiphysics software package to simulate the E-field distribution and the absorption spectra of the devices. We apply the time-averaged Maxwell’s stress tensor [27] method to calculate the optical gradient force acting on a 20 nm PS particle. The geometric parameters used in numerical simulations are: $d_{out}=285$ nm, $\Lambda=360$ nm, $w_{slot}=40$ nm, and $d_{in}=0,~{}150,~{}175,~{}200$ nm. We assume that the 20 nm particles are trapped 5 nm away from the surface of the device. To obtain good resolution for the mesh size at the particle’s surface, we choose the nanoslot width to be 20 nm larger than the particle diameter. The Maxwell’s stress tensor is applied on a surrounding shell 2 nm away from the particle’s surface. Figure 1(c) shows an example of numerical simulations of the E-field distribution for the xy- and yz-planes with a particle positioned at x = 0 nm and z = 20 nm (the equilibrium position).

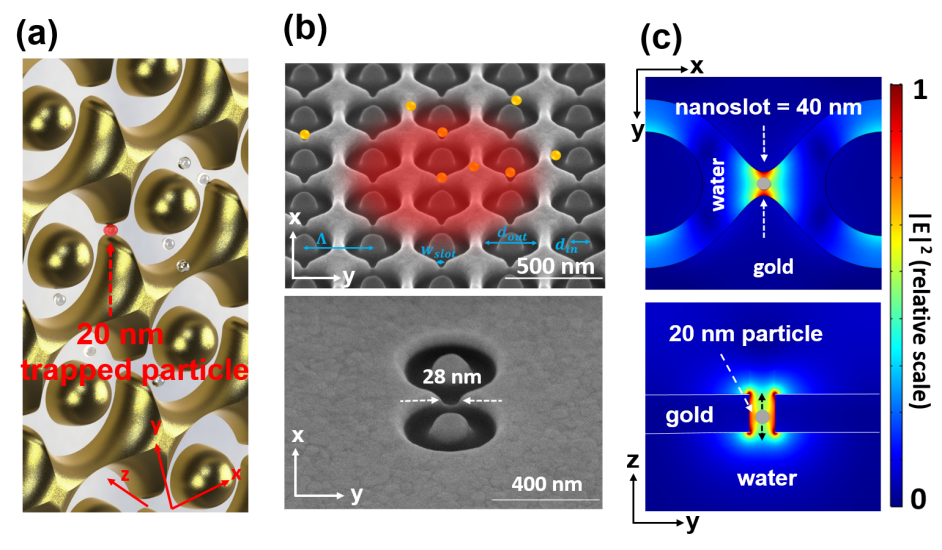
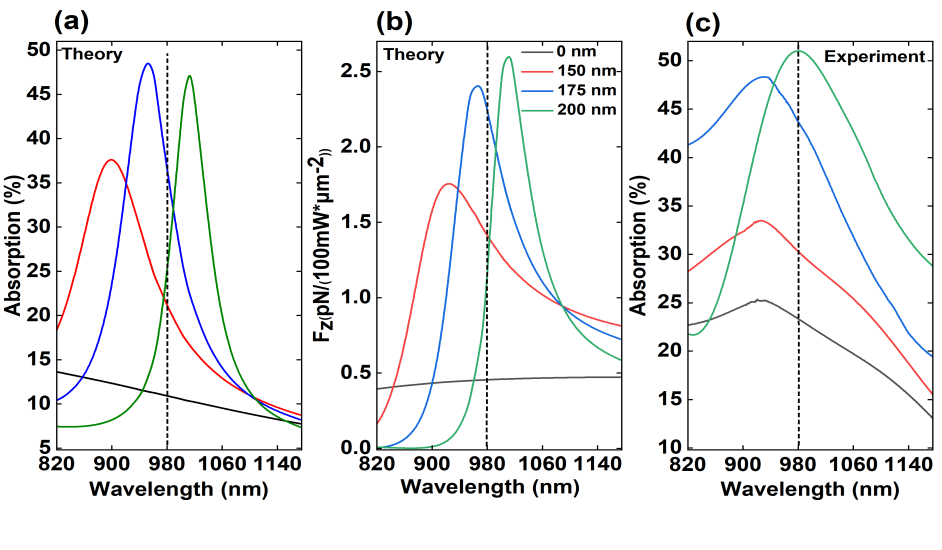
Absorption peak spectra are used as indicators of the resonance positions for the various structures used in the study. Figure 2(a) shows the theoretical absorption spectra for all the structures with varying inner disk diameters, $d_{in}$ = 0 - 200 nm, in water solution. Note that, with increased inner disk size, the absorption peak is red-shifted, which allows us to tune the required excitation laser towards the experimental wavelength of 980 nm. Of the four devices, the 175 nm inner disk design shows the highest theoretical absorption peak at 980 nm (vertical dotted line in Fig. 2(a)). In Figure 2(b), we plot the theoretical optical trapping force along the z-axis (light propagation direction), acting on a 20 nm PS nanoparticle at ($x,y,z)~{}=~{}(0,0,-4)$ nm position, where the localised field intensity is highest, as a function of the excitation laser wavelength. For excitation at 980 nm, the 175 nm design exerts the strongest theoretical optical force, of about 2.24 pN/(100 mW$\cdot$ $\mu$m^-2), on the nanoparticle. We see that the theoretical absorption spectra and $z$-component of the optical trapping force show similar curve trends. However, the theoretical trapping force peak positions show a slight red-shift towards the 980 nm excitation wavelength compared to the theoretical absorption resonance peaks. It is worth noting that the optical force is relatively constant for the 0 nm design (no inner disk) within this wavelength range.

To perform the experimental measurement of absorption, a microspectrophotometer (MCRAIC 20/30 PV) is used to measure the reflection, R, and transmission, T, spectra of the plasmonic devices in deionized water. The absorption, A, is determined from the following : ${A(\%)}=100({\%})-T(\%)-R(\%)$ and indicates the resonance peak position for the nanoring array structures, see Fig. 2(c). We see that the wavelength is blue-shifted by approximately 20 nm compared to the theoretical curves (Fig. 2(a)). We will discuss this discrepancy in the following sections. Moreover, absorption spectra artifacts were observed for inner disk diameters of 0 nm, 150 nm, and 175 nm. This is a systematic error caused by the detector changes (from the visible to the near-infrared regime) and leads to spurious peaks on the absorption spectrum, (Fig. 2(c)). However, the experimental trapping laser beam at 980 nm is at a value far from these peaks. This allows us to extract information on the enhancement of the absorption spectrum for each plasmonic configuration.

The optical trapping force, its corresponding potential, and trap stiffness for a 20 nm PS particle in the proximity of the 3D plasmonic nanoslot area are numerically calculated using the COMSOL Multiphysics software package. We assume that the particle is in the water domain of the xy-plane and sweep the particle along the z-axis (see Fig. 1(b)). We obtain the potentials by integrating the corresponding forces along the z-axis. The incident laser intensity is 100 mW/$\mu$m² at 980 nm.

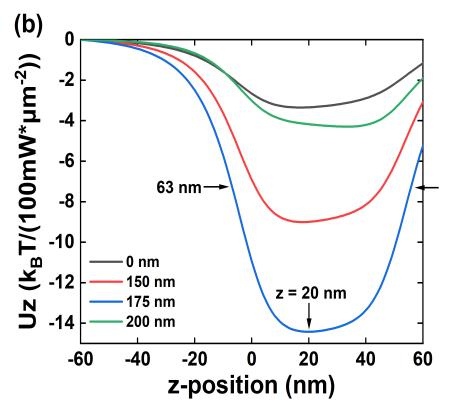
In our model, the plane at z = 0 nm is the boundary between the Au film and the water domain. The thickness of the Au film is 50 nm, thus for positions in the range of 0 - 50 nm along $z$ the particle is within the water-filled nanoslot region of the Au film. The optical force has a positive sign when the particle is attracted towards the SiO₂ domain and a negative sign indicates a repulsive force in the opposite direction. Moreover, the equilibrium position for trapped particles is located at z = 20 nm, i.e., inside the nanoslot area, for all designs. Figures 3(a) and (b) show the calculated optical forces and their corresponding potentials along the z-axis for four different nanodisk structures.

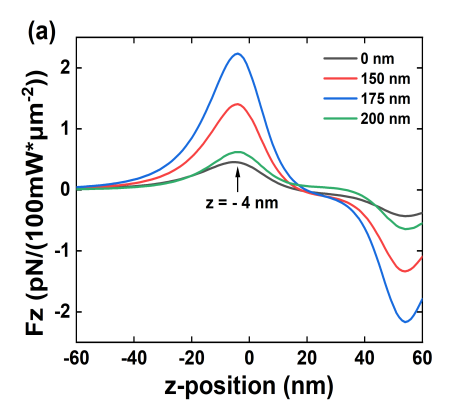
We also calculate the trapping potentials along the x- and y-axis for the 175 nm inner disk diameter and at the z = -4  nm plane, where the strongest optical force is observed (data not shown). We obtain a full-width-at-half-maximum (FWHM) of the trapping wells in the x-direction to be 44 nm and 14.4 nm in the y-direction, which is almost four times narrower due to stronger trapping. This arises since the E-field is highly confined (i.e., stronger gradient) at the nanoslot along the y-direction.

Finally, the trap stiffness, $\kappa$, is calculated for the 175 nm inner disk design, along all three axes. We use the harmonic oscillator equation, $F=\kappa\Delta r$, where $F$ is the maximum optical force acting on the nanoparticle for each axis and $\Delta r$ is the FWHM/2. We also normalise all values to 1 mW/$\mu$m² incident light intensity. We determine that $\kappa_{x}=0.55$ fN/nm, $\kappa_{y}=~{}3.72$ fN/nm, and $\kappa_{z}=~{}0.71$ fN/nm. The total trap stiffness is $\kappa_{tot}=\sqrt{\kappa_{x}^{2}+\kappa_{y}^{2}+\kappa_{z}^{2}}=3.82$ fN/nm.

The structure with the 175 nm inner disk diameter has the highest theoretical absorbance efficiency, provides the maximum theoretical optical force on a 20 nm particle, and creates the deepest trapping potential of -14.42$k_{B}$T/(100 mW/$\mu$m²). As mentioned previously, there is a 20 nm blue-shift of the experimental absorption peak positions compared to theoretical calculations. We observe that the fabricated 200 nm design nanodisk shows the strongest experimental absorbance at 980 nm (vertical dashed line in Fig. 2(c)). We assume that this discrepancy arises from imperfections during the fabrication process leading to rounded edges in the structure’s features, in contrast to sharp edges in simulations. Based on theoretical interpretations, we conclude here that the 175 nm nanodisk structure should provide the strongest experimental optical trapping force on a 20 nm PS particle in water solution for the excitation wavelength of 980nm.

The experimental approach is described in our previous work [25]. In brief, for nanoparticle trapping experiments, a tunable, continuous-wave (cw) Ti:Sapphire laser (MBR110 Coherent) is used at 980 nm. The laser spot diameter at the sample plane is around 2 $\mu$m. The number of nanorings that can be excited on the plasmonic substrates is 25, based on the size of the incident trapping laser spot. A high numerical aperture (N.A.= 1.3) oil immersion objective lens (OLYMPUS UPlanFL N 100$\times$) is used to focus the trapping beam onto the plasmonic substrate. We control the incident power of the trapping beam, which is limited to a maximum of 7.7 mW, at the sample plane, while the polarisation of the trapping laser is along the y-direction (see Fig. 1). A trapping event is detected by collecting the transmitted laser light through a 50$\times$ objective lens (Nikon CF Plan) and sending it to an avalanche photodiode (APD430A/M, Thorlabs). The APD signal is recorded using a data acquisition board at a frequency of 100 kHz with a LabVIEW program. When a 20 nm particle is trapped in one connecting nanoslot, a sharp increase in transmission is observed. The transmission level returns to its initial value when there is no particle at the trapping point. The plasmonic substrate is attached to a cover glass with adhesive microscope spacers, forming a microwell. The microwell contains 8 $\mu$L of PS nanoparticles with a mean diameter of 20 nm (Thermo Fisher Scientific, F8786) in heavy water with a concentration of 14 $\times$ 10¹¹ particles/ml. A small amount of surfactant (Detergent Tween 20 with 0.1% volume concentration) is used to minimize particle aggregation. The microwell is mounted and fixed on top of a piezoelectric translation stage.

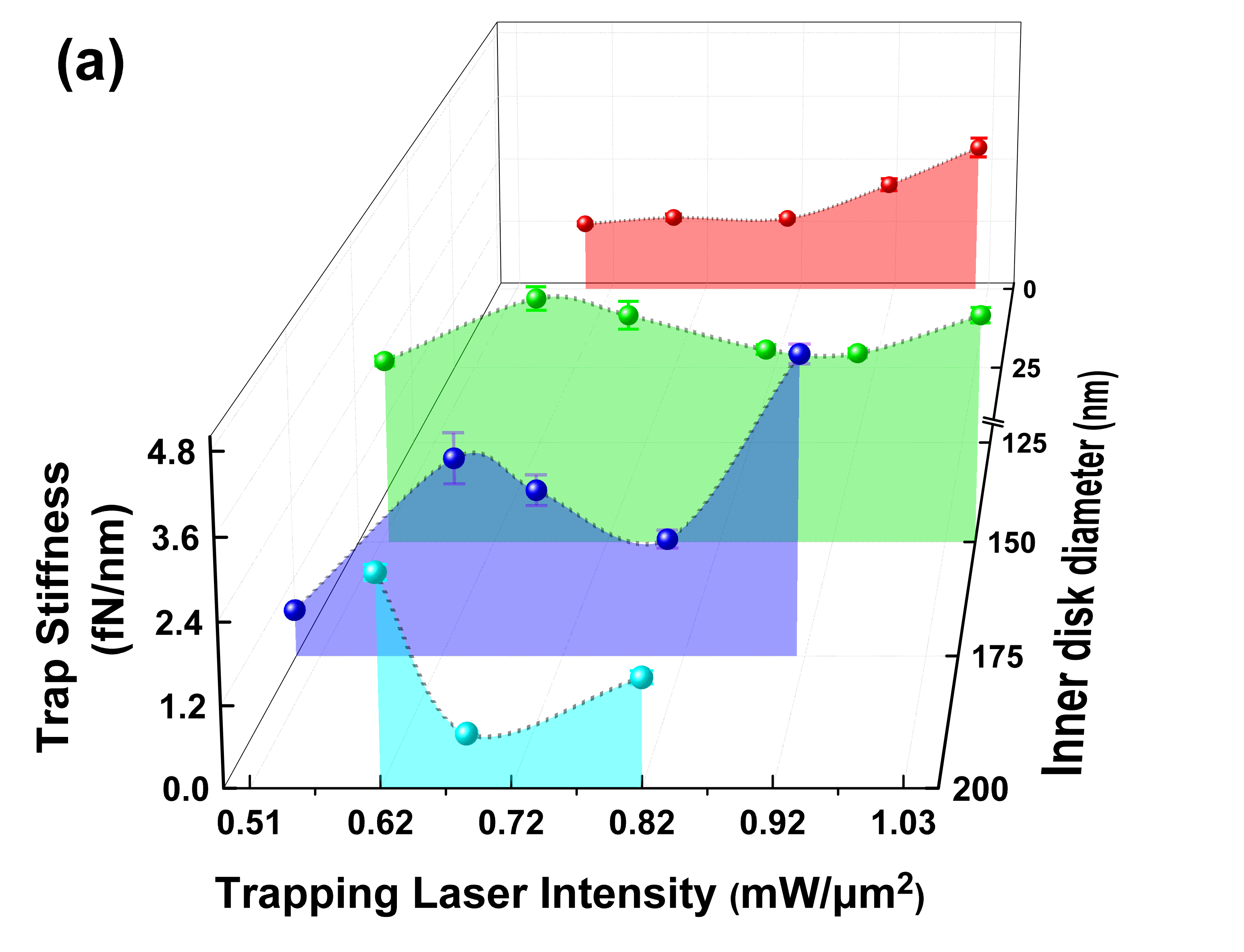
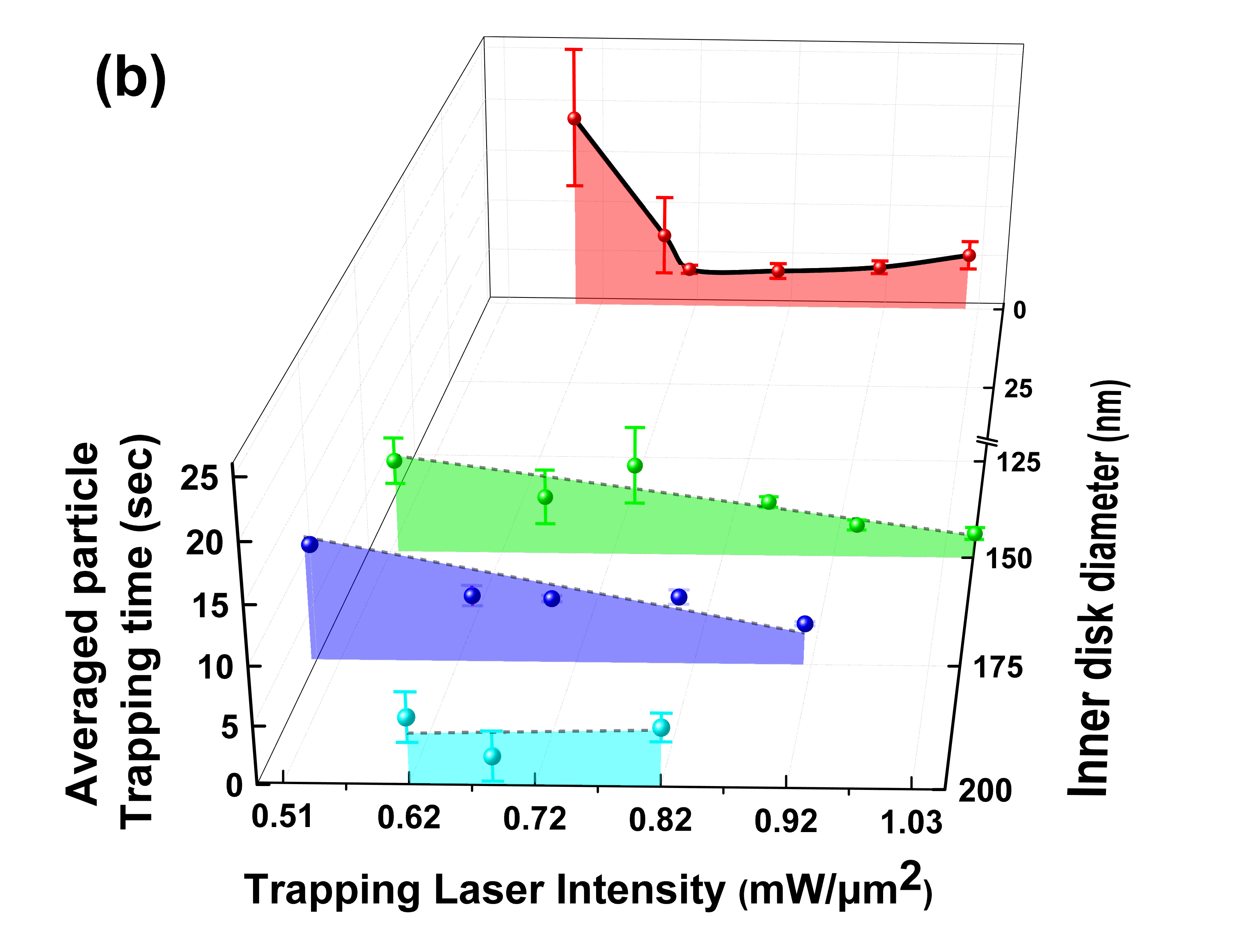
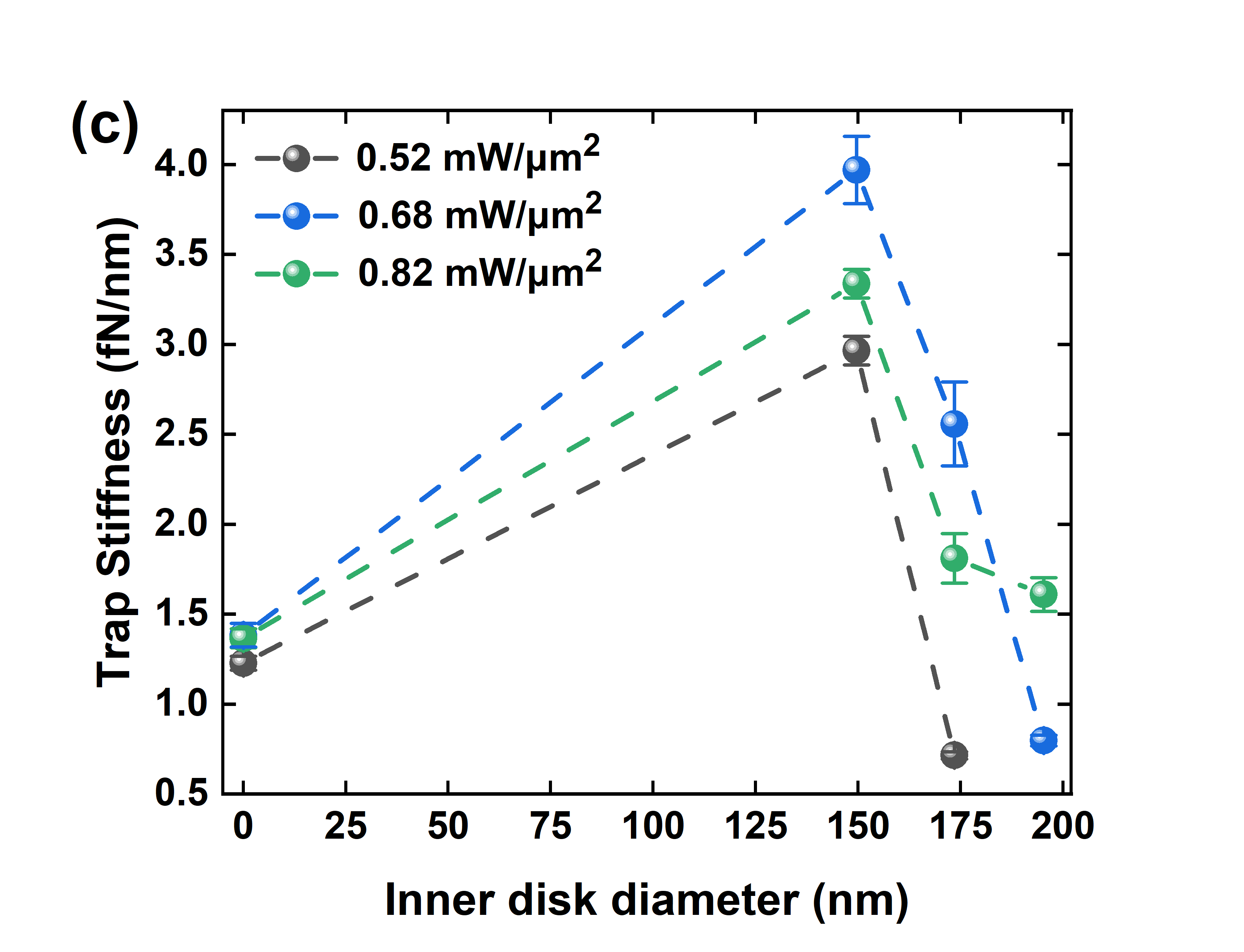
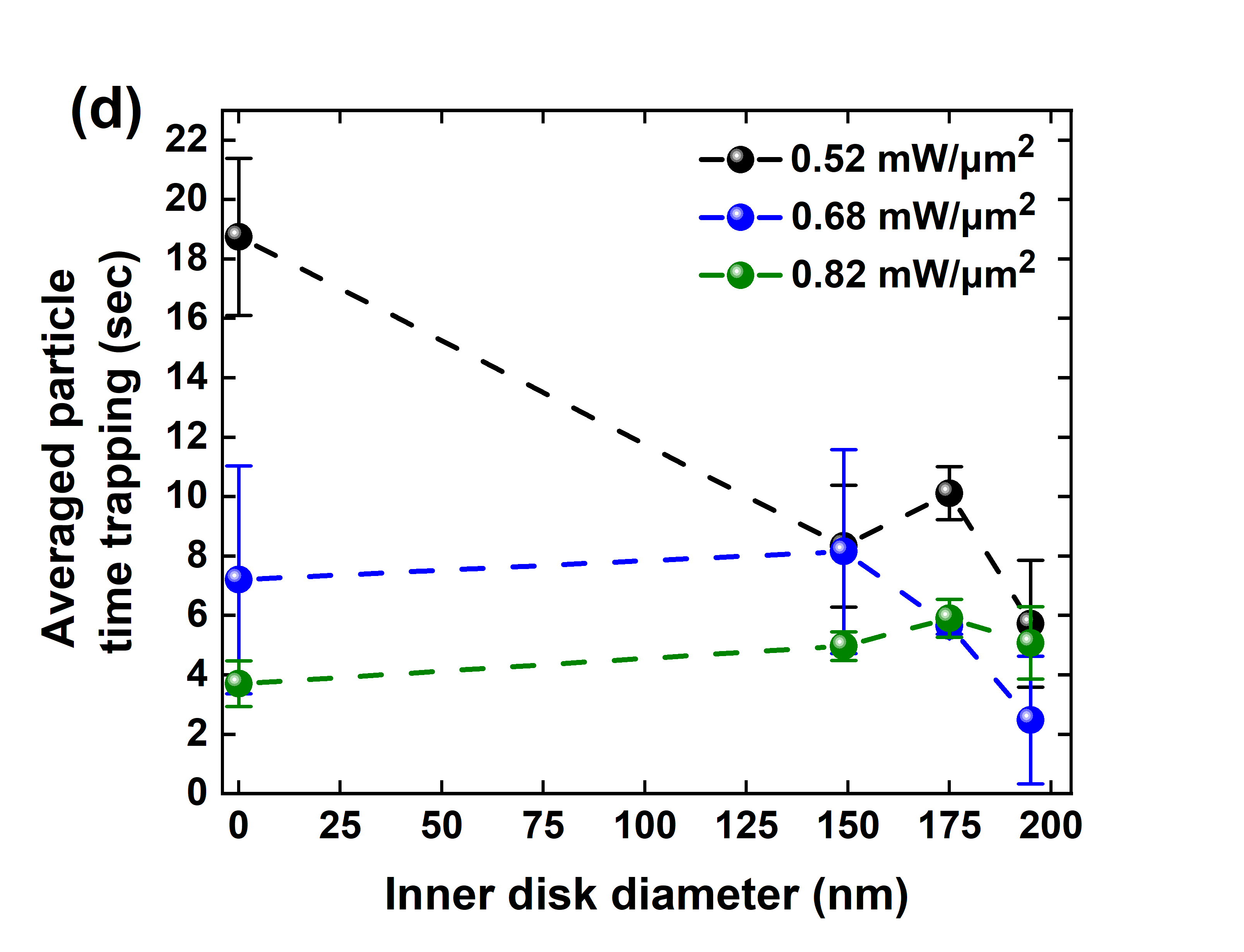
Figure 4(a) shows the measured trap stiffnesses, $\mathrm{\kappa}_{exp}$, for four different inner disk diameters, $d_{in}$, as a function of the incident laser intensity. We use the transient time method as discussed elsewhere [26, 24, 25]. We also consider Faxén’s correction to introduce a factored drag force that arises due to the surface roughness of the nanoring structure wall, as previously reported for nanoparticle trapping [26, 24, 25]. The trapping laser intensity ranges from 0.48 mW/$\mu$m² to 1.03 mW/$\mu$m². The experimental trap stiffness is the average over three multiple runs for each laser intensity. It should be noted that the range of the laser intensity varies for each configuration due to difficulties in achieving single particle trapping.

As expected, we observe an increase to the measured trap stiffnesses for larger inner disk structures compared to the no-disk configuration. When there is no disk (red curve in Fig. 4(a)), the trap stiffness is relatively constant for trapping laser intensities below 0.75 mW/$\mu$m² and increases linearly for higher trapping laser intensities. This behaviour changes for the nanoring array with $d_{in}$ = 149 nm (green curve in Fig. 4(a)), where the trap stiffness does not vary significantly as the incident laser intensity increases to 1.03 mW/$\mu$m². Surprisingly, as the inner disk diameter increases, larger fluctuations of the trap stiffness are evident and the expected linear behaviour is not observed. A maximum trap stiffness is achieved for the 149 nm inner disk configuration (purple curve in Fig. 4(a)). We also note that the 195 nm inner disk diameter device (blue curve in Fig 4(a)), which is expected to produce the highest optical trapping force, does not provide the maximum trap stiffness for both low, 0.52 mW/$\mu$m², and high, 0.82 mW/$\mu$m², laser intensities, (Fig. 4(c)). Instead, the trap stiffness for larger inner disk diameters of 173 nm and 195 nm decreases compared to the 149 nm inner disk structure. Assuming that, as the inner disk diameter increases, thermal energy dissipation via the Joule effect increases upon resonant excitation, an increase of the spatial temperature distribution would result. This is due to collective heating of several hotspots in the illumination area of the nano-aperture array. This photo-induced plasmonic heating produces a temperature gradient across the device, resulting in the creation of a strong thermal fluidic flow, which could influence the trap stiffness values.

The maximum $\kappa_{exp}=3.50\pm 0.17$ fN/nm is obtained for the nanoring array with 149 nm inner disk diameter. The stiffness enhancement factor is approximately 2.9, 1.8, and 0.6 times for the nanoring arrays of $d_{in}$ = 149 nm, $d_{in}$ = 173 nm, and $d_{in}$ = 195 nm, respectively, when compared to the standard, $d_{in}$ = 0 nm, nanohole array configuration for an incident laser intensity of 1.0 mW/$\mu$m² at 980 nm. The high trap stiffness for the 149 nm inner disk diameter indicates the ability of this device to perform stable trapping and to hold nanoparticles at specific positions for long periods of time, thereby providing opportunities for effective low-power nanomanufacturing of nanoscale objects.

Figure 4(b) shows the average time taken to trap a single 20 nm particle as a function of the trapping laser intensity for different inner disk diameters. The trapping time is defined as the time from when the trapping laser is turned on (t = 0) to the transmission signal’s first observed discrete step, indicating the first particle trapping event. The experimental trapping time is taken from the average values observed over three multiple runs. The error bars represent the standard deviation of the average trapping time measurements. We also assume that, as the trapping laser intensity increases, the spatial temperature distribution increases, producing buoyancy-driven natural convection due to the fluid’s density gradient. This leads to an increase in the probability of trapping a nanoparticle in the flow, delivering it to the illuminated area, thus reducing the average particle trapping time. We also note that, for low laser intensities, the array of nano-apertures (0 nm inner disk) provides the longest particle diffusion times (Fig. 4(d)). Specifically, for 0.55 mW/$\mu$m² laser intensity, the trapping time for the 0 nm and 149 nm inner disk designs is 18.7 sec and 8.3 sec, respectively. A linear behaviour of the average particle trapping time as a function of laser intensity is observed for configurations with 149 nm and 173 nm inner disk diameters with slopes of 1.72 $\pm$ 0.35 s/(mW/$\mu$m²) and 2.53 $\pm$ 0.65 s/(mW/$\mu$m²), respectively. Figure 4(d) shows that the average particle trapping time approaches a minimum value at around 4 seconds for all nanodisk designs when higher laser intensities up to 0.82 mW/$\mu$m² are used.

The authors would like to thank M. Ozer and S. P. Mekhail for technical assistance, M. Sergides for initial contributions to the experimental work, and OIST editing section for reviewing the manuscript.

This work was partly funded by the Okinawa Institute of Science and Technology Graduate University, Onna-San, Okinawa, Japan. DGK acknowledges support from JSPS Grant-in-Aid for Scientific Research (C) Grant Number GD1675001.