Planar two-region multi-partite maximally entangled states
Abstract
In entanglement theory, there are different methods to consider one state being more entangled than another. The ”maximally”
entangled states in a multipartite system can be defined from an axiomatic perspective. According to different criteria for selection, there are many specific types of quantum maximally entangled states, such as absolutely maximally entangled state, planar maximally entangled state and so on. In this paper we propose a new type of maximally entangled states, the planar two-region multipartite maximally entangled state. The requirement condition of this maximally entangled state is weak than that of the absolutely maximally entangled state and different from that of the planar maximally entangled state. We show that there are the two-region four-partite maximally entangled states in 4-qubit and 7-qubit planar systems, although there is no absolutely maximally entangled state in these systems. It is proved that there are the planar two-region four-partite maximally entangled states in both even particle quantum systems and odd particle quantum systems. Additionally, based on some planar two-region four-partite maximally entangled states, the new planar two-region four-partite maximally entangled states are generated. We also provide some important examples of the planar two-region multi-partite maximally entangled states.
pacs:
03.67.Mn, 03.65.Ud, 03.67.-aI Introduction
Multipartite quantum entanglement Einstein ; Werner ; Horodecki is a distinctive feature of quantum mechanics and responsible for numerous practical tasks Nielsen . So quantum entanglement is an essential constituent part of quantum information and at the same time the subject of philosophical debates Horodecki . By far bipartite entangled states have been studied sufficiently, however the knowledge about multipartite states is far from perfect. From both a theoretical and practical perspective, multipartite entangled states are a very important resource in quantum information science.
It is well-known that the maximally entangled states (MES) play a very important role in practical quantum information processing. However, in fact there are different ways to consider one state to be more entangled than another. A method for defining ”maximally” entangled states in multipartite systems is based on an axiomatic approach. By using this method Gisin and Bechmann-Pasquinucci identify -qubit Greenberger-Horne-Zeilinger (GHZ) states as maximally entangled in -qubit systems Gisin . The reason for regarding these states as maximally entangled may be that GHZ states of qubits maximally violate the Bell-Klyshko inequalities Klyshko . Moreover, Chen proved that GHZ states in -qubit systems and the states obtained from them by local unitary transformations are the unique family of states which show such a maximal violation Chen . Recently, the absolutely maximally entangled (AME) states have been defined and discussed Helwig ; Raissi ; limaosheng . The characterization of AME states of an -particle quantum system is that any collection of particles are in a maximally mixed state, where, is the floor function. Well-known examples are the Bell and GHZ states on two and three parties respectively. Obviously, the 4-qubit GHZ state is not a absolutely maximally entangled state.
According to different criteria 1 ; 2 ; 3 ; 4 ; 5 ; 6 , the maximally entangled states can be divided into multiple types 7 ; 8 ; 9 ; 10 ; 11 , such as the AME state and planar maximally entangled (PME) state. PME states have the property that any collection of adjacent particles in a planar -particle quantum system are in a completely mixed state 26 . Various maximally entangled states can be applied to quantum parallel teleportation Helwig ; 12 ; 13 ; 14 ; 15 , quantum secret sharing 16 ; 17 ; 18 and so on.
AME states do not exist in all possible Hilbert spaces . It has been demonstrated that for any -particle system, when the dimension of the Hilbert space of the subsystem is chosen large enough, one can find the AME states; however, for low local dimensions there are severe constraints. The existence of AME states composed of two-level systems was recently solved. For qubit systems (=2), AME states do only exist for , and 6 parties, whereas it has been shown that no AME states exist for 4, 7, 8, and more than 8 qubits Helwig ; 20 ; 21 ; 22 ; Higuchi ; Scott ; FHuber .
Compared with AME state, the PME state is one with a lower number of constraints. Hence there are many more PME states than AME states, and the PME states are a wider class of entangled states than the AME states. The AME states are a subclass of PME states, that is, any AME state is a PME state, but the converse is not true 26 . Is there other class of maximally entangled states except the AME states and PME states? In this paper we solve this problem by proposing a new class of maximally entangled states, called the planar two-region multipartite maximally entangled states. In Sec. II, we investigate a special case, the planar two-region four-partite maximally entangled states. Then in Sec. III, we study the exactly definition of this kind of maximally entangled states and prove that there exists this kind of maximally entangled state. A summary with some remarks is provided in Sec. IV.
II Planar two-region four-partite maximally entangled state
It was shown that there exist various PME states for any even number of qudits, and there are two distinct multiparameter classes of four-qudit PMEs 26 . One may ask if it is possible to search for a wider class of entangled states except AME states and PME states.
In this section we will answer the above problem by defining the planar two-region four-partite maximally entangled state first. Then we will show that there is this kind of maximally entangled state.
Assume that the structure of the planar quantum system consisting of particles can be divided into two regions , , and each region has two disconnected parts. In the region , one part has adjacent particles, and the other part has adjacent particles. At the same time we also require that one part of region has adjacent particles and the other part of the region has adjacent particles. As the two parts of region are not connected, so the only neighboring parts of each part of region are that of region . Evidently, for a given planar quantum system there can exist many structures. If a quantum state of the system satisfies that every subset of region in each possible quantum structure, is in a completely mixed state, then this state is called a planar two-region four-partite maximally entangled state, simply written as PKME state. Here is the dimension of the Hilbert space of single particle. Apparently, the requirement condition of this kind of maximally entangled state is weak than that of AME state and different from that of the planar maximally entangled state.
Next we will prove that there are PKME states for even and odd , respectively.
Suppose that a partition of particles of a quantum system is parted into parts and with , then a pure state of the quantum system can be written as 26
| (1) |
So the density matrix of part is
| (2) |
For to be the completely mixed state , it is necessary to demand that the states are orthogonal and with equal norm, and the states form a basis for the Hilbert space of the part 26 .
II.1 PKME states in a quantum system consisting of even number of particles
II.1.1 PKME state in a 4-qudit planar system
We start from a special case, in which there are qudits in a planar system, where is a positive integer. This planar -qudit system is depicted in figure 1.

It is easy to see that there are quantum structures satisfying the requirements of the PKME state. That is, there exist particle distributions satisfying that region consists of two nonadjacent parts and , region consists of two nonadjacent parts and , and each of , , and , has adjacent particles.
One can deduce that a state in a Hilbert space of qudits,
| (3) |
is a PKME state, where denotes a -dimensional complex space. Figure 2 shows the corresponding state structure.

Therefore, there exists the PKME state of a planar -qudit system.
II.1.2 The family of PKME states of a 4-qubit planar system
Let us consider a 4-qubit quantum system. The qubits are numbered as respectively. Clearly, there are two quantum structures in this system, which are
and can only be 1. Next we will give the family of the PKME states.
The state of the 4-qubit planar system can be expressed as
| (4) |
Then it can be written as
| (5) |
where
| (6) | ||||
According to the generalized Schmidt decomposition of multipartite quantum states Carteret , one can always take
| (7) |
by choosing a suitable basis. Thus we have
| (8) | ||||
Obviously, if and only if , quantum state can satisfy . As a matter of fact implies that the matrix
| (9) |
is a unitary matrix.
It is well-known that a unitary matrix has the properties: (a) Two different rows (columns) are orthogonal; (b) If there is an element whose magnitude is unit module, then all the other elements in the row and column are all 0 except for this element; (c) There is phase freedom globally.
Using the orthogonality of the first, second and third rows, one can obtain
| (10) |
The solutions of above equation can be divided the following two cases.
(i) . In this case, one must have and . Without loss of generality, we can choose , which means . Then the matrix becomes
| (11) |
where the matrix is a unitary matrix.
Therefore the quantum state can be expressed as
| (12) | ||||
It is easy to deduce that . Hence, the quantum state is a family of PKME(4, 1, 4, 2) states of 4-qubit planar system.
(ii) . In this case we can obtain by Eq.(10). Similarly, we get by using the orthogonality of the first, second and third columns. Thus the matrix reads
| (13) |
Evidently, if and only if the inner matrix and outer matrix are unitary matrices, then the matrix is a unitary matrix.
Hence in this case we have
| (14) | ||||
One can also derive that . Therefore is a PKME(4,1,4,2) state of a 4-qubit planar system, if and outer matrix are unitary matrices.
We use to denote the intersection set of and . Obviously, one has
| (15) |
where is a unitary matrix. Of course, the union consists of all PKME(4, 1, 4,2) states of a 4-qubit planar system. So there are PKME(4,1,4,2) states of the 4-qubit planar system, although there is no AME state of 4-qubit system.
Additionally, here we provide an example of PKME state of a 6-qubit planar system. The qubits are denoted as 1,2,3,4,5,6 in a planar circle. Clearly, there are 12 quantum structures
One can easily check that a quantum state in a Hilbert space
| (16) |
is a PKME(6,1,4,2) state, where .
II.1.3 The constructed PKME states of the quantum systems with even number of particles
Suppose that is a PKME state of a -qudit quantum system. We can construct a more complicated PKME state by using the controlled operators . Here and represent the control site and target site respectively, is a unitary matrix acting on the -th qudit 30 . That is
| (17) |
Evidently,
| (18) |
is also a PKME state of a -qudit planar quantum system.
For example, from an 8-qudit PKME state
| (19) |
one can make another PKME state
| (20) | ||||
where states must satisfy . Figure 3 shows that when the input state is state, namely an 8-qudit PKME state, then the output state is also a PKME.

By changing the order of action of the controlled operator in Eq.(18), we can construct another PKME state
| (21) |
The difference between Eq. (18) and Eq. (21) is the order of action of the controlled operators . By using state in Eq. (19), a new PKME state of an 8-qudit planar quantum system is
| (22) | ||||
which is illustrated in figure 4.

II.1.4 PKME state of the particle system
Let us first consider a special case , i.e., a 5-qubit quantum system. Five qubits in a planar circle system are numbered as 1,2,3,4,5, respectively. It is not difficult to check that the quantum state
| (23) |
is a PKME state. Here there are 5 quantum structures
Therefore, there exist PKME states of the planar quantum system with odd-particles.
Now we consider the generalized case, a -qubit planar system in a circle, where is an arbitrary positive integer. Each quantum structure consists of four parts . Here , , , and contain , , , and neighboring particles, respectively; region is composed of parts and , region is composed of parts and , as shown in figure 5. Clearly, there are quantum structures in this planar system.

A quantum state in a Hilbert space of the qubits
| (24) | ||||
is a PKME state, which is plotted in figure 6.

II.1.5 Constructed PKME state of a quantum system with odd number of particles
Suppose that state is a PKME state of a -qudit quantum system. One can generate a new PKME state
| (25) |
For example, one can use a 5-qubit PKME state
| (26) |
to construct another PKME state
| (27) | ||||
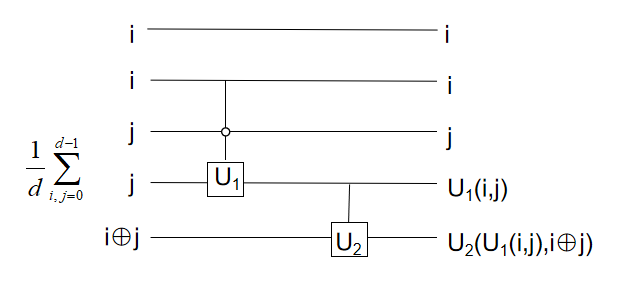
as depicted in figure 7, where and the state satisfies .

By changing the order of action of the controlled operators in Eq.(25) we can construct another PKME state
| (28) |
The difference between this state and the state stated by Eq.(25) is only the order of action of the controlled operator . Taking state in Eq.(26) as an example, the new PKME state of this 5-qubit system reads
| (29) | ||||
which is illustrated in figure 8. Here .
II.1.6 PKME(7,2,4,2) state
Let us consider a 7-qubit quantum system. There are 7 quantum structures
It is easy to prove that a quantum state in a Hilbert space of 7-qubit system
| (30) |
is a PKME(7,2,4,2) state. However, AME state of seven qubits do not exist.
III Planar two-region multi-partite maximally entangled state
In this section, we will generalize the definition of two-region four-partite maximally entangled state to the more generalized case. That is we will define two-region multi-partite maximally entangled state and prove that this kind of maximally entangled states do exist.
Consider a quantum system composed of particles in a planar circle, where the Hilbert space of each particle is a -dimensional complex space . Suppose that one can divide the particles into two-region , where () consists of parts (), and the particles in each part are adjacent, however are not neighbors, so do . Each is called a quantum structure. We also demand that region contains particles, region consists of particles. We use to denote the corresponding particle numbers of parts respectively. Here , . Obviously, for an particle system and fixed there are many quantum structures.
If a quantum state in the Hilbert space of the particle system satisfies that every subset of region in each possible quantum structure, is in a completely mixed state, then this state is called a planar two-region multi-partite maximally entangled state, simply written as PKME state. Here is the dimension of the Hilbert space of single particle and .
Clearly, the requirement condition of PKME states is weak than that of the absolutely maximally entangled state and different from that of the planar maximally entangled state.
Next we will give two examples of the planar two-region multi-partite maximally entangled states.
Example 1. Consider a -qubit system. It is easy to demonstrate that the quantum state in Hilbert space
| (31) | ||||
is a PKME state, with .
Therefore, there exists the planar two-region multi-partite maximally entangled state of the planar -qubit system, where both and are positive integers larger than or equal to 1.
Example 2. Assume , are positive integers larger than or equal to 1. Let us consider a qubit system. One can verify that a quantum state in the Hilbert space
| (32) | ||||
is just a PKME state, with .
Thus, there is the planar two-region multi-partite maximally entangled state of the planar -qubit system, where both and are positive integers larger than or equal to 1.
IV Summary
In this paper, we discuss a new kind of maximally entangled states, the planar two-region multi-partite maximally entangled states. It is demonstrated that there are the planar two-region four-partite maximally entangled states in 4-qubit and 7-qubit planar systems, although there is no AME state in 4-qubit and 7-qubit systems. Furthermore we show that there are the planar two-region four-partite maximally entangled states whether in the quantum system with even particles or in that with odd particles. Additionally, based on some planar two-region four-partite maximally entangled states, we also construct the new planar two-region four-partite maximally entangled states. Some important examples of the planar two-region four-partite and multi-partite maximally entangled states are provided.
Evidently, the virtue of two-region multi-partite maximally entangled states may induce many applications, especially in quantum parallel teleportation and quantum secret sharing. One can easily design the protocols of quantum parallel teleportation and quantum secret sharing by using the similar method provided by the authors of Ref. 26 . We hope these protocols can be realized in the future experiments.
Acknowledgements.
This work was supported by the National Natural Science Foundation of China under Grant Nos. 62271189, 12071110, and the Hebei Central Guidance on Local Science and Technology Development Foundation of China under Grant No. 236Z7604G.References
- (1) A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete?, Phys. Rev. 47, 777 (1935).
- (2) R. F. Werner, Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model, Phys. Rev. A 40, 4277 (1989).
- (3) R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki, Quantum entanglement, Rev. Mod. Phys. 81, 865 (2009).
- (4) M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, England, 2010).
- (5) N. Gisin and H. Bechmann-Pasquinucci, Bell inequality, Bell states and maximally entangled states for n qubits, Phys. Lett. A 246, 1 (1998).
- (6) D. N. Klyshko, The Bell and GHZ theorems: a possible three-photon interference experiment and the question of nonlocality, Phys. Lett. A 172, 399 (1993).
- (7) Z. Q. Chen, Bell-Klyshko inequalities to characterize maximally entangled states of n qubits, Phys. Rev. Lett. 93, 110403 (2004).
- (8) W. Helwig, W. Cui, J. I. Latorre, A. Riera, and H. K. Lo, Absolute maximal entanglement and quantum secret sharing, Phys. Rev. A 86, 052335 (2012).
- (9) Z. Raissi, C. Gogolin, A. Riera, and A. Acín, Optimal quantum error correcting codes from absolutely maximally entangled states, J. Phys. A: Math. Theor. 51, 075301 (2018).
- (10) M. S. Li and Y. L. Wang, -uniform quantum states arising from orthogonal arrays, Phys. Rev. A 99, 042332 (2019).
- (11) X. Wang and M. M. Wilde, Cost of quantum entanglement simplified, Phys. Rev. Lett. 125, 040502 (2020).
- (12) A. Streltsov, H. Kampermann, and D. Bruß, Linking quantum discord to entanglement in a measurement, Phys. Rev. Lett. 106, 160401 (2011).
- (13) F. Giraldi and P. Grigolini, Quantum entanglement and entropy, Phys. Rev. A 64, 032310 (2001).
- (14) M. F. Cornelio, M. C. de Oliveira, and F. F. Fanchini, Entanglement irreversibility from quantum discord and quantum deficit, Phys. Rev. Lett. 107, 020502 (2011).
- (15) Y. Hong, T. Gao, and F. L. Yan, Measure of multipartite entanglement with computable lower bounds, Phys. Rev. A 86, 062323 (2012).
- (16) T. Gao, F. L. Yan, and S. J. van Enk, Permutationally invariant part of a density matrix and nonseparability of N-qubit states, Phys. Rev. Lett. 112, 180501 (2014).
- (17) F. L. Yan, T. Gao, and E. Chitambar, Two local observables are sufficient to characterize maximally entangled states of N qubits, Phys. Rev. A 83, 022319 (2011).
- (18) F. C. Khanna, J. M. C. Malbouisson, A. E. Santana, and E. S. Santos, Maximum entanglement in squeezed boson and fermion states, Phys. Rev. A 76, 022109 (2007).
- (19) P. Facchi, G. Florio, G. Parisi, and S. Pascazio, Maximally multipartite entangled states, Phys. Rev. A 77, 060304 (2008).
- (20) M. Alexanian, Dynamical generation of maximally entangled states in two identical cavities, Phys. Rev. A 84, 052302 (2011).
- (21) J. Batle, M. Casas, A. Plastino, and A. R. Plastino, Maximally entangled mixed states and conditional entropies, Phys. Rev. A 71, 024301 (2005).
- (22) M. Doroudiani and V. Karimipour, Planar maximally entangled states, Phys. Rev. A 102, 012427 (2020).
- (23) S. Strelchuk, M. Horodecki, and J. Oppenheim, Generalized teleportation and entanglement recycling, Phys. Rev. Lett. 110, 010505 (2013).
- (24) D. Verdon and J. Vicary, Tight quantum teleportation without a shared reference frame, Phys. Rev. A 98, 012306 (2018).
- (25) A. E. Ulanov, D. Sychev, A. A. Pushkina, I. A. Fedorov, and A. I. Lvovsky, Quantum teleportation between discrete and continuous encodings of an optical qubit, Phys. Rev. Lett. 118, 160501 (2017).
- (26) D. Bacon and S. T. Flammia, Adiabatic gate teleportation, Phys. Rev. Lett. 103, 120204 (2009).
- (27) S. K. Singh and R. Srikanth, Generalized quantum secret sharing, Phys. Rev. A 71, 012328 (2005).
- (28) A. Keet, B. Fortescue, D. Markham, and B. C. Sanders, Quantum secret sharing with qudit graph states, Phys. Rev. A 82, 062315 (2010).
- (29) L. Y. Hsu, Quantum secret-sharing protocol based on Grover’s algorithm, Phys. Rev. A 68, 022306 (2003).
- (30) F. Huber, O. Ghne, and J. Siewert, Absolutely maximally entangled states of seven qubits do not exist, Phys. Rev. Lett. 118, 200502 (2017).
- (31) D. Alsina and M. Razavi, Absolutely maximally entangled states, quantum-maximum-distance-separable codes, and quantum repeaters, Phys. Rev. A 103, 022402 (2021).
- (32) D. Goyeneche, D. Alsina, J. I. Latorre, A. Riera, and K. yczkowski, Absolutely maximally entangled states, combinatorial designs, and multiunitary matrices, Phys. Rev. A 92, 032316 (2015).
- (33) A. Higuchi and A. Sudbery, How entangled can two couples get? Phys. Lett. A 273, 213 (2000).
- (34) A. J. Scott, Multipartite entanglement, quantum-error-correcting codes, and entangling power of quantum evolutions, Phys. Rev. A 69, 052330 (2004).
- (35) F. Huber, C. Eltschka, J. Siewert, and O. Ghne, Bounds on absolutely maximally entangled states from shadow inequalities, and the quantum MacWilliams identity, J. Phys. A: Math. Theor. 51, 175301 (2018).
- (36) H. A. Carteret, A. Higuchi, and A. Sudbery, Multipartite generalisation of the Schmidt decomposition, J. Math. Phys. 41, 7932 (2000).
- (37) J. E. Harriman, Reduced-density-matrix cumulants and correlation, Phys. Rev. A 75, 032513 (2007).
- (38) C. L. Benavides-Riveros, J. Wolff, M. A. L. Marques, and C. Schilling, Reduced density matrix functional theory for bosons, Phys. Rev. Lett. 124, 180603 (2020).
- (39) M. A. L. Marques and N. N. Lathiotakis, Empirical functionals for reduced-density-matrix-functional theory, Phys. Rev. A 77, 032509 (2008).
- (40) D. Goyeneche and K. yczkowski, Genuinely multipartite entangled states and orthogonal arrays, Phys. Rev. A 90, 022316 (2014).
- (41) M. Owari and M. Hayashi, Asymptotic local hypothesis testing between a pure bipartite state and the completely mixed state, Phys. Rev. A 90, 032327 (2014).
- (42) C. S. Yu, X. X. Yi, and H. S. Song, Evolution of entanglement for quantum mixed states, Phys. Rev. A 78, 062330 (2008).
- (43) A. Soeda, P. S. Turner, and M. Murao, Entanglement cost of implementing controlled-unitary operations, Phys. Rev. Lett. 107, 180501 (2011).