Pinned planar -elasticae
Abstract.
Building on our previous work, we classify all planar -elasticae under the pinned boundary condition, and then obtain uniqueness and geometric properties of global minimizers. As an application we establish a Li–Yau type inequality for the -bending energy, and in particular discover a unique exponent for full optimality. We also prove existence of minimal -elastic networks, extending a recent result of Dall’Acqua–Novaga–Pluda.
Key words and phrases:
-Elastica, pinned boundary condition, Li–Yau inequality, network.2020 Mathematics Subject Classification:
49Q10, 53A04, and 33E05.1. Introduction
This paper is a continuation of our study of -elasticae [19], wherein we have classified all planar -elasticae and obtained their explicit parameterizations as well as optimal regularity. In this paper, we turn to a boundary value problem and classify all planar -elasticae subject to the pinned boundary condition, with some applications to a Li–Yau type inequality and minimal networks.
1.1. Classification of pinned planar -elasticae
For and immersed curves in the Euclidean plane , the -bending energy is defined by
where denotes the signed curvature and denotes the arclength parameter of , respectively. A critical point of the -bending energy under the fixed-length constraint is called -elastica; in other words, its signed curvature is a (weak) solution to the Euler–Lagrange equation formally given by
where denotes the arclength derivative and denotes a multiplier due to the fixed-length constraint. Classification of planar elasticae () is classic and given by Euler in the 18th century. Planar -elasticae are just recently classified by the authors [19], with optimal regularity and closed formulae in terms of newly introduced -elliptic functions. In particular, in the degenerate case the obtained family includes Watanabe’s flat-core solutions [28] (see also [25]), which are of qualitatively novel type compared to . See [19] and references therein for details.
Boundary value problems for (-)elasticae are in general more advanced because we need to detect the precise values of the multiplier or other geometric parameters for compatibility with the given boundary data, and thus need to solve the corresponding system of transcendental equations.
As a first step we focus on the so-called pinned boundary condition, which prescribes the endpoints up to zeroth order. More precisely, for given and such that , we define the admissible space by
| (1.1) |
where denotes the length functional , and denotes the set of immersed -curves:
We call a critical point of in pinned -elastica (cf. Definition 2.11).
In the case of elastica () the pinned boundary value problem has been completely solved on the level of critical points and global minimizers [30, 17] (see also [15, 14, 1]). Roughly speaking, if , then all pinned elasticae are part of “figure-eight”, while if , then the curves are “arcs” and “loops” (like Figure 1). In any case, for given boundary data there are countably many critical points but the global minimizer is uniquely given by a “single arc” up to invariances.
Our primary result here extends the known classification of pinned planar elasticae for to all . In particular, in the degenerate case , we find a critical distance of the endpoints at which the number of pinned -elasticae changes from countable to uncountable. Following terminology in Definition 3.2, our result is summarized as follows (see also Figures 1 and 2).
Theorem 1.1 (Classification of pinned -elasticae).
Let . Let and such that
Suppose that is a critical point of in . Then the following assertions hold true.
-
(i)
If , then is an -fold figure-eight -elastica for some .
-
(ii)
If , then is either a -arc for some , or a -loop for some .
-
(iii)
If , then is either a -arc for some , or a -flat-core for some , , and subject to relation (3.5).


Remark 1.2 (Countability-uncountability transition).
If , then so the only possible cases are (i) and (ii), and hence the classification is qualitatively parallel to the classical case . Case (iii) is of novel type and occurs if and only if and the endpoints are sufficiently distant. In particular, if and , then there are uncountably many critical points, and otherwise countably many (up to isometry and reparameterization). The uncountability is due to the freedom of the length of the flat parts as in Figure 2.
Remark 1.3 (Loss of regularity).
Critical points in Theorem 1.1 are always of class but may not in general, particularly at the points where the curvature vanishes. More precisely, if is an odd integer (i.e., ), then any arclength-parameterized critical point is always of class , but otherwise may not. For example, if is not an integer, then any arclength-parameterized -arc and -loop are not of class , where . We emphasize that this loss of regularity occurs even for , since at the endpoints the curvature vanishes. In addition, if and if , then any arclength-parameterized -flat-core is not of class , where . For more details as well as optimal regularity in terms of Sobolev class, see [19].
Now we focus on global minimizers. Existence follows by a standard direct method. In addition, comparing the -bending energy of all the above critical points, we obtain uniqueness of global minimizers.
Theorem 1.4 (Unique existence of global minimizers).
Let , , and such that . Then there exists a global minimizer of in , and in addition any global minimizer is uniquely given by a -arc (up to isometry and reparameterization).
A particularly useful case is where the endpoints agree . In this case, by Theorems 1.1 and 1.4 we deduce that a half-fold (i.e., -fold) figure-eight -elastica is a unique global minimizer, extending [17, Proposition 2.6] from to in the planar case. Here we apply this fact to obtain a Li–Yau type inequality and existence of minimal networks in the same spirit as [17]. In view of these applications it would be informative if we could know the precise geometric properties of the figure-eight -elastica, in particular how the crossing angle depends on . Fortunately we succeed in ensuring the following key monotonicity, cf. Figure 3:
Theorem 1.5 (Monotonicity of the crossing angle).
For , let be the angle between the tangent vectors at the two endpoints of a half-fold figure-eight -elastica, cf. (4.9). Then the function is continuous and strictly decreasing from to .


This monotonicity is easy to infer from the numerical pictures but its analytic verification seems not straightforward. Our proof involves an indirect argument.
In what follows we discuss the aforementioned applications in detail. We also expect that our classification would be useful in other contexts, e.g. to detect the limit curves of gradient flows for the -bending energy under the natural boundary condition. For recent developments of such flows, see e.g. [21, 22, 3, 4, 23].
1.2. Li–Yau type inequality
We first apply our result to deduce a Li–Yau type inequality involving the normalized -bending energy , defined as the -bending energy normalized by the length to be scale-invariant:
| (1.2) |
In their celebrated study, Li and Yau obtained the sharp inequality that the Willmore energy of a closed surface is bounded below by times multiplicity [12]. A one-dimensional counterpart has also been studied by several authors [24, 27, 29, 20], and recently (almost) optimized in [17]: If an immersed closed -curve in () has a point of multiplicity , then
| (1.3) |
Here denotes the normalized bending energy of a half-fold figure-eight elastica, and we say that a curve has a point of multiplicity if the preimage contains at least distinct points.
A typical characteristic of the 1D Li–Yau type inequality (compared to 2D) is the presence of a new algebraic obstruction for optimality of the inequality. In fact, it is proven in [17] that equality in (1.3) is attained if and only if or is even, and also is an -leafed elastica. In particular, for and any odd multiplicity , the inequality is not optimal because of the irrationality of .
In this paper we first extend inequality (1.3) to all in the plane, and then reveal some new phenomena on its optimality arising from the generality of . Let and denote the set of immersed closed -curves. Let denote the normalized -bending energy of a half-fold figure-eight -elastica, which will be given by formula (5.1); in particular, . Finally, we say that is an -leafed -elastica if the curve consists of half-fold figure-eight -elasticae of same length (see Definition 5.3 for details). Then, applying Theorem 1.4, we establish the following
Theorem 1.6 (Li–Yau type inequality and rigidity).
Let , and an integer. If a closed curve has a point of multiplicity , then
| (1.4) |
Equality in (1.4) is attained if and only if is a closed -leafed -elastica.
In addition, as in the case of [17], it is easy to see that if the multiplicity is even, then our inequality is always optimal.
Theorem 1.7 (Optimality for even multiplicity).
Let . If is an even integer, then there exists a closed curve with a point of multiplicity such that
In particular, we can take to be an -fold figure-eight -elastica.
As for odd multiplicity, the optimality is much more delicate (and does not hold for as discussed). However, for we can apply Theorem 1.5 to find many new phenomena that recover optimality, even for closed planar curves with odd multiplicity. For example, there is a dense set such that each exponent retrieves the optimality for all but a finite number of odd multiplicities (Theorem 5.11). In particular, as a very peculiar example, we discover a unique exponent for which inequality (1.4) becomes fully optimal.
Theorem 1.8 (Unique exponent for full optimality).
There exists a unique exponent with the following property: For every integer there exists a closed curve with a point of multiplicity such that
The unique exponent is given by defined as
| (1.5) |
Moreover, for an odd , if we define , then the corresponding closed planar -leafed -elastica is unique (up to invariances) and has -fold rotational symmetry, cf. Figure 4. These exponents can be used to ensure a “thresholding” phenomenon; for any given odd integer there is an exponent for which optimality holds if and only if the multiplicity is none of (see Theorem 5.12).


1.3. Minimal -elastic networks
Another application is about existence of planar networks composed by three curves minimizing the normalized -bending energy. Such a network structure is of recent interest particularly in geometric variational problems or flows as a model case with possible structural changes. See [2, 8, 6, 10, 7, 11, 21, 17] for some instances of static and dynamical studies of elastic networks.
In this paper, for given , a triplet of immersed curves is called -network with angles if and , and if in addition the curves satisfy the angle condition
where we interpret . Let denote the class of all -networks with angles , and for we define
where and . Applying Theorems 1.4 and 1.5, we can obtain the existence of minimal -networks in a certain range of the angle :
Theorem 1.9 (Existence of minimal -elastic -networks).
Let and . Let be the angle defined in (4.9). Suppose that
| (1.6) |
Then there exists a network such that
| (1.7) |
In particular, focusing on the special “homogeneous” angle condition , we may rephrase Theorem 1.9 in terms of defined by (1.5).
Corollary 1.10.
If , then there exists a network such that
Corollary 1.10 directly extends Dall’Acqua–Novaga–Pluda’s existence result for [7] (see also [17]) to . Recall that numerically . Analytically we can ensure at least thanks to Theorem 1.5 with the fact that (cf. [17, Lemma 3.11]).
In general, the existence of minimal elastic networks does not follow from a standard direct method due to the lack of compactness, namely the possibility that a component-curve degenerates into a point (see Section 6 for details). Our proof of Theorem 1.9 follows the general strategy of [17] strongly inspired by [7]. Although the proof in [7] contains a numerical part, the one in [17] gives a different analytic proof. Our proof here is also fully analytic. Along the way we establish and use new monotonicity results involving -elliptic integrals.
We close the introduction by mentioning a few of many open problems. Concerning uniqueness of global minimizers, here we addressed the pinned boundary condition (Theorem 1.4), but as for the clamped boundary condition, only a few results are available even for (see e.g. [16] for the straightened case and [18] for the cuspidal case) and in particular it is widely open for (except for the obvious closed case). Concerning the Li–Yau type inequality, the shape of a minimizer of among -immersed closed planar curves with an odd multiplicity is totally open unless equality in (1.4) is attained; in particular, if , it is open for all odd . Finally, concerning minimal -elastic networks, it is not clear whether the assumption in Corollary 1.10 (or (1.6) in Theorem 1.9) is optimal. We expect that the same existence result would not hold at least for sufficiently close to , but even this is remained open.
1.4. Organization of the paper
Acknowledgments
The first author is supported by JSPS KAKENHI Grant Numbers 18H03670, 20K14341, and 21H00990, and by Grant for Basic Science Research Projects from The Sumitomo Foundation. The second author is supported by JSPS KAKENHI Grant Number 22K20339.
2. Preliminary
In this section we first recall the definitions and fundamental properties of -elliptic integrals and functions introduced in [19], which we use throughout this paper. Then we rigorously define pinned -elasticae, and recall some known facts for -elasticae.
Hereafter, we always let denote an arbitrary exponent unless an additional condition is specified.
2.1. -Elliptic integrals
Definition 2.1 (-Elliptic integrals of the first kind).
The incomplete -elliptic integrals of the first kind and of modulus , where , are defined by
and also the corresponding complete -elliptic integrals and by
In addition, for ,
and
| (2.1) |
Definition 2.2 (-Elliptic integrals of the second kind).
The incomplete -elliptic integrals of the second kind and of modulus , where , are defined by
and also the corresponding complete -elliptic integrals and by
Remark 2.3.
Since , both and are well defined for each and . By definition and periodicity of the integrand we deduce the following quasiperiodicity:
| (2.2) | ||||
for any , , , and .
Remark 2.4.
In particular we also have the following alternative representations:
| (2.3) |
| (2.4) |
Now we discuss some basic properties. As in the classical case , the complete -elliptic integrals and are not only monotone with respect to modulus but also related by explicit derivative formulae:
Proposition 2.5.
The function is strictly increasing with respect to (including if ), and the function is strictly decreasing with respect to . Moreover, for ,
| (2.5) | ||||
In fact, the above derivative formulae are special cases of those for more general elliptic integrals obtained by Takeuchi [26]: For and , let
By [26, Proposition 2], letting and , we have
| (2.6) | ||||
Proof of Proposition 2.5.
We will also consider the ratio of the first and second complete -elliptic integrals.
Lemma 2.6 ([28, Lemma 2]).
Let be defined by
| (2.8) |
Then is strictly decreasing on . Moreover, satisfies and
| (2.9) |
By this monotonicity of we can define the unique modulus corresponding to “figure-eight”, which we will use frequently:
Definition 2.7 (Modulus of figure-eight).
Let denote a unique solution to the equation .
2.2. -Elliptic functions
Next we recall the -elliptic functions.
Definition 2.8 (-Elliptic functions).
Let . The amplitude functions and with modulus are defined by the inverse functions of and , respectively, i.e., for ,
The -elliptic sine and -elliptic cosine with modulus are defined by, for ,
| (2.10) |
The -delta amplitude with modulus is defined by
In addition, a typical part of and is interpreted as the -hyperbolic secant function.
Definition 2.9 (-Hyperbolic functions).
The -hyperbolic secant is defined by
| (2.11) |
If , then we regard as . Moreover, the -hyperbolic tangent is defined by
In general our -elliptic functions satisfy fundamental properties such as periodicity and monotonicity similar to the classical Jacobian elliptic functions (). In particular we recall some of those about and for later use.
Proposition 2.10 ([19, Proposition 3.10]).
Let and be given by (2.10) and (2.11), respectively.
-
(i)
For , is an even -antiperiodic function on and, in , strictly decreasing from to .
-
(ii)
If , then is an even positive function on , and strictly decreasing in . Moreover, and as .
-
(ii’)
If , then is an even nonnegative function on , and strictly decreasing in . Moreover, and as . In particular, is continuous on .
2.3. The Euler–Lagrange equation and pinned -elastica
Now we rigorously define pinned (planar) -elasticae, and recall their known properties.
Definition 2.11 (Pinned -elastica).
Let and such that . Let be the admissible space defined in (1.1).
-
•
For , we call a one-parameter family admissible perturbation of in if and if the derivative exists.
-
•
We say that is a critical point of in the admissible space if for any admissible perturbation of in the first variation of vanishes:
We also call such a critical point pinned -elastica in general.
Let be a pinned -elastica. Then, by the Lagrange multiplier method (cf. Proposition A.5), there is a multiplier such that
| (2.12) |
for with , where and are the Fréchet derivatives of and at , respectively. Using the arclength parameterization of , we can rewrite (2.12) as
| (2.13) |
for with (cf. Proposition A.8). Moreover, we can translate (2.13) in terms of the signed curvature; indeed, according to [19, Proposition 2.1], if satisfies (2.13), then its signed curvature (parameterized by the arclength) belongs to , and further satisfies
| (EL) |
for all with (although the class of test functions is different from [19], the derivation is parallel).
In particular, we find that any pinned -elastica in the sense of Definition 2.11 is always a -elastica in the sense of [19, Definition 1.1] by restricting test functions to in (2.13). The complete classification of -elasticae is already known. In order to state the classification, we prepare the notation on a concatenation of curves. For with , we define by
and inductively define . We also write
We now recall the classification of -elasticae:
Proposition 2.12 ([19, Theorems 1.2 and 1.3]).
Let be a -elastica. Then up to similarity (i.e., translation, rotation, reflection, and dilation) and reparameterization, the curve is represented by with some , where is one of the following arclength parameterizations:
-
•
(Case I — Linear -elastica) , where .
-
•
(Case II — Wavelike -elastica) For some ,
(2.14) In this case, and
-
•
(Case III — Borderline -elastica, )
In this case, and
-
•
(Case III’ — Flat-core -elastica, ) For some integer , signs , and nonnegative numbers ,
(2.15) where and are defined by
(2.16) The curves have and for . In particular,
(2.17) -
•
(Case IV — Orbitlike -elastica) For some ,
In this case, and
-
•
(Case V — Circular -elastica) , where .
Here denotes the tangential angle , and the (counterclockwise) signed curvature .
The optimal regularity of -elasticae is known to depend on . Here we recall a weak general regularity (independent of ), which will be sufficient for our purpose.
Proposition 2.13 ([19, Theorem 1.7]).
Let be a -elastica. Then has continuous (arclength parameterized) signed curvature.
3. Classification of pinned -elasticae
In this section we give the complete classification of pinned -elasticae, thus proving Theorem 1.1.
As a key fact for reducing the possible candidates, we first deduce that any pinned -elastica satisfies an additional (natural) boundary condition that the curvature vanishes at the endpoints.
Lemma 3.1.
If is a pinned -elastica, then the arclength parameterized signed curvature of satisfies
Proof.
Recall that by Proposition 2.13 so that is defined pointwise. From the fact that satisfies (EL) we deduce that the function
satisfies
| (3.1) |
for any . Moreover, it is shown in [19, Lemma 4.3] that also satisfies (3.1) in the classical sense, i.e.,
| (3.2) |
By choosing with and in (3.1), and integrating by parts, we obtain
where we used , , , and (3.2). Therefore, , so that holds. In the same way we obtain . ∎
By Proposition 2.12 and Lemma 3.1, with the obvious fact that linear -elasticae are ruled out by , if is a pinned -elastica, then must be
This fact drastically reduces the candidates of pinned -elasticae. Motivated by this reduction, we prepare terminology for the following special -elasticae — we will later show that those curves are indeed the only possibilities.
Definition 3.2 (Arc, loop, and flat-core).
Let , , and .
-
•
A curve is called -arc if, up to similarity and reparameterization, is given by
where is defined by (2.14) and is a unique solution of
(3.3) -
•
A curve is called -loop if and, up to similarity and reparameterization, is given by
where is defined by (2.14) and is a unique solution of
(3.4) -
•
In particular, we call a -arc, or equivalently a -loop, -fold figure-eight -elastica. A -fold figure-eight -elastica is also called half-fold figure-eight -elastica.
-
•
A curve is called -flat-core if , , and there are and such that, up to similarity and reparameterization, is given by
where and are given by (2.16), and in addition and satisfy
(3.5)
Remark 3.3.
The monotonicity in Lemma 2.6 implies uniqueness of solutions to equations (3.3) and (3.4), respectively. By and (2.9), equation (3.3) always admits a solution, while (3.4) admits a solution if and only if , or equivalently . In order to define the flat-core case, the condition is obviously required since flat-core elasticae only appear for ; the condition is also necessary and sufficient since this is equivalent to the nonnegativity of the right-hand side of (3.5).
Remark 3.4.
One can observe from the above definition that, loosely speaking, the given parameter characterizes the modulus in Proposition 2.12.
In what follows we verify that any pinned -elastica is either a -arc, a -loop, or a -flat-core. We first obtain necessary conditions for pinned wavelike -elasticae:
Lemma 3.5 (Pinned wavelike -elasticae).
Proof.
By Proposition 2.12, up to similarity and reparameterization, the curve is represented by
| (3.7) |
for some and , where is defined by (2.14). Let (resp. ) denote the length (resp. the distance between the endpoints) of . Note that . We see that the signed curvature of is
By Lemma 3.1, we have . Moreover, in view of the fact that
| (3.8) |
and the fact that is a -antiperiodic function (cf. Proposition 2.10), without loss of generality, we can choose in (3.7). Furthermore, since also follows from Lemma 3.1, we see that for some . To compute , set
It follows from (2.14) that
Combining this with (3.8) and , we see that . Hence holds. Since , we find that in (3.7) has to satisfy
| (3.9) |
Now we compute the numerator. By (2.2) we have and hence by definition of ,
By this fact and (2.2) we deduce
Consequently, we obtain
Therefore, the left-hand side of both equalities in (3.9) are reduced to
which implies that in (3.7) has to satisfy (3.3) or (3.4). The proof is complete. ∎
Next we obtain necessary conditions for pinned flat-core -elasticae.
Lemma 3.6 (Pinned flat-core -elasticae).
Let and such that . Let be a critical point of in . Suppose that is a flat-core -elastica. Then it is necessary that
| (3.10) |
Moreover, up to similarity and reparameterization, is given by
| (3.11) |
for some , , and such that (3.5) holds.
Proof.
By Proposition 2.12, clearly , and in addition, up to similarity and reparameterization, the curve is represented by for with some , where is given by (2.15) and is the length of the curve after dilation. Let be the signed curvature of . Since follows from Lemma 3.1, there are , , such that for ,
| (3.12) |
where and are defined by (2.16). Given the form of the right-hand side of (3.12), we notice that
| (3.13) |
Set . Similar to the proof of Lemma 3.5, we consider the condition to satisfy . We infer from [19, Lemma 5.7] that the distance between the endpoints of is . Therefore it follows that
This together with (3.13) yields
which is equivalent to (3.5). Thus we find that (3.10) is also necessary since the right-hand side of (3.5) must be nonnegative. ∎
Now we complete the proof of Theorem 1.1.
Proof of Theorem 1.1.
Let be a pinned -elastica. By Lemma 3.1, is either a wavelike -elastica or a flat-core -elastica.
We first consider the case . In view of (3.10), flat-core -elasticae are ruled out in this case, so it suffices to consider being a wavelike -elastica. Then we infer from Lemma 3.5 that, up to similarity and reparameterization, is given by (3.6) for some , where is a solution to (3.3) with , that is, in Definition 2.7. This implies that is an -fold figure-eight -elastica.
Remark 3.7 (Sufficiency).
Conversely, all the candidates in Theorem 1.1 are indeed pinned -elasticae as long as the curves are admissible.
Below we put down some geometric properties of arcs and loops, which follow by explicit formulae. Although we focus on the one-fold case, the general case is obtained by its antiperiodic extension (cf. Figure 1) and hence the symmetry is inherited in a certain sense.
Lemma 3.8.
Let and . Let be either a -arc or a -loop. Then is reflectionally symmetric in the sense that, up to similarity and reparameterization, the curve has an arclength parameterization satisfying that
In addition, if and is a -loop, then has a self-intersection, i.e., there is such that .
Proof.
Reflection symmetry follows since by Definition 3.2, up to similarity and reparameterization, is given by , cf. Proposition 2.12, for which it is easy to check that and .
Now we check that a -loop has a self-intersection. By the above symmetry it suffices to find such that . By the fact that and , and by the intermediate value theorem, it is now sufficient to show that . This follows since , cf. (3.4), where and . ∎
A parallel argument shows that each loop of a flat-core is also a symmetric curve with a self-intersection.
4. Unique existence and geometric properties of global minimizers
In this section we compute the normalized -bending energy of each pinned -elastica and detect a unique global minimizer, thus proving Theorem 1.4. We then investigate geometric properties of the half-fold figure-eights and prove Theorem 1.5.
4.1. Unique existence
We first prove the existence of minimizers of in by the standard direct method.
Proposition 4.1.
Given and such that , there exists a solution to the following minimization problem
Proof.
Let be a minimizing sequence of in , i.e.,
| (4.1) |
Up to reparameterization, we may suppose that is of constant speed so that . By (4.1) there is such that for any , and hence the assumption of constant-speed implies that
| (4.2) |
where stands for the arclength parameterization of . This yields the uniform estimate of . Using and the boundary condition, we also obtain the bounds on the -norm. Therefore, is uniformly bounded in so that there is a subsequence (without relabeling) that converges in the senses of -weak and topology. Thus the limit curve satisfies , , , and , which implies that . Moreover, similar to (4.2), we infer from that
This together with the weak lower semicontinuity for ensures that
This with (4.1) implies that is a minimizer of in . ∎
Note that any minimizer of in is a pinned -elastica. Thanks to the classification in the previous section, for detecting a minimizer it is sufficient to compute the -bending energy of each pinned -elastica. To this end it is sufficient to compute the normalized -bending energy
cf. (1.2), since we compare the energy of curves of same length. The energy has the advantage of being scale-invariant in the sense that for any curve and , if we define , then . Thus we need not adjust the length of pinned -elasticae but can use their natural length involving complete -elliptic integrals.
First, we address the wavelike case. To this end, we prepare the following
Lemma 4.2.
For each (including if ),
Proof.
Fix ( if ) arbitrarily. By definition of , we have
where we used the change of variables . Keeping the definitions of and in mind, we compute
The proof is complete. ∎
Using this formula, we can compute the normalized -bending energy of -arcs and -loops.
Proposition 4.3.
Proof.
Since the proof is completely parallel, we only consider the case that is a -arc. Since is invariant with respect to similar transformation and reparameterization, by Definition 3.2, we may assume that
where is a solution of (3.3). Then we have
where we used the fact that is an even -antiperiodic function (cf. Proposition 2.10). Combining this with Lemma 4.2, we obtain (4.3). ∎
Next we turn to the flat-core case.
Proposition 4.4.
Let , , and such that (3.10) holds. Let be a -flat-core. Then the normalized -bending energy of is given by
| (4.4) |
Proof.
Let be a -flat-core, i.e., there are and such that is given by (3.11). As discussed in (3.13), it follows that . Noting that satisfies (3.5), we obtain
| (4.5) |
In view of (2.17), we have
Moreover, since is even (cf. Proposition 2.10), we obtain
where we also used the fact that in and Lemma 4.2. This together with (4.5) yields (4.4). The proof is complete. ∎
The following lemma plays an important role for the quantitative comparison of the normalized -bending energy among pinned -elasticae.
Lemma 4.5.
Let be the function defined by
| (4.6) |
and let if . Then, for ,
| (4.7) |
In particular, is strictly increasing with respect to (including if ).
Proof.
We are in a position to prove the uniqueness of minimizers in .
Proof of Theorem 1.4.
The existence of minimizers of in follows from Proposition 4.1. Fix any minimizer . Then is a pinned -elastica. We divide the proof into three cases along the classification in Theorem 1.1.
First we consider the case . Then is an -fold figure-eight -elastica, i.e., a -arc for some . By Proposition 4.3, the normalized -bending energy of a -arc is times that of a -arc, and hence a half-fold figure-eight -elastica (corresponding to ) is a unique minimizer.
Next we consider the case . Then is either a -arc or a -loop for some . Let and denote the corresponding values of the normalized -bending energy. Then, using a solution of (3.3) and the function defined by (4.6), we have
Similarly, using a solution of (3.4), we obtain
Therefore, we see that and for any . Furthermore, since , we infer from Proposition 2.5 and Lemma 4.5 that
Consequently a -arc is a unique minimizer.
Finally we turn to the case . In this case, is either a -arc or a -flat-core. Let denote the value of the normalized -bending energy of a -flat-core (which is independent of , cf. Proposition 4.4). Then we infer from (4.4) that
Since by (3.10), using Proposition 2.5 and Lemma 4.5, we obtain
for any . As a result a -arc is a unique minimizer. ∎
4.2. Properties of a half-fold figure-eight -elastica
In this subsection, we discuss some properties of a half-fold figure-eight -elastica, and in particular, we prove Theorem 1.5.
To begin with, we collect the basic properties of a half-fold figure-eight -elastica.
Proposition 4.6 (Basic properties of a half-fold figure-eight -elastica).
Let be a half-fold figure-eight -elastica. Then up to similarlity and reparameterization, is given by, for ,
| (4.8) | ||||
where . In addition, the following properties hold.
-
(i)
The tangential angle is .
-
(ii)
The curve defined by (4.8) takes the origin if and only if .
-
(iii)
Let be
(4.9) Then , where stands for the counterclockwise rotation matrix through angle .
Proof.
By Proposition 2.12 and by definition of a half-fold figure-eight -elastica, up to similarity and reparameterization, we have implying (4.8) and property (i). Property (ii) follows from (4.8). We finally prove property (iii). By property (i) we have and . By definition of , it follows that . This together with yields and hence property (iii). ∎
From the previous proposition we see that characterizes the crossing angle of a figure-eight -elastica, cf. Figure 3. Notice that the parameterization in (4.8) rotated through angle represents the left curve in Figure 3.
Hereafter we investigate properties of through the analysis of . Noting that is a unique solution of , cf. (2.8), we introduce
| (4.10) |
Since , the roots of and coincide. Both and have own advantages; in general the former is easy to compute at least for a fixed , but we will later discover that the latter has a remarkable monotone structure as varies, cf. Figure 6.
Lemma 4.7.
Let be the function defined by (4.10). Then is strictly decreasing and strictly concave. In addition, if , then
| (4.11) |
Proof.
By Proposition 2.5, and are strictly decreasing, and hence so is . By the change of variables, we can rewrite (2.7) as
| (4.12) | ||||
In particular we have
| (4.13) |
Differentiating once more, we obtain for
This implies the concavity of . It remains to show (4.11) for . Combining (2.9) with the fact that (cf. (2.1)), we obtain (4.11). ∎
In what follows we prove that is continuously decreasing from to as varies from to (cf. Figure 5). First we prepare some basic properties of .

Proposition 4.8.
Let be given by (4.9). Then satisfies the following properties.
-
(i)
for any .
-
(ii)
as .
-
(iii)
as .
-
(iv)
is continuously differentiable on .
Proof.
First we check property (i). To this end, by (4.9) it suffices to show that for any . From the fact that
and monotonicity of (cf. Lemma 2.6), it follows that . By definition of , it also follows that .
Next we show property (ii). In view of (4.9), it suffices to show that as . By concavity of (cf. Lemma 4.7), it turns out that
| (4.14) |
By definition we have
from which it follows that
| (4.15) |
In addition, using (4.13), we obtain
| (4.16) | ||||
Combining this with (4.14) and (4.15), we have
which yields as .
We turn to property (iii). To this end, we show that as . By Lemma 4.7, if , then is well defined, and we infer from concavity of that
| (4.17) |
Moreover, concavity of and also imply that
| (4.18) |
This together with (4.11) and (4.17) gives
where we also used (4.16). The right-hand side tends to be zero since
Consequently, we obtain as .
It remains to prove property (iv). Let be a function defined by . Then, is continuously differentiable with respect to and . Indeed, it follows that
From definition of and (4.18), we infer that
Hence, by the implicit function theorem, for each there exists a neighborhood of and a function such that . Moreover, Lemma 2.6 implies uniqueness of solutions to for each , and hence we see that in . Furthermore, by differentiability of , we notice that . Consequently the map is continuously differentiable with respect to . The proof is complete. ∎
In order to obtain monotonicity of , we here prove the key fact that has a remarkable monotone structure with respect to as in the left of Figure 6, in contrast to as in the right of Figure 6.


Proposition 4.9.
If , then
| (4.19) |
Proof.
Fix arbitrarily and define
First we show that there is such that
| (4.20) |
Note that (4.12) yields , where . Combining this with
we obtain
where we also used . Moreover, it follows from (4.12) that
Therefore, using the Beta function , we see that
By the well-known relations and , where denotes the Gamma function, we obtain
This implies that is strictly increasing with respect to , so we have . This together with yields (4.20).
Now we are ready to prove (4.19), i.e.,
| (4.22) |
With the help of (4.20), in order to obtain (4.22), it suffices to show that for any . We prove this by contradiction. Suppose that there is such that . In view of (4.20) we may assume that . Combining with (4.21), we have
| (4.23) |
Note that Proposition 2.5 and yield . Since , we infer from (4.23) that . However, this together with the fact that in contradicts . Thus we obtain (4.22). ∎
5. Li–Yau type multiplicity inequality
This section is devoted to discussing the Li–Yau type multiplicity inequality of the form (1.4). In Subsection 5.1 we first prove Theorem 1.6. The key fact to prove Theorem 1.6 is that a half-fold figure-eight -elastica is a unique minimizer of in . From the proof we observe that whether the equality in (1.4) is attained is equivalent to whether there exists a closed -leafed -elastica, i.e., a -concatenation of half-fold figure-eight -elasticae. Then we discuss existence of closed -leafed -elasticae in Subsection 5.2, and observe new phenomena related to optimality in Subsection 5.3. Here the angle monotonicity in Theorem 1.5 plays a key role.
5.1. Multiplicity inequality
Corollary 5.1.
Let be a constant given by
| (5.1) |
and satisfy . Then
where equality is attained if and only if is a half-fold figure-eight -elastica.
Proof.
Fix an arbitrary such that and let be a half-fold figure-eight -elastica. It follows from Theorem 1.4 that , and equality is attained if and only if is also a half-fold figure-eight elastica. Recalling the fact that , we infer from (4.3) with and that
which coincides with (5.1). The proof is complete. ∎
In order to prove inequality (1.4), we first prove its open-curve counterpart.
Theorem 5.2 (Multiplicity inequality for open curves).
Let be a curve with a point of multiplicity . Then
| (5.2) |
Proof.
By the assumption on multiplicity, there are such that . If , then follows and it suffices to show that . Therefore we may assume that . Similarly, we may assume that . Set for . Then we infer from Corollary 5.1 that
| (5.3) |
Note that and . It follows from (5.3) that
| (5.4) |
For the case , it follows from Hölder’s inequality that
This together with (5.4) yields
| (5.5) | ||||
where we used the HM-AM inequality. For the case , it follows from Hölder’s inequality that
Combining this with (5.4), we see that
| (5.6) | ||||
where we used the HM-AM inequality. The proof is complete. ∎
We later show that inequality (1.4) follows from a special consequence of Theorem 5.2. In order to discuss optimality, we introduce leafed -elasticae as in [17].
Definition 5.3 (Leafed -elastica).
Let and .
-
(1)
We call -leafed -elastica if there are such that for each the curve is a half-fold figure-eight -elastica, and also .
-
(2)
We call closed -leafed -elastica if there is such that the curve defined by is an -leafed -elastica.
We mention an obvious example in the following lemma. The proof is safely omitted since it follows immediately by definition.
Lemma 5.4 (Closed -leafed -elasticae for even ).
For any and any even , an -fold figure-eight -elastica is a closed -leafed -elastica.
It is also easy to see that leafed -elasticae indeed attain equality in (5.2).
Proposition 5.5 (Energy of -leafed -elastica).
Let . Then any -leafed (resp. closed -leafed) elastica has a point of multiplicity (resp. ), and its normalized -bending energy is .
Proof.
Let be an -leafed -elastica. Let denote the length of each half-fold figure-eight elastica , cf. Definition 5.3. Then . In addition, since , the additivity of yields . Thus we get . ∎
We now prove that for open curves, not only rigidity but also optimality always holds.
Theorem 5.6 (Optimality and rigidity for open curves).
Let and . Then there exists with a point of multiplicity such that
| (5.7) |
In addition, equality (5.7) is attained if and only if is an -leafed -elastica.
Proof.
By definition, an -fold figure-eight -elastica is an open curve with a point of multiplicity , and attains equality. From this fact the existence of an optimal curve follows. In addition, any -leafed -elastica attains equality (5.7) by Proposition 5.5.
We now prove rigidity. Suppose that attains (5.7). As in the proof of Theorem 5.2, there are such that . Then and must be and , respectively. Set for . Then equality holds for all the inequalities in the proof of Theorem 5.2, i.e., (5.4), (5.5), and (5.6). Focusing on Hölder’s inequality and the HM-AM inequality, we have . Moreover, in view of (5.4), we also have for all , and hence by Corollary 5.1 each curve needs to be a half-fold figure-eight -elastica. This means that is an -leafed -elastica. ∎
Proof of Theorem 1.6.
First, we prove inequality (1.4). Let be a curve with a point of multiplicity . Then we can create an open curve with a point of multiplicity after cutting at the original point of multiplicity and opening the domain to . Applying Theorem 5.2 to the curve , we obtain (1.4).
We turn to optimality and rigidity. By Proposition 5.5, any closed -leafed -elastica attains equality in (1.4). Conversely, suppose that attains equality in (1.4). As in the previous procedure, by creating an open curve with a point of multiplicity , and applying Theorem 5.6 to , we see that must be a closed -leafed -elastica. ∎
5.2. Closed -leafed -elasticae
Here we seek for exponents admitting closed leafed -elasticae with odd multiplicities.
We first prepare the following lemma in the same spirit of [17, Lemma 3.7], which states that whether there exists a closed -leafed -elastica can be characterized by whether the leaves can be joined up to first order. By Proposition 4.6 (iii), the angle plays a fundamental role.
Lemma 5.7 (Characterization of closed -leafed -elasticae).
Let be an integer and . Let be the set of all -tuples of unit-vectors such that holds for any , where we interpret .
If is a unit-speed closed -leafed -elastica, then holds for and , where is a point of multiplicity .
Conversely, for any element , there exists a unique unit-speed closed -leafed -elastica such that and for .
The proof of Lemma 5.7 is straightforward and safely omitted. Instead, we discuss a typical example: Let be a closed -fold figure-eight -elastica. Up to similarity and reparameterization we may assume that is of unit-speed and is a point of multiplicity . Then setting for , we see that if is even, and (up to reflection) if is odd. Hence, clearly .
Now we discuss the existence issue for special exponents. For an odd integer , and with so that , we define by
| (5.8) |
Such an exponent uniquely exists by Theorem 1.5. If we also write
| (5.9) |
For this we will create closed leafed elasticae with odd multiplicities.
To gain insight, we first discuss the special exponent for which we can construct closed leafed elasticae even for all odd multiplicities.
Example 5.8 (Closed -leafed -elasticae).
Let be a half-fold figure-eight -elastica. Then, by , cf. (5.9), and by Proposition 4.6 (iii), (up to reflection) the concatenation is a closed -leafed -elastica, unique up to invariances. For a general with , we can construct a closed -leafed -elastica by concatenating a closed -leafed -elastica and an -fold figure-eight -elastica.
This kind of construction extends to a general multiplicity:
Proposition 5.9 (Closed -leafed -elasticae for odd ).
Let and be integers such that is odd and , and let be defined by (5.8). Let be an odd integer. If , then there exists a closed -leafed -elastica. In addition, in the case of , there exists a closed -leafed -elastica if and only if .
Proof.
First, we show existence of a closed -leafed -elastica. For simplicity, hereafter we write , cf. (5.8). Fix any , and inductively define for . Then and hence the -tuple is an element of . Therefore, Lemma 5.7 ensures existence of a closed -leafed -elastica (corresponding to the case of ).
Next let be an odd integer with . Fix any , and inductively define for . For , we define if is even and if is odd. Then we see that , and hence thanks to Lemma 5.7 there exists a closed -leafed -elastica.
In the rest of the proof, provided that so that , we show nonexistence of closed -leafed -elasticae if . We argue by contradiction. Suppose that there exists a closed -leafed -elastica for an odd integer . Then, by Lemma 5.7, there is an -tuple of unit-vectors . Here we note that holds for if and only if or . From this fact there is an -tuple of rotation matrices such that is either or and , where denotes the identity matrices. In particular, there is a sequence such that . However, we infer from (5.9) and that , and also infer from oddness of that . This contradicts , and the proof is complete. ∎
In general, for a given integer , there may be multiple exponents that admit -leafed -elasticae. For example, there exist -leafed -elasticae if is (cf. Remark 5.8), , or , see Figure 7.
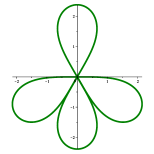


However, the exponent admitting a -leafed -elastica is uniquely determined:
Proposition 5.10.
Let . There exists a closed -leafed -elastica if and only if , where .
5.3. Optimality for odd multiplicity
Now we translate the phenomena observed above into optimality of our Li–Yau type multiplicity inequality.
Theorem 5.11 (Optimality for ).
Let be the set of all exponents with integers and such that is odd and , cf. (5.8). Then is dense in . In addition, for any , and for any odd integer , there exists a curve with a point of multiplicity such that .
Proof.
Note that the set of all angles with under consideration is dense in . Since is the preimage of under the continuous and bijective map (cf. Theorem 1.5), the set is also dense in .
In particular, if , then we can obtain a complete classification of multiplicity which ensures optimality.
Theorem 5.12 (Thresholding phenomenon).
Let be an odd integer and be defined by (5.9). Let be an integer. Then there exists a curve with a point of multiplicity such that if and only if is even or .
Proof.
We close this section by completing the proof of Theorem 1.8, i.e., showing that an exponent which can recover optimality for every multiplicity is unique.
Proof of Theorem 1.8.
If an integer is even (resp. odd), then by Lemma 5.4 (resp. Proposition 5.9) there exists a closed -leafed -elastica. Hence the assertion holds for . We turn to uniqueness. Assume that an exponent satisfies the assertion of the theorem. Then, by the rigidity part of Theorem 1.6, there exists a closed -leafed -elastica for any odd , in particular for . Therefore, Proposition 5.10 implies . ∎
6. Existence of minimal -elastic networks
In this final section we prove Theorem 1.9. Note that, up to rescaling, our problem (1.7) is equivalent to minimizing (as is done in [7, 17]). Indeed, for and a curve , if we set , then and . Hence, with the choice of , we find that
| (6.1) |
Clearly, the same is true for replaced by a network , and the set is closed under rescaling, so that the desired equivalency holds.
The main concern here is the lack of compactness of the set (cf. [7, 9, 17] for the case ). More precisely, the length of one component-curve of a minimizing sequence may vanish; in other words, a family of networks composed by three curves may converge to “two-component network” (cf. Lemma 6.2). In order to prevent such a phenomenon, in this paper, we construct a certain -network whose energy is less than the minimal energy among the class of “two-component network”. The assumption (1.6) is needed to construct such a -network which consists of exactly three curves (cf. Lemma 6.4).
We will use Fenchel’s theorem for piecewise closed curves obtained in [7, Theorem A.1] or [17, Lemma 5.2].
Lemma 6.1 ([7, Theorem A.1], [17, Lemma 5.2]).
Let be immersed curves such that for , where we interpret . For all , let denote the external angle at the vertex , i.e.,
Then
Lemma 6.2.
Let be a sequence such that . Then, up to reparameterization, translation, dilation, and taking a subsequence (all without relabeling), either of the following two assertions holds:
-
(i)
There exists a -network such that for each , the sequence converges to as in the -weak and topology. In particular, .
-
(ii)
Up to permutations of the index , as . In addition, there are such that and such that the sequence (resp. ) converges to (resp. ) as in the -weak and topology. In particular,
(6.2)
Proof.
Throughout the proof we may suppose that, after translation, , and also, after rescaling as in (6.1) (i.e., replacing with ),
| (6.3) |
In addition, we may suppose that after reparameterization, each curve is of constant speed. Furthermore, all of these transformations do not change . In what follows we adopt ideas from [7, 17].
We first consider the case where . Then, as discussed in (4.2), the assumption of constant-speed implies that
This together with (6.3) yields the -boundedness of for each . By the assumption of the constant-speed and , the -boundedness of also follows. Therefore, for each , there exists such that, up to a subsequence, the sequence converges to in the -weak and topology. In particular, the -convergence and the assumption that ensure that satisfies the angle condition to be a -network with angles . Since (cf. (4.2)), since converges to a positive value, and since the weak lower semicontinuity holds for , we deduce that .
Next, we consider the case that, after permutations, holds but we still have . In this case, the same argument as above ensures the desired convergence of and so that the assertion (ii) holds.
We finally prove that only the above cases are possible to occur. For each pair of with , the angle condition implies that the curves and form a piecewise closed curve with exactly two jumps of angle or , and hence by Lemma 6.1 we have . Noting that follows from Hölder’s inequality, we obtain
Then energy-boundedness (6.3) implies that . By the arbitrariness of the choice of and , up to taking a subsequence, there are at least two indices such that . ∎
Next, applying our new Li–Yau type inequality, we give a lower bound on when the assertion (ii) holds in Lemma 6.2.
Lemma 6.3.
Let satisfy . Then
| (6.4) |
where equality is attained if and only if the curves are half-fold figure-eight -elasticae of same length.
Proof.
Up to a rigid motion for , we may assume that and are parallel. Then up to reparametrization we may regard the concatenation of and as a single open curve with a point of multiplicity , whose normalized -bending energy is equal to the right-hand side of (6.4). The assertion follows by applying Theorem 5.2 to . ∎
Now the main issue is reduced to showing that there exists a -network of less energy than the minimal energy of degenerate networks. More precisely, we prove
Lemma 6.4.
Suppose (1.6) holds. Then there exists a -network such that .
Proof.
Let be a half-period of a wavelike -elastica given by in (2.14) with . Then it follows that
| (6.5) |
In addition, since the curvature of is , we infer from Lemma 4.2 that
| (6.6) | ||||
where is given by (4.6).
We define (up to reparameterization) a triplet of curves for by
where denotes the refection with respect to the -axis and for . It is clear that and . Combining this with (6.5) and (6.6), we see that
which yields
| (6.7) |
In particular, by this representation, and by definition of and , we have
Let be a constant satisfying . We now prove that gives the desired -network with angles .
Next, we show that . In view of Case II in Proposition 2.12, the tangential angles of at two endpoints are and . This together with ensures the angle condition.
It remains to show that
To this end, by the fact that , it is sufficient to prove that the energy in (6.7) is strictly increasing with respect to . We calculate
| (6.8) | ||||
It follows from Proposition 2.5 and Lemma 4.5 that
| (6.9) |
We now show that
| (6.10) |
In view of (2.5) and (4.7), we see that
Here, we infer from Proposition 2.5 that
Therefore we obtain
which ensures (6.10). Combining (6.8) with (6.9) and (6.10), we see that is strictly increasing in . ∎
We are now ready to complete the proof of Theorem 1.9.
Proof of Theorem 1.9.
Let be a minimizing sequence such that . Then, possibly after rescaling, translation, reparameterization, and taking a subsequence, either assertion (i) or (ii) in Lemma 6.2 holds. However, assertion (ii) does not occur in view of (6.2). Indeed, since the curves and in (ii) satisfy the assumption of Lemma 6.3, we have ; on the other hand, Lemma 6.4 implies that
Therefore we have assertion (i). Then the limit network is a desired minimizer in view of the fact that . ∎
Appendix A First variation and multiplier method
A.1. Preliminary estimates
We collect elementary inequalities of power type.
Lemma A.1.
Let and . Then
| (A.1) | |||
| (A.2) |
where is a constant depending only on .
Proof.
A.2. First variation of the -bending energy
In this subsection we compute the Fréchet derivative of . Note that the Fréchet differentiability is nontrivial due to the strong nonlinearity of . First, let us mention a known formula for the Gâteaux derivative of (see [19, Lemma A.1] for a rigorous derivation). Let . For an immersed curve (), let be the line element in the sense of a weighted measure on . Let denote the arclength derivative along , i.e., . In particular, the curvature vector is then represented by
Lemma A.3.
Let and . For an immersed curve , let be the -bending energy defined by
Then the Gâteaux derivative of at is given by, for ,
In the following we prove that is Fréchet differentiable by showing the sufficient condition that is continuous with respect to (cf. [32, Proposition 4.8]). For a Banach space , let and denote the operator norm
Lemma A.4.
Let and . Let . Then the Gâteaux derivative of is continuous at every in .
Proof.
Fix an arbitrary satisfying in . Then in also follows, and hence there is independent of such that for sufficiently large . The proof is completed by showing that
| (A.4) |
In what follows, we use the same notation for positive constants depending only on and .
Fix an arbitrary such that . Let denote the arclength derivative along . Let First we compute
| (A.5) | ||||
We demonstrate the estimate of in the right hand side. It follows that
We apply Lemma A.1 and Hölder’s inequality, as in Remark A.2, to obtain
Since and , we have . On the other hand, since , Hölder’s inequality combined with some -estimates for first derivatives and implies that
Similarly, we obtain
From the facts that in and that and , it follows that
Combining this with (A.5) and a well-known embedding , we obtain
which implies (A.4). ∎
By Lemma A.4, the Fréchet derivative coincides with .
A.3. Lagrange multiplier theorem
Since our problem involves a non-local constraint, we use a Lagrange multiplier method (see e.g. [31, Proposition 43.21]). In the following, for let
Proposition A.5.
Let . Let be an open neighborhood of and be Fréchet differentiable at , and denote
Let . Then either of the following holds:
-
(a)
for all ,
-
(b)
is a critical point of in if and only if there exists such that
(A.6)
Remark A.6.
In the case of and , when (a) is satisfied, i.e., , then is nothing but a line segment, which also satisfies . Therefore in our setting it suffices to consider (b) only.
Remark A.7 (Clamped boundary condition).
Thanks to Lemmata A.3 and A.4, we can explicitly calculate (A.6) for the case and . Note that for any the arclength function is of class , has strictly positive derivative, and maps to . Hence the arclength reparameterization is an element of with . Applying the change of variables to Lemma A.3 combined with Lemma A.4, and setting for , we obtain the representation of (A.6) in terms of the arclength parameterization:
Proposition A.8.
Let . A curve satisfies
for any with if and only if the arclength parametrization of satisfies
for any with .
References
- [1] J. J. Arroyo, O. J. Garay, and A. Pámpano. Boundary value problems for Euler-Bernoulli planar elastica. A solution construction procedure. J. Elasticity, 139(2):359–388, 2020.
- [2] J. W. Barrett, H. Garcke, and R. Nürnberg. Elastic flow with junctions: variational approximation and applications to nonlinear splines. Math. Models Methods Appl. Sci., 22(11):1250037, 57, 2012.
- [3] S. Blatt, C. Hopper, and N. Vorderobermeier. A regularized gradient flow for the -elastic energy. Adv. Nonlinear Anal., 11(1):1383–1411, 2022.
- [4] S. Blatt, C. P. Hopper, and N. Vorderobermeier. A minimising movement scheme for the -elastic energy of curves. J. Evol. Equ., 22(2):Paper No. 41, 25, 2022.
- [5] T. Cazenave, D. Fang, and Z. Han. Continuous dependence for NLS in fractional order spaces. Ann. Inst. H. Poincaré C Anal. Non Linéaire, 28(1):135–147, 2011.
- [6] A. Dall’Acqua, C.-C. Lin, and P. Pozzi. Elastic flow of networks: long-time existence result. Geom. Flows, 4(1):83–136, 2019.
- [7] A. Dall’Acqua, M. Novaga, and A. Pluda. Minimal elastic networks. Indiana Univ. Math. J., 69(6):1909–1932, 2020.
- [8] A. Dall’Acqua and A. Pluda. Some minimization problems for planar networks of elastic curves. Geom. Flows, 2(1):105–124, 2017.
- [9] G. Del Nin, A. Pluda, and M. Pozzetta. Degenerate elastic networks. J. Geom. Anal., 31(6):6128–6170, 2021.
- [10] H. Garcke, J. Menzel, and A. Pluda. Willmore flow of planar networks. J. Differential Equations, 266(4):2019–2051, 2019.
- [11] H. Garcke, J. Menzel, and A. Pluda. Long time existence of solutions to an elastic flow of networks. Comm. Partial Differential Equations, 45(10):1253–1305, 2020.
- [12] P. Li and S. T. Yau. A new conformal invariant and its applications to the Willmore conjecture and the first eigenvalue of compact surfaces. Invent. Math., 69(2):269–291, 1982.
- [13] P. Lindqvist. Notes on the -Laplace equation (second edition). University Jyväskylä, Department of Mathematics and Statistics, Report 161, 2017.
- [14] A. Linnér. Explicit elastic curves. Ann. Global Anal. Geom., 16(5):445–475, 1998.
- [15] A. E. H. Love. A treatise on the Mathematical Theory of Elasticity. Dover Publications, New York, 1944. Fourth Ed.
- [16] T. Miura. Elastic curves and phase transitions. Math. Ann., 376(3-4):1629–1674, 2020.
- [17] T. Miura. Li–Yau type inequality for curves in any codimension, arXiv:2102.06597.
- [18] T. Miura, M. Müller, and F. Rupp. Optimal thresholds for preserving embeddedness of elastic flows. to appear in Amer. J. Math., arXiv:2106.09549.
- [19] T. Miura and K. Yoshizawa. Complete classification of planar -elasticae, arXiv:2203.08535v2.
- [20] M. Müller and F. Rupp. A Li-Yau inequality for the 1-dimensional Willmore energy. Adv. Calc. Var., 16(2):337–362, 2023.
- [21] M. Novaga and P. Pozzi. A second order gradient flow of -elastic planar networks. SIAM J. Math. Anal., 52(1):682–708, 2020.
- [22] S. Okabe, P. Pozzi, and G. Wheeler. A gradient flow for the -elastic energy defined on closed planar curves. Math. Ann., 378(1-2):777–828, 2020.
- [23] S. Okabe and G. Wheeler. The -elastic flow for planar closed curves with constant parametrization. J. Math. Pures Appl. (9), 173:1–42, 2023.
- [24] A. Polden. Curves and surfaces of least total curvature and fouth-order flows. PhD thesis, Universität Tübingen, 1996.
- [25] N. Shioji and K. Watanabe. Total -powered curvature of closed curves and flat-core closed -curves in . Comm. Anal. Geom., 28(6):1451–1487, 2020.
- [26] S. Takeuchi. Legendre-type relations for generalized complete elliptic integrals. J. Class. Anal., 9(1):35–42, 2016.
- [27] H. von der Mosel. Minimizing the elastic energy of knots. Asymptot. Anal., 18(1-2):49–65, 1998.
- [28] K. Watanabe. Planar -elastic curves and related generalized complete elliptic integrals. Kodai Math. J., 37(2):453–474, 2014.
- [29] G. Wheeler. On the curve diffusion flow of closed plane curves. Ann. Mat. Pura Appl. (4), 192(5):931–950, 2013.
- [30] K. Yoshizawa. The critical points of the elastic energy among curves pinned at endpoints. Discrete Contin. Dyn. Syst., 42(1):403–423, 2022.
- [31] E. Zeidler. Nonlinear functional analysis and its applications. III. Springer-Verlag, New York, 1985.
- [32] E. Zeidler. Nonlinear functional analysis and its applications. I. Springer-Verlag, New York, 1986.