Photoproduction $\gamma p\to K^{+}\Lambda(1520)$ in an effective Lagrangian approach

The traditional $\pi N$ elastic and inelastic scattering experiments have provided us with abundant knowledge of the mass spectrum and decay properties of the nucleon resonances ($N^{\ast}$’s). Nevertheless, both the quark model Isgur:1977ef ; Koniuk:1979vy and lattice QCD Edwards:2011jj ; Edwards:2012fx calculations predict more resonances than have been observed in the $\pi N$ scattering experiments. The resonances predicated by quark model or lattice QCD but not observed in experiments are called “missing resonances”, which are supposed to have small couplings to the $\pi N$ channel and, thus, escape from experimental detection. In the past few decades, intense efforts have been dedicated to search for the missing resonances in meson production reaction channels other than $\pi N$. In particular, the $\rho N$, $\phi N$, and $\omega N$ production reactions in the nonstrangeness sector and the $KY$, $K^{\ast}Y$ ($Y=\Lambda,\Sigma$) production reactions in the strangeness sector have been widely investigated both experimentally and theoretically.

In the present paper, we focus on the $\gamma p\to K^{+}\Lambda(1520)$ reaction process. The threshold of the $K^{+}\Lambda(1520)$ photoproduction is about $2.01$ GeV, and, thus, this reaction provides a chance to study the $N^{\ast}$ resonances in the $W\sim 2.0$ GeV mass region in which we have infancy information as shown in the latest version of the Review of Particle Physics (RPP) Tanabashi:2018oca . Besides, the isoscalar nature of $\Lambda(1520)$ allows only the $I=1/2$ $N^{\ast}$ resonances exchanges in the $s$ channel, which simplifies the reaction mechanisms of the $K^{+}\Lambda(1520)$ photoproduction.

Experimentally, the cross sections for the reaction $\gamma p\to K^{+}\Lambda(1520)$ have been measured at SLAC by Boyarski et al. in 1971 for photon energy $E_{\gamma}=11$ GeV Boyarski:1970yc , and by the LAMP2 group in 1980 at $E_{\gamma}=2.8$$-$$4.8$ GeV Barber:1980zv . In 2010, the LEPS Collaboration measured the differential cross sections and photon-beam asymmetries ($\Sigma$) at Spring-8 for $\gamma p\to K^{+}\Lambda(1520)$ at energies from threshold up to $E_{\gamma}=2.6$ GeV at forward $K^{+}$ angles Kohri:2009xe . In 2011, the SAPHIR Collaboration measured the cross sections at the Electron Stretcher Accelerator (ELSA) for the $K^{+}\Lambda(1520)$ photoproduction in the energy range from threshold up to $E_{\gamma}=2.65$ GeV Wieland:2010cq . Recently, the differential and total cross sections for the $K^{+}\Lambda(1520)$ photoproduction were reported by the CLAS Collaboration at energies from threshold up to the center-of-mass energy $W=2.86$ GeV over a large range of the $K^{+}$ production angle Moriya:2013hwg .

Theoretically, the $K^{+}\Lambda(1520)$ photoproduction reaction has been extensively investigated based on effective Lagrangian approaches by four theory groups in $11$ publications Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga ; Yu:2017kng . In Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au , Nam et al. found that the contact term and the $t$-channel $K$ exchange are important to the cross sections of $\gamma p\to K^{+}\Lambda(1520)$, while the contributions from the $t$-channel $K^{\ast}$ exchange and the $s$-channel nucleon resonance exchange are rather small. In Refs. Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb , Xie, Wang, and Nieves et al. found that apart from the contact term and the $t$-channel $K$ exchange, the $u$-channel $\Lambda$ exchange and the $s$-channel $N(2120)3/2^{-}$ [previously called $D_{13}(2080)$] exchange are also important in describing the cross-section data for $\gamma p\to K^{+}\Lambda(1520)$, while the contribution from the $t$-channel $K^{\ast}$ exchange is negligible in this reaction. In Refs. He:2012ud ; He:2014gga , He and Chen found that the contribution from the $t$-channel $K^{\ast}$ exchange in $\gamma p\to K^{+}\Lambda(1520)$ is also considerable besides the important contributions from the contact term, the $t$-channel $K$ exchange, the $u$-channel $\Lambda$ exchange, and the $s$-channel $N(2120)3/2^{-}$ exchange. In Ref. Yu:2017kng , Yu and Kong studied the $\gamma p\to K^{+}\Lambda(1520)$ reaction within a Reggeized model, and they claimed that the important contributions to this reaction are coming from the contact term, the $t$-channel $K$ exchange, and the $t$-channel $K^{\ast}_{2}$ exchange, while the contribution from the $t$-channel $K^{\ast}$ exchange is minor.

One observes that the common feature reported in all the above-mentioned publications of Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga ; Yu:2017kng is that the contributions from the contact term and the $t$-channel $K$ exchange are important to the $\gamma p\to K^{+}\Lambda(1520)$ reaction. Even so, the reaction mechanisms of $\gamma p\to K^{+}\Lambda(1520)$ claimed by those four theory groups are quite different. In particular, there are no conclusive answers which can be derived from Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga ; Yu:2017kng for the following questions: Are the contributions from the $t$-channel $K^{\ast}$ exchange and $u$-channel $\Lambda$ exchange significant or not in this reaction, does one inevitably need to introduce nucleon resonances in the $s$ channel to describe the data, and if yes, is the $N(2120)3/2^{-}$ resonance the only candidate needed in this reaction and what are the parameters of it?

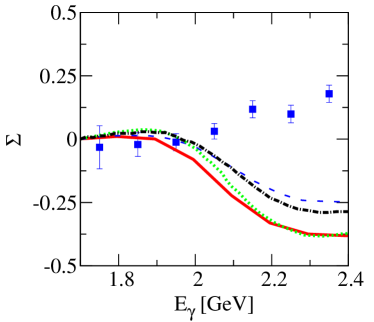
On the other hand, the data on photon-beam asymmetries for $\gamma p\to K^{+}\Lambda(1520)$ reported by the LEPS Collaboration in 2010 Kohri:2009xe have never been well reproduced in previous publications of Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga . As an illustration, we show in Fig. 1 the theoretical results on photon-beam asymmetries from Refs. Xie:2010yk ; He:2012ud ; Xie:2013mua ; He:2014gga calculated at $\cos\theta=0.8$ and compared with the data located at $0.6<\cos\theta<1$. It is true that the data bins in scattering angles are wide; nevertheless, it has been checked that the averaged values of theoretical beam-asymmetry results in $0.6<\cos\theta<1$ are comparable with those calculated at $\cos\theta=0.8$. One sees that, in the energy region $E_{\gamma}>2$ GeV, even the signs of the photon-beam asymmetries predicated by these theoretical works are opposite to the data. In the Regge model analysis of Ref. Yu:2017kng , the photon-beam asymmetries have indeed been analyzed, but there the differential cross-section data have been only qualitatively described, and the structures of the angular distributions exhibited by the data were missing due to the lack of nucleon resonances in the $s$-channel interactions.

The purpose of the present work is to perform a combined analysis of the available data on both the differential cross sections and the photon-beam asymmetries for $\gamma p\to K^{+}\Lambda(1520)$ within an effective Lagrangian approach, and, based on that, we try to get a clear understanding of the reaction mechanism of $\gamma p\to K^{+}\Lambda(1520)$. In particular, we aim to clarify whether the $t$-channel $K^{\ast}$ exchange and the $u$-channel $\Lambda$ exchange are important or not and what the resonance contents and their associated parameters are in this reaction. As discussed above, previous publications of Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga can describe only the differential cross-section data, and they gave diverse answers to these questions. It is expected that more reliable results on the resonance contents and the roles of $K^{\ast}$ and $\Lambda$ exchanges in this reaction can be obtained from the theoretical analysis which can result in a satisfactory description of the data on both the differential cross sections and the photon-beam asymmetries.

The present paper is organized as follows. In Sec. II, we briefly introduce the framework of our theoretical model, including the effective interaction Lagrangians, the resonance propagators, and the phenomenological form factors employed in this work. The results of our model calculations are shown and discussed in Sec. III. Finally, a brief summary and conclusions are given in Sec. IV.

The full amputated photoproduction amplitude for $\gamma N\to K\Lambda(1520)$ in our tree-level effective Lagrangian approach can be expressed as Wang:2017tpe ; Wang:2018vlv ; Wang:2020mdn ; Wei:2019imo

with $\nu$ and $\mu$ being the Lorentz indices for outgoing $\Lambda(1520)$ and incoming photon, respectively. The first three terms $M^{\nu\mu}_{s}$, $M^{\nu\mu}_{t}$, and $M^{\nu\mu}_{u}$ stand for the amplitudes resulted from the $s$-channel $N$ and $N^{\ast}$ exchanges, the $t$-channel $K$ and $K^{\ast}$ exchanges, and the $u$-channel $\Lambda$ exchange, respectively, as diagrammatically depicted in Fig. 2. They can be calculated straightforward by using the effective Lagrangians, propagators, and form factors provided in the following part of this section. The last term in Eq. (1) represents the interaction current arising from the photon attaching to the internal structure of the $\Lambda(1520)NK$ vertex. In practical calculation, the interaction current $M^{\nu\mu}_{\rm int}$ is modeled by a generalized contact current Haberzettl:1997 ; Haberzettl:2006 ; Haberzettl:2011zr ; Huang:2012 ; Huang:2013 ; Wang:2017tpe ; Wang:2018vlv ; Wei:2019imo ; Wang:2020mdn ; Wei:2020fmh :

Here $\Gamma_{\Lambda^{\ast}NK}^{\nu}(q)$ is the vertex function of $\Lambda(1520)NK$ coupling governed by the Lagrangian of Eq. (16):

with $q$ being the four-momentum of the outgoing $K$ meson; $M^{\nu\mu}_{\rm KR}$ is the Kroll-Ruderman term governed by the Lagrangian of Eq. (15):

with $Q_{K}$ being the electric charge of outgoing $K$ meson and $\tau$ being the isospin factor of the Kroll-Ruderman term; $f_{t}$ is the phenomenological form factor attached to the amplitude of $t$-channel $K$ exchange, which is given by Eq. (39); $C^{\mu}$ is an auxiliary current introduced to ensure the gauge invariance of the full photoproduction amplitude of Eq. (1). Note that the photoproduction amplitudes will automatically be gauge invariant in the cases that there are no form factors and the electromagnetic couplings are obtained by replacing the partial derivative by its covariant form in the corresponding hadronic vertices. In practical calculation, one has to introduce the form factors in hadronic vertices (cf. Sec. II.3) which violate the gauge invariance. The auxiliary current $C^{\mu}$ is then introduced to compensate the gauge violation caused by the form factors. Following Refs. Haberzettl:2006 ; Haberzettl:2011zr ; Huang:2012 , for the $\gamma N\to K\Lambda(1520)$ reaction, the auxiliary current $C^{\mu}$ is chosen to be

with

Here $p$, $q$, and $k$ denote the four-momenta for incoming $N$, outgoing $K$, and incoming photon, respectively; $Q_{K}$ and $Q_{N}$ are electric charges of $K$ and $N$, respectively; $f_{s}$ and $f_{t}$ are phenomenological form factors for $s$-channel $N$ exchange and $t$-channel $K$ exchange, respectively; $\hat{h}$ is an arbitrary function going to unity in the high-energy limit and set to be $1$ in the present work for simplicity; $\tau$ depicts the isospin factor for the corresponding hadronic vertex. Alternatively, one can rewrite the auxiliary current $C^{\mu}$ in Eq. (5) as

One sees clearly that if there are no form factors, i.e., $f_{t}=f_{s}=1$, one has $C^{\mu}\to 0$ and, consequently, $M^{\nu\mu}_{\rm int}\to M^{\nu\mu}_{KR}$. We mention that the auxiliary current $C^{\mu}$ in Eq. (5) works for both real and virtual photons; i.e., the amplitudes we constructed in Eq. (1) are gauge invariant for both photo- and electroproduction of $K^{+}\Lambda(1520)$. In Ref. Nam2013 , another prescription for keeping gauge invariance of the $K^{+}\Lambda(1520)$ electroproduction amplitudes was introduced, where additional terms are considered besides those for photoproduction reactions.

In the rest of this section, we present the effective Lagrangians, the resonance propagators, the form factors, and the interpolated $t$-channel Regge amplitudes employed in the present work.

As discussed in the introduction section of this paper, the reaction $\gamma p\to K^{+}\Lambda(1520)$ has been theoretically investigated based on effective Lagrangian approaches by four theory groups in $11$ publications Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga ; Yu:2017kng . The common feature of the results from these theoretical works is that the contributions from the contact term and the $t$-channel $K$ exchange are important for the $\gamma p\to K^{+}\Lambda(1520)$ reaction. Apart from that, no common ground has been found by these theoretical works for the reaction mechanisms of $\gamma p\to K^{+}\Lambda(1520)$. In particular, different groups gave quite different answers for the following questions: Are the contributions from the $t$-channel $K^{\ast}$ exchange and $u$-channel $\Lambda$ exchange significant or not in this reaction, are the nucleon resonances introduced in the $s$ channel indispensable or not to describe the available data, and, if yes, what are the resonance contents and their associated parameters in this reaction? On the other hand, we notice that even though the data on photon-beam asymmetries for $\gamma p\to K^{+}\Lambda(1520)$ have been reported by the LEPS Collaboration in 2010, they have never been well reproduced in previous theoretical publications of Refs. Nam:2005uq ; Nam:2006cx ; Nam:2009cv ; Nam:2010au ; Toki:2007ab ; Xie:2010yk ; Xie:2013mua ; Wang:2014jxb ; He:2012ud ; He:2014gga . One believes that these photon-beam-asymmetry data will definitely put further constraints on the reaction amplitudes. In Ref. Yu:2017kng , the photon-beam-asymmetry data have indeed been analyzed, but there, the structures of the angular distributions exhibited by the data are missed due to the lack of nucleon resonances. In a word, all previous theoretical publications in regards to $\gamma p\to K^{+}\Lambda(1520)$ are divided over the reaction mechanism and the resonance contents and parameters of this reaction. A simultaneous description of the differential cross-section data and the photon-beam-asymmetry data still remains to be accomplished.

The purpose of the present work is to get a clear understanding of the reaction mechanism of $\gamma p\to K^{+}\Lambda(1520)$ based on a combined analysis of the available data on both the differential cross sections and the photon-beam asymmetries within an effective Lagrangian approach. As the differential cross-section data exhibit clear bump structures in the near-threshold region, apart from the $N$, $K$, $K^{\ast}$, and $\Lambda$ exchanges and the interaction current in the nonresonant background, we introduce as few as possible near-threshold nucleon resonances in the $s$ channel in constructing the $\gamma p\to K^{+}\Lambda(1520)$ reaction amplitudes to reproduce the data.

In the most recent version of RPP Tanabashi:2018oca , there are six nucleon resonances near the $K^{+}\Lambda(1520)$ threshold, namely, the $N(2000)5/2^{+}$, $N(2040)3/2^{+}$, $N(2060)5/2^{-}$, $N(2100)1/2^{+}$, $N(2120)3/2^{-}$, and $N(2190)7/2^{-}$ resonances. If none of these nucleon resonances are introduced in the construction of the $s$-channel reaction amplitudes, we find that it is not possible to achieve a simultaneous description of both the differential cross-section data and the photon-beam-asymmetry data in our model. We then try to reproduce the data by including one of these six near-threshold resonances. If we include one of the $N(2000)5/2^{+}$, $N(2040)3/2^{+}$, $N(2100)1/2^{+}$, and $N(2190)7/2^{-}$ resonances, we find that the obtained theoretical results for differential cross sections and photon-beam asymmetries have rather poor fitting qualities. As an illustration, we show in Fig. 3 the differential cross sections at a few selected scattering angles as a function of the incident photon energy which are obtained by including one of the $N(2000)5/2^{+}$ (black solid lines), $N(2040)3/2^{+}$ (red dot-double-dashed lines), $N(2100)1/2^{+}$ (blue dashed lines), and $N(2190)7/2^{-}$ (green dot-dashed lines) resonances and compared with the corresponding data Kohri:2009xe ; Moriya:2013hwg . One sees clearly from Fig. 3 that the fits with one of the $N(2040)3/2^{+}$, $N(2100)1/2^{+}$, and $N(2190)7/2^{-}$ resonances fail to describe the differential cross sections at $\cos\theta=0.95$, and the fit with the $N(2000)5/2^{+}$ resonance fails to reproduce the differential cross-section data at the other three selected scattering angles. In a word, none of these four fits that includes one of the $N(2000)5/2^{+}$, $N(2040)3/2^{+}$, $N(2100)1/2^{+}$, and $N(2190)7/2^{-}$ resonances can well describe the differential cross-section data. Thus, they are excluded to be acceptable fits. On the other hand, if either the resonance $N(2060)5/2^{-}$ or the resonance $N(2120)3/2^{-}$ is considered, a simultaneous description of both the differential cross-section data and the photon-beam-asymmetry data can be satisfactorily obtained, which will be discussed below in detail. Consequently, these two fits, i.e., the ones including the $N(2060)5/2^{-}$ or the $N(2120)3/2^{-}$ resonance, are treated as acceptable. When an additional resonance is further included, the fit quality will be improved a little bit, since one has more adjustable model parameters. But, in this case, one would obtain too many solutions with similar fitting qualities, and meanwhile the fitted error bars of adjustable parameters are also relatively large. As a consequence, no conclusive conclusion can be drawn about the resonance contents and parameters extracted from the available data for the considered reaction. We thus conclude that the available differential cross-section data and the photon-beam-asymmetry data for $\gamma p\to K^{+}\Lambda(1520)$ can be described by including one of the $N(2060)5/2^{-}$ and $N(2120)3/2^{-}$ resonances and postpone the analysis of these available data with two or more nucleon resonances until more data for this reaction become available in the future.